RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2

RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS

Question 1.
A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold? [NCERT]
Solution:
Length of water tank (l) = 6 m
Breadth (b) = 5 m
and depth (h) = 4.5 m

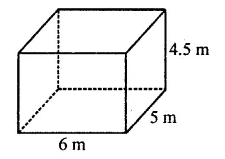
∴ Volume of water in it = lbh
= 6 x 5 x 4.5 m³ = 135 m³
Capacity of water in litres = 135 x 1000 litres (1 m³ = 1000 l)
= 135000 litres

Question 2.
A cubical vessel is 10 m long and 8 m wide. How high must it be made to hold 380 cubic metres of a liquid? [NCERT]
Solution:
Length of vessal (l) = 10 m
Breadth (b) = 8 m
Volume = 380 m³

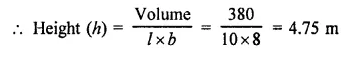
Question 3.
Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3 m deep at the rate of ₹30 per m³. [NCERT]
Solution:
Length of pit (l) = 8m
Width (b) = 6 m
and depth (h) = 3 m
∴ Volume of earth digout = lbh
= 8 x 6 x 3 = 144 m³
Cost of digging the pit at the rate of ₹30 per m³
= 144 x 30 = ₹4320

Question 4.
If the areas of three adjacent faces of a cuboid are 8 cm², 18 cm² and 25 cm². Find the volume of the cuboid.
Solution:
Let x, y, z be the three adjacent faces of the cuboid, then
x = 8 cm², y = 18 cm², z = 25 cm²
and let l, b, h are the dimensions of the cuboid, then
x = lb = 8 cm²
y = bh = 18 cm²
z = hl = 25 cm²
∴ Volume = lbh

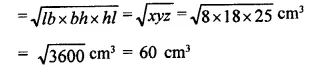
Question 5.
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu. dm. Find its dimensions.
Solution:
Let breadth of a room (b) = x

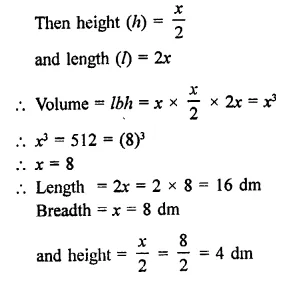
Question 6.
Three metal cubes with edges 6 cm, 8 cm and 10 cm respectively are melted together and formed into a single cube. Find the volume, surface area and diagonal of the new cube.
Solution:
Edge of first cube = 6 cm
Edge of second cube = 8 cm
and edge of third cube = 10 cm
∴ Volume of 3 cubes = (6)³ + (8)³ + (10)3 cm³
= 216 + 512 + 1000 cm³
= 1728 cm³
∴ Edge of so formed cube

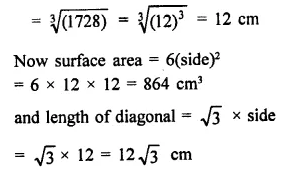
Question 7.
Two cubes, each of volume 512 cm³ are joined end to end. Find the surface area of the resulting cuboid.
Solution:
Volume of each volume = 512 cm³
∴ Side (edge) = \(\sqrt [ 3 ]{ 512 }\)
=\(\sqrt [ 3 ]{ { 8 }^{ 3 } }\)  = 8 cm
Now by joining two cubes, then Length of so formed cuboid (l)
= 8 + 8 = 16 cm
Breadth (b) = 8 cm
and height (h) = 8 cm
∴ Surface area = 2(lb + bh + hl)
= 2[16 x 8 + 8 x 8 + 8 x 16] cm²
= 2[128 + 64 + 128] cm²
= 2 x 320 = 640 cm²

Question 8.
A metal cube of edge 12 cm is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 6 cm and 8 cm, find the edge of the third smaller cube.
Solution:
Edge of metal cube = 12 cm
∴ Its volume = (Edge)³ = (12)³ cm3³
= 1728 cm³
It is melted and form 3 cubes
Edge of one smaller cube = 6 cm
and edge of second smaller cube = 8 cm
∴ Volume of two smaller cubes = (6)³ + (8)³ cm³
= 216 + 512 cm³ = 728 cm³
∴ Volume of third smaller cube = 1728 – 728 = 1000 cm³
∴ Edge of the third cube = \(\sqrt [ 3 ]{ 1000 }\)
= \(\sqrt [ 3 ]{ (10)3 }\)  cm = 10 cm

Question 9.
The dimensions of a cinema hall are 100 m, 50 m and 18 m. How many persons can sit in the hall, if each person requires 150 m3 of air?
Solution:
Length of cinema hall (l) = 100 m
Breadth (b) = 50 m
and height (h) = 18 m
∴ Volume of air in it = lbh
= 100 x 50 x 18 m³ = 90000 m³
Air required for one person = 150 m³
∴ Number of persons in the hall = \(\frac { 90000 }{ 150 }\) = 600 persons

Question 10.
Given that 1 cubic cm of marble weighs 0.25 kg, the weight of marble block 28 cm in width and 5 cm thick is 112 kg. Find the length of the block.
Solution:
Weight of 1 cm3 = 0.25 kg
Breadth of the block (b) = 28 cm
Thickness (h) = 5 cm
and total weight of the block = 112 kg

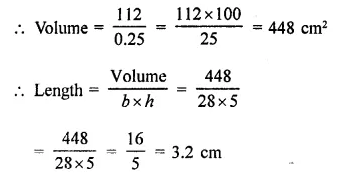
Question 11.
A box with lid is made of 2 cm thick wood. Its external length, breadth and height are 25 cm, 18 cm and 15 cm respectively. How much cubic cm of a liquid can be placed in it? Also, find the volume of the wood used in it.
Solution:
Outer length of the closed wooden box (l) = 25 cm
Breadth (b) = 18 cm
and height (h) = 15 cm
Width of wood = 2 cm

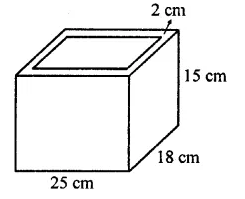
∴ Inner length = 25 – 2×2 = 25- 4 = 21cm
Breadth =18- 2×2 = 18-4 = 14 cm
and height =15- 2×2 = 15- 4=11 cm
Now outer volume = 25 x 18 x 15 cm³ = 6750 cm³
and inner volume = 21 x 14 x 11 cm³ = 3234 cm³
(i) Inner volume = 3234 cm³
(ii) Volume of wood = 6750 – 3234 = 3516 cm³

Question 12.
The external dimensions of a closed wooden box are 48 cm, 36 cm, 30 cm. The box is made of 1.5 cm thick wood. How many bricks of size 6 cm x 3 cm x 0.75 cm can be put in this box?
Solution:
External length of a closed wooden box (L) = 48 cm
Width (B) = 36 cm
and height (H) = 30 cm
Thickness of wood = 1.5 cm

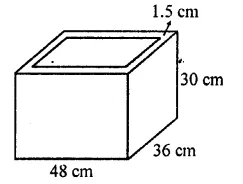
∴ Internal length (l) = 48 – 2 x 1.5 cm = 48 – 3 = 45 cm
Width (b) = 36 – 2 x 1.5 cm
= 36 – 3 = 33 cm
and height (h) = 30 – 2 x 1.5 cm
= 30 – 3 = 27 cm
Now volume of internal box
= lbh = 45 x 33 x 27 cm³
Volume of one bricks = 6 x 3 x 0.75 cm³

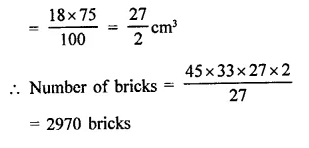
Question 13.
A cube of 9 cm edge is immersed completely in a rectangular vessel containing water. If the dimensions of the base are 15 cm and 12 cm, find the rise in water level in the vessel.
Solution:
Edge of a cube = 9 cm
Volume of cube = (9)³ cm³
= 729 cm³
Now length of vessel (l) = 15 cm
and breadth (b) = 12 cm

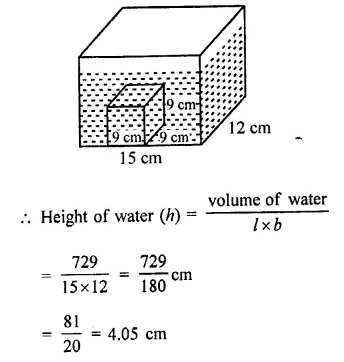
Question 14.
A field is 200 m long and 150 m broad. There is a plot, 50 m long and 40 m broad, near the field. The plot is dug 7 m deep and the earth taken out is spread evenly on the field. By how many metres is the level of the field raised? Give the answer to the second place of decimal.
Solution:
Length of a field (l) = 200 m
Breadth (b) = 150 m
Length of plot = 50 m
and breadth = 40 m
Depth of plot = 7 m

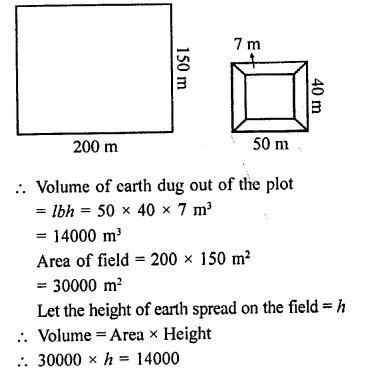
Question 15.
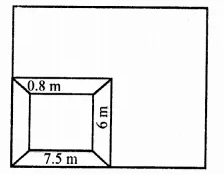
A field is in the form of a rectangle of length 18 m and width 15 m. A pit, 7.5 m long, 6 m broad and 0.8 m deep, is dug in a comer of the field and the earth taken out is spread- over the remaining area of the field. Find out the extent to which the level of the field has been raised.
Solution:
Length of a field (L) = 18m
and width (B) = 15 m
Length of pit (l) = 7.5 m
Breadth (b) = 6 m
and depth (h) = 0.8 m

∴ Volume of earth dugout = lbh
= 7.5 x 6 x 0.8 m³
= 45 x 0.8 = \(\frac { 45 x 4 }{ 5 }\) = 36 m3
Total area of the field = L x B
= 18 x 15 = 270 m²
and area of pit = lb = 7.5 x 6 = 45 m²
∴ Remaining area of the field excluding pit
= 270 – 45 = 225 m²
Let by spreading the earth on the remaining part of the field, the height = h
= 225 x h = 36
⇒ h = \(\frac { 36 }{ 225 }\) = \(\frac { 4 }{ 25 }\)= 0.16 m = 16 cm
∴ Level of field raised = 16 cm

Question 16.
A village having a population of 4000 requires 150 litres of water per head per day. It has a tank measuring 20 m x 15m x 6 m. For how many days will the water of this tank last? [NCERT]
Solution:
Population of a village = 4000
Water required per head per day = 150 litres
∴ Total water required = 4000 x 150 litres = 600000 litres
Dimensions of a tank = 20mx 15mx6m
∴ Volume of tank = 20 x 15 x 6 m3 = 1800 m³
Capacity of water in litres = 1800 x 1000 litres (1 m³ = 1000 litres)
= 1800000 litres
The water will last for = \(\frac { 1800000 }{ 600000 }\) = 3 days

Question 17.
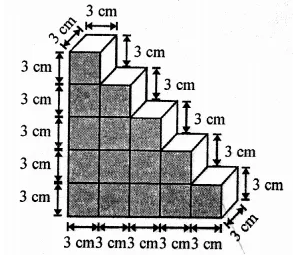
A child playing with building blocks, which are of the shape of the cubes, has built a structure as shown in the figure. If the edge of each cube is 3 cm, find the volume of the structure built by the child. [NCERT]

Solution:
No. of cubes at the given structure = 1+ 2 + 3+ 4 + 5 = 15
Edge of one cube = 3 cm
∴ Volume of one cube = (3)³ = 3 x 3 x 3 cm³ = 27 cm³
∴Volume of the structure = 27 x 15 cm³ = 405 cm³

Question 18.
A godown measures 40 m x 25 m x 10 m. Find the maximum number of wooden crates each measuring 1.5 m x 1.25 m x 0.5 m that can be stored in the godown. [NCERT]
Solution:
Length of godown (L) = 40 m
Breadth (B) = 25 m
and height (H) = 10 m
∴ Volume of godown = LBH
= 40 x 25 x 10 = 10000 m³
Dimension of one wooden crates = 1.5 m x 1.25 m x 0.5 m
∴Volume of one crate = 1.5 x 1.25 x 0.5 m³ = 0.9375 m³
∴ Number of crates to be stored in the

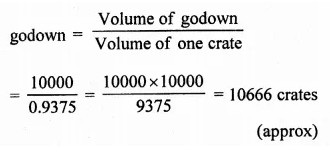
Question 19.
A wall of length 10 m was to be built across an open ground. The height of the wall is 4 m and thickness of the wall is 24 cm. If this wall is to be built up with bricks whose dimensions are 24 cm x 12 cm x 8 cm, how many bricks would be required? [NCERT]
Solution:
Length of wall (L) = 10 m = 1000 cm
Height (H) = 4 m = 400 cm
Thickness (B) = 24 cm = 24 cm
∴ Volume of wall = LBH = 1000 x 24 x 400 cm3 = 9600000 cm³
Dimensions of one brick = 24 cm x 12 cm x 8 cm = 2304 cm³

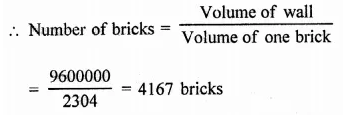
Question 20.
If V is the volume of a cuboid of dimensions a, b, c and S is its surface area, then prove that

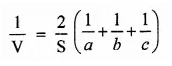
Solution:
a, b, c are the dimensions of a cuboid S is the surface area and V is the volume
∴ V = abc and S = 2(lb + bc + ca)

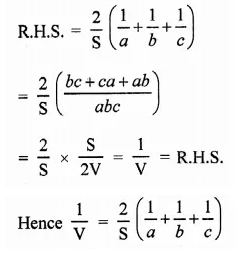
Question 21.
The areas of three adjacent faces of a cuboid are x, y and z. If the volume is V, prove that V² = xyz.
Solution:
Let a, b, c are the dimensions of a cuboid then,
x = ab, y = bc, z = ca
and V = abc
Now L.H.S. = V²
= (abc)² = a²b²c²
= ab.bc.ca = xyz = R.H.S.
Hence V² = xyz

Question 22.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute? [NCERT]
Solution:
Speed of water in a river = 2 km/hr

Question 23.
Water in a canal 30 dm wide and 12 dm deep, is flowing with a velocity of 100 km per hour. How much area will it irrigate in 30 minutes if 8 cm of standing water is desired?
Solution:
Width of canal (b) = 30 dm = 3 m
Depth (h) = 12 dm = 1.2 m
Speed of water = 100 km/hr
Length of water flow in 30 minutes = \(\frac { 1 }{ 2 }\) hr

Question 24.
Half cubic metre of gold-sheet is extended by hammering so as to cover an area of 1 hectare. Find the thickness of the gold- sheet.
Solution:

Question 25.
How many cubic centimetres of iron are there in an open box whose external dimensions are 36 cm, 25 cm and 16.5 cm, the iron being 1.5 cm thick throughout? If 1 cubic cm of iron weighs 15 g, find the weight of the empty box in kg.
Solution:
External length of open box (L) = 36 cm
Breadth (B) = 25 cm
and Height (H) = 16.5 cm
Width of iron sheet used = 1.5 cm
∴ Inner length (l) = 36 – 1.5 x 2 = 36 – 3 = 33 cm
Breadth (b) = 25 – 2 x 1.5 = 25 – 3 = 22 cm
and Height (h) = 16.5 – 1.5 = 15 cm
∴ Volume of the iron used = Outer volume – Inner volume
= 36 x 25 x 16.5 – 33 x 22 x 15
= 14850 – 10890 = 3960 cm3
Weight of 1 cm3 = 15 g

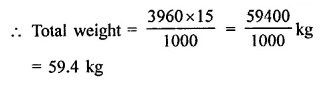
Question 26.
A rectangular container, whose base is a square of side 5 cm, stands on a horizontal table, and holds water upto 1 cm from the top. When a cube is placed in the water it is completely submerged, the water rises to the top and 2 cubic cm of water overflows. Calculate the volume of the cube and also the length of its edge.
Solution:
Base of the container = 5 cm x 5 cm
Level of water upto 1 cm from the top After placing a cube in it, the water rises to the top and 2 cubic cm of water overflows,
(i) ∴ Volume of water = 5 x 5 x 1 + 2 = 25 + 2 = 27 cm³
∴ Volume of cube = 27 cm³

Question 27.
A rectangular tank is 80 m long and 25 m broad. Water-flows into it through a pipe whose cross-section is 25 cm², at the rate of 16 km per hour. How much the level of the water rises in the tank in 45 minutes.
Solution:
Length of tank (l) = 80 m
Breadth (b) = 25 m
Area of cross section of the month of pipe = 25 cm²
and speed of water-flow =16 km/h
∴ Volume of water is 45 minutes

Question 28.
Water in a rectangular reservoir having base 80 m by 60 m is 6.5 m deep. In what time can the water be emptied by a pipe of which the cross-section is a square of side 20 cm, if the water runs through the pipe at the rate of 15 km/hr.
Solution:
Length of reservoir (l) = 80 m
Breadth (b) = 60 m
and depth (h) = 6.5 m
∴ Volume of water in it = lbh = 80 x 60 x 6.5 m³ = 31200 m³
Area of cross-section of the month of pipe = 20 x 20 = 400 cm²

Hope given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.