RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
Other Exercises
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
- RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS
Question 1.
If the heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm respectively. Find the mean height.
Solution:
Heights of 5 persons are 140 cm, 150 cm, 152 cm, 158 cm and 161 cm
Question 2.
Find the mean of 994, 996, 998, 1002 and 1000.
Solution:
Mean of 994, 996, 998, 1002 and 1000
Question 3.
Find the mean of first five natural numbers.
Solution:
First five natural numbers are 1, 2, 3, 4, 5
∴ Mean = \(\overline { x } =\frac { 1+2+3+4+5 }{ 5 } =\frac { 15 }{ 5 } \) = 3
Question 4.
Find the mean all factors of 10.
Solution:
Factors of 10 = 1, 2, 5, 10
∴ Mean = \(\overline { x } =\frac { 1+2+5+10 }{ 4 } =\frac { 18 }{ 4 } \) = 4.5
Question 5.
Find the mean of first 10 even natural numbers.
Solution:
First 10 even natural numbers are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
∴ Mean = \(\overline { x } =\frac { 2+4+6+8+10+12+14+16+18+20 }{ 10 } =\frac { 110 }{ 10 } \) = 11
Question 6.
Find the mean of x, x + 2, x + 4, x + 6, x + 8.
Solution:
Sum = x + x + 2+ x + 4 + x + 6 + x + 8 = 5x + 20
∴ Mean = \(\overline { x } =\frac { \sum { { x }_{ i } } }{ n } \frac { 5x+20 }{ 5 } =x+4 \)
Question 7.
Find the mean of first five multiples of 3.
Solution:
First 5 multiples of 3 are = 3, 6, 9, 12, 15
∴ Mean = \(\overline { x } =\frac { 3+6+9+12+15 }{ 5 } =\frac { 45 }{ 5 } \) = 9
Question 8.
Following are the weights (in kg) or 10 new born babies in a hospital on a particular day:
3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6. Find the mean \(\overline { X } \).
Solution:
Weights of 10 new bom babies are 3.4, 3.6, 4.2, 4.5, 3.9, 4.1, 3.8, 4.5, 4.4, 3.6
∴ Mean \(\overline { X } \) = \(\frac { 3.4+3.6+4.2+4.5+3.9+4.1+3.8+4.5+4.4+3.6 }{ 10 } \)
= \(\frac { 40.0 }{ 10 } \) = 4kg
Question 9.
The percentage of marks obtained by students of a class in mathematics are : 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1. Find their mean.
Solution:
Percentage of 12 students are 64, 36, 47, 23, 0, 19, 81, 93, 72, 35, 3, 1
∴ Mean \(\overline { X } \) = \(\frac { 64+36+47+23+0+19+81+93+72+35+3+1 }{ 12 } \)
= \(\frac { 474 }{ 12 } \) = 39.5
Question 10.
The numbers of children in 10 families of a locality are : 2, 4, 3, 4, 2, 0, 3, 5, 1, 1, 5. Find the mean number of children per family.
Solution:
Number of children in 10 families are 2, 4, 3, 4, 2, 0, 3, 5, 1, 1, 5
∴ Mean \(\overline { X } \) = \(\frac { 2+4+3+4+2+0+3+5+1+1+5 }{ 10 } \)
= \(\frac { 30 }{ 10 } \) = 3
Question 11.
Explain, by taking a suitable example, how the arithmetic mean alters by (i) adding a constant k to each term, (ii) subtracting a constant k from each them, (iii) multiplying each term by a constant k and (iv) dividing each term by a non-zero constant k.
Solution:
Let x1, x2, x3, x4, x5 are five numbers whose mean is \(\overline { x } \) i.e. = \(\frac { x1+x2+x3+x4+x5 }{ 5 } \) = \(\overline { x } \)
Hence we see that in each case, the mean is changed.
Question 12.
The mean of marks scored by 100 students was found to be 40. Later on its was discovered that a score of 53 was misread as 83. Find the correct mean.
Solution:
Mean score of 100 students = 40
∴Total = 100 x 40 = 4000
Difference in one score by mistake = 83 – 53 = 30
Actual total scores = 4000 – 300 = 3970
Actual mean = \(\frac { 3970 }{ 100 } \) = 39.70 = 39.7
Question 13.
The traffic police recorded the speed (in km/hr) of 10 motorists as 47, 53, 49, 60, 39, 42, 55, 57, 52, 48. Later on an error in recording instrument was found. Find the correct average speed of the motorists if the instrument recorded 5 km/hr less in each case.
Solution:
Speed of 10 motorist as recorded = 47, 53, 49, 60, 39, 42, 55, 57, 52, 48
Total of speed of 10 motorists = 47 + 53 + 49 + 60 + 39 + 42 + 55 +57 + 52 + 48 = 502

Question 14.
The mean of five numbers is 27. If one number is excluded, their mean is 25. Find the excluded number.
Solution:
Mean of 5 numbers = 27
Total = 27 x 5 = 135
By excluded one number, then mean of remaining 4 numbers = 25
Total = 4 x 25 = 100
Excluded number = 135 – 100 = 35
Question 15.
The mean weight per student in a group of 7 students is 55 kg. The individual weights of 6 of them (in kg) are 52, 54, 55, 53, 56 and 54. Find the weight of the seventh student.
Solution:
Mean weight of 7 students = 55 kg
Total weight of 7 students = 55 x 7 kg = 385 kg
Total weights of 6 students among them = 52 + 54 + 55 + 53 + 56 + 54 = 324 kg
Weight of 7th student = 385 – 324 = 61 kg
Question 16.
The mean weight of 8 numbers is 15. If each number is multiplied by 2, what will be the new mean?
Solution:
Weight of 8 numbers =15
By multiplying each number by 2, then the average will be = 15 x 2 = 30
New average = 30
Question 17.
The mean of 5 numbers is 18. If one number is excluded, their mean is 16. Find the excluded number.
Solution:
Mean of 5 numbers = 18
Total = 18 x 5 = 90
By excluding one number, the mean of remaining 5 – 1=4 numbers = 16
Total = 16 x 4 = 64
Excluded number = 90 – 64 = 26
Question 18.
The mean of 200 items was 50. Later on, it was discovered that the two items were misread as 92 and 8 instead of 192 and 88. Find the correct mean.
Solution:
Mean of 200 items = 50
Total = 50 x 200 = 10000
The number were misread as 92 instead of 192 and 8 instead of 88
Difference = 192 – 92 + 88 – 8 = 180
New total = 10000 + 180 = 10180
and new mean = \(\frac { 10180 }{ 200 } \) = 50.9
Question 19.
If M is the mean of x1, x2, xr3, x4, x5 and x6, prove that
(x1 – M) + (x2 – M) + (x3 – M) + (x4 – M) + (x5 – M) + (x6 – M) = 0.
Solution:
∵ M is the mean of x,, x2, x3, x4, x5, x6
Then M = \(\frac { x1+x2+x3+x4+x5+x6 }{ 6 } \)
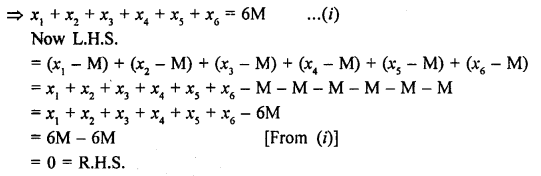
Question 20.
Durations of sunshine (in hours) in Amritsar for first 10 days of August 1997 as reported by the Meteorological Department are given below:
9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9
(i) Find the mean \(\overline { X }\)
(ii) Verify that \( \sum _{ i=1 }^{ 10 }{ \left( { x }_{ i }-\overline { X } \right) } \) = 0
Solution:
Duration of sun shine for 10 days (in hours)
= 9.6, 5.2, 3.5, 1.5, 1.6, 2.4, 2.6, 8.4, 10.3, 10.9

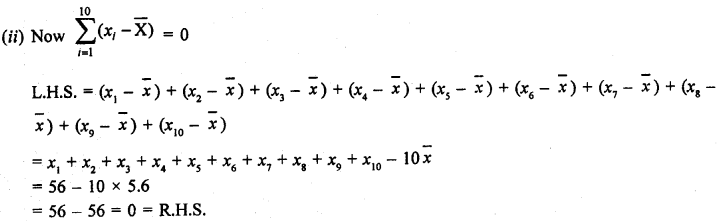
Question 21.
Find the values of n and X in each of the following cases:
(i) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-12 \right) } =-10\quad and\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-3 \right) } =62\)
(ii) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-10 \right) } =30\quad and\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-6 \right) } =150\)
Solution:
(i) \(\sum _{ i=1 }^{ n }{ \left( { x }_{ i }-12 \right) } =-10\)…(i)

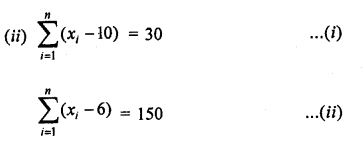

Question 22.
The sums of the deviations of a set of n values x1, x2,… xn measured from 15 and -3 are -90 and 54 respectively. Find the value of n and mean.
Solution:
In first case,
(x1 – 15) + (x2 – 15) + (x3 – 15) + … + (xn – 15) = – 90
=> x1 + x2 + x3 + … + xn – 15 x n = – 90

Question 23.
Find the sum of the deviations of the variate values 3, 4, 6, 7, 8, 14 from their mean.
Solution:
Mean of 3, 4, 6, 7, 8, 14 = \(\frac { 42 }{ 6 } \) = 7
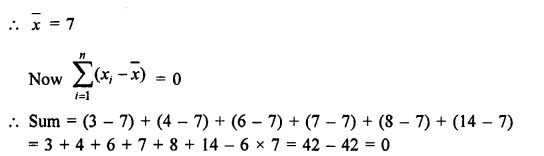
Question 24.
If \(\overline { X } \) is the mean of the ten natural numbers x1, x2, x3, …, x10, show that (x1 – \(\overline { X } \)) + (x2 – \(\overline { X } \)) + … + (x10 – \(\overline { X } \)) = 0.
Solution:
\(\overline { X } \) is the mean of 10 natural numbers
x1, x2, x3, …, x10
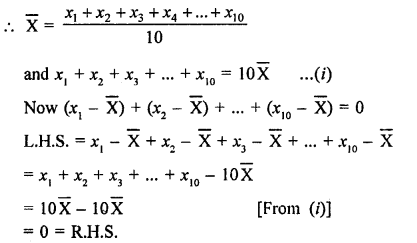
Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.