RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.1
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.2
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.3
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency Ex 24.4
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS
• RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS

Mark the correct alternative in each of the following:

Question 1.
Which one of the following is not a measure of central value?
(a) Mean
(b) Range
(c) Median
(d) Mode
Solution:
Range (b)

Question 2.
The mean of n observations is \(\overline { X } \) . If k is added to each observation, then the new mean is
(a) \(\overline { X } \)
(b) \(\overline { X } \) + k
(c) \(\overline { X } \) – k
(d) k\(\overline { X } \)
Solution:
Mean of n observation = \(\overline { X } \)
By adding k to each observation the new mean will be \(\overline { X } \) + k (b)

Question 3.
The mean of n observations is \(\overline { X } \) . If each observation is multiplied by k, the mean of new observations is
(a) k\(\overline { X } \)
(b) \(\frac { \overline { X } }{ k } \)
(c) \(\overline { X } \) + k
(d) \(\overline { X } \) – k
Solution:
Mean of n observations = \(\overline { X } \)
By multiplying each observation by k,
the new mean = k\(\overline { X } \) (a)

Question 4.
The mean of a set of seven numbers is 81. If one of the numbers is discarded, the mean of the remaining numbers is 78. The value of discarded number is
(a) 98
(b) 99
(c) 100
(d) 101
Solution:
Mean of 7 numbers = 81
Total = 7 x 81 = 567
By discarding one number, the mean of the remaining 7 – 1 = 6 numbers = 78
Total = 6 x 78 = 468
Discarded number = 567 – 468 = 99 (b)

Question 5.
For which set of numbers do the mean, median and mode all have the same value?
(a) 2, 2, 2, 2, 4
(b) 1, 3, 3, 3, 5
(c) 1, 1, 2, 5, 6
(d) 1, 1, 1, 2, 5
Solution:
a) In set 2, 2, 2, 2, 4

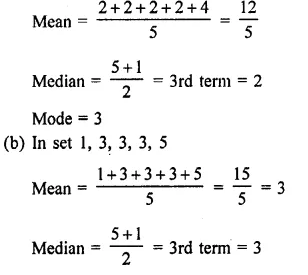
Mode = 3 as it come in maximum times
This set has mean, median and mode same (b)

Question 6.
For the set of numbers 2, 2, 4, 5 and 12, which of the following statements is true?
(a) Mean = Median
(b) Mean > Mode
(c) Mean < Mode
(d) Mode = Median
Solution:
The given set is 2, 2, 4, 5, 12

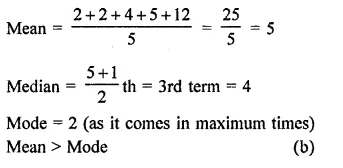
Question 7.
If the arithmetic mean of 7, 5, 13, x and 9 is 10, then the value of x is
(a) 10
(b) 12
(c) 14
(d) 16
Solution:
Arithmetic mean of 7, 5, 13, x, 9 is 10

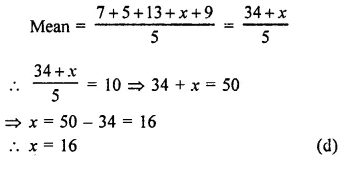
Question 8.
If the mean of five observations x, x + 2, x + 4, x + 6, x + 8, is 11, then the mean of first three observations is
(a) 9
(b) 11
(c) 13
(d) none of these
Solution:
Mean = 11
But mean of x, x + 2, x + 4, x+ 6, x + 8

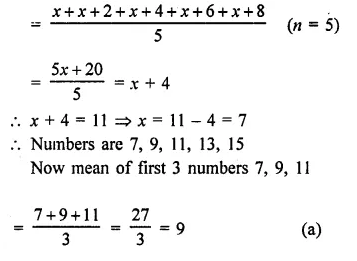
Question 9.
Mode is
(a) least frequent value
(b) middle most value
(c) most frequent value
(d) none of these
Solution:
Mode is most frequent value (c)

Question 10.
The following is the data of wages per day: 5, 4, 7, 5, 8, 8, 8, 5, 7, 9, 5, 7, 9, 10, 8 The mode of the data is
(a) 7
(b) 5
(c) 8
(d) 10
Solution:
Wages per day
5, 4, 7, 5, 8, 8, 8, 5, 7, 9, 5, 7, 9, 10, 8
=> 4, 5, 5, 5, 5, 7, 7, 7, 8, 8, 8, 8, 9, 9, 10
Here 8 comes in maximum times
Mode = 8 (c)

Question 11.
The median of the following data :
is ,
(a) 0
(b) -1.5
(c) 2
(d) 3.5
Solution:
Arranging in ascending order,
-3, -3, -1, 0, 2, 2, 2, 5, 5, 5, 5, 6, 6, 6

Question 12.
The algebraic sum of the deviations of a set of n values from their mean is
(a) 0
(b) n – 1
(c) n
(d) n + 1
Solution:
The algebraic sum of deviation of a set of n values from that mean

Question 13.
A, B, C are three sets of values of X:
A : 2, 3, 7, 1, 3, 2, 3
B: 7, 5, 9, 12, 5, 3, 8
C: 4, 4, 11, 7 ,2, 3, 4
Which one of the following statements is
correct?
(a) Mean of A = Mode of C
(b) Mean of C = Median of B
(c) Median of B = Mode of A
(d) Mean, Median and Mode of A are equal.
Solution:
Arranging the sets in ascending order
A{2, 3, 7, 1,3,2,3)
= {1, 2, 2, 3, 3, 3, 7)
B = {7, 5, 9, 12, 5, 3, 8)
= {3, 5, 5, 7, 8, 9, 12)
C = {4, 4, 11,7,2,3,4)
= {2, 3, 4, 4, 4, 7, 11)

Mode = 5 {as it comes max times}
(c) Mean of set C = \(\\ \frac { 2+3+4+4+4+7+11 }{ 7 } \)
= \(\\ \frac { 35 }{ 7 } \) = 5
Median = \(\\ \frac { 7+1 }{ 2 } \) th =\(\\ \frac { 8 }{ 2 } \) =4th term = 4
Mode =4 {as it comes max times}
In set A,mean = median = mode = 3 (d)

Question 14.
The empirical relation between mean, mode and median is
(a) Mode = 3 Median — 2 Mean
(b) Mode 2 Median — 3 Mean
(c) Median 3 Mode — 2 Mean
(d) Mean = 3 Median —2 Mode
Solution:
The empirical relations between mean, mode
and median is
Mode = 3 Median — 2 Mean (a)

Question 15.
The mean of a, b, c, d and e is 28. If the mean of a, c, and e is 24, what is the mean of b and d?
(a) 31
(b) 32
(c) 33
(d) 34
Solution:
Mean of a, b, c, d and e = 28
Total of a, b, c, d and e = 28 x 5 = 140
Mean of a, c and e is = 24
Total of a, c, e = 24 x 3 = 72
Total of b and d = 140 – 72 = 68
Mean = \(\\ \frac { 68 }{ 2 } \) = 34 (d)

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.