RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS

Other Exercises

Question 1.
If the ratio of mode and median of a certain data is 6 : 5, then find the ratio of its mean and median.
Solution:
We know that
Mode = 3 median – 2 mean…(i)
and \(\frac { mode }{ median } \) = \(\frac { 6 }{ 5 } \)
Mode = \(\frac { 6 }{ 5 } \)median
∴From (i), \(\frac { 6 }{ 5 } \) median = 3 median – 2 mean
=> 2 mean = 3 median – \(\frac { 6 }{ 5 } \)median
2 mean = \(\frac { 15-6 }{ 5 } \)median = \(\frac { 9 }{ 5 } \)median
\(\frac { mean }{ median } \) = \(\frac { 9 }{ 5X2 } \) = \(\frac { 9 }{ 10 } \)
∴Ratio = 9:10

Question 2.
If the mean of x + 2, 2x + 3, 3x + 4, 4x + 5 is x + 2, find x.
Solution:
Mean of x + 2, 2x + 3, 3x + 4, 4x + 5 = x + 2
=> \(\frac { x + 2+2x + 3+3x + 4+4x + 5 }{ 4 } \) = x + 2
=> 10x + 14 = 4x + 8
=> 10x – 4x = 8 – 14
=> 6x= – 6
∴ x = – 1

Question 3.
If the median of scores ,\(\frac { x }{ 2 } \), \(\frac { x }{ 3 } \), \(\frac { x }{ 4 } \), \(\frac { x }{ 5} \) and \(\frac { x }{ 6 } \) (where x > 0) is 6, then find the value \(\frac { x }{ 6 } \)
Solution:
\(\frac { x }{ 2 } \), \(\frac { x }{ 3 } \), \(\frac { x }{ 4 } \), \(\frac { x }{ 5} \), \(\frac { x }{ 6 } \)
Here n = 5
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 5+1 }{ 2 } \) th
\(\frac { 6 }{ 2 } \) = 3rd term = \(\frac { x }{ 4 } \)
\(\frac { x }{ 4 } \) = 6 => x = 24
\(\frac { x }{ 6 } \) = \(\frac { 24 }{ 6 } \) = 4
∴Hence = \(\frac { x }{ 6 } \) = 4

Question 4.
If the mean of 2, 4, 6, 8, x, y is 5, then find the value of x + y.
Solution:
Mean of 2, 4, 6, 8, x, y is 5
\(\frac { 2+4+6+8+x+y }{ 6 } \) = 5
\(\frac { 20+x+y }{ 6 } \) = 5
=> 20 + (x +y) = 30
=> x + y = 30 – 20 = 10
∴x + y = 10

Question 5.
If the mode of scores 3, 4, 3, 5, 4, 6, 6, x is 4, find the value of x.
Solution:
Mode of 3, 4, 3, 5, 4, 6, 6, x is 4
∴ 4 comes in maximum times
But here ,
3 2
4 2
5 1
6 2
3, 4 and 6 are equal in number
∴ x must be 4 so that it becomes in maximum times

Question 6.
If the median of 33, 28, 20. 25, 34, x is 29. find the maximum possible value of x.
Solution:
Median of 33, 28, 20, 25, 34, x is 29
Now arranging in ascending order 20, 25, 28, x, 33, 34
Here n = 6
Median = \(\frac { 1 }{ 2 } \left[ \frac { 6 }{ 2 } th\quad term+\left( \frac { 6 }{ 2 } +1 \right) th\quad term \right] \)
29 = \(\frac { 1 }{ 2 } \) [3rd term + 4th term]
29 = \(\frac { 1 }{ 2 } \) [28+x]
58 = 28 + x
=> x = 58 – 28 = 30
∴Possible value of x = 30

Question 7.
If the median of the scores 1, 2, x, 4, 5 (where 1 <2 <x <4 <5) is 3, then find the mean of the scores.
Solution:
Scores are 1, 2, x, 4, 5 and median 3
Here n = 5 which is odd
Median = \(\frac { n+1 }{ 2 } \) th term = \(\frac { 5+1 }{ 2 } \) = \(\frac { 6 }{ 2 } \) th
=> 3 = 3rd term = x
=> 3 = x
∴ x = 3
Mean of the score = \(\frac { 1+2+3+4+5 }{ 5 } \) = 3

Question 8.
If the ratio of mean and median of a certain data is 2 : 3, then find the ratio of its mode and mean.
Solution:
We know that mode = 3 median – 2 mean
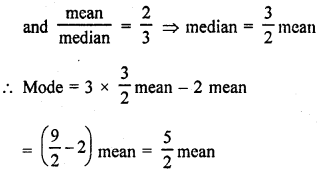
RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS 8.1
\(\frac { mode }{ mean } \) = \(\frac { 5 }{ 2 } \)
Ratio in mode and mean = 5 : 2

Question 9.
The arithmetic mean and mode of a data are 24 and 12 respectively, then find the median of the data.
Solution:
Mean = 24
Mode = 12
We know that mode = 3 median – 2 mean
12 = 3 median – 2 x 24
12 = 3 median – 48
3 median 12 + 48 = 60
Median = \(\frac { 60 }{ 3 } \) = 20

Question 10.
If the difference of mode and median of a data is 24, then find the difference of median and mean.
Solution:
Mode – Median = 24
Mode = 24 + median
But mode = 3 median – 2 mean
3 median – 2 mean = 24 + median
3 median – median – 2 mean = 24
=> 2 median – 2 mean = 24
=> Median – Mean = 12 (Dividing by 2)

Hope given RD Sharma Class 9 Solutions Chapter 24 Measures of Central Tendency VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.