RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1

Question 1.
Evaluate each of the following using identities:
(i) (2x –\(\frac { 1 }{ x }\))2
(ii)  (2x + y) (2x – y)
(iii) (a2b – b2a)2
(iv) (a – 0.1) (a + 0.1)
(v) (1.5.x2 – 0.3y2) (1.5x2 + 0.3y2)
Solution:
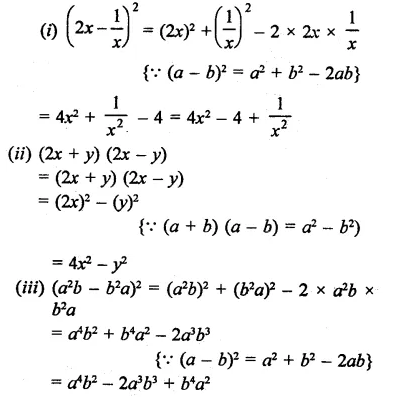
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q1.1
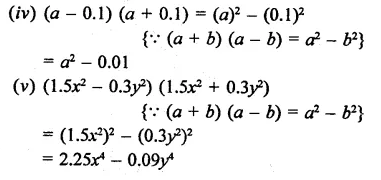
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q1.2

Question 2.
Evaluate each of the following using identities:
(i) (399)2
(ii) (0.98)2
(iii) 991 x 1009
(iv) 117 x 83
Solution:
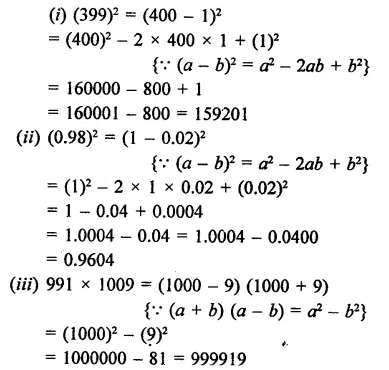
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q2.1
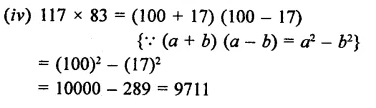
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q2.2

Question 3.
Simplify each of the following:
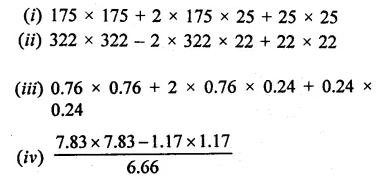
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q3.1
Solution:
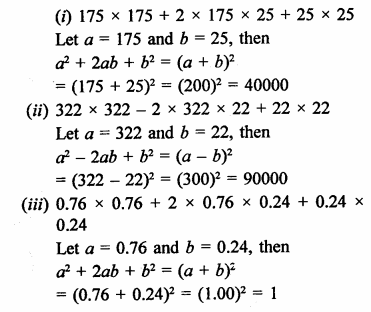
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q3.2
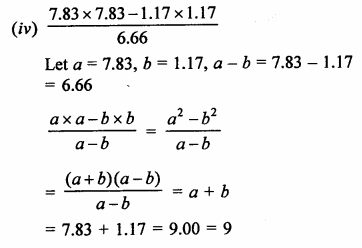
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q3.3

Question 4.
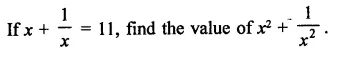
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q4.1
Solution:
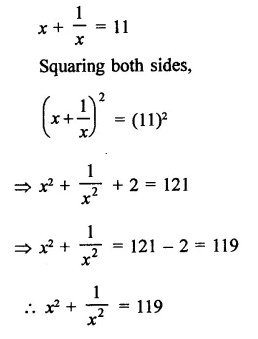
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q4.2

Question 5.
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q5.1
Solution:
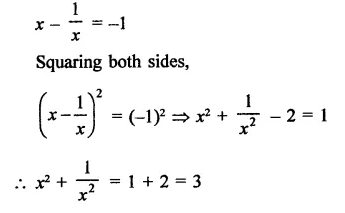
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q5.2

Question 6.
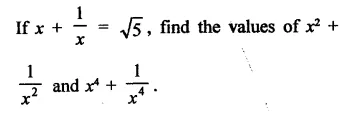
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q6.1
Solution:
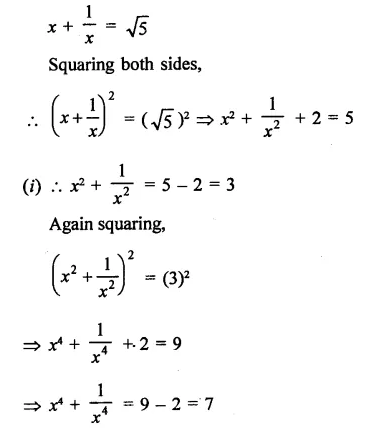
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q6.2
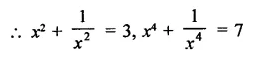
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q6.3

Question 7.
If 9x2 + 25y2 = 181 and xy = -6, find the value of 3x + 5y.
Solution:
9x2 + 25y2 = 181, and xy = -6
(3x + 5y)2 = (3x)2 + (5y)2 + 2 x 3x + 5y
⇒ 9X2 + 25y2 + 30xy
= 181 + 30 x (-6)
= 181 – 180 = 1
= (±1 )2
∴ 3x + 5y = ±1

Question 8.
If 2x + 3y = 8 and xy = 2, find the value of 4X2 + 9y2.
Solution:
2x + 3y = 8 and xy = 2
Now, (2x + 3y)2 = (2x)2 + (3y)2 + 2 x 2x x 3y
⇒  (8)2 = 4x2 + 9y2 + 12xy
⇒ 64 = 4X2 + 9y2 + 12 x 2
⇒ 64 = 4x2 + 9y2 + 24
⇒ 4x2 + 9y2 = 64 – 24 = 40
∴ 4x2 + 9y2 = 40

Question 9.
If 3x -7y = 10 and xy = -1, find the value of 9x2 + 49y2
Solution:
3x – 7y = 10, xy = -1
3x -7y= 10
Squaring both sides,
(3x – 7y)2 = (10)2
⇒ (3x)2 + (7y)2 – 2 x 3x x 7y = 100
⇒  9X2 + 49y2 – 42xy = 100
⇒  9x2 + 49y2 – 42(-l) = 100
⇒ 9x2 + 49y2 + 42 = 100
∴ 9x2 + 49y2 = 100 – 42 = 58

Question 10.
Simplify each of the following products:
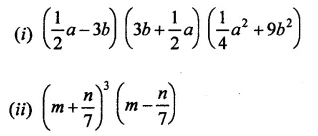
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q10.1
Solution:
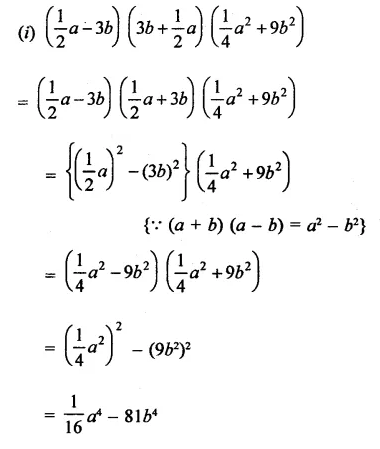
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q10.2
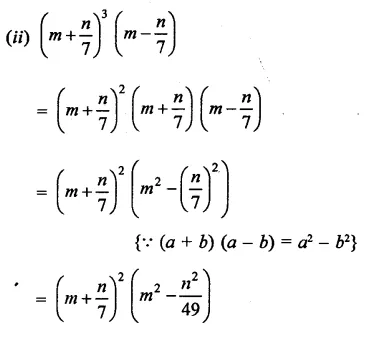
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q10.3

Question 11.
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q11.1
Solution:
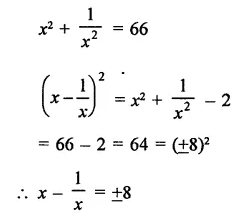
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q11.2

Question 12.
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q12.1
Solution:
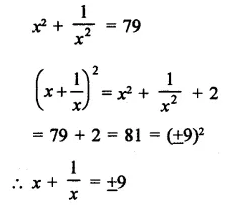
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q12.2

Question 13.
Simplify each of the following products:
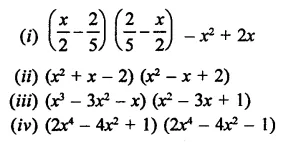
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q13.1
Solution:
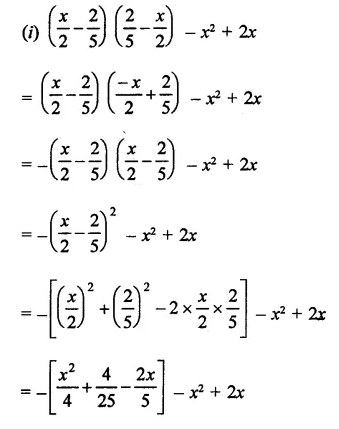
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q13.2
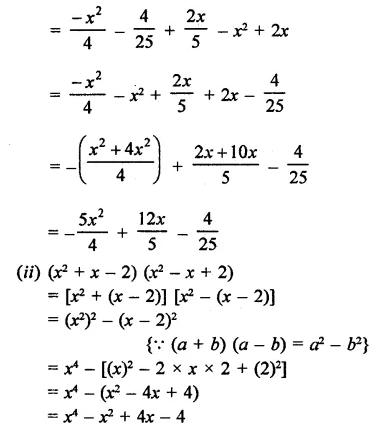
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q13.3
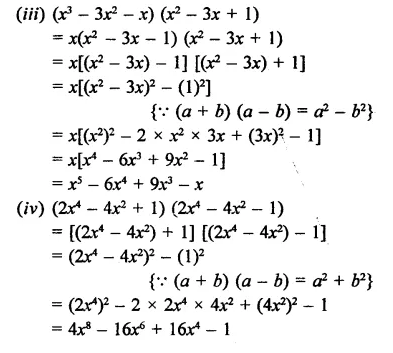
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q13.4

Question 14.
Prove that a2 + b2 + c2 – ab – bc – ca is always non-negative for all values of a, b and c.
Solution:
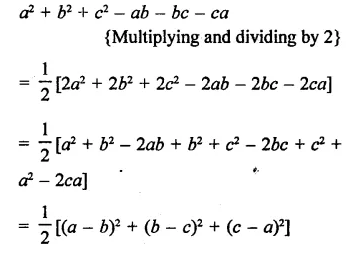
RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 Q14.1
∵  The given expression is sum of these squares
∴ Its value is always positive Hence the given expression is always non-­negative for all values of a, b and c

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.