RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

Factorize
Question 1.
x³ + x – 3x² – 3
Solution:
x³ + x – 3x² – 3
x³ – 3a² + x – 3
⇒  x²(x – 3) + 1(x – 3)
= (x – 3) (x² + 1)

Question 2.
a(a + b)³ – 3a²b(a + b)
Solution:
a(a + b)³ – 3a²b(a + b)
= a(a + b) {(a + b)² – 3ab}
= a(a + b) {a² + b² + 2ab – 3ab}
= a{a + b) {a² – ab + b²)

Question 3.
x(x³ – y³) + 3xy(x – y)
Solution:
x(x³ – y³) + 3xy(x – y)
= x(x – y) (x² + xy + y²) + 3xy(x – y)
= x(x – y) (x² + xy + y² + 3y)
= x(x – y) (x² + xy + y² + 3y)

Question 4.
a²x² + (ax² +1)x + a
Solution:
a²x² + (ax² + 1)x + a
= a²x² + a + (ax² + 1)x
= a(ax² + 1) + x(ax² + 1)
= (ax² + 1) (a + x)
= (x + a) (ax² + 1)

Question 5.
x² + y – xy – x
Solution:
x² + y – xy – x
= x²-x-xy + y = x(x- l)-y(*- 1)
= (x – 1) (x – y)

Question 6.
X³ – 2x²y + 3xy² – 6y³
Solution:
x³ – 2x²y + 3xy² – 6y³
= x²(x – 2y) + 3y²(x – 2y)
= (x – 2y) (x² + 3y²)

Question 7.
6ab – b² + 12ac – 2bc
Solution:
6ab – b² + 12ac – 2bc
= 6ab + 12ac – b² – 2bc
= 6a(b + 2c) – b(b + 2c)
= (b + 2c) (6a – b)

Question 8.
x(x – 2) (x – 4) + 4x – 8
Solution:
x(x – 2) (x – 4) + 4x – 8
= x(x – 2) (x – 4) + 4(x – 2)
= (x – 2) [x(x – 4) + 4]
= (x – 2) (x² – 4x + 4)
= (x – 2) [(x)² – 2 x x x 2 + (2)²]
= (x – 2) (x – 2)² = (x – 2)³

Question 9.
(a – b + c)² + (b – c + a)² + 2(a – b + c) (b – c + a)
Solution:
(a – b + c)² + ( b- c+a)² + 2(a – b + c) (b – c + a)      {∵ a² + b² + 2ab = (a + b)²}
= [a – b + c + b- c + a]²
= (2a)² = 4a²

Question 10.
a² + 2ab + b² – c²
Solution:
a² + 2ab + b² – c²
= (a² + 2ab + b²) – c²
= (a + b)² – (c)²         {∵  a² – b² = (a + b) (a – b)}
= (a + b + c) (a + b – c)

Question 11.
a² + 4b² – 4ab – 4c²
Solution:

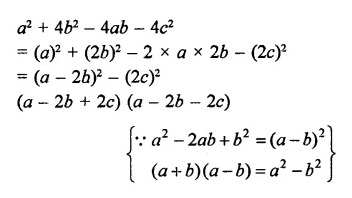
Question 12.
x² – y² – 4xz + 4z²
Solution:
x² – y² – 4xz + 4z²
= x² – 4xz + 4z² – y²
= (x)² – 2 x x x 2z + (2z)² – (y)²
= (x – 2z)² – (y)²
= (x – 2z + y) (x – 2z – y)
= (x +y – 2z) (x – y – 2z)

Question 13.

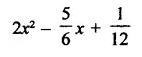
Solution:

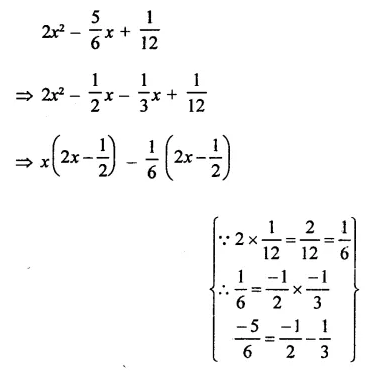
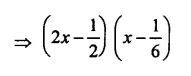
Question 14.

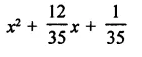
Solution:

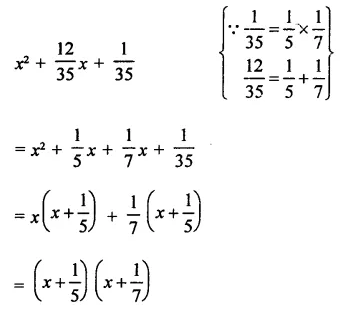
Question 15.

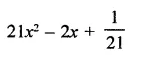
Solution:

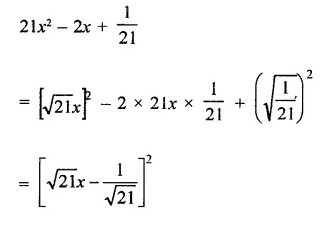
Question 16.
Give possible expression for the length and breadth of the rectangle having 35y² + 13y – 12 as its area.
Solution:
Area of a rectangle = 35y² + 13y – 12
= 35y² + 28y- 15y- 12

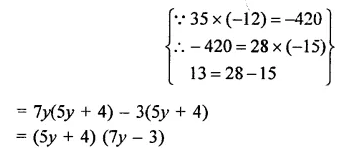
(i) If length = 5y + 4, then breadth = 7y – 3
(ii) and if length = 7y-3, then length = 5y+ 4

Question 17.
What are the possible expressions for the dimensions of the cuboid whose volume is 3x² – 12x.
Solution:
Volume 3x² – 12x
= 3x(x – 4)
∴ Factors are 3, x, and x – 4
Now, if length = 3, breadth = x and height = x – 4
if length =3, breadth = x – 4, height = x
if length = x, breadth = 3, height = x – 4
if length = x, breadth = x – 4, height = 3
if length = x – 4, breadth = 3, height = x
if length – x – 4, breadth = x, height = 3

Question 18.

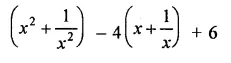
Solution:

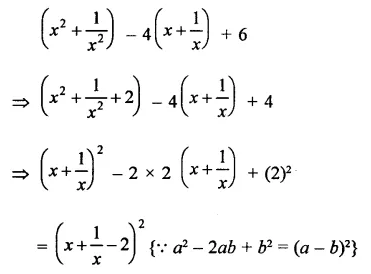
Question 19.
(x + 2) (x² + 25) – 10x² – 20x
Solution:
(x + 2) (x² + 25) – 10x² – 20x
= (x + 2) (x² + 25) – 10x(x + 2)
= (x + 2) [x² + 25 – 10x]
= (x + 2) [(x)² – 2 x x x 5 + (5)²]
= (x + 2) (x – 5)²

Question 20.
2a² + 2\(\sqrt { 6 } \) ab +3b²
Solution:
2a² + 2\(\sqrt { 6 } \)  ab +3 b²
= (\(\sqrt { 2 } \) a)²+ \(\sqrt { 2 } \) a x \(\sqrt { 3 } \) b+ (\(\sqrt { 3 } \) b)²
= (\(\sqrt { 2 } \)a + \(\sqrt { 3 } \) b)2

Question 21.
a² + b² + 2(ab + bc + ca)
Solution:
a² + b² + 2(ab + bc + ca)
= a² + b² + 2 ab + 2 bc + 2 ca
= (a + b)² + 2c(b + a)
= (a + b)² + 2c(a + b)
= (a + b) (a + b + 2c)

Question 22.
4(x – y)² – 12(x -y) (x + y) + 9(x + y)²
Solution:
4(x – y)² – 12(x – y) (x + y) + 9(x + y)²
= [2(x – y)² + 2 x 2(x – y) x 3(x + y) + [3 (x+y]²        {∵ a² + b² + 2 abc = (a + b)²}
= [2(x – y) + 3(x + y)]²
= (2x-2y + 3x + 3y)²
= (5x + y)²

Question 23.
a² – b² + 2bc – c²
Solution:
a² – b² + 2bc – c²
= a² – (b² – 2bc + c²)                                           {∵ a² + b² – 2abc = (a – b)²}
= a² – (b – c)²
= (a)² – (b – c)²          {∵ a² – b² = (a + b) (a – b)}
= (a + b – c) (a – b + c)

Question 24.
xy⁹ – yx⁹
Solution:
xy⁹ – yx⁹ = xy(y⁸ – x⁸)
= -xy(x⁸ – y⁸)
= -xy[(x⁴)² – (y⁴)²]
= -xy (x⁴ + y⁴) (x⁴ – y⁴)                                         {∵ a²-b² = (a + b) (a – b)}
= -xy (x⁴ + y⁴) {(x²)² – (y²)²}
= -xy(x⁴ + y⁴) (x² + y²) (x² – y²)
= -xy (x⁴ +y⁴) (x² + y²) (x + y) (x -y)
= -xy(x – y) (x + y) (x² + y²) (x⁴ + y⁴)

Question 25.
x⁴ + x²y² + y⁴
Solution:
x⁴ + x²y² + y⁴  = (x²)² + 2x²y² + y⁴ – x²y²           (Adding and subtracting x²y²)
= (x² + y²)² – (xy)²                                                        {∵ a² – b² = (a + b) (a – b)}
= (x² + y² + xy) (x² + y² – xy)
= (x² + xy + y²) (x² – xy + y²)

Question 26.
x² + 6\(\sqrt { 2 } \)x + 10
Solution:

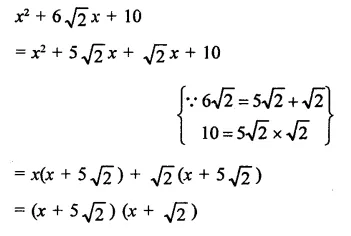
Question 27.
x² + 2\(\sqrt { 2 } \)x- 30
Solution:

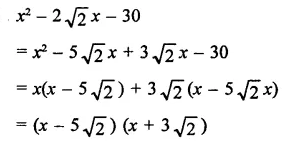
Question 28.
x² – \(\sqrt { 3 } \)x – 6
Solution:

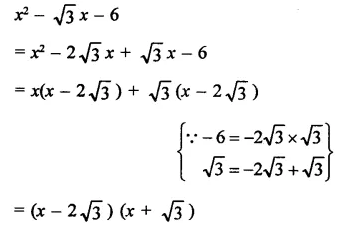
Question 29.
x² + 5 \(\sqrt { 5 } \)x + 30
Solution:

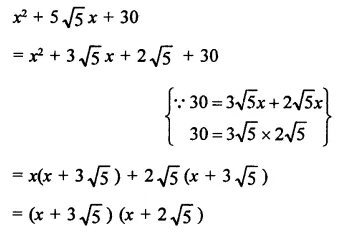
Question 30.
x² + 2 \(\sqrt { 3 } \)x – 24
Solution:

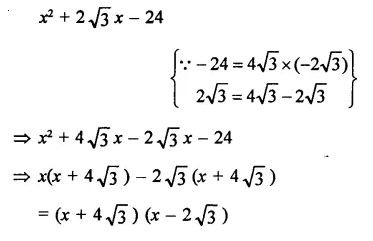
Question 31.
5 \(\sqrt { 5 } \)x² + 20x + 3\(\sqrt { 5 } \)
Solution:

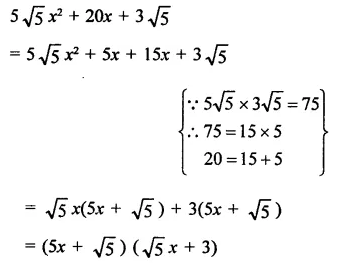
Question 32.
2x² + 3\(\sqrt { 5 } \) x + 5
Solution:

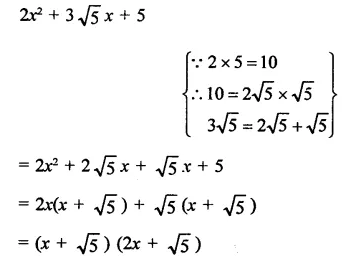
Question 33.
9(2a – b)² – 4(2a – b) – 13
Solution:

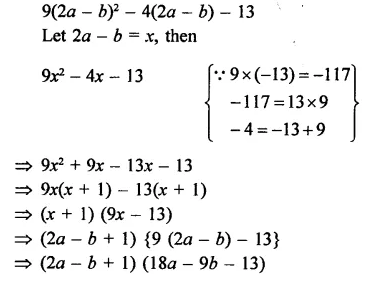
Question 34.
7(x-2y) – 25(x-2y) +12
Solution:

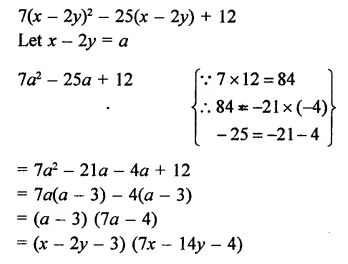
Question 35.
2(x+y) – 9(x+y) -5
Solution:
2(x+y) – 9(x+y) -5

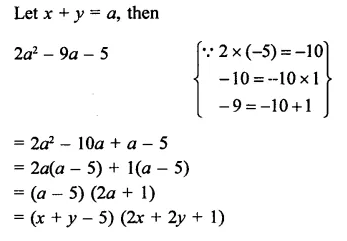
Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.