RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2

Other Exercises

Question 1.
If f(x) = 2x³ – 13x² + 17x + 12, find
(i) f (2)
(ii) f (-3)
(iii) f(0)
Solution:
f(x) = 2x³ – 13x² + 17x + 12
(i) f(2) = 2(2)³ – 13(2)² + 17(2) + 12
= 2 x 8-13 x 4+17 x 2+12
= 16-52 + 34 + 12
= 62 – 52
= 10
(ii) f(-3) = 2(-3)³ – 13(-3)² + 17 x (-3) + 12
= 2 x (-27) – 13 x 9 + 17 x (-3) + 12
= -54 – 117 -51 + 12
= -222 + 12
= -210
(iii) f(0) = 2 x (0)³ – 13(0)² + 17 x 0 + 12
= 0-0 + 0+ 12 = 12

Question 2.
Verify whether the indicated numbers are zeros of the polynomials corresponding to them in the following cases: [NCERT]
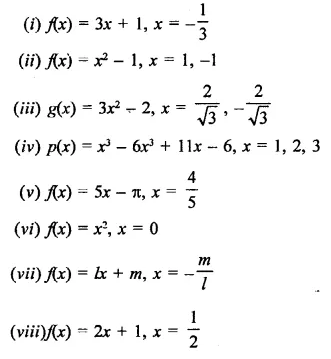
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2 Q2.1
Solution:

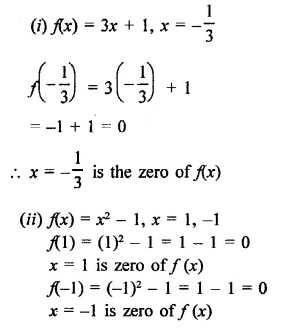
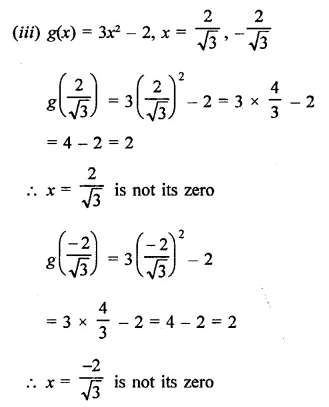
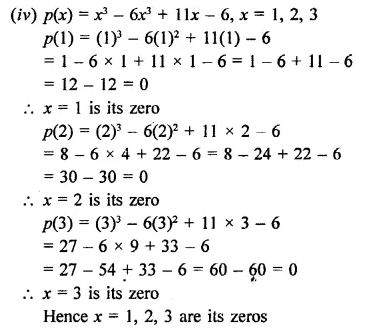
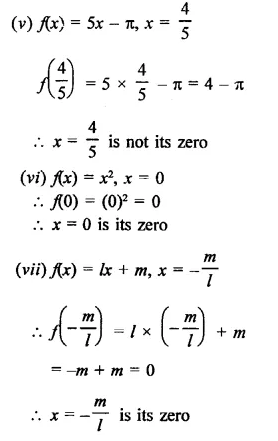
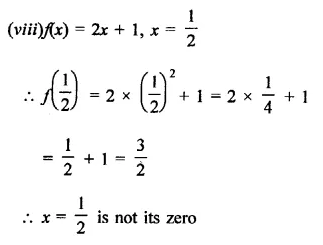
Question 3.
If x = 2 is a root of the polynomial f(x) = 2x²-3x + la, find the value of a.
Solution:
p(x) = 2x² – 3x + 7a
∵ x = 2 is its zero, then
p(0) = 0
∴ p( 2) = 2(2)² – 3×2 + la = 0
⇒2 x 4-3 x2 + 7a = 0
⇒ 8 – 6 + 7o = 0
⇒2 + 7a = 0
⇒ 7a = -2 ⇒ a =\(\frac { -2 }{ 7 }\)
∴ Hence a = \(\frac { -2 }{ 7 }\)

Question 4.
If x = –\(\frac { 1 }{ 2 }\) is a zero of the polynomial p(x) = 8x³ – ax² – x + 2, find the value of a.
Solution:
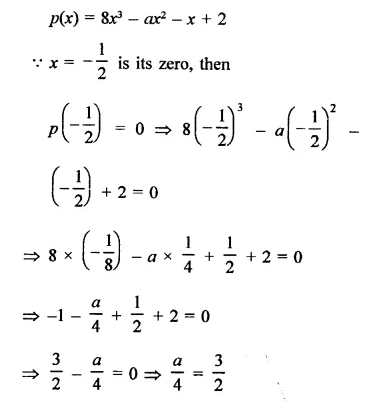
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2 Q4.1

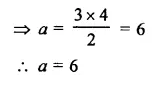
Question 5.
If x = 0 and x = -1 are the roots of the polynomial f(x) = 2x³ – 3x² + ax + b, find the value of a and b.
Solution:
f(x) = 2x³ – 3x² + ax + b
∵ x = 0 and x = -1 are its zeros
∴ f(0) = 0 and f(-1) = 0
Now, f(0) = 0
⇒ 2(0)³ – 3(0)² + a x 0 + b = 0
⇒ 0-0 + 0 + b= 0
∴ b = 0
and f(-1) = 0
⇒ 2(-1)³ – 3(-1)² + a(-1) + b = 0
⇒ 2 x (-1) – 3 x 1 + a x (-1) + b = 0
⇒ -2 -3-a + b = 0
⇒ -2-3-a + 0 = 0
⇒ -5- a = 0=>a =-5
Hence a = -5, b = 0

Question 6.
Find the integral roots of the polynomial f(x) = x³ + 6x² + 11x + 6.
Solution:
f(x) = x³ + 6x² + 11x + 6
Construct = 6 = ±1, ±2, +3, ±6
If x = 1, then
f(1) = (1)³ + 6(1)² + 11 x 1 + 6
= 1+ 6+11+ 6 = 24
∵ f(x) ≠ 0, +0
∴ x = 1 is not its zero
Similarly, f(-1) = (-1)³ + 6(-1)² + 11(-1) + 6
= -1 + 6 x 1-11+6
=-1+6-11+6
= 12-12 = 0
∴ x = -1 is its zero
f(-2) = (-2)³ + 6(-2)² + 11 (-2) + 6
= -8 + 24 – 22 + 6
= -30 + 30 = 0
∴ x = -2 is its zero
f(-3) = (-3)³ + 6(-3)² + 11 (-3) + 6
= -27 + 54 – 33 + 6 = 60 – 60 = 0
∴ x = -3 is its zero
x = -1, -2, -3 are zeros of f(x)
Hence roots of f(x) are -1, -2, -3

Question 7.
Find the rational roots of the polynomial f(x) = 2x³ + x² – 7x – 6.
Solution:
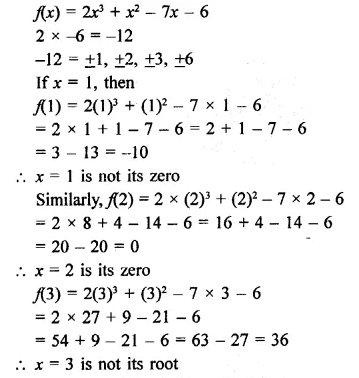
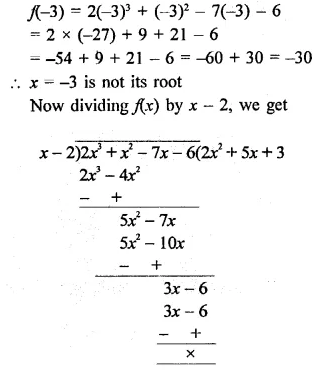
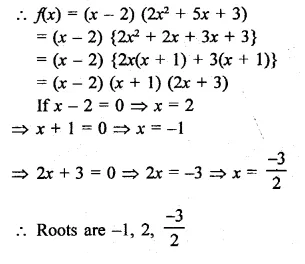
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2 Q7.1