RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4

Other Exercises

Question 1.
Give the geometric representations of the following equations.
(a) on the number line
(b) on the cartesian plane.
(i) x – 2
(ii) y + 3 = 0
(iii) y = 3
(iv) 2x + 9 = 0
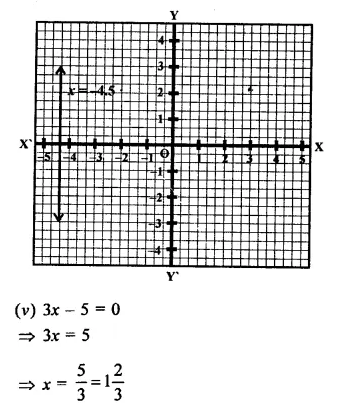
(v) 3x – 5 = 0
Solution:
(i) x = 2
(i) on the number line
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q1.1
(ii) x = 2 is a line parallel to 7-axis at a distance of 2 units to right of y-axis.
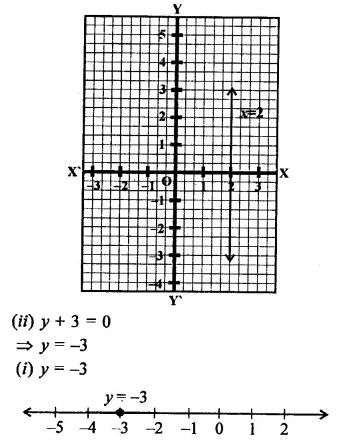
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q1.2
(ii) y = -3 is a line parallel to x-axis at a distance of 3 units below x-axis.
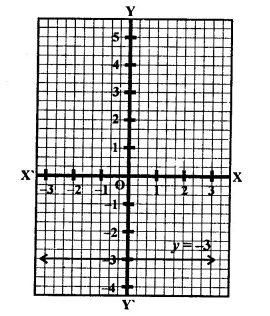
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q1.3
(iii) y = 3
(i) y = 3
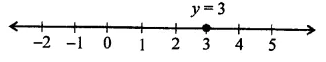
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q1.4
(ii) y = 3 is a line parallel to x-axis at a distance of 3 units above x-axis.
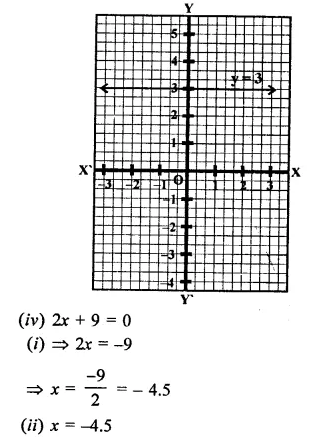
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q1.5
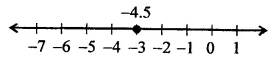
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q1.6
x = -4.5 is a line parallel to 7-axis at a distance of 4.5 units to left of y-axis.
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q1.7
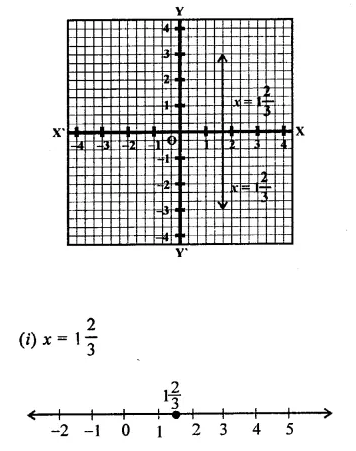
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q1.8
(ii) x = 1\(\frac { 2 }{ 3 }\) is a line parallel to y-axis at a  distance of 1\(\frac { 2 }{ 3 }\) unit to right side of y-axis.

Question 2.
Give the geometrical representation of 2x + 13 = 0 as an equation in
(i) One variable
(ii) Two variables
Solution:
(i) In one variable,
2x + 13 = 0
⇒ 2x = – 13
⇒ x = \(\frac { -13 }{ 2 }\)
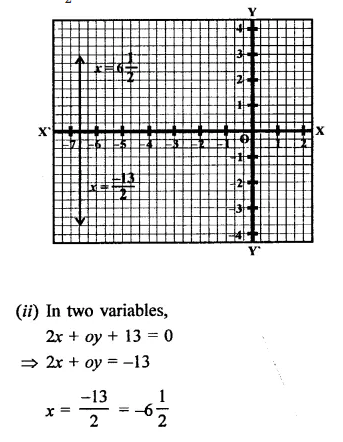
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q2.1
is a line parallel to y-axis at a distance of -6 \(\frac { 1 }{ 2 }\) units on the left side of y-axis.

Question 3.
Solve the equation 3x + 2 = x -8, and represent on
(i) the number line
(ii) the Cartesian plane.
Solution:
3x + 2 = x – 8
⇒  3x – x = -8 – 2
⇒  2x = -10
⇒  x = \(\frac { -10 }{ 2 }\) = -5
(i) on the number line s = -5
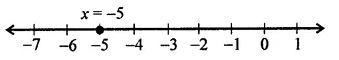
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q3.1
(ii) x = -5 is a line parallel to  y-axis at a distance of 5 knot’s left of y-axis.
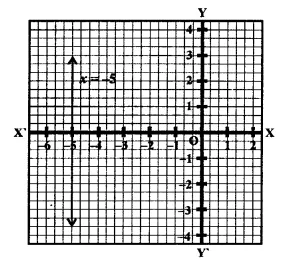
RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 Q3.2

Question 4.
Write the equal of the line that is parallel to x-axis and passing through the points.
(i) (0, 3)                     
(ii)  (0, -4)
(iii) (2, -5)                     
(iv)    (3, 4)
Solution:
∵  A line parallel to x-axis will be of the type y = a
∴ (i) y = 3
(ii) y = -4
(iii) y = -5 and y = 4 are equations of the lines parallel to x-axis

Question 5.
Write the equation of the line that is parallel to y-axis and passing through the points.
(i) (4, 0)                      
(ii) (-2, 0)
(iii) (3, 5)                    
(iv) (-4, -3)
Solution:
∵  A line parallel to y-axis will be of the type x = a
∴  (i) x = 4, (ii)  x = -2, x = 3 and x = -4 are the equations of the lines parallel to y-axis.

Hope given RD Sharma Class 9 Solutions Chapter 7 Introduction to Euclid’s Geometry Ex 7.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.