RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers MCQS

RS Aggarwal Class 10 Solutions Chapter 1 Real Numbers MCQS

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQS.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1A
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1B
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1C
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1D
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Ex 1E
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQs
• RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers Test Yourself

Choose the correct answer in each of the following questions.
Question 1.
Solution:
(b) We know that HCF of two co-prime number is 1
HCF of 14, 35 is 7
HCF of 18, 25 is 1
HCF of 31, 93 is 31
HCF of 32, 60 is 4
Required co-prime number is (18, 25)

Question 2.
Solution:
(b) a = (2² x 3³ x 5⁴), b = (2³ x 3² x 5)
HCF = 2² x 3² x 5 = 2 x 2 x 3 x 3 x 5 = 180

Question 3.
Solution:
(c) HCF of 2³ x 3² x 5, 2² x 3³ x 5², 2⁴ x 3 x 5³ x 7
HCF = 2² x 3 x 5 = 2 x 2 x 3 x 5 = 60

Question 4.
Solution:
(d) LCM of 2³ x 3 x 5, 2⁴ x 5 x 7 = 2⁴ x 3 x 5 x 7
=2 x 2 x 2 x 2 x 3 x 5 x 7
= 1680

Question 5.
Solution:
(d) HCF of two numbers = 27
LCM = 162
One number = 54

Question 6.
Solution:
(c) Product of two numbers = 1600
HCF = 5

Question 7.
Solution:
(c) Largest number that divides each one of 1152 and 1664
HCF of 1152 and 1664 =128

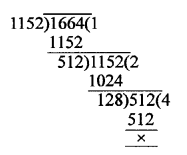
Question 8.
Solution:
(a) Largest number that divides 70 and 125 leaving remainders as 5 and 8 respectively.
Required number = 70 – 5 = 65
and 125 – 8= 117
HCF of 65, 117 = 13

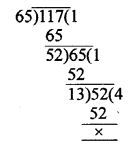
Question 9.
Solution:
(b) Largest number that divides 245 and 1029 leaving remainder as 5 in each case. .
Required number = 245 – 5 = 240 and 1029 – 5 = 1024
Now, HCF of 240 and 1020 = 16

Question 10.
Solution:
(d)

Question 11.
Solution:
(c) In a = bq + r
r must satisfy i.e. 0 ≤ r < b

Question 12.
Solution:
(d) Let the given number when divided by 143 gives q as quotient and 31 as remainder.
Number = 143q + 31
= (13 x 11) q + 31
= 13 x 11 q+ 13 x 2 + 5
= 13 (110 + 2) + 5
The number where divided by 73, gives 5 as remainder.

Question 13.
Solution:
(d) 3.141141114… is irrational because it is non terminating non-repeating.

Question 14.
Solution:
(c) π is an irrational number.

Question 15.
Solution:
(b) \(2.\bar { 35 }\) is a rational number as it is non-terminating repeating decimal.

Question 16.
Solution:
(c) 2.13113111311113… is an irrational number.
It is non-terminating non-repeating decimal.

Question 17.
Solution:
(b) 3.24636363…
= \(3.24\bar { 63 }\)
It is non-terminating repeating decimal.
It is a rational number.

Question 18.
Solution:
(c) \(\frac { 2027 }{ 625 }\) = \(\frac { 2027 }{ { 5 }^{ 4 } }\) is a rational because it has terminating decimal as q = 5⁴ which is in form of 2^m x 5ⁿ.

Question 19.
Solution:
(b)

Question 20.
Solution:
(d)

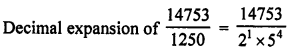
Question 21.
Solution:
(b) 1.732 is a rational number.
As it is terminating decimal.

Question 22.
Solution:
(a) Least prime factor of a positive integer a is 3 and b is 5
2 is neither a factor of a nor of b
a and b are odd
Then (a + b) = even
(Sum of two odd numbers is even)
(a + b) is divisible by 2
Which is the least prime factor.

Question 23.
Solution:
(b) √2 is an irrational number.

Question 24.
Solution:
(c)

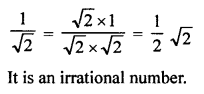
Question 25.
Solution:
(c) 2 + √2 is an irrational number as sum of a rational and an irrational is an irrational

Question 26.
Solution:
(c) LCM of 1 to 10 = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Hope given RS Aggarwal Solutions Class 10 Chapter 1 Real Numbers MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.