RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11A

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Question 1.
Solution:
(i) 9, 15, 21, 27, …
Here, 15 – 9 = 6,
21 – 15 = 6,
27 – 21 = 6
d = 6 and a = 9
Next term = 27 + 6 = 33
(ii) 11, 6, 1, -4, …
Here, 6 – 11 = -5,
1 – 6 = -5,
-4 – 1 = -5
d = -5 and a = 11
Next term = -4 – 5 = -9

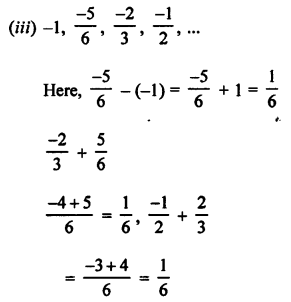
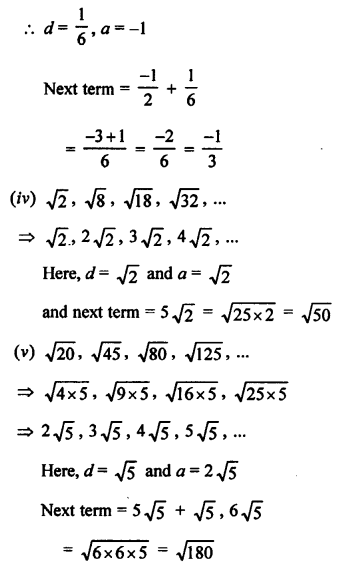
Question 2.
Solution:
(i) AP is 9, 13, 17, 21, ……
Here, a = 9, d = 13 – 9 = 4

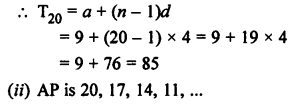
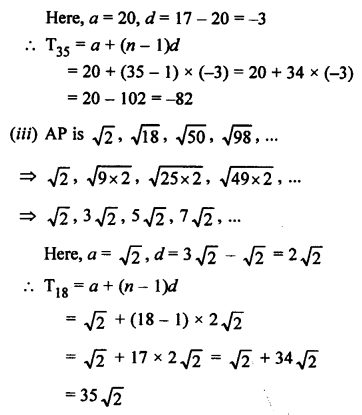
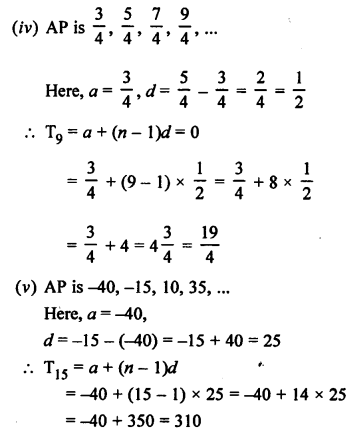
Question 3.
Solution:

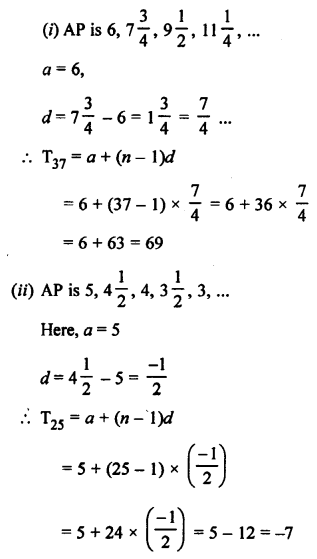
Question 4.
Solution:
If the terms are in AP, then
a₂ – a₁ = a₃ – a₂ = …….
a₂ = 3p + 1
a₁ = 2p – 1
a₃ = 11
⇒ (3p + 1) – (2p – 1) = 11 – (3p + 1)
⇒ 3p + 1 – 2p + 1 = 11 – 3p – 1
⇒ p + 2 = 10 – 3p
⇒ 4p = 8
⇒ p = 2
Then for p = 2, these terms are in AP.

Question 5.
Solution:
(i) AP is 5, 11, 17, 23, ……
Here, a = 5, d = 11 – 5 = 6
T_n = a (n – 1)d = 5 + (n – 1) x 6 = 5 + 6n – 6 = (6n – 1)
(ii) AP is 16, 9, 2, -5, ……
Here, a = 16 d = 9 – 16 = -7
T_n = a + (n – 1)d = 16 + (n – 1) (-7)
= 16 – 7n + 7 = (23 – 7n)

Question 6.
Solution:
nth term = 4n – 10
Substituting the value of 1, 2, 3, 4, …, we get
4n – 10
= 4 x 1 – 10 = 4 – 10 = -6
= 4 x 2 – 10 = 8 – 10 = -2
= 4 x 3 – 10 = 12 – 10 = 2
= 4 x 4 – 10 = 16 – 10 = 6
We see that -6, -2, 2, 6,… are in AP
(i) Whose first term = -6
(ii) Common difference = -2 – (-6) = -2 + 6 = 4
(iii) 16th term = 4 x 16 – 10 = 64 – 10 = 54

The common difference calculator takes the input values of sequence and difference and shows you the actual results.

Question 7.
Solution:
In AP 6, 10, 14, 18,…, 174
Here, a = 6, d= 10 – 6 = 4
nth or l = 174
T_n = a + (n – 1)d
⇒ 174 = 6 + (n – 1) x 4
⇒ 174 – 6 = (n – 1) x 4
⇒ n – 1 = \(\frac { 168 }{ 4 }\) = 42
n = 42 + 1 = 43
Hence, there are 43 terms in the given AP.

Question 8.
Solution:
In AP 41, 38, 35,…, 8
a = 41, d = 38 – 41 = -3, l = 8
Let l be the nth term
l = T_n = a + (n – 1) d
⇒ 8 = 41 + (n – 1)(-3)
⇒ 8 – 41 = (n – 1)(-3)
⇒ n – 1 = 11
⇒ n = 11 + 1 = 12
There are 12 terms in the given AP.

Question 9.
Solution:
the AP is 8, 15\(\frac { 1 }{ 2 }\) , 13, …, -47

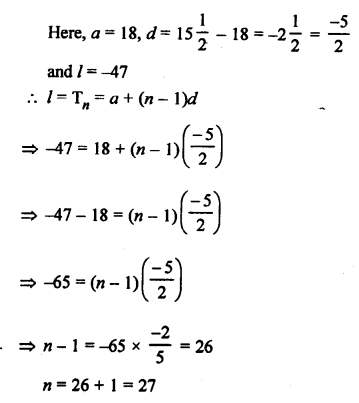
There are 27 terms in the given AP.

Question 10.
Solution:
Let 88 be the nth term
Now, in AP 3, 8, 13, 18, …
a = 3, d = 8 – 3 = 5
T_n = a + (n – 1) d
88 = 3 + (n – 1)(5)
⇒ 88 – 3 = (n – 1) x 5
⇒ \(\frac { 88 }{ 5 }\) = n – 1
⇒ 17 = n – 1
n= 17 + 1 = 18
88 is the 18th term.

Question 11.
Solution:
In the AP 72, 68, 64, 60, …..
Let 0 be the nth term
Here, a = 72, d = 68 – 72 = -4
T_n = a + (n – 1)d
0 = 72 + (n – 1)(-4)
⇒ -72 = -4(n – 1)
⇒ n – 1 = 18
⇒ n = 18 + 1 = 19
0 is the 19th term.

Question 12.
Solution:

n = 13 + 1 = 14
3 is the 14th term.

Question 13.
Solution:
In the AP 21, 18, 15, ……
Let -81 is the nth term
a = 21, d = 18 – 21 = -3
T_n = a + (n – 1)d
⇒ -81 = 21 + (n – 1)(-3)
⇒ -81 – 21 = (n – 1)(-3)
⇒ -102 = (n – 1)(-3)
⇒ n – 1 = 34
n = 34 + 1 = 35
-81 is the 35th term

Question 14.
Solution:
In the given AP 3, 8, 13, 18,…
a = 3, d = 8 – 3 = 5
T₂₀ = a + (n – 1)d = 3 + (20 – 1) x 5 = 3 + 19 x 5 = 3 + 95 = 98
The required term = 98 + 55 = 153
Let 153 be the nth term, then
T_n = a + (n – 1)d
⇒ 153 = 3 + (n – 1) x 5
⇒ 153 – 3 = 5(n – 1)
⇒ 150 = 5(n – 1)
⇒ n – 1 = 30
⇒ n = 30 + 1 = 31
Required term will be 31st term.

Question 15.
Solution:
AP is 5, 15, 25,…
a = 5, d = 15 – 5 = 10
T₃₁ = a + (n – 1)d = 5 + (31 – 1) x 10 = 5 + 30 x 10 = 5 + 300 = 305
Now the required term = 305 + 130 = 435
Let 435 be the nth term, then
T_n = a + (n – 1)d
⇒ 435 = 5 + (n – 1)10
⇒ 435 – 5 = (n – 1)10
⇒ n – 1 = 43
⇒ n = 43 + 1 = 44
The required term will be 44th term.

Question 16.
Solution:
Let a be the first term and d be the common difference, then

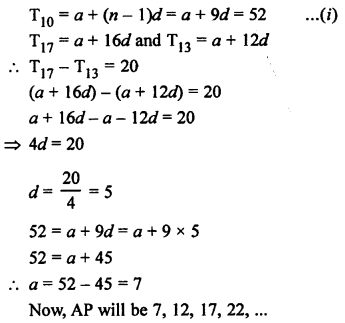
Question 17.
Solution:

T₁₆ = 6 + (16 – 1)7 = 6+ 15 x 7 = 6 + 105 = 111

Question 18.
Solution:
AP is 10, 7, 4, …, (-62)
a = 10, d = 7 – 10 = -3, l = -62
l = T_n = a + (n – 1)d
⇒ -62 = 10 + (n – 1) x (-3)
⇒ -62 – 10 = -3(n- 1)
-72 = -3(n – 1)
n = 24 + 1 = 25
Middle term = \(\frac { 25 + 1 }{ 2 }\) th = 13th term
T₁₃ = 10 + (13 – 1)(-3) = 10+ 12 x (-3)= 10 – 36 = -26

Question 19.
Solution:

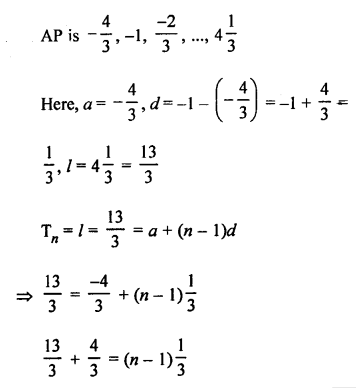
Question 20.
Solution:
AP is 7, 10, 13,…, 184
a = 7, d = 10 – 7 = 3, l = 184
nth term from the end = l – (n – 1)d
8th term from the end = 184 – (8 – 1) x 3 = 184 – 7 x 3 = 184 – 21 = 163

Question 21.
Solution:
AP is 17, 14, 11, …,(-40)
Here, a = 17, d = 14 – 17 = -3, l = -40
6th term from the end = l – (n – 1)d
= -40 – (6 – 1) x (-3)
= -40 – [5 x (-3)]
= -40 + 15
= -25

Question 22.
Solution:
Let 184 be the nth term of the AP
3, 7, 11, 15, …
Here, a = 3, d = 7 – 3 = 4
T_n = a + (n – 1)d
⇒ 184 = 3 + (n – 1) x 4
⇒ 184 – 3 = (n – 1) x 4
⇒ \(\frac { 181 }{ 4 }\) = n – 1
⇒ n = \(\frac { 181 }{ 4 }\) + 1 = \(\frac { 185 }{ 4 }\) = 46\(\frac { 1 }{ 4 }\)
Which is in fraction.
184 is not a term of the given AP.

Question 23.
Solution:
Let -150 be the nth term of the AP
11, 8, 5, 2,…

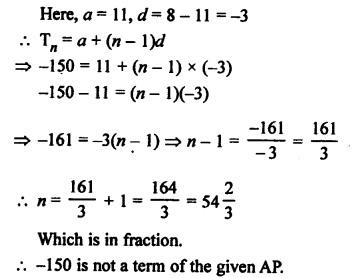
Question 24.
Solution:
Let nth of the AP 121, 117, 113,… is negative

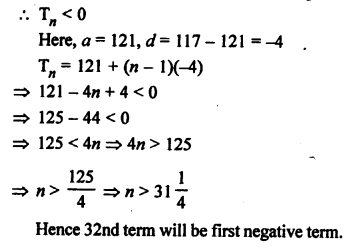
Question 25.
Solution:

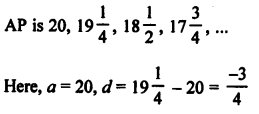
Question 26.
Solution:
Let a be the first term and d be the common difference of an AP
T_n = a + (n – 1)d
T₇ = a + (7 – 1)d = a + 6d = -4 …(i)
T₁₃ = a + 12d = -16 …..(ii)
Subtracting (i) from (ii),
6d = -16 – (-4) = -16 + 4 = -12
From (i), a + 6d = -4
a + (-12) = -4
⇒ a = -4 + 12 = 8
a = 8, d = -2
AP will be 8, 6, 4, 2, 0, ……

Question 27.
Solution:
Let a be the first term and d be the common difference of an AP.
T₄ = a + (n- 1)d = a + (4 – 1)d = a + 3d
a + 3d = 0 ⇒ a = -3d
Similarly,
T₂₅ = a + 24d and T₁₁ = a + 10d = -3d + 24d = 21d
It is clear that T₂₅ = 3 x T₁₁

Question 28.
Solution:
Given, a₆ = 0
⇒ a + 5d = 0
⇒ a = -5 d
Now, a₁₅ = a + (n – 1 )d
= a + (15 – 1)d = -5d + 14d = 9d
and a₃₃ = a + (n – 1 )d = a + (33 – 1)d = -5d + 32d = 27d
Now, a₃₃ : a₁₂
⇒ 27d : 9d
⇒ 3 : 1
a₃₃ = 3 x a₁₅

Question 29.
Solution:
Let a be the first term and d be the common difference of an AP.
T_n = a + (n – 1)d
T₄ = a + (4 – 1)d = a + 3d
a + 3d = 11 …(i)
Now, T₅ = a + 4d
and T₇ = a + 6d
Adding, we get T₅ + T₇ = a + 4d + a + 6d = 2a + 10d
2a + 10d = 34
⇒ a + 5d = 17 …(ii)
Subtracting (i) from (ii),
2d = 17 – 11 = 6
⇒ d = 3
Hence, common difference = 3

Question 30.
Solution:
Let a be the first term and d be the common difference of an AP.

Question 31.
Solution:
Let a be the first term and d be the common difference, then

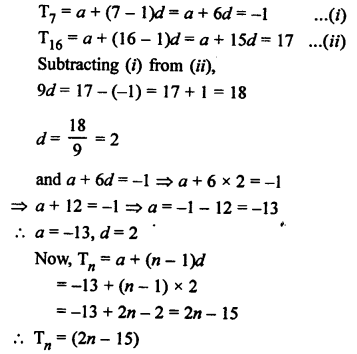
Question 32.
Solution:
In an AP,
Let a be the first term and d be the common difference, then

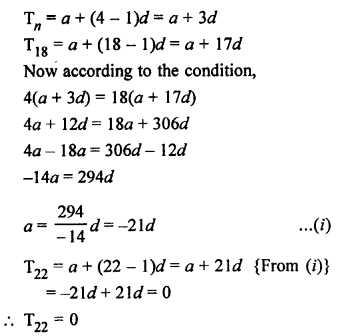
Question 33.
Solution:
Let a be the first term and d be the common difference in an AP, then

Question 34.
Solution:
In an AP,
Let d be the common difference,
First term (a) = 5
Sum of first 4 terms
= a + a + d + a + 2d + a + 3d = 4a + 6d
Sum of next 4 terms
= a + 4d + a + 5d + a + 6d + a + 7d = 4a + 22d
According to the condition,

Question 35.
Solution:
Let a be the first term and d be the common difference in an AP, then

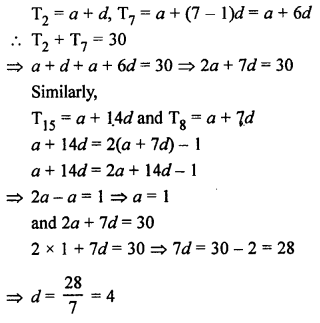
a = 1, d = 4
AP = 1, 5, 9, 13, 17, …

Question 36.
Solution:
In AP 63, 65, 67, …..

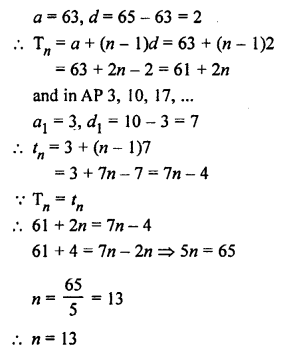
Question 37.
Solution:
Let first term of AP = a
and common difference = d

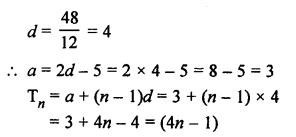
Question 38.
Solution:
Let a be the first term and d be the common difference, then

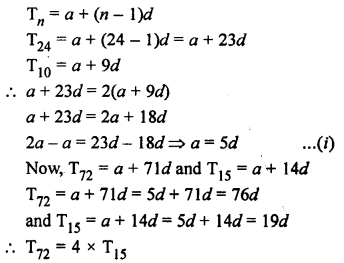
Question 39.
Solution:
Let a be the first term and d be the common difference, then

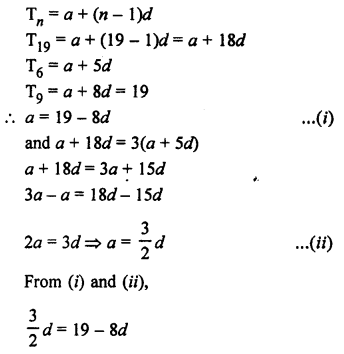
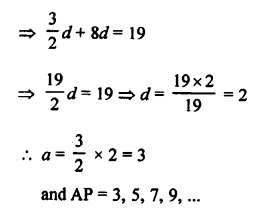
Question 40.
Solution:
Let a be the first term and d be the common difference, then

Question 41.
Solution:
Let a be the first term, d be the common difference, then

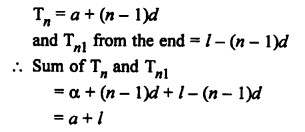
Question 42.
Solution:
Two-digit numbers are 10 to 99 and two digit numbers divisible by 6 will be
12, 18, 24, 30, …, 96

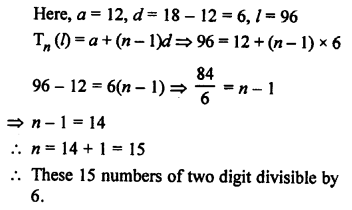
Question 43.
Solution:
Two digit numbers are 10 to 99 and
Two digit numbers which are divisible by 3 are
12, 15, 18, 21, 24, … 99

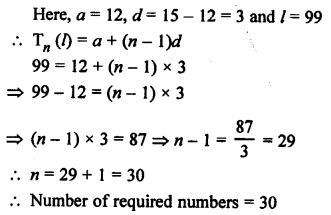
Question 44.
Solution:
Three digit numbers are 100 to 999 and numbers divisible by 9 will be
108, 117, 126, 999

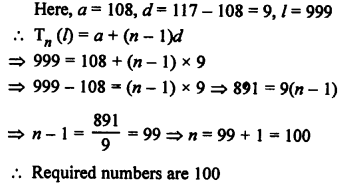
Question 45.
Solution:
Numbers between 101 and 999 which are divisible both by 2 and 5 will be
110, 120, 130,…, 990

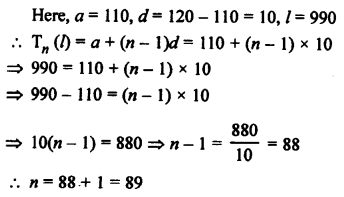
Question 46.
Solution:
Let number of from a rows are in the flower bed, then

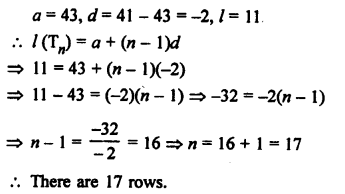
Question 47.
Solution:
Total amount = ₹ 2800
and number of prizes = 4
Let first prize = ₹ a
Then second prize = ₹ a – 200
Third prize = a – 200 – 200 = a – 400
and fourth prize = a – 400 – 200 = a – 600
But sum of there 4 prizes are ₹ 2800
a + a – 200 + a – 400 + a – 600 = ₹ 2800
⇒ 4a – 1200 = 2800
⇒ 4a = 2800 + 1200 = 4000
⇒ a = 1000
First prize = ₹ 1000
Second prize = ₹ 1000 – 200 = ₹ 800
Third prize = ₹ 800 – 200 = ₹ 600
and fourth prize = ₹ 600 – 200 = ₹ 400

Question 48.
Solution:
The first term between 200 and 500 divisible by 8 is 208, and last term is 496.
So, first term (a) = 208
Common difference (d) = 8
Now, an = a + (n – 1 )d
⇒ 496 = 208 + (n – 1) x 8
⇒ (n – 1) = \(\frac { 288 }{ 8 }\)
⇒ n – 1 = 36
⇒ n = 36 + 1 = 37
Hence, there are 37 integers between 200 and 500 which are divisible by 8.

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.