RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11B
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
- RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
- RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
- RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
- RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS
Question 1.
Solution:
(3k – 2), (4k – 6) and (k + 2) are three consecutive terms of an AP.
(4k – 6) – (3k – 2) = (k + 2) – (4k – 6)
⇒ 2(4k – 6) = (k + 2) + (3k – 2)
⇒ 8k – 12 = 4k + 0
⇒ 8k – 4k = 0 + 12
⇒ 4k = 12
k = 3
Question 2.
Solution:
(5x + 2), (4x – 1) and (x + 2) are in AP.
(4x – 1) – (5x + 2) = (x + 2) – (4x – 1)
⇒ 2(4x – 1) = (x + 2) + (5x + 2)
⇒ 8x – 2 = 6x + 2 + 2
⇒ 8x – 2 = 6x + 4
⇒ 8x – 6x = 4 + 2
⇒ 2x = 6
x = 3
Question 3.
Solution:
(3y – 1), (3y + 5) and (5y + 1) are the three consecutive terms of an AP.
(3y + 5) – (3y – 1) – (5y + 1) – (3y + 5)
⇒ 2(3y + 5) = 5y + 1 + 3y – 1
⇒ 6y + 10 = 8y
⇒ 8y – 6y = 10
⇒ 2y = 10
⇒ y = 5
y = 5
Question 4.
Solution:
(x + 2), 2x, (2x + 3) are three consecutive terms of an AP.
2x – (x + 2) = (2x + 3) – 2x
⇒ 2x – x – 2 = 2x + 3 – 2x
⇒ x – 2 = 3
⇒ x = 2 + 3 = 5
x = 5
Question 5.
Solution:
(a – b)², (a² + b²) and (a + b)² will be in AP.
If (a² + b²) – (a – b)² = (a + b)² – (a² + b²)
If (a² + b²) – (a² + b² – 2ab) = a² + b² + 2ab – a² – b²
2ab = 2ab which is true.
Hence proved.
Question 6.
Solution:
Let the three numbers in AP be
a – d, a, a + d
a – d + a + a + d = 15
⇒ 3a = 15
⇒ a = 5
and (a – d) x a x (a + d) = 80
a(a² – d²) = 80
⇒ 5(5² – d²) = 80
⇒ 25 – d² = 16
⇒ d² = 25 – 16 = 9 = (±3)²
d = ±3
Now, a = 5, d = +3
Numbers are 5 – 3 = 2
5 and 5 + 3 = 8
= (2, 5, 8) or (8, 5, 2)
Question 7.
Solution:
Let the three numbers in AP be a – d, a and a + d
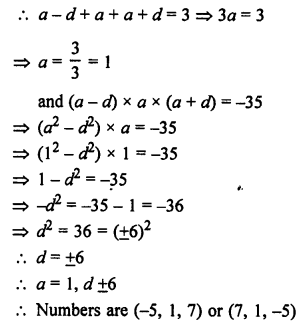
Question 8.
Solution:
Sum of three numbers = 24
Let the three numbers in AP be a – d, a, a + d
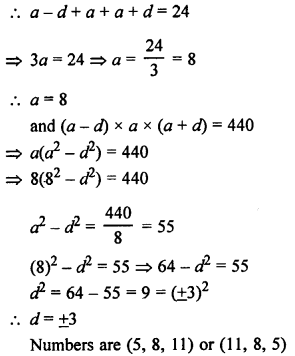
Question 9.
Solution:
Let three consecutive in AP be a – d, a, a + d
a – d + a + a + d = 21
⇒ 3a = 21
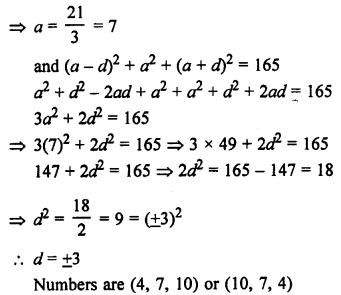
Question 10.
Solution:
Sum of angles of a quadrilateral = 360°
Let d= 10
The first number be a, then the four numbers will be
a, a + 10, a + 20, a + 30
a + a + 10 + a + 20 + a + 30 = 360
4a + 60 = 360
4a = 360 – 60 = 300
Angles will be 75°, 85°, 95°, 105°
Question 11.
Solution:
Let the four numbers in AP be a – 3d, a – d, a + d, a + 3d, then
a – 3d + a – d + a + d + a + 3d = 28
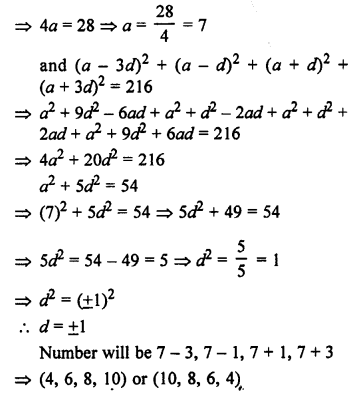
Question 12.
Solution:
Let the four parts of 32 be a – 3d, a – d, a + d, a + 3d
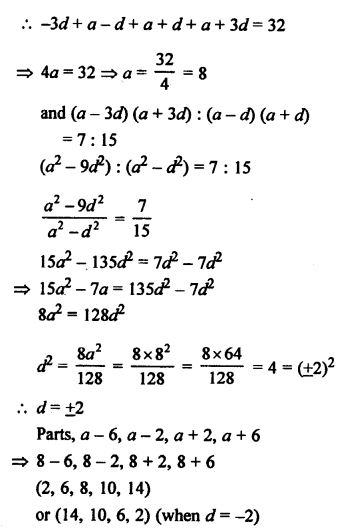
Question 13.
Solution:
Let the three terms be a – d, a, a + d
a – d + a + a + d = 48
⇒ 3a = 48
⇒ a = 16
and (a – d) x a = (a + d) + 12
⇒ a(a – d) = 4 (a + d) + 12
⇒ 16 (16 – d) = 4(16 + d) + 12
⇒ 256 – 16d = 64 + 4d + 12 = 4d + 76
⇒ 256 – 76 = 4d + 16d
⇒ 180 = 20d
⇒ d = 9
Numbers are (16 – 9, 16), (16 + 9) or (7, 16, 25)
Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.