RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11C

RS Aggarwal Class 10 Solutions Chapter 11 Arithmetic Progressions Ex 11C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11A
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11B
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11D
• RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions MCQS

Question 1.
Solution:

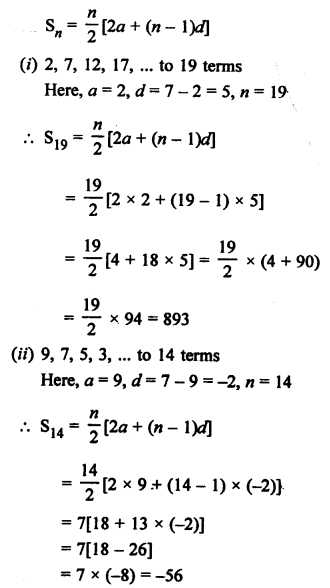
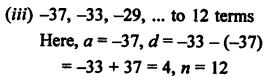
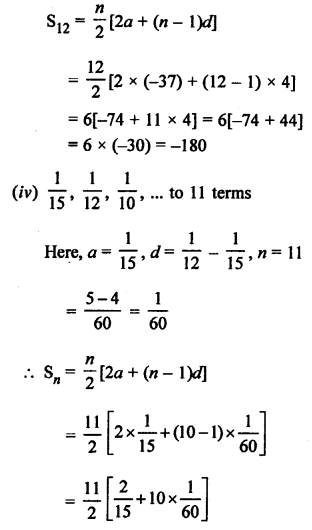
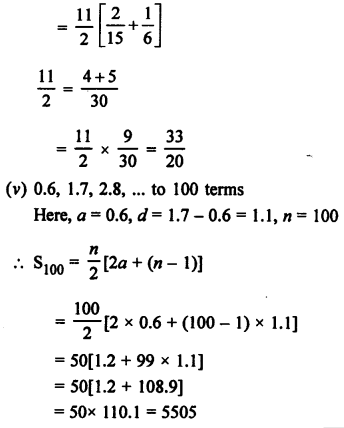
Question 2.
Solution:

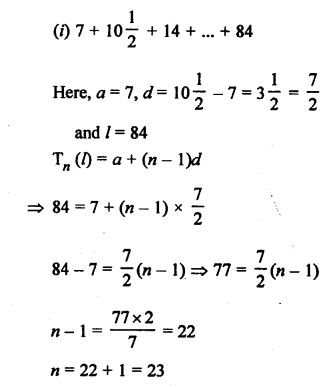
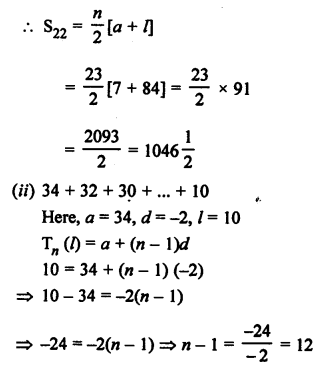
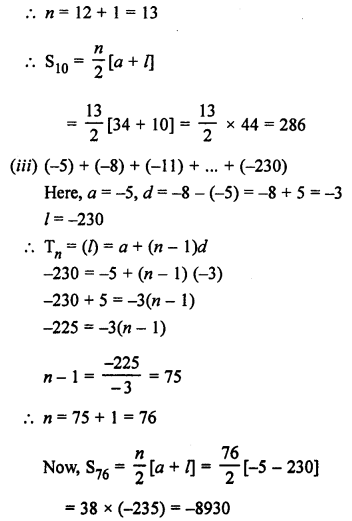
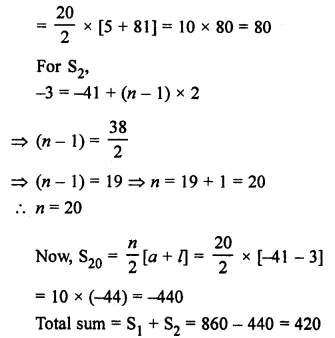
Question 3.
Solution:

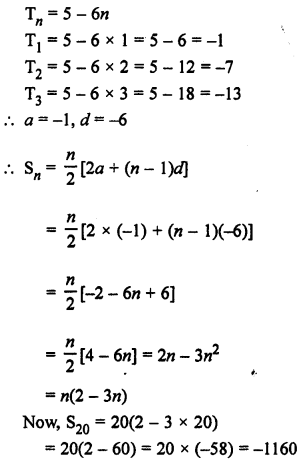
Question 4.
Solution:
S_n = 3n² + 6n

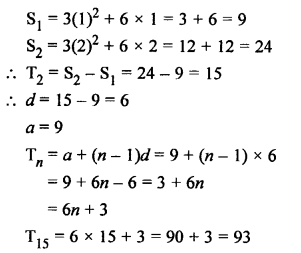
Question 5.
Solution:
S_n = 3n² – n
S₁ = 3(1)² – 1 = 3 – 1 = 2
S₂ = 3(2)² – 2 = 12 – 2 = 10
T₂ = 10 – 2 = 8 and
T₁ = 2
(i) First term = 2
(ii) Common difference = 8 – 2 = 6
T_n = a + (n – 1) d = 2 + (n – 1) x 6
= 2 + 6n – 6 = 6n – 4

Question 6.
Solution:

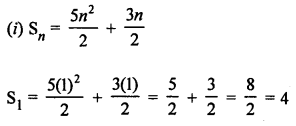
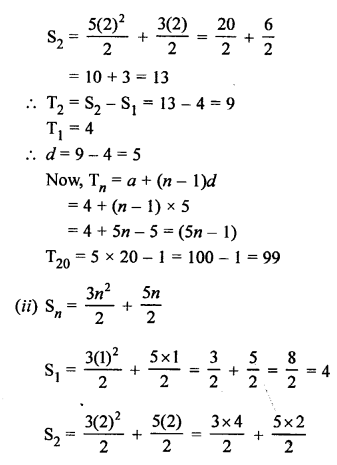
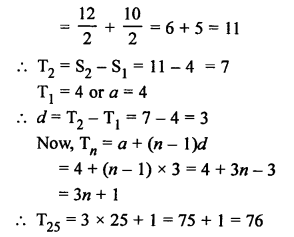
Question 7.
Solution:
Let a be first term and d be the common difference of an AP.
Since, we have,
a_m = a + (m – 1) d = \(\frac { 1 }{ n }\) …(i)

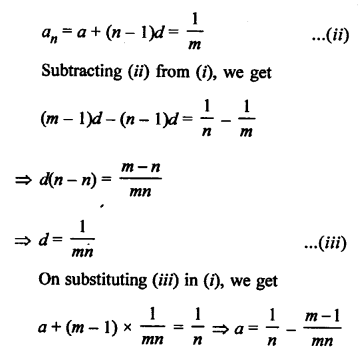
Question 8.
Solution:
AP is 21, 18, 15,…
Here, a = 21,
d = 18 – 21 = -3,
sum = 0
Let number of terms be n, then

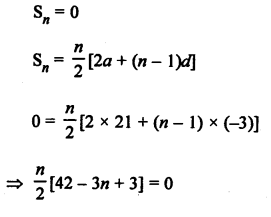
Question 9.
Solution:
AP is 9, 17, 25,…
Here, a = 9, d = 17 – 9 = 8
Sum of terms = 636
Let number of terms be n, then

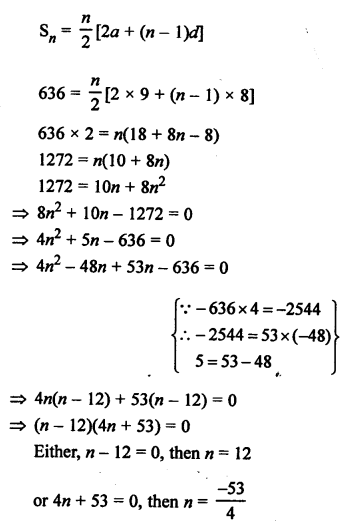
Which is not possible being negative and fraction.
n = 12
Number of terms = 12

Question 10.
Solution:
AP is 63, 60, 57, 54,…
Here, a = 63, d = 60 – 63 = -3 and sum = 693
Let number of terms be n, then

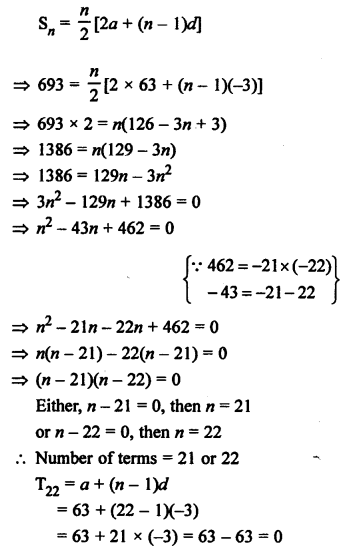
22th term is zero.
There will be no effect on the sum.
Number of terms are 21 or 22.

Question 11.
Solution:

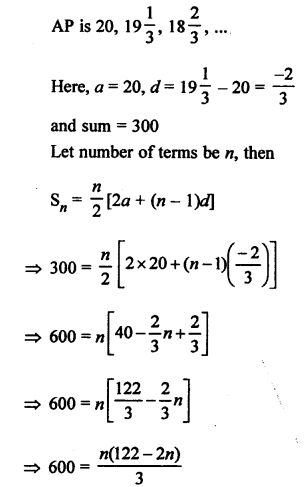
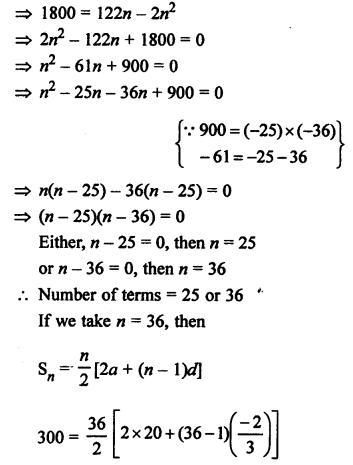
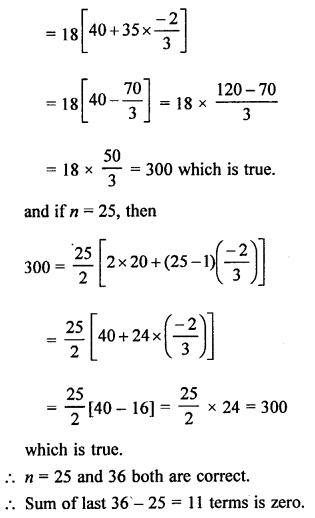
Question 12.
Solution:
Odd numbers between 0 and 50 are 1, 3, 5, 7, 9, …, 49
Here, a = 1, d = 3 – 1 = 2, l = 49

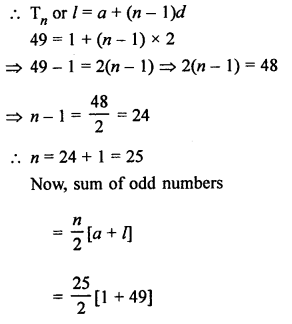
= \(\frac { 25 }{ 2 }\) x 50 = 25 x 25 = 625

Question 13.
Solution:
Numbers between 200 and 400 which are divisible by 7 will be 203, 210, 217,…, 399
Here, a = 203, d = 7, l = 399

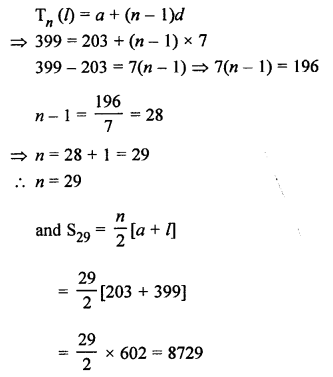
Question 14.
Solution:
First forty positive integers are 0, 1, 2, 3, 4, …
and numbers divisible by 6 will be 6, 12, 18, 24, … to 40 terms
Here, a = 6, d = 12 – 6 = 6, n = 40 .

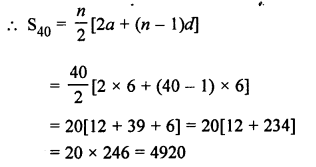
Question 15.
Solution:
First 15 multiples of 8 are 8, 16, 24, 32, … to 15 terms
Here, a = 8, d = 16 – 8 = 8 , n = 15

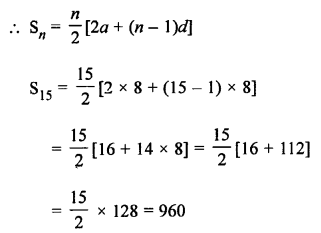
Question 16.
Solution:
Multiples of 9 lying between 300 and 700 = 306, 315, 324, 333, …, 693
Here, a = 306, d = 9, l = 693

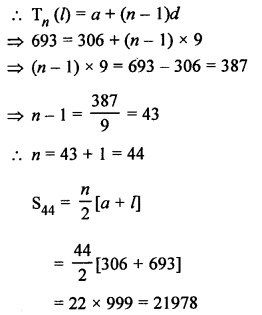
Question 17.
Solution:
Three digit numbers are 100, 101, …, 999
and numbers divisible by 13, will be 104, 117, 130, …, 988
Here, a = 104, d = 13, l = 988
T_n (l) = a + (n – 1) d

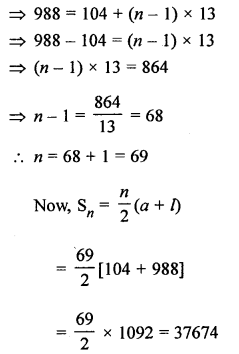
Question 18.
Solution:
Even natural numbers are 2, 4, 6, 8, 10, …
Even natural numbers which are divisible by 5 will be
10, 20, 30, 40, … to 100 terms
Here, a = 10, d = 20 – 10 = 10, n = 100

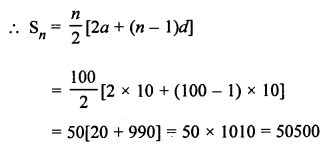
Question 19.
Solution:

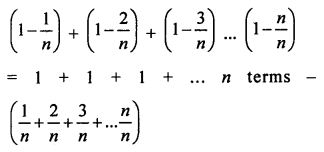
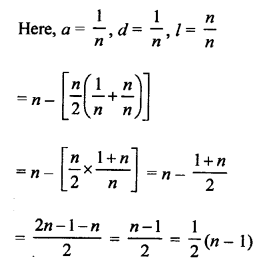
Question 20.
Solution:
Let a be the first term and d be the common difference of the AP, then

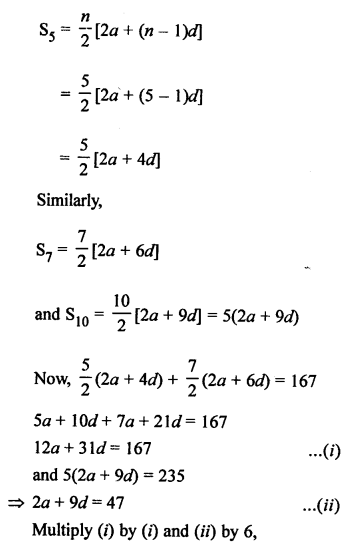
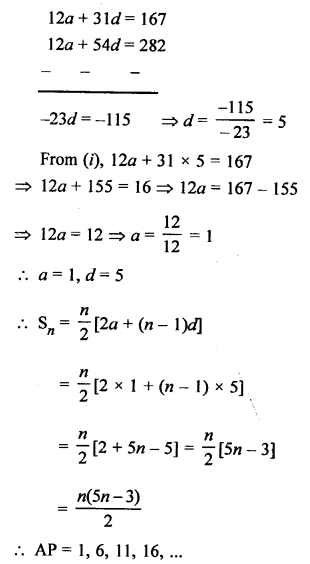
Question 21.
Solution:
Let a be the first term and d be the common difference, then

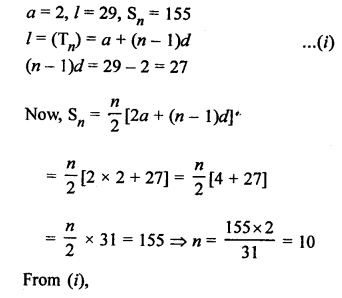
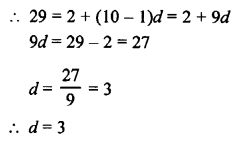
Question 22.
Solution:
Let a be the first term and d be the common difference, then

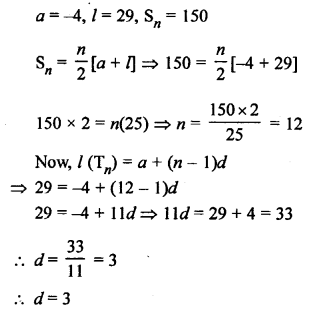
Question 23.
Solution:
In an AP
a = 17, d = 9, l = 350
Let number of terms be n, then

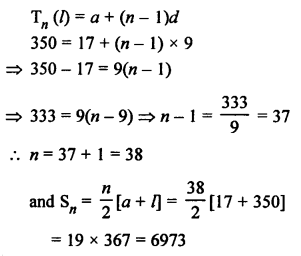
Question 24.
Solution:
Let a be the first term, d be the common difference, then

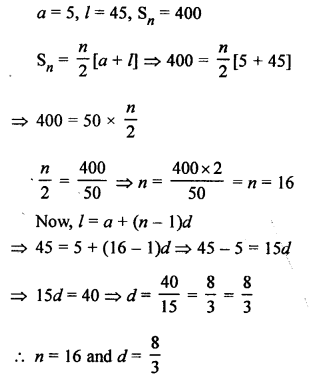
Question 25.
Solution:
In an AP, let a be the first term and d be the common difference, then

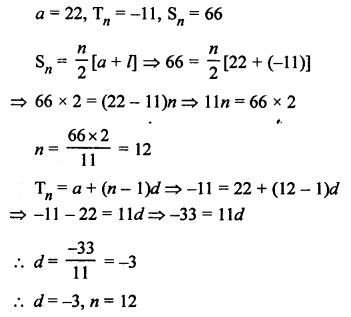
Question 26.
Solution:
Let a be the first term and d be the common difference of an AP, then

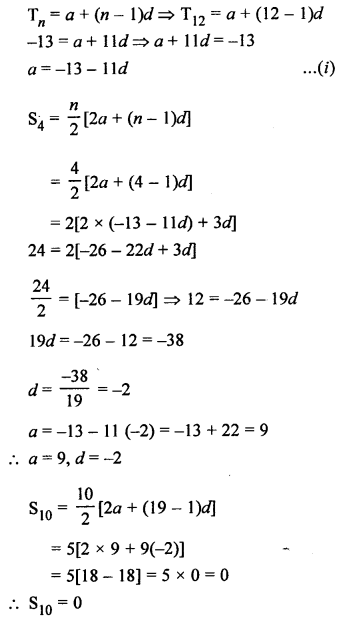
Question 27.
Solution:
Let a be first term and d be the common difference, then

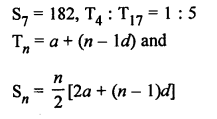
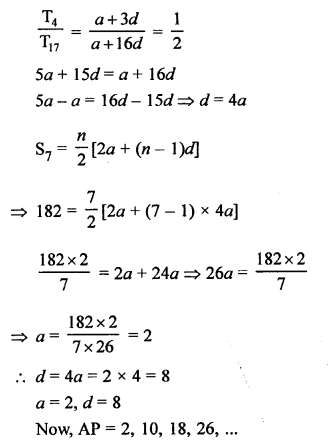
Question 28.
Solution:
Let first term be a and d be the common difference in an AP, then

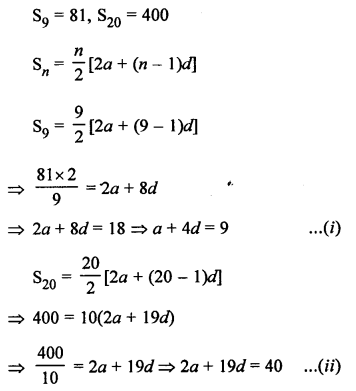
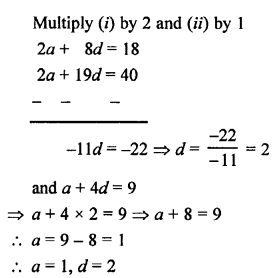
Question 29.
Solution:
Let a be the first term and d be the common difference of an AP, then

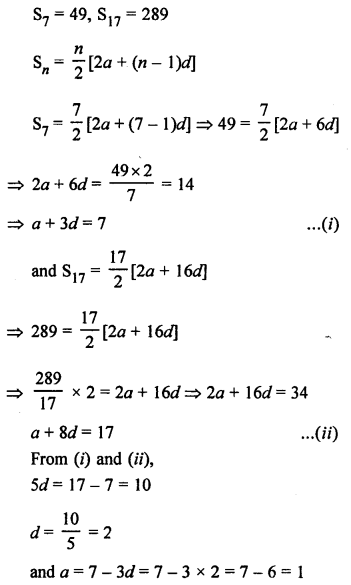
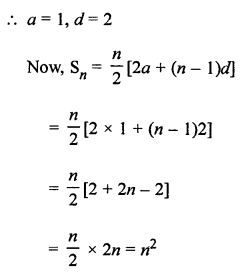
Question 30.
Solution:
Let a₁ and a₂ be the first terms of the two APs and d be the common difference, then
a₁ = 3, a₂ = 8

Question 31.
Solution:
Let a be the first term and d be the common difference, then
S₁₀ = -150

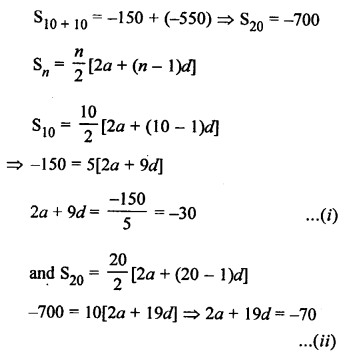
Question 32.
Solution:
Let a be the first term and d be the common difference, then

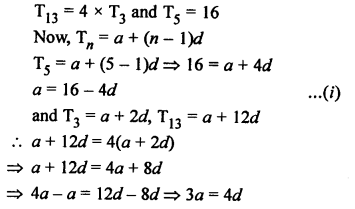
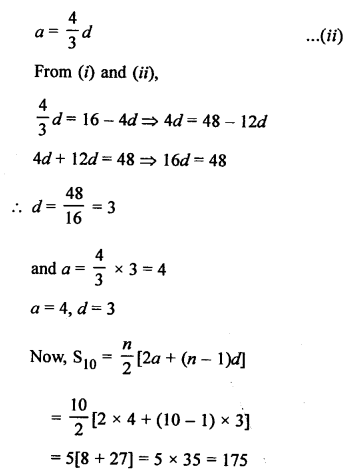
Question 33.
Solution:
Let a be the first term and d be the common difference of an AP, then

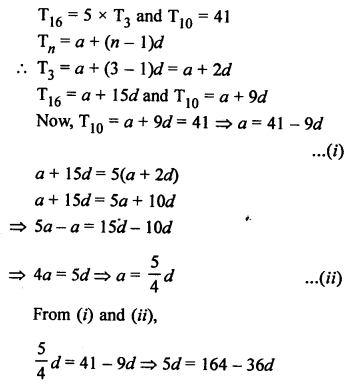
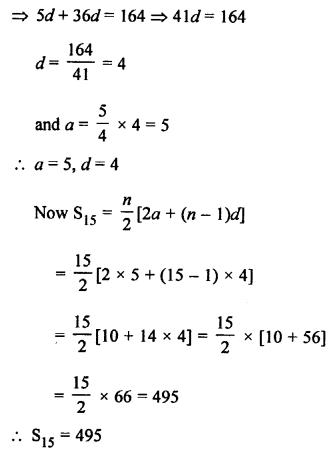
Question 34.
Solution:
(i) AP is 5, 12, 19,… to 50 terms
Here, a = 5, d = 12 – 5 = 7, n = 50

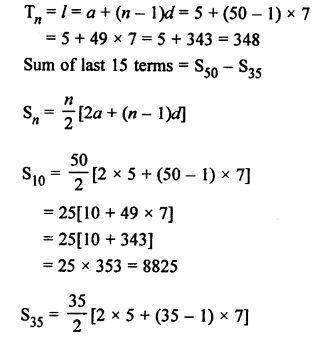
Question 35.
Solution:
Let a₁, a₂ be the first term and d₁, d₂ be common difference of the two AP’s respectively.
Given, ratio of sum of first n terms =

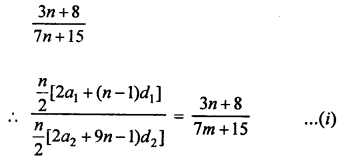
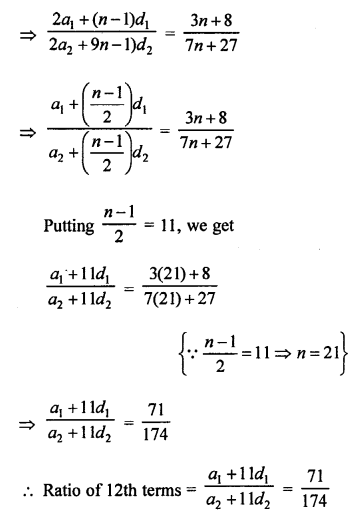
Question 36.
Solution:
Let a be the first term and d be the common difference of an AP.

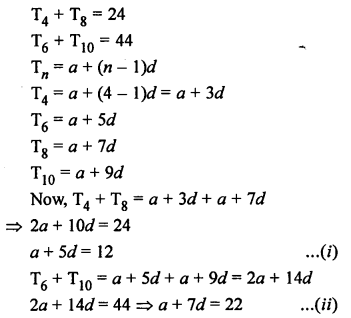
Question 37.
Solution:

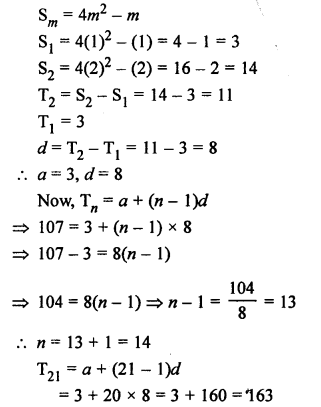
Question 38.
Solution:

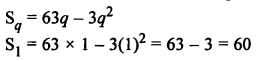
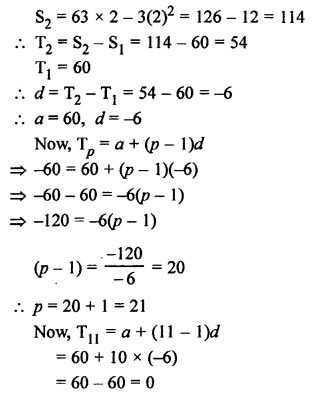
Question 39.
Solution:
AP is -12, -9, -6,…, 21
Here, a = -12, d = -9 – (-12) = -9 + 12 = 3, l = 21

Question 40.
Solution:
S₁₄ = 1505
Let a be the first term and d be the common difference, then
a = 10

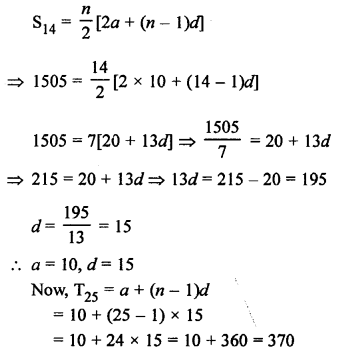
Question 41.
Solution:
Let a be the first term and d be the common difference of an AP, then

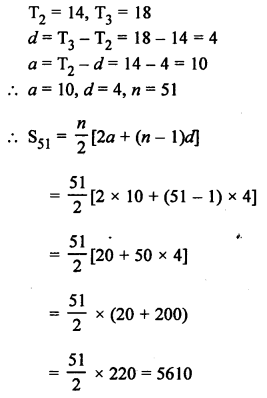
Question 42.
Solution:
In the school, there are 12 classes, class 1 to 12 and each class has two sections.
Each class plants double of the class
i.e. class 1 plants two plant, class 2 plants 4 plants, class 3 plants 6 plants, and so on.
So, total plants will be for each class each sections = 2 + 4 + 6 + 8 … + 24
Here, a = 2, d = 2, l = 24, n = 12

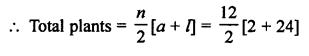
Each class has. two sections.
Plants will also be doubt
i.e. Total plants = 156 x 2 = 312

Question 43.
Solution:
In a potato race,
Bucket is at 5 m from first potato and then the distance between the two potatoes is 3m.
There are 10 potatoes.
The player, pick potato and put it in the bucket one by one.
Total distance in m to be covered, for 1st, 2nd, 3rd, … potato.

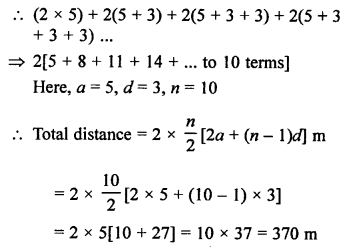
Question 44.
Solution:
Total number of trees = 25
Distance between them = 5 m in a line.
There is a water tank which is 10 m from the first tree.
A gardener waters these plants separately.
Total distance for going and coming back

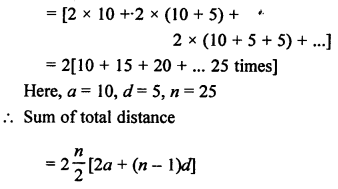
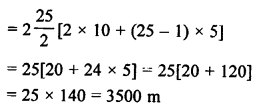
Question 45.
Solution:
Total sum = ₹ 700
Number of cash prizes = 7
Each prize in ₹ 20 less than its preceding prize.
Let first prize = ₹ x
Then second prize = ₹ (x – 20)
Third prize = ₹ (x – 40) and so on.

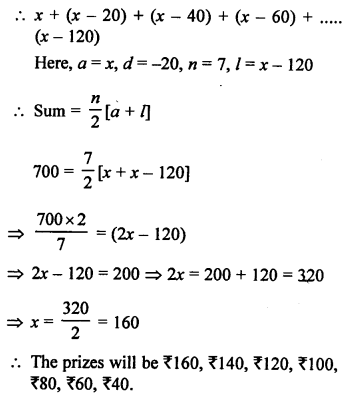
Question 46.
Solution:
Total savings = ₹ 33000
Total period = 10 months
Each month, a man saved ₹ 100 more than its preceding of month.
Let he saves ₹ x in the first month.

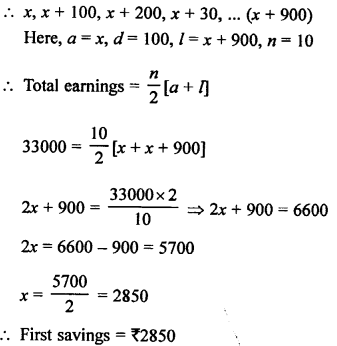
Question 47.
Solution:
Total debt to be paid = ₹ 36000
No. of monthly installments = 40
After paying 30 installments, \(\frac { 1 }{ 3 }\) of his debt left
i.e. ₹ 36000 x \(\frac { 1 }{ 3 }\) = ₹ 12000
and amount paid = ₹ 36000 – ₹ 12000 = ₹ 24000
Monthly installments are in AP.
Let first installment = x
and common difference = d

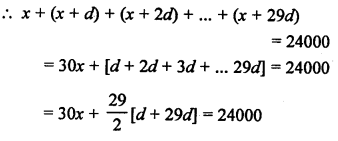
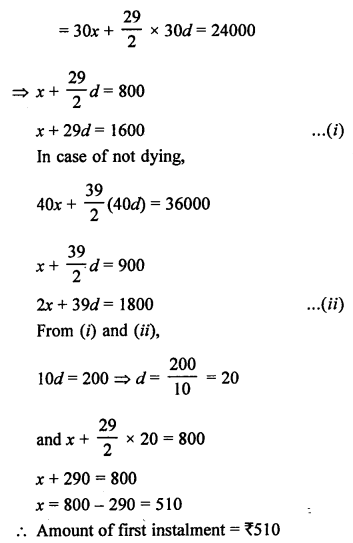
Question 48.
Solution:
A contractor will pay the penalty for not doing the work in time.
For the first day = ₹ 200
For second day = ₹ 250
For third day = ₹ 300 and so on
The work was delayed for 30 days
Total penalty, he paid
200 + 250 + 300 + ….. to 30 terms
Here, a = 200, d = 50, n = 30
Total sum = \(\frac { n }{ 2 }\) [2a + (n – 1) d]
= \(\frac { 30 }{ 2 }\) [2 x 200 + (30 – 1) x 50]
= 15 [400 + 29 x 50]
= 15 [400 + 1450]
= 15 x 1850 = ₹ 27750

Question 49.
Solution:
Child will put 5 rupee on 1st day, 10 rupee (2 x 5 rupee)
on 2nd day, 15 rupee (3 x 5 rupee) on 3rd day etc.
Total saving = 190 coins = 190 x 5 = 950 rupee
The above problem can be written as Arithmetic Progression series
5, 10, 15, 20, ……
with a = 5, d = 5, S_n = 950
Let n be the last day when piggy bank become full.

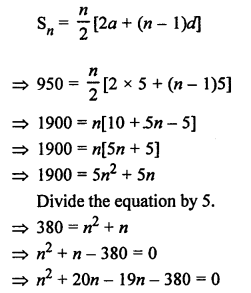
⇒ n (n + 20) – 19 (n + 20) = 0
⇒ (n + 20) (n – 19) = 0
⇒ n + 20 = 0 or n – 19 = 0
⇒ n = -20 or n = 19
cannot be negative, hence n = 19
She can put money for 19 days.
Total saving is 950 rupees.

Hope given RS Aggarwal Solutions Class 10 Chapter 11 Arithmetic Progressions Ex 11C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.