RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4D

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
For the given triangle to be right-angled, the sum of the squares of the two smaller sides must be equal to the square of the largest side.
(i) 9 cm, 16 cm, 18 cm
Longest side = 18
Now (18)² = 324
and (9)² + (16)² = 81 + 256 = 337
324 ≠ 337
It is not a right triangle.
(ii) 1 cm, 24 cm, 25 cm
Here longest side = 25 cm
(25)² = 625
and (7)² x (24)² = 49 + 576 = 625
625 = 625
It is a right triangle
(iii) 1.4 cm, 4.8 cm, 5 cm
Here longest side = 5 cm
(5)² = 25
and (1.4)² + (4.8)² = 1.96 + 23.04 = 25.00 = 25
25 = 25
It is a right triangle
(iv) 1.6 cm, 3.8 cm, 4 cm
Here longest side = 4 cm
(4 )² = 16
and (1.6)² + (3.8)² = 2.56 + 14.44 = 17.00 = 17
16 ≠ 17
It is not a right triangle
(v) (a- 1) cm, 2√a cm, (a + 1) cm
Here longest side = (a + 1) cm
(a + 1)² = a² + 2a + 1
and (a – 1)² + (2 √a )² = a² – 2a + 1 + 4a = a² + 2a + 1
a² + 2a + 1 = a² + 2a + 1
It is a right triangle.

Question 2.
Solution:
A man goes 80 m from O to east side and reaches A, then he goes 150 m due north from A and reaches B.
Join OB.

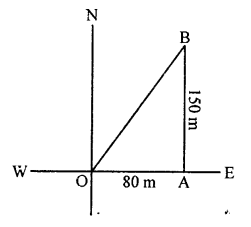
In right ∆OAB,
OB² = OA²+² (Pythagoras Theorem) = (80)² + (150)² = 6400 + 22500 = 28900
⇒ OB = √28900 = 170

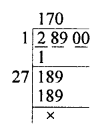
He is 170 m away from the starting point.

Question 3.
Solution:
A man goes 10 m due south from O and reaches A and then 24 m due west from A and reaches B.
Join OB.

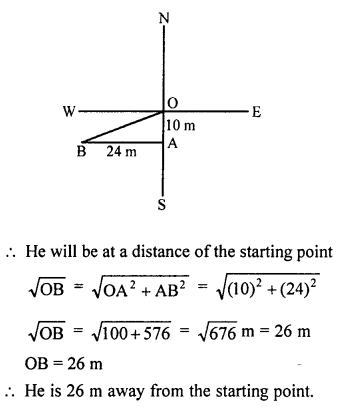
Question 4.
Solution:
Length of a ladder = 13 m
Height of the window = 12 m
Distance between the foot of the ladder and building.
In the figures,

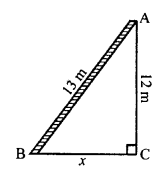
AB is ladder, A is window of building AC
AB² = AC² + BC² (Pythagoras Theorem)
⇒ (13)² = (12)² + x²
⇒ 169 = 144 + x²
⇒ x² = 169 – 144 = 25 = (5)²
x = 5
Hence, distance between foot of ladder and building = 5 m.

Question 5.
Solution:
Let length of ladder AB = x m
Height of window AC = 20 m
and distance between the foot of the ladder and the building (BC) = 15 m

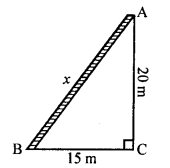
AB² = AC² + BC² (Pythagoras Theorem)
⇒ x² = 20² + 15² = 400 + 225 = 625 = (25)²
x = 25
Length of ladder = 25 m

Question 6.
Solution:
Height of first pole AB = 9 m
and of second pole CD = 14 m

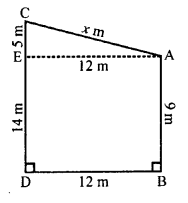
Let distance between their tops CA = x m
From A, draw AE || BD meeting CD at E.
Then EA = DB = 12 m CE = CD – ED = CD – AB = 14-9 = 5 m
In right ∆AEC,
AC² = AE² + CE² = 122 + 52 = 144 + 25 = 169 = (13)²
AC = 13
Distance between their tops = 13 m

Question 7.
Solution:
Height of the pole AB = 18 m
and length of wire AC = 24 m

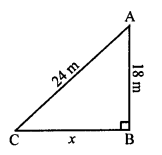
Distance between the base of the pole and other end of the wire
BC = x m (suppose)
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
(24)² = (18)² + x²
⇒ 576 = 324 + x²
⇒ x² = 576 – 324 = 252

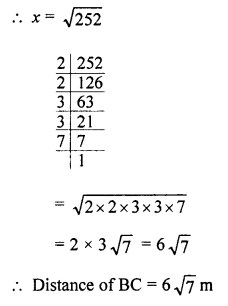
Question 8.

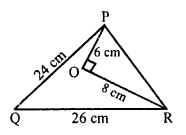
Solution:
In ∆PQR, O is a point in it such that
OP = 6 cm, OR = 8 cm and ∠POR = 90°
PQ = 24 cm, QR = 26 cm
To prove : ∆PQR is a right angled.
In ∆POR, ∠O = 90°
PR² = PO² + OR² = (6)² + (8)² = 36 + 64 = 100 = (10)²
PR = 10
Greatest side QR is 26 cm
QR² = (26)² = 676
and PQ² + PR² = (24)² + (10)² = 576 + 100 = 676
676 = 676
QR² = PQ² + PR²
∆PQR is a right angled triangle and right angle at P.

Question 9.
Solution:
In isosceles ∆ABC, AB = AC = 13 cm
AL is altitude from A to BC
and AL = 5 cm

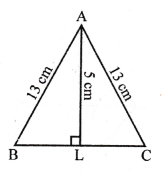
Now, in right ∆ALB
AB² = AL² + BL²
(13)² = (5)² + BL²
⇒ 169 = 25 + BL²
⇒ BL² = 169 – 25 = 144 = (12)²
BL = 12 cm
L is mid point of BC
BC = 2 x BC = 2 x 12 = 24 cm

Question 10.
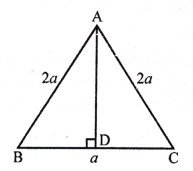
Solution:
In an isosceles ∆ABC in which
AB = AC = 2a units, BC = a units

Question 11.
Solution:
∆ABC is an equilateral triangle
and AB = BC = CA = 2a

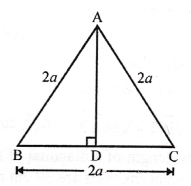
AD ⊥ BC
D is mid point of BC
BD = DC = \(\frac { 1 }{ 2 }\) BC
= \(\frac { 1 }{ 2 }\) x 2a = a
Now, in right ∆ADB,
AB² = AD² + BD² (Pythagoras Theorem)
(2a)² = AD² + a²
⇒ 4a² – a² = AD²
⇒ AD² = 3a² = (√3 a)²
AD = √3 a = a√3 units

Question 12.
Solution:
∆ABC is an equilateral triangle in which
AB = BC = CA = 12 cm

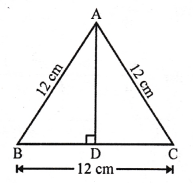
AD ⊥ BC which bisects BC at D
BD = DC = \(\frac { 1 }{ 2 }\) BC = \(\frac { 1 }{ 2 }\) x 12 = 6cm
Now, in right ∆ADB,
AB² = AD² + BD²
⇒ (12)² = AD² + (6)²
⇒ 144 = AD² + 36
AD² = 144 – 36 = 108
AD = √108 = √(36 x 3) = 6√3 cm

Question 13.
Solution:
Let ABCD is a rectangle in which adjacent sides.
AB = 30 cm and BC = 16 cm

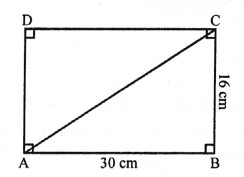
AC is its diagonal.
In right ∆ABC,
AC² = AB² + BC² (Pythagoras Theorem)
= (30)² + (16)² = 900 + 256 = 1156 = (34)²
Diagonal AC = 34 cm

Question 14.
Solution:
ABCD is a rhombus
Its diagonals AC and BD bisect each other at O.

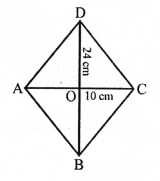
AO = OC = \(\frac { 1 }{ 2 }\) AC.
and BO = OD = \(\frac { 1 }{ 2 }\) BD
BD = 24 cm and AC = 10 cm
BO = \(\frac { 1 }{ 2 }\) x BD = \(\frac { 1 }{ 2 }\) x 24 = 12 cm
AO = \(\frac { 1 }{ 2 }\) x AC = \(\frac { 1 }{ 2 }\) x 10 = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² = (5)² + (12)² = 144 + 25 = 169 = (13)²
AB = 13
Hence, each side of rhombus = 13 cm

Question 15.
Solution:
Given : In ∆ABC, AC > AB.
D is the mid point of BC and AE ⊥ BC.
AD is joined.

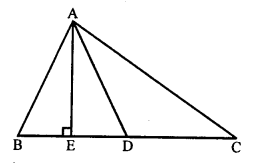
To prove: AB² = AD² – BC x DE + \(\frac { 1 }{ 4 }\) BC2
Proof: In ∆AEB, ∠E = 90°
AB² = AE² + BE² …..(i) (Pythagoras Theorem)
In ∆AED, ∠E = 90°
AD² = AE² + DE²
⇒ AE² = AD² – DE² …..(ii)
Now, substitute eq. (ii) in eq. (i)
AB² = AE² + BE²
AB² = AD² – DE² + BE² [from (ii)]
AB² = (AD² – DE²) + (BD – DE)² [BE = BD – DE²]

Question 16.
Solution:

Question 17.
Solution:
Given : In ∆ABC, D is the mid point of BC, AE ⊥ BC,
BC = a, AC = b, AB = c, ED = x, AD =p and AE =
AD is joined.
To prove :

Question 18.
Solution:
Given : In ∆ABC, AB =AC
BC is produced to D and AD is joined.
To prove : (AD² – AC²) = BD x CD
Construction : Draw AE ⊥ BC.

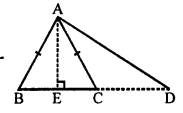
Proof: In ∆ABC,
AB = AC and AE ⊥ BC
BE = EC
Now, in right ∆AED, ∠E = 90°
AD² = AE² + ED² …..(i)
and in right ∆AEC, ∠E = 90°
AC² = AE² + EC² …..(ii)
Now, subtracting (i) and (ii),
AD² – AC² = (AE² + ED²) – (AE² + EC²)
= AE² + ED² – AE² – EC²
= ED² – EC²
= (ED + EC) (ED – EC) (BE = EC proved above)
= BD x CD = BD x CD
AD² – AC² = BD x CD
Hence proved.

Question 19.
Solution:
Given : In ∆ABC, AB = BC and ∠ABC = 90°
∆ACD and ∆ABE are similar to each other.

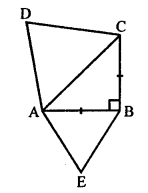
To prove : Ratio between area ∆ABE and area ∆ACD.
Proof: Let AB = BC = x
Now, in right ∆ABC,
⇒ AC² = AB² + BC² = AB² + AB² = 2AB² = 2x²
∆ABE and ∆ACD are similar

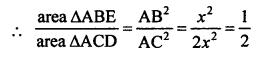
Ratio between the areas of ∆ABE and ∆ACD = 1 : 2

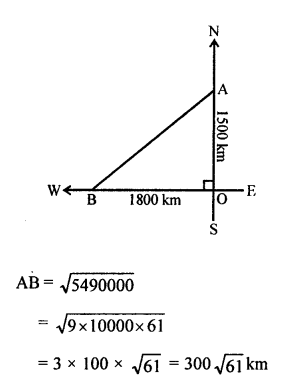
Question 20.
Solution:
An aeroplane flies from airport to north at the speed of 1000 km/hr.
Another aeroplane flies from the airport to west at the speed of 1200 km/hr.
Period = 1\(\frac { 1 }{ 2 }\) hours
Distance covered by the first plane in 1\(\frac { 1 }{ 2 }\) hours = 1000 x \(\frac { 3 }{ 2 }\) km = 1500 km
and distance covered by another plane in 1\(\frac { 1 }{ 2 }\) hours = 1200 x \(\frac { 3 }{ 2 }\) km = 1800 km
At present, the distance between them
AB² = (BO)² + (AO)²
= (1800)² + (1500)²
= 3240000 + 2250000
= 5490000

Question 21.
Solution:
Given : In ∆ABC,
D is the mid point of BC and AL ⊥ BC
AD is joined.
To prove:

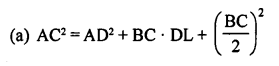
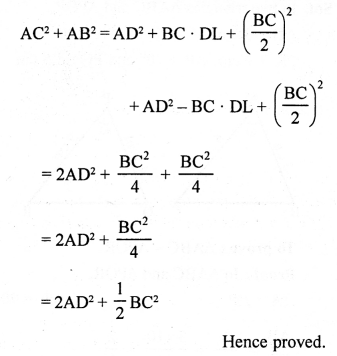
Question 22.
Solution:
AM is rod and BC is string out of rod.
In ∆BMC,
BC² = BM² + CM² = (1.8)² + (2.4)²

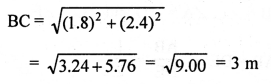
Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.