RS Aggarwal Class 7 Solutions Chapter 7 Linear Equations in One Variable Ex 7B

RS Aggarwal Class 7 Solutions Chapter 7 Linear Equations in One Variable Ex 7B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 7 Linear Equations in One Variable Ex 7B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 7 Linear Equations in One Variable Ex 7A
• RS Aggarwal Solutions Class 7 Chapter 7 Linear Equations in One Variable Ex 7B
• RS Aggarwal Solutions Class 7 Chapter 7 Linear Equations in One Variable Ex 7C
• RS Aggarwal Solutions Class 7 Chapter 7 Linear Equations in One Variable CCE Test Paper

Question 1.
Solution:
Let the required number = x
Then 2x – 7 = 45
2x = 45 + 7 = 52
x = 26
Required number = 26

Question 2.
Solution:
Let the required number = x Then
3x + 5 = 44
⇒ 3x = 44 – 5 = 39
x = 13
Required number = 13

Question 3.
Solution:
Let the required fraction = x
then 2x + 4 = \(\frac { 26 }{ 5 }\)

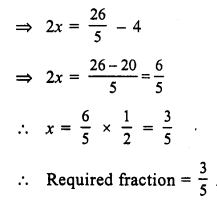
Question 4.
Solution:
Let the required number = x
and half of .the number = \(\frac { x }{ 2 }\)

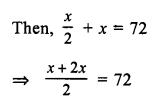
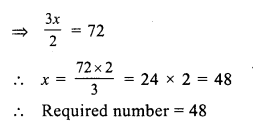
Question 5.
Solution:
Let the required number = x
Two third of the number = \(\frac { 2 }{ 3 }\) x

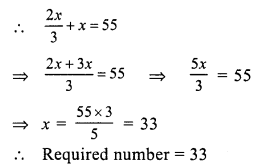
Question 6.
Solution:
Let the required number = x
Then, 4x = x + 45
⇒ 4x – x = 45
⇒ 3x = 45
⇒ x = 15
Required number = 15

Question 7.
Solution:
Let the required number = x
Then x – 21 = 71 – x
⇒ x + x = 71 + 21
⇒ 2x = 92
⇒ x = 46

Question 8.
Solution:
Let the original number = x
Then \(\frac { 2 }{ 3 }\) of the number = \(\frac { 2 }{ 3 }\) x

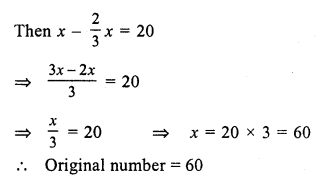
Question 9.
Solution:
Let the second number = x
then first number = \(\frac { 2 }{ 5 }\) x
their sum = 70

Question 10.
Solution:
Let the required number = x

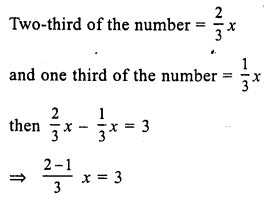
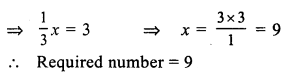
Question 11.
Solution:
Let the required number = x
Fifth part of the number = \(\frac { x }{ 5 }\)
Fourth part of the number = \(\frac { x }{ 4 }\)

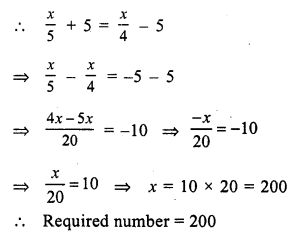
Question 12.
Solution:
Let first natural number = x then
next number = x + 1
x + x + 1 = 63
⇒ 2x = 63 – 1 = 62
x = 31
first number = 31
and second number = 31 + 1 = 32
Numbers are 31, 32

Question 13.
Solution:
Let first odd number = 2x + 1
second odd number = 2x + 3
2x + 1 + 2x + 3 = 76
⇒ 4x + 4 = 76
⇒ 4x = 76 – 4 = 72
x = 18
First number = 2x + 1 = 2 x 18 + 1 = 36 + 1 = 37
Second number = 2x + 3 = 2 x 18 + 3 = 36 + 3 = 39
Numbers are 37, 39

Question 14.
Solution:
Let first positive even number = 2x
Second number = 2x + 2
Third number = 2x + 4
2x + 2x +2 + 2x + 4 = 90
⇒ 6x + 6 = 90
⇒ 6x = 90 – 6 = 84
x = 14
First even number = 2x = 2 x 14 = 28
Second number = 2x + 2 = 2 x 14 + 2 = 28 + 2 = 30
Third number = 30 + 2 = 32
Required numbers are 28, 30, 32

Question 15.
Solution:
Sum of two numbers = 184
Let first number = x
Then second number = 184 – x

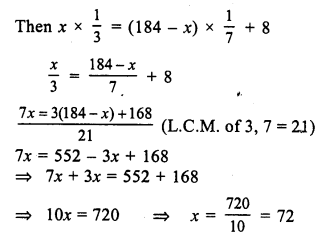
First part = 72
Second part = 184 – 72 = 112
Hence parts are 72, 112

Question 16.
Solution:
Total number of notes = 90
Let number of notes of Rs. 5 = x
Then number of notes of Rs.10 = 90 – x
Then x x 5 + (90 – x) x 10 = 500
⇒ 5x + 900 – 10x = 500
⇒ -5x = 500 – 900 = -400
x = 8
Number of 5 rupees notes = 80
and ten rupees notes = 90 – 80 = 10

Question 17.
Solution:
Amount of coins = Rs. 34
Let 50 paisa coins = x
then 25 paisa coins = 2x

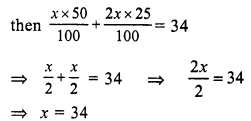
Number of 50 paisa coins = 34
and number of 25 paisa coins = 2x = 2 x 34 = 68

Question 18.
Solution:
Let present age of Raju’s cousin = x years
then age of Raju = (x – 19) years
After 5 years,
Raju’s age = x – 19 + 5 = (x – 14) years
and his cousin age = x + 5
(x – 14) : (x + 5) = 2 : 3
⇒ \(\frac { x – 14 }{ x + 5 }\) = \(\frac { 2 }{ 3 }\)
⇒ 3(x – 14) = 2 (x + 5) (By cross multiplication)
⇒ 3x – 42 = 2x + 10
⇒ 3x – 2x = 10 + 42
⇒ x = 52
Raju’s age = x – 19 = 52 – 19 = 33 years
and his cousin age = 52 years.

Question 19.
Solution:
Let present age of son = x years
Age of father = (x + 30) years
12 years after,
Father’s age = x + 30 + 12 = (x + 42) years
and son’s age = (x + 12) years
(x + 42) = 3(x + 12)
⇒ x + 42 = 3x + 36
⇒ 3x + 36 = x + 42
⇒ 3x – x = 42 – 36
⇒ 2x = 6
⇒ x = 3
Son’s age = 3 years
Father’s age = 3 + 30 = 33 years

Question 20.
Solution:
Ratio in present ages of Sonal and Manoj = 7 : 5
Let Sonal’s age = 7x
then Manoj’s age = 5x
10 years hence,
Sonal’s age will be = 7x + 10
and Manoj’s age = 5x + 10

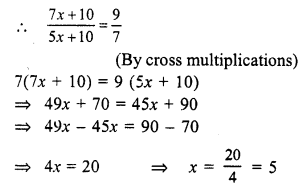
Sonal’s present age = 7x = 7 x 5 = 35 years
and Manoj’s age = 5x = 5 x 5 = 25 years

Question 21.
Solution:
Five years ago,
Let Son’s age = x years
and father’s age = 7x years
Present age of son = (x + 5) years
and age of father = (7x + 5) years
5 years hence,
father’s age = 7x + 5 + 5 = 7x + 10
and Son’s age = x + 5 + 5 = x + 10
(7x + 10) = 3(x + 10)
⇒ 7x + 10 = 3x + 30
⇒ 7x – 3x = 30 – 10
⇒ 4x = 20
⇒ x = 5
Father present age = 7x + 5 = 7 x 5 + 5 = 35 + 5 = 40 years
and son’s age = x + 5 = 5 + 5 = 10 years

Question 22.
Solution:
Let age of Manoj 4 years ago = x
then his present age = x + 4
After 12 years his age will be = x + 4 + 12 = x + 16
x + 16 = 3(x)
x + 16 = 3x
⇒ 16 = 3x – x
⇒ 2x = 16
x = 8
His present age = 8 + 4 = 12 years

Question 23.
Solution:
Let total marks = x
Pass marks = 40% of x = \(\frac { 40x }{ 100 }\) = \(\frac { 2 }{ 5 }\) x
No. of marks got by Rupa = 185
No. of marks by which she failed = 15
Pass marks = 185 + 15 = 200
\(\frac { 2 }{ 5 }\) x = 200
⇒ x = \(\frac { 200 x 5 }{ 2 }\) x
⇒ x = 500
Hence total marks = 500

Question 24.
Solution:
Sum of digits = 8
Let units digit = x
Then tens digit = 8 – x
and number will be x + 10 (8 – x) ….(i)
By adding 18, the digits are reversed then
units digit = 8 – x
and tens digit = x
Number = (8 – x) = 10x
According to the condition,
(8 – x) + 10x = 18 + x + 10 (8 – x)
⇒ 8 – x + 10x = 18 + x + 80 – 10x
⇒ 10x – x – x + 10x = 18 + 80 – 8
⇒ 18x = 90
⇒ x = 5
Number is
x + 10(8 – x) = 5 + 10(8 – 5) = 5 + 10 x 3 = 35

Question 25.
Solution:
Cost of 3 tables and 2 chairs = 1850
Cost of table = Rs. 75 + cost of a chair
Let cost of chair = Rs. x,
then Cost of table = Rs. 75 + x
According to the condition,
3 (75 + x) + 2x = 1850
⇒ 225 + 3x + 2x = 1850
⇒ 225 + 5x = 1850
⇒ 5x = 1850 – 225 = 1625
x = 325
Cost of chair = Rs. 325
and cost of table = Rs. 325 + 75 = Rs. 400

Question 26.
Solution:
S.P of article = Rs. 495
gain = 10%
Let cost price = Rs. x

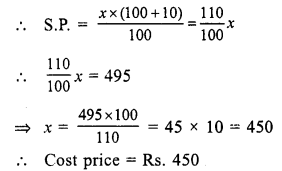
Question 27.
Solution:
Perimeter of field = 150 m
Length + Breadth = \(\frac { 150 }{ 2 }\) = 75 m
[Perimeter = 2(l + b)]
Let length = x Then breadth = 75 – x
Then x = 2(75 – x)
⇒ x = 150 – 2x
⇒ x + 2x = 150
⇒ 3x = 150
⇒ x = \(\frac { 150 }{ 3 }\) = 50
Length = 50 m
and breadth = 75 – 50 = 25 m

Question 28.
Solution:
Perimeter of an isosceles triangle = 55 m
Let the third side of an isosceles triangle = x
Then each equal side = (2x – 5) m
According to the condition,
x + 2 (2x – 5) = 55
⇒ x + 4x – 10 = 55
⇒ 5x = 55 + 10
⇒ 5x = 65
⇒ x = 13
and 2x – 5 = 2 x 13 – 5 = 21 m
Sides will be 13m, 21m, 21m

Question 29.
Solution:
Sum of two complementary angles = 90°
Let first angle = x
then second = 90° – x
x – (90 – x) = 8
⇒ x – 90 + x = 8
⇒ 2x = 8 + 90
⇒ 2x = 98
⇒ x = 49
first angle = 49°
and second angle = 90° – 49° = 41°
Hence angles are 41°, 49°

Question 30.
Solution:
Sum of two supplementary angles = 180°
Let first angle = x
Then second angle = 180° – x
x – (180° – x) = 44°
⇒ x – 180° + x = 44°
⇒ 2x = 44° + 180° = 224°
⇒ 2x = 224°
⇒ x = 112°
First angle = 112°
and second angle = 180° – 112° = 68°
Hence angles are 68°, 112°

Question 31.
Solution:
In an isosceles triangle
Let each equal base angles = x
Then vertex angle = 2x
According to the condition,
x + x + 2x = 180° (sum of angles of a triangle)
⇒ 4x = 180°
⇒ x = 45°
Then vertex angle = 2x = 2 x 45° = 90°
Angles of the triangle are 45°, 45° and 90°

Question 32.
Solution:
Let length of total journey = x km
According to the condition,

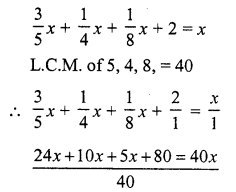
⇒ 39x + 80 = 40x
⇒ 40x – 39x = 80
⇒ x = 80
Total journey = 80km

Question 33.
Solution:
No. of days = 20 Let no. of days he worked = x
Then he will receive amount = x x Rs. 120 = Rs. 120x
No. of days he did not work = 20 – x
Fine paid = (20 – x) x Rs. 10 = Rs. 10(20 -x)
120x – 10 (20 – x) = 1880
⇒ 120x – 200 + 10x = 1880
⇒ 130x = 1880 + 200 = 2080
x = 16
No. of days he remained absent = 20 – x = 20 – 16 = 4 days

Question 34.
Solution:
Let value of property = x

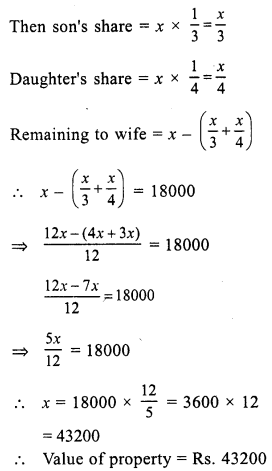
Question 35.
Solution:
Solution = 400 mL
Quantity of alcohol = 15% of 400 mL
= \(\frac { 400 x 15 }{ 100 }\) = 60 mL
Let pure alcohol added = x mL
Total solution = 400 + x
and total alcohol = (x + 60)
Now (400 + x) x 32% = x + 60
⇒ (400 + x) x \(\frac { 32 }{ 100 }\) = x + 60
⇒ 32 (400 + x) = 100 (x + 60)
⇒ 12800 + 32x = 100x + 6000
⇒ 12800 – 6000 = 100x – 32x
⇒ 6800 = 68x
⇒ x = 6800
Pure alcohol added = 100 mL

Hope given RS Aggarwal Solutions Class 7 Chapter 7 Linear Equations in One Variable Ex 7B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.