RS Aggarwal Class 7 Solutions Chapter 8 Ratio and Proportion Ex 8C

RS Aggarwal Class 7 Solutions Chapter 8 Ratio and Proportion Ex 8C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8A
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8B
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8C
• RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion CCE Test Paper

Objective questions :
Mark (✓) against the correct answers in each of the following :
Question 1.
Solution:
(d) a : b = 3 : 4, b : c = 8 : 9

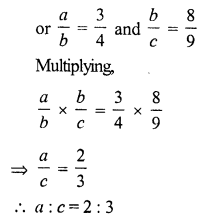
Question 2
Solution:
(a) A : B = 2 : 3, B : C = 4 : 5

Question 3.
Solution:
(d)

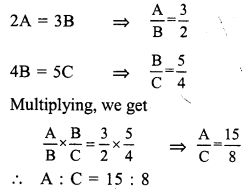
Question 4.
Solution:
(b) 15% of A = 20% of B

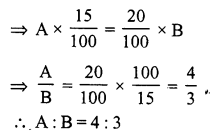
Question 5.
Solution:
(a)

Question 6.
Solution:
(b) A : B = 5 : 7, B : C = 6 : 11
LCM of 7, 6 = 42

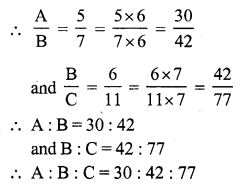
Question 7.
Solution:
(c) 2A = 3B = 4C = x

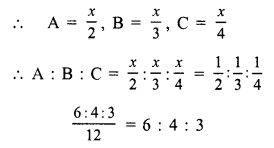
Question 8.
Solution:
(a)
\(\frac { A }{ 3 }\) = \(\frac { B }{ 4 }\) = \(\frac { C }{ 5 }\) = 1(suppose)
A = 3, B = 4, C = 5
A : B : C = 3 : 4 : 5

Question 9.
Solution:
(b)

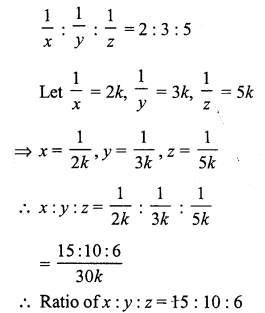
Question 10.
Solution:
(c)

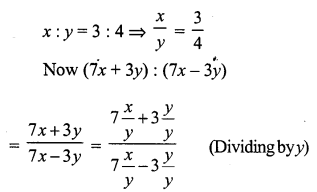
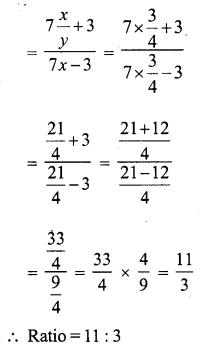
Question 11.
Solution:
(c) (3a + 5b) : (3a – 5b) = 5 : 1

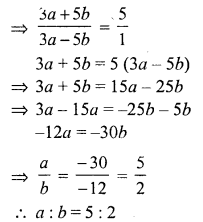
Question 12.
Solution:
(c) 7 : x :: 35 : 45

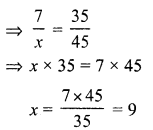
x = 9

Question 13.
Solution:
(b) Let x to be added to each term of 3 : 5
Then \(\frac { 3 + x }{ 5 + x }\) = \(\frac { 5 }{ 6 }\)
By cross multiplication
18 + 6x = 25 + 5x
6x – 5x = 25 – 18
x = 7
7 is to be added

Question 14.
Solution:
(d) Ratio in two numbers = 3 : 5
Let first number = 3x
Then second number = 5x
According to the condition,
\(\frac { 3x + 10 }{ 5x + 10 }\) = \(\frac { 5 }{ 7 }\)
(By cross multiplication)
25x + 50 = 21x + 70
25x – 21x = 70 – 50
4x = 20
x = 5
First number = 3 x 5 = 15
and second number = 5 x 5 = 25
Sum of numbers = 15 + 25 = 40

Question 15.
Solution:
(a)
Let x be subtracted from each of the term
\(\frac { 15 – x }{ 19 – x }\) = \(\frac { 3 }{ 4 }\)
⇒ 4 (15 – x) = 3 (19 – x)
⇒ 60 – 4x = 57 – 3x
⇒ -4x + 3x = 57 – 60
⇒ -x = -3
x = 3
Required number = 3

Question 16.
Solution:
(a)
Amount = Rs. 420
and ratio = 3 : 4
Sum of ratios = 3 + 4 = 7
A’s share = \(\frac { 420 x 3 }{ 7 }\) = Rs. 60 x 3 = Rs. 180

Question 17.
Solution:
(d)
Let number of boys = x, then
x : 160 : : 8 : 5
⇒ x x 5 = 160 x 8
x = \(\frac { 160 x 8 }{ 5 }\) = 32 x 8 = 256
Number of total students of the school = 256 + 160 = 416

Question 18.
Solution:
(a)

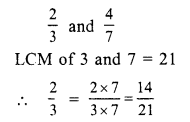
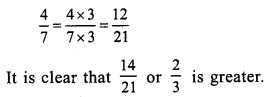
Question 19.
Solution:
(c)
Let x be the third proportional to 9 and 12 then
9 : 12 :: x : 12
⇒ 9 x x = 12 x 12
⇒ x = \(\frac { 12 x 12 }{ 9 }\) = \(\frac { 144 }{ 9 }\) = 16
Third proportional = 16

Question 20.
Solution:
Answer = (b)
Mean proportional of 9 and 16 = √(9 x 16) = √144 = 12

Question 21.
Solution:
(a)
Let age of A = 3x
and age of B = 8x
6 years hence, their ages will be 3x + 6 and 8x + 6
\(\frac { 3x + 6 }{ 8x + 6 }\) = \(\frac { 4 }{ 9 }\)
⇒ 9 (3x + 6) = 4 (8x + 6)
⇒ 27x + 54 = 32x + 24
⇒ 32x – 27x = 54 – 24
⇒ 5x = 30
⇒ x = 6
A’s age = 3x = 3 x 6 = 18 years

Hope given RS Aggarwal Solutions Class 7 Chapter 8 Ratio and Proportion Ex 8C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.