Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24A

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency (Mean, Median, Quartiles and Mode) Ex 24A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 24 Measures of Central Tendency (Mean, Median, Quartiles and Mode) Ex 24A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24E

Question 1.
Find the mean of following set of numbers:
(i) 6, 9, 11, 12 and 7
(ii) 11, 14, 23, 26, 10, 12, 18 and 6.
Solution:

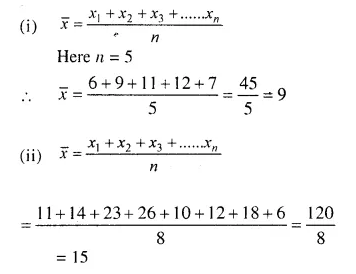
Question 2.
Marks obtained (in mathematics) by a students are given below :
60, 67, 52, 76, 50, 51, 74, 45 and 56
(a) Find the arithmetic mean
(b) If marks of each student be increased by 4;
what will be the new value of arithmetic mean.
Solution:
(a) Hence x = 9

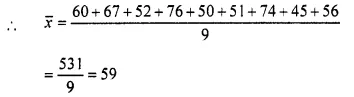
(b) If marks of each students be increased by 4 then new mean will be = 59 + 4 = 63

Question 3.
Find the mean of natural numbers from 3 to 12.
Solution:
Numbers betweeen 3 to 12 are 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Here n = 10

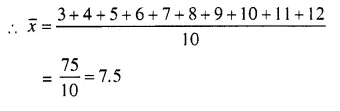
Question 4.
(a) Find the means of 7, 11, 6, 5 and 6. (b) If each number given in (a) is diminished by 2; find the new value of mean.
Solution:
(a) The mean of 7, 11, 6, 5 and 6.

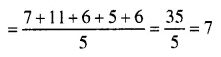
(b) If we subtract 2 from each number, then the mean will be 7 – 2 = 5

Question 5.
If the mean of 6, 4, 7, a and 10 is 8. Find the value of ‘a’.
Solution:
No. of terms = 5
Mean = 8
∴ Sum of number (Σx_i) = 5 x 8 = 40 …(i)
But Σx_i = 6 + 4 + 7 + a+10 = 27 + a ….(ii)
From (i) and (ii)
27 + a = 40 ⇒ a = 40 – 27
∴ a = 13

Question 6.
The mean of the number 6, y, 7, x and 14 is 8. Express y in terms of x.
Solution:
No. of terms = 5 and
mean = 8
∴ Sum of numbers (Σx_i) = 5 x 8 = 40 ….(i)
But sum of numbers given = 6 + y + 7 + x + 14
= 21 + y + x + ….(ii)
From (i) and (ii)
27 + y + x = 40
⇒ y = 40 – 27 – x
⇒ y= 13 – x

Question 7.
The ages of 40 students are given in the following table :

Find the arithmetic mean.
Solution:

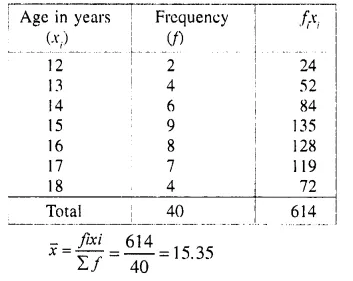
Question 8.
If 69.5 is the mean of 72, 70, x, 62, 50, 71, 90, 64, 58 and 82, find the value of x.
Solution:
No. of terms = 10
Mean = 69.5
∴ Sum of numbers = 69,5 x 10 = 695 ….(i)
But sum of given number = 72 + 70 + x + 62 + 50 + 71 + 90 + 64 + 58 + 82 = 619+x ….(ii)
From (i) and (ii)
619 + x = 695
⇒ x = 695 – 619 = 76

Question 9.
The following table gives the heights of plants in centimeter. If the mean height of plants is 60.95 cm; find the value of ‘f’.

Solution:

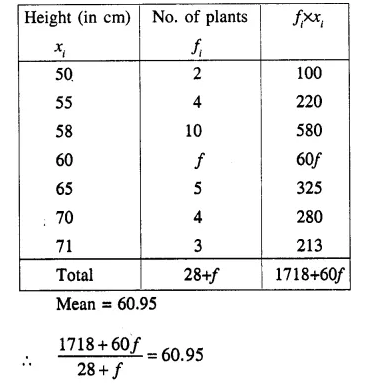
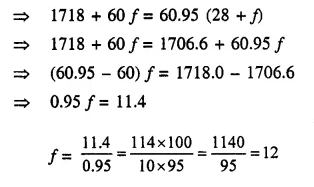
Question 10.
From the data given below, calculate the mean wage, correct to the nearest rupee.

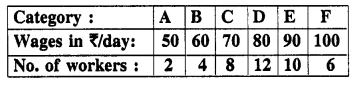
(i) If the number of workers in each category is doubled, what would be the new mean wage? [1995]
(ii) If the wages per day in each category are increased by 60%; what is the new mean wage?
(iii) If the number of workers in each category is doubled and the wages per day per worker are reduced by 40%. What would be the new mean wage?
Solution:

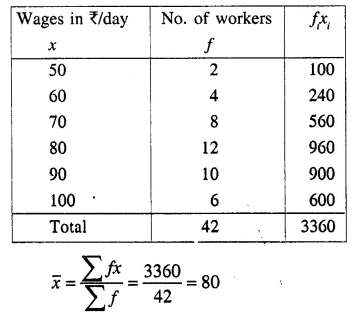
(i) Mean remains the same if the number of workers in each catagory is doubled.
∴ Mean = 80.
(ii) Mean will be increased by 60% if the wages per day per worker is increased by 60%.
∴ New mean = 80 x \(\frac { 160 }{ 100 }\)= 128
(iii) No change in the mean if the number of worker is doubled but if wages per worker is reduced by 40%, then
New mean = 80 x \(\frac { 60 }{ 100 }\)= 48

Question 11.
The contents of 100 match boxes were checked to determine the number of matches they contained.

(i) Calculate, correct to one decimal place, the mean number of matches per box.
(ii) Determine how many extra matches would have to be added to the total contents of the 100 boxes to bring the mean up to exactly 39 matches. [1997]
Solution:

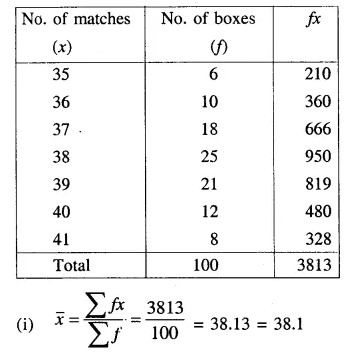
(ii) In the second case,
New mean = 39 matches
∴ Total contents = 39 x 100 = 3900
But total no of matches already given = 3813
∴ Number of new matches to be added = 3900 – 3813 = 87

Question 12.
If the mean of the following distribution is 3, find the value of p.

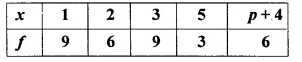
Solution:
Mean = 3

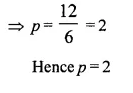
Question 13.
In the following table, Σf= 200 and mean = 73. Find the missing frequencies f₁ and f₂.

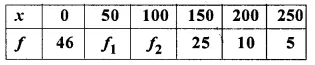
Solution:

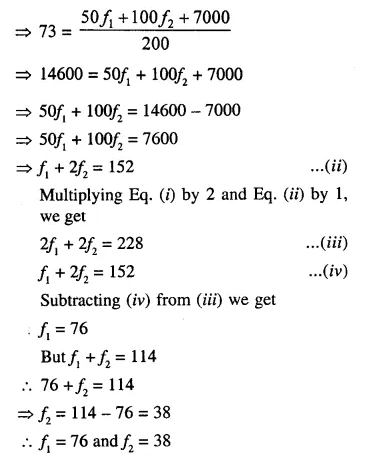
Question 14.
Find the arithmetic mean (correct to the nearest whole-number) by using step-deviation method.

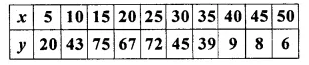
Solution:
Let the Assumed mean = 30

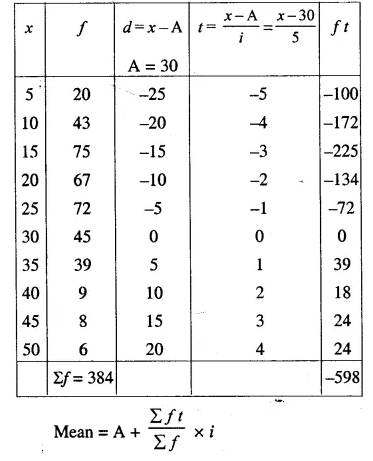
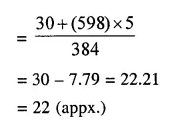
Question 15.
Find the mean (correct to one place of decimal) by using short-cut method.

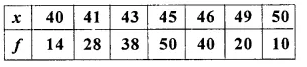
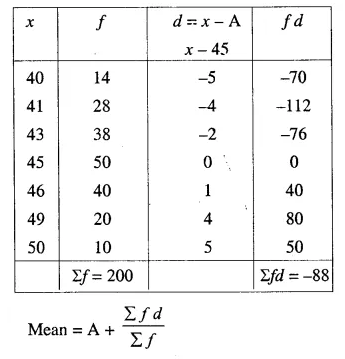
Solution:
Let the Assumed mean A = 45

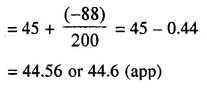
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 24 Measures of Central Tendency Ex 24A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.