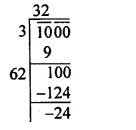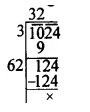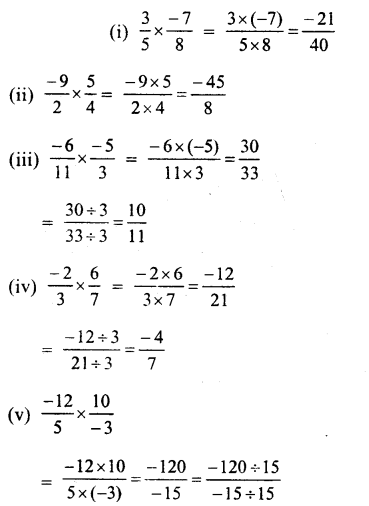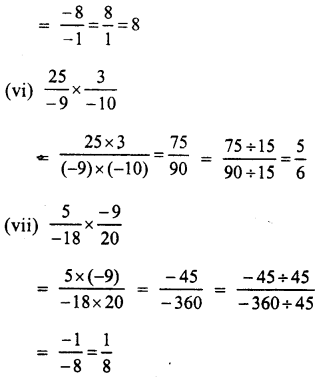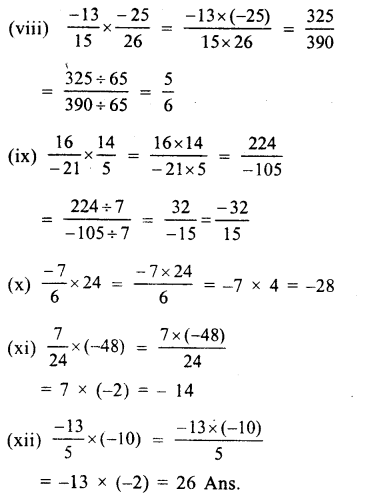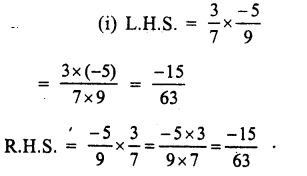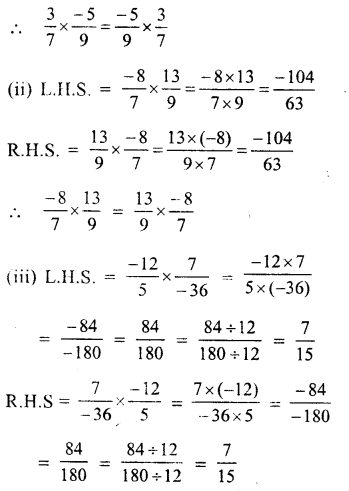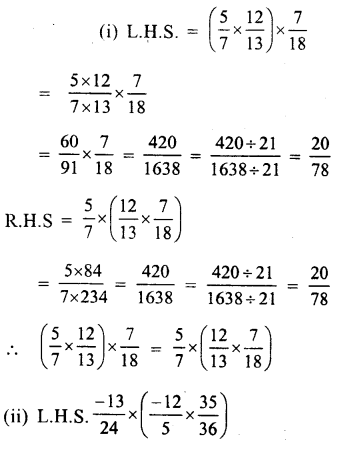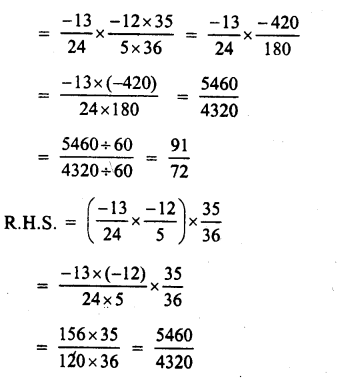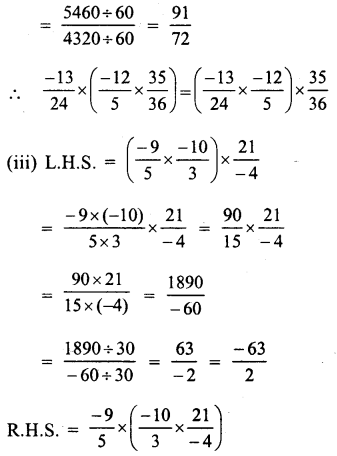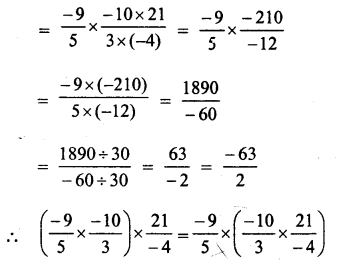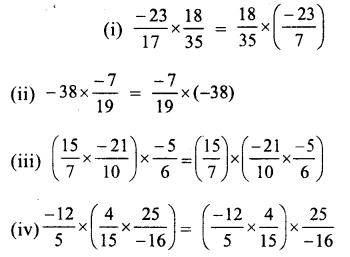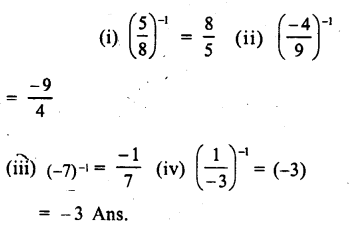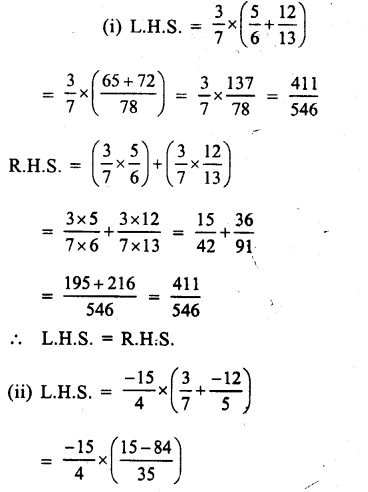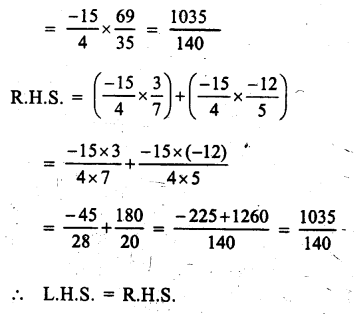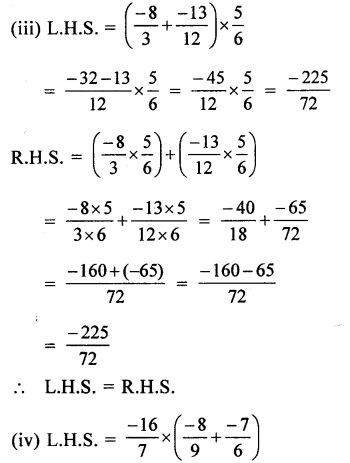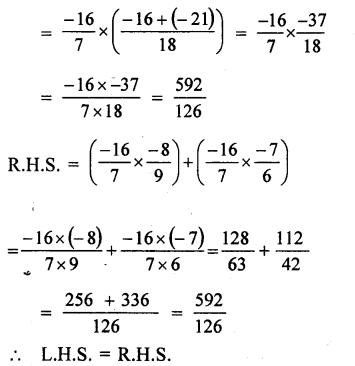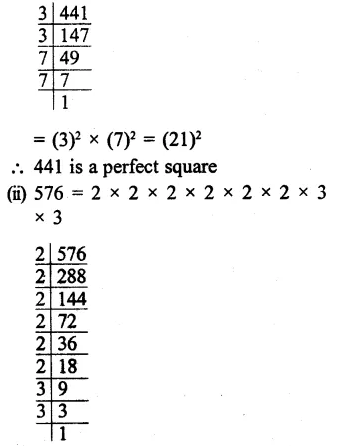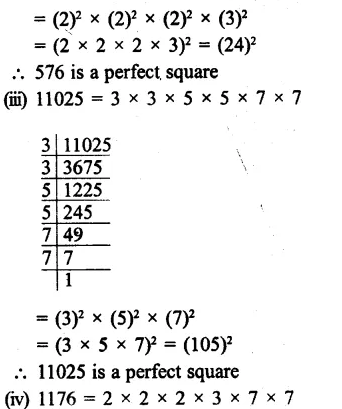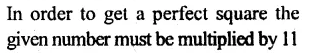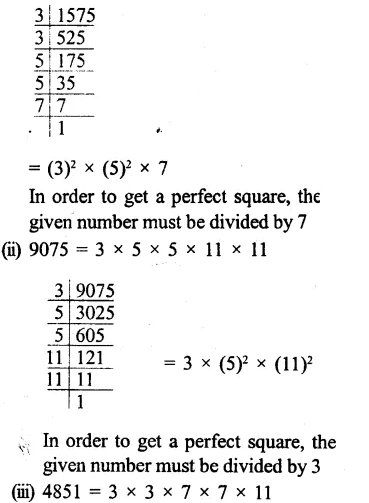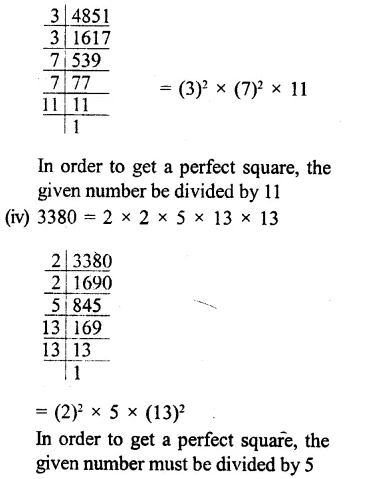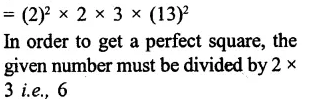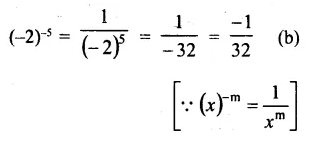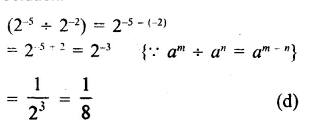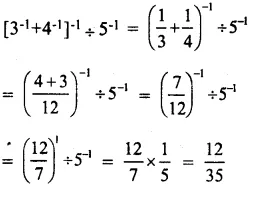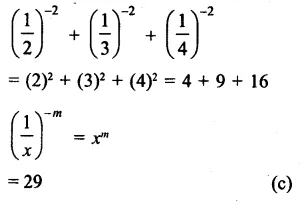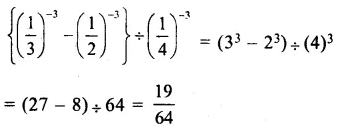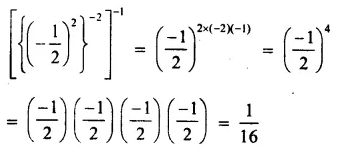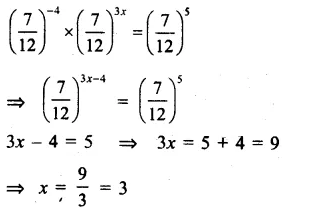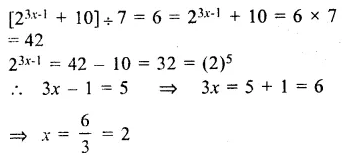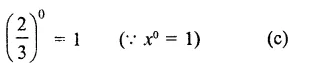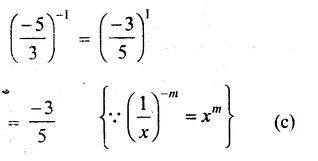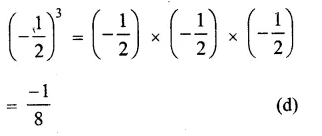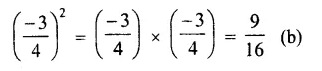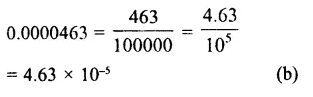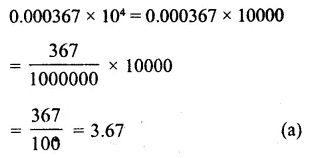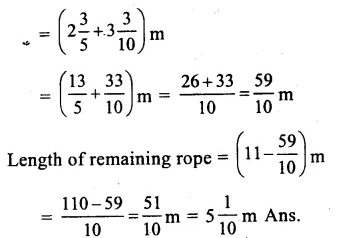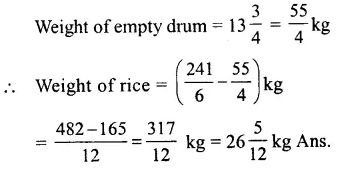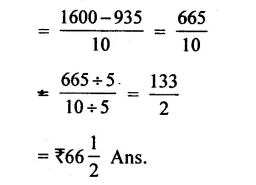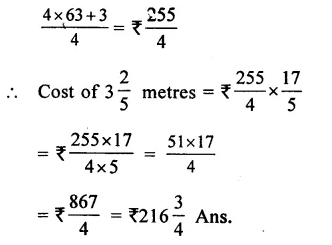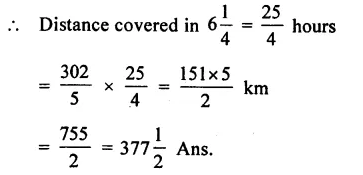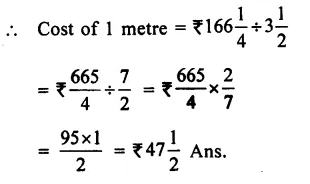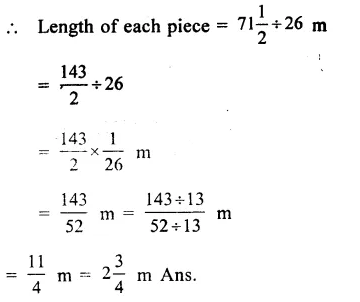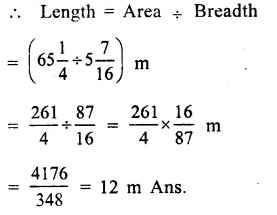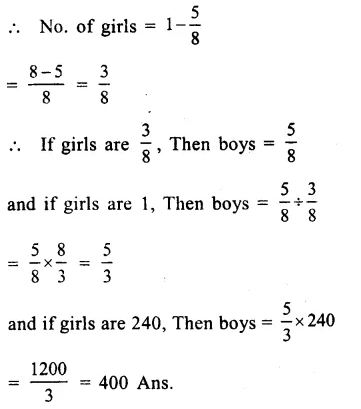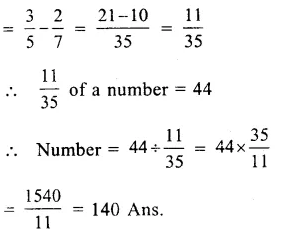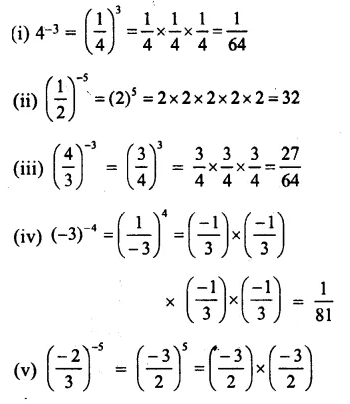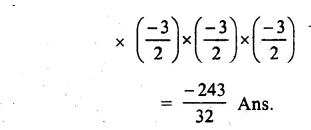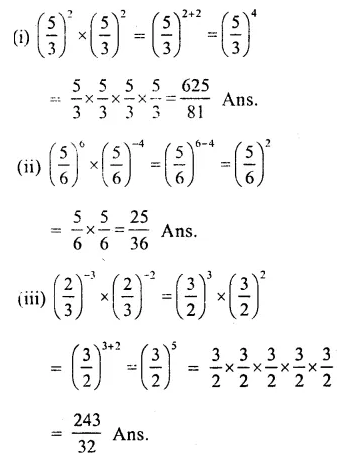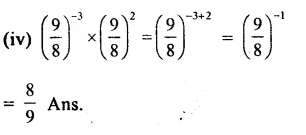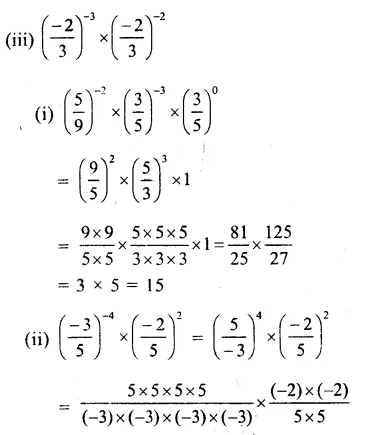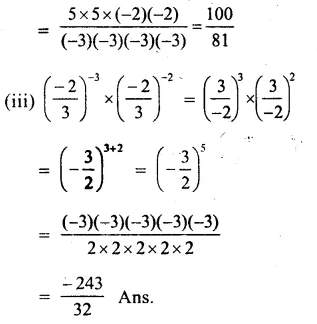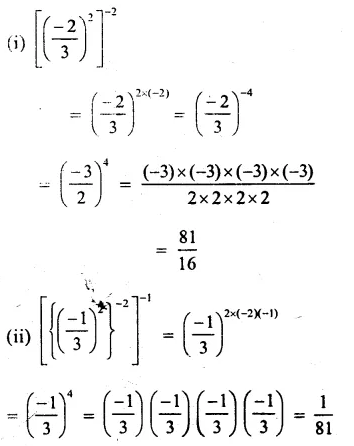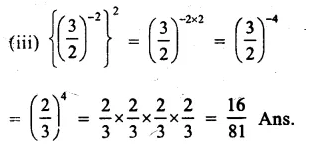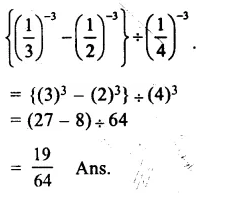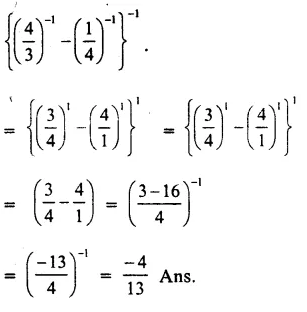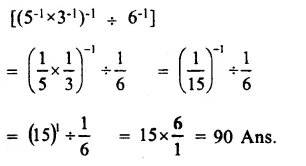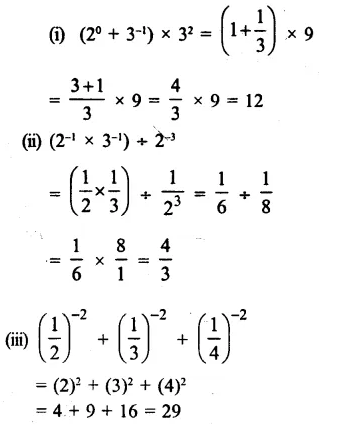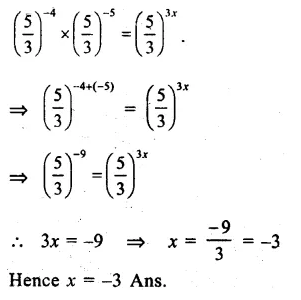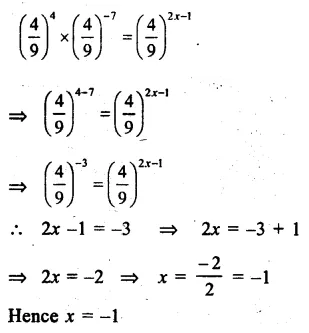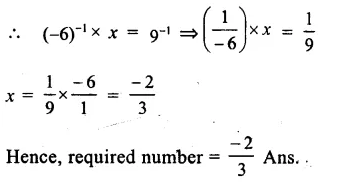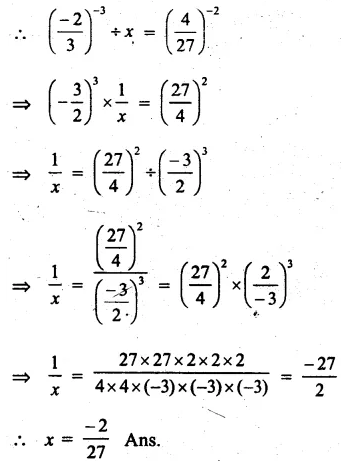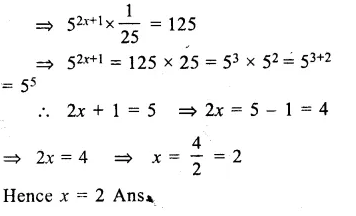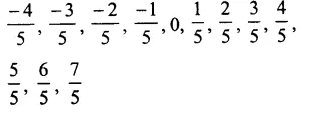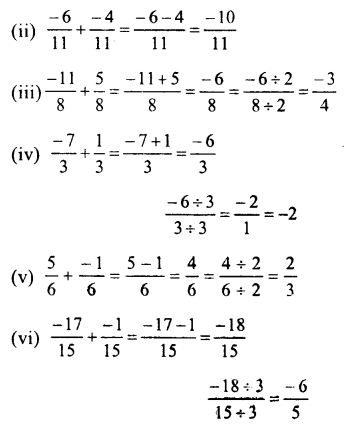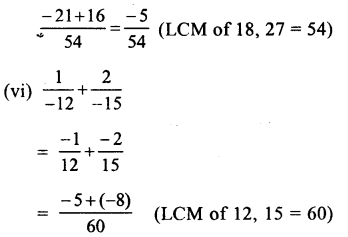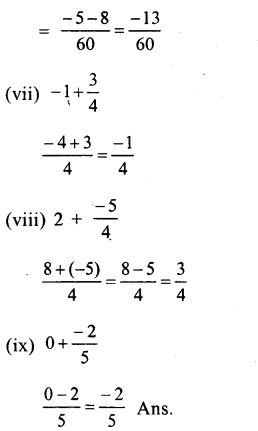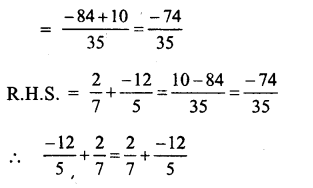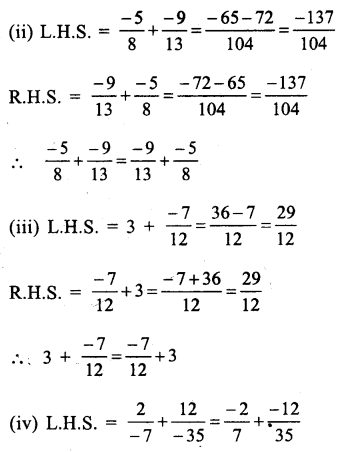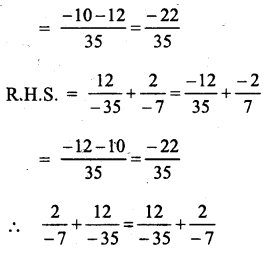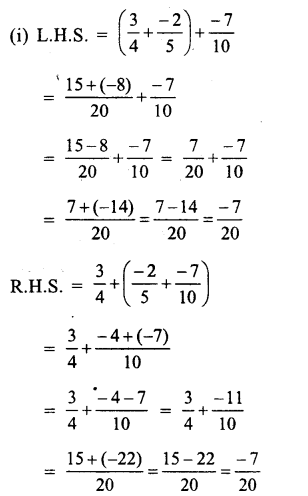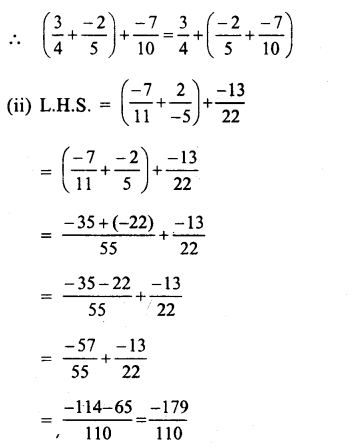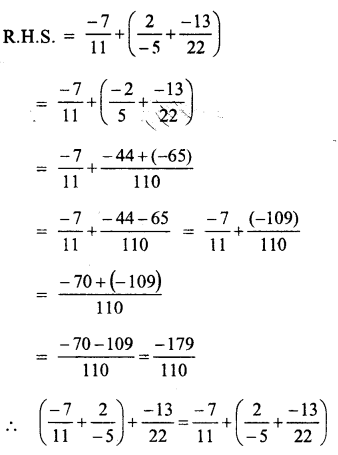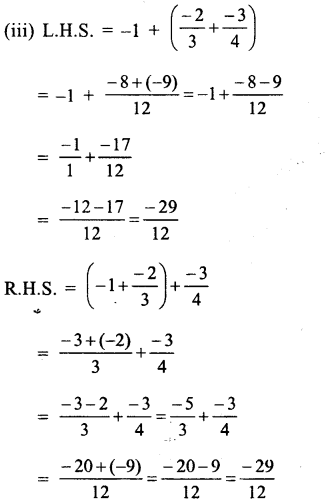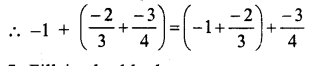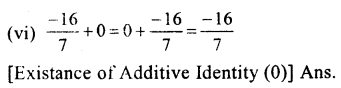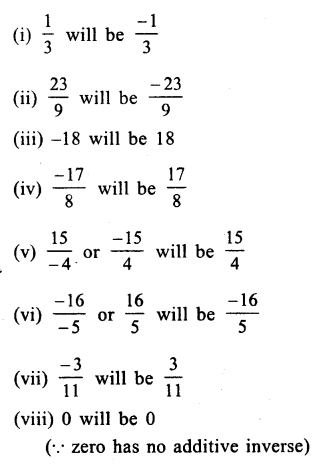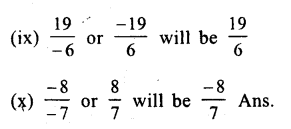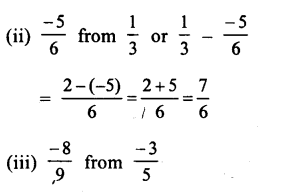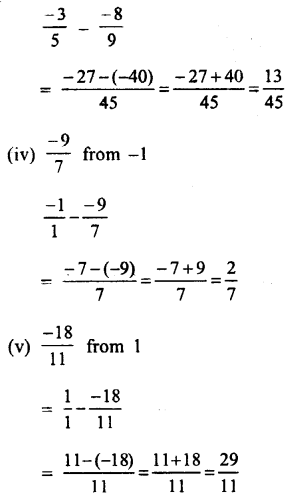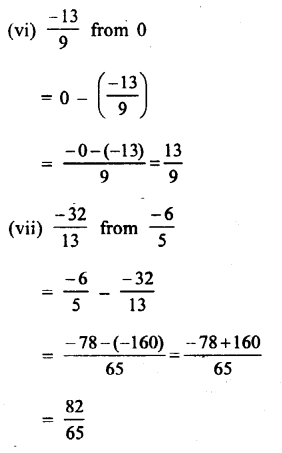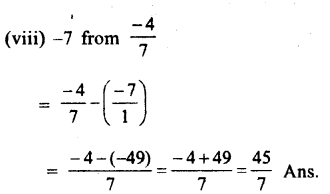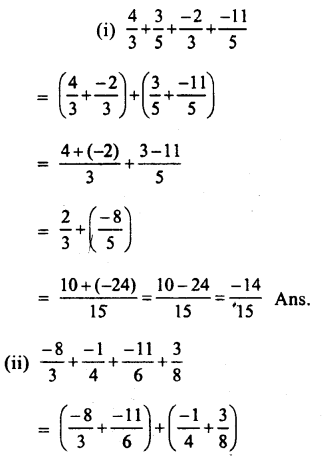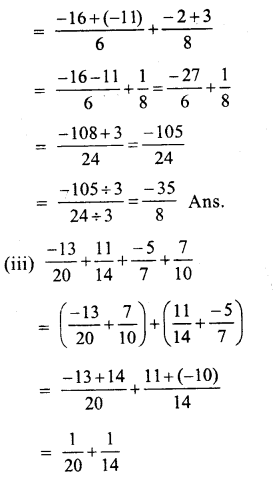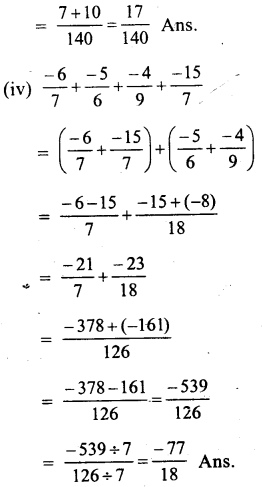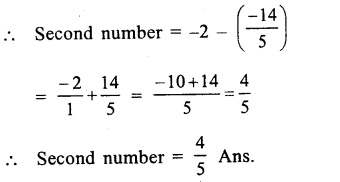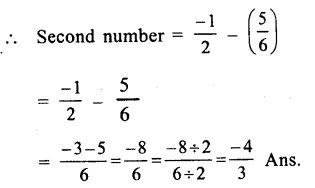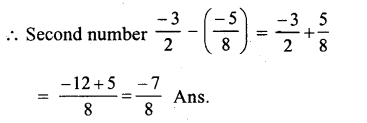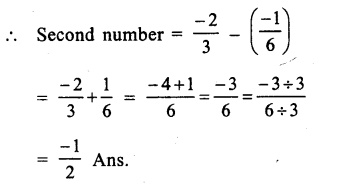RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1E
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1E.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1A
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1B
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1C
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1D
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1E
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1F
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1G
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1H
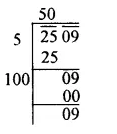
Question 1.
Solution:
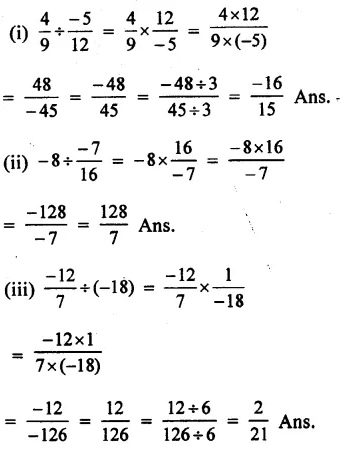
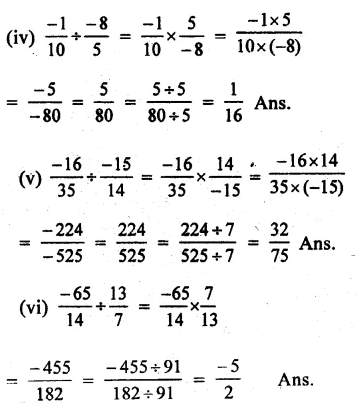
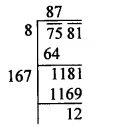
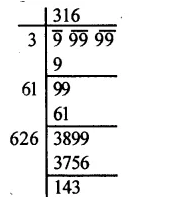
Question 2.
Solution:

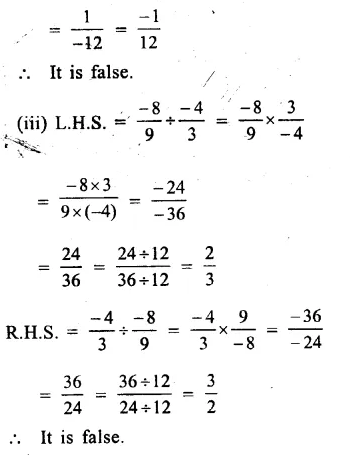
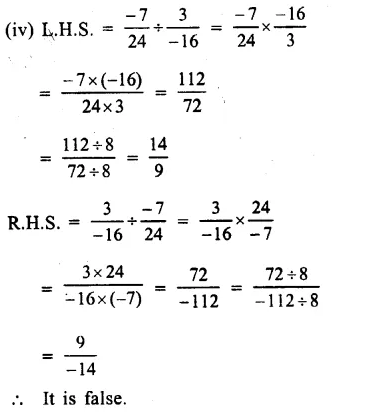
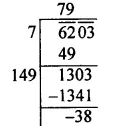
Question 3.
Solution:

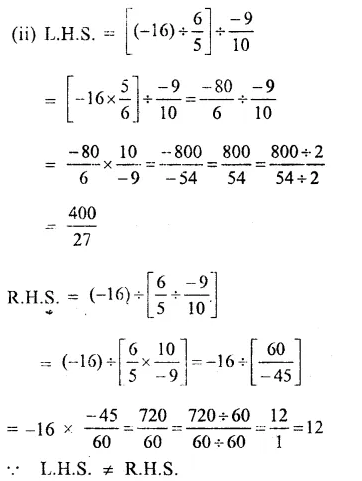
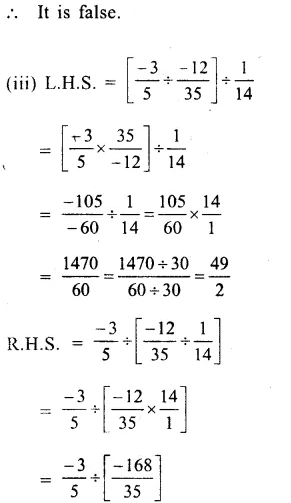
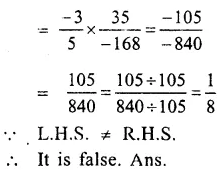
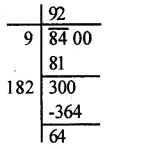
Question 4.
Solution:
Product of two numbers = – 9
one number = – 12
Let second number = x
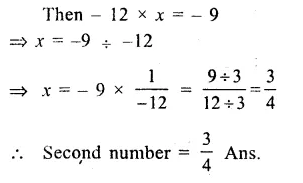
Question 5.
Solution:
Product of two rational numbers = \(\\ \frac { -16}{ 9 } \)
One number = \(\\ \frac { -4 }{ 3 } \)
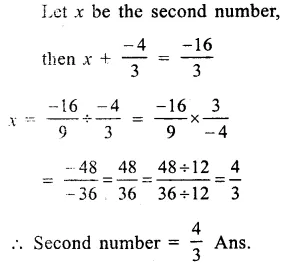
Question 6.
Solution:
Let x be multiplied

Question 7.
Solution:
Let x be multiplied
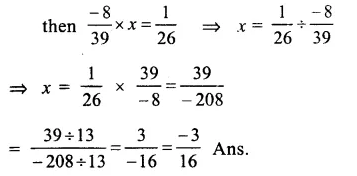
Question 8.
Solution:
Let required number = x
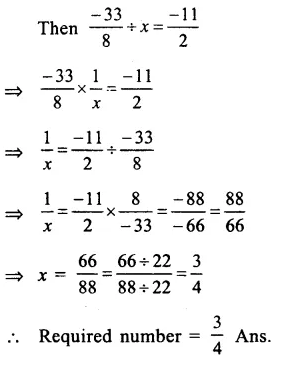
Question 9.
Solution:
sum of \(\\ \frac { 13 }{ 5 } \) and \(\\ \frac { -12 }{ 7 } \)
= \(\\ \frac { 13 }{ 5 } \) + \(\\ \frac { -12 }{ 7 } \)
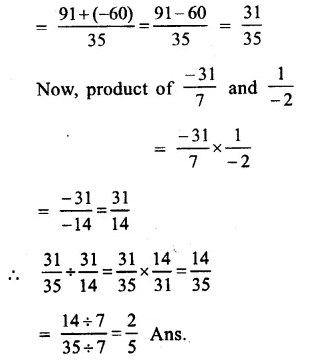
Question 10.
Solution:
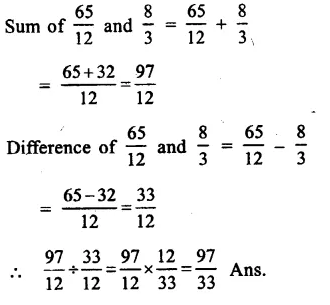
Question 11.
Solution:


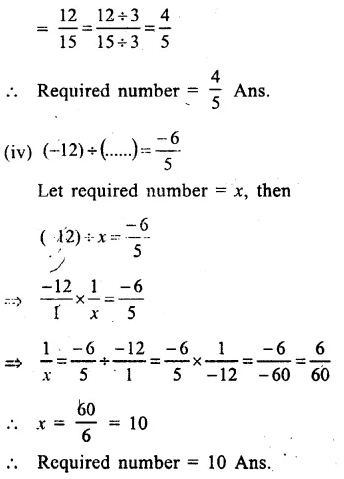
Question 12.
Solution:
(i) No, not always closed under division.
(ii) No, not always commutative.
(iii) No, not always associative.
(iv) No. It is not possible to divide any number by zero.
Hope given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1E are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.