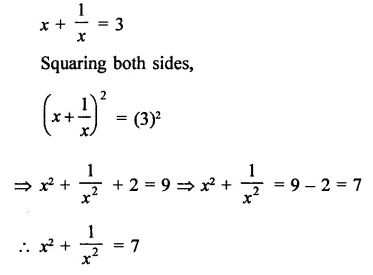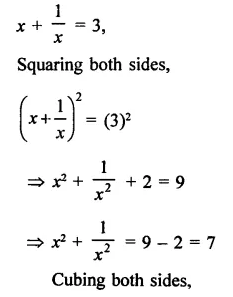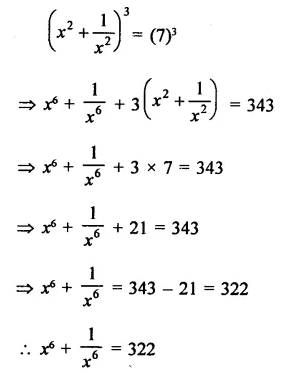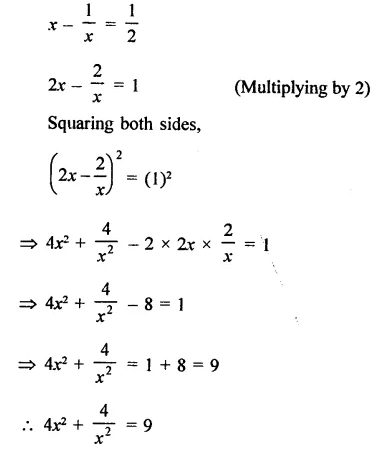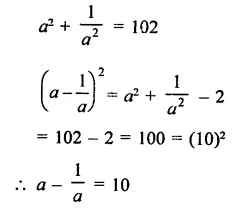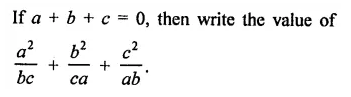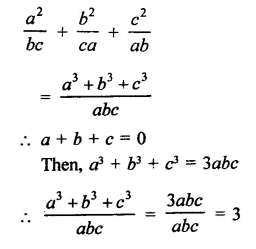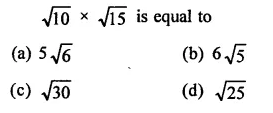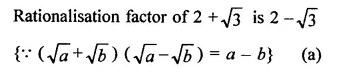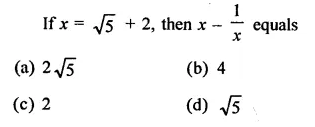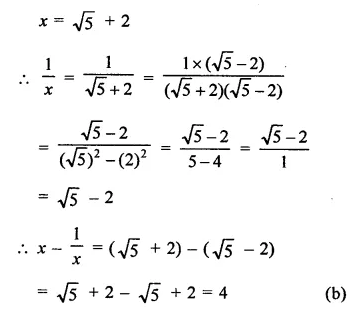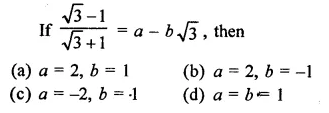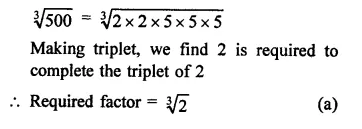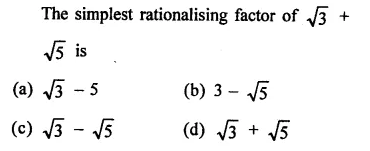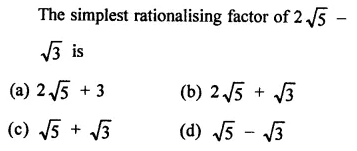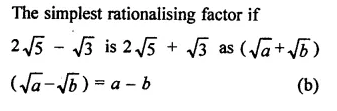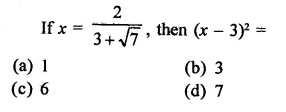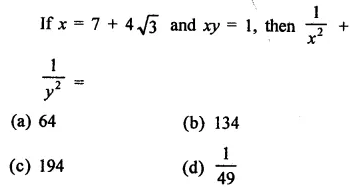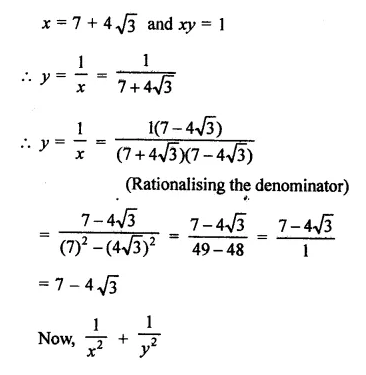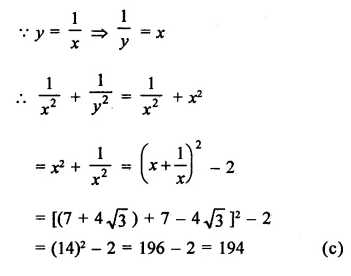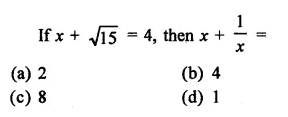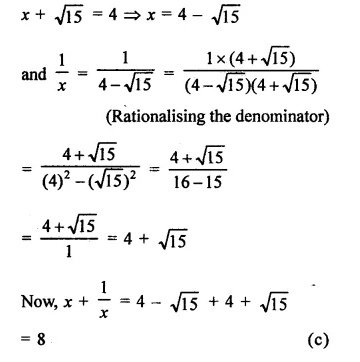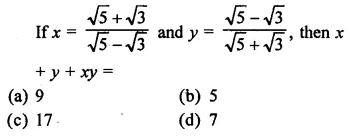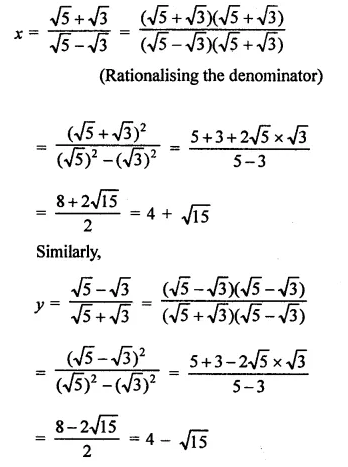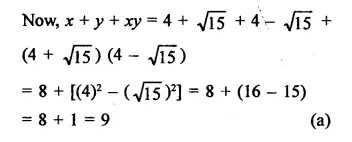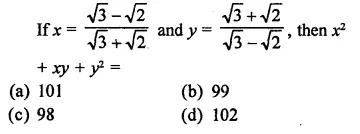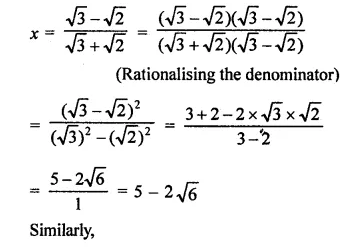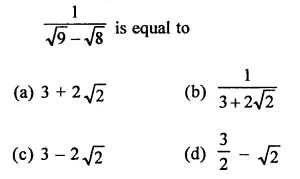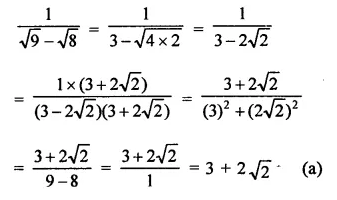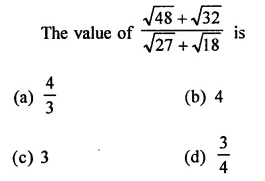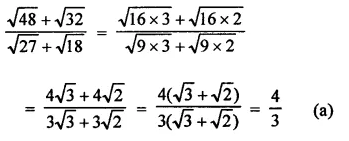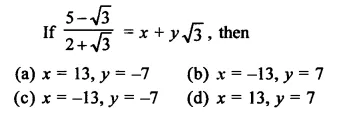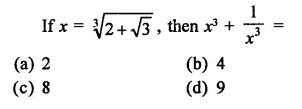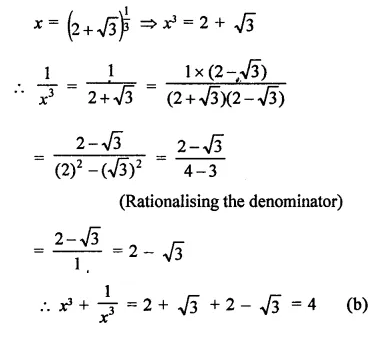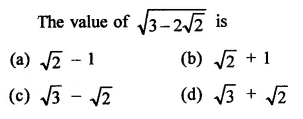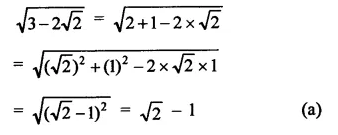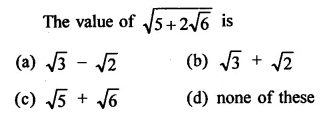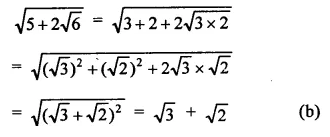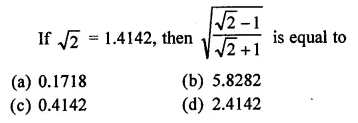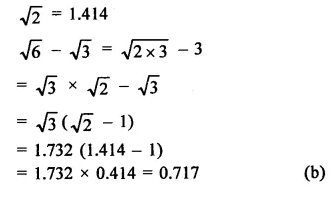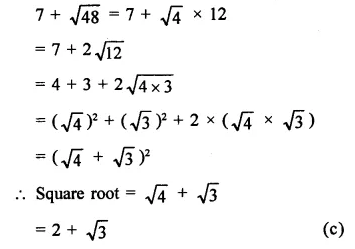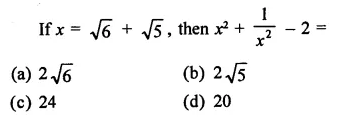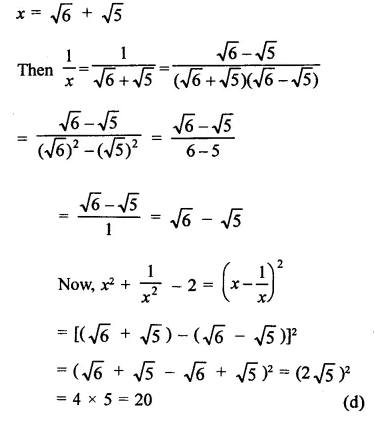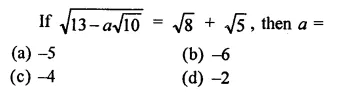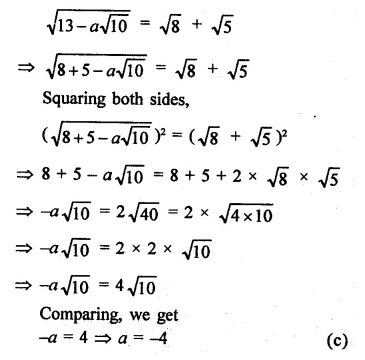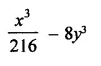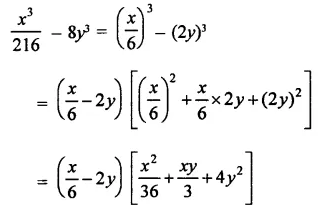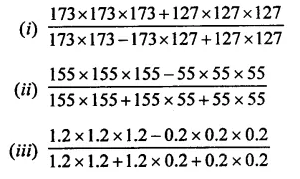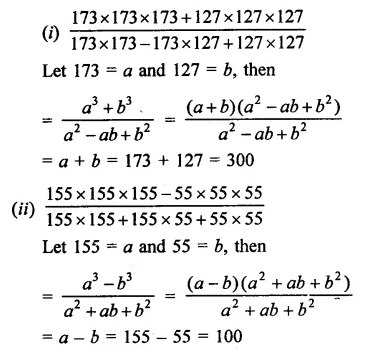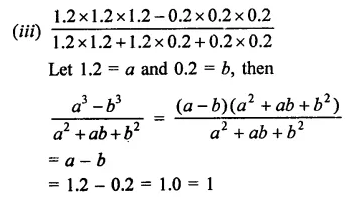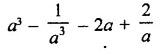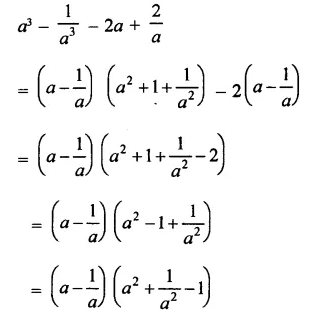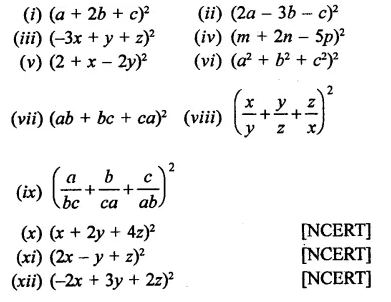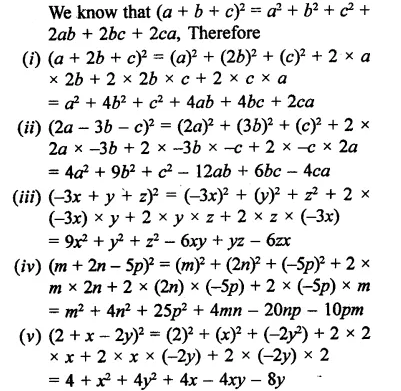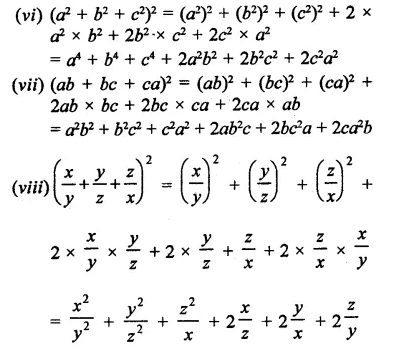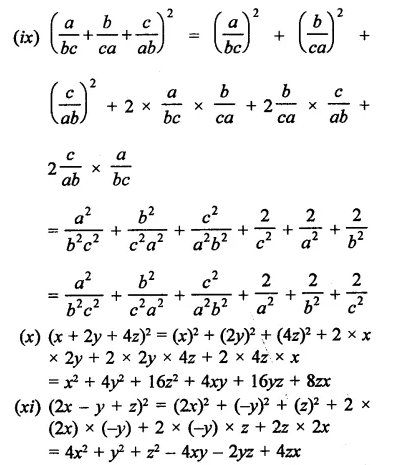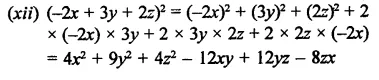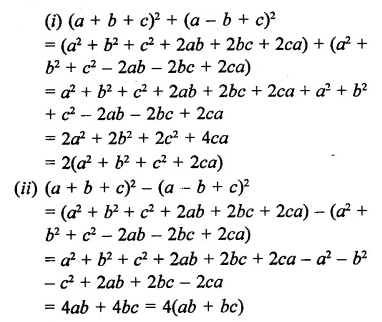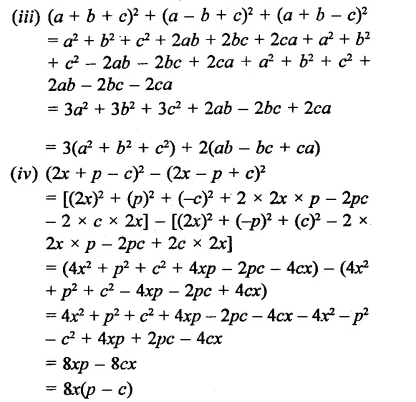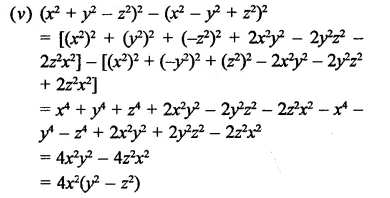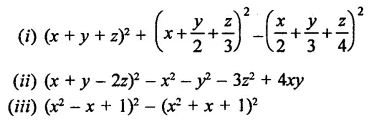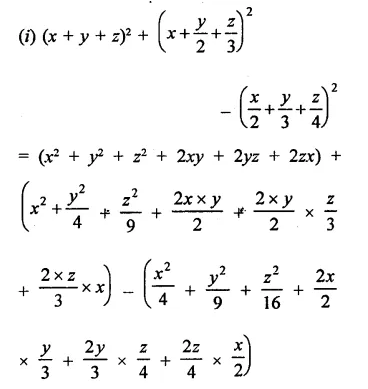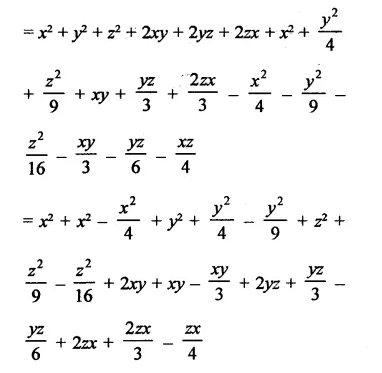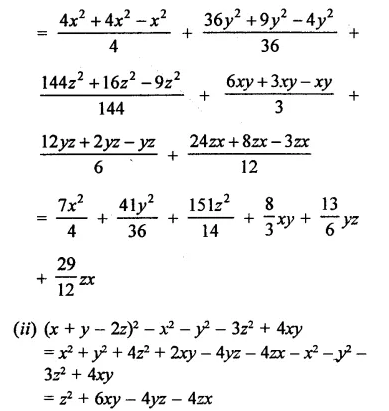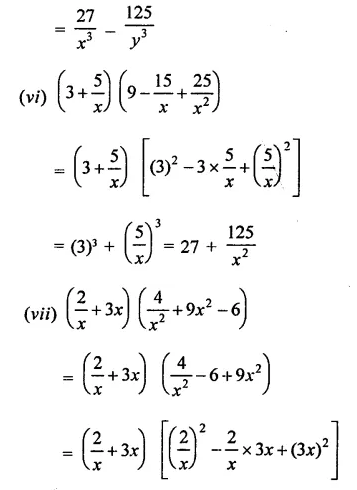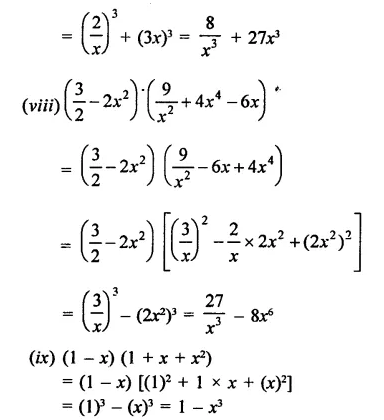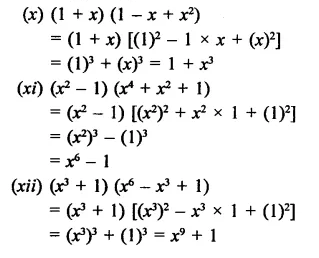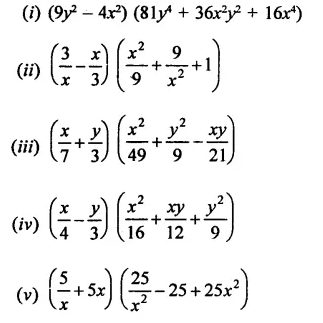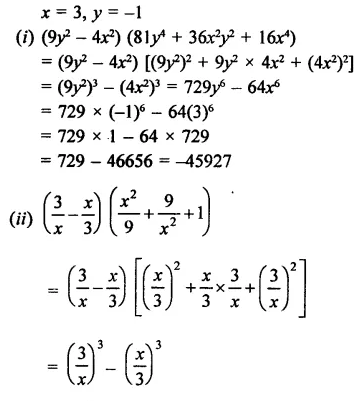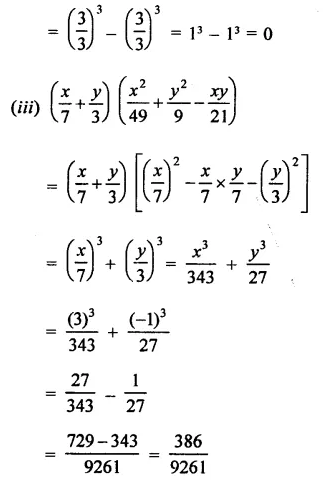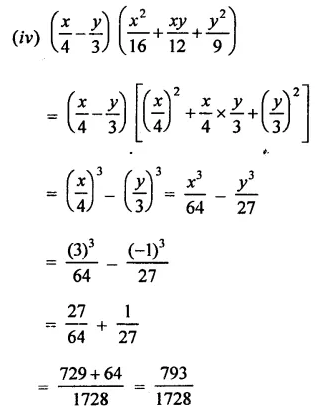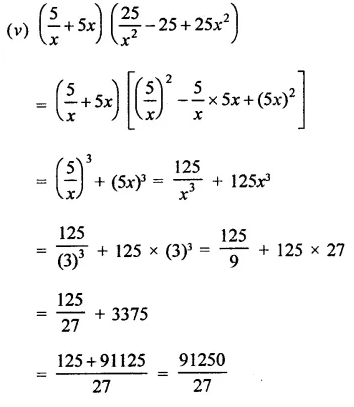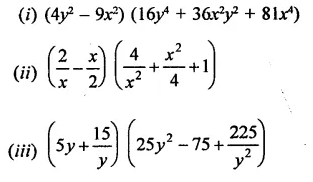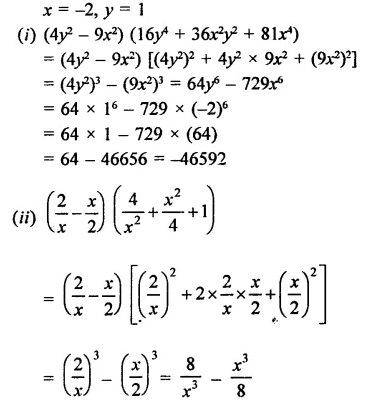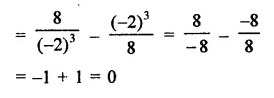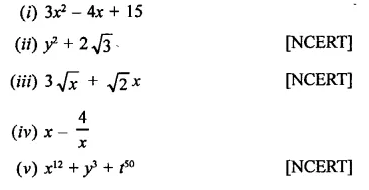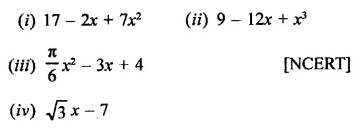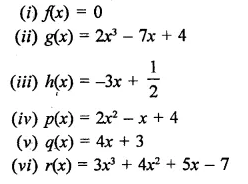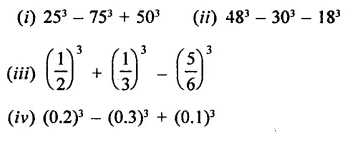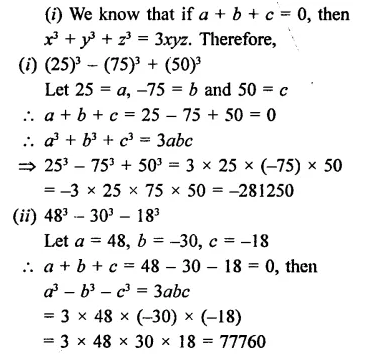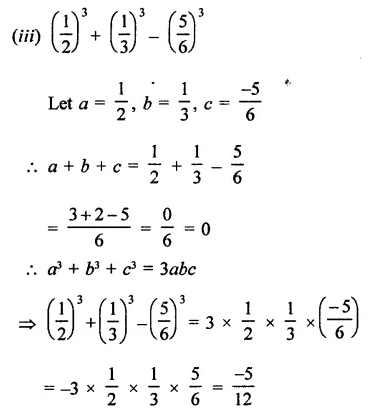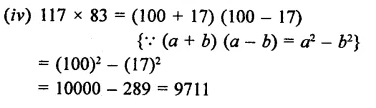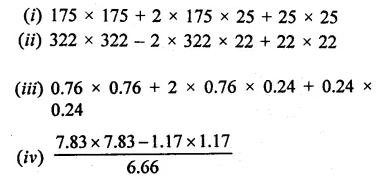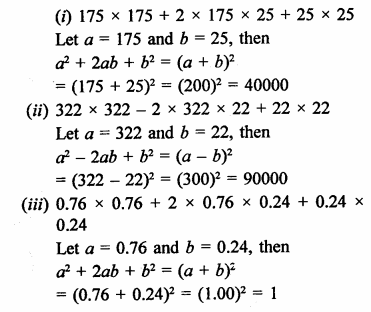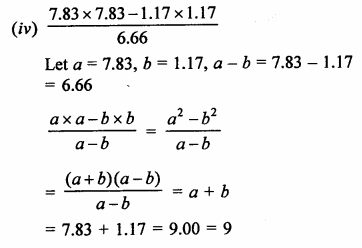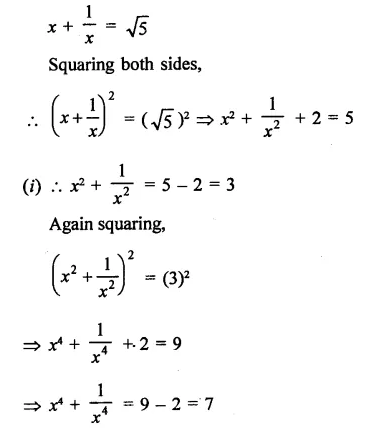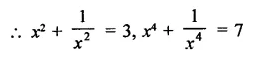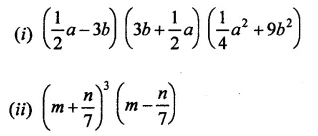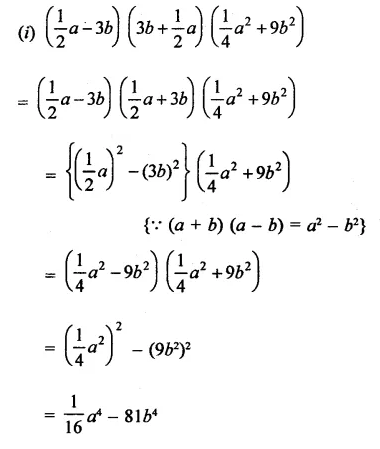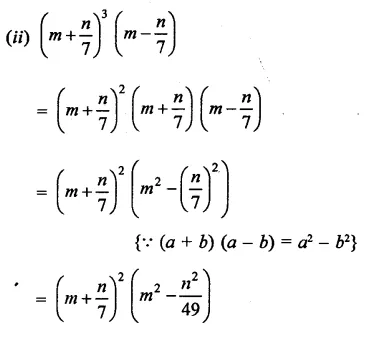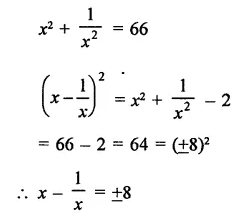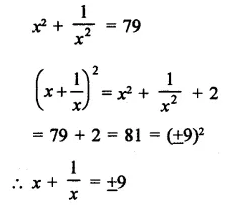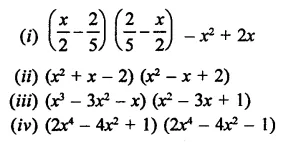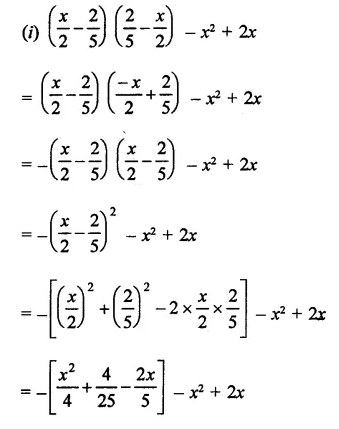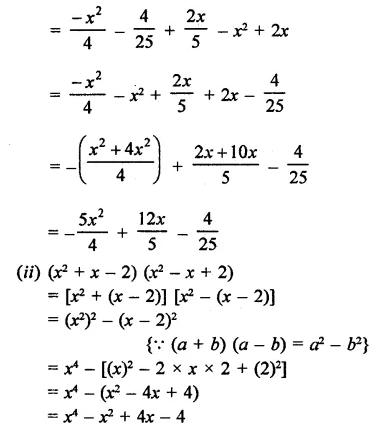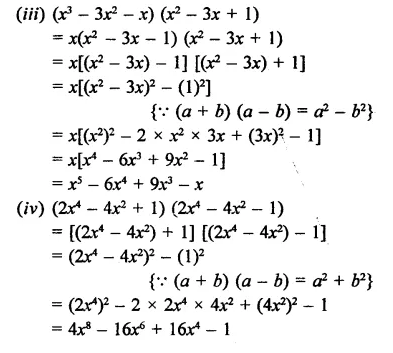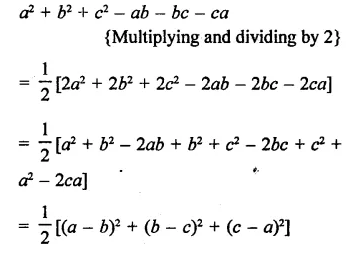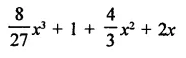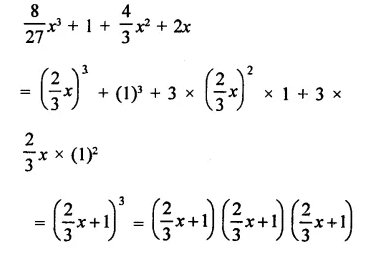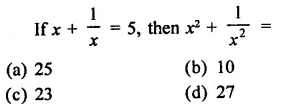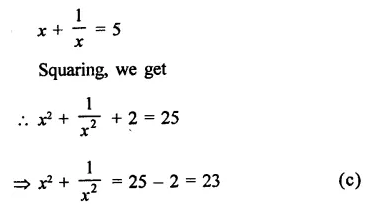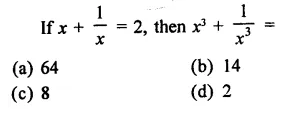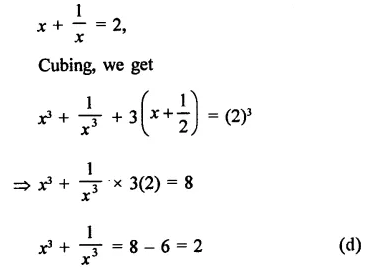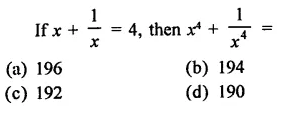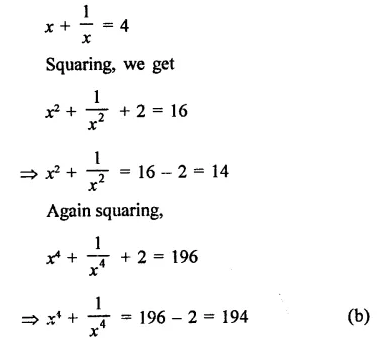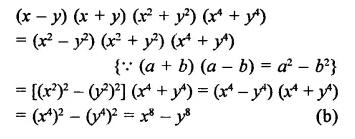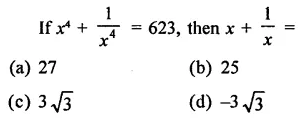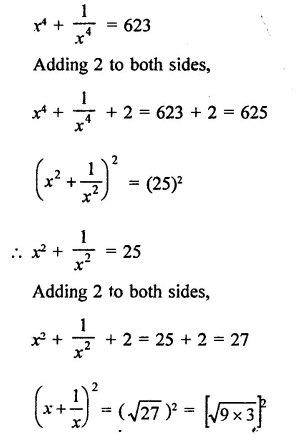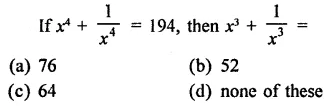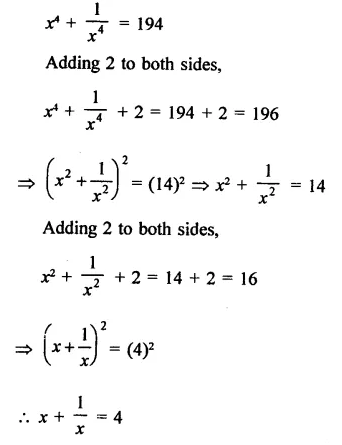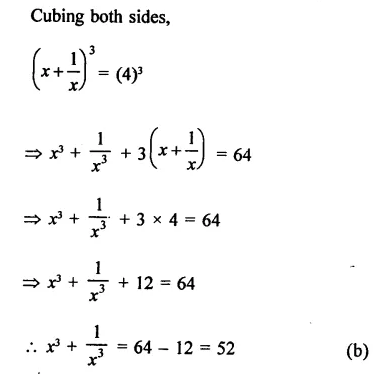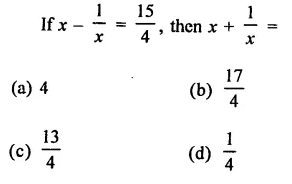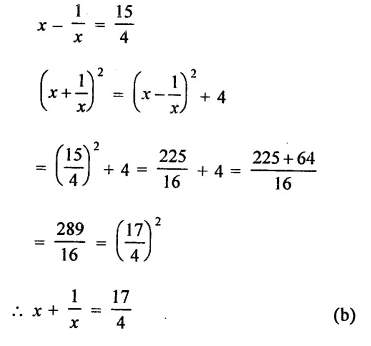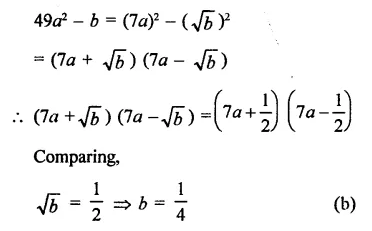Tag: Maths RD Sharma Solutions Class 9

RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2

Question 1.
Rationalise the denominators of each of the following(i – vii):
>
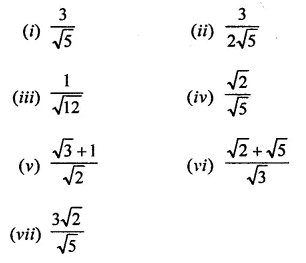Solution:

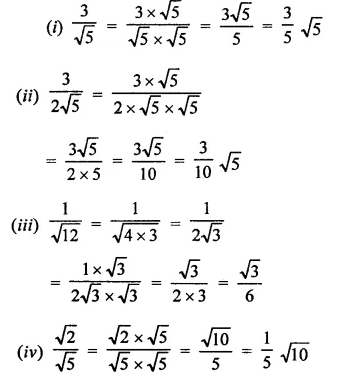
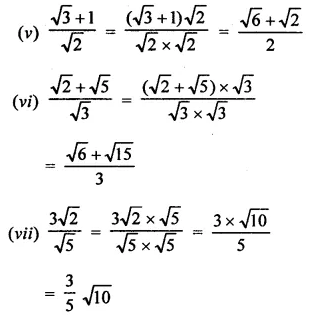
Question 2.
Find the value to three places of decimals of each of the following. It is given that

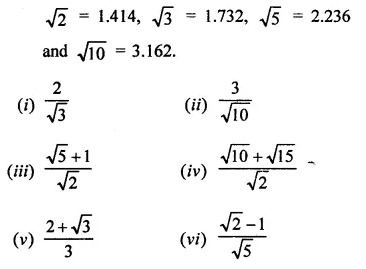
Solution:

Question 3.
Express each one of the following with rational denominator:

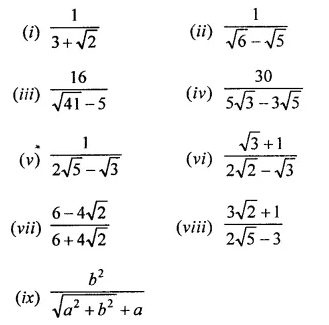
Solution:

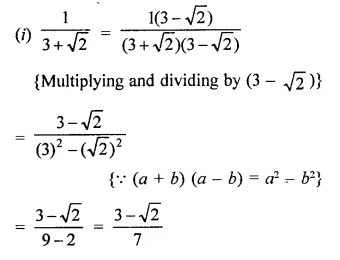
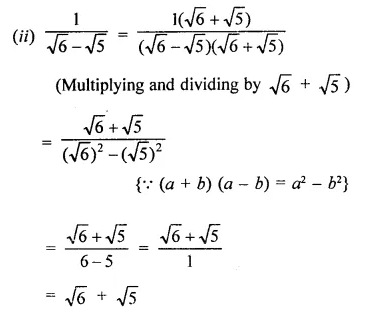
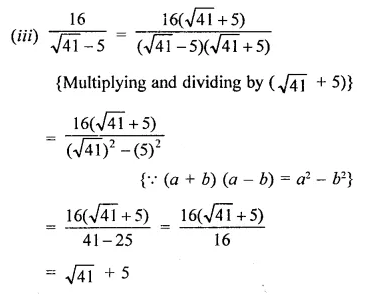
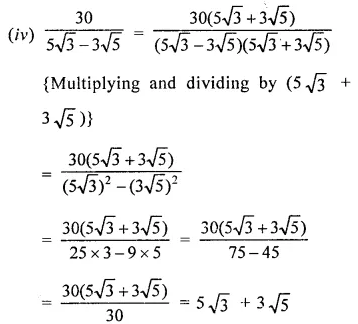
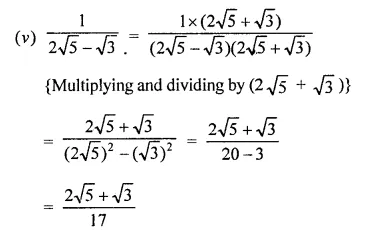
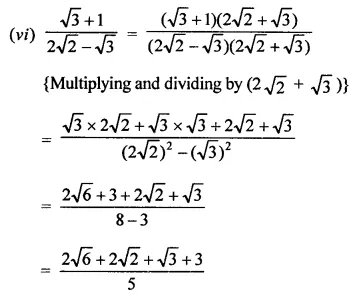
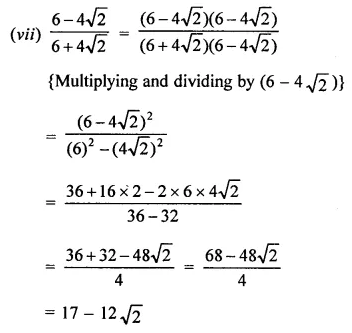
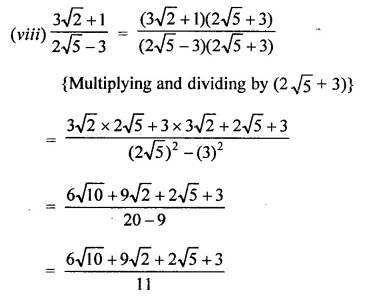
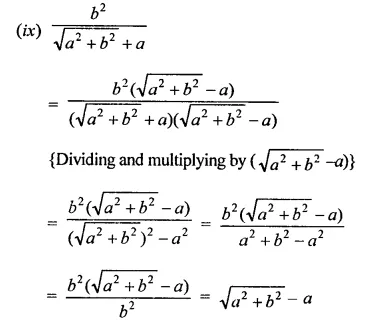
Question 4.
Rationales the denominator and simplify:

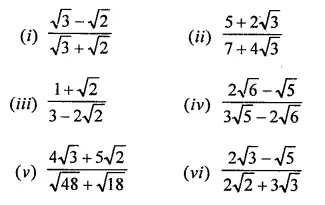
Solution:

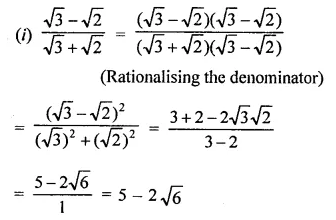
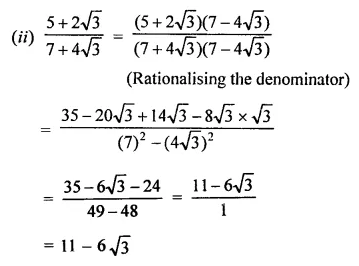
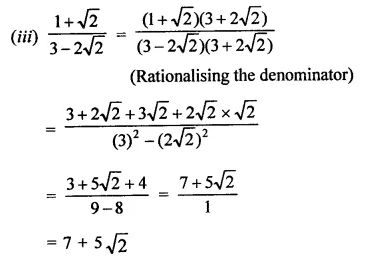
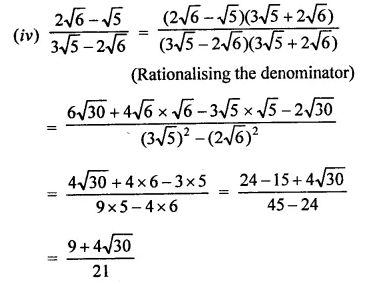
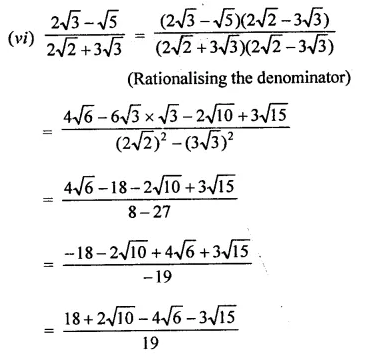
Question 5.
Simplify:

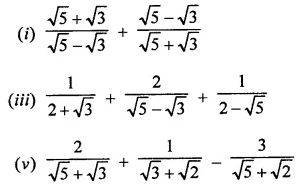
Solution:

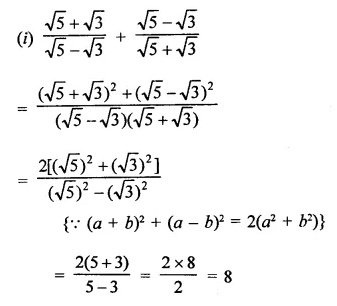
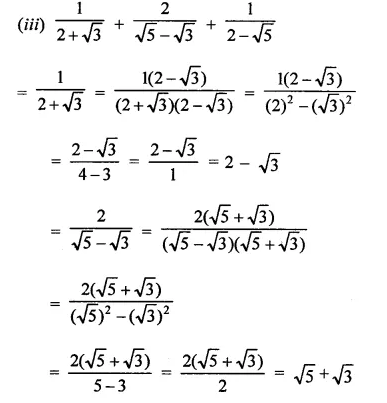
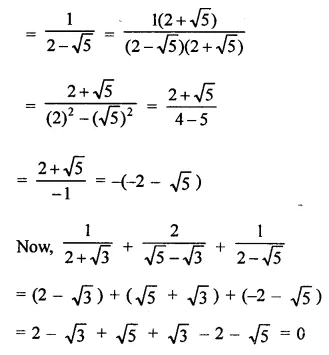
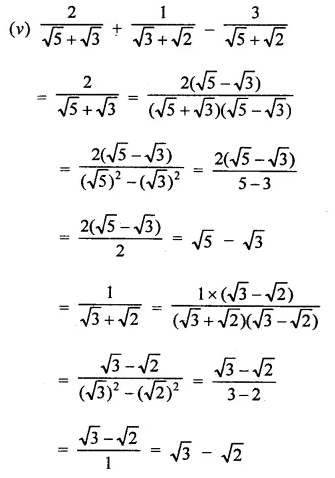
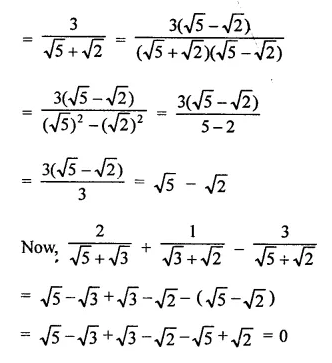
Question 6.
In each of the following determine rational numbers a and b:

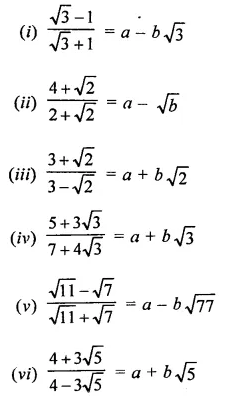
Solution:

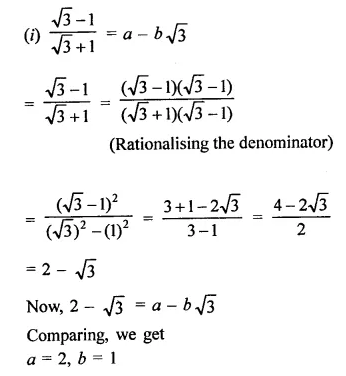
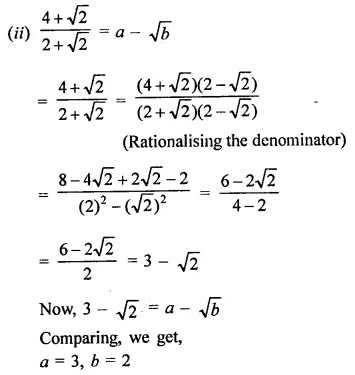
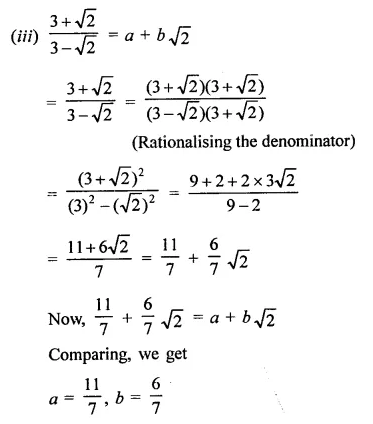
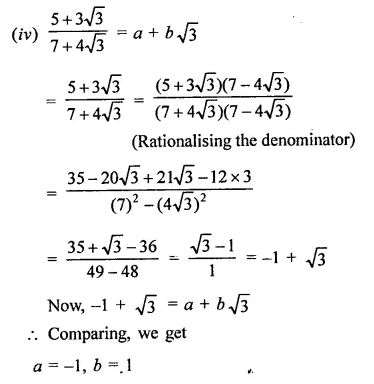
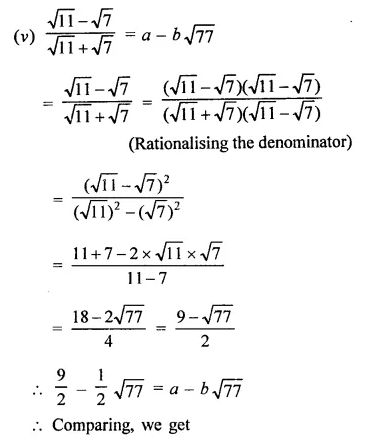
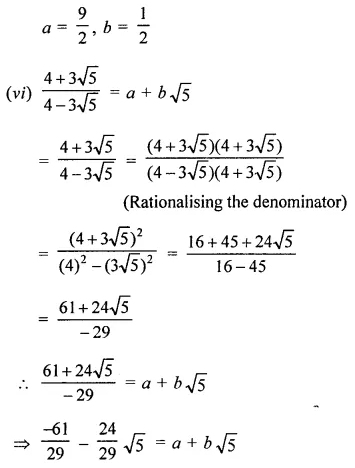
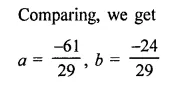
Question 7.

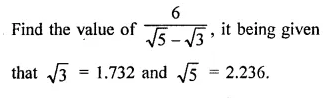
Solution:

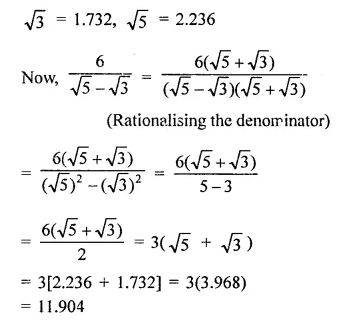
Question 8.
Find the values of each of the following correct to three places of decimals, it being given that \(\sqrt { 2 } \)  = 1.4142, \(\sqrt { 3 } \) = 1-732, \(\sqrt { 5 } \)  = 2.2360, \(\sqrt { 6 } \) =  2.4495 and \(\sqrt { 10 } \)  = 3.162.

Solution:

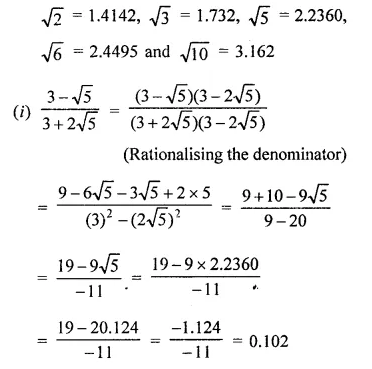
Question 9.
Simplify:

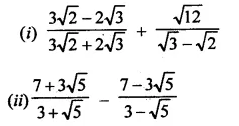
Solution:

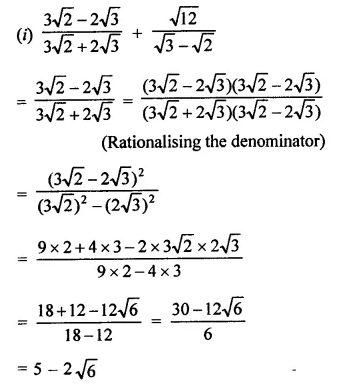
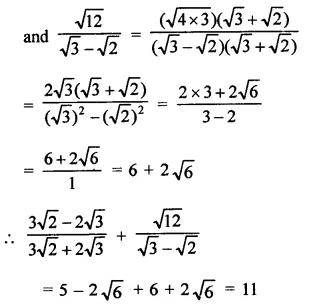
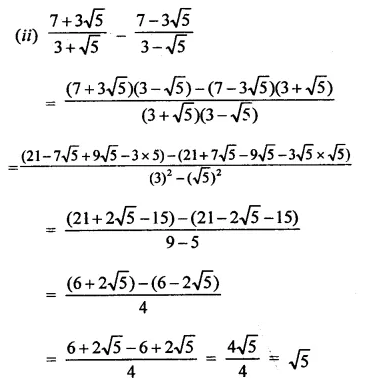
Question 10.

Solution:

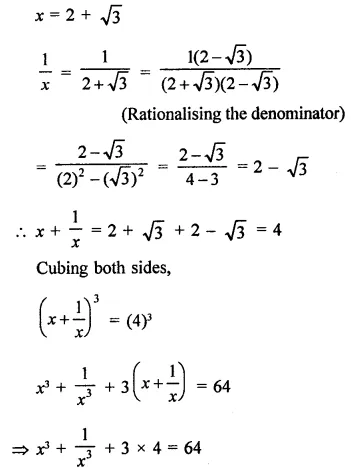
Question 11.

Solution:

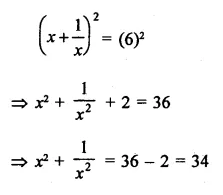
Question 12.

Solution:

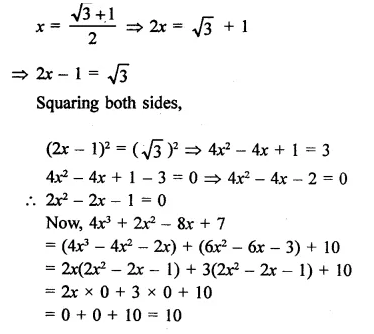
Hope given RD Sharma Class 9 Solutions Chapter 3 Rationalisation Ex 3.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities VSAQS

Question 1.

Solution:

Question 2.

Solution:

Question 3.
If a + b = 7 and ab = 12, find the value of a² + b².
Solution:
a + b = 7, ab = 12
Squaring both sides,
(a + b)² = (7)²
⇒  a² + b² + 2ab = 49
⇒  a² + b² + 2 x 12 = 49
⇒ a² + b² + 24 = 49
⇒ a² + b² = 49 – 24 = 25
∴ a² + b² = 25

Question 4.
If a – b = 5 and ab = 12, find the value of a² + b² .
Solution:
a – b = 5, ab = 12
Squaring both sides,
⇒ (a – b)² = (5)²
⇒  a² + b² – 2ab = 25
⇒  a² + b² – 2 x 12 = 25
⇒  a² + b² – 24 = 25
⇒  a² + b² = 25 + 24 = 49
∴ a² + b² = 49

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 3 Rationalisation MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 3 Rationalisation MCQS

Mark the correct alternative in each of the following:
Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.
The rationalisation factor of 2 + \(\sqrt { 3 } \)  is
(a) 2 – \(\sqrt { 3 } \)
(b) \(\sqrt { 2 } \) + 3
(c)  \(\sqrt { 2 } \) – 3
(d) \(\sqrt { 3 } \) – 2
Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Question 21.

Solution:

Question 22.

Solution:

Question 23.

Solution:

Question 24.

Solution:

Question 25.

Solution:

Hope given RD Sharma Class 9 Solutions Chapter 3 Rationalisation MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

Factorize each of the following expressions:
Question 1.
p³ + 27
Solution:
We know that a³ + b³ = (a + b) (a² – ab + b²)
a³ – b³ = (a – b) (a² + aft + b²)
p³ + 21 = (p)³ + (3)³
= (p + 3) (p²– p x 3 + 3²)
= (p + 3) (p² – 3p + 9)

Question 2.
y³ + 125
Solution:
y³ + 125 = (p)³ + (5)³
= (p + 5) (p² – 5y + 5²)
= (P + 5) (p² – 5y + 25)

Question 3.
1 – 21a³
Solution:
1 – 21a³ = (1)³ – (3a)³
= (1 – 3a) [1² + 1 x 3a + (3a)²]
= (1 – 3a) (1 + 3a + 9a²)

Question 4.
8x³y³ + 27a³
Solution:
8x³y³ + 27a³
= (2xy + 3a) [(2xy)² – 2xy x 3a + (3a)²]
= (2xy + 3a) (4x²y – 6xya + 9a²)

Question 5.
64a³ – b³
Solution:
64a³ – b³ = (4a)³ – (b)³
= (4a – b) [(4a)² + 4a x b + (b)²]
= (4a – b) (16a² + 4ab + b²)

Question 6.

Solution:

Question 7.
10x⁴– 10xy⁴
Solution:
I0x⁴y- 10xy⁴ = 10xy(x³ -y³)
= 10xy(x – y) (x² + xy + y²)

Question 8.
54x⁶y + 2x³y⁴
Solution:
54 x⁶y + 2x³y⁴ = 2x³y(27x³ + y³)
= 2x³y[(3x)³ + (y)³]
= 2x³y(3x + y) [(3x)² -3x x y + y²]
= 2x³y(3x + y) (9x² -3xy + y²)

Question 9.
32a³ + 108b³
Solution:
32a³ + 108b³
= 4(8a³ + 27b³) = 4 [(2a)³ + (3 b)³]
= 4(2a + 3b) [(2a)² – 2a x 3b + (3b)²]
= 4(2a + 3b) (4a² – 6ab + 9b²)

Question 10.
(a – 2b)³ – 512b³
Solution:
(a – 2b)³ – 512b³
= (a – 2b)³ – (8b)³
= (a – 2b- 8b) [(a – 2b)² + (a – 2b) x 8b + (8b)²]
= (a – 10b) [a² + 4b² – 4ab + 8ab – 16b² + 64b²]
= (a – 10b) (a² + 4ab + 52b²)

Question 11.
8x²y³ – x⁵
Solution:
8x²y³ – x⁵ = x²(8y³ – X³)
= x²(2y)³ – (x)³]
= x²[(2y – x) (2y)² + 2y x x + (x)²]
= x²(2y – x) (4y² + 2xy + x²)

Question 12.
1029 -3x³
Solution:
1029 – 3X³ = 3(343 – x³)                       ‘
= 3 [(7)³ – (x)³]
= 3(7 – x) (49x + 7x + x²)

Question 13.
x³y³+ 1
Solution:
x³y³ + 1 = (xy)³ + (1)³
= (xy + 1) [(xy)² – xy x 1 + (1)²]
= (xy + 1) (x²y² – xy + 1)
= (xy + 1) (x²y – xy + 1)

Question 14.
x⁴y⁴ – xy
Solution:
x⁴y⁴ – xy = xy(x³y³ – 1)
= xy[(xy³-(1)³]
= xy (xy – 1) [x²y² + 2xy + 1]

Question 15.
a³ + b³ + a + b
Solution:
a³ + b³ + a + b
= (a + b) (a² – ab + b²) + 1 (a + b)
= (a + b) (a² – ab + b² + 1)

Question 16.
Simplify:

Solution:

Question 17.
(a + b)³ – 8(a – b)³
Solution:
(a + b)³ – 8(a – b)³
= (a + b)² – (2a – 2b)³
= (a+ b – 2a + 2b) [(a + b)² + (a + b) (2a-2b) + (2a – 2b)²)]
= (3b – a) [a² + b² + 2ab + 2a² – 2ab + 2ab – 2b² + 4a² – 8ab + 4b²]
= (3b – a) [7a² – 6ab + 3b²]

Question 18.
(x + 2)³ + (x- 2)³
Solution:
(x + 2)³ + (x – 2)³
= (x + 2 + x – 2) [(x + 2)² – (x + 2) (x – 2) + (x – 2)²]
= 2x [x² + 4x + 4 – (x² + 2x – 2x – 4) + x² 4x + 4]
= 2x[x² + 4x + 4- x²-2x + 2x + 4+ x²– 4x + 4]
= 2x[x² + 12]

Question 19.
x⁶ +y⁶
Solution:
x⁶ + y⁶ = (x²)³ + (y²)³
= (x² + y²) [x⁴ – x²y² + y⁴]

Question 20.
a¹² + b¹²
Solution:
a¹² + b¹² = (a⁴)³ + (b⁴)³
= (a⁴ + b⁴) [(a⁴)² – a⁴b⁴ + (b⁴)²]
= (a⁴ + b⁴) (a⁸ – a⁴b⁴ + b⁸)

Question 21.
x³ + 6x² + 12x + 16
Solution:
x³ + 6x² + 12x + 16
= (x)³ + 3.x².2 + 3.x.4 + (2)³ + 8           {∵ a³ + 3a²b + 3ab² +b³ = (a + b)³}
= (x + 2)³ + 8 = (x + 2)³ + (2)³
= (x + 2 + 2) [(x + 2)² – (x + 2) x 2 + (2)²] {∵ a³ + b² = (a + b) (a² – ab + b²}
= (x + 4) (x² + 4x + 4 – 2x – 4 + 4)
= (x + 4) (x² + 2x + 4)

Question 22.

Solution:

Question 23.
a³ + 3a²b + 3ab² + b³ – 8
Solution:
a³ + 3a²b + 3ab² + b³ – 8
= (a + b)³ – (2)³
= (a + b -2)[(a + b)² + (a +b)x2 + (2)²]
= (a + b-2) (a² + b² + 2ab + 2a + 2b + 4)
= (a + b – 2) (a² + b² + 2ab + 2(a + b) + 4]
= (a + b – 2) [(a + b)² + 2(a + b) + 4}

Question 24.
8a³ – b³ – 4ax + 2bx
Solution:
8a³ – b³ – 4ax + 2bx
(2a)³ – (b)³ – 2x(2a – b)
= (2a-b)[(2a)² + 2a x b + (b)²]- 2x(2a-b)
= (2a – b) [4a² + 2ab + b²] – 2x(2a – b)
= (2a – b) [4a² + 2ab + b² – 2x]

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.2

Question 1.
Write the following in the expanded form:

Solution:

Question 2.
If a + b + c = 0 and a² + b² + c² = 16, find the value of ab + be + ca.
Solution:
a + b+ c = 0
Squaring both sides,
(a + b + c)² = 0
⇒ a² + b² + c² + 2(ab + bc + ca) = 0
16 + 2(ab + bc + c) = 0
⇒ 2(ab + bc + ca) = -16
⇒  ab + bc + ca =-\(\frac { 16 }{ 2 }\) = -8
∴ ab + bc + ca = -8

Question 3.
If a² + b² + c² = 16 and ab + bc + ca = 10, find the value of a + b + c.
Solution:
(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
= 16 + 2 x 10
= 16 + 20 = 36
= (±6)²
∴ a + b + c = ±6

Question 4.
If a + b + c = 9 and ab + bc + ca = 23, find the value of a² + b² + c².
Solution:
(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
⇒ (9)² = a² + b² + c² + 2 x 23
⇒ 81= a² + b² + c² + 46
⇒  a² + b² + c² = 81 – 46 = 35
∴ a² + b² + c² = 35

Question 5.
Find the value of 4x² + y² + 25z² + 4xy – 10yz – 20zx when x = 4, y = 3 and z = 2.
Solution:
x = 4, y – 3, z = 2
⇒ 4x² + y² + 25z² + 4xy – 10yz – 20zx
= (2x)² + (y)² + (5z)² + 2 x2 x x y-2 x y x 5z – 2 x 5z x 2x
= (2x + y- 5z)²
= (2 x 4 + 3- 5 x 2)²
= (8 + 3- 10)²
= (11 – 10)²
= (1)² = 1

Question 6.
Simplify:
(i)  (a + b + c)² + (a – b + c)²
(ii) (a + b + c)² –  (a – b + c)²
(iii) (a + b + c)² +   (a – b + c)² + (a + b – c)²
(iv) (2x + p – c)² – (2x – p + c)²
(v) (x² + y² – z²)² – (x² – y² + z²)²
Solution:

Question 7.
Simplify each of the following expressions:

Solution:

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4

Question 1.
Find the following products:
(i) (3x + 2y) (9X² – 6xy + Ay²)
(ii) (4x – 5y) (16x² + 20xy + 25y²)
(iii) (7p⁴ + q) (49p⁸ – 7p⁴q + q²)

Solution:

Question 2.
If x = 3 and y = -1, find the values of each of the following using in identity:

Solution:

Question 3.
If a + b = 10 and ab = 16, find the value of a² – ab + b² and a² + ab + b².
Solution:
a + b = 10, ab = 16 Squaring,
(a + b)² = (10)²
⇒ a² + b² + lab = 100
⇒ a² + b² + 2 x 16 = 100
⇒  a² + b² + 32 = 100
∴ a² + b² = 100 – 32 = 68
Now, a² – ab + b² = a² + b² – ab = 68 – 16 = 52
and a² + ab + b² = a² + b² + ab = 68 + 16 = 84

Question 4.
If a + b = 8 and ab = 6, find the value of a³ + b³.
Solution:
a + b = 8, ab = 6
Cubing both sides,
(a + b)³ = (8)3
⇒ a³ + b³ + 3 ab{a + b) = 512
⇒  a³ + b³ + 3 x 6 x 8 = 512
⇒  a³ + b³ + 144 = 512
⇒  a³ + b³ = 512 – 144 = 368
∴ a³ + b³ = 368

Question 5.
If a – b = 6 and ab = 20, find the value of a³-b³.
Solution:
a – b = 6, ab = 20
Cubing both sides,
(a – b)3 = (6)³
⇒  a³ – b³ – 3ab(a – b) = 216
⇒  a³ – b³ – 3 x 20 x 6 = 216
⇒  a³ – b³ – 360 = 216
⇒  a³ -b³ = 216 + 360 = 576
∴ a³ – b³ = 576

Question 6.
If x = -2 and y = 1, by using an identity find the value of the following:

Solution:

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
• RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS

Question 1.
Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer:

Solution:
(i) 3x² – 4x + 15,
(ii) y² + 2\(\sqrt { 3 } \) are polynomial is one variable. Others are not polynomial or polynomials in one variable.

Question 2.
Write the coefficient of x² in each of the following:

Solution:
Coefficient of x²,
in (i) is 7
in (ii) is 0 as there is no term of x² i.e. 0 x²

Question 3.
Write the degrees of each of the following polynomials:
(i) 7x³ + 4x² – 3x + 12
(ii) 12 – x + 2x³
(iii) 5y – \(\sqrt { 2 } \)
(iv) 7
(v) 0
Solution:
(i) Degree of the polynomial 7x³ + 4x² – 3x + 12 is 3
(ii) Degree of the polynomial 12 – x + 2x³ is 3
(iii) Degree of the polynomial 5y – \(\sqrt { 2 } \)is 1
(iv) Degree of the polynomial 7 is 0
(v) Degree of the polynomial 0 is 0 undefined.

Question 4.
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
(i) x + x² + 4
(ii) 3x – 2
(iii) 2x + x² [NCERT]
(iv) 3y
(v) t² + 1
(v) 7t⁴ + 4t³ + 3t – 2
Solution:
(i)  x + x² + 4 It is a quadratic polynomial.
(ii) 3x – 2 : It is a linear polynomial.
(iii) 2x + x²: It is a quadratic polynomial.
(iv) 3y It is a linear polynomial.
(v) t²+ 1 It is a quadratic polynomial.
(vi) 7t⁴ + 4t³ + 3t – 2 It is a biquadratic polynomial.

Question 5.
Classify the following polynomials as polynomials in one-variable, two-variables etc.
(i) x²-xy +7y²
(ii) x² – 2tx + 7t² – x + t
(iii) t³ -3t² + 4t-5
(iv) xy + yz + zx
Solution:
(i) x² – xy + 7y²: It is a polynomial in two j variables x, y.
(ii) x² – 2tx + 7t² – x + t: It is a polynomial in two variables in x, t.
(iii) t³ – 3t² + 4t – 5 : It is a polynomial in one variable in t.
(iv) xy +yz + zx : It is a polynomial in 3 variables in x, y and

Question 6.
Identify polynomials in the following:

Solution:

Question 7.
Identify constant, linear, quadratic and cubic polynomials from the following polynomials:

Solution:
(i) f(x) = 0 : It is a constant polynomial as it has no variable.
(ii) g(x) = 2x³ – 7x + 4 : It is a cubic polynomial.
(iii) h(x) = -3x + \(\frac { 1 }{ 2 }\) : It is a linear polynomial.
(iv) p(x) = 2x² – x + 4 : It is a quadratic polynomial.
(v) q(x) = 4x + 3 : It is linear polynomial.
(vi) r(x) = 3x³ + 4x² + 5x – 7 : It is a cubic polynomial.

Question 8.
Give one example each of a binomial of degree 35 and of a monomial of degree 100.   [NCERT]
Solution:
Example of a binomial of degree 35 = 9x³⁵ + 16
Example of a monomial of degree 100 = 2y¹⁰⁰

 

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.5

Question 1.
Find the following products:
(i) (3x + 2y + 2z) (9x² + 4y² + 4z² – 6xy – 4yz – 6zx)
(ii) (4x -3y + 2z) (16x² + 9y²+ 4z² + 12xy + 6yz – 8zx)
(iii) (2a – 3b – 2c) (4a² + 9b² + 4c² + 6ab – 6bc + 4ca)
(iv) (3x -4y + 5z) (9x² + 16y² + 25z² + 12xy- 15zx + 20yz)
Solution:
(i) (3x + 2y + 2z) (9x² + 4y² + 4z² – 6xy – 4yz – 6zx)
= (3x + 2y + 2z) [(3x)² + (2y)² + (2z)² – 3x x 2y + 2y x 2z + 2z x 3x]
= (3x)³ + (2y)³  + (2z)³ – 3 x 3x x 2y x 2z
= 27x³ + 8y³ + 8Z³ – 36xyz
(ii) (4x – 3y + 2z) (16x² + 9y² + 4z² + 12xy + 6yz – 8zx)
= (4x -3y + 2z) [(4x)² + (-3y)² + (2z)² – 4x x (-3y + (3y) x (2z) – (2z x 4x)]
= (4x)³ + (-3y)³ + (2z)³ – 3 x 4x x (-3y) x (2z)
= 64x³ – 27y³ + 8z³ + 72xyz
(iii) (2a -3b- 2c) (4a² + 9b² + 4c² + 6ab – 6bc + 4ca)
= (2a -3b- 2c) [(2a)² + (3b)² + (2c)² – 2a x (-3b) – (-3b) x (-2c) – (-2c) x 2a]
= (2a)³ + (3b)³ + (-2c)³ -3x 2a x (-3 b) (-2c)
= 8a³ – 21b³ -8c³ – 36abc
(iv) (3x – 4y + 5z) (9x² + 16y² + 25z² + 12xy – 15zx + 20yz)
= [3x + (-4y) + 5z] [(3x)² + (-4y)² + (5z)² – 3x x (-4y) -(-4y) (5z) – 5z x 3x]
= (3x)³ + (-4y)³ + (5z)³ – 3 x 3x x (-4y) (5z)
= 27x³ – 64y³ + 125z³ + 180xyz

Question 2.
Evaluate:

Solution:

Question 3.
If x + y + z = 8 and xy + yz+ zx = 20, find the value of x³ + y³ + z³ – 3xyz.
Solution:
We know that
x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² -xy -yz – zx)
Now, x + y + z = 8
Squaring, we get
(x + y + z)² = (8)²
x² + y² + z² + 2(xy + yz + zx) = 64
⇒ x² + y² + z² + 2 x 20 = 64
⇒  x² + y² + z² + 40 = 64
⇒  x² + y² + z² = 64 – 40 = 24
Now,
x³ + y³ + z³ – 3xyz = (x + y + z) [x² + y² + z² – (xy + yz + zx)]
= 8(24 – 20) = 8 x 4 = 32

Question 4.
If a +b + c = 9 and ab + bc + ca = 26, find the value of a³ + b³ + c³ – 3abc.
Solution:
a + b + c = 9, ab + be + ca = 26
Squaring, we get
(a + b + c)² = (9)²
a² + b² + c² + 2 (ab + be + ca) = 81
⇒  a² + b² + c² + 2 x 26 = 81
⇒ a² + b² + c² + 52 = 81
∴  a² + b² + c² = 81 – 52 = 29
Now, a³ + b³ + c³ – 3abc = (a + b + c) [(a² + b² + c² – (ab + bc + ca)]
= 9[29 – 26]
= 9 x 3 = 27

Question 5.
If a + b + c = 9, and a² + b² + c² = 35, find the value of a³ + b³ + c³ – 3abc.
Solution:
a + b + c = 9
Squaring, we get
(a + b + c)² = (9)²
⇒  a² + b² + c² + 2 (ab + be + ca) = 81
⇒  35 + 2(ab + bc + ca) = 81
2(ab + bc + ca) = 81 – 35 = 46
∴  ab + bc + ca = \(\frac { 46 }{ 2 }\) = 23
Now, a³ + b³ + c³ – 3abc
= (a + b + c) [a² + b² + c² – (ab + bc + ca)]
= 9[35 – 23] = 9 x 12 = 108

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1

Question 1.
Evaluate each of the following using identities:
(i) (2x –\(\frac { 1 }{ x }\))²
(ii)  (2x + y) (2x – y)
(iii) (a²b – b²a)²
(iv) (a – 0.1) (a + 0.1)
(v) (1.5.x² – 0.3y²) (1.5x² + 0.3y²)
Solution:

Question 2.
Evaluate each of the following using identities:
(i) (399)²
(ii) (0.98)²
(iii) 991 x 1009
(iv) 117 x 83
Solution:

Question 3.
Simplify each of the following:

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.
If 9x² + 25y² = 181 and xy = -6, find the value of 3x + 5y.
Solution:
9x² + 25y² = 181, and xy = -6
(3x + 5y)² = (3x)² + (5y)² + 2 x 3x + 5y
⇒ 9X² + 25y² + 30xy
= 181 + 30 x (-6)
= 181 – 180 = 1
= (±1 )²
∴ 3x + 5y = ±1

Question 8.
If 2x + 3y = 8 and xy = 2, find the value of 4X² + 9y².
Solution:
2x + 3y = 8 and xy = 2
Now, (2x + 3y)² = (2x)² + (3y)² + 2 x 2x x 3y
⇒  (8)² = 4x² + 9y² + 12xy
⇒ 64 = 4X² + 9y² + 12 x 2
⇒ 64 = 4x² + 9y² + 24
⇒ 4x² + 9y² = 64 – 24 = 40
∴ 4x² + 9y² = 40

Question 9.
If 3x -7y = 10 and xy = -1, find the value of 9x² + 49y²
Solution:
3x – 7y = 10, xy = -1
3x -7y= 10
Squaring both sides,
(3x – 7y)² = (10)²
⇒ (3x)² + (7y)² – 2 x 3x x 7y = 100
⇒  9X² + 49y² – 42xy = 100
⇒  9x² + 49y² – 42(-l) = 100
⇒ 9x² + 49y² + 42 = 100
∴ 9x² + 49y² = 100 – 42 = 58

Question 10.
Simplify each of the following products:

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.
Simplify each of the following products:

Solution:

Question 14.
Prove that a² + b² + c² – ab – bc – ca is always non-negative for all values of a, b and c.
Solution:

∵  The given expression is sum of these squares
∴ Its value is always positive Hence the given expression is always non-­negative for all values of a, b and c

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities Ex 4.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.1
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.2
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.4
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions VSAQS
• RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions MCQS

Factorize:
Question 1.
64a³ + 125b³ + 240a²b + 300ab²
Solution:
64a³ + 125b³ + 240a²b + 300ab²
= (4a)³ + (5b)³ + 3 x (4a)² x 5b + 3(4a) + (5b)²
= (4a + 5b)³
= (4a + 5b) (4a + 5b) (4a + 5b)

Question 2.
125x³ – 27y³ – 225x²y + 135xy²
Solution:
125x³ – 27y³ – 225x²y + 135xy²
= (5x)³ – (3y)³ – 3 x (5x)² x (3y) + 3- x 5x x (3y)²
= (5x – 3y)³
= (5x – 3y) (5x – 3y) (5x – 3y)

Question 3.

Solution:

Question 4.
8x³ + 27y³ + 36x²y + 54xy²
Solution:
8x³ + 27y³ + 16x²y + 54xy²
= (2x)³ + (3y)³ + 3 x (2x)² x 3y  +  3 x 2x x (3y)²
= (2x + 3y)³
= (2x + 3y) (2x + 3y) (2x + 3y)

Question 5.
a³ – 3a²b + 3ab² – b³ + 8
Solution:
a³ – 3a²b + 3ab² – b³ + 8
= (a – b)³ + (2)³
= (a – b + 2) [(a -b)²– (a – b) x 2 + (2)²]
= (a- b + 2) (a² + b² -2ab – 2a + 2b + 4)

Question 6.
x³ + 8y³ + 6x²y + 12xy²
Solution:
x³ + 8y³ + 6x²y + 12xy²
= (x)³ + (2y)³ + 3 x x²x 2y + 3 x x x (2y)²
= (x + 2y)³
= (x + 2y) (x + 2y) (x + 2y)

Question 7.
8x³ + y³ + 12x²y + 6xy²
Solution:
8x³ + y³ + 12x²y + 6xy²
= (2x)³ + (y)³ + 3 x (2x)² x y + 3 x 2x x y²
= (2x + y)³
= (2x + y) (2x + y) (2x + y)

Question 8.
8a³ + 27b³ + 36a²b + 54ab²
Solution:
8a³ + 27b³ + 16a²b + 54ab²
= (2a)³ + (3b)³ + 3 x (2a)² x 3b + 3 x 2a x (3b)²
= (2a + 3b)³
= (2a + 3b) (2a + 3b) (2a + 3b)

Question 9.
8a³ – 27b³ – 36a²b + 54ab²
Solution:
8a³ – 27b³ – 36a²b + 54ab²
= (2a)³ – (3b)³ – 3 x (2a)² x 3b + 3 x 2a x (3b)²
= (2a – 3b))³
= (2a – 3b) (2a – 3b) (2a – 3b)

Question 10.
x³ – 12x(x – 4) – 64
Solution:
x³ – 12x(x – 4) – 64
= x³ – 12x² + 48x – 64
= (x)³ – 3 x x² x 4 + 3 x x x (4)²– (4)³
= (x – 4)³
= (x – 4) (x – 4) (x – 4)

Question 11.
a³x³ – 3a²bx² + 3ab²x – b³
Solution:
a³x³ – 3a²bx² + 3ab²x – b³
= (ax)³ – 3 x (ax)² x  b + 3 x ax x (b)²– (b)³
= (ax – b)³
= (ax – b) (ax – b) (ax – b)

 

Hope given RD Sharma Class 9 Solutions Chapter 5 Factorisation of Algebraic Expressions Ex 5.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities MCQS

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.
If a + b + c = 9 and  ab + bc + ca = 23, then a² + b² + c² =
(a) 35
(b) 58
(c) 127
(d) none of these
Solution:
a + b + c = 9, ab + bc + ca = 23
Squaring,
(a + b+ c) = (9)²
a² + b² + c² + 2 (ab + bc + ca) = 81
⇒ a² + b² + c² + 2 x 23 = 81
⇒  a² + b²+ c² + 46 = 81
⇒  a² + b²+ c² = 81 – 46 = 35   (a)

Question 9.
(a – b)³ + (b – c)³ + (c – a)³ =
(a) (a + b + c) (a² + b² + c² – ab – bc – ca)
(d) (a -b)(b- c) (c – a)
(c) 3(a – b) (b – c) (c – a)
(d) none of these
Solution:
(a – b)³ + (b- c)³ + (c- a)³
∵ a – b + b – c + c – a = 0
∴ (a – b)³ + (b – c)³ + (c – a)³
= 3 (a -b)(b- c) (c – a)        (c)

Question 10.

Solution:

Question 11.
If a – b = -8 and ab = -12 then a³ – b³ =
(a) -244
(b) -240
(c) -224
(d) -260
Solution:
a – b = -8, ab = -12
(a – b)³ = a³ – b³ – 3ab (a – b)
(-8)³ = a³ – b³ – 3 x (-12) (-8)
-512 = a³-b³– 288
a³ – b³ = -512 + 288 = -224      (c)

Question 12.
If the volume of a cuboid is 3x² – 27, then its possible dimensions are
(a) 3, x², -27x
(b) 3, x – 3, x + 3
(c) 3, x², 27x
(d) 3, 3, 3
Solution:
Volume = 3x² -27 = 3(x² – 9)
= 3(x + 3) (x – 3)
∴ Dimensions are   = 3, x – 3, x   +  3        (b)

Question 13.
75 x 75 + 2 x 75 x 25    + 25 x 25 is equal to
(a) 10000
(b) 6250
(c) 7500
(d) 3750
Solution:

Question 14.
(x – y) (x + y)(x² + y²) (x⁴ + y⁴) is equal to
(a) x¹⁶ – y¹⁶
(b) x⁸ – y⁸
(c) x⁸ + y⁸
(d) x¹⁶ + y¹⁶
Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.
If a² + b² + c² – ab – bc – ca = 0, then
(a) a + b = c
(b) b + c = a
(c) c + a = b
(d) a = b = c
Solution:
a² + b² + c² – ab – bc – ca = 0
2 {a² + b² + c² – ab – be – ca) = 0 (Multiplying by 2)
⇒  2a² + 2b² + 2c²– 2ab – 2bc – 2ca = 0
⇒  a² + b² – 2ab + b² + c² – 2bc + c² + a² – 2ca = 0
⇒  (a – b)² + (b – c)² + (c – a)² = 0
(a – b)² = 0, then a – b = 0
⇒ a = b
Similarly, (b – c)² = 0, then
b-c = 0
⇒ b = c
and (c – a)² = 0, then c-a = 0
⇒ c = a
∴ a = b – c           (d)

Question 20.

Solution:

Question 21.

Solution:

Question 22.
If a + b + c = 9 and ab + bc + ca = 23, then a³ + b³ + c³ – 3 abc =
(a) 108
(b) 207
(c) 669
(d) 729
Solution:
a³ + b³ + c³ – 3abc
= (a + b + c) [a² + b² + c² – (ab + bc + ca)
Now, a + b + c = 9
Squaring,
a² + b² + c² + 2 (ab + be + ca) = 81
⇒  a² + b² + c² + 2 x 23 = 81
⇒  a² + b² + c² + 46 = 81
⇒  a² + b² + c² = 81 – 46 = 35
Now, a³ + b³ + c³ – 3 abc = (a + b + c) [(a² + b² + c²) – (ab + bc + ca)
= 9[35 -23] = 9 x 12= 108                     (a)

Question 23.

Solution:

Question 24.
The product (a + b) (a – b) (a² – ab + b²) (a² + ab + b²) is equal to
(a) a⁶ +   b⁶
(b) a⁶ – b⁶
(c) a³ – b³
(d) a³ + b³
Solution:
(a + b) (a – b) (a² – ab + b²) (a² + ab +b²)
= (a + b) (a²-ab + b²) (a-b) (a² + ab + b²)
= (a³ + b³) (a³ – b³)
= (a³)² – (b³)² = a⁶ – b⁶   (b)

Question 25.
The product (x² – 1) (x⁴ + x² + 1) is equal to
(a) x⁸ –   1
(b) x⁸ + 1
(c) x⁶ –   1
(d) x⁶ + 1
Solution:
(x² – 1) (x⁴ + x² + 1)
= (x²)³ – (1)³ = x⁶ – 1                            (c)

Question 26.

Solution:

Question 27.

Solution:

Hope given RD Sharma Class 9 Solutions Chapter 4 Algebraic Identities MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.