RS Aggarwal Class 6 Solutions Chapter 16 Triangles Ex 16B
These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B
Other Exercises
- RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A
- RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B
Objective questions
Mark against the correct answer in each of following.
Question 1.
Solution:
(c) ∵ It has three sides and three angles i.e. six.
Question 2.
Solution:
(b) ∵ Sum of three angles of a triangle is 180°.
Question 3.
Solution:
(b) ∵ Largest angle
\(=\frac { { 180 }^{ O }\times 4 }{ 2+3+4 } =\frac { { 180 }^{ O }\times 4 }{ 9 } \)
= 80°
Question 4.
Solution:
(d) ∵ A triangle has 180° and if two angles are complementary i.e. sum of two angles is 90°, then third angle will be 180° – 90° = 90°.
Question 5.
Solution:
(c) ∵ Sum of three angles is 180° and sum of two equal angles = 70° + 70° = 140°, then third angle will be 180°- 140° = 40°.
Question 6.
Solution:
(c) ∵ A scalene triangle has different sides.
Question 7.
Solution:
In an isosceles ∆ABC, ∠B = ∠C and bisector of ∠B and ∠C meet at O and ∠A = 40°
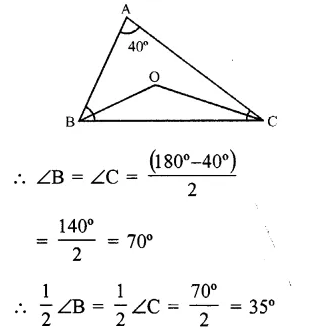
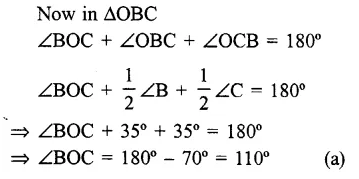
Question 8.
Solution:
Side of a triangle are in the ratio 3:2:5 and perimeter = 30 m
Length of longest side = \(\frac { 30\times 5 }{ 3+2+5 } \)
= \(\frac { 30\times 5 }{ 10 } \) cm
= 15 cm (b)
Question 9.
Solution:
Two angles of a triangle are 30° and 25° But sum of three angles of a triangle – 180°
Third angle = 180° – (30 + 25°)
= 180° – 55° = 125° (d)
Question 10.
Solution:
Each angles of an equilateral triangle = 60°
as each angle of an equilateral triangle are equal
Each angle = \(\\ \frac { 180 }{ 3 } \) = 60° (c)
Question 11.
Solution:
In the figure, P lies on AB
Its lies on the ∆ABC (c)
Hope given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.