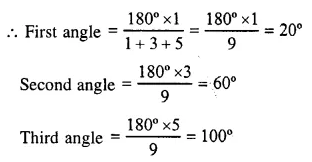Tag: RS Aggarwal Maths Solutions Class 6

RS Aggarwal Class 6 Solutions Chapter 16 Triangles Ex 16B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A
• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Objective questions
Mark against the correct answer in each of following.

Question 1.
Solution:
(c) ∵ It has three sides and three angles i.e. six.

Question 2.
Solution:
(b) ∵ Sum of three angles of a triangle is 180°.

Question 3.
Solution:
(b) ∵ Largest angle
\(=\frac { { 180 }^{ O }\times 4 }{ 2+3+4 } =\frac { { 180 }^{ O }\times 4 }{ 9 } \)
= 80°

Question 4.
Solution:
(d) ∵ A triangle has 180° and if two angles are complementary i.e. sum of two angles is 90°, then third angle will be 180° – 90° = 90°.

Question 5.
Solution:
(c) ∵ Sum of three angles is 180° and sum of two equal angles = 70° + 70° = 140°, then third angle will be 180°- 140° = 40°.

Question 6.
Solution:
(c) ∵ A scalene triangle has different sides.

Question 7.
Solution:
In an isosceles ∆ABC, ∠B = ∠C and bisector of ∠B and ∠C meet at O and ∠A = 40°

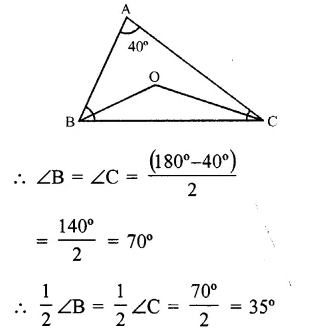
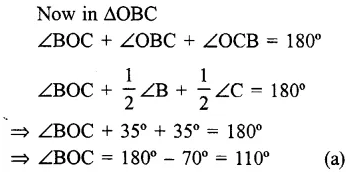
Question 8.
Solution:
Side of a triangle are in the ratio 3:2:5 and perimeter = 30 m
Length of longest side = \(\frac { 30\times 5 }{ 3+2+5 } \)
= \(\frac { 30\times 5 }{ 10 } \) cm
= 15 cm (b)

Question 9.
Solution:
Two angles of a triangle are 30° and 25° But sum of three angles of a triangle – 180°
Third angle = 180° – (30 + 25°)
= 180° – 55° = 125° (d)

Question 10.
Solution:
Each angles of an equilateral triangle = 60°
as each angle of an equilateral triangle are equal
Each angle = \(\\ \frac { 180 }{ 3 } \) = 60° (c)

Question 11.
Solution:
In the figure, P lies on AB
Its lies on the ∆ABC (c)

Hope given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10A
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D

Question 1.
Solution:
(i) 4, 6, 8, 12
If it is in proportion, then
If ad = bc if 4 x 12 = 6 x 8
If 48 = 48
Which is true
∴ 4, 6, 8, 12 are in proportion
(ii) 7, 42, 13, 78
7 : 42 :: 13 : 78
If ad = bc if 7 x 78 = 42 x 13
If 546 = 546
Which is true
∴ 7, 42, 13, 78 are in proportion
(iii) 33, 121, 9, 96 or 33 : 121 :: 9 : 96
are in proportion
If ad = bc
If 33 x 96 = 121 x 9
If 3168 = 1089
Which is not true
∴ 33, 121,9, 96 are not in proportion
(iv) 22, 33, 42, 63 or 22 : 33 :: 42 : 63
are in proportion
If ad = bc
If 22 x 63 = 33 x 42
If 1386 = 1386
Which is true
∴ 22, 33, 42, 63 are in proportion
(v) 32, 48, 70, 210 or 32 : 48 :: 70 : 210
are in proportion
If ad = bc
If 32 x 210 = 48 x 70
If 6720 = 3360
Which is not true
∴ 32, 48, 70, 210 are not in proportion
(vi) 150, 200, 250, 300 or
150 : 200 :: 250 : 300 are in proportion
If ad = bc if 150 x 300 = 200 x 250
If 45000 = 50000
Which is not true
∴ 150, 200,250, 300 are not in proportion

Question 2.
Solution:
(i) We have 60 : 105 :: 84 : 147
Product of means = 105 x 84 = 8820
Product of extremes = 60 x 147 = 8820
∴ Product of means = Product of extremes
Hence 60 : 105 :: 84 : 147 is verified.
(ii) We have 91 : 104 :: 119 : 136
Product of means = 104 x 119 = 12376
Product of extremes = 91 x 136 = 12376
Product of means = Product of extremes
Hence 91 : 104 :: 119 : 136 is verified.
(iii) We have 108 : 72 :: 129 : 86
Product of means = 72 x 129 = 9288
Product of extremes = 108 x 86 = 9288
Product of means = Product of extremes
Hence 108 : 72 :: 129 : 86 is verified.
(iv) We have 39 : 65 :: 141 : 235
Product of means = 65 x 141 = 9165
Product of extremes = 39 x 235 = 9165
∴ Product of means = Product of extremes
Hence 39 : 65 :: 141 : 235 is verified.

Question 3.
Solution:
(i) We have 55 : 11 :: x : 6
Product of means = 11 × x = 11x
Product of extremes = 55 x 6 = 330

Question 4.
Solution:
(i) We have, 51 : 68 = \(\\ \frac { 51 }{ 68 } \)
= \(\\ \frac { 3 }{ 4 } \)

Question 5.
Solution:
(i) 25 cm : 1 m and Rs. 40 : Rs. 160
= \(\\ \frac { 25cm }{ 1000cm } \) = \(\\ \frac { 1 }{ 4 } \),
\(\\ \frac { Rs.40 }{ Rs.160 } \) = \(\\ \frac { 1 }{ 4 } \)

Question 6.
Solution:
Let the third term be x.
Then 51 : 68 :: x : 108
Now, product of means = x × 68
And, product of extremes = 51 × 108
x × 68 = 51 × 108
=> x = \(\\ \frac { 51\times 108 }{ 68 } \)
= 3 × 27 = 81
x = 81
Hence the third term of the given proportion is 81

Question 7.
Solution:
1st term =12, third term = 8 and fourth term = 14
Let 2nd term = x, then

Question 8.
Solution:
(i) The given numbers 48, 60, 75 are in
continued proportion if 48 : 60 :: 60 : 75.
Now, product of means = 60 x 60 = 3600
And, product of extremes = 48 x 75 = 3600
∴ Product of means = Product of extremes
So, 48 : 60 :: 60 : 75
Hence, the numbers 48, 60, 75 are in continued proportion.
(ii) The given numbers 36, 90, 225 are in
continued proportion of 36 : 90 :: 90 : 225
Now, product of means = 90 x 90 = 8100
And, product of extremes = 36 x 225 = 8100
∴ Product of means = Product of extremes
So, 36 : 90 :: 90 : 225
Hence, the numbers 36, 90, 225 are in continued proportion.
(iii)The given numbers 16, 84, 441 are in
continued proportion if 16 : 84 :: 84 : 441.
Now, product of means = 84 x 84 = 7056
And, product of extremes = 16 x 441 = 7056
Product of means = Product of extremes.
So, 16 : 845 :: 84 : 441
Hence 16, 84, 441 are in continued proportion.
(iv) The given numbers 27, 36, 48 are
in continued proportion if 27 : 36 :: 36 : 48
Now, product of means = 36 x 36 = 1296
And, product of extremes = 27 x 48 = 1296
∴ Product of means = Product of extremes.
So, 27 : 36 :: 36 : 48
Hence, the numbers 27, 36, 48 are in continued proportional.

Question 9.
Solution:
It is given that 9, x, x, 49 are in proportion, that is, 9 : x :: x : 49
∴ Product of means = Product of extremes

Question 10.
Solution:
Let the height of the pole be x metres.

Question 11.
Solution:
5 : 3 :: x : 6

Hope given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 16 Triangles Ex 16A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A
• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Question 1.
Solution:
A, B and C are three non-collinear points in a plane. AB, BC and CA are joined.

(i) The side opposite ∠C is AB
(ii) The angle opposite to the side BC is ∠A
(iii) The vertex opposite to the side CA is B
(iv) The side opposite to the vertex B is CA

Question 2.
Solution:
The measures of two angles of a triangle are 72° and 58°
But measure of three angles of a triangle is 180°
Third angle will be = 180 – (72° + 58°)
= 180° – 130°
= 50°

Question 3.
Solution:
Sum of three angles of a triangle = 180°
Ratio of three angles = 1 : 3 : 5

Hence, three angles are 20°, 60° and 100°
Ans.

Question 4.
Solution:
Sum of three angles of a right triangle = 180°
Sum of two acute angles = 180°- 90°
= 90°
Measure of one angle = 50°
Second acute angle = 90° – 50° = 40°
Ans.

Question 5.
Solution:
Let the measure of each of the equal angles be x°. Then,
x° + x°+ 110°= 180°
(Angle sum property of a triangle)
=> 2x°+110°= 180°
=> 2x° = 180° – 110° = 70°
=> \({ x }^{ O }={ \left( \frac { 70 }{ 2 } \right) }^{ O }={ 35 }^{ O }\)
The measure of each of the equal angles is 35°.

Question 6.
Solution:
Let the three angles of a triangle be ∠A, ∠B, ∠C. Then, ∠A = ∠B + ∠C
Adding ∠A to both sides, we get ∠A + ∠A = ∠A + ∠B + ∠C
=> 2 ∠A = 180°
(Angle sum property of a triangle)
=> ∠A = \({ \left( \frac { 180 }{ 2 } \right) }^{ O }={ 90 }^{ O }\)
One of the angles of the triangle is a right angle.
Hence, the triangle is a right triangle

Question 7.
Solution:
In a ∆ABC,
3∠A = 4∠B = 6∠C = 1 (say)

Question 8.
Solution:
(i) It is obtuse triangle.
(ii) It is acute triangle.
(iii) It is right triangle.
(iv) It is obtuse triangle.

Question 9.
Solution:
(i) It is an isosceles triangle as it has two equal sides.
(ii) It is an isosceles triangle as it has two equal sides.
(iii) It is a scalene triangle as its sides are different in length.
(iv) It is an equilateral triangle as its all sides are equal.
(v) It is an equilateral triangles as its angles are equal, so its sides will also be equal.
(vi) It is an isosceles triangle as its two base angles are equal, so its two sides are equal.
(vii) It is a scalene triangle as its angles are different, so its sides will also be different or unequal.

Question 10.
Solution:
In ∆ABC, D is a point on BC and AD is joined
Now we get triangles ∆ABC, ∆ABD and ∆ADC

Question 11.
Solution:
(i) No
(ii) No
(iii) Yes
(iv) No
(v) No
(vi) Yes.

Question 12.
Solution:
(i) three, three, three.
(ii) 180°
(iii) different
(iv) 60°
(v) equal
(vi) perimeter.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 15 Polygons Ex 15

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 15 Polygons Ex 15

Question 1.
Solution:
(a), (b), (d) and (f) are simple closed figures.

Question 2.
Solution:
(a), (b) and (c) are polygons.

Question 3.
Solution:
(i) two
(ii) triangle
(iii) quadrilateral
(iv) 3, 3
(v) 4, 4
(vi) closed figure.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 15 Polygons Ex 15 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 14 Constructions (Using Ruler and a Pairs of Compasses) Ex 14B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14A
• RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14B

Question 1.
Solution:
(1) 60°
Steps of construction :
(i) Draw a ray OA.

(ii) With centre O and with a suitable radius drawn an arc meeting OA at E.
(iii) With centre E and with same radius, draw another arc cutting the first arc at F.
(iv) Join OF and produce it to B Then ∠AOB = 60°
(2) 120°
Steps of construction :
(i) Draw a ray OA
(ii) With centre O and with a suitable radius draw an arc meeting OA at E
(iii) With centre E and with the same radius cut off the first arc firstly at F and then at G i.e. EF = FG.
(iv) Join OG and produce it to B.
Then, ∠AOB = 120°

(3) 90°
Steps of construction :
(i) Draw a ray OA

(ii) With centre O and a suitable radius draw an arc meeting OA at E.
(iii) With centre E and A with same radius cut off the arc first at F and then from F with same radius cut off arc at G.
(iv) With centres F and G with a suitable radius, draw two arcs intersecting each other at H.
(v) Join OH and produce it to B.
Then, ∠AOB = 90°.

Question 2.
Solution:
Steps of Construction :
(i) Draw a ray OA.

(ii) With O as centre and any suitable radius draw an arc above OA, cutting it at a point B.
(iii) With B as centre and same radius as before draw another arc to cut the previous arc at C.
(iv) Join OC and produce it to D. Then ∠AOD = 60° is the required angle. To bisect the angle ∠AOD, with B as centre and radius more than half BC draw an arc. With C as centre and the same radius draw another are cutting the previous arc at E. Join OE and produce it. Then, OE is the required bisector of ∠AOD.

Question 3.
Solution:
Steps of constructions :
(i) Draw a ray OA.
(ii) With centre O and a suitable radius draw an arc meeting OA at E.
(iii) With centre E and with same radius, cut the first arc firstly at F and then from F with same radius cut act at G.
(iv) With centres F and G, with suitable radius, draw arcs intersecting each other at H.

(v) Join OH intersecting the first arc at L and produce it to C.
(vi) With centre E and L and with suitable radius draw arcs intersecting each other at M.
(vii) Join OM and produce it to B.
Then ∠AOB = 45°

Question 4.
Solution:
(i) Steps of Construction :
1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc cutting OA at G.
3. With G as centre and same radius cut the arc at B and then B as centre and same radius cut the arc at C. Again, with C as centre and same radius cut the arc at D.

4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE and produce it to F.
Then ∠AOF = 150°
(ii) Steps of Construction :
1. Draw a ray OA.
2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.

3. With B as centre and same radius as before draw another arc to cut the previous arc at C. Join OC and prouce it to D.
4. Draw the bisector OE of ∠AQD. Then ∠AOE = 30°.
5. Draw the bisector OF of ∠AOE. Then ∠AOF = 15° is the required angle.
(iii) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
3. With B as centre and same radius as before draw another arc to cut the previous arc at C. With C as centre and same radius draw the arc to cut it at D. Again with D as centre and same radius cut the arc at E.
4. Join OD and produce it to G. Then ∠AOG = 120°.
5. With D as centre and radius more than half DE draw an arc.
6. With E as centre and same radius draw another arc to cut the previous arc at F. Join OF.
7. Draw the bisector OH of ∠GOF. Then ∠AOH = 135° is the required angle.
(iv) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc above OA, cutting it at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.
8. Draw the bisector OG of ∠AOF.
Then ∠AOG = \(22 \frac { 1 }{ 2 } \) ° is the required angle.
(v) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc cutting OA at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Also join OD and produce it to F.
7. Draw the bisector OG of ∠EOF Thus, ∠AOG = 105° is the required angle.
(vi) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc cutting OA at B.
3. With B as centre and same radius* cut the previous arc at C and then with C as centre cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Also join OC and produce it to G.
7. Draw the bisector OF of ∠EOG. Then, ∠AOF = 75° is the required angle.
(vii) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any suitable radius draw an arc above OA to cut it B.
With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of ∠AOE.
8. Draw the bisector OG of ∠EOF.
Then ∠AOG = \(67 \frac { 1 }{ 2 } \) ° is the required angle.
(viii) Steps of Construction :
1. Draw a ray OA.

2. With O as centre and any su itable radius draw an arc above OA to cut it at B.
3. With B as centre and same radius cut the previous arc at C and then with C as centre and same radius cut the arc at D.
4. With C as centre and radius more than half CD, draw an arc.
5. With D as centre and same radius draw another arc to cut the previous arc at E.
6. Join OE. Then ∠AOE = 90°.
7. Draw the bisector OF of angle ∠AOE. Then, ∠AOF = 45° is the required angle.

Question 5.
Solution:
Steps of Construction :
1. Draw a line-segment AB = 5 cm with the help of a rular.

2. With Aas centre and suitable radius draw an arc cutting AB at C.
3. With C as centre and same radius cut the previous arc at D and then with D as centre and same radius cut the arc at E
4. With D as centre and radius more than half DE draw an arc.
5. With E as centre and same radius draw another arc to cut the previous arc at F.
6. Join AF and produce it to G such that AG = 3.5 cm. Then ∠BAG = 90°.
7. With G as centre and radius equal to AB draw an arc. With B as centre and radius equal to AG draw another arc to cut the previous arc at H.
8. Join GH and BH. Then, AB HG is the required rectangle.

Question 6.
Solution:
Steps of Construction :
1. With the help of a ruler draw a line segment AB = 5 cm.

2. With A as centre and any suitable radius draw an arc cutting AB at C.
3. With C as centre and same radius cut the previous arc at D and then with D as centre and same radius cut the arc at E.
4. With D as centre and radius more than half DE draw an arc.
5. With E as centre and same radius draw another arc to cut the previous arc at F.
6. Join AF and produce it to G such that AG = 5 cm.
7. With G as centre and radius equal to AB draw an arc. With B as centre and same radius draw another arc to cut the previous arc at H.
8. Join GH and BH. Then, AB HG is the required square.

Hope given RS Aggarwal Solutions Class 6 Chapter 14 Constructions Ex 14B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9C.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A
• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9B
• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9C

Question 1.
Solution:
Let the required number be x.
Then, x + 9 = 36
=> x = 36 – 9
(Transposing 9 to R.H.S.)
=> x = 27
The required number = 27.

Question 2.
Solution:
Let the required number be x. Then,
4x – 11 = 89
=> 4x = 89 + 11

Question 3.
Solution:
Let the required number be x. Then,
x x 5 = x + 80
=> 5x = x + 80
=> 5x – x = 80

Question 4.
Solution:
Let the three consecutive numbers be x,
x + 1 and x + 2. Then,
x + (x + 1) + (x + 2) = 114
=> x – x + 1 + x + 2 = 114

Question 5.
Solution:
Let the required number be x. Then
x x 17 + 4 = 225
=> 17x + 4 = 225
=> 17x = 225 – 4

Question 6.
Solution:
Let the required number be x. Then
3 x + 5 = 50
=> 3 x = 50 – 5

Question 7.
Solution:
Let the smaller number be x.
Then the other number = x + 18
According to question,
x + (x + 18) = 92
=> 2 x + 18 = 92
=> 2 x = 92 – 18
(Transposing 18 to R.H.S.)
=> 2 x = 74
=> x = 37
(Dividing both sides by 2)
One number = 37
Another number = 37 + 18
= 55.

Question 8.
Solution:
Let the smaller number be x.
Then, the other number = 3 x
According to question, x + 3 x = 124
=> 4 x = 124

Question 9.
Solution:
Let the smallest number be x.
Then, the other number = 5 x
According to question,
5 x – x = 132
=> 4 x = 132

Question 10.
Solution:
Let the two consecutive even number be x and x + 2.
Then x + x + 2 = 74
=> 2 x + 2 = 74
=> 2 x = 74 – 2
(Transposing 2 to RHS.)
=> 2x = 72
=> x = 36
(Dividing both sides by 2)
The required numbers are 36 and (36 + 2) i.e. 36 and 38.

Question 11.
Solution:
Let the three consecutive odd numbers be x, (x + 2) and (x + 4).
According to the question,
x + (x + 2) + (x + 4) = 21
3x + 6 = 21
=> 3 x = 21 – 6
(Transposing 6 to R.H.S.)
=> 3 x = 15
=> x = 5
(Dividing both sides by 3)
The required numbers are 5, 5 + 2 and 5 + 4 i.e. 5, 7 and 9.

Question 12.
Solution:
Let the present age of Ajay be x years. Then, the present age of Reena = (x + 6) years
According to the question,
x + (x + 6) = 28
2x + 6 = 28
=> 2x = 28 – 6
(Transposing 6 to R.H.S.)
=> 2 x = 22
=> x = 11
(Dividing both sides by 2)
Present age of Ajay = 11 years
and present age of Reena = 11 + 6
= 17 years.

Question 13.
Solution:
Let the present age of Vikas be x years.
Then, the present age of Deepak = 2x years
According to the question,
2x – x = 11
=> x = 11
Present age of Vikas = 11 years
and present age of Deepak = 2 x 11
= 22 years.

Question 14.
Solution:
Let the present age of Rekha be x years
Then, the present age of Mrs. Goel = (x + 27) years
Rekha’s age after 8 years = (x + 8) years
Mrs. Goel’s age after 8 years = (x + 27 + 8) years
= (x + 35) years
According to the question,
x + 35 = 2 (x + 8)
=> x + 35 = 2x + 16
=> x – 2x = 16 – 35
(Transposing 2x to L.H.S. and 35 to R.H.S.)
=> – x = – 19
=> x = 19
Present age of Rekha =19 years and present age of Mr. Goel = 19 + 27 = 46 years.

Question 15.
Solution:
Let the present age of the son be A years.
Then, the present age of the man
= 4 x years
Son’s age after 16 years = (x + 16) years Man’s age after 16 years
= (4 x + 16) years According to the question,
4x + 16 = 2 (x + 16)
=> 4x + 16 = 2x + 32
=> 4x – 2x = 32 – 16
(Transposing 2 x to L.H.S. and 16 to R.H.S.)
=> 2x = 16
=> x = 8 (Dividing both sides by 2)
Present age of the son = 8 years and present age of the man = 8 x 4 = 32 years.

Question 16.
Solution:
Let the present age of the son be x years.
Then, the present age of the man = 3x years
five years ago, the age of the son = (x – 5) years
five years ago, the age of the man = (3x – 5) years
According to the question, 3x – 5 = 4(x – 5)
=>3x – 5 = 4x – 20
=>3x – 4x = – 20 + 5
(Transposing 4 x to L.H.S. and – 5 to R.H.S.)
=> – x = – 15 => x = 15
Present age of the son = 15 years and present age of the man = 3 x 15 = 45 years.

Question 17.
Solution:
Let the present age of Fatima be A years. According to the question,
x + 16 = 3 x
=> x – 3x = – 16
(Transposing 3 x to L.H.S. and 16 to R.H.S.)
=> – 2 x = – 16
=> x = 8
(Dividing both sides by – 2)
Present age of Fatima = 8 years.

Question 18.
Solution:
Let the present age of Rahim be x years
Rahim’s age after 32 years = (x + 32) years
Rahim’s age 8 years ago = (x – 8) years
According to the question, x + 32 = 5 (x – 8)
=> x + 32 = 5 x – 40
=> x – 5x = – 40 – 32
(Transposing 5 x to L.H.S. and 32 to R.H.S.)
– 4 x = – 72
x= 18
(Dividing both sides by – 4)
Present age of Rahim =18 years

Question 19.
Solution:
Let the number of 50 paisa coins be x.
Then, the number of 25 paisa coins = 4x
Total value of 50 paisa coins = 50 x paisa
and total value of 25 paisa coins
= 25 x 4 = 100 x paisa
But total value of both the coins
= Rs. 30 (Given)
= 30 x 100 paisa
= 3000 paisa
According to the question,
50 x + 100 x = 3000
=> 150 x = 3000
\(\\ \frac { 150x }{ 150 } \) = \(\\ \frac { 3000 }{ 150 } \)
(Dividing both sides by 150)
x = 20
Number of 50 paisa coins = 20
and number of 25 paisa coins = 4 x 20
= 80

Question 20.
Solution:
Let the price of the pen be x rupees. According to the question,
5 x = 3 x + 17
5 x – 3 x = 17
(Transposing 3 x to L.H.S.)
=> 2 x = 17
=> x = \(\\ \frac { 17 }{ 2 } \)
(Dividing both sides by 2)
Price of the pen = \(\\ \frac { 17 }{ 2 } \) rupees
= Rs. 8.50.

Question 21.
Solution:
Let the number of girls in the school be x.
Then, the number of boys in the school = (x + 334)
According to the question, x + (x + 334) = 572
=> 2 x + 334 = 572
=> 2 x = 572 – 334
(Transposing 334 to L.H.S.)
2 x = 238
=> x = \(\\ \frac { 238 }{ 2 } \)
(Dividing both sides by 2) => x = 119
Number of girls in the school = 119.

Question 22.
Solution:
Let the breadth of the park be x metres.
Then, the length of die park=3x metres.
According to the question,
Perimeter of the park = 168 metres
=> 2 (x + 3 x) = 168
=> 2 x 4x = 168
=> 8 x = 168
=> x = 21
(Dividing both sides by 8)
Breadth of the park = 21 metres and length of the park = 3 x 21 = 63 metres.

Question 23.
Solution:
Let the breadth of the hall be x metres.
Then, the length of the hall = (x + 5) metres .
According to question,
Perimeter of the hall = 74 metres
=> 2 (x + x + 5) = 74
=> 2 (2 x + 5) = 74
=> 4 x + 10 = 74
=> 4 x = 74 – 10
(Transposing 10 to R.H.S.)
4x = 64
=> \(\\ \frac { 4x }{ 4 } \) = \(\\ \frac { 64 }{ 4 } \)
(Dividing both sides by 4)
=> x = 16
Breadth of the hall = 16 metres
and length of the hall = 16 + 5 = 21 metres.

Question 24.
Solution:
Since a wire of length 86 cm is bent to form die rectangle, so the perimeter of the rectangle = 86 cm.
Let the breadth of the rectangle = x cm
Then, die length of the rectangle = (x + 7) cm
2 (x + x + 7) = 86
=> 2 (2 x + 7) = 86 .
=> 4 x + 14 = 86
=> 4x = 86 – 14
(Transposing 14 to R.H.S.)
=> 4 x = 72
\(\\ \frac { 4x }{ 4 } \) = \(\\ \frac { 72 }{ 4 } \) = 18
(Dividing both sides by 4)
Breadth of the rectangle = 18 cm
Length of the rectangle = (18 + 7) = 25 cm.

Hope given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A
• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9B
• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9C

Solve each of the following equations and verify the answer in each case :

Question 1.
Solution:
x + 5 = 12
=> x + 5 – 5 = 12 – 5
(Subtracting 5 from both sides)
=> x = 7
.’. x = 7 is the solution of the given equation.
Check : Substituting x = 7 in the given equation, we get
L.H.S. = 7 + 5 = 12 and R.H.S. = 12
∴When x = 7, we have L.H.S. = R.H.S.

Question 2.
Solution:
x + 3 = – 2
=>x + 3 – 3 = – 2 – 3
(Subtracting 3 from both sides)
=> x = – 5
∴ x = – 5 is the solution of the given equation.
Check : Substituting x = – 5 in the given equation, we get:
L.H.S. = – 5 + 3 = – 2 and R.H.S. = – 2
When x = – 5,
∴we have L.H.S. = R.H.S.

Question 3.
Solution:
x – 7 = 6
=>x – 7 + 7 = 6 + 7
(Adding 7 to both sides)
=> x – 13
So, x = 13 is the solution of the given equation.
Check : Substituting x – 13 in the given equation, we get
L.H.S.= 13 – 7 = 6 and R.H.S. = 6
∴When x = 13, we have L.H.S. = R.H.S.

Question 4.
Solution:
x – 2 = – 5
=> x – 2 + 2 = – 5 + 2
(Adding 2 on both sides)
=> x = – 3
So, x = – 3 is the solution of the given equation.
Check : Substituting x = – 3 in the given equation, we get
L.H.S. = – 3 – 2 = – 5 and R.H.S. = – 5 When x = – 3,
we have
L.H.S. = R.H.S.

Question 5.
Solution:
3x – 5 = 13
=>3x – 5 + 5 = 13 + 5
(Adding 5 on both sides)
=> 3x = 18
=>\(\\ \frac { 3x }{ 3 } \) = \(\\ \frac { 18 }{ 3 } \)
(Dividing both sides by 3)
=> x = 6
x = 6 is the solution of the given equation.
Check : Substituting x = 6 in the given equation, we get
L.H.S. = 3 x 6 – 5 = 18 – 5 = 13 and R.H.S. = 13
∴ When x = 6, we have L.H.S. = R.H.S

Question 6.
Solution:
4x + 7 = 15
=> 4x + 7 – 7 = 15 – 7
(Subtracting 7 from both sides)
=> 4x = 8
=> \(\\ \frac { 4x }{ 4 } \) = \(\\ \frac { 8 }{ 4 } \)
(Dividing both sides by 4)
=> x = 2
x = 2 is the solution of the given equation.
Check : Substituting x = 2 in the given equation, we get
L.H.S. = 4 x 2 + 7 = 8 + 7 = 15 and R.H.S. = 15
∴When x = 2, we have L.H.S. = R.H.S.

Question 7.
Solution:
\(\\ \frac { x }{ 5 } \) = 12
=> \(\\ \frac { x }{ 5 } \) x 5 = 12 x 5
(Multiplying both sides by 5)
=> x = 60
x = 60 is the solution of the given equation.
Check : Substituting x = 60 in the given equation, we get
L.H.S. = \(\\ \frac { 60 }{ 5 } \) = 12 and R.H.S. = 12
When x = 60, we have
∴L.H.S. = R.H.S.

Question 8.
Solution:
\(\\ \frac { 3x }{ 5 } \) = 15
=> \(\\ \frac { 3x }{ 5 } \) x \(\\ \frac { 5 }{ 3 } \) = 15 x \(\\ \frac { 5 }{ 3 } \)

Question 9.
Solution:
5x – 3 = x + 17
=> 5x – x = 17 + 3

So. x = 5 is a solution of the given
equation.
Check : Substituting x = 5 in the given
equation, we get
L.H.S. = 5 x 5 – 3 = 25 – 3 = 22
R.H.S. 5 + 17 = 22
∴When x = 5, we have L.H.S. = R.H.S.

Question 10.
Solution:
2x – \(\\ \frac { 1 }{ 2 } \) = 3
=> 2x = 3 + \(\\ \frac { 1 }{ 2 } \)

Question 11.
Solution:
3(x + 6) = 24
=> \(\\ \frac { 3(x+6) }{ 3 } \) = \(\\ \frac { 24 }{ 3 } \)
(Dividing both sides by 3)
x + 6 = 8
=> x = 8 – 6
(Transposing 6 to R.H.S.)
=> x = 2
x = 2 is a solution of the given equation.
Check : Substituting the value of x = 2
in the given equation, we get
L.H.S. = 3(2 + 6 ) = 3 x 8 = 24
and RH.S. = 24
∴When x = 2, we have L.H.S. = R.H.S.

Question 12.
Solution:
6x + 5 = 2x + 17
=> 6x – 2x = 17 – 5
(Transposing 2 x to L.H.S. and 5 to R.H.S.)
=> 4x = 12
=> \(\\ \frac { 4x }{ 4 } \) = \(\\ \frac { 12 }{ 4 } \)
(Dividing both sides by 4)
=> x = 3
x = 3 is a solution of the given
equation.
Check : Substituting x = 3 in the given
equation, we get
L.H.S.= 6 x 3 + 5 = 18 + 5 = 23
R.H.S.= 2 x 3 + 17 = 6 + 17 = 23
∴When x = 3, we have L.H.S. = R.H.S.

Question 13.
Solution:
\(\\ \frac { x }{ 4 } \) – 8 = 1
=> \(\\ \frac { x }{ 4 } \) = 1 + 8

R.H.S = 1
∴When x = 36,we have L.H.S. = R.H.S.

Question 14.
Solution:
\(\\ \frac { x }{ 2 } \) = \(\\ \frac { x }{ 2 } \) + 1
=> \(\\ \frac { x }{ 2 } \) – \(\\ \frac { x }{ 3 } \) = 1

Question 15.
Solution:
3(x + 2) – 2(x – 1) = 7
=> 3x + 6 – 2x + 2 = 7
(Removing brackets)
3x – 2x + 6 + 2 = 7
x + 8 = 7
x = 7 – 8
(Transposing 8 to R.H.S.)
x = – 1 is a solution of the given
equation.
Check : Substituting x = – 1 in the given
equation, we get
L.H.S. = 3 ( – 1 + 2) – 2( – 1 – 1)
= 3 x 1 + ( – 2 x – 2)
= 3 + 4 = 7 and
R.H.S. = 7
When x = – 1, we have
L.H.S. = R.H.S.

Question 16.
Solution:
5 (x- 1) + 2 (x + 3) + 6 = 0
= 5 (x – 1) + 2 (x + 3) = – 6
(Transposing 6 to R.H.S.)
= 5x – 5 + 2x + 6 = – 6

Question 17.
Solution:
6(1 – 4 x) + 7 (2 + 5 x) – 53
=> 6 – 24x + 14 + 35 x = 53
(Removing brackets)
=> – 24 x + 35 x + 14 + 6 = 53
=> 11 x + 20 = 53
=> 11 x = 53 – 20
=> 11 x = 33
(Transposing 20 to R.H.S.)

Question 18.
Solution:
16 (3x – 5) – 10 (4x – 8) = 40
=> 48x – 80 – 40x + 80 = 40
(Removing brackets)
=> 48x – 40 x – 80 + 80 = 40
=> 8x = 40

Question 19.
Solution:
3 (x + 6) + 2 (x + 3) = 64
=> 3x + 18 + 2x + 6 = 64
(Removing brackets)
=> 3x + 2x + 18 + 6 = 64
=> 5x + 24 = 64
=> 5x = 64 – 24

Question 20.
Solution:
3(2 – 5x) – 2 (1 – 6x) = 1
=> 6 – 15x – 2 + 12x = 1
(Removing brackets)
=> 6 – 2 – 15x + 12x = 1
=> 4 – 3x = 1
– 3x = 1 – 4

Question 21.
Solution:
\(\\ \frac { n }{ 4 } -5\) = \(\\ \frac { n }{ 6 } \) + \(\\ \frac { 1 }{ 2 } \)
Multiplying each term by 12, the L.C.M. of 4, 6, 2, we get

Question 22.
Solution:
\(\\ \frac { 2m }{ 3 } +8\) = \(\\ \frac { m }{ 2 } -1\)
Multiplying each term by 6, the L.C.M. of 2 and 3, we get
\(\\ \frac { 2m }{ 3 } \) x 6 + 8 x 6 = \(\\ \frac { m }{ 2 } \) x 6 – 1 x 6

Question 23.
Solution:
\(\\ \frac { 2x }{ 5 } \) – \(\\ \frac { 3 }{ 2 } \) = \(\\ \frac { x }{ 2 } +1\)
Multiplying each term by 10, the L.C.M. of 5 and 2, we get

Question 24.
Solution:
\(\\ \frac { x-3 }{ 5 } \) – 2 = \(\\ \frac { 2x }{ 5 } \)
multiplying each term by 5, we get

Question 25.
Solution:
\(\\ \frac { 3x }{ 10 } \) – 4 = 14
=> \(\\ \frac { 3x }{ 10 } \) = 14 + 4

Question 26.
Solution:
\(\\ \frac { 3 }{ 4 } (x-1)\) = (x – 3)

Hope given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 9 Linear Equations in One Variable Ex 9A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A
• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9B
• RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9C

Question 1.
Solution:
Let x be the given number, then
(i) 5x = 40
(ii) x + 8 = 15
(iii) 25 – x = 7
(iv) x – 5 = 3
(v) 3x – 5 = 16
(vi) x – 12 = 24
(vii) 19 – 2x = 11
(viii) \(\\ \frac { x }{ 8 } \) = 7
(ix) 4x – 3 = 17
(x) 6x = x + 5

Question 2.
Solution:
(i) 7 less than from the number x is 14.
(ii) Twice the number y is 18.
(iii) 11 increased by thrice the number x is 17.
(iv) 3 less than twice the number x is 13.
(v) 30 less than 12 times the number is 6.
(vi) Quotient of twice the number z and 3 is

Question 3.
Solution:
(i) The given equation is 3x – 5 = 7
Substituting x = 4, we get
L.H.S. = 3 x – 5
= 3 x 4 – 5
= 12 – 5
= 7 = R.H.S.
It is verified that x = 4 is the root of the given equation.
(ii) The given equation is 3 + 2 x = 9
Substituting x = 3, we get L.H.S. = 3 + 2x
= 3 + 2 x 3
= 3 + 6 = 9
= R.H.S.
It is verified that x = 3 is the root of the given equation.
(iii) The given equation is 5x – 8 = 2x – 2
Substituting x = 2, we get
L.H.S. = 5x – 8
=5 x 2 – 8
= 10 – 8
= 2
R.H.S. = 2x – 2
= 2 x 2 – 2
= 4 – 2
= 2
L.H.S. = R.H.S.
Hence, it is verified that x = 2, is the root of the given equation.
(iv) The given equation is 8 – 7y = 1 Substituting y = 1, we get L.H.S. = 8 – 7y
= 8 – 7 x 1
= 8 – 7
= 1
= R.H.S.
Hence, it verified that y = 1 is the root of the given equation.
(v) The given equation is \(\\ \frac { z }{ 7 } \) = 8
Substituting the value of z = 56, we get
L.H.S.= \(\\ \frac { 56 }{ 7 } \)
= 8
= R.H.S.
Hence, it is verified that z = 56 is the root of the given equation.

Question 4.
Solution:
(i) The given equation is y + 9 = 13
We try several values of y and find L.H.S. and the R.H.S. and stop when L.H.S. = R.H.S.

When y = 4, we have L.H.S. = R.H.S.
So y = 4 is the solution of the given equation.
(ii) The given equation is x – 1 = 10
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When x = 17, we hive L.H.S. = R.H.S
So x = 17 is the solution of the given equation.
(iii) The given equation is 4x = 28
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When x = 7, we have L.H.S. = R.H.S.
So x = 7 is the solution of the given equation.
(iv) The given equation is 3y = 36
We guess and try several values of y to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When y = 12, we have L.H.S. = R.H.S.
So y = 12 is the solution of the given equation.
(v) The given equation is 11 + x = 19
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When x = 8, we have L.H.S. = R.H.S.
So, x = 8 is the solution of the given equation.
(vi) The given equation is \(\\ \frac { x }{ 3 } \) = 4
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When x = 12, we have L.H.S. = R.H.S.
So, x = 12 is the solution of the given equation.
(vii) The given equation is 2 x – 3 = 9
We guess and try several values of x to find L.H.S. and R.H.S. and stop when

.’. When x = 6, we have L.H.S. = R.H.S.
So, x = 6 is the solution of the given equation.
L.H.S. = R.H.S.
(viii) The given equation is \(\\ \frac { 1 }{ 2 } \) x + 7 = 11
We guess and try several values of x to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When x = 8, we have L.H.S. = R.H.S.
So, x = 8 is the solution of the given equation.
(ix) The given equation is 2y + 4 = 3y (x)
We guess and try several values of z to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S.

When y = 4, we have L.H.S. = R.H.S. So, y = 4 is the solution of the given equation
(x) The given equation is z – 3 = 2z – 5
We guess and try several values of z to find L.H.S. and R.H.S. and stop when L.H.S. = R.H.S

When z = 2, we have L.H.S. = R.H.S. So, z = 2 is the solution of the given equation.

Hope given RS Aggarwal Solutions Class 6 Chapter 9 Linear Equations in One Variable Ex 9A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8D.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8A
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8B
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8C
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8D

Simplify :

Question 1.
Solution:
We have : a – (b – 2a)
= a – b + 2a
= a + 2a – b
= (1 + 2) a – b
= 3a – b.

Question 2.
Solution:
We have : 4x – (3y – x + 2z)
= 4x – 3y + x – 2z
= 4x + x – 2y – 2z
= 5x – 3y – 2z

Question 3.
Solution:
We have :
(a² + b² + 2ab) – (a² + b² – 2ab)
= a² + b² + 2ab – a² – b² + 2ab
= a² – a² + b² – b² + 2ab + 2ab
= 0 + 0 + (2 + 2) ab
= 4 ab

Question 4.
Solution:
We have :
– 3 (a + b) + 4 (2a – 3b) – (2a – b)
= – 3a – 3b + 8a – 12b – 2a + b
= – 3a + 8a – 2a – 3b – 12b + b
= ( – 3 + 8 – 2) a + ( – 3 – 12 + 1) b
= 3a – 14 b.

Question 5.
Solution:
We have :
– 4x² + {(2x² – 3) – (4 – 3x²)}
= – 4x² + {2x² – 3 – 4 + 3x²}
[removing grouping symbol]
= – 4x² + {5x² – 7)
= – 4x² + 5x² – 7
(removing grouping symbol {})
= x² – 7

Question 6.
Solution:
We have :
– 2 (x² – y² + xy) – 3 (x² + y² – xy)
= – 2x² + 2y² – 2xy – 3x² – 3y² + 3xy
= – 2x² – 3x² + 2y² – 3y² – 2xy + 3xy
= ( – 2 – 3)x² + (2 – 3) y² + ( – 2 + 3)xy
= – 5x² – y² + xy

Question 7.
Solution:
a – [2b – {3a – (2b – 3c)}]
= a – [2b – {3a – 2b + 3c}]
[removing grouping symbol( )]
= a – [2b – 3a + 2b – 3c]
(removing grouping symbol {})
= a – [4b – 3a – 3c]
= a – 4b + 3a + 3c
(removing grouping symbol [ ])
= 4a – 4b + 3c

Question 8.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have :
– x + [5y – {x – (5y – 2x)}]
= – x + [5y – {x – 5y + 2x}]
= – x + [5y – {3x – 5y}]
= – x + [5y – 3x + 5y]
= – x + [ 10y – 3x]
= – x + 10y – 3x
= – x – 3x + 10y
= – 4x + 10y

Question 9.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have :
86 – [15x – 7 (6x – 9) – 2 {10x – 5(2 – 3x)}]
= 86 – [15x – 42x + 63 – 2 {10x – 10 + 15x}
= 86 – [ 15x – 42x + 63 – 2 {25x – 10}]
= 86 – [15x – 42x + 63 – 50x + 20]
= 86 – 15x + 42x – 63 + 50x – 20
= (86 – 63 – 20) – 15x + 42x + 50x
= (86 – 83) + (- 15 + 42 + 50) x
= 3 + 77x

Question 10.
Solution:
Removing the innermost grouping ‘ symbol () first, then { } and then [ ], we have :
12x – [3x³ + 5x² – {7x² – (4 – 3x – x³) + 6x³} – 3x]
= 12x – [3x³ – 5x² – {7x² – 4 + 3x + x³ + 6x³} – 3x]
= 12x – [3x³ + 5x² – {7x² – 4 + 3x + 7x³} – 3x]
= 12x – [3x³ + 5x² – 7x² + 4 – 3x – 7x³ – 3x]
= 12x – [3x³ – 7x³ + 5x² – 7x² + 4 – 3x – 3x]
= 12x – [ – 4x³ + 2x² + 4 – 6x]
= 12x + 4x³ + 2x² – 4 + 6x
= 12x + 6x + 4x³ + 2x² – 4
= 18x + 4x³ + 2x² – 4
= 4x³ + 2x² + 18x – 4

Question 11.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have
5a – [a² – {2a (1 – a + 4a²) – 3a (a² – 5a – 3)}] – 8a
= 5a – [a² – {2a – 2a² + 8a³ – 3a³ + 15a² + 9a}] – 8a
= 5a – [a² – {2a + 9a – 2a² + 15a² + 8a³ – 3a³}] – 8a
= 5a – [a² – {11a + 13a² + 5a³}] – 8a
= 5a – [a² – 11a – 13a² – 5a³] – 8a
= 5a – a² + 11a + 13a² + 5a³ – 8a
= 5a + 11a – 8a – a² + 13a² + 5a³
= 8a + 12a² + 5a³
= 5a3 + 12a² + 8a.

Question 12.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have :
3 – [x – {2y – (5x + y – 3) + 2x²} – (x² – 3y)]
= 3 – [x – {2y – 5x – y + 3 + 2x²} – x² + 3y]
= 3 – [x – {y – 5x + 3 + 2x²} – x² + 3y]
= 3 – [x – y + 5x – 3 – 2x² – x² + 3y]
= 3 – [6x + 2y – 3 – 3x²]
= 3 – 6x – 2y + 3 + 3x²
= 6 – 6x – 2y + 3x²

Question 13.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have :
xy – [yz – zx – {yx – (3y – xz} – (xy – zy)}]
= xy – [yz – zx – {yx – 3y + xz – xy + zy}]
= xv – [yz – zx – {- 3y + xz + zy}]
= xy – [yz – zx + 3y – xz – zy]
= xy – [ – 2xz + 3y]
= xy + 2xz – 3y

Question 14.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have
2a – 3b – [3a – 2b – {a – c – (a – 2b)}]
= 2a – 3b – [3a – 2b – {a – c – a + 2b}]
= 2a – 3b – [3a – 2b – { – c + 2b}]
= 2a – 3b – [3a – 2b + c – 2b]
= 2a – 3b – 3a + 2b – c + 2b
= 2a – 3a – 3b + 2b + 2b – c
= – a + b – c

Question 15.
Solution:
Removing the innermost grouping symbol () first, then { } and ten [ ], we have:
– a – [a + {a + b – 2a – (a – 2b)} – b]
= – a – [a + {a + b – 2a – a + 2b} – b]
= – a – [a + { – 2a + 3b} – b]
= – a – [a – 2a + 3b – b]
= – a – a + 2a – 3b + b
= – 2a + 2a – 2b
= – 2 b

Question 16.
Solution:
Removing the innermost grouping symbol ‘—’ first, then ( ), then { } and then [ ], we have
2a – [4b – {4a – (3b – \(\overline { 2a+2b } \))}]
= 2a – [4b – {4a – (3b – 2a – 2b)}]
= 2a – [4b – {4a – (b – 2a)}]
= 2a – [4b – {4a – b + 2a}]
= 2a – [4b – {6a – b}]
= 2a – [4b – 6a + b]
= 2a – [5b – 6a]
= 2a – 5b + 6a
= 8a – 5b.

Question 17.
Solution:
Removing the innermost grouping < symbol ( ) first, then { } and then [ ], we have :
5x – [4y – {7x – (3z – 2y) + 4z – 3(x + 3y – 2z)}]
= 5x – [4y – {7x – 3z + 2y + 4z – 3x – 9y + 6z}]
= 5x – [4y – {4x + 7z – 7y}]
= 5x – [4y – 4x – 7z + 7y]
= 5x – [11y – 4x – 7z]
= 5x – 11y + 4x + 7z
= 9x – 11y + 7z

Hope given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8C.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8A
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8B
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8C
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8D

Question 1.
Solution:
(i) The required sum
= 3x + 7x
= (3 + 7) x
= 10x

Question 2.
Solution:
(i) Adding columnwise,
we get

Question 3.
Solution:
(i) Arranging the like terms columnwise and adding, we get :

Question 4.
Solution:
(i) We have :
2x – 5x = (2 – 5)x = – 3x
(ii) We have :
6x – y – (- xy) = 6xy + xy = 7xy
(iii) We have : 5b – 3a
(iv) We have : 9y – ( – 7x) = 9y + 7x
(v) We have : – 7x² – 10x² = ( – 7 – 10)x²
= – 17x²
(vi) We have : b² – a² – (a² – b²)
= b² – a² – a² + b²
= b² + b² – a² – a²
= (1 + 1) b² + ( – 1 – 1) a²
= 2b² – 2a²

Question 5.
Solution:
(i) Arranging the like terms columnwise, we get :

Question 6.
Solution:
(i) Rearranging and collecting the like terms, we get :

Question 7.
Solution:
We have:

Question 8.
Solution:
We have :
A = 7x² + 5xy – 9y²
B = – 4x² + xy + 5y²
C = 4y² – 3x² – 6xy

= 0+0+0 = 0
Hence the result

Question 9.
Solution:
Required expression

Question 10.
Solution:
Substituting the values of P, Q, R and S, we have :
P + Q + R + S = (a² – b² + 2ab)

Question 11.
Solution:
Required expression

Question 12.
Solution:
Required expression

Question 13.
Solution:
Required expression

Question 14.
Solution:
Required expression

Question 15.
Solution:
Sum of 5x – 4y + 6z and – 8x + y – 2z
= 5x – 4y + 6z – 8x + y – 2z
= 5x – 8x – 4y + y + 6z – 2z
= – 3x – 3y + 4z
Sum of 12x – y + 3z and – 3x + 5y – 8z
= 12x – y + 3z – 3x + 5y – 8z
= 12x – 3x – y + 5y + 3z – 8z
= 9x + 4y – 5z

Question 16.
Solution:
Required expression

Question 17.
Solution:
Required expression

Hope given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8A
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8B
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8C
• RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8D

Question 1.
Solution:
(i) Substituting a = 2 and b = 3 in the , given expression, we get :
a + b = 2 + 3 = 5
(ii) Substituting a = 2 and b = 3 in the given expression, we get :
a² + ab = (2)² + 2 x 3
= 4 + 6 = 10
(iii) Substituting a = 2 and b = 3 in the given expression, we get :
ab – a² = 2 x 3 – (2)²
= 6 – 4 = 2
(iv) Substituting a = 2 and b = 3 in the given expression, we get :
2a – 3b = 2 x 2 – 3 x 3
= 4 – 9 = – 5
(v) Substituting a = 2 and b = 3 in the given expression, we get :
5a² – 2ab = 5 x (2)² – 2 x 2 x 3
= 5 x 4 – 4 x 3
= 20 – 12 = 8
(vi) Substituting a = 2 and b = 3 in the given expression, we get :
a³ – b³ = (2)³ – (3)³ = 2 x 2 x 2 – 3 x 3 x 3
= 8 – 27 = – 19

Question 2.
Solution:
(i) Substituting x = 1, y = 2 and z = 5 in the given expression, we get :
3x – 2y + 4z = 3 x 1 – 2 x 2 + 4 x 5
= 3 – 4 + 20 = 23 – 4 = 19

Question 3.
Solution:
(i) Substituting p = – 2, q = – 1 and r = 3
in the given expression, we get :

Question 4.
Solution:
(i) The coefficient of x in 13x is 13
(ii) The coefficient of y in – 5y is – 5
(iii) The coefficient of a in 6ab is 6b
(iv) The coefficient of z in – 7xz is – 7x
(v) The coefficient of p in – 2pqr is – 2qr
(vi) The coefficient of y² in 8xy²z is 8xz
(vii) The coefficient of x³ in x³ is 1
(viii) The coefficient of x² in – x² is -1

Question 5.
Solution:
(i) The numerical coefficient of ab is 1
(ii) The numerical coefficient of – 6bc is – 6
(iii) The numerical coefficient of 7xyz is 7
(iv) The numerical coefficient of – 2x³y²z is – 2.

Question 6.
Solution:
(i) The constant term is 8
(ii) The constant term is – 9
(iii) The constant term is \(\\ \frac { 3 }{ 5 } \)
(iv) The constant term is \(– \frac { 8 }{ 3 } \)

Question 7.
Solution:
(i) The given expression contains only one term, so it is monimial.
(ii) The given expression contains only two terms, so it is binomial.
(iii) The given expression contains only one term, so it is monomial.
(iv) The given expression contains three terms, so it is trinomial.
(v) The given expression contains three terms, so it is trinomial.
(vi) The given expression contains only one term, so it is monomial.
(vii) The given expression contains four terms, so it is none of monomial, binomial and trinomial.
(viii) The given expression contains only one term so it is monomial.
(ix) The given expression contains two terms, so it is binomial.

Question 8.
Solution:
(i) The terms of the given expression 4x⁵ – 6y⁴ + 7x²y – 9 are :
4x⁵, – 6y⁴, 7x²y, – 9
(ii) The terms of the given expression 9x³ – 5z⁴ + 7x³y – xyz are :
9x³, – 5z⁴, 7x³y, – xyz.

Question 9.
Solution:
(i) We have : a², b², – 2a², c², 4a
Here like terms are a², – 2a²
(ii) We have : 3x, 4xy, – yz, \(\\ \frac { 1 }{ 2 } \) zy
Here like terms are – yz, \(\\ \frac { 1 }{ 2 } \) zy
(iii) We have : – 2xy², x²y, 5y²x, x²z
Here like terms are – 2xy², 5y²x
(iv) We have :
abc, ab²c, acb², c²ab, b²ac, a²bc, cab²
Here like terms are ab²c, acb², b²ac, cab².

Hope given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.