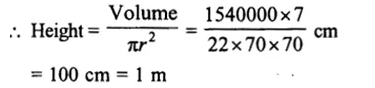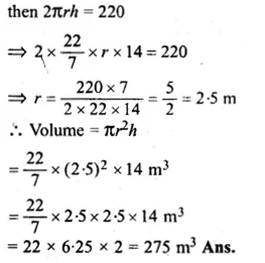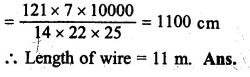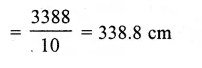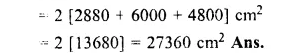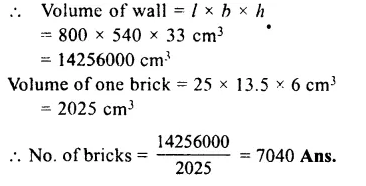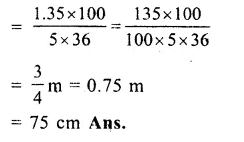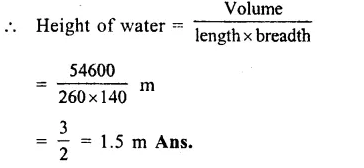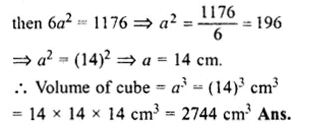RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A
- RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B
- RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C
Tick the correct answer in each of the following:
Question 1.
Solution:
Answer = (b)
Length (l) = 12 cm
Breadth (b) = 9cm
height (h) = 8 cm

Question 2.
Solution:
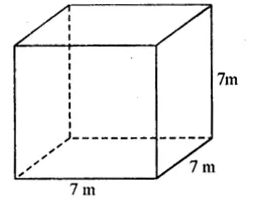
Total surface area of cube = 150 cm2
Side = \( \sqrt { \frac { 150 }{ 6 } } \)
= √25
= 5 cm
Volume = (side)3
= (5)3
= 125 cm3 (b)
Question 3.
Solution:
Volume of cube = 343 cm2
Side = \( \sqrt [ 3 ]{ 343 } =\sqrt [ 3 ]{ 7\times 7\times 7 } \)
= 7 cm
Total surface area = 6 (side)2
= 6 x (7)2
= 6 x 49 cm2
= 294 cm2 (c)
Question 4.
Solution:
Rate of painting = 10 paise per cm2
Total cost = Rs. 264.60

Question 5.
Solution:
Answer = (c)
Length of wall (l) = 8m = 800 cm
Breadth (b) = 22.5 cm
Height (h) = 6 m
= 600 cm

Question 6.
Solution:
Answer = (c)
Edge of cube = 10 cm
Volume = a3 = (10)3 = 1000 cm3
Edge of box = 1 m = 100 cm
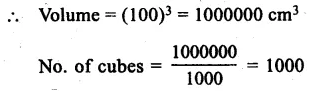
Question 7.
Solution:
Answer = (a)
Ratio in sides of a cuboid = 1 : 2 : 3
Surface area = 88 cm2
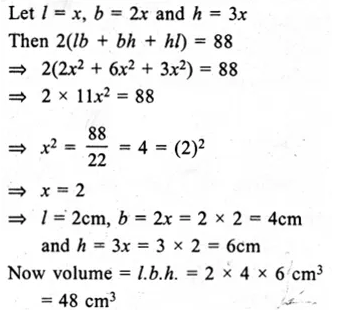
Question 8.
Solution:
Ratio in the two volumes = 1 : 27
Let volume of first volume = x3
and volume of second volume = 27x3
Side of first cube = x

Question 9.
Solution:
Surface area of a brick of measure 10 cm x 4 cm x 3 cm
= 2 (l x b + b x h + h x l)
= 2 [10 x 4 + 4 x 3 + 3 x 10] cm2
= 2 [40 + 12 + 30]
= 82 x 2
= 164 cm2 (c)
Question 10.
Solution:
Length of beam (l) = 9 m

Question 11.
Solution:
Water in rectangular reservoir = 42000
Volume = \(\\ \frac { 42000 }{ 1000 } \) = 42 m3
Length (l) = 6 m
Breadth (b) = 3.5 m
Depth = \(\\ \frac { volume }{ l\times b } \)
= \(\\ \frac { 42 }{ 6\times 3.5 } \)
= 2 m (c)
Question 12.
Solution:
Dimensions of a room are 10 m, 8 m, 3.3 m
Volume of air in it = lbh
= 10 x 8 x 3.3 = 264 m3
Air required for one man = 3 m3
No. of men = \(\\ \frac { 264 }{ 3 } \)
= 88 (b)
Question 13.
Solution:
Length of water tank (l) = 3 m
Width (b) = 2 m
and height (h) = 5 m
Volume = lbh = 3 x 2 x 5 = 30 m3
Water in it = 30 x 1000
= 30000 (a)
Question 14.
Solution:
Size of box = 25 cm, 15 cm, 8 cm
Surface area = (lb + bh + hl)
= 2 ( 25 x 15 + 15 x 8 + 8 x 25) cm2
= 2 (375 + 120 + 200) cm2
= 2(695)
= 1390 cm2 (b)
Question 15.
Solution:
Diagonal of cube = 4√3
Side = \( \frac { 4\sqrt { 3 } }{ \sqrt { 3 } } \)
= 4 cm
Volume = a3 = (4)3
= 64 cm3 (d)
Question 16.
Solution:
Diagonal of cube = 9√3 cm
Side = \( \frac { 9\sqrt { 3 } }{ \sqrt { 3 } } \)
= 9 cm
Surface area = 6a2
= 6 (9)2 = 6 x 81 cm2
= 486 cm2 (b)
Question 17.
Solution:
Let side of cube in first case = a
Then volume = a3
If side of cube is doubled, then side = 2a
Volume (2a)3 = 8a3
Becomes 8 times (d)
Question 18.
Solution:
Let side of cube in first case = a
Then surface area = 6a2
and side of second cube = 2a
Surface area = 6 (2a)2 = 6 x 4a2 = 24a2
Ratio = \(\frac { { 24a }^{ 2 } }{ { 6a }^{ 2 } } \) = 4
Becomes 4 times (b)
Question 19.
Solution:
Sides (edges) of 3 cubes are 6 cm, 8 cm, and 10 cm respectively
Volume of first cube = (6)3 = 216 cm3
Volume of second cube = (8)3 = 512 cm3
and volume of third cube
= (10)3 = 1000 cm3
Sum of volumes of 3 cubes = 216 + 512 + 1000
= 1728 cm3
Volume of new single cube = 1728 cm3
Edge = \(\sqrt [ 3 ]{ 1728 } \)
\(\sqrt [ 3 ]{ { \left( 12 \right) }^{ 3 } } \)
= 12 cm (a)
Question 20.
Solution:
Each edge of 5 cubes = 5 cm
Placing than adjacent to each other
Length of new cuboid (l)
= 5 x 5 = 25 cm
Breadth (b) = 5 cm
and height (h) = 5 cm
Volume of new cuboid = lbh
= 25 x 5 x 5 cm3
= 625 cm3 (d)
Question 21.
Solution:
Diameter of circular well = 2n
Radius = \(\\ \frac { 2 }{ 2 } \) = 1 m
Depth(h) = 14 m
Volume of earth dug out = πr2h
= \(\\ \frac { 22 }{ 7 } \) x 1 x 1 x 14
= 44 m (d)
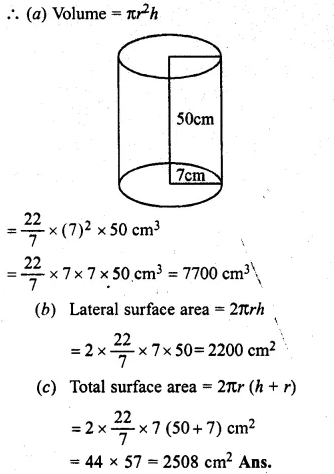
Question 22.
Solution:
Capacity of cylindrical tank = 1848 m3
Diameter = 14 m
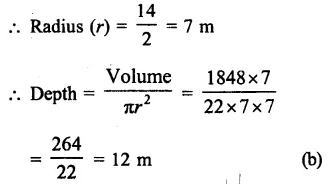
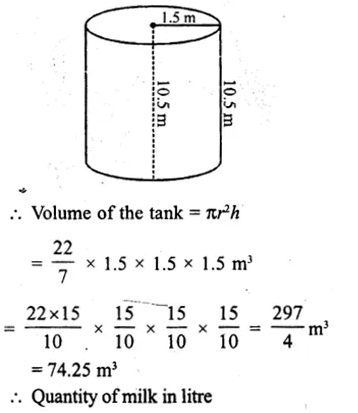
Question 23.
Solution:
Radius of a cylinder (r) = 20 cm
and height (h) = 60 cm

Question 24.
Solution:
Radius of each coin (r) = 0.75 cm
and thickness (h) = 0.2 cm

Question 25.
Solution:
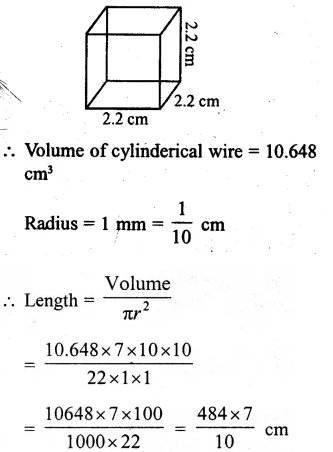
Volume of silver = 66 cm3
Diameter of wire = 1 mm = \(\\ \frac { 1 }{ 10 } \)

Question 26.
Solution:
Diameter of cylinder = 10 cm
Radius (r) = \(\\ \frac { 10 }{ 2 } \) = 5 cm
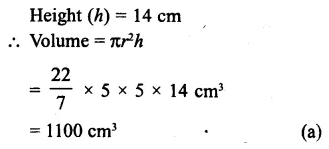
Question 27.
Solution:
Diameter of cylinder = 7 cm
Radius (r) = \(\\ \frac { 7 }{ 2 } \) cm

Question 28.
Solution:
Curved surface area of a cylinder = 264 cm3
Height (h) = 14 cm

Question 29.
Solution:
Diameter of cylinder = 14 cm
Radius (r) = 7 cm
Curved surface area = 220 cm2

Question 30.
Solution:
Ratio in radii of two cylinder = 2 : 3
and ratio in their height = 5 : 3
Let radii of two cylinder = 2x and 3x
and corresponding heights = 5y, 3y

Hope given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.