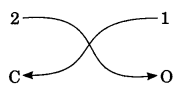Prasanna

On this page, you will find Lines and Angles Class 9 Notes Maths Chapter 4 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 4 Lines and Angles will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 4 Notes Lines and Angles

Lines and Angles Class 9 Notes Understanding the Lesson

Point: A point is a dot made by a sharp pen or pencil. It is represented by capital letter.

Line: A straight and endless path on both the directions is called a line.

 

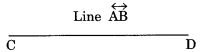
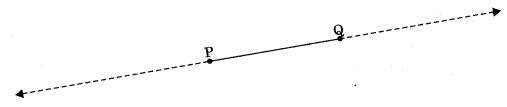
Line segment: A line segment is a straight path between two points.

Ray: A ray is a straight path which goes forever in one direction.

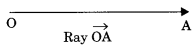
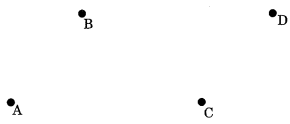
Collinear points: If three or more than three points lie on the same line, then they are called collinear points.

Non-collinear points: If three or more than three points does not lie on the same line, then they are called non-collinear points.

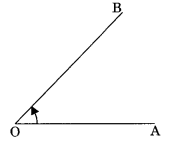
Angle: The space between two straight lines that diverge from a common point or between two planes that extend from a common line.

Types of Angles
1. Acute angle: An angle between 0° and 90° is called acute angle.

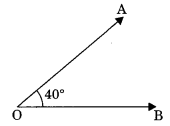
2. Right angle: An angle which is equal to 90° is called right angle.

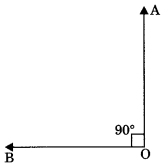
3. Obtuse angle: An angle which is more than 90° but less than 180° is called obtuse angle.

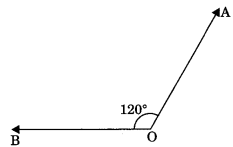
4. Straight angle: An angle whose measure is 180° is called straight angle.

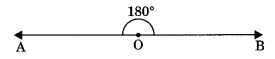
5. Reflex angle: An angle whose measure is between 180° and 360° is called reflex angle.

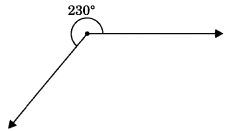
6. Complete angle: An angle which is equal to 360° is called complete angle

Pairs of Angles

1.Complementary angles: Two angles are said to be complementary if the sum of their degree measure is 90°.

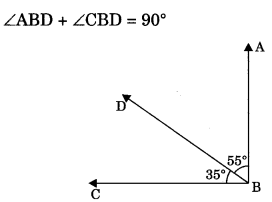
For example, pair of complementary angles are 35° and 55°.

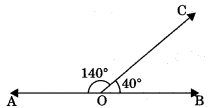
2. Supplementary angles: Two angles are said to be supplementary if the sum of their degree measure is 180°.
∠AOC + ∠BOC = 180°

3. Bisector of angle: A ray which divides an angle into two equal parts is called bisector of the angle.
∠AOC = ∠BOC

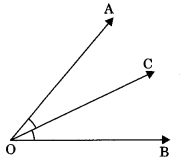
4. Adjacent angles: Two angles are said to be adjacent angles if

• They have a common vertex (O)
• They have a common arm (OC)
• and their non-common arms are on either side of common arm (OA and OB).
  ∠AOB = ∠AOC +∠BOC

5. Linear pair: Two adjacent angles are said to be linear pair if their sum is equal to 180°.

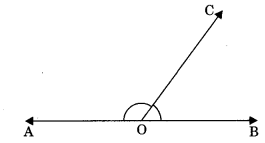
∠AOC + ∠BOC = 180°
Axiom 6.1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
Axiom 6.2: If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.

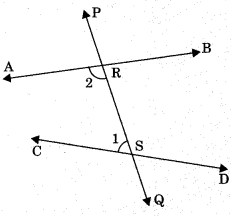
6. Vertically opposite angles: Vertically opposite angles are those angles which are opposite to each other (or not adjacent) when two lines cross each other.

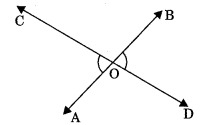
Theorem 6.1: If two lines intersect each other, then the vertically opposite angles are equal.
To prove: If lines AB and CD mutually intersect at point O, then
(a) ∠AOC = ∠BOD (Vertically opposite angles)
(b) ∠AOD = ∠BOC

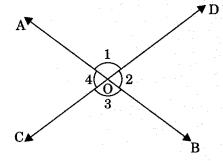
Proof: Lines AB intersect CD at O.
∠1 + ∠2 = 180° (Linear pair)
∠2 + ∠3 = 180° (Linear pair)
From eqn. (1) and (2), ∠1 + ∠2 = ∠2 + ∠3
⇒ ∠1 = ∠3 ⇒ ∠AOD = ∠BOC
Similarly, ∠AOC = ∠BOD

Parallel Lines
If distance between two lines is the same at each and every point on two lines, then two lines are said to be parallel.
If lines l and m do not intersect each other at any point then l || m.

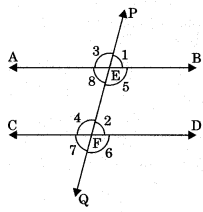
Transversal line: A line is said to be transversal which intersect two or more lines at distinct points.

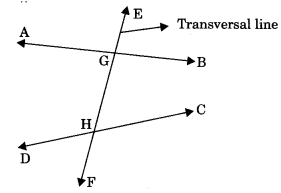
1. Corresponding angles: Pair of angles having different vertex but lying on same side of the transversal are called corresponding angles. Note that in each pair one is interior and other is exterior angle.

• ∠1 and ∠2
• ∠3 and ∠4
• ∠5 and ∠6
• ∠1 and ∠8

These angles are pair of corresponding angles.

2. Alternate interior angles: Pair of angles having distinct vertices and lying can either side of the transversal are called alternate interior angles.

• ∠1 and ∠2
• ∠3 and ∠4

These angles are alternate interior angles

3. Consecutive interior angles: Pair of interior angles of same side of transversal line.

• ∠1 and ∠2
• ∠2 and ∠4

These angles are consecutive interior angles or co-interior angles

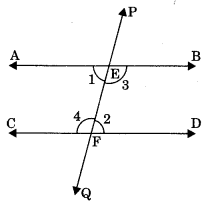
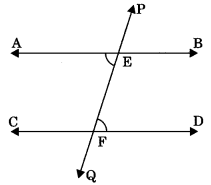
Axiom 6.3: If two parallel lines are intersected by a transversal then each pair of corresponding angles are equal.
If AB || CD, then

• ∠PEB = ∠EFD
• ∠PEA = ∠EFC
• ∠BEF = ∠DFQ
• ∠AEF = ∠CFQ

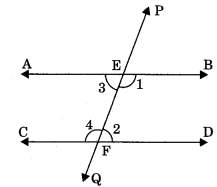
Theorem 6.2: If two parallel lines are intersected by a transversal then pair of alternate interior angles are equal.
If AB || CD, then ?

• ∠AEF = ∠EFD
• ∠BEF = ∠CFE

 

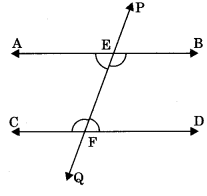
Theorem 6.3: If two parallel lines are intersected by a transversal then the ! sum of consecutive interior angles of same side of transversal is equal to 180°. If AB || CD then
(i) ∠BEF + ∠DFE = 180°
(ii) ∠AEF + ∠CFE = 180°

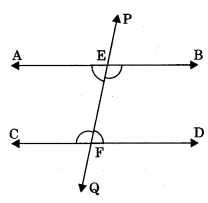
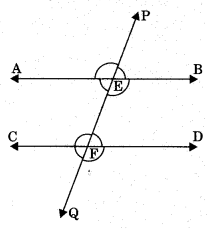
Axiom 6.4: If two lines are intersected by a transversal and a pair of corresponding angles are equal, then two lines are parallel.
(i) If ∠PEB = ∠EFD (corresponding angles), then AB || CD

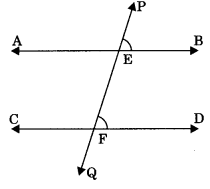
Theorem 6.4: If two lines intersected by a transversal and a pair of alternate interior angles are equal, then two lines are parallel. If ∠AEF = ∠EFD (alternate interior angles), then AB || CD.

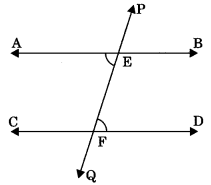
Theorem 6.5: If two lines are intersected by a transversal and the sum of consecutive interior angles of same side of transversal is equal to 180°, the lines are parallel. If ∠AEF + ∠CFE = 180°, then AB || CD.

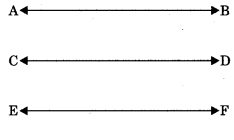
Theorem 6.6: Lines which are parallel to the same line are parallel to each other.
If AB || EF and CD || EF then AB || CD

 

 

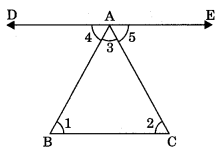
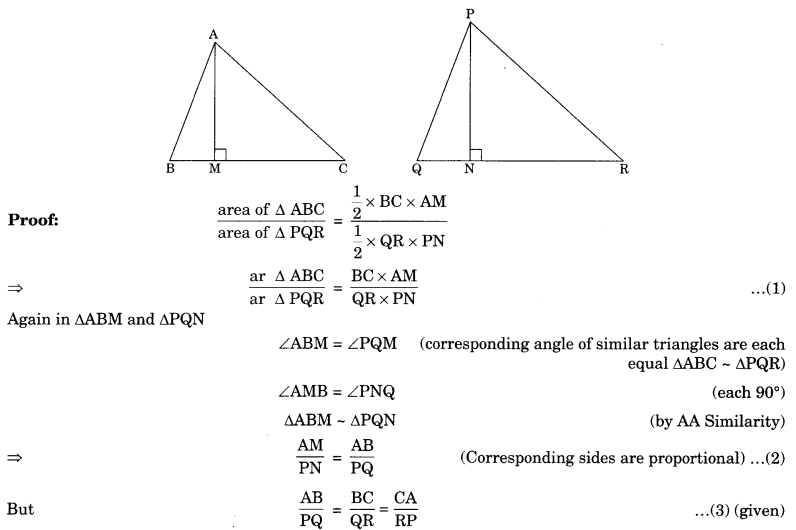
Theorem 6.7: The sum of the angles of a triangle is equal to 180°.
Given: ΔABC
To prove: ∠A + ∠B + ∠C = 180°
Construction: Draw DE || BC
Proof: DE || BC
then ∠1 = ∠4 …(1) (alternate interior angles)
∠2 = ∠5 …(2) (alternate interior angles)
Adding equations (1) and (2),
∠1 + ∠2 = ∠4 +∠5
Adding ∠3 on both sides,
∠1 +∠2 + ∠3 = ∠3 + ∠4 + ∠5
⇒ ∠A + ∠B + ∠C = 180° (Sum of angles at a point on same side of a line is 180°)

Theorem 6.8: If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
Given: AABC in which, side BC is produced to D.
To Prove: ∠ACD = ∠BAC + ∠ABC
Proof: ∠ACD + ∠ACB = 180° …(1) (Linear pair)
∠ABC + ∠ACB + ∠BAC = 180° …(2)
From eqn. (1) and (2), ∠ACD + ∠ACB
= ∠ABC + ∠ACB + ∠BAC
= ∠ACD = ∠ABC + ∠BAC

 

On this page, you will find Introduction to Euclid’s Geometry Class 9 Notes Maths Chapter 3 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 3 Introduction to Euclid’s Geometry will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 3 Notes Introduction to Euclid’s Geometry

Introduction to Euclid’s Geometry Class 9 Notes Understanding the Lesson

1. The word ‘geometry is derived from the Greek Word ‘Geo’ means Earth and ‘matrein’ means to measure,

2. In India the excavations of Harappa and Mohenjo-daro show the industrially civilisation (about 300 BCE) made use of geometry.

3. Sulbasutras were the manuals of geometrical constructions in (800 BCE to 500 BCE)

4. The Sriyantra (given in Atharvaveda) which consist 9 interwoven isosceles triangles. These triangles are arranged in such a way that they produce 43 subsidiary triangles.

5. Thales was a great mathematician who gives the proof and statement that a circle is bisected by its diameter.

6. Thales famous pupil was Pythagoaras (572 BCE). He and his group developed the theory of geometry to a great extent.

7. Euclid was a teacher of mathematics at Alexandria in Egypt collect all the famous work and arranged it in his famous treatise called ‘Elements’. He divided the elements in thirteen chapters which are each called a book. These books influenced the whole worlds to understand geometry.

Definitions which are given by Euclid

• Point-, a point is that which has no part.
• Line: A line is breadthless length.
• The ends of a line are points.
• Straight line: It is a line which lies evenly with the points on itself.
• Surface: A surface is that which has length and breadth only.
• Edge: The edges of a surface are lines.
• Plane surface: A plane surface is a surface which lies evenly with the straight lines on itself

If we study these definitions, we find the some of terms like part, length, breadth, evenly, etc. need to be further described clearly. Euclid assumed certain properties, which were not to be proved. Euclid’s assumptions are universal truths,

• Axiom: The basic facts which are taken for granted without proofs are called axiom.
• Statement: A sentence which is either true or false but both is called a statement.
• Theorem: A statement which requires proof.

Euclid’s Axioms

• Things which are equal to the same thing are equal to one another.
• If equals are added to equals, the wholes are equal.
• If equals are subtracted from equals the remainders are equal.
• Things which coincide with one another are equal to one another.
• The whole is greater than the part.
• Things which are double of the same things are equal to one another.
• Things which are halves of the same things are equal to one another.

Collinear points: Three or more points are said to be collinear, if they all lie in the same line.

Plane: A plane is a flat, two dimensional surface that extends infinitely in all directions. Intersecting lines: Two lines land m are said to be intersecting lines if l and m have only one point common.

Playfair Axiom: Two intersecting lines cannot both be parallel to a same line.

Plane figure: A figure that exist in a plane is called a plane figure.

Note:

• Common notions often called axioms.
• Postulates were the assumptions that are specific for geometry.

Axiom 5.1: There is a unique line that passes through two distinct points.

1. Through a given point infinitely many lines can be drawn.

2. A line contains infinitely many points.

Euclid’s five postulates
Postulate 1: A straight line may be drawn from any one point to any other point.
Note: This postulate tells us that one and only one (unique) line passes through two distinct points.

Postulate 2: A terminated line can be produced indefinitely.
This postulate tells us that a line segment can be extended on either side to form a line.

Postulate 3: A circle can be drawn with any centre and any radius.

Postulates 4: All right angles are equal to one another.

Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

Example: Sum of ∠1 and ∠2 is less than 180°. Therefore, the lines AB and CD will enventually intersect on the left side of PQ. Nowadays, axioms and postulates are used in same sense.

 

Note: The statements that were proved are called propositions or theorems.
I Euclid deduced 465 propositions in a logical chain by using his axioms,

Theorem 5.1
Two distinct lines can not have more than one point in common,
Proof: Let us suppose that two lines l and m intersect in two distinct points say P and Q. Therefore two lines passing through two distinct points P and Q. But our assumption clashes with the axiom that only one line can pass through two distinct points. So, the assumption was wrong that we started with, that two lines can pass through two distinct points is wrong. Hence two distinct lines can passe through one common point.

On this page, you will find Atoms and Molecules Class 9 Notes Science Chapter 3 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 3 Atoms and Molecules will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 3 Notes Atoms and Molecules

Atoms and Molecules Class 9 Notes Understanding the Lesson

1. The structure of matter has been a subject of speculation from a very early time. The ancient Indian and Greek philosophers regarded matter to be discontinuous and made up of infinitely small particles. Around the same period, Greek philosopher, Democritus, suggested that if we go on dividing matter into smaller parts, a stage would be reached when particles obtained cannot be divided further. He called these particles ‘Atoms’ meaning indivisible.

2. After Democritu’s death, little more was done with atomic theory until the end of the 18th century, when Antoine Lavoisier introduced modern chemistry to the world. He put forward two important laws of chemical combination which formed the basis of Dalton’s atomic theory which were published in 1808.

3. Laws of Chemical Combination: Whenever reactants react together to form the products or the elements combine together to form a compound, they do so according to certain laws. These laws are called “Laws of Chemical Combination”.

4. Laws of Conservation of Mass: Law of Conservation of Mass states that mass can neither be created nor destroyed in a chemical reaction.

5. Law of Constant Proportions: This law was stated by Proust as “In a chemical substance, the elements are always present in definite proportion by mass”. For example: In a compound such as water, the ratio of the mass of hydrogen to the mass of oxygen is always 1: 8, whatever the source of water. Thus, if 9 g of water is decomposed, 1 g of hydrogen and 8 g of oxygen are always obtained.

6. As the law of constant proportions is true, it helps us to calculate the percentage of any element in the given compound, using the following expression:

7. Dalton’s Atomic Theory : On the basis of laws of chemical combination, John Dalton, proposed that behaviour of matter could be explained using an atomic theory.

8. Postulates of Dalton’s Atomic Theory

• All matter is made of very tiny particles called atoms.
• Atoms are indivisible particles, which cannot be created or destroyed in a chemical reaction.
• Atoms of a given element are identical in mass and chemical properties.
• Atoms of different elements have different masses and chemical properties.
• Atoms combine in the ratio of small whole numbers to form compounds.
• The relative number and kinds of atoms are constant in a given compound.

9. Limitations of Dalton’s Atomic Theory

• It failed to explain how atoms of different elements differ from each other i.e., it did not tell anything about internal structure of the atom.
• It could not explain how and why atoms of different elements combine with each other to form compound- atoms or molecules.
• It failed to explain the nature of forces that hold together different atoms in a molecule.
• It did not make any distinction between ultimate particle of an element that takes part in reaction (atom) and ultimate particle that has independent existence (molecule).

Question 10.
Atom
Answer:
An atom is defined as the smallest particle of an element which may not be capable of free existence. However, it is the smallest particle that takes part in a chemical reaction.

Question 11.
How big are atoms?
Answer:
Atoms are very small, they are smaller than anything that we can imagine or compare with more than millions of atoms when stacked would make a layer barely as thick as a thin sheet of paper.

Atoms are very small in size. The size of an atom is expressed in terms of atomic radius. Atomic radius is measured in nanometers (nm).
\(1 \mathrm{nm}=\frac{1}{10^{9}} \mathrm{m}=10^{-9} \mathrm{m}\)

Radii of most of the atoms are the order of 0.1 nm or 10_1° m. For example, atomic radius of hydrogen is
0. 037 nm while that of gold atom is 0.144 nm.

Question 12.
Symbols used to represent atoms of different elements
Answer:
Daltons suggested symbols for the atoms of different elements. He was the first scientist to use the symbols for elements in a quantitative sense. When he used symbol for an element he meant a definite quantity of that element, that is, one atom of the element.

Question 13.
Modern Symbols of Elements
Answer:
1. The symbol of an element is the “first letter and another letter” of the English or Latin name of the element. However, in all cases, the first letter is always capital and the other letter (if added) is always a small letter.
For example: Hydrogen is represented by ‘H’, oxygen by ‘O’, carbon by ‘C’ etc.

2. The necessity of adding another letter arises only in case of elements whose names start with the same
letter. However, the other letter added is not always the second letter of the name. Further, the other – letter added may be a letter from the Latin name of the element.

For example: Carbon, Calcium, Cobalt, Chlorine and Copper all start with the first letter ‘C’ Hence carbon is represented by C and calcium is represented by Ca, cobalt by Co, chlorine by Cl and copper by Cu

Element	Symbol	Element	Symbol	Element	Symbol
Aluminium	A1	Copper	Cu	Nitrogen	N
Argon	Ar	Fluorine	F	Oxygen	O
Barium	Ba	Gold	Au	Potassium	K
Boron	B	Hydrogen	H	Silicon	Si
Bromine	Br	Iodine	I	Silver	Ag
Calcium	Ca	Iron	Fe	Sodium	Na
Carbon	C	Lead	Pb	Sulphur	S
Chlorine	Cl	Magnesium	Mg	Uranium	U
Cobalt	CO	Neon	Ne	Zinc	Zn

Question 14.
Atomic Mass
Answer:
The atomic mass of an element is the relative mass of its atoms as compared with the mass of an atom of carbon -12 isotope taken as 12 units.
\(\text { Atomic mass }=\frac{\text { Mass of } 1 \text { atom of the element }}{\frac{1}{12} \text { of the mass of an atom of Carbon-12 }}\)

Since atomic masses are relative masses, they are pure numbers and are often given without units. In case of most of the elements, all the atoms of the elements do not have same relative mass. The atoms of an element having different relative masses are called isotopes. For example: Chlorine contains two types of atoms having relative masses 35 u and 37 u and their relative abundance is 3:1.
\(\text { Atomic mass of chlorine }=\frac{35 \times 3+37 \times 1}{4}=35.5 \mathrm{u}\)

Question 15.
What is a Molecule?
Answer:
A molecule can be defined as the smallest particle of an element or a compound that is capable of an independent existence and shows all the properties of that substance.

Question 16.
Molecule of an element
Answer:
Molecule of an element means one, two or more atoms of the same element existing as one species in the free state.
(i) Monoatomic molecules: Noble gases like helium, neon, etc., exist as single atom. Hence, their molecules are monoatomic.

(ii) Diatomic molecules: For example, in a molecule of hydrogen, two atoms of hydrogen exist together. Its molecule is, therefore, represented by H₂, i.e., it is a diatomic molecule.

(iii) Triatomic molecules: For example, in a molecule of ozone, three atoms of oxygen exist together as one species. Hence, it is triatomic with formula O₂

(iv) Tetratomic molecules: For example; Phosphorus P₄ is a triatomic molecule.

Molecules containing more than four atoms are generally called polyatomic.

The number of atoms present in one molecule of the substance is called its atomicity.

Molecules of a compound: Atoms of different elements join together in definite proportion to form molecules of compounds. For example, H₂O represents the molecule of a compound in which two atoms of hydrogen are combined with one atom of oxygen, or hydrogen and oxygen are combined in the fixed proportion, i.e., 1 : 8 by mass.

Molecular mass: The molecular mass of a substance (an element or a compound) may be defined as the average relative mass of a molecule of the substance as compared with mass of an atom of carbon (C-12 isotope) taken as 12 u.
\(\text { Molecular mass }=\frac{\text { Mass of } 1 \text { molecule of the substance }}{\frac{1}{12} \text { of the mass of an atom of } \mathrm{C}-12}\)

For example, molecular mass of CO₂ is 12 x 1+ 16 x 2 = 44.
Formula mass: Formula mass of an ionic compound is obtained by adding atomic masses of all the atoms in a formula unit of the compound.
For example, formula mass of potassium chloride (KCl)
= Atomic mass of potassium + atomic mass of chlorine
= 39 + 35.5
= 74.5

Question 17.
What is an ion?
Answer:
An atom or a group of atoms which contains positive or negative charge are called ions.

• A positively charged ion called ‘cation’.
• A negatively charged ion is called ‘anion’.
• The ions consisting of only single atoms are called monoatomic ions.
• The ions consisting of a group of atoms is called polyatomic ion.

Question 18.
Writing chemical formula
Answer:
Chemical formula of a compound represents the actual number of atoms of different elements present in one molecule of the compound. For example, chemical formula of water is H₂O.

Valency is defined as the combining capacity of the element. It is equal to the number of hydrogen atoms or number of chlorine atoms or double the number of oxygen atoms with which one atom of the element combines.

For example, valency of oxygen is 2. This means that one atom of oxygen can combine with two atoms of hydrogen. Hence, the formula of the compound formed is H₂O.

Rules for writing the chemical formula

• Formula of compound is given by writing the symbols of constituent elements side by side.
• Symbol of the more metallic element is written first in the formula.
• Number of atoms of each of the constituent elements present in the molecule is indicated by subscript.
• When either of the ions or both the ions are polyatomic and their valency is more than 1, we enclose the polyatomic ions in brackets. No brackets are riecessary if the valencies of polyatomic ions are 1.
• While writing formula of a compound if the valency numbers have a highest common factor [H.C.F.], divide the valency numbers by H.C.F. to get a simple ratio between the combining elements.

The simplest compounds, which are made up of two different elements are called binary compounds and formula can be written by criss crossing the valencies of elements present in a molecule of the compound. Formula of the compound can be derived by following steps

Step – 1: Write the constituent elements and their valencies as shown.

Step – 2: Reduce the valency numerals to the simplest whole numbers by dividing by some common factor, if any

Step – 3: Criss-cross the reduced valency numerals and write them as subscripts at the bottom right-hand side of the symbols.

The subscript 1 is not written. Thus, the formula of the compound is CO₂.

Mole concept: A mole of particles (atoms, ions or molecules) is defined as that amount of the substance which contains the same number of particles as there are C-12 atoms in 12 g, i.e., 0.012 kg of C-12 isotope.

Te number of particles (atoms, molecules or ions) present in 1 mole of any substance is fixed, with a value 6.022 x 10²³. This number is called avogadro’s number. Avogadro’s number (N_A or N₀) = 6.022 x 10²³

The volume occupied by one mole of molecules of a gaseous substance is called molar volume or gram molecular volume.

Class 9 Science Chapter 3 Notes Important Terms

Element: A chemical substance that cannot be decomposed by chemical means into simpler parts. It contains same kind of atoms. There are 118 elements known, out of which 94 are natural.

Compound: When two or more atoms of different elements chemically combine, the molecule of a compound is obtained. The examples of some compounds are water, ammonia, sugar, etc.

Molar mass: Molar mass is the sum of the atomic masses of the elements present in a molecule. It is obtained by multiplying the atomic mass of each element by the number of its atoms and adding them together.

Ion: Any atom or molecule which has a resultant electric charge due to loss or gain of valence electrons.

Valency: It is the capacity of atoms of a given element that tend to combine with, or replace atoms of hydrogen. In HCl gas, valency of chlorine is 1.

Atomicity: It corresponds to the number of atoms present in a given molecule of an element. For example, ozone (O₃) has an atomicity of 3 and benzene (C₆H₆) has an atomicity of 12.

Mole: [Historically the word ‘mole’ was introduced about hundred years back by Wilhelm Ostwald. He derived this word from the Latin word ‘moles’ meaning ‘ heap or a pile’]. A mole is the amount of a substance that contains as many elementary entities (atoms, molecules or other particles) as there are atoms in exactly 0.012 kg of the carbon-12 isotope.

On this page, you will find Constructions Class 10 Notes Maths Chapter 11 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 11 Constructions will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 11 Notes Constructions

Constructions Class 10 Notes Understanding the Lesson

Division of a line segment internally in the given ratio.

Let AB be a line segment of certain length. We need a point P on AB dividing it internally in the ratio m : n
Steps of Construction: Let m = 4, n = 3.

• Draw a line segment AB of given length.
• Make an acute ∠BAX with AB
• Use a compass of any radius and mark 7(i.e. m + n) points A₁, A₂,…… , A₇
  such that AA₁ = A₁A₂ = A₂A₃ =………………= A₆A₇
  
  
• Join BA₇
• Through the point A₄ [m = 4], draw a line parallel to BA₇ by making an angle equal to AA₇B at A₄ intersecting AB at P. Then AP : PB = 4 : 3.

Construction of a Triangle similar to a given Triangle as per given scale factor.
1. Scale Factor  \(\frac{m}{n}\)(where m < n)
Steps of construction: Let \(\frac{m}{n}=\frac{3}{4}\)

• Construct a triangle ABC by using given data.
• Make an acute angle ∠BAX below the base AB.
• Along AX, mark 4 points [the greater of 3 and 4 in \(\frac{3}{4}\)] as A₁, A₂,A₃, A₄ such that
  AA₁ = A₁A₂ = A₂A₃ = A₃A₄.
• Join A₄ B
  
• From A₃, draw A_gB’ || A₄B, meeting AB at B’.
  From B’, draw B’C’ || BC, meeting AC at C’.

Thus, ΔAB’C’ is the required triangle each of whose sides is \(\frac{3}{4} \)of the corresponding side of ΔABC.

2. Scale Factor \(\frac{m}{n} \) (where m > n)
Steps of construction:
Let \(\frac{m}{n}=\frac{5}{3}\)

• Construct ΔABC using given data.
• Make an acute angle ∠BAX below the base AB. Extend AB to AY and AC to AZ.

• Along AX, mark 5 points [the greater of 5 and 3 in \(\frac{5}{3} \)
  such that AA₁ = A₁A₂ =………. = A₄A₅.
• Join A₃B.
• From A_g, draw A₅B’ || A₃B, meeting AY produced at B’.
• From B’, draw B’C’ || BC, meeting AZ produced at C’.
  Thus, ΔAB’C’ is the required triangle, each of whose sides is \(\frac{5}{3}\) of the corresponding side of ΔABC.

Construction of the pair of tangents from an external point to a circle.

Let O is the centre of the circle and a point A is external point to a circle.

Steps of construction

• Join AO and bisect it. Let M be the mid-point of AO.
• Taking M as centre and MO as radius, draw a circle.
  Let it intersects the given circle at the points B and C.
• Join AB and AC.
  Thus, AB and AC are the required tangents.

On this page, you will find Polynomials Class 9 Notes Maths Chapter 2 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 2 Polynomials will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 2 Notes Polynomials

Polynomials Class 9 Notes Understanding the Lesson

1. An expression which is the combination of constants and variables and are connected by some or all the operations addition, subtraction, multiplication and division is known as an algebraic expression.
Example: 7 + 9x – 2x² + \(\frac{5}{6}\) xy

2. Constant: Which has fixed numerical value.
Example: 7, -4, \(\frac{3}{4}\) , n etc.

3. Variable: A symbol which has no fixed numerical value is known as a variable.
Example: 2x, 5x²

4. Terms: These are the parts of an algebraic expression which are separated by operations, like addition or subtraction are known as terms.
Example: In the expression 5x³ + 9x² + 7x – 3, terms are 5x³, 9x², 7x and -3

5. Polynomial: An algebraic expression of which variables have non-negative integral powers is called a polynomial.
Example:
(a) 5x² + 7x + 3
(b) 9y³ – 7y² + 3y + 7

6. Coefficient: A coefficient is the numerical value in a term.
Note: If a term has no coefficient, the coefficient is an unwritten 1.
Example: 5x³ – 7x² – x + 3

7. Degree of a polynomial (in one variable): The highest power of the variable is called the degree of the polynomial.
Example: 5x + 4 is a polynomial in x of degree 1.

8. Degree of a polynomial in two or more variables: The highest sum of powers of variables is called the degree of the polynomial.
Example: 7x³ + 2x²y² – 3ry + 8

9. Degree of polynomial = 4 (Sum of the powers of variables x and y )

10. Types of Polynomial

(i) Linear polynomial: A polynomial of degree one is called a linear polynomial.
Example: 2x + 3 is a linear polynomial in x.

(ii) Quadratic polynomial: A polynomial of degree 2 is called a quadratic polynomial.
Example: 5x² – 7x + 4 is a quadratic polynomial.

(iii) Cubic polynomial: A polynomial of degree 3 is called a cubic polynomial.
Example: 3x³ + 7x² – 4x + 9 is a cubic polynomial.

(iv) Biquadratic polynomial: A polynomial of degree 4 is called a biquadratic polynomial.
Example: 7x⁴ – 2x³ + 4x + 9 is a biquadratic polynomial.

11. Number of Terms in a Polynomial
Categories of the polynomial according to their terms:

(i) Moflomil A polynomial which has only one non-zero term is called a monomial.
Example: 7, 4x, \(\frac{4}{5}\) xy, 7x²y³z⁵, all are monomials.

(ii) Binomial: A polynomial which has only two non-zero terms is called binomial.
Example: 2x + 7, 9x² + 3, 3x²yz + 4x³y³z², all are binomials.

(iii) Trinomial: A polynomial which has only three non-zero terms is called a trinomial.
Example: 5x² + lx + 9, 5xy + 7xy² + 3x³yz, all are trinomials.

(iv) Constant polynomial: A polynomial which has only one term and that is a constant is called a constant polynomial.
Example: \(\frac{-3}{4}\), 7, 5 all are constant polynomials. 4
Note: The degree of constant non-zero polynomial is zero.

(v) Zero polynomial. A polynomial which has only one term i.e., 0 is called a zero polynomial.
Note: Degree of a zero polynomial is not defined.

12. Value of a Polynomial

Value of a polynomial is obtained, when variable of a given polynomial is interchanged or replaced by a ; constant.    Let p(x) is a polynomial then value of polynomial at x = a is p(a).
Zero or root of a polynomial: A zero or root of a polynomial is the value of that variable for which value of polynomial p(x) becomes zero i.e., p(x) = 0.
Let p(x) be the polynomial and x – a.
If p(a) = 0 then real value a is called zero of a polynomial.

13. Remainder Theorem
Let p(x) be a polynomial of degree ≥ 1 and a be any real number. If p(x) is divided by the linear polynomial x-a, then the remainder is p(a).

Proof: Let p(x) be any polynomial of degree greater than or equal to 1. When p(x) is divided by x – a, the quotient is q(x) and remainder is r(x).
i.e.,p(x) = (x-a) q(x) + r(x)
Since degree of x – a is 1 and the degree of r(x) is less than the degree of x – a so the degree of r(x) = 0.
It: means r(x) is a constant, say r.
Therefore, for every value of x,  r(x) = r
then   p(x) = (x-a) q(x) + r
When x = a, then  p(a) = (a – a) q(x) + r ⇒ p(a) = r

14. Factor Theorem
If p(x) is a polynomial of degree greater than or equal to 1 and a be any real number, then

• x – a is a factor of p(x) i.e., p(x) – (x-a) q(x) which shows x – a is a factor of p(x)
• Since x – a is a factor of p(x)
  p(x) = (x-a)g(x) for same polynomial g(x). In this case,p(a) = (a-a) g (a) = 0

15. Factorisation of the Polynomial ax² + bx + c by Splitting the Middle Term
Let           p(x) = ax² + bx + c
and factor of polynomial p(x) = (px + q) and (rx + s)
then   ax² + bx + c = (px + q) (rx + s) = prx² + (ps +qr)x+ qs
Comparing the coefficient of x² on both sides
a = pr …………. (1)
Comparing the coefficient of x
b =ps + qr …………. (2)
and comparing the constant terms
c = qs ……………..(3)
which shows that b is the sum of two numbers ps + qr.
Product of two numbers ps x qr =pr x qs = ac
So for factors ax² + bx + c, we should write b as sum of two numbers whose product is ac.
Example: Factorise 6x² + 17x + 5
Here,  b = p + q = 17
and   ac = 6 x 5 = 30 (= pq)
then we get factors of 30,      1 x 30, 2 x 15, 3 x 10, 5 x 6,
Among above factors of 30, the sum of 2 and 15 is 17
i.e.,p + q = 2 + 15 = 17
∴ 6x² + 17x + 5 = 6x² + (2 + 15)x + 5 = 6x² + 2x + 15x + 5
= 2x(3x + 1) + 5(3x + 1) = (3x + 1) (2x + 5)

16. Algebraic Indentities

On this page, you will find Is Matter Around Us Pure Class 9 Notes Science Chapter 2 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 2 Is Matter Around Us Pure will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 2 Notes Is Matter Around Us Pure

Is Matter Around Us Pure Class 9 Notes Understanding the Lesson

1. Pure substance: A pure substance is defined as a material which contains only one kind of atoms or molecules. In pure substance all the constituting particles have the same chemical nature. Thus, a pure substance con¬sists of a single type of particles.

2. Pure substances are always homogeneous.

• Element: A pure substance which is made up of only one kind of atom.
• Compound: A pure substance which is made up of only one kind of molecules.

3. Mixtures: It is a form of matter in which two or more elements or compounds combine physically in any proportion by weight.

4. Types of Mixtures

• Homogeneous mixture: A mixture which has same composition throughout. Solutions are homogeneous mixtures. For example, air, sea water, grass, vinegar, etc.
• Heterogeneous mixture: A mixture which has different compositions in different parts. For example, sand, mud, iron filings, sulphur, etc.

5. Characteristics of Mixture

• Mixture may be homogeneous and heterogeneous.
• Mixture does not have a fixed melting point.
• In a mixture, the different constituents combine physically in any proportion by mass.
• The constituents of a mixture do not loose their identical property.
• Usually, no energy change take place during the formation of a mixture.

6. Solution
It is a homogeneous mixture of two or more non-reacting substances.

7. Solvent is the substance in which a solute is dissolved.

8. On the basis of the size of particles, solutions can be classified as:

• True solution
• Colloidal solution
• Suspension

9. True Solution : A homogeneous system in which the particle size is less than 1 nm. For example, sugar solution.

10. Properties of True Solution

• A solution is a homogeneous mixture.
• The particles of a solution are smaller than 1 nm in diameter. So, they cannot be seen by the naked eye.
• Because of very small particle size, they do not scatter a beam of light passing through the solution. So, the path of light is not visible in a solution.
• The solute particles cannot be separated from the mixture by the process of filtration. The solute particles do not settle down when left undisturbed that is, a solution is stable.

11. Concentration of solution
There are two methods for expressing the concentration of solution.
Saturated solution: A solution in which no more of solute can be dissolved at a given temperature is called a saturated solution.
(i) Mass by Mass percentage of a Solution =\(\frac{\text { Mass of solute }}{\text { Mass of solution }} \times 100\)

(ii) Mass by Volume percentage of a Solution \(=\frac{\text { Mass of solute }}{\text { Volume of solution }} \times 100\)

12. Unsaturated solution: A solution in which more of the solute can be dissolved at a given temperature is called an unsaturated solution.
Suspension

13. A suspension: is a heterogeneous mixture in which one substance having particle size greater than 100 nm in diameter is spread throughout another substance. For example, muddy water, dust storm, aluminium paint, etc.

14. Properties of Suspension

• A suspension is a heterogeneous mixture.
• The particles of a suspension do not pass through a filter paper. Hence, it is possible to separate them by ordinary filtration.
• The particles of a suspension settle down when a suspension is left undisturbed. Thus, a suspension is unstable.
• The particles of suspension can be seen with naked eyes or with the help of a simple microscope.
• The size of particle in a suspension is greater than 100 nm in diameter.
• A suspension is not transparent to light.

15. Colloidal solutions
A solution in which the size of particles lies in between those of true solutions and suspensions are called colloidal solutions or colloids.
Colloidal solution is heterogeneous in nature and consists of two phases:

• Dispersed phase: It is the component present in small proportion and consists of particles of colloidal dimensions (1 nm to 100 nm).
• Dispersion medium: The solvent like medium in which colloidal particles are dispersed is called dispersion medium.

16. Properties of Colloidal Solutions

(i) Heterogeneous Nature: A colloidal solution is heterogeneous in nature. It consists of two phases— dispersed phase and dispersion medium.

(ii) Filtrability: The size of the colloidal particles is less than the pores of a filter paper,, and, therefore, they easily pass through a filter paper. Colloidal particles, however, cannot pass through the parchment paper or an animal membrane or ultra-filter.

(iii) Tyndall Effect: When a strong beam of light is passed through a colloidal solution placed in a dark place, the path of the beam gets illuminated by a bluish light. This phenomenon is called Tyndall effect. The phenomenon is due to scattering of light by the colloidal particles. The same phenomenon is noticed when a beam of sunlight enters a dark room through a small slit, due to scattering of light by dust particles in the air.

(iv) Visibility: Colloidal particles are too small to be seen by the naked eye. They, however, scatter light and become visible when viewed through an ultramicroscope.

(v) Brownian Movement: When colloidal particles are seen under an ultramicroscope, the particles are found to be in constant motion in zig-zag path in all possible directions. This zig-zag motion of colloidal particles is called Brownian movement. The movement of the particles is due to the collisions with the molecules of the dispersion medium.

(vi) Diffusion: Colloidal particles diffuse from a region of higher concentration to that of lower concentration. However, because of their bigger sizes colloidal particles move slowly and hence diffuse at a slower rate.

(vii) Sedimentation or Settling: Under the influence of gravity, the solute particles tend to settle down very slowly. This rate of settling down or sedimentation can be accelerated by the use of high speed centrifuge called ultracentrifuge.

17. Common methods for the separation mixtures are:

(a) Filtration: Filtration is the process of separating solids that are suspended in liquids by pouring the mixture into a filter funnel. As the liquid passes through the filter, the solid particles remain behind on the filter.

(b) Distillation: Distillation is the process of heating a liquid to form vapour and then cooling the vapour to get back the liquid. This is a method by which a mixture containing volatile substances can be separated into its components.

(c) Sublimation: This is the process of conversion of a solid directly into vapour on heating. Substances showing this property are called sublimate, e.g., iodine, naphthalene, camphor. This method is used to separate a sublimate from non-sublimate substances.

(d) Crystallisation: It is the process of separating solids having different solubilities in a particular solvent.

(e) Magnetic separation: This process is based upon the fact that a magnet attracts magnetic components from a mixture of magnetic and non-magnetic substances. The non-magnetic substance remains unaffected. Thus, it can be used to separate magnetic components from non-magnetic components.

(f) Atmolysis: This method is based upon rates of diffusion of gases and used for their separation from a gaseous mixture.

18. Physical Change: A temporary change which includes change in the shape, size, physical states and appearance of a substance,but not its chemical composition is known as physical change. Physical change is temporary and reversible. Chemical composition of the substance remains the same.
Examples:

• Heating of sulphur
• Sublimation of camphor
• Drying of wet clothes
• Breaking of glass

19. Chemical Change: A permanent change in which the chemical substance loses its own characteristics and composition and gives one or more new substances is called a chemical change. Chemical change is generally permanent and irreversible. Chemical change gives one or more new substances as products.
Examples

• Rusting of iron
• Digestion of food
• Burning of wood
• Ripening of fruit

20. Types of Pure Substances

1. Element: An element is defined as the simplest form or the basic form of a pure substance which can neither be broken into nor built up from simpler substances by any physical or chemical changes.

Properties of metals

• They have a lustre (shine).
• They have silvery-grey or golden-yellow colour.
• They conduct heat and electricity.
• They are ductile (can be drawn into wires).
• They are malleable (can be hammered into thin sheets).
• They are sonorous (make a ringing sound when hit).
  Examples of metals: Gold, silver, copper, iron, etc.

Properties of non-metals:

• They are poor conductors of heat and electricity.
• They are not lustrous, sonorous or malleable.
• They display a variety of colours.
  Examples of non-metals: Hydrogen, oxygen, iodine, bromine, chlorine, etc.
  Metalloids: Elements having certain properties of metals and non-metals are called metalloids.
  Examples: Arsenic, germanium, antimony and bismuth.

2. Compound: A compound is a substance composed of two or more elements, chemically combined with one another in a fixed proportion. For example: Water is compound of hydrogen and oxygen elements and these elements are present in water in the ratio of
1 : 8 by mass.
Characteristics of compound:

• In a compound constituents are presents in definite proportion by mass.
• The properties of the compound are different from the properties of the constituents (elements) that make up the compound.
• The constituents of a compound cannot be separated by simple physical processes.
• A compound has a fixed melting point and boiling point.
• A compound is always homogeneous in nature.

Difference between mixture and compound

Mixture	Compound
1. In a mixture, the constituents can be present in any proportion by mass. Thus, a mixture does not have any definite formula.	1. In a compound, constituents are present in  definite proportion by mass. A compound has a definite formula.
2. A mixture shows the properties of its constituents.	2. The properties of a compound are different from the properties of its constituent elements.
3. A mixture can be separated into its constituents by physical methods such as distillation, sublimation, filtration, etc.	3. The constituent of a compound can be separated only by chemical methods.
4. Formation of a mixture is not accompanied by much energy change.	4. Formation of a compound is generally accompanied by the evolution of energy in the form of heat or light.
5. A mixture does not have a fixed melting point and boiling point.	5. A compound has fixed melting point and boiling point.
6. A mixture may be homogeneous or heterogeneous.	6. A compound is always homogeneous.

Class 9 Science Chapter 2 Notes Important Terms

1. Matter is defined as anything that has weight and occupies space.

2. Intermolecular force is the force of attraction between the consituent particles of matter.

3. Alloys are mixtures of two or more metals or a metal and a non-metal and cannot be separated into their components by physical methods.

4. Solution is a homogeneous mixture of two or more substances. The major component of a solution is called the solvent, and the minor, the solute.

5. Colloids are heterogeneous mixtures in which the particle size is too small to be seen with the naked eyes, but is big enough to scatter light.

On this page, you will find Circles Class 10 Notes Maths Chapter 10 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 10 Circles will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 10 Notes Circles

Circles Class 10 Notes Understanding the Lesson

1. Circle: A circle is a collection of all points in a plane which are at a constant distance from a fixed point. Here
Fixed point is called centre of the circle. Constant distance is called radius of the circle.

2. Considering a circle with centre ‘O’ and radius V and a line T in a plane.
Three different situations are there:

• When there is no common point between the circle and the line. Then the line is known as a non¬intersecting line
• When the line passes the circle in two points, the line is called a secant
• When a line meets the circle at a point, the line is called a tangent
  The point at which the tangent touches the circle is called point of contact.

Facts related to tangent of circle.

Given: A circle with centre 0 and radius r.
A tangent XY at point P to the circle.
To prove: OP ⊥ XY
Construction: Take a point Q on XY other than P. Join OQ.
Proof: Point Q lies outside the circle.

If point Q lies inside the circle then XY will become a secant and not a tangent to the circle.
∴ OQ > OP
which is true for every point on the line XY except the point P.
⇒ OP is the shortest of all the distances of the point O to the points of XY.
OP ⊥ XY
[ ∵ Shortest length from the point outside the line to the line is perpendicular]
Remark: A line drawn through the end point of radius and perpendicular to it, is the tangent to the circle.

Theorem 10.2: The lengths of tangents drawn from an external point to a circle are equal.
Given: PT and PS are tangents from point P to circle with centre 0.
To prove: PT = PS
Construction: Join OP, OT and OS.
Proof: In ΔOTP and ΔOSP
OT = OS [Radii of same circle]

OP = QP
∠OTP = ∠OSP [Each 90º]
∴ ΔOTP ≅ ΔOSP  [RHS]
⇒ PT = PS   [CPCT]

On this page, you will find Matter in Our Surroundings Class 9 Notes Science Chapter 1 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 1 Matter in Our Surroundings will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 1 Notes Matter in Our Surroundings

Matter in Our Surroundings Class 9 Notes Understanding the Lesson

1. Matter is everything around you. Everything in this universe is made up of material which in scientific term is called matter.

2. Matter can be defined as anything that occupies space possesses mass, offers resistance and can be felt by one or more of our senses.

3. Examples: Water, air, plant, animal, stones, clouds, etc.
Matter is classified on the basis of their physical and chemical nature.

• Physical classification: On the basis of physical properties, matter has been classified as solid, liquid and gas.
• Chemical classification: On the basis of chemical composition, matter has been classified as element, compound and mixture.

4. Properties of Matter

• Matter is made up of small particles.
• Particles of matter have space between them.
• Particles of matter are continuously moving.
• Particles of matter attract each other because of force of attraction.

5. States of Matter
This classification is done on the basis of arrangement among particles, energy of particles and the distance between the particles.
(i) Solids:

• They have fixed shape and definite volume.
• They have small interparticle distances.
• They are incompressible.
• They are rigid.
• They have high density and do not diffuse.
• They have strong intermolecular forces of attraction.
• Their constituent particles are very closely packed.
• Their kinetic energy is very less.
  Examples: Sugar, salt, etc.

(ii) Liquids:

• They do not have fixed shape but have fixed volume.
• Their interparticle distances are larger than solids.
• They are almost incompressible.
• They have low density than solids.
• Their interparticle forces of attraction are weaker than solids.
• Their constituent particles are less closely packed.
• They assume the shape of the portion of the container they occupy.
• They can flow and thus can be called fluids.
• The kinetic energy of particles is more than that of solids.
• Examples: Milk, water, etc.

(iii) Gases:

• They have neither fixed shape nor fixed volume.
• Their interparticle distances are largest among the three states of matter.
• They have high compressibility.
• They have least density and diffuse.
• Their interparticle forces of attraction are weakest.
• Their constituent particles are free to move about.
• They can expand to occupy larger volume.
• They are also called vapour.
• The particles of gases have maximum kinetic energy.
• Examples: H₂, N₂, CO₂ etc.

6. Interchange of States of Matter

• Matter can be changed from one state to another state.
• Most of the metals, which are solid change into liquid on heating and then into vapour on further heating.
• The change of state of matter depends on:
  (i) Temperature
  (ii) Pressure

7. Effect of Change of Temperature

8. The temperature effect on heating a solid varies depending on the nature of the solid and the conditions required for bringing the change.

9. Generally on heating, temperature of substances increases. But during state transformation, temperature remains same.

10. On heating: The kinetic energy of particles increases which overcomes the force of attraction between the particles thereby solid melts and is converted to a liquid.

11. Melting point: It is the temperature at which a solid changes to a liquid at atomospheric pressure.

12. Different substances have different melting points.

13. Higher the melting point means large forces of attraction between the particles.

14. Melting point of ice is 273.16 K.

15. The process of melting is also known as fusion.

16. Melting point is characteristic propertyof a substance.

17. Latent heat: The hidden heat which breaks the force of attraction between the molecule is called latent heat.

18. It is the heat supplied to a substance during the change of its state.

19. It is the heat energy hidden in the bulk of matter.

20. Latent heat of fusion: Amount of heat energy required to convert 1 kg of a solid into a liquid at atmospheric pressure at its melting point is known as latent heat of fusion of a substance.

21. A solid having stronger interparticle forces has greater latent heat of fusion.

22. Latent heat of fusion of water is 333.7 kJ/kg.

23. Boiling point: The temperature at which a liquid starts boiling at atmospheric pressure is known as its boiling point.

24. A liquid having weaker interparticle forces has lower boiling point and is more volatile.

25. Latent heat of vapourisation: The amount of heat energy required to convert 1 kg of a liquid into a gas at atmospheric pressure at its boiling point is known as latent heat of vapourisation of the substance.

26. Latent heat of vapourisation of water is 2259 kJ/kg. Thus 1 kg of water in the form of steam at 373 K has 2259 kJ more energy than 1 kg of water at 373 K.

27. Condensation: The change of state from gas to liquid is called condensation.

28. The condensation process is reverse of vapourisation.

29. Freezing: The change of state from liquid to solid is called freezing.

30. Freezing is the reverse of melting or fusion.

31. Sublimation: Sublimation involves direct conversion of a solid into the gaseous state on heating and vice-versa.

32. Dry ice sublimes at -78 °C (195 K).

33. Camphor, ammonium chloride, iodine and naphthalene are some substances which undergo sublimation.

34. Effect of Change of Pressure

In the gaseous state, the interparticle spaces are very large and attractive forces between the particles are negligible. Because of large interparticle space, gases are highly compressible. When pressure is applied on a gas, enclosed in a cylinder, its molecules move closer and the gas undergoes appreciable compression. As the molecules move closer, the attractive forces between the molecules increase. At a sufficiently high pressure, the gas changes into liquid.

(i) Solid CO₂ is stored under high pressure. At a pressure of 1 atmosphere, solid CO₂ changes directly into gas without passing through the liquid state. Solid CO₂ is known as dry ice. Thus, we can conclude that we can liquefy gas by applying pressure and reducing temperature.

(ii) Change in volume from gaseous state to liquid state is very large whereas change in volume from liquid state to solid state is very small (negligible). This is due to the reason that in liquid the interparticle spaces are very small in a liquid.

(iii) Atmospheric pressure: The pressure exerted by the atmosphere or air is called atmospheric pressure. It decreases with increase in height.

(iv) Atmosphere (atm) is a unit of pressure.

(v) The SI unit of pressure is pascal (pa).
1 atm = 1.01 x 10⁵pa
1 bar = 1 x 10⁵ pa 1
bar = 1.01 atm.

(vi) Evaporation: The phenomenon of change of a liquid into vapour at any temperature below its boiling point is called evaporation.

(vii) Particles of matter possess kinetic energy. At a particular temperature, in a sample of liquid all the particles do not have same kinetic energy. There is a small fraction of molecule which has enough kinetic energy to overcome the attractive forces of other particles. If such a particle happens to come near the surface, it escapes into vapour state and evaporation takes place.

35. Factors Affecting the Rate of evaporation

(i) Surface area: Evaporation is a surface phenomenon, i.e., only the particles on the surface of the liquid gets converted into vapour. Thus, greater is the surface area, more is the rate of evaporation. For example, clothes dry faster when they are well spread out.

(ii) Increase in temperature: The rate of evaporation increases with increase in temperature. At higher temperature greater number of particles have enough kinetic energy to escape into the vapour state. For example, clothes dry faster in summer than in winter.

(iii) Decrease in humidity: The amount of water vapour present in air is referred to as humidity. The air cannot hold more than a definite amount of water vapour at a given temperature. If the humidity is more, the rate of evaporation decreases. For example, clothes do not dry easily during rainy season because the rate of evaporation is less due to high moisture content in the air.

(iv) Increase in the speed of the wind: With the increase in wind speed, the particles of water vapour move away with the wind, decreasing the amount of water vapour in the surrounding. For example, wet clothes dry faster on a windy day.

(v) Nature of liquid: Different liquids have different rates of evaporation. A liquid having weaker interparticle attractive forces evaporates at a faster rate because less energy is required to overcome the attractive forces. For example, acetone evaporates faster than water.

(vi) Evaporation causes cooling: Only the liquid particles having high kinetic energy leave the surface of the liquid and get converted into vapour. As a result, the average kinetic energy of the remaining particles of the liquid decreases and hence the temperature falls. Thus, evaporation causes cooling.

Class 9 Science Chapter 1 Notes Important Terms

Melting Point: It is the temperature at which a solid changes into liquid at atmospheric pressure.

Freezing point: The temperature at which a liquid freezes to become a solid at atmospheric pressure is called the freezing point.

Boiling point: The temperature at which a liquid starts boiling at atmospheric pressure is called its boiling point.

Latent heat of vapourisation: The amount of heat energy that is required to change 1 kg of liquid into vapour at atmospheric pressure at its boiling point is called latent heat of vapourisation.

Condensation: The process of changing a gas (or vapour) to a liquid by cooling is called condensation. Sublimation: Sublimation involves direct conversion of a solid into the gaseous state on heating and vice-versa.

Latent heat: The hidden heat which breaks the force of attraction between the molecules is known as latent heat.

Latent heat of fusion: The heat of energy required to convert 1 kg of a solid into liquid at atmospheric pressure, as its melting point, is known as latent heat of fusion.

Boiling: Boiling is a bulk phenomenon. Particles from the bulk (whole) of the liquid change into vapour state.

Evaporation: Evaporation is a surface phenomenon. Particles from the surface gain enough energy to overcome the force of attraction present in the liquid and change into vapour state.

On this page, you will find Some Applications of Trigonometry Class 10 Notes Maths Chapter 9 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 9 Some Applications of Trigonometry will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 9 Notes Some Applications of Trigonometry

Some Applications of Trigonometry Class 10 Notes Understanding the Lesson

Trigonometry is the study of relationships between the sides and angles of a triangle. In this chapter you will study about some ways in which trigonometry is used:

• It is used in geography and in navigation.
• It is used in constructing maps, determine the position of an island in relation to the longitudes and latitudes.
• It is used for calculating the height and distance of various objects without measuring it.

Terms related to height and distance:

1. Line of sight: The line joining the eyes of the observer and the objects which he/she observes is called line of sight.

2. Angle of elevation: (When object is above the horizontal)
The angle between the line of sight and the horizontal is called the angle of elevation.

3. Angle of depression: (When object is below the horizontal)
The angle between the horizontal line and the line of sight is called the angle of depression.

Trigonometric formulae used:

On this page, you will find Triangles Class 10 Notes Maths Chapter 6 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 6 Triangles will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 6 Notes Triangles

Triangles Class 10 Notes Understanding the Lesson

In X standard we have learnt about congruent figures.

Congruent figure: Those two geometric figures having the same shape and size are known as congruent figures.

Rules of Congruency

1. SAS (Side-Angle-Side): Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.

2. ASA (Angle-Side-Angle): Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.

3. AAS (Angle-Angle-Side): Two triangles are Congruent if any two pairs of angles and a pair of corresponding sides are equal.

4. SSS (Side-Side-Side): If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.

5. RHS (Right angle-Hypotenuse-Side: In two right angle triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.

Note: All congruent figures or triangles are similar.

Similar Figure: Two figure which are of same shape (but not necessarily the same size) are called similar figures. For example,

• All line segments are similar.
• All circles are similar.
• Two or more squares are similar.
• Two or more equilateral triangles are similar.

Note:

• All rectangles are not similar.
• All triangles are not similar.

Similar Polygons: Two polygons with the same number of sides are similar, if (1) their corresponding angles are equal. (2) their corresponding sides in the same ratio.

Similarity of Triangles

Two triangles are similar if

• Their corresponding angles are equal; and
• Their corresponding sides are in the same ratio

Famous Greek mathematician Militus Thales gives the relation to the two equiangular triangle is known as BPT or Thales theorem.

Equiangular triangles: If corresponding angles of two triangles are equal then they are equiangular triangles

Theorem 6.1: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Given: A AABC in which a line DE || BC intersects the other two sides AB and AC at D and E respectively.
To Prove that \(\frac{A D}{D B}=\frac{A E}{E C}\)
Construction: Join BE and CD and draw DM ⊥ AC and EN ⊥ AB

(Because both are on the same base DE and between the same parallels BC and DE) from eqn (1), (2) and (3) AD AE

Theorem 6.2: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.

AD AE Given: In ΔABC, \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
To prove: DE || BC

Construction: Let us suppose that DE is not parallel to BC, so we draw a line DF || BC
Proof: DF || BC
Therefore by Basic Proportionality Theorem,

which is not possible. We come at the contradiction. So our supposition was wrong, it is only possible, if point F will coincide the point E.
Therefore DE || BC.

Criteria for Similarity of Triangles

In previous section, we have studied that two triangles are similar, if (I) their corresponding angles are similar (II) their corresponding sides are proportional (or are in the same ratio).

Theorem 6.3: AAA Criterion: If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) and hence the two triangles are similar.

In ΔABC and ΔDEF,

Remark : AA Similarity Creterian: If two angles of a triangle are equal to two angles of another triangle, then their corresponding angles are equal and the triangles are similar.

In ΔABC and ΔDEF
∠A =∠D, ∠C = ∠F then ΔABC ~ ΔDEF (by AA similarity)

Theorem 6.4: SSS Similarity Criterion: If the corresponding sides of two triangles are proportional (i.e. in the same ratio), then their corresponding angles are equal and the triangles are similar.

In ΔABC and ΔDEF
\(\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F} DF \)then ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
Hence ΔABC ~ ΔDEF

Theorem 6.5: SAS Similarity Criterion: If one angle of a triangle is equal to one angle of the other and the sides including these angles are proportional, the triangles are similar.

In ΔABC and ΔDEF
∠BAC = ∠EDF
\(\frac{A B}{D E}=\frac{A C}{D F}\)
Hence ΔABC ~ ΔDEF

Areas of Similar Triangles
We have study in two similar triangles. Ratio of the corresponding sides of two similar triangles is same.

Theorem 6.6: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

Given: ΔABC ~ ΔPQR

Theorem 6.7: If a perpendicular is drawn from the verities of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other.

• ΔADB ~ ΔABC
• ΔBDC ~ ΔABC
• ΔADB ~ ΔBDC

Theorem 6.8: In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Given: ABC is a right angle triangle which is right angled at B.
To prove:  AC² = AB² + BC²
Construction: Draw BD ⊥  AC
Proof:  ΔADB ~ ΔABC
(If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other)

From equation (2) and (3)
Adding eqn (1) and (2)
(If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse than triangles on both sides of the perpendicular are similar to the whole triangle and to each other)
AB² + BC² = AD . AC + CD . AC
⇒ AB² + BC² = AC (AD + CD)
⇒ AB² + BC² = AC x AC
⇒ AB² + BC² = AC²
⇒ AC² = AB² + BC²

Theorem 6.9: In a triangle, if square of one side is equal to the sum of the squares of the other two sides. Then the angle opposite the first side is a right angle.

Given: We have ΔABC in which
AC² = AB² + BC²
To prove: ∠ABC = 90°
Construction: Construct a ΔDEF right angled at E such that EF = BC and DE = AB

Proof: In ΔDEF
DF² = EF² + DE² (Pythagoras theorem) (given)
DF² = BC² + AB²…(1) (by construction)
But AC² = BC² + AB²…(2)

From eqn (1) and (2)
AC² = DF²
⇒ AC = DF… (3)

In ΔABC and ΔDEF
AB = DE(by construction)
BC = EF(by construction)
AC = DF(proved above in eqn (3))
ΔABC ≅ ΔDEF(by SSS congruence)
⇒ ∠ABC = ∠DEF (by CPCT)
Therefore ∠ABC = 90°

On this page, you will find Number Systems Class 9 Notes Maths Chapter 1 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 1 Number Systems will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 1 Notes Number Systems

Number Systems Class 9 Notes Understanding the Lesson

1. Number: A number is a mathematical object which is used in counting and measuring.

2. Number system: A number system defines a set of values used to represent a quantity.

3. Natural numbers: A set of counting numbers is called the natural numbers.
N = {1,2, 3, 4, 5,…}
These are infinite in number. Here first natural number is 1 whereas there is no last natural number.

4. Whole numbers: A set of natural numbers including zero is called the whole numbers.
W = {0, 1, 2, 3, 4, 5,…}

Note: All natural numbers are whole numbers but all whole numbers are not natural numbers.
Integers: A set of all whole numbers including negative of all the natural numbers.
Z = {…, – 7, – 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5, 6, 7, …}

5. Rational Numbers
A number is called rational number if it can be expressed in the form of \(\frac{p}{q}\), where p and q are integers and q≠ 0.
Example: \(\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{7}{9}, \text { etc. }\)

Note:

• Every fractional number and integer is a rational number because they can be expressed in the form\(\frac{p}{q}\)
• Between two rational numbers, infinite number of rational numbers can be possible. A rational number between two rational numbers a and b can be found as \(\frac{1}{2}\)(a + b)by using mean method.
• The sum, difference and product of the rational numbers is always a rational number.
• The quotient of a division of one rational number by a non-zero rational number is a rational number.

6. Types of Rational Numbers
1. The natural numbers form a subset of the integers.
2. Natural numbers with zero are referred to as non-negative integers.
3. The natural numbers without zero are known as positive integers.
4. When negative of a positive integer is added to the corresponding positive integer then it produces 0.

• Terminating decimal: It has a finite number of digits after the decimal point.
  \(\frac{3}{8}\)=0.375
• Non-terminating recurring decimal or repeating decimal: It has a digit or group of digits after the decimal point that repeat endlessly.
  

7. Irrational Numbers
Those numbers which cannot be expressed in the form of \(\frac{p}{q}\), where p and q are integers and
q ≠0. They neither terminate nor do they repeat. They are also known as non-terminating non-repeating numbers. Example: \(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}, \sqrt{13}, \sqrt{\frac{7}{3}}, \ldots 5+\sqrt{7}\) are irrational numbers.
An irrational number between two rational numbers a and b can be found as the square root of their product \(\sqrt{a b}\)

Note:

• Euler’s number ‘e’ is an irrational whose first few digits are 2.71828….
• The sum, difference, multiplication and division of irrational numbers are not always irrational.
• Rational number and irrational number can be represented on a number line.
• Irrational numbers like \(\sqrt{2}, \sqrt{3}, \sqrt{5}\) etc. can be represented on a number line by using Pythagoras theorem.

8. Number line: A number line is a line which represent all the numbers. It is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point.

9. Real Numbers”
The union of the set of rational numbers and the set of irrational numbers.
A group of rational or irrational numbers is called real numbers. It can be represented on a number line.

10. Successive Magnification

• Let us suppose we locate 4.46 on the number line. We know 4.46 lies between 4 and 5.
• Now let us divide the portion between 4 and 5 into 10 equal parts and represent 4.1, 4.2, 4.3, …, 4.9.
• We know that 4.46 lies between 4.4 and 4.5 so further divide the portion into 10 equal parts, then these points will represent 4.41, 4.42, 4.43, …, 4.49 on number line. Thus we can locate the given number 4.46 on the number line.