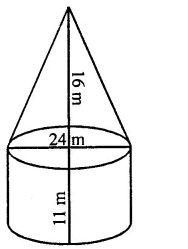
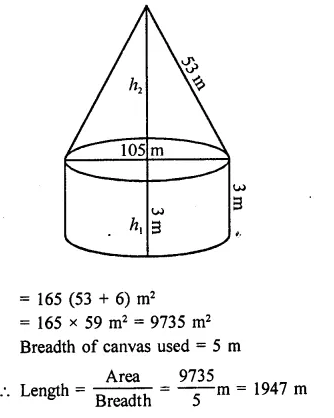
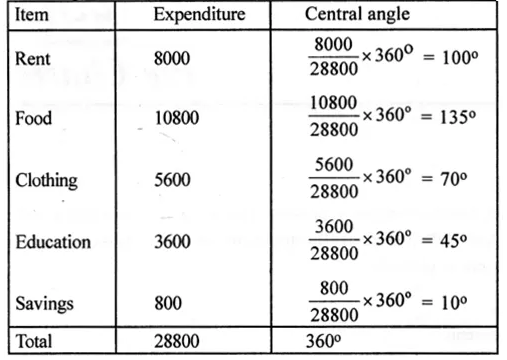
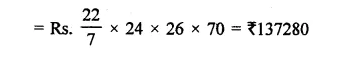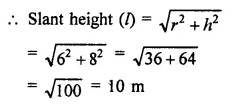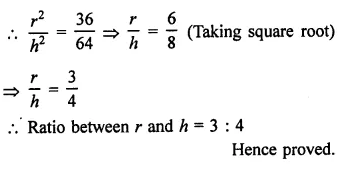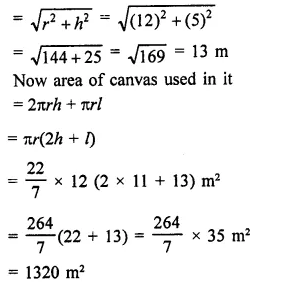RS Aggarwal Class 8 Solutions Chapter 19 Three-Dimensional Figures Ex 19A
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19A.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19A
- RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19B
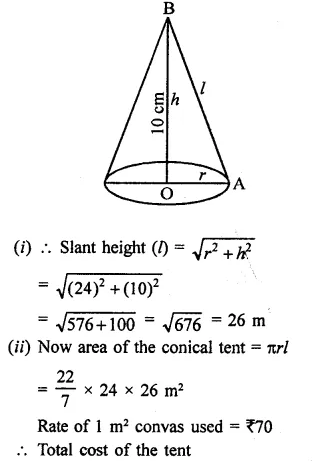
Question 1.
Solution:
(i) Cuboid : It has 6 faces.
(ii) Cube : It has 6 faces.
(iii) Triangular prism : It has 5 faces.
(iv) Square Pyramid : It has 5 faces.
(v) Tetrahedron : It has 4 faces. Ans.
Question 2.
Solution:
(i) Tetrahedron : It has 6 edges.
(ii) Rectangular pyramid : It has 8 edges
(iii) Cube : It is 12 edges.
(iv) Triangular prism : It has 9 edges Ans.
Question 3.
Solution:
(i) Cuboid : It has 8 vertices
(ii) Square pyramid : It has 5 vertices.
(iii) Tetrahedron : It is 4 vertices.
(iv) Triangular prism : It has 6 vertices
Question 4.
Solution:
(i) A cube has 8 vertices 12 edges and 6 faces.
(ii) The point at which three faces of a figure meet is known as vertex.
(iii) A cuboid is also known as a rectangular prism.
(iv) A triangular pyramid is called a tetrahedron.
Hope given RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.