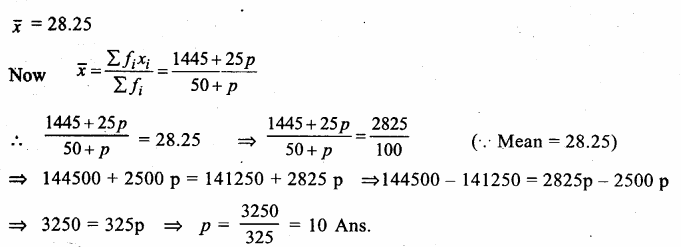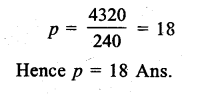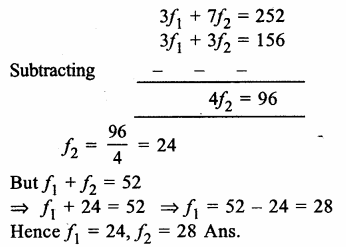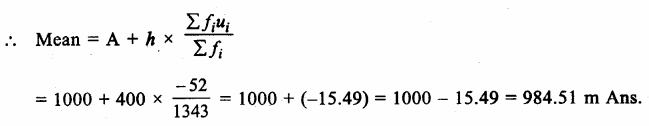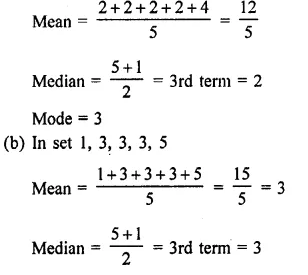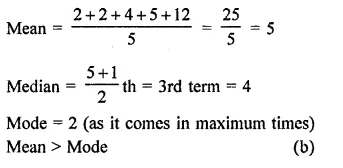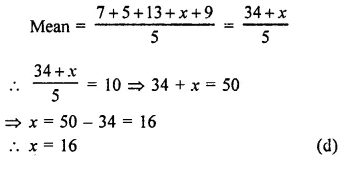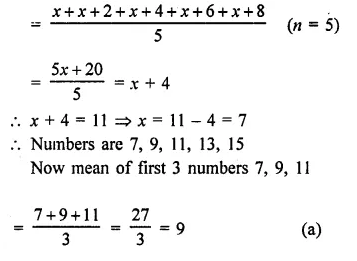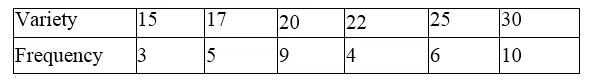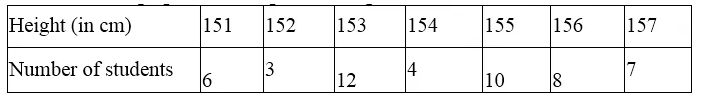RS Aggarwal Class 9 Solutions Chapter 14 Statistics Ex 14H
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14H.
Other Exercises
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14A
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14B
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14C
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14D
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14E
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14F
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14G
- RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14H
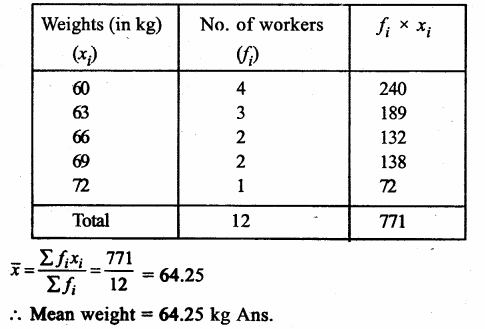
Question 1.
Solution:
Arranging the given data in ascending order :
0, 0, 1, 2, 3, 4, 5, 5, 6, 6, 6, 6
We see that 6 occurs in maximum times.
Mode = 6 Ans.
Question 2.
Solution:
Arranging in ascending order, we get:
15, 20, 22, 23, 25, 25, 25, 27, 40
We see that 25 occurs in maximum times.
Mode = 25 Ans.
Question 3.
Solution:
Arranging in ascending order we get:
1, 1, 2, 3, 3, 4, 5, 5, 6, 6, 7, 8, 9, 9, 9, 9, 9
Here, we see that 9 occurs in maximum times.
Mode = 9 Ans.
Question 4.
Solution:
Arranging in ascending order, we get:
9, 19, 27, 28, 30, 32, 35, 50, 50, 50, 50, 60
Here, we see that 50 occurs in maximum times.
Modal score = 50 scores Ans.
Question 5.
Solution:
Arranging in ascending order, we get:
10, 10, 11, 11, 12, 12, 13, 14,15, 17
Here, number of terms is 10, which is even
∴ Median = \(\frac { 1 }{ 2 } \left[ \frac { 10 }{ 2 } th\quad term+\left( \frac { 10 }{ 2 } +1 \right) th\quad term \right]\)
= \(\frac { 1 }{ 2 } \) (5th term + 6th term)
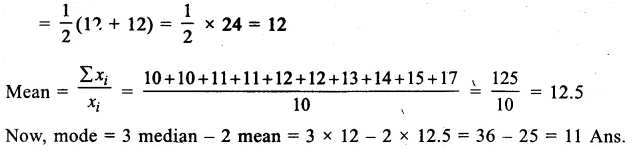
Question 6.
Solution:
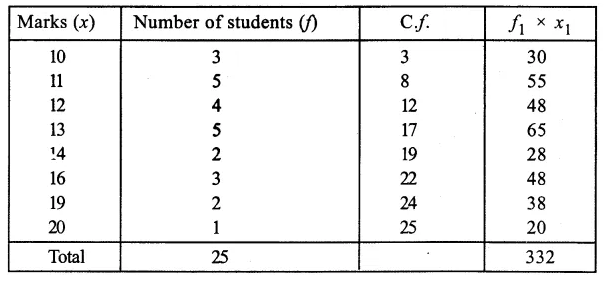
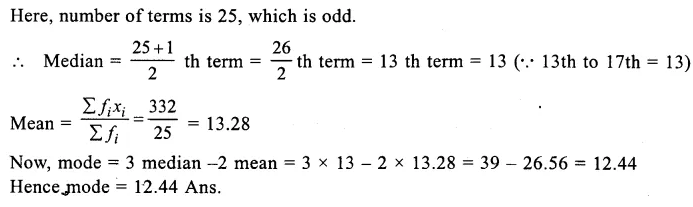
Question 7.
Solution:
Writing its cumulative frequency table

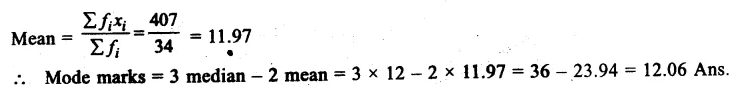
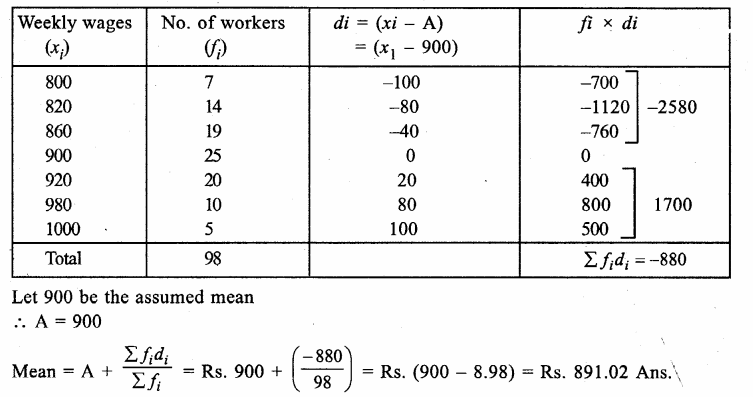
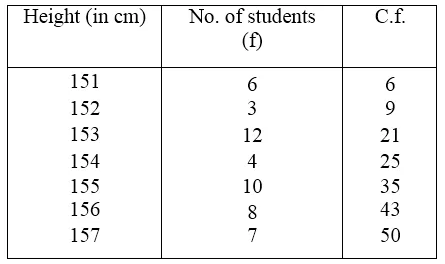
Question 8.
Solution:
Writing its cumulative frequency table
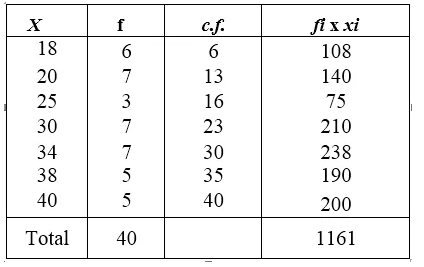
Here, number of items is 40 which is even.
∴ Median = \(\frac { 1 }{ 2 } \left[ \frac { 40 }{ 2 } th\quad term+\left( \frac { 40 }{ 2 } +1 \right) th\quad term \right]\)
= \(\frac { 1 }{ 2 } \) (20th term + 21th term)
= \(\frac { 1 }{ 2 } \) (30 + 30) = \(\frac { 1 }{ 2 } \) x 60 = 30
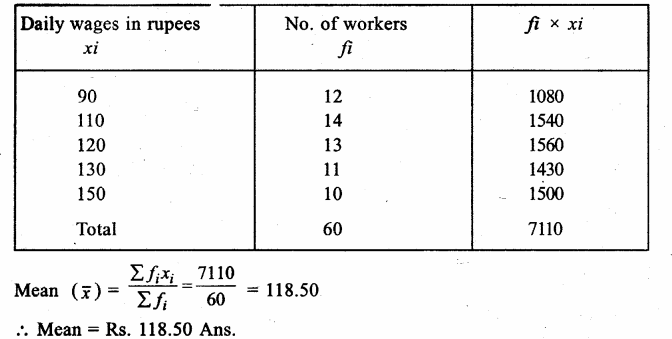
Mean= \(\frac { \sum { { f }_{ i }{ x }_{ i } } }{ \sum { { f }_{ i } } } \) = \(\frac { 1161 }{ 40 } \) = 29.025
∴Mode = 3 median – 2 mean = 3 x 30 – 2 x 29.025 = 90 – 58.05 = 31.95
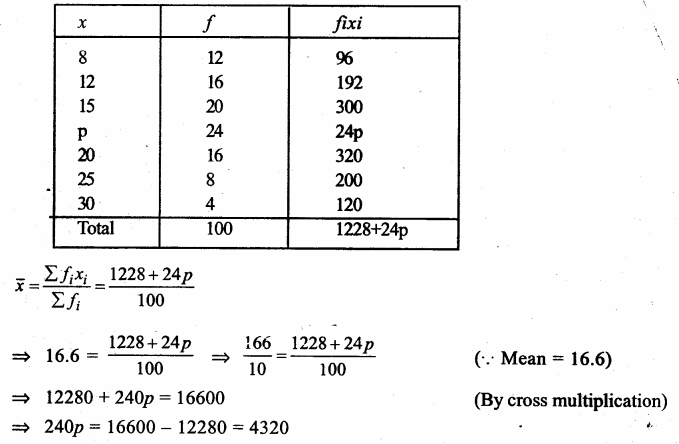
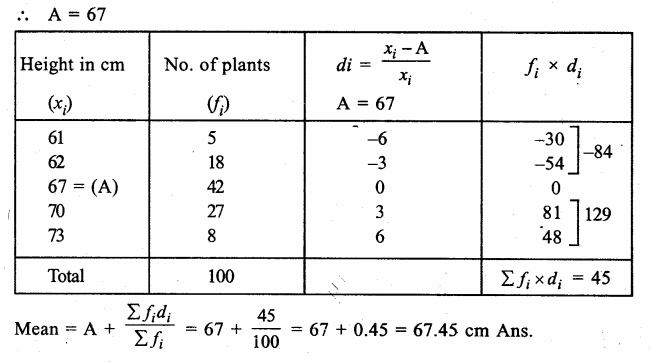
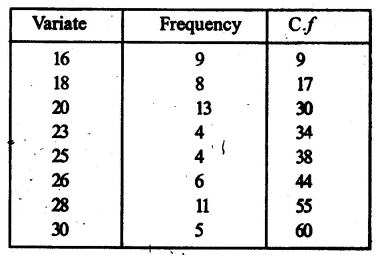
Question 9.
Solution:
Preparing its cumulative frequency table we get:
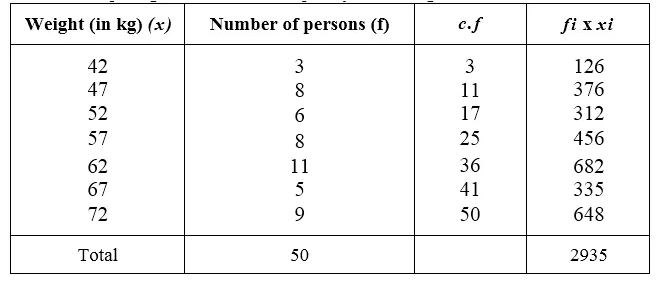
Here number of terms is 50, which is even
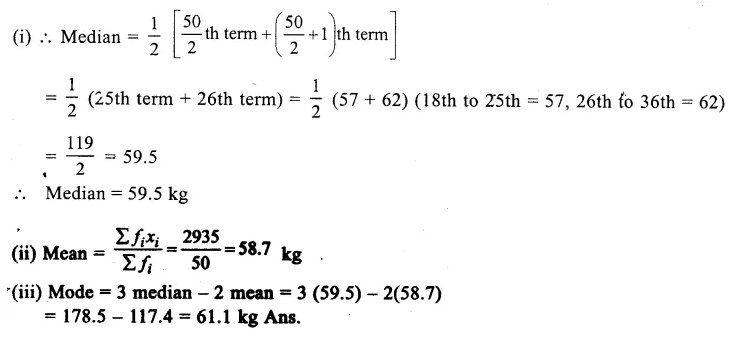
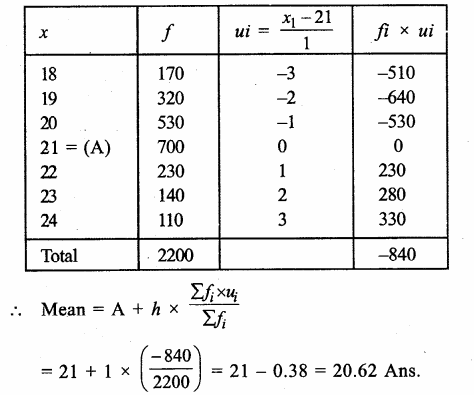
Question 10.
Solution:
Preparing its cumulative frequency table :

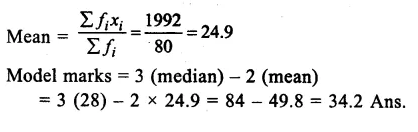
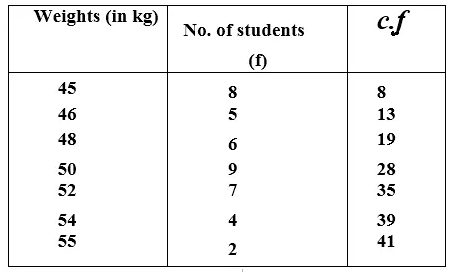
Question 11.
Solution:
Preparing its cumulative frequency table we have,

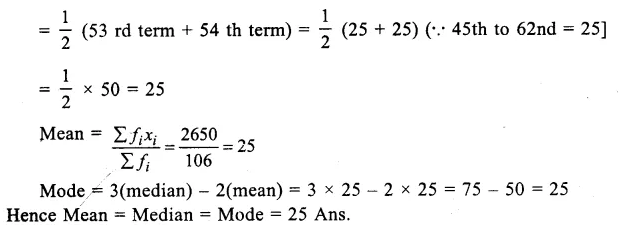
Question 12.
Solution:
Preparing its cumulative frequency table we have,

Hope given RS Aggarwal Solutions Class 9 Chapter 14 Statistics Ex 14H are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.