Prasanna

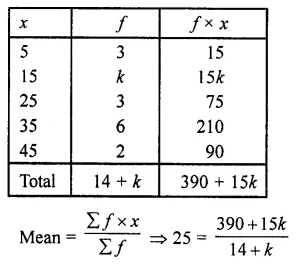
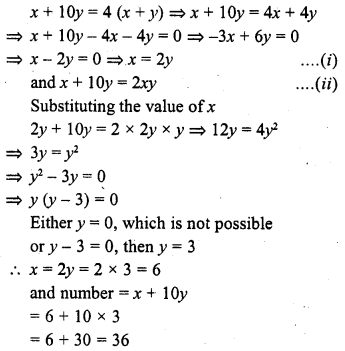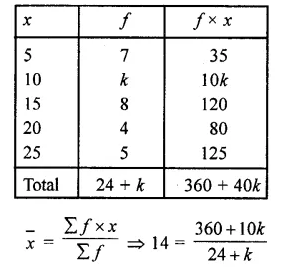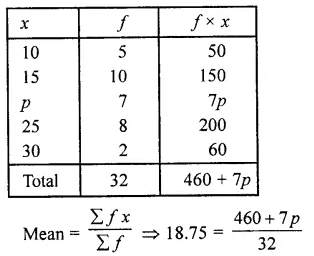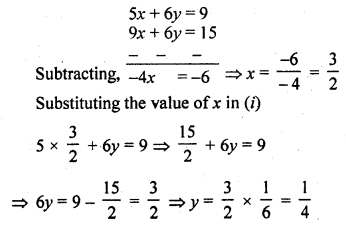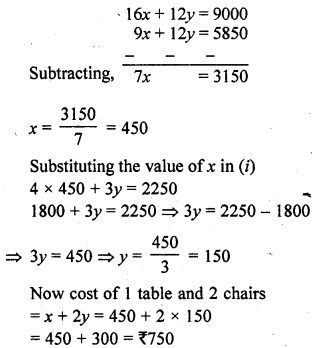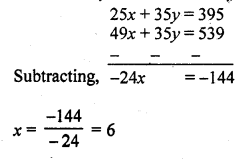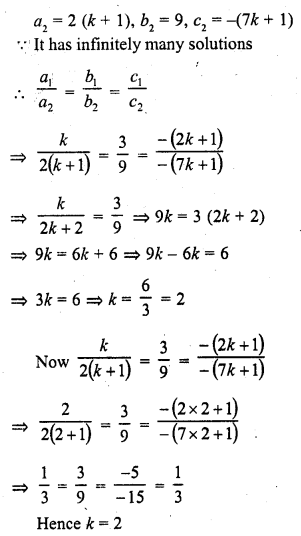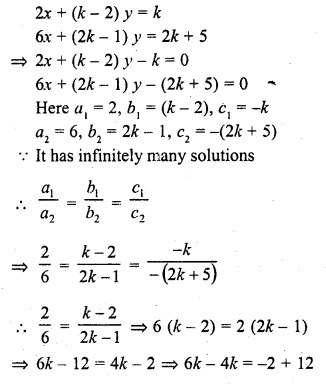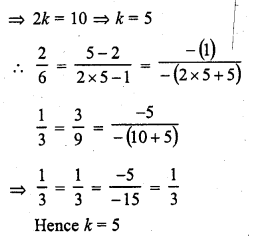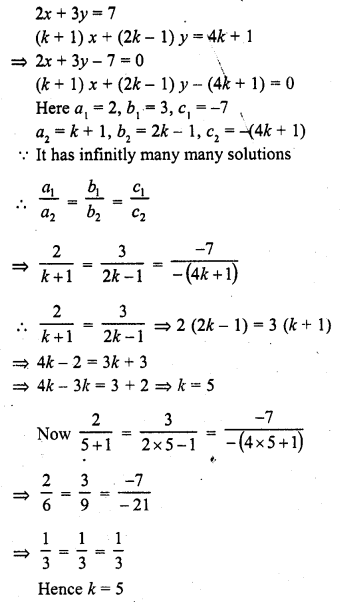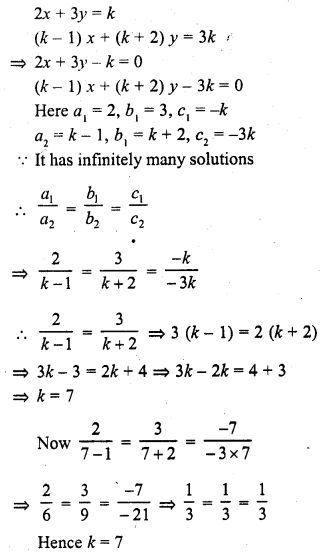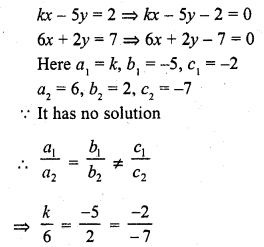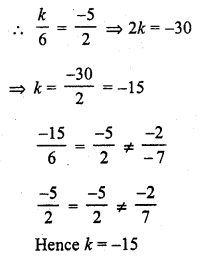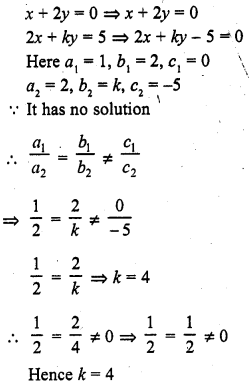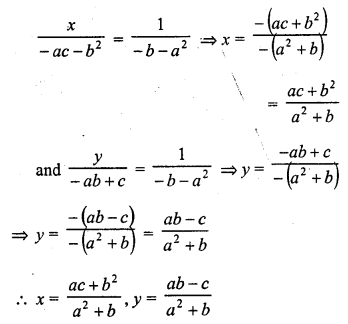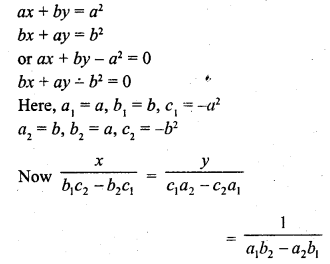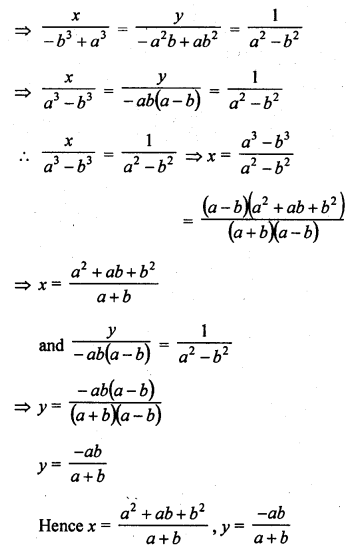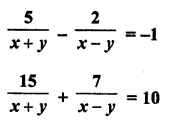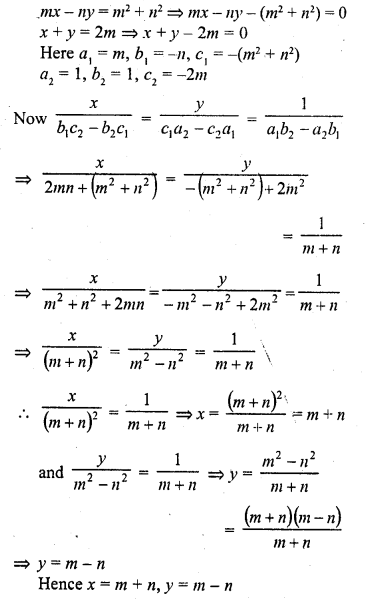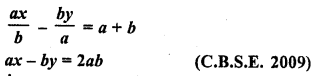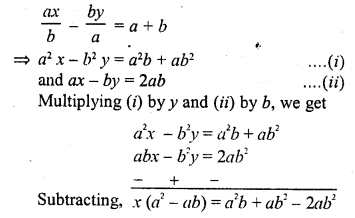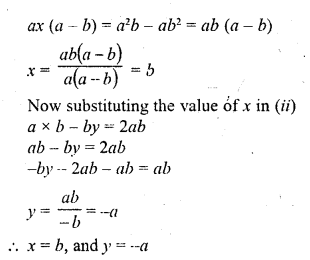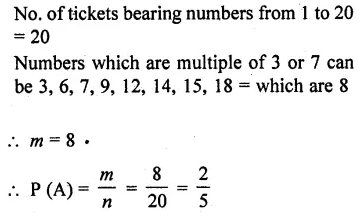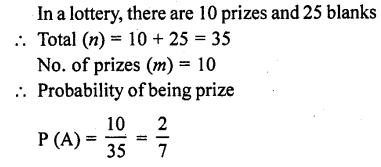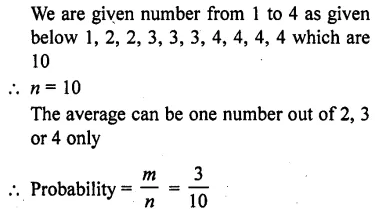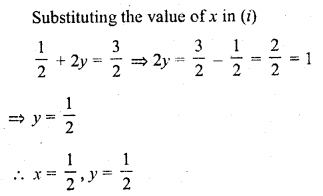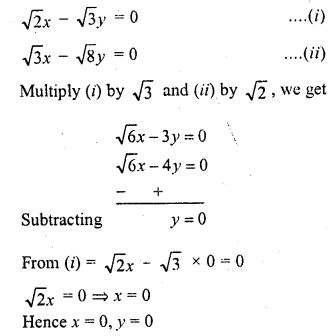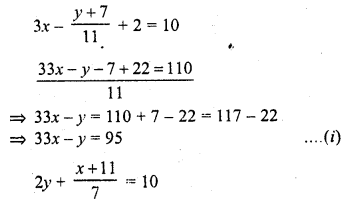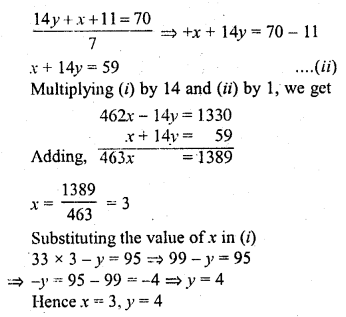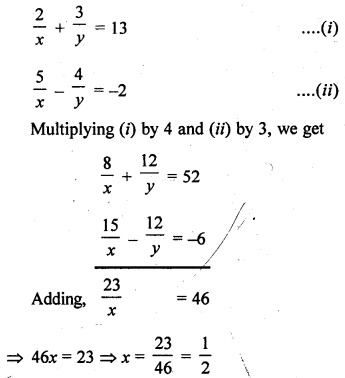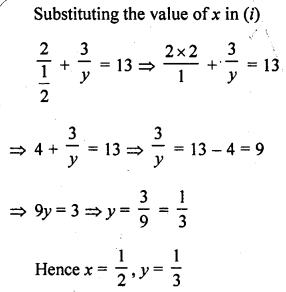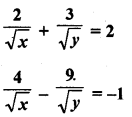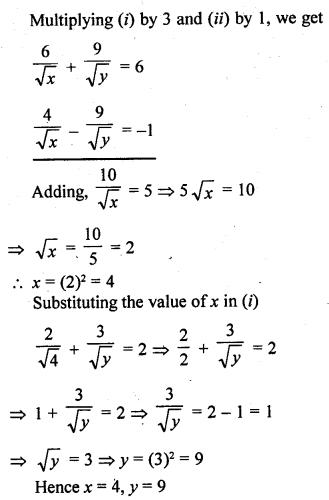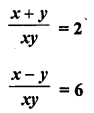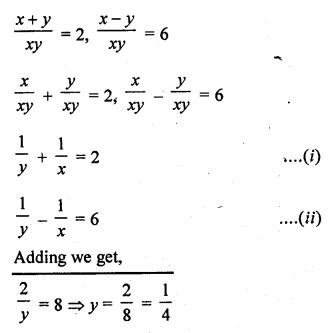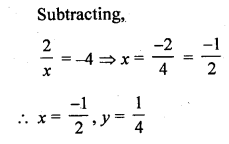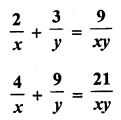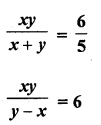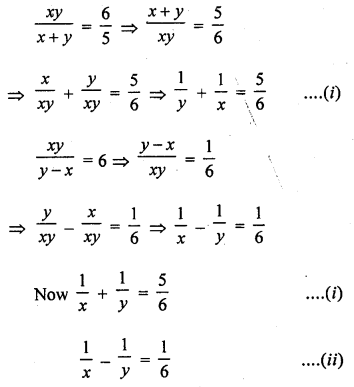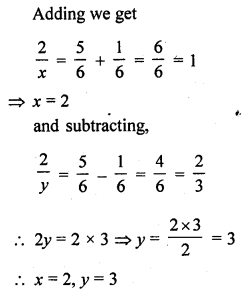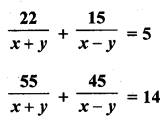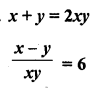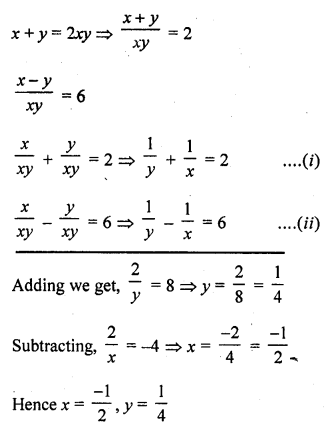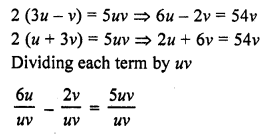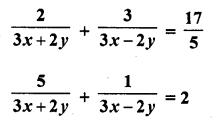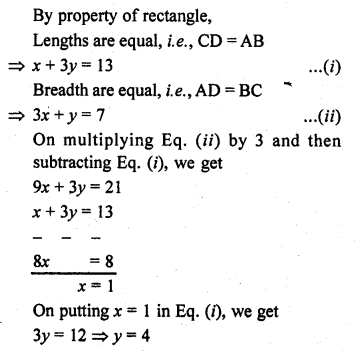RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

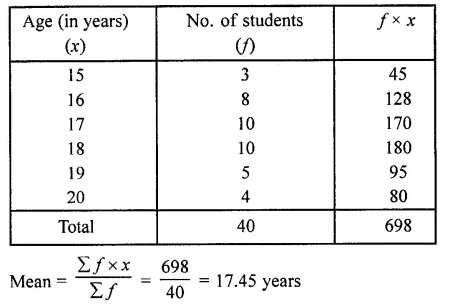
Question 1.
The. number of telephone calls received at an exchange per interval for 250 successive one-minute intervals are given in the following frequency table:

Compute the mean number of calls per interval.
Solution:
Let assumed mean (A) = 4

Hence mean number of calls per interval = 3.54

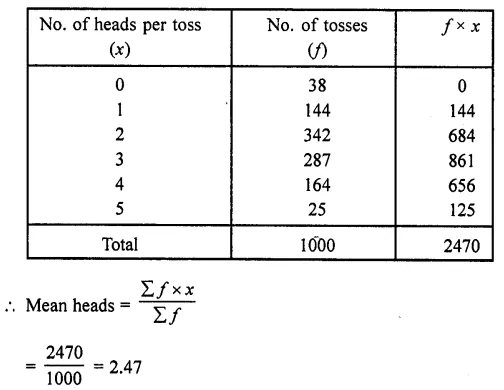
Question 2.
Five coins were simultaneously tossed 1000 times, and at each toss the number of heads was observed. The number of tosses during which 0, 1, 2, 3, 4, and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss

Solution:
Let assumed means (A) = 3

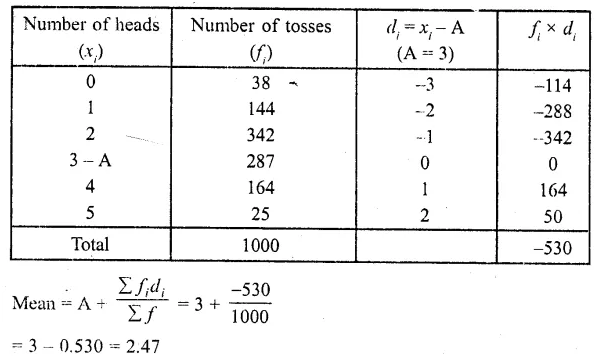
Hence mean number of tosses per head = 2.47

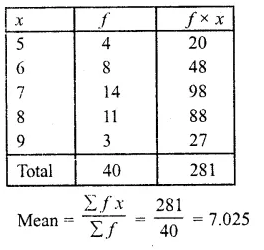
Question 3.
The following table gives the number of branches and number of plants in the garden of a school.

Calculate the average number of branches per plant.
Solution:
Let assumed mean (A) = 4

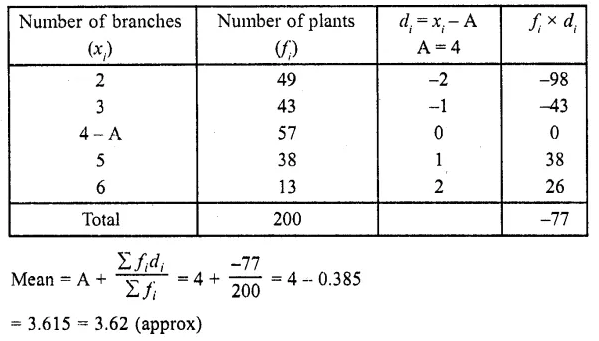
∴Mean number of branches per plant = 3.62

Question 4.
The following table gives the number of children of 150 families in a village

Find the average number of children per family.
Solution:
Let assumed mean (A) = 3

= 3 – 0.65 = 2.35
Hence mean number of children per family = 2.35

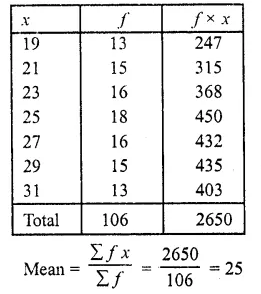
Question 5.
The marks obtained out of 50, by 102 students in a Physics test are given in the frequency table below:

Find the average number of marks.
Solution:

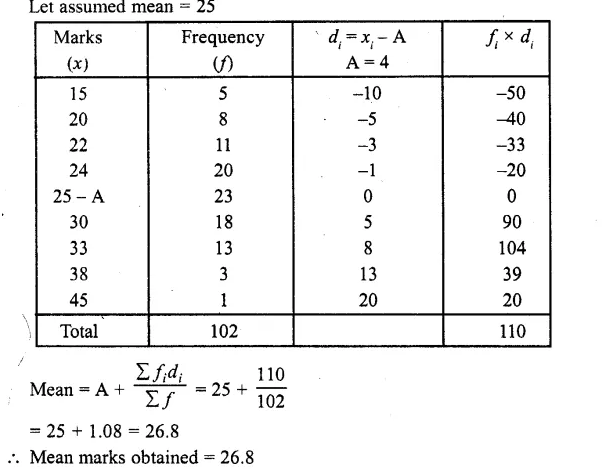
Question 6.
The number of students absent in a class were recorded every day for 120 days and the

Solution:
Let assumed mean = 3

= 3 + 0.525 = 3.525 = 3.53 (approx)

Question 7.
In the first proof reading of a book containing 300 pages the following distribution of misprints was obtained:

Find the average number of misprints per page.
Solution:
Let assumed mean (A) = 2

= 2 – 127 = 0.73
∴ Average of number of misprints per page = 0.73

Question 8.
The following distribution gives the number of accidents met by 160 workers in a factory during a month.

Find the average number of accidents per worker.
Solution:
Let assumed mean = 2

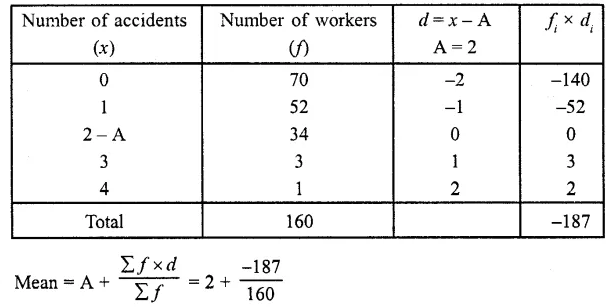
= 2 – 1.168 = 2 – 1.17 = 0.83 (approx)
∴ Average number of accidents per worker = 0.83

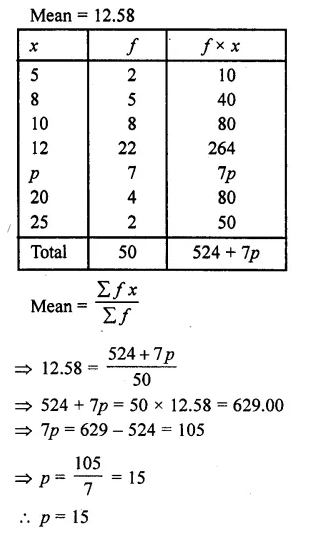
Question 9.
Find the mean from the following frequency distribution of marks at a test in statistics

Solution:
Let assumed mean = 25

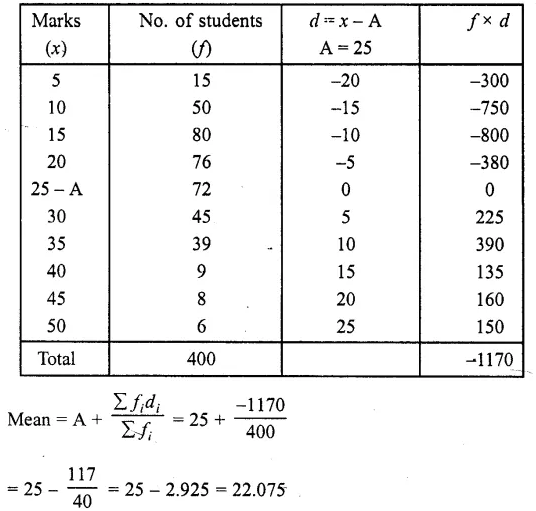
∴Average of marked obtained per student = 22.075

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 8 ….(i)
and x + y = 4 (x – y)
=> 4 (x – y) = 8
=> x – y = 2 ….(ii)
Adding (i) and (ii),
2x = 10 => x = 5
Subtracting (ii) from (i),
2y = 6 => y = 3
Numbers are 5, 3

Question 2.
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits, the result is 45. What is the number ?
Solution:
Let unit’s digit = x
and ten’s digit = y
Number = x + 10y
Now according to the condition
x + y = 13 ….(i)
Number after interchanging their digits,
y + 10x
Now y + 10x – x – 10y = 45
9x – 9y = 45
=> x – y = 5
x – y = 5 ….(ii)
Adding (i) and (ii),
2x = 18 => x = 9
subtracting 8
2y = 8 => y = 4
Number = x + 10y = 9 + 4 x 10 = 9 + 40 = 49

Question 3.
A number consists of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
Solution:
Let units digit = x
and ten’s digit = y
Number = x + 10y
and number by reversing their digits = y+ 10x
Now according to the conditions,
x + y = 5 ….(i)
and y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9x – y = 1 ….(ii)
(Dividing by 9)
Adding we get:
2x = 6 => x = 3
and subtracting,
2y = 4 => y = 2
Number = x + 10y = 3 + 10 x 2 = 3 + 20 = 23

Question 4.
The sum of digits of a two digit number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number. (C.B.S.E. 2004)
Solution:
Let the ones digit = x
and tens digit = y
Number = x + 10y
and number by reversing the order of digits = y +10x
According to the conditions,
x + y = 15 ….(i)
y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9
=>x – y = 1 ……..(ii)
(Dividing by 9)
Adding (i) and (ii)
2x = 16
x = 8
and subtracting, 2y = 14 => y = 7
Number = x + 10y = 8 + 10 x 7 = 8 + 70 = 78

Question 5.
The sum of a two-digit number and the number formed by reversing the order of digits is 66. If the two digits differ by 2, find the number. How many such numbers are there ? [NCERT]
Solution:
Sum of two-digit number and number formed by reversing its digits = 66
Let units digit = x
Then tens digit = x + 2
Number = x + 10 (x + 2) = x + 10x + 20 = 11x + 20
and by reversing its digits
Unit digit = x + 2
and tens digit = x
Number = x + 2 + 10x = 11x + 2
11x + 20 + 11x + 2 = 66
=> 22x + 22 = 66
=> 22x = 66 – 22 = 44
=> x = 2
Number = 11x + 20 = 11 x 2 + 20 = 22 + 20 = 42
and number by reversing its digits will be 11x + 2 = 11 x 2 + 2 = 22 + 2 = 24
Hence numbers are 42 and 24

Question 6.
The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 1000 ……..(i)

Question 7.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number. (C.B.S.E. 2002)
Solution:
Let the unit’s digit of the number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits, the new number will be = y +10x
According to the condition,
x + 10y + y + 10x = 99
=> 11x + 11y = 99
=> x + y = 9 ….(i)
and x – y = 3 ….(ii)
Adding we get,
2x = 12
x = 6
and subtracting, 2y = 6
y= 3
Number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 8.
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let the unit digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the order of digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y)
=> x + 10y = 4x + 4y
=> 4x + 4y – x – 10y = 0
=> 3x – 6y = 0
=> x – 2y = 0
=> x = 2y ….(ii)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> – 9x + 9y = -18
=> x – y = 2 ….(ii)
(Dividing by – 9)
=> 2y – y = 2 {From (i}
=> y = 2
x = 2y = 2 x 2 = 4
Number = x + 10y = 4 + 10 x 2 = 4 + 20 = 24

Question 9.
A two-digit number is 3 more than 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let unit digit of the number = x
and ten’s digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y) + 3
=> x + 10y = 4x + 4y + 3
=> x + 10y – 4x – 4y = 3
=> -3x + 6y = 3
=> x – 2y = -1 ….(i)
(Dividing by -3)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> -9x + 9y = -18
=>x – y = 2 ….(ii)
(Dividing by 9)
Subtracting (i) from (ii)
y = 3
x – 3 = 2
=>x = 2 + 3 = 5 {From (ii)}
Number = x + 10y = 5 + 10 x 3 = 5 + 30 = 35

Question 10.
A two digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let units digit of the number = x
and ten’s digit = y
then number = x + 10y
The number by reversing the digits = y+ 10x
According to the condition given,
x + 10y = 6 (x + y) + 4
=> x + 10y = 6x + 6y + 4
=> x + 10y – 6x – 6y = 4
=> -5x + 4y = 4 ….(i)
and x + 10y – 18 = y + 10x
=> x + 10y – y – 10x = 18
=> -9x + 9y = 18
=> x – y = -2 ….(ii)
(Dividing by 9)
=> x = y – 2
Substituting in (i),
-5 (y – 2) + 4y = 4
-5y + 10 + 4y = 4
-y = 4 – 10 = – 6
y = 6
Number = x + 10y = 4 + 10 x 6 = 4 + 60 = 64

Question 11.
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find-the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
According to the conditions given,

Question 12.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after interchanging its digits = y + 10x
According to the conditions,
xy = 20

Question 13.
The difference between two pumbers is 26 and one number is three times the other. Find them.
Solution:
Let first number = x
and second number = y
x – y = 26 ……….(i)
x = 3y ….(ii)
Substituting the value of x in (i)
3y – y = 26
=> 2y = 26
=>y = 13
x = 3y = 3 x 13 = 39
Numbers are 39, 13

Question 14.
The sum of the digits o,f a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Solution:
Let the units digit of the number = x
and tens digit number = y
Number = x + 10y
and the number by reversing the order of the digits = y + 10x
According to the condition;
x + y = 9 …..(i)
9 (x + 10y) = 2 (y + 10x)
=> 9x + 90y = 2y + 20x
=> 9x + 90y – 2y – 20x = 0
=> -11x + 88y = 0
=> x – 8y = 0 (Dividing by -11)
=> x = 8y
Substituting the value of x in (i)
8y + y = 9
=> 9y = 9
=> y= 1
x = 8y = 1 x 8 = 8
Number = x + 10y = 8 + 10 x 1 = 8 + 10 = 18

Question 15.
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x – y = 3 ….(i)
and 7 (x + 10y) = 4 (y + 10x)
=> 7x + 70y = 4y + 40x
=> 7x + 70y – 4y – 40x = 0
=> -33x + 66y = 0
=> x – 2y = 0 (Dividing by -33)
=> x = 2y
Substituting the value of x in (i),
2y – y = 3 => y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 16.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers. [NCERT Exemplar]
Solution:
Let the two numbers be x and y.
Then, by the first condition, ratio of these two numbers = 5 : 6
x : y = 5 : 6

Question 17.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number. [NCERT Exemplar]
Solution:
Let the two-digit number = 10x + y
Case I : Multiplying the sum of the digits by 8 and then subtracting 5 = two-digit number
=> 8 x (x + y) – 5 = 10x + y

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Calculate the mean for the following distribution :

X	5	6	7	8	9
f	4	8	14	11	3

Solution:

Question 2.
Find the mean of the following data:

X	19	21	23	25	27	29	31
f	13	15	16	18	16	15	13

Solution:

Question 3.
If the mean of the following data is 20.6. Find the value of p. (C.B.S.E. 1997)

X	10	15	p	25	35
y	3	10	25	7	5

 Solution:

Question 4.
If the mean of the following data is 15, find p. (C.B.S.E. 1992C)

X	5	10	15	20	25
f	6	P	6	10	5

Solution:

Question 5.
Find the value of p for the following distribution whose mean is 16.6.

X	8	12	15	P	20	25	30
f	12	16	20	24	16	8	4

Solution:
Mean = 16.6

Question 6.
Find the missing value of p for the following distribution whose mean is 12.58. (C.B.S.E. 1992C)

X	5	8	10	12	P	20	25
f	2	5	8	22	7	4	2

Solution:

Question 7.
Find the missing frequency (p) for the following distribution whose mean is 7.68.

X	3	5	7	9	11	13
f	6	8	15	P	8	4

 Solution:

Question 8.
The following table gives the number of boys of a particular age in a class of 40 students. Calculate the mean age of the students

Age (in years)	15	16	17	18	19	20
No. of students	3	8	10	10	5	4

Solution:

Question 9.
Candidates of four schools appear in a mathematics test. The data were as follows :

Schools	No. of Candidates	Average Score
I	60	75
II	48	80
III	Not available	55
IV	40	50

If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:

Question 10.
Five coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.

No. of heads per toss	No. of tosses
0	38
1	144
2	342
3	287
4	164
5	25
Total	1000

 Solution:

Question 11.
The arithmetic mean of the following data is 14, find the value of k. (C.B.S.E. 2002C)

X	5	10	15	20	25
f	7	k	8	4	5

Solution:
Mean=14

⇒ 14 (24 + k) = 360 + 10k
⇒ 336 + 14k = 360 + 10k
⇒ 14k- 10k- 360 -336 24
⇒ 4k = 24
⇒ k= \(\frac { 24 }{ 4 }\) = 6 4
Hence k = 6

Question 12.
The arithmetic mean of the following data is 25, find the value of k. (C.B.S.E. 2001)

X	5	15	25	35	45
f	3	k	3	6	2

Solution:
Mean =25

⇒ 25 (14 + k) = 390 + 15k
⇒ 350 + 25k= 390 + 15k
⇒ 25k- 15k = 390 -350
⇒ 10k = 40 ⇒ k = \(\frac { 40 }{ 10 }\) = 4
Hence k = 4

Question 13.
If the mean of the following data is 18.75. Find the value of p.

X	10	15	P	25	30
f	5	10	7	8	2

Solution:

⇒ 460 + 7p = 32 (18.75)
⇒ 460 + 7p = 600
⇒ 7p = 600 – 460 = 140
⇒ p =  \(\frac { 140 }{ 7 }\) = 20
∴ p = 20

Question 14.
Find the value of p, if the mean of the following distribution is 20.

X	15	17	19	20 + p	23
f	2	3	4	5p	6

Solution:

⇒ 5p² + 100p + 295 = 20 (15 + 5p)
⇒ 5p² + 100p + 295 = 300 + 100p
⇒ 5p² + 100p – 100p = 300 – 295
⇒  5p² = 5 ⇒  p²  =  \(\frac { 5 }{ 5 }\)  = 1
⇒ P= ±1
P = -1 i s not possible
∴ p= 1

Question 15.
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
5 pens and 6 pencils together cost ₹ 9 and 3 pens and 2 pencils cost ₹ 5. Find the cost of 1 pen and 1 pencil. (C.B.S.E. 1991)
Solution:
Let cost of 1 pen = ₹ x
and cost of 1 pencil = ₹ y
According to the conditions,
5x + 6y = 9 ….(i)
3x + 2y = 5 …(ii)
Multiplying (i) by 1 and (ii) by 3, we get

Cost of one pen = ₹ \(\frac { 3 }{ 2 }\)
and cost of one pencil = ₹ \(\frac { 1 }{ 4 }\)

Question 2.
7 audio cassettes and 3 video cassettes cost ₹ 1110, while 5 audio cassettes and 4 video cassettes cost ₹ 1350. Find the cost of an audio cassette and a video cassette. (C.B.S.E. 1992)
Solution:
Let the cost of 1 audio cassette = ₹ x
and cost of 1 video cassette = ₹ y
According to the condition,
7x + 3y= 1110 ….(i)
5x + 4y = 1350 ….(ii)
Multiplying (i) by 4 and (ii) by 3,

Question 3.
Reena has pens and pencils which together are 40 in number. If she has 5 more pencils and 5 less pens, then number of pencils would become 4 times the number of pens. Find,.the original number of pens and pencils. (C.B.S.E 1992C)
Solution:
Let number of pens = x
and number of pencils = y
x + y = 40 ….(i)
In second case,
number of pens = x – 5
and number of pencils = y + 5
(y + 5) = 4 (x – 5) => y + 5 = 4x – 20
4x – y = 5 + 20 => 4x – y = 25 ….(ii)
Adding (i) and (ii)
5x = 65 => x = 13 [From (i) ]
13 + y = 40 => y = 40 – 13 = 27
Hence number of pens = 13
and number of pencils = 27

Question 4.
4 tables and 3 chairs, together, cost ₹ 2,250 and 3 tables and 4 chairs cost ₹ 1950. Find the cost of 2 chairs and 1 table.
Solution:
Let cost of 1 table = ₹ x
and cost of 1 chair = ₹ y
According to the conditions,
4x + 3y = 2250 ….(i)
3x + 4y= 1950 ….(ii)
Multiplying (i) by 4 and (ii) by 3, we get

Question 5.
3 bags and 4 pens together cost ₹ 257 whereas 4 bags and 3 pens together cost ₹ 324. Find the total cost of 1 bag and 10 pens. (C.B.S.E. 1996)
Solution:
Let cost of 1 bag = ₹ x
and cost of 1 pen = ₹ y
According to the conditions,
3x + 4y = 257 ….(i)
4x + 3y = 324 ….(ii)
Multiplying (i) by 3 and (ii) by 4, we get

Question 6.
5 books and 7 pens together cost ₹ 79 whereas 7 books and 5 pens together cost ₹ 77. Find the cost of 1 book and 2 pens. (C.B.S.E. 1996)
Solution:
Let the cost 1 book = ₹ x
and cost of 1 pen = ₹ y
Now according to the conditions,
5x + 7y = 79 ….(i)
7x + 5y = 77 ….(ii)
Multiplying (i) by 5 and (ii) by 7, we get

Substituting the value of x in (i)
5 x 6 + 7y = 79
=> 30 + 7y = 79
=> 7y = 79 – 30 = 49
y = 7
Cost of 1 book and 2 pens = 6 + 2 x 7 = 6 + 14 = 20

Question 7.
Jamila sold a table and a chair for ₹ 1050, thereby making a profit of 10% on a table and 25% on the chair. If she had taken profit of 25% on the table and 10% on the chair she would have got ₹ 1065. Find the cost price of each. [NCERT Exemplar]
Solution:
Let the cost price of the table be ₹ x
and the cost price of the chair by ₹ y.
The selling price of the table, when it is sold at a profit of 10%

110x + 125y = 105000
and 125x + 110y = 106500
On adding and subtracting these equations, we get
235x + 235y = 211500
and 15x – 15y= 1500
i.e., x + y = 900 …(iii)
and x – y = 100 …(iv)
Solving equation (iii) and (iv), we get
2x = 1000
x = 500
500 + y = 900
=> y = 900 – 500
y = 400
x = 500, y = 400
So, the cost price of the table is ₹ 500 and the cost price of the chair is ₹ 400.

Question 8.
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received ₹ 1860 as annual interest. However, had she interchanged the amount of investment in the two schemes, she would have received 720 more as annual interest. How much money did she invest in each scheme?
[NCERT Exemplar]
Solution:
Let the amount of investments in schemes A and B be ₹ x and ₹ y, respectively.
Case I:
Interest at the rate of 8% per annum on scheme A + Interest at the rate of 9% per annum on scheme B = Total amount received

Case II:
Interest at the rate of 9% per annum on scheme A + Interest at the rate of 8% per annum on scheme B = ₹ 20 more as annual interest

Question 9.
The coach of a cricket team buys 7 bats and 6 balls for ₹ 3800. Later, he buys 3 bats and 5 balls for ₹ 1750. Find the cost of each bat and each ball.
Solution:
Let cost of 1 bat = ₹ x
and cost of 1 ball = ₹ y
According to the conditions,
7x + 6y = 3800 ….(i)
3x + 5y = 1750 ….(ii)
Multiplying (i) by 5 and (ii) by 6, we get

Question 10.
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day;
Solution:
Let the fixed charge for the book = ₹ x
and let extra charge for each day = ₹ y
According to the given conditions,
x + 4y = 27 ….(i)
x + 2y = 21 ….(ii)
Subtracting,
2y = 6 => y = 3
Substituting the value of y in (i)
x + 4 x 3 = 27
=> x + 12 = 27
=> x = 27 – 12 = 15
Amount of fixed charge = ₹ 15
and charges for each extra day = ₹ 3

Question 11.
The cost of 4 pens and 4 pencil boxes is ₹ 100. Three times the cost of a pen is ₹ 15 more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and pencil box. [NCERT Exemplar]
Solution:
Let the cost of a pen be ₹ x and the cost of a pencil box be ₹ y.
Then, by given condition,
4x + 4y = 100 => x + y = 25 …(i)
and 3x = y + 15
=> 3x – y = 15 …(ii)
On adding Eqs. (i) and (ii), we get
4x = 40 => x = 10
By substituting x = 10, in Eq. (i) we get
y = 25 – 10 = 15
Hence, the cost of a pen and a pencil box are ₹ 10 and ₹ 15, respectively.

Question 12.
One says, “Give me a hundred, friend! I shall then become twice as rich as you.” The other replies, “If you give me ten, I shall be six times as rich as you.” Tell me what is the amount of their respective capital?
Solution:
Let the amount of first person = ₹ x
and amount of second = ₹ y
According to the first condition,
x + 100 = 2 (y- 100)
=> x + 100 = 2y – 200
=> x – 2y = -200 – 100
=> x – 2y = -300 …….(i)
According to the second condition,
6(x – 10) = (y + 10)
6x – 60 = y + 10
6x – y = 10 + 60
6x – y = 70 ….(ii)
Multiplying (i) by 1 and (ii) by 2, we get


Hence first person has money = ₹ 40 and second person has = ₹ 170

Question 13.
A and B each have a certain number of mangoes. A says to B, “if you give 30 of your mangoes, I will have twice as many as left with you.” B replies, “if you give me 10, I will have thrice as many left with you.” How many mangoes does each have ?
Solution:
Let A has mangoes = x
and B has mangoes = y
According to the first condition,
x + 30 = 2 (y – 30)
x + 30 = 2y – 60
x – 2y = -60 – 30
=> x – 2y = -90 ….(i)
and according to the second condition
3 (x – 10) = (y + 10)
=> 3x – 30 = y + 10
=> 3x – y = 10 + 30
=> 3x – y = 40 ….(ii)
From (i) x = -90 + 2y Substituting in (i)
3 (-90 + 2y) – y = 40
– 270 + 6y – y = 40
=> 5y = 40 + 270 = 310
=> y = 62
and x = – 90 + 2y = – 90 + 2 x 62 = 124 – 90 = 34
A has mangoes = 34
and B has mangoes = 62

Question 14.
Vijay had some bananas, and he divided them into two lots A and B. He sold first lot at the rate of ₹ 2 for 3 bananas and the second lot at the rate of ₹ 1 per banana and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per banana and the second lot at the rate of ₹ 4 per five bananas, his total collection would have been ₹ 460. Find the total number of bananas he had. [NCERT Exemplar]
Solution:
Let the number of bananas in lots A and B be x and y, respectively.
Case I:
Cost of the first lot at the rate of ₹ 2 for 3 bananas + Cost of the second lot at the rate of ₹ 1 per banana = Amount received
=> \(\frac { 2 }{ 3 }\) x + y = 400
=> 2x + 3y= 1200 …(i)
Case II:
Cost of the first lot at the rate of ₹ 1 per banana + Cost of the second lot at the rate of ₹ 4 for 5 bananas = Amount received
=> x + \(\frac { 4 }{ 5 }\) y = 460
=> 5x + 4y = 2300 …(ii)
On multiplying in the Eq. (i) by 4 and Eq. (ii) by 3 and then subtracting them, we get,

Now, putting the value of x in Eq. (i), we get,
2 x 300 + 3y = 1200
=> 600 + 3y = 1200
=> 3y = 1200 – 600
=> 3y = 600
=> y = 200
Total number of bananas = Number of bananas in lot A + Number of bananas in lot B
= x + y
= 300 + 200 = 500
Hence, he had 500 bananas.

Question 15.
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains ₹ 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss. He gains ₹ 1500 on the transaction. Find the actual prices of T.V. and fridge.
Solution:
Let the price of T.V. = ₹ x
and price of Fridge = ₹ y
According to first condition,


\(\frac { y }{ 10 }\) = 2000 – 1000 = 1000
=> y = 10 x 1000 = 10000
Hence price of T.V. = ₹ 20000 and of fridge = ₹ 10000

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

In each of the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it : (1 – 4)
Question 1.
x – 3y = 3
3x – 9y = 2 (C.B.S.E. 1994)
Solution:

Question 2.
2x + y = 5
4x + 2y = 10 (C.B.S.E. 1995C)
Solution:

Question 3.
3x – 5y = 20
6x – 10y = 40 (C.B.S.E. 1993)
Solution:

Question 4.
x – 2y = 8
5x – 10y = 10 (C.B.S.E. 1993)
Solution:

Find the value of k for which the following system of equations has a unique solution: (5 – 8)
Question 5.
kx + 2y = 5
3x + y = 1 (C.B.S.E. 1990C, 92C)
Solution:

Question 6.
4x + ky + 8 = 0
2x + 2y + 2 = 0 [NCERT]
Solution:

Question 7.
4x – 5y = k
2x – 3y = 12
Solution:

Question 8.
x + 2y = 3
5x + ky + 7 = 0
Solution:

Find the value of k for which each of the following systems of equations have infinitely many solution : (9 – 19)
Question 9.
2x + 3y – 5 = 0
6x + ky – 15 = 0 (C.B.S.E. 1991)
Solution:

Question 10.
4x + 5y = 3
kx + 15y = 9 (C.B.S.E. 1990C)
Solution:

Question 11.
kx – 2y + 6 = 0
4x – 3y + 9 = 0
Solution:

Question 12.
8x + 5y = 9
kx + 10y = 18 (C.B.S.E. 1999)
Solution:

Question 13.
2x – 3y = 7
(k + 2) x + (2k + 1) y = 3 (2k – 1) (C.B.S.E. 1999)
Solution:

Question 14.
2x + 3y = 2
(k + 2)x + (2k + 1) y = 2 (k – 1) (C.B.S.E. 2000, 2003)
Solution:

Question 15.
x + (k + 1) y = 4
(k + 1) x + 9y = 5k + 2 (C.B.S.E. 2000C)
Solution:

Question 16.
kx + 3y = 2k + 1
2(k+ 1) x + 9y = 7k + 1 (C.B.S.E. 2000C)
Solution:

Question 17.
2x + (k – 2) y = k
6x + (2k – 1) y = 2k + 5 (C.B.S.E. 2000C)
Solution:

Question 18.
2x + 3y = 7
(k + 1) x + (2k – 1)y = 4k + 1 (C.B.S.E. 2001)
Solution:

Question 19.
2x + 3y = k
(k – 1) x + (k + 2) y = 3k (C.B.S.E. 2001)
Solution:

Find the value of k for which the following system of equations has no solution : (20 – 25) :
Question 20.
kx – 5y = 2
6x + 2y = 1 (C.B.S.E. 1994C)
Solution:

Question 21.
x + 2y = 0
2x + ky = 5 (C.B.S.E. 1993C)
Solution:

Question 22.
3x – 4y + 7 = 0
kx + 3y – 5 = 0 (C.B.S.E. 1996)
Solution:

Question 23.
2x – ky + 3 = 0
3x + 2y – 1 = 0 (C.B.S.E. 1996)
Solution:

Question 24.
2x + ky = 11
5x – 7y = 5 (C.B.S.E. 1995)
Solution:

Question 25.
kx + 3y = 3
12x + ky = 6
Solution:

Question 26.
For what value of k, the following system of equations will be inconsistant ?
4x + 6y = 11
2x + ky = 1 (C.B.S.E. 1994C)
Solution:

Question 27.
For what value of a, the system of equations
αx + 3y = α – 3
12x + αy = α
will have no solution. (C.B.S.E. 2003)
Solution:

Question 28.
Find the value of k for which the system
kx + 2y = 5
3x + y = 1
has (i) a unique solution, and (ii) no solution.
Solution:

k = 6

Question 29.
Prove that there is a value of c (≠ 0) for which the system
6x + 3y = c – 3
12x + cy = c
has infinitely many solutions. Find this value.
Solution:

Question 30.
Find the values of k for which the system
2x + k y = 1
3x – 5y = 7
will have (i) a unique solution, and (ii) no solution.
Is there a value of k for which the system has infinitely many solutions?
Solution:

Question 31.
For what value of k, the following system of equations will represent the coincident lines ?
x + 2y + 7 = 0
2x + ky + 14 = 0 (C.B.S.E. 1992)
Solution:

Question 32.
Obtain the condition for the following system of linear equations to have a unique solution
ax + by = c
lx + my = n (C.B.S.E. 1991C)
Solution:

Question 33.
Determine the values of a and b so that the following system of linear equations have infinitely many solutions ?
(2a – 1) x + 3y – 5 = 0
3x + (b – 1) y – 2 = 0 (C.B.S.E. 2001C)
Solution:

Question 34.
Find the values of a and b for which the following system of linear equations has infinite number of solutions :
2x – 3y = 7
(a + b) x – (a + b – 3) y = 4a + b (C.B.S.E. 2002)
Solution:

Question 35.
Find the values of p and q for which the following system of linear equations has infinite number of solutions:
2x + 3y = 9
(p + q) x + (2p – q) y = 3 (p + q + 1)
Solution:

Question 36.
Find the value of a and b for which the following system of equations has infinitely many solutions :
(i) (2a – 1) x – 3y = 5
3x + (b – 2) y = 3 (C.B.S.E. 2002C)
(ii) 2x – (2a + 5) y = 5
(2b + 1) x – 9y = 15 (C.B.S.E. 2002C)
(iii) (a – 1) x + 3y = 2
6x + (1 – 2b) y = 6 (C.B.S.E. 2002C)
(iv) 3x + 4y = 12
(a + b) x + 2 (a – b) y = 5a – 1 (C.B.S.E. 2002C)
(v) 2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
(vi) 2x + 3y – 7 = 0 [CBSE 2010]
(a – 1) x + (a + 1) y = (3a – 1)
(vii) 2x + 3y = 7
(a – 1) x + (a + 2) y = 3a [CBSE 2010]
(viii) x + 2y = 1
(a – b) x + (a + b) y = a + b – 2 [NCERT Exemplar]
(ix) 2x + 3y = 7
2ax + ay = 28 – by [NCERT Exemplar]
Solution:

Question 37.
For which value(s) of λ, do the pair of linear equations λx + y = λ² and x + λy = 1 have
(i) no solution ?
(ii) infinitely many solutions ?
(iii) a unique solutions ? [NCERT Exemplar]
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 16 Probability Ex VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 16 Probability VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.1
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.2
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex MCQS

Question 1.
Cards each marked with one of the numbers 4, 5, 6, …….. 20 are placed in a box and mixed thoroughly. One card is drawn at random from the box what is the probability of getting an even number ?
Solution:

Question 2.
One card is drawn from a well shuffled deck of 52 playing cards. What is the probability of getting a non-face card ?
Solution:

Question 3.
A bag contains 5 red, 8 green and 7 white balls. One ball is drawn at random from the bag. What is the probability of getting a white ball or a green ball ?
Solution:

Question 4.
A die is thrown once. What is the probability of getting a prime number?
Solution:

Question 5.
A die is thrown once. What is the probability of getting a number lying between 2 and 6 ?
Solution:

Question 6.
A die is thrown once. What is the probability of getting an odd number ?
Solution:

Question 7.
If \(\bar { E }\) denoted the complement or negation of an even E, what is the value of P(E) + P(\(\bar { E }\))?
Solution:

Question 8.
One card is drawn at random from a well shuffled deck of 52 cards. What is the probability of getting an ace ?
Solution:

Question 9.
Two coins are tossed simultaneously. What is the probability of getting at least one head ?
Solution:

Question 10.
Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn bears a number which is a multiple of 3?
Solution:

Question 11.
From a well shuffled pack of cards, a card is drawn at random. Find the probability of getting a black queen.[C.B.S.E. 2008]
Solution:

Question 12.
A die is thrown once. Find the probability of getting a number less than 3. [CBSE 2008]
Solution:

Question 13.
Two coines are tossed simultaneously. Find the probability of getting exactly one head. [CBSE 2009]
Solution:

Question 14.
A die is thrown once. What is the probability of getting a number greater than 4 ? [CBSE 2010]
Solution:

Question 15.
What is the probability that a number selected at random from the numbers 3, 4, 5,…, 9 is a multiple of 4 ? [CBSE 2010]
Solution:

Question 16.
A letter of English alphabet is chosen at random. Determine the probability that the chosen letter is a consonant.
Solution:

Question 17.
A bag contains 3 red and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is not red? [CBSE 2017]
Solution:

Question 18.
A number is chosen at random from the numbers, -3, -2, -1, 0,1, 2, 3. What will be the probability that the square of this number is less than or equal tori?
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 16 Probability VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.1
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.2
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex MCQS

Question 1.
Suppose you drop a tie at random on the rectangular region shown in the figure. What is the probability that it will land inside the circle with diameter 1 m?

Solution:

Question 2.
In the accompanying diagram a fair spinner is placed at the centre O of the circle. Diameter AOB and radius OC divide the circle into three rigions labelled X, Y and Z. If ∠BOC = 45°. What is the probability that the spinner will land in the region X?

Solution:

Question 3.
A target shown in the figure consists of three concentric circles of radii 3, 7 and 9 cm respectively. A dart is thrown and lands on the target. What is the probability that the dart will land on the shaded region ?

Solution:

Question 4.
In the figure, points A, B, C and D arc the centres of four circles that each have a radius of length one unit. If a point is selected at random from the interior o’ square ABCD. What is the probability that the point will be chosen from th; shaded region ?

Solution:

Question 5.
In the figure, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of ∆JAB?

Solution:

Question 6.
In the figure, a square dart board is shown. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will land in the interior of the smaller square ?

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Solve each of the following systems of equations by the method of cross multiplication.
Question 1.
x + 2y + 1 = 0
2x – 3y – 12 = 0 (C.B.S.E. 1992)
Solution:

Question 2.
3x + 2y + 25 = 0
2x + y + 10 = 0 (C.B.S.E. 1992)
Solution:

Question 3.
2x + y = 35
3x + 4y = 65 (C.B.S.E. 1993)
Solution:

Question 4.
2x – y = 6
x – y = 2 (C.B.S.E. 1994)
Solution:

Question 5.
\(\frac { x+y }{ xy } =2,\quad \frac { x-y }{ xy } =6\)
Solution:

Question 6.
ax + by = a – b
bx – ay = a + b
Solution:
ax + by = a – b
bx – ay = a + b

Question 7.
x + ay = b
ax – by = c
Solution:
x + ay = b

Question 8.
ax + by = a²
bx + ay = b²
Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.
\(\frac { x }{ { a } } +\frac { y }{ b } =a+b\)
\(\frac { x }{ { { a }^{ 2 } } } +\frac { y }{ { b }^{ 2 } } =2\)
Solution:

Question 14.
\(\frac { x }{ { { a } } } =\frac { y }{ { b } }\)
ax + by = a² + b²
Solution:

Question 15.
2ax + 3by = a + 2b
3ax + 2by = 2a + b
Solution:

Question 16.
5ax + 6by = 28
3ax + 4by = 18
Solution:

Question 17.
(a + 2b) x + (2a – b) y = 2
(a – 2b) x + (2a + b) y = 3
Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.
(a – b) x + (a + b) y = 2a² – 2b²
(a + b) (x + y) = 4ab
Solution:

Question 21.
a²x + b²y = c²
b²x + a²y = d²
Solution:

Question 22.
ax + by = \(\frac { a + b }{ 2 }\)
3x + 5y = 4
Solution:


Hence x = \(\frac { 1 }{ 2 }\) , y = \(\frac { 1 }{ 2 }\)

Question 23.
2 (ax – by) + a + 4b = 0
2 (bx + ay) + b – 4a = 0 (C.B.S.E. 2004)
Solution:

Question 24.
6 (ax + by) = 3a + 2b
6 (bx – ay) = 3b – 2a (C.B.S.E. 2004)
Solution:

Question 25.
\(\frac { { a }^{ 2 } }{ x } -\frac { { b }^{ 2 } }{ y } =0\)
\(\frac { { a }^{ 2 }b }{ x } -\frac { { b }^{ 2 }a }{ y } =a+b\quad ,\quad x,y\quad \neq 0\)
Solution:

Question 26.
mx – ny = m² + n²
x + y = 2m (C.B.S.E. 2006C)
Solution:

Question 27.

Solution:

Question 28.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.1
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.2
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 16 Probability Ex MCQS

Question 1.
The probability that it will rain tomorrow is 0.85. What is the probability that it will not rain tomorrow ?
Solution:

Question 2.
A die is thrown. Find the probability of getting :
(i) a prime number
(ii) 2 or 4
(iii) a multiple of 2 or 3
(iv) an even prime number
(v) a number greater than 5 (CBSE 2008)
(vi) a number lying between 2 and 6 [NCERT]
Solution:

Question 3.
Three coins are tossed together. Find the probability of getting:
(i) exactly two heads
(ii) at most two heads
(iii) at least one head and one tail
(iv) no tails
Solution:

Question 4.
A and B throw a pair of dice. If A throws 9, find B’s chance of throwing a higher number.
Solution:

Question 5.
Two unbiased dice are thrown. Find the probability that the total of the numbers on the dice is greater than 10.
Solution:

Question 6.
A card is drawn at random from a pack of 52 cards. Find the probability that the card drawn is
(i) a black king
(ii) either a black card or a king
(iii) black and a king
(iv) a jack, queen or a king
(v) neither a heart nor a king
(vi) spade or an ace
(vii) neither an ace nor a king
(viii) neither a red card nor a queen [CBSE 2005]
(ix) other than an ace
(x) a ten
(xi) a spade
(xii) a black card
(xiii)the seven of clubs
(xiv) jack
(xv) the ace of spades
(xvi) a queen
(xvii) a heart
(xviii) a red card
(xix) neither a king nor a queen [CBSE 2013]
Solution:

Question 7.
In a lottery of 50 tickets numbered 1 to 50, one ticket is drawn. Find the probability that the drawn ticket bears a prime number.
Solution:

Question 8.
An urn contains 10 red and 8 white balls. One ball is drawn at random. Find the probability that the ball drawn is white.
Solution:

Question 9.
A bag contains 3 red balls, 5 black balls and 4 white balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is:
(i) white?
(ii) red?
(iii) black?
(iv) not red? [CBSE2008]
Solution:

Question 10.
What is the probability that a number selected from the numbers 1, 2, 3…… 15 is a multiple of 4 ?
Solution:

Question 11.
A bag contains 6 red, 8 black and 4 white balls. A ball is drawn at random. What is the probability that ball drawn is not black?
Solution:

Question 12.
A bag contains 5 white and 7 red balls. One ball is drawn at random. What is the probability that ball drawn is white ?
Solution:

Question 13.
Tickets numbered from 1 to 20 are mixed up and a ticket is drawn at random. What is the probability that the ticket drawn has a number which is a multiple of 3 or 7?
Solution:

Question 14.
In a lottery there are 10 prizes and 25 blanks. What is the probability of getting a prize ?
Solution:

Question 15.
If the probability of winning a game is 0.3, what is the probability of loosing it ?
Solution:

Question 16.
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
(i) red
(ii) black or white
(iii) not black
Solution:

Question 17.
A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
(i) white
(ii) red
(iii) not black
(iv) red or white [CBSE 2004]
Solution:

Question 18.
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting:
(i) a king of red suit
(ii) a face card
(iii) a red face card
(iv) a queen of black suit
(v) a jack of hearts
(vi) a spade [NCERT]
Solution:

Question 19.
Five cards ten, jack, queen, king and an ace of diamonds are shuffled face downwards. One card is picked at I j random.
(i) What is the probability that the card is a queen ?
(ii) If a king is drawn first and put aside, what is the probability that the second card picked up is the (i) ace (ii) king?
Solution:

Question 20.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is:
(i) red
(ii) black
Solution:

Question 21.
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to one of the number, 1, 2, 3,………12 as shown in the figure. What is the probability that it will point to:

(i) 10?
(ii) an odd number?
(iii) a number which is multiple of 3?
(iv) an even number?

Question 22.
In a class, there are 18 girls and 16 boys. The class teacher wants to choose one pupil for class monitor. What she does, she writes the name of each pupil on a card and puts them into a basket and mixes thoroughly. A child is asked to pick one card from the basket. What is the probability that the name written on the card is: .
(i) the name of a girl
(ii) the name of a boy?
Solution:

Question 23.
Why is tossing a coin considered to be a fair way of deciding which team should choose ends in a game of cricket ?
Solution:
When we toss a coin, there are two outcomes of being a head and a tail equally So, the result of an individual coin toss is complelery are predictable. That is why, coin is tossed to decide which team should choose the end for the game

Question 24.
What is the probability that a number selected at random from the number 1, 2,2,3,3,3,4,4,4,4 will be their average?
Solution:

Question 25.
There are 30 cards, of same size, iiTa bag on which numbers 1 to 30 are written. One card is taken out of the bag at random. Find the probability that the number on the selected card is not divisible by 3. [CBSE 2005]
Solution:

Question 26.
A bag contains 5 red, 8 white and 7 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is (i) red or white (ii) not black (iii) neither white nor black. [CBSE 2005]
Solution:

Question 27.
Find the probability that a number selected from a number 1 to 25 is not a prime number when each of the given numbers is equally likely to be selected. [CBSE 2005]
Solution:

Question 28.
A bag contains 8 red, 6 white and 4 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is
(i) red or white
(ii) not black
(iii) neither white nor black.
Solution:

Question 29.
Find the probability that a number selected at random from the numbers 1, 2, 3,….. , 35 is a
(i) prime number
(ii) multiple of 7
(iii) a multiple of 3 or 5 [CBSE 2006C]
Solution:

Question 30.
From a pack of 52 playing cards Jacks, queens, kings and aces of red colour, are removed. From the remaining, a card is drawn at random. Find the probability that the card drawn is
(i) a black queen
(ii) a red card
(iii) a black jack
(iv) a picture card (Jacks, queens and kings are picture cards).
Solution:

Question 31.
A bag contains lemon flavoured candies only. Malini takes out one candy without looking into the bag. ‘What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy? [NCERT]
Solution:

Question 32.
It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday? [NCERT]
Solution:
n a group of 3 students, the probability of 2 students not having the same birthday=0.992 Probability of 2 students having the same birthday = 1 – 0.992 = 0.008

Question 33.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is (i) red? (ii) not red?
Solution:

Question 34.
A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be (i) red? (ii) white? (iii) not green? [NCERT]
Solution:

Question 35.
A lot consists of 144 ball pens of which 20 are defective and others good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) She will buy it?
(ii) She will not buy it?
Solution:

Question 36.
12 defective pens are accidently mixed with 132 good ones. It is not possible to just look at pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is good one.
Solution:

Question 37.
Five cards the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen ?
(ii) If the queen is drawn and put a side, what is the probability that the second card picked up is (a) an ace? (b) a queen?
Solution:

Question 38.
Harpreet tosses two different coins simultaneously (say, one is of ₹1 and other of ₹2). What is the probability that the gets at least one head ?
Solution:

Question 39.
Cards marked with numbers 13, 14, 15,……. 60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that, number on the card drawn is
(i) divisible by 5
(ii) a number is a perfect square [CBSE 2007]
Solution:

Question 40.
A bag contains tickets numbered 11, 12, 13,……..,30. A ticket is taken out from
the bag at random. Find the probability that the number on the drawn ticket
(i) is a multiple of 7
(ii) is greater than 15 and a multiple of 5. [CBSE 2008]
Solution:

Question 41.
Fill in the blanks :
(i) Probability of a sure event is …….
(ii) Probability of an impossible event is …….. .
(iii) The probability of an event (other than sure and impossible event) lies between …… .
(iv) Every elementary event associated to a random experiment has ……… probability.
(v) Probability of an event A + Probability of event ‘not A’ = …….. .
(vi) Sum of the probabilities of each outcome in an experiment is ……… .
Solution:
(i) Probability of a sure event is 1.
(ii) Probability of an impossible event is 0 (zero).
(iii) The probability of an event (other than sure and impossible event) lies between 0 and 1
i. e., 0 < probability <1.
(iv) Every elementary event associated to a random experiment has equal probability.
(v) Probability of an event A + Probability of event ‘not A’ = 1 (∵ \(\bar { A }\) + A = 1)
(vi) Sum of the probabilities of each outcome in an experiment is 1.

Question 42.
Examine each of the following statements and comment:
(i) If two coins are tossed at the same time, there are 3 possible outcomes two heads, two tails, or one of each. Therefore, for each outcome, the probability of occurrence is 1/3.
(ii) If a die is thrown once, there are two possible outcomes an odd number of an even number. Therefore, the probability of obtaining an odd number is 1/2 and the probability of obtaining an even number is 1/2.
Solution:

Question 43.
A box contains 100 red cards, 200 yellow cards and 50 blue cards. If a card is drawn at random from the box, then find the probability that it will be (i) a blue card (ii) not a yellow card (iii) neither yellow nor a blue card. [CBSE 2012]
Solution:

Question 44.
A box contains cards numbered 3,5,7,9, .., 35,37. A card is drawn at random from the box. Find te probability that the number on the drawn card is a prime number. [CBSE 2013]
Solution:

Question 45.
A group consists of 12 persons, of which 3 are extremely patient, other 6 are extremely honest and rest are extremely kind. A person from the group is selected at random. Assuming that each person is equally likely to be selected, find the probability of selecting a person who is (i) extremely patient (ii) extremely kind or honest. Which of the above you prefer more. [CBSE 2013]
Solution:

Question 46.
Cards numbered 1 to 30 are put in a bag. A card is drawn at random from this bag. Find the probability that the number on the drawn card is [CBSE 2014]
(i) not divisible by 3
(ii) a prime number great than 7
(iii) not a perfect square number.
Solution:

Question 47.
A piggy bank contains hundred 50 paise, fifty ₹1 coins, twenty ₹2 coins and ten ₹5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, find the probability that the coins which fell
(i) will be a 50 paise win
(ii) will be of value more than ₹1
(iii) will be of value less than ₹5
(iv) will be a ₹1 or ₹2 coins [CBSE 2014]
Solution:

Question 48.
A bag contains cards numbered from 1 to 49. A card is drawn from the bag at random, after mixing the card thoroughly. Find the probability that the number on the drawn card is
(i) an odd number
(ii) a multiple of 5
(iii) a perfect square
(iv) an even prime number. [CBSE 2014]
Solution:

Question 49.
A box contains 20 cards numbered from 1 to 20. A card is drawn at random from the box. Find the probability that the number on the drawn card is
(i) divisible by 2 or 3
(ii) a prime number [CBSE 2015]
Solution:

Question 50.
In a simultaneous throw of a pair of dice, find the probability of getting.
(i) 8 as the sum
(ii) a doublet
(iii) a doublet of prime numbers
(iv) a doublet of odd numbers
(v) a sum greater than 9
(vi) an even number on first
(vii) an even number on one and h multiple of 3 on the other
(viii)neither 9 nor 11 as the sum of the numbers on the faces
(ix) a sum less than 6
(x) a sum less than 7
(xi) a sum more than 7
(xii) at least once
(xiii)a number other than 5 on any dice.
(xiv) even number on each die [CBSE 2014,2015]
(xv) 5 as the sum [CBSE 2014,2015]
(xvi) 2 will come up at least once [CBSE 2015]
(xvii) 2 will not come either time [CBSE 2015]
Solution:

Question 51.
What is the probability that an ordinary year has 53 Sundays ?
Solution:

Question 52.
What is the probability that a leap year has 53 Sundays and 53 Mondays ?
Solution:

Question 53.
A black die and a white die are thrown at the same time. Write all the possible outcomes. What is the probability that :
(i) the sum of the two numbers that turn up is 8?
(ii) of obtaining a total of 6?
(iii) of obtaining a total of 10?
(iv) of obtaining the same number on both dice?
(v) of obtaining a total more than 9?
(vi) that the sum of the two numbers appearing on the top of the dice is 13?
(vii) that the sum of the numbers appearing on the top of the dice is less than or equal to 12?
(viii)that the product of numbers appearing on the top of the dice is less than 9.
(ix) that the difference of the numbers appearing on the top of the two dice is 2.
(x) that the numbers obtained have a product less than 16. [CBSE 2017]
Solution:

Question 54.
A bag contains cards which are numbered from 2 to 90. A card is drawn at random from the bag. Find the probability that it bears
(i) a two digit number
(ii) a number which is a perfect square.
Solution:

Question 55.
The faces of a red cube and a yellow cube are numbered from 1 to 6. Both cubes are rolled. What is the probability that the top face of each cube will have the same number ?
Solution:

Question 56.
The probability of selecting a green marble at random from a jar that contains only green, white and yellow marbles is 1/4. The probability of selecting a white marble at random from the same jar is 1/3. If this jar contains 10 yellow
marbles. What is the total number of marbles in the jar?
Solution:

Question 57.
(i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and not replaced. Now bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Solution:

Question 58.
A box contains 90 discs which are numbered from 1 to 90. If one discs is drawn at random from the box, find the probability that it bears
(i) a two digit number
(ii) a perfect square number
(iii) a number divisible by 5.
Solution:

Question 59.
Two dice, one blue and one grey, are thrown at the same time. Complete the following table:
From the above table a student argues that there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10,11 and 12. Therefore, each of them has a probability \(\frac { 1 }{ 11 }\). Do you agree with this
argument ?
Solution:

Question 60.
A bag contains 6 red balls and some blue balls. If the probability of drawing a blue ball from the bag is twice that of a red ball, find the number of blue balls in the bag.
[CBSE 2007]
Solution:

Question 61.
The king, queen and jack of clubs are removed from a deck of 52 playing cards and the remaining cards are shuffled. A card is drawn from the remaining cards. Find the probability of getting a card of (i) heart (ii) queen (iii) clubs (iv) a face card (v) a queen of diamond.
Solution:

Question 62.
Two dice are thrown simultaneously. What is the probability that :
(i) 5 will not come up on either of them ?
(ii) 5 will come up on at least one ?
(iii) 5 will come up at both dice? [CBSE 2009]
Solution:

Question 63.
A number is selected at random from first 50 natural numbers. Find the probability that it is a multiple of 3 and 4.
Solution:

Question 64.
A dice is rolled twice. Find the probability that
(i) 5 will not come up either time.
(ii) 5 will come up exactly one time. [CBSE 2014]
Solution:

Question 65.
All the black face cards are removed from a pack of 52 cards. The remaining cards are well shuffled and then a card is drawn at random. Find the probability to getting a
(i) face card
(ii) red card
(iii) black card
(iv) king.
Solution:

Question 66.
Cards numbered from 11 to 60 are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn cards is
(i) an odd number
(ii) a perfect square number
(iii) divisible by 5
(iv) a prime number less than 20. [CBSE 2014]
Solution:

Question 67.
All kings and queens are removed from a pack of 52 cards. The remaining cards are well-shuffled and then a card is randomly drawn from it. Find the probability that this card is
(i) a red face card
(ii) a black card. [CBSE 2014]
Solution:

Question 68.
All jacks, queens and kings are removed from a pack of 52 cards. The remaining cards are well-shuffled and then a card is randomly drawn from it. Find the probability that this cards is
(i) a black face card
(ii) a red card. [CBSE 2014]
Solution:

Question 69.
Red queens and blackjacks are removed from a pack of 52 playing cards. A cards is drawn at random from the remaining cards, after reshuffling them. Find the probability that the card drawn is
(i) a king
(ii) of red colour
(iii) a face card
(iv) a queen [CBSE 2014]
Solution:

Question 70.
In a bag there are 44 identical cards with figure of circle or square on them. There are 24 circles, of which 9 are blue and rest are green and 20 squares of which 11 are blue and rest are green. One card is drawn from the bag at random. Find the probability that it has the figure of (i) square (ii) green colour, (iii) blue circle and (iv) green square. [CBSE 2015]
Solution:

Question 71.
All red face cards are removed from a pack of playing cards. The remaining cards are well shuffled and then a card is drawn at random from them. Find the probability that the drawn card is (i) a red card, (ii) a face card and (ii) a card of clubs. [CBSE 2015]
Solution:

Question 72.
Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any one day as on another. What is the probability that both will visit the shop on:
(i) the same day?
(ii) different days?
(iii) consecutive days?
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Solve the following systems of equations:
Question 1.
11x + 15y + 23 = 0
7x – 2y – 20 = 0
Solution:
11x + 15y + 23 = 0 => 11x + 15y = -23 ……..(i)
7x – 2y – 20 = 0 => 7x – 2y = 20 ……….(ii)
Multiply (i) by 2 and (ii) 15, we get
22x + 30y = -46
105x – 30y = 300
Adding we get
127x = 254 => x = \(\frac { 254 }{ 127 }\) = 2
7 x 2 – 2y = 20 => 14 – 2y = 20
-2y = 20 – 14 = 6
y = -3

Question 2.
3x – 7y + 10 = 0
y – 2x – 3 = 0
Solution:

Question 3.
0.4x + 0.3y = 1.7
0.7x – 0.2y = 0.8
Solution:

Question 4.

Solution:

Question 5.
7(y + 3) – 2(x + 2) = 14
4(y – 2) + 3(x – 3) = 2
Solution:

Question 6.
\(\frac { x }{ 7 } +\frac { y }{ 3 } =5\)
\(\frac { x }{ 2 } -\frac { y }{ 9 } =6\)
Solution:

Question 7.
\(\frac { x }{ 3 } +\frac { y }{ 4 } = 11\)
\(\frac { 5x }{ 6 } -\frac { y }{ 3 } = -7\)
Solution:

Question 8.
\(\frac { 4 }{ x }\) + 3y = 8
\(\frac { 6 }{ x }\) – 4y = -5
Solution:

Question 9.
x + \(\frac { y }{ 2 }\) = 4
\(\frac { x }{ 3 }\) + 2y = 5
Solution:

Question 10.
x + 2y = \(\frac { 3 }{ 2 }\)
2x + y = \(\frac { 3 }{ 2 }\)
Solution:

Question 11.
√2x – √3y = 0
√3x – √8y = 0
Solution:

Question 12.
3x – \(\frac { y + 7 }{ 11 }\) + 2 = 10
2y + \(\frac { y + 11 }{ 7 }\) = 10
Solution:

Question 13.
2x – \(\frac { 3 }{ y }\) = 9
3x + \(\frac { 7 }{ y }\) = 2, y ≠ 0
Solution:

Hence x = 3, y = -1

Question 14.
0.3x + 0.7y = 0.74
0.3x + 0.5y = 0.5
Solution:

Question 15.

Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.

Solution:

Question 19.

Solution:

Question 20.

Solution:

Question 21.

Solution:

Question 22.

Solution:

Question 23.

Solution:

Question 24.

Solution:

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Question 31.

Solution:

Question 32.

Solution:

Question 33.

Solution:

Question 34.
x + y = 5xy
3x + 2y = 13xy
Solution:

Question 35.

Solution:

Question 36.
2 (3u – v) = 5uv
2 (u + 3v) = 5uv
Solution:

Question 37.

Solution:

Question 38.

Solution:

Question 39.

Solution:

Question 40.

Solution:

Question 41.

Solution:

Question 42.

Solution:

Question 43.
152x – 378y = -74
– 378x + 152y = -604
Solution:
152x – 378y = -74 ……..(i)
– 378x + 152y = -604 ………(ii)
Adding (i) and (ii), we get
– 226x – 226y = 678
Dividing by -226,
x + y = 3 ……..(iiii)
and subtracting (ii) from (i)
530x – 530y = 530
Dividing by 530,
x – y = 1 ……..(iv)
Adding (iii) and (iv)
2x = 4
x = 2
From (iii), 2 + y = 3
y = 3 – 2 = 1
Hence x = 2, y = 1

Question 44.
99x + 101y = 499
101x + 99y = 501
Solution:
99x + 101 y = 499 ….(i)
101x + 99y = 501 ……(ii)
Adding we get
200x + 200y = 1000
x + y = 5 ……(iii)
(Dividing by 200)
Subtracting we get
-2x + 2y = -2
=> x – y = 1 ….(iv)
(Dividing by -2)
Now adding (iii) and (iv)
2x = 6 => x = 3
and subtracting (iv) from (iii)
2y = 4 => y = 2
Hence x = 3, y = 2

Question 45.
23x – 29y = 98
29x – 23y = 110
Solution:
23x – 29y = 98 ….(i)
29x – 23y = 110 ….(ii)
Adding (i) and (ii) we get
52x – 52y = 208
x – y = 4 ….(iii)
(Dividing by 52)
Subtracting (ii) from (i)
6x + 6y = 12
=> x + y = 2 ….(iv)
(Dividing by 6)
Adding (iii) and (iv)
2x = 6 => x = 3
Subtracting (iv) from (iii)
2y = -2 => y = -1
Hence x = 3, y = -1

Question 46.
x – y + z = 4
x – 2y – 2z = 9
2x + y + 3z = 1
Solution:
x – y + z = 4 ……(i)
x – 2y – 2z = 9 ……(ii)
2x + y + 3z = 1 ……(iii)

Question 47.
x – y + z = 4
x + y + z = 2
2x + y – 3z = 0
Solution:
x – y + z = 4 ….(i)
x + y + z = 2 ….(ii)
2x + y – 3z = 0 ….(iii)
From (i)
z = 4 – x + y
Substituting the values of z in (ii) and (iii)
x + y + 4 – x + y = 2
2y = 2 – 4 = -2
y = -1
and 2x + y – 3(4 – x + y) = O
2x + y – 12 + 3x – 3y = 0
5x – 2y = 12
5x – 2(-1) = 12
5x + 2 = 12
5x = 12 – 2 = 10
x = 2
From (i),
2 – (-1) + z = 4
2 + 1 + z = 4
3 + z = 4
z = 4 – 3 = 1
Hence x = 2, y = 1, z = 1

Question 48.
21x + 47y = 110
47x + 21y = 162
Solution:
We have,
21x + 47y = 110 …(i)
47x + 21y = 162 …(ii)
Multiplying equation (i) by 47 and Equation (ii) by 21, we get
987x + 2209y = 5170 …(iii)
987x + 441y = 3402 …(iv)
Subtracting equation (iv) from equation (iii),
we get
1768y = 1768
y = 1
Substituting value of y in equation (i), we get
21x + 47 = 110
or 21x = 63
or x = 3
So, x = 3, y = 1

Question 49.
If x + 1 is a factor of 2x³ + ax² + 2bx + 1, then find the values of a and b given that 2a – 3b = 4
Solution:

Question 50.

Solution:

Question 51.
Find the values of x and y in the following rectangle

Solution:

Hence, the required values of x and y are 1 and 4, respectively.

Question 52.
Write an equation of a line passing through the point representing solution of the pair of linear equations x + y = 2 and 2x – y = 1. How many such lines can we find?
Solution:


Plotting the points A (2, 0) and B (0, 2), we get the straight line AB. Plotting the points C (0, -1) and D (\(\frac { 1 }{ 2 }\) , 0) we get the straight line CD. The lines AB and CD intersect at E (1, 1).
Hence, infinite lines can pass through the intersection point of linear equations x + y = 2 and 2x – y = 1
¡.e.,E(1, 1) like as y = x, 2x + y = 3, x + 2y = 3, so on.

Question 53.
Write a pair of linear equations which has the unique solution x = -1, y = 3. How many such pairs can you write?
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.