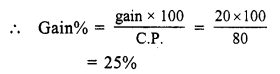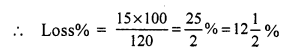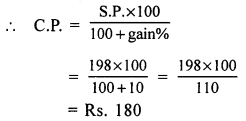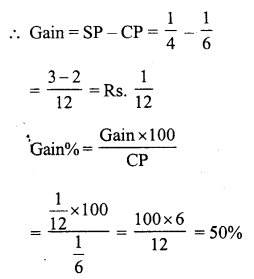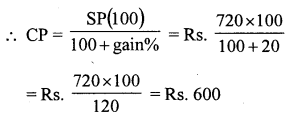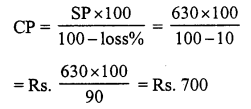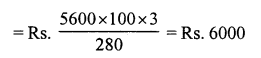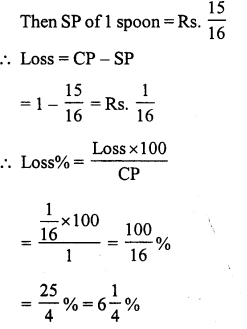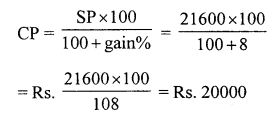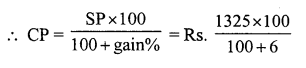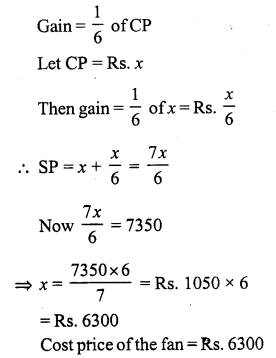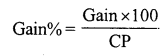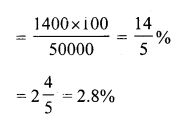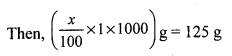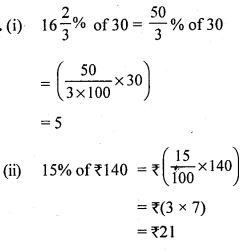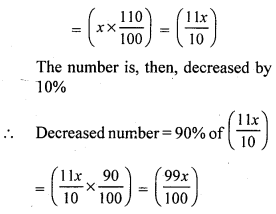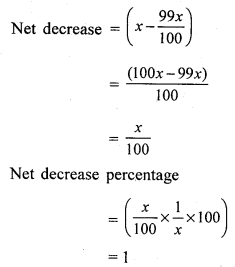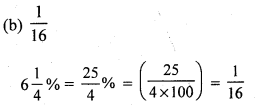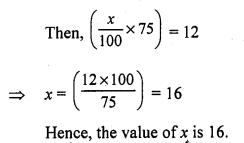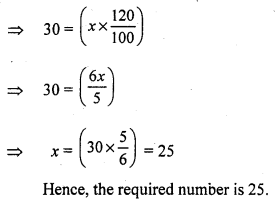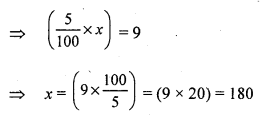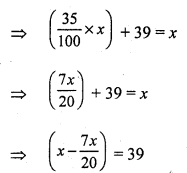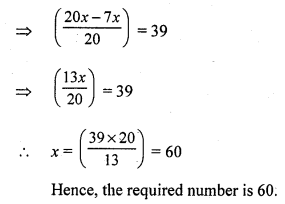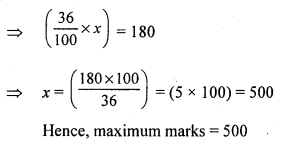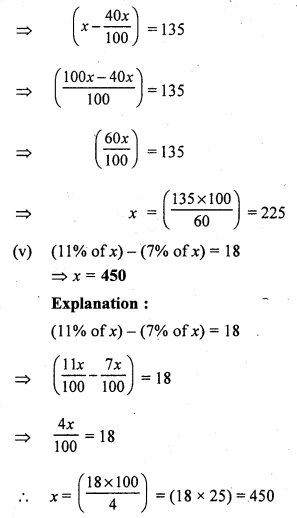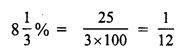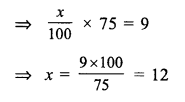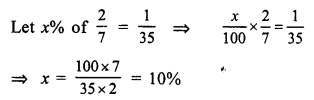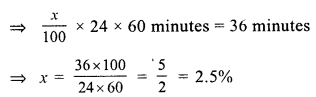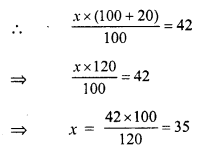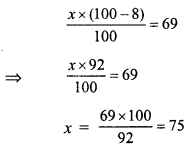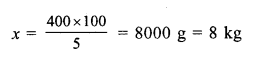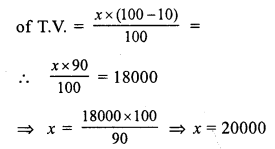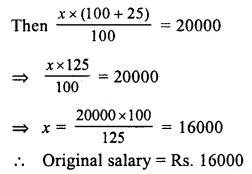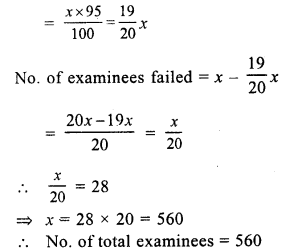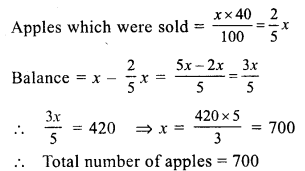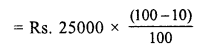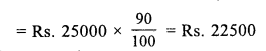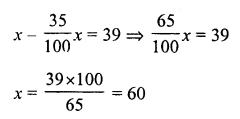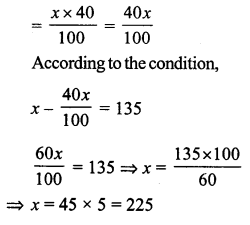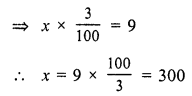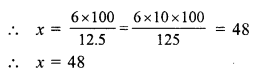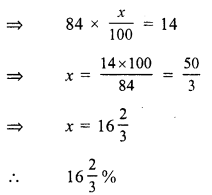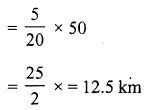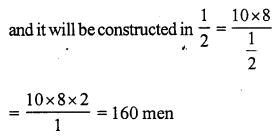Raju

RS Aggarwal Class 7 Solutions Chapter 11 Profit and Loss CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper

Question 1.
Solution:
SP of the chair = ₹ 1375
Gain% = 10
CP of the chair

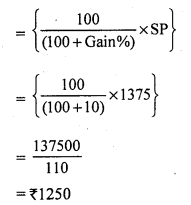
Question 2.
Solution:
Let the cost of each pen be ₹ 1
CP of 10 pens = ₹ 10
SP of 10 pens = CP of 14 pens = ₹ 14
Gain = SP – CP = 14 – 10 = ₹ 4

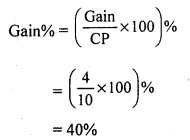
Question 3.
Solution:
Let the cost price of the fan be ₹ x

Question 4.
Solution:
Cost price of six lemons = ₹ 10

Question 5.
Solution:
SP of the bat = ₹ 486
Loss = 10%
CP of the bat

Mark (✓) against the correct answer in each of the following :
Question 6.
Solution:
(b) ₹ 85
SP of a football = ₹ 100
Gain = ₹ 15
Gain = SP – CP
⇒ 15 = 100 – CP
⇒ CP = ₹ (100 – 15)
⇒ CP = ₹ 85

Question 7.
Solution:
(c) 15.2%
Cost price of 12 bananas = ₹ 25
Cost price of one banana = ₹ \(\frac { 25 }{ 12 }\)
Cost price of five bananas = 5 x \(\frac { 25 }{ 12 }\)
= \(\frac { 125 }{ 12 }\) = 10.42
He shells five bananas at the cost (SP) of ₹ 12.
Gain = SP – CP = ₹ (12 – 10.42) = ₹ 1.58

Question 8.
Solution:
(c) ₹ 196
Let the cost price of the jug be ₹ x

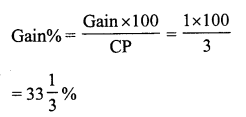
Question 9.
Solution:
(c) 66\(\frac { 2 }{ 3 }\) %
Let the cost price of each banana be ₹ 1
Cost price of three bananas = ₹ 3
SP of three bananas = CP of five bananas = ₹ 5
Gain = SP – CP = ₹ (5 – 3) = ₹ 2

Question 10.
Solution:
(i) Loss = (CP) – (SP).

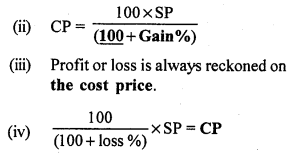
Question 11.
Solution:
(i) False
Gain or loss is always reckoned on the cost price.
(ii) True
(iii) True
(iv) True

Hope given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 11 Profit and Loss Ex 11B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper

Objective Questions :
Mark (✓) against the correct answer in each of the following :
Question 1.
Solution:
(b)
C.P. = Rs. 80
S.P. = Rs. 100
Gain = S.P. – C.P. = Rs. 100 – 80 = Rs. 20

Question 2.
Solution:
(a)
C.P. = Rs. 120
S.P. = Rs. 105
Loss = C.P. – S.P. = Rs. 120 – 105 = Rs. 15

Question 3.
Solution:
(b)
S.P. = Rs. 100
Gain = Rs. 20
C.P. = S.P. – gain = Rs. 100 – 20 = Rs. 80

Question 4.
Solution:
(a)
S.P. = Rs. 198
Gain = 10%

Question 5.
Solution:
(a)
First S.P. of jug = Rs. 144
Loss = \(\frac { 1 }{ 7 }\) of C.P.
Let C.P. = x

Question 6.
Solution:
(d)
First S.P. of a pen = Rs. 48
Loss = 20%

Question 7.
Solution:
(a)
C.P. of 12 pencils = S.P. of 15 pencils = Re 1 (suppose)

Question 8.
Solution:
(d)
Let CP of 4 toffees = SP of 3 toffee = Rs. 12
(LCM of 4, 3 = 12)
CP of 1 toffee = Rs. \(\frac { 12 }{ 4 }\) = Rs. 3
SP of 1 toffee = Rs. \(\frac { 12 }{ 3 }\) = 4
Gain = Rs. 4 – 3 = Re 1

Question 9.
Solution:
(c) SP of an article = Rs. 144
Loss% = 10%

Question 10.
Solution:
(a)
CP of 6 lemons = Re 1
CP of 1 lemon = Re \(\frac { 1 }{ 6 }\)
SP of 4 lemons = Re 1
SP of 1 lemon = Re \(\frac { 1 }{ 4 }\)

Question 11.
Solution:
(d)
SP of chair = Rs. 720
Gain% = 20%

Question 12.
Solution:
(c)
SP of stool = Rs. 630
Loss% = 10%

Hope given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 11 Profit and Loss Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11B
• RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss CCE Test Paper

Question 1.
Solution:
(i) C.P. = Rs. 950

Question 2.
Solution:
(i) CP = Rs. 2400
SP = Rs. 2592
Gain = SP – CP = Rs. 2592 – Rs. 2400 = Rs. 192

Question 3.
Solution:
(i) S.P. = Rs. 924
Gain% = 10%

Question 4.
Solution:
C.P. of an almirah = Rs. 13600
Amount spent on transportation = Rs. 400
Total cost price (CP) = Rs. 13600 + Rs. 400 = Rs. 14000
SP = Rs. 16800
Total gain = SP – CP
= Rs. 16800 – Rs. 14000 = Rs. 2800

Question 5.
Solution:
CP of an old house = Rs. 765000
Amount spent on repairs = Rs. 115000
Total cost price (CP) = Rs. 765000 + Rs. 115000 = Rs. 880000
Gain = 5%

Question 6.
Solution:
CP of 1 dozen or 12 lemons = Rs. 25
SP of 5 lemons = Rs. 12

Question 7.
Solution:
SP of 12 pens = CP of 15 pens
Let CP of 1 pen = Re. 1
The CP of 15 pens = Rs. 15
and SP of 12 pens = Rs. 12

Question 8.
Solution:
SP of 16 spoons = CP of 15 spoons
Let CP of 1 spoon = Re. 1
Then CP of 15 spoons = Rs. 15
and SP of 16 spoons = Rs. 15

Question 9.
Solution:
For Manoj
CP of video = Rs. 12000
Gain = 10%

Question 10.
Solution:
SP of sofa set = Rs. 21600
Gain = 8%

Question 11.
Solution:
SP of a watch = Rs. 11400
Loss = 5%

Question 12.
Solution:
SP of calculator = Rs. 1325
Gain = 6%

Question 13.
Solution:
SP of computer = Rs. 24480
Loss = 4%

Question 14.
Solution:
In first case gain =15%
and in second case, gain = 20%
Difference = 20 – 15 = 5%
Now 5% of the CP = Rs. 108
CP = \(\frac { 108 x 100 }{ 5 }\) = Rs. 2160

Question 15.
Solution:
In first case, loss = 8%
and in second case gain = 6%
Difference = 8 + 6 = 14%
Now 14% of CP = Rs. 3360
CP = Rs. \(\frac { 3360 x 100 }{ 14 }\) = Rs. 24000

Question 16.
Solution:
SP of first cycle = Rs. 2376
Gain = 10%

Question 17.
Solution:
SP of an exhaust fan = Rs. 7350

Question 18.
Solution:
Let CP of watch for Mohit = Rs. 100
Gain =10%
SP for Mohit = Rs. 100 + 10 = Rs. 110
CP for Karim = Rs. 110
Gain = 4%

Question 19.
Solution:
Retail price or S.P. of the machine for retailer = Rs. 37950
Gain = 25%

Question 20.
Solution:
CP of video = Rs. 20000
and CP of television = Rs. 30000
Loss on video = 5%
and gain on TV = 8%

Total CP of video and TV = Rs. 20000 + 30000 = Rs. 50000
and SP of video and TV = Rs. 190000 + 32400 = RS. 51400
Gain = SP – CP = Rs. 51400 – 50000 = Rs. 1400

Question 21.
Solution:
SP of 36 oranges = CP of 36 oranges – loss = CP of 36 oranges – SP of 4 oranges
⇒ SP of 36 oranges + SP of 4 oranges = CP of 3 6 oranges
⇒ SP of 40 oranges = CP of 36 oranges
Let CP of each orange = Re. 1
CP of 36 oranges = Rs. 36
and SP of 40 of 40 oranges = Rs. 36

Question 22.
Solution:
We know that C.P. = S.P. – gain
C.P. of 8 dozen pencils = S.P. of 8 dozen pencils – S.P. of 1 dozen pencils
= S.P. of 7 dozen pencils = Rs. 100 (suppose)
C.P. of 1 dozen = Rs.\(\frac { 100 }{ 8 }\)

 

Hope given RS Aggarwal Solutions Class 7 Chapter 11 Profit and Loss Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 10 Percentage CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper

Question 1.
Solution:
We have :

Question 2.
Solution:
(i) Let x% of 1 kg be 125 g

Question 3.
Solution:

Question 4.
Solution:
(i) Let x be the required number.

Question 5.
Solution:
Let x be the number
The number is increased by 10%
Increased number = 110% of x

Question 6.
Solution:
The present value of the machine = ₹ 10000
The decrease in its value after the 1 st year = 10% of ₹ 10000
\(\frac { 10 }{ 100 }\) x 10000 = ₹ 1000
The depreciated value of the machine after the 1 st year = ₹ (10000 – 1000) = ₹ 9000
The decrease in its value after th 2nd year = 10% of ₹ 9000
\(\frac { 10 }{ 100 }\) x 9000 = 900
The depreciated value of the machine after the 2nd year = ₹ (9000 – 900) = ₹ 8100
Hence, the value of the machine after two years will be ₹ 8100.

Question 7.
Solution:
The present population of the town = 16000
Increase in population after 1 year = 5% of 16000
= (\(\frac { 5 }{ 100 }\) x 16000) = 800
Thus, population after one year = 16000 + 800 = 16800
Increase in population after 2 years = 5% of 16800
= \(\frac { 5 }{ 100 }\) x 16800 = 840
Population after two years = 16800 + 840 = 17640
Hence, the population of the town after two years will be 17,640.

Question 8.
Solution:
Let us assume that the original price of the tea set is Increase in price = 5%
So, value increased on the tea set = 5% of ₹ x

Hence, the original price of the tea set is ₹ 420.

Mark (✓) against the correct answer in each of the following :
Question 9.
Solution:

Question 10.
Solution:
(c) 12
Given that x% of 75 = 12

Question 11.
Solution:
(c) 25
Let the number be x. Then, we have:
120% of x = increased number

Question 12.
Solution:
(d) 180
Let the required number be x.
Then, we have :
5% of x = 9

Question 13.
Solution:
(a) 60
Let the number be x According to question, we get:
(35 % of x) + 39 = x

Question 14.
Solution:
(c) 500
Let x be the maximum marks Pass marks = (160 + 20) = 180
36 % of x = 180

Question 15.
Solution:
(i) 3 : 4 = (75) %
Explanation:
3 : 4 = \(\frac { 3 }{ 4 }\)
= (\(\frac { 3 }{ 4 }\) x 100) %
= (3 x 25)% = 75%
(ii) 0.75 = (75)%
Explanation : (0.75 x 100)% = 75%
(iii) 6% = 0.06 (express in decimals)
Explanation :
6% = \(\frac { 6 }{ 100 }\) = 0.06
(iv) If x decreased by 40% gives 135, then x = 225
Explanation :
Let the number be x.
According to question, we have :
x – 40% of x = 135

Question 16.
Solution:
(i) True (T)

Hope given RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 10 Percentage Ex 10C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper

Objective Questions :
Mark (✓) against the correct answer in each of the following :
Question 1.
Solution:
(b) \(\frac { 3 }{ 4 }\) = \(\frac { 3 }{ 4 }\) x 100 = 75 %

Question 2.
Solution:
(c)
2 : 5 = \(\frac { 2 }{ 5 }\) = \(\frac { 2 }{ 5 }\) x 100 = 40%

Question 3.
Solution:
(c)

Question 4.
Solution:
(c) x% of 75 = 9

Question 5.
Solution:
(d)

Question 6.
Solution:
(b)
Let x% of 1 day = 36 minutes

Question 7.
Solution:
(a)
Let x be the required number

Question 8.
Solution:
(b)
Let x be the required number, then

Question 9.
Solution:
(d)
Let ore = x, then
5% of x = 400g
\(\frac { x x 5 }{ 100 }\) 400

Question 10.
Solution:
(b)
Let gross value of T.V = x
Commission = 10%
After deducting commission, the value

Question 11.
Solution:
(b)
Increase in salary = 25%
Let original salary = x

Question 12.
Solution:
(c)
Let x be the number of total examinees
No. of examinees passed

Question 13.
Solution:
(c)
Let total number of apples = x

Question 14.
Solution:
(b)
Present value of machine = Rs. 25000
Rate of depreciation = 10% p.a.
Value of machine after one year

Question 15.
Solution:
(c) Let x be numbers

Question 16.
Solution:
(c) 60% of 450
= \(\frac { 60 }{ 100 }\) x 450 = 270

Question 17.
Solution:
(d) Rate of reduction = 6%
Price after reduction = Rs. 658

Question 18.
Solution:
(b) Boys = 70% of students
No. of girls = 240
Girls percentage = 100 – 70 = 30%

Question 19.
Solution:
(c) Let number = x
11% of x – 7% of x = 18

Question 20.
Solution:
(a) Let number = x
35% of x + 39 = x

Question 21.
Solution:
(c) Pass marks = 36%
A students get =145 marks
But failed by 3 5 marks
Then pass marks = 145 + 35 = 180
Maximum marks = \(\frac { 180 x 100 }{ 36 }\) = 500

Question 22.
Solution:
(d) Let number be = x
Then decreasing by 40%

Hope given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 14 Properties of Parallel Lines Ex 14

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 14 Properties of Parallel Lines Ex 14.

Question 1.
Solution:
A transversal t intersects two parallel lines l and m.
∠ 1 = ∠ 5 (corresponding angles)
But ∠ 5 = 70° (given)
∠ 1 = 70°

But ∠ 3 = ∠ 5 (Alternate angles)
∠ 3 = 70°
∠4 + ∠5 = 180° (Sum of co-interior angles)
⇒ ∠4 + 70° = 180°
⇒ ∠4 = 180° – 70°
⇒ ∠4 = 110°
But ∠ 4 = ∠ 8 (corresponding angles)
∠ 8 = 110°
Hence ∠ 1 = 70°, ∠3 = 70°, ∠4 = 110° and ∠ 8 = 110°

Question 2.
Solution:
A transversal t intersects two parallel lines l and m
∠1 : ∠2 = 5 : 7
But ∠ 1 + ∠ 2 = 180° (Linear pair)


But ∠ 3 = ∠ 1 (vertically opposite angles)
∠ 3 = 75°
∠ 8 = ∠ 4 (corresponding angles)
and ∠ 4 = ∠ 2 (vertically opposite angles)
∠8 = ∠2 = 105°
Hence ∠ 1 = 75°, ∠2 = 105°, ∠3 = 75° and ∠ 8 = 105°

Question 3.
Solution:
A transversal t intersects two parallel lines l and m interior angles of the same side of t are (2x – 8)° and (3x – 7)°
(2x – 8)° + (3x – 7)° = 180° (sum of co-interior angles)
⇒ 2x – 8 + 3x – 7 = 180°
⇒ 5x – 15° = 180°
⇒ 5x = 180° + 15°
⇒ 5x = 195°

⇒ x = \(\frac { 195 }{ 5 }\) = 39°
First angle = 2x – 8° = 2 x 39° – 8° = 78° – 8° = 70°
Second angle = 3x – 7 = 3 x 39° – 7° = 117° – 7° = 110°

Question 4.
Solution:
l || m and two transversals intersect these lines but s is not parallel to t.

∠ 5 = ∠ 1 (vertically opposite angles)
∠ 5 = 50°
But l || m and s the transversal
∠ 5 + ∠ 2 = 180° (sum of co-interior angles)
⇒ 50° + x = 180°
⇒ x = 180° – 50° – 130°
x = 130°
∠ 4 = ∠ 6 (vertically opposite angles)
∠ 6 = y
But l || m and t is the transversal
∠ 6 + ∠ 3 = 180° (sum of co-interior angles)
⇒ y + 65° = 180°
⇒ y = 180° – 65° = 115°
y = 115°
Hence x = 130° and y = 115°

Question 5.
Solution:
In the figure, ABC is a triangle, DAE || BC
∠B = 65°, ∠C = 45°
∠ DAB = x° and ∠ EAC = y°
DAE || BC and AB is transversal
∠ DAB = ∠ B (Alternate angles)

⇒ x° = 65°
Similarly ∠ EAC = ∠ C (Alternate angles)
y° = 45°
Hence x = 65° and y = 45°

Question 6.
Solution:
In ∆ABC, AB || CE
∠BAC = 80°, ∠ECD = 35°
AB || CE and BCD is the transversal
∠ABC = ∠ECD (corresponding angles)

⇒ ∠ABC = 35° (∠ECD = 35°)
Again AB || CE and AC is the transversal
∠ BAC = ∠ ACE (alternate angles)
∠ACE = 80° (∠BAC = 80°)
In ∆ABC
∠A + ∠B + ∠ACB = 180° (Sum of angles of a triangle)
∠ 80° + ∠ 35° + ∠ACB = 180°
⇒ ∠ACB + ∠ 115° = 180°
⇒ ∠ACB = 180° – 115° = 65°
Hence ∠ ACE = 80°, ∠ ACB = 65° and ∠ ABC = 35°

Question 7.
Solution:
In the figure,
AO || CD, DB || CE and ∠AOB = 50°
AO || CD and CD is the transversal
∠ AOB = ∠ CDB (corresponding angles)

∠ CDB = 50° (∠ AOB = 50°)
Similarly CE || OB and CD in transversal
∠ECD + ∠CEB = 180° (sum of co-interior angles)
⇒ ∠ECD + 50° = 180°
⇒ ∠ECD = 180° – 50° = 130°
∠ECD = 130°

Question 8.
Solution:
In the fig, AB || CD
∠ABO = 50° and ∠CDO = 40°
From O, draw EOF || AB or CD
AB || EF and BO is the transversal

∠ABO = ∠ 1 (Alternate angles) …(i)
∠ CDO = ∠ 2 (Alternate angles) …(ii)
Similarly, EF || CD and OD is the transversal
Adding (i) and (ii),
∠ 1 + ∠ 2 = ∠ABO + ∠CDO
⇒ ∠BOD = 50° + 40° = 90°
Hence ∠ BOD = 90°

Question 9.
Solution:
Given : In the figure, AB || CD and EF is a transversal which intersects them at G and H respectively
GL and HM are the angle bisectors or ∠ AGH and ∠ GHD respectively.
To prove : GL || HM.
Proof : AB || CD and EF is a transversal
∠ AGH = ∠ CHD (Alternate angles)
GL is the bisector of ∠ AGH
∠ 1 = ∠2 = \(\frac { 1 }{ 2 }\) ∠ AGH

Similarly, HM is the bisectors of ∠ GHD
∠3 = ∠4 = \(\frac { 1 }{ 2 }\) ∠ GHD
∠ AGH = ∠ GHD (proved)
∠ 1 = ∠3
But, these are alternate angles
BL || HM
Hence proved.

Question 10.
Solution:
In the given figure,
AB || CD
∠ ABE = 120° and ∠ECD = 100° ∠ BEC = x°
From E, draw FG || AB or CD.
AB || EF

∠ABE + ∠1 = 180° (sum of co-interior angles)
⇒ 120° + ∠1 = 180°
⇒ ∠1 = 180°- 120° = 60°
Similarly CD || EG
∠ECD + ∠2 = 180°
⇒ 100° + ∠2 = 180°
⇒ ∠2 = 180° – 100°
∠ 2 = 80°
But ∠1 + ∠x + ∠2 = 180° (Angles on one side of a straight line)
⇒ 60° + x + 80° = 180°
⇒ x + 140° = 180°
⇒ x = 180° – 140° = 40°
x = 40°

Question 11.
Solution:
Given : In the figure, ABCD is a quadrilateral in which AB || DC and AD || BC
To prove : ∠ADC = ∠ABC
Proof : AB || DC and DA is the transversal
∠ADC + ∠ DAB = 180° (co-interior angles)

Similarly, AD || BC and AB is the transversal
∠DAB + ∠ABC = 180° …(ii)
from (i) and (ii),
∠ ADC + ∠ DAB = ∠DAB + ∠ABC
⇒ ∠ADC = ∠ABC
Hence ∠ ADC = ∠ ABC
Hence proved.

Question 12.
Solution:
In the figure,
l || m and p || q.
∠1 = 65°
∠ 2 = ∠ 1 (vertically opposite angles)

∠ 2 = 65°
⇒ a = 65°
p || q and l is the transversal
∠ 2 + ∠ 3 = 180° (co-interior angles)
⇒ a + b= 180°
⇒ 65° + b = 180°
⇒ b = 180° – 65° = 115°
Again l || m and p is the transversal
∠ 3 + ∠4 = 180°
⇒ b + c = 180°
⇒ 115° + c = 180°
⇒ c = 180° – 115° = 65°
l || m and q is the transversal
∠ 2 + ∠ 5 = 180°
⇒ a + d = 180°
⇒ 65° + d = 180°
⇒ d = 180° – 65° = 115°
Hence a = 65°, b = 115°, c = 65° and d = 115°

Question 13.
Solution:
In the given figure, AB || DC and AD || BC and AC is the diagonal of parallelogram ABCD.

∠BAC = 35°, ∠CAD = 40°, ∠ACB = x° and ∠ ACD = y°. .
AB || DC and CA is the transversal
∠ DCA = ∠ CAB (Alternate angles)
⇒ y = 35°
and similarly AD || BC and AC is the transversal
∠ CAD = ∠ ACB (Alternate angles)
⇒ 40° = x°
x = 40° and y = 35°

Question 14.
Solution:
In the figure, AB || CD and CD has been produced to E so that
∠ BAE = 125° ∠ BAC = x°, ∠ ABD = x°, ∠ BDC = y° and ∠ ACD = z°
DAE is a straight line and AB stands on it.

∠ BAD + ∠ BAE = 180° (Linear pair)
⇒ x + 125° = 180°
⇒ x = 180° – 125° = 55°
But ∠ABC = x = 55°
DC || AB and CB is the transversal
∠ABC + ∠ BCD = 180° (co-interior angles)
⇒ x + y = 180°
⇒ 55° + y = 180°
⇒ y = 180° – 55° = 125°
Again DC || AB and DAE is its transversal
∠ CDA = ∠ BAE (corresponding angles).
z = 125°
Hence x = 55°, y = 125° and z = 125°

Question 15.
Solution:
Given : In each figure,
l and m are two lines and t is the transversal
To prove : l || m or not
Proof:
(i) fig. (i)
A transversal t intersects two lines l and m

and ∠ 1 = 40°, ∠2 = 130°
But ∠ 1 + ∠3 = 180° (Linear pair)
⇒ 40° + ∠ 3 = 180°
⇒ ∠3 = 180° – 40° = 140°
l || m,
If ∠ 3 = ∠ 2
⇒ 140° = 130°
Which is not possible.
l is not parallel to m.
(ii) fig. (ii)
Transversal t, intersects l and m and ∠ 1 = 35°, ∠2 = 145°
But ∠ 1 = ∠ 3 (vertically opposite angles).
∠3 = 35°
l || m,
if ∠3 + ∠2 = 180°
if 35° + 145° = 180°

if 180°= 180°
which is true
l || m
(iii) Transversal t, intersects l and m.
∠ 1 = 125°, ∠ 2 = 60°

But ∠ 1 = ∠ 3 (vertically opposite angles)
∠ 3 = 125°
l || m
If ∠3 + ∠2 = 180° (co-interior angles)
If 125° + 60° = 180°
If 185° =180°
which is not possible.
Hence l is not parallel to m.

Hope given RS Aggarwal Solutions Class 7 Chapter 14 Properties of Parallel Lines Ex 14 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 13 Lines and Angles Ex 13

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 13 Lines and Angles Ex 13.

Question 1.
Solution:
(i) The given angle = 35°
Let x be its complementary, then
x + 35° = 90°
⇒ x = 90° – 35° = 55°
Complement angle = 55°
(ii) The given angle = 47°
Let x be its complement, then
x + 47° = 90 ⇒ x = 90° – 47° = 43°
Complement angle = 43°
(iii) The given angles = 60°
Let x be its complement angle
x + 60° = 90° ⇒ x = 90° – 60° = 30°
Complement angle = 30°
(iv) The given angle = 73°
Let x be its complement angle
x + 73° = 90°
⇒ x = 90° – 73° = 17°
Complement angle = 17°

Question 2.
Solution:
(i) Given angle = 80°
Let x be its supplement angle, then
x + 80° = 180°
⇒ x = 180° – 80° = 100°
Supplement angle = 100°
(ii) Given angle = 54°
Let x be its supplement angle, then
x + 54° = 180°
⇒ x = 180° – 54° = 126°
Supplement angle = 126°
(iii) Given angle = 105°
let x be its supplement angle, then
x + 105° = 180°
⇒ x = 180° – 105° = 75°
Supplement angle = 75°
(iv) Given angle = 123°
Let x be its supplement angle, then
x + 123° = 180°
⇒ x = 180° – 123° = 57°
⇒ Supplement angle = 57°

Question 3.
Solution:
Let smaller angle =x
Then larger angle = x + 36°
But x + x + 36° = 180° (Angles are supplementary)
2x = 180° – 36°= 144°
x = 72°
Smaller angle = 72°
and larger angle = 72° + 36° = 108°

Question 4.
Solution:
Let angle be = x
Then other supplement angle = 180°- x
x = 180° – x
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = 90°
Hence angles are 90°, and 90°

Question 5.
Solution:
Sum of two supplementary angles is 180°
If one is acute, then second will be obtuse or both angles will be equal
Hence both angles can not be acute or obtuse
Both can be right angles only

Question 6.
Solution:
In the given figure,
AOB is a straight line and the ray OC stands on it.
∠AOC = 64° and ∠BOC = x°

∠AOC + ∠BOC = 180° (Linear pair)
⇒ 64° + x = 180°
⇒ x = 180° – 64° = 116°
Hence x = 116°

Question 7.
Solution:
AOB is a straight line and ray OC stands on it ∠AOC = (2x – 10)°, ∠BOC = (3x + 20)°

∠AOC + ∠BOC = 180° (Linear pair)
⇒ 2x – 10° + 3x + 20° = 180°
⇒ 5x + 10° = 180°
⇒ 5x = 170°
⇒ x = 34°
∠AOC = (2x – 10)° = 2 x 34° – 10 = 68° – 10° = 58°
∠BOC = (3x + 20)° = 3 x 34° + 20° – 102° + 20° = 122°

Question 8.
Solution:
AOB is a straight line and rays OC and OD stands on it ∠AOC = 65°, ∠BOD = 70° and ∠COD = x

But ∠AOC + ∠COD + ∠BOD = 180° (Angles on one side of the straight line)
⇒ 65° + x + 70° = 180°
⇒ 135° + x = 180°
⇒ x = 180° – 135°
⇒ x = 45°
Hence x = 45°

Question 9.
Solution:
Two straight lines AB and CD intersect each other at O.

∠AOC = 42°
AB and CD intersect each other at O.
∠AOC = ∠BOD (Vertically opposite angles)
and ∠AOD = ∠BOC
But ∠AOC = 42°
∠BOD = 42°
AOB is a straight line and OC stands on it
∠AOC + ∠BOC = 180°
⇒ 42° = ∠BOC = 180°
⇒ ∠BOC = 180° – 42° = 138°
But ∠AOD = ∠BOC (vertically opposite angles)
∠AOD = 138°
Hence ∠AOD = 138°, ∠BOD = 42° and ∠COB =138°

Question 10.
Solution:
Two straight lines PQ and RS intersect at O.
∠POS = 114°
Straight lines,

PQ and RS intersect each other at O
∠POS = ∠QOR (Vertically opposite angles)
But ∠POS = 114°
∠QOR = 114° or ∠ROQ = 114°
But ∠POS + ∠POR = 180° (Linear pair)
⇒ 114° + ∠POR = 180°
⇒ ∠POR = 180° – 114° = 66°
But ∠QOS = ∠POR (vertically opposite angles)
∠QOS = 66°
Hence ∠POR = 66°, ∠ROQ =114° and ∠QOS = 66°

Question 11.
Solution:
In the given figure, rays OA, OB, OC and OD meet at O and ZAOB – 56°,
∠BOC = 100°, ∠COD = x and ∠DOA = 74°

But ∠AOB + ∠BOC + ∠COD + ∠DOA = 360° (Angles at a point)
56° + 100° + x° + 74° = 360°
⇒ 230° + x° = 360°
⇒ x° = 360° – 230° = 130°
⇒ x = 130°

Hope given RS Aggarwal Solutions Class 7 Chapter 13 Lines and Angles Ex 13 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 10 Percentage Ex 10A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10B
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10C
• RS Aggarwal Solutions Class 7 Chapter 10 Percentage CCE Test Paper

Question 1.
Solution:

Question 2.
Solution:

Question 3.
Solution:

Question 4.
Solution:

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:

Question 9.
Solution:
Let x is the required number

Question 10.
Solution:
Let x be the required number

Question 11.
Solution:
10 % of Rs. 90 = 90 x \(\frac { 10 }{ 100 }\) = Rs. 9
Required amount = Rs. 90 + Rs. 9 = Rs. 99

Question 12.
Solution:
20 % of Rs. 60 = \(\frac { 60 x 20 }{ 100 }\) = 12
Required amount = Rs. 60 – 12 = Rs. 48

Question 13.
Solution:
3 % of x = 9

Question 14.
Solution:
12.5 % of x = 6
⇒ x x \(\frac { 12.5 }{ 100 }\) = 6

Question 15.
Solution:
Let x % of 84 = 14

Question 16.
Solution:

Hope given RS Aggarwal Solutions Class 7 Chapter 10 Percentage Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method CCE Test Paper

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Question 1.
Solution:
Cost of 8 toys = ₹ 192
Cost of 1 toys = ₹ \(\frac { 192 }{ 8 }\) = ₹ 24
Cost of 14 toys = 24 x 14 = ₹ 336

Question 2.
Solution:
Distance covered with 15L of petrol = 270 km
Distance covered with 1L of petrol 270 = \(\frac { 270 }{ 15 }\) km
Distance covered with 8L of petrol 270 = \(\frac { 270 }{ 15 }\) x 8 km = 144 km

Question 3.
Solution:
Cost of 15 envelopes = ₹ 11.25
Cost of 1 envelope = ₹ \(\frac { 11.25 }{ 15 }\)
Cost of 20 envelopes = \(\frac { 11.25 }{ 15 }\) x 20 = ₹ 15

Question 4.
Solution:
24 cows can graze a field in = 20 days
1 cow can graze a field in = 20 x 24 days
15 cows can graze a field in = \(\frac { 20 x 24 }{ 15 }\)
= 32 days

Question 5.
Solution:
Time taken to finish the work by 8 men = 15 h
Time taken to finish the work by 1 man = 8 x 15 h
Time taken to finish the work by 20 men = \(\frac { 8 x 15 }{ 20 }\) h = 6 h
[More men, less time taken]

Question 6.
Solution:
Time taken to fill \(\frac { 4 }{ 5 }\) of the cistern = 1 min
Time taken to fill 1 cistern = \(\frac { 1 }{ \frac { 4 }{ 5 } }\) = \(\frac { 5 }{ 4 }\)
= 1.25 min = 1 min 15 sec
Hence, it will take 1 min 15 sec to fill the empty cistern.

Question 7.
Solution:
Time taken to cover the distance at a speed of 45 km/h = 3 h 20 min
Time taken to cover the distance at a speed of 1 km/h = 45 x 3.33 h
[Less speed, more time taken] (20 min = 0.33 hour)
Time taken to cover the distance at a speed of 50 km/h
= \(\frac { 45 x 3.33 }{ 50 }\) h
= 3h [More speed, less time taken]

Question 8.
Solution:
Number of days with enough food for 120 men = 30
Number of days with enough food for 1 man = 30 x 120 [Less men, more days]
Number of days with enough food for 100 men = \(\frac { 30 x 120 }{ 100 }\)
= 36 [More men, less days]

Mark (✓) against the correct answer in each of the following :
Question 9.
Solution:
(c) 644 km
1 cm represents km 80.5 cm represents = 8 x 80.5 = 644 km

Question 10.
Solution:
(a) 24 days
16 men can reap the field in 30 days.
1 man can reap the field in 30 x 16 days [Less men, more days]
20 men can reap the field in \(\frac { 30 x 16 }{ 20 }\)
= 24 days [More men, less days]

Question 11.
Solution:
(b) 49
Number of cows that eat as much as 15 buffaloes = 21
Number of cows that eat as much as 1 buffalo = \(\frac { 21 }{ 15 }\)
Number of cows that eat as much as 35 buffaloes = \(\frac { 21 }{ 15 }\) x 35 = 49

Question 12.
Solution:
Number of cows that graze the field in 12 days = 45
Number of cows that graze the field in 1 day = 45 x 12
Number of cows that graze the field in 9 days = \(\frac { 45 x 12 }{ 2 }\) = 60

Question 13.
Solution:
(b) ₹ 162
Cost of 72 eggs = ₹ 108
Cost of 1 egg = ₹ \(\frac { 108 }{ 72 }\)
Cost of 108 eggs = ₹ \(\frac { 108 x 108 }{ 72 }\)
= ₹ 162

Question 14.
Solution:
(i) 588 days
42 men can dig the trench in 14 days 1 men can dig the trench in = 42 x 14 = 588 days
(ii) ₹48
15 oranges cost ₹ 60
12 oranges will cost ₹ \(\frac { 60 }{ 15 }\) x 12 = ₹ 48
(iii) 10.8 kg
A rod of length 10m weighs 18 kg
A rod of length 6 m will weigh = \(\frac { 18 }{ 10 }\) x 6 = 10.8 kg
(iv) 3 h 12 min
12 workers finish the work in 4 h
15 workers will finish the work in \(\frac { 4 x 12 }{ 15 }\) = 3.2 h = 3h 12 min

Question 15.
Solution:
(i) False
10 pipes fill the tank in = 24 min.
1 pipe will fill the tank in = 24 x 10 min. [Less pipes, more time taken]
8 pipes will fill the tank in = \(\frac { 24 x 10 }{ 8 }\)
= 30 min. [More pipes, less time taken]
(ii) True
8 men finish the work in = 40 days
1 man finishes the work in = 8 x 40 days [Less men, more days taken]
10 men will finish the work in = \(\frac { 8 x 40 }{ 10 }\)
= 32 days [More men, less days taken]
(iii) True
A 6 m tall tree casts a shadow of length = 4 m.
Aim tall tree cast a shadow of length = \(\frac { 4 }{ 6 }\) m
A 75 m tall pole will cast a shadow of length = \(\frac { 4 }{ 6 }\) x 75 = 50 m
(iv) True
1 toy is made in = \(\frac { 2 }{ 3 }\) h. [Less toys, less time taken]
12 toys can be made in = \(\frac { 2 }{ 3 }\) x 12
= 8h [More toys, more time taken]

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method Ex 9C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Objective Questions.
Marks (✓) against the correct answer in each of the following :
Question 1.
Solution:
(c)
Weight of 4.5 m rod = 17.1 kg

Question 2.
Solution:
(d) None of these 0.8 cm represent the map = 8.8 km

Question 3.
Solution:
(c) In 20 minutes, Raghu covers = 5 km
in 1 minutes, he will cover = \(\frac { 5 }{ 20 }\) km
and in 50 minutes, he will cover

Question 4.
Solution:
(d)
No. of men in the beginning = 500
More men arrived = 300
No. of total men = 500 + 300 = 800
For 500 men, provision are for = 24 days
For 1 man, provision will be = 24 x 500 days (less men, more days)
and for 800 men, provision will be = \(\frac { 24 }{ 800 }\) x 500 days
(more men less days)
= 15 days

Question 5.
Solution:
(b) Total cistern = 1
Filled in 1 minute = \(\frac { 4 }{ 5 }\)
Unfilled = 1 – \(\frac { 4 }{ 5 }\) = \(\frac { 1 }{ 5 }\)
\(\frac { 4 }{ 5 }\) of cistern is filled in = 1 minutes = 60 seconds
1 full cistern can be filled in = \(\frac { 60 x 5 }{ 4 }\) = 75 seconds
More time = 75 – 60 = 15 seconds

Question 6.
Solution:
(a)
15 buffaloes can eat as much as = 21 cows
1 buffalo will eat as much as = \(\frac { 21 }{ 15 }\) cows
35 buffaloes will eat as much as
= \(\frac { 21 x 35 }{ 15 }\) cm = 49 cows

Question 7.
Solution:
(b) 4 m long shadow is of a tree of height = 6 m
1 m long shadow of flagpole will of height = \(\frac { 6 }{ 4 }\) m
50 m long shadow, the height of pole 6 will be = \(\frac { 6 }{ 4 }\) x 50 = 75 m

Question 8.
Solution:
(b) 8 men can finish the work in = 40 days
1 man will finish it in=40 x 8 days (less men, more days)
8 + 2 = 10 men will finish it in = \(\frac { 40 x 8 }{ 10 }\) days
(more men, less days)
= 32 days

Question 9.
Solution:
(b)
16 men can reap a field in = 30 days
1 man will reap the field in = 30 x 16 days
and 20 men will reap the field in = \(\frac { 30 x 16 }{ 20 }\) = 24 days

Question 10.
Solution:
(c) 10 pipe can fill tank in = 24 minutes
1 pipe will fill it in = 24 x 10 minutes (less pipe, more time)
and 10 – 2 = 8 pipes will fill the tank in
= \(\frac { 24 x 10 }{ 8 }\) = 30 minutes

Question 11.
Solution:
(d) 6 dozen or 6 x 12 = 72 eggs
Cost of 72 eggs is = Rs. 108
Cost of 1 egg will be = Rs. \(\frac { 108 }{ 72 }\)
and cost of 132 eggs will be 108
= Rs. \(\frac { 108 }{ 72 }\) x 132 = Rs. 198

Question 12.
Solution:
(b) 12 workers take to complete the work = 4 hrs.
1 worker will take = 4 x 12 hrs. (less worker, more time)
15 workers will take = \(\frac { 4 x 12 }{ 15 }\) hrs. (more workers, less time)
= \(\frac { 16 }{ 5 }\) hr. = 3 hrs. 12 min

Question 13.
Solution:
(a) 27 days – 3 days = 24 days
Men = 500 + 300 = 800
For 500 men, provision is sufficient = 24 days
For 1 man, provision will be = 24 x 500 (less man, more days)
and for 500 + 300 = 800 men provision
will be sufficient = \(\frac { 24 x 500 }{ 800 }\) = 15 days
(more men, less days)

Question 14.
Solution:
(c) No. of rounds of rope = 140
Radius of base of cylinder = 14 cm
Radius of second cylinder of cylinder = 20 cm
If radius is 14 cm, then rounds of rope are = 140
If radius is 1 cm, then round = 140 x 14 (less radius more rounds)
and if radius is 20 cm, then rounds will
be = \(\frac { 140 x 14 }{ 20 }\) = 98 (more radius less rounds)

Question 15.
Solution:
(d) A worker makes toy in \(\frac { 2 }{ 3 }\) hr= 1
He will make toys in 1 hr = 1 x \(\frac { 3 }{ 2 }\)
and will make toys in \(\frac { 22 }{ 3 }\) hrs. = 1 x \(\frac { 3 }{ 2 }\) x \(\frac { 22 }{ 3 }\)
= 11 (more time more toys)

Question 16.
Solution:
(d) A wall is constructed in 8 days by = 10 men
It will be constructed in 1 day by = 10 x 8 men (less time, more men)
10 x 8

More men required = 160 – 10 = 150

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 9 Unitary Method Ex 9B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9A
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9C
• RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method CCE Test Paper

Question 1.
Solution:
48 men can dig a trench in = 14 days
1 man will dig the trench in = 14 x 48 days (less men more days)
28 men will dig the trench m = \(\frac { 14 x 48 }{ 28 }\) (more men less days)
= 24 days

Question 2.
Solution:
In 30 days, a field is reaped by = 16 men
In 1 day, it will be reaped by = 16 x 30 (less days, more men)
and in 24 days, it will be reaped by = \(\frac { 16 x 30 }{ 24 }\) men (more days, less men)
= \(\frac { 480 }{ 24 }\)
= 20 men

Question 3.
Solution:
In 13 days, a field is grazed by = 45 cows.
In 1 day, the field will be grazed by = 45 x 13 cows (less days, more cows)
and in 9 days the field will be grazed by = \(\frac { 45 x 13 }{ 9 }\) cows (more days, less cows)
= 5 x 13 = 65 cows

Question 4.
Solution:
16 horses can consume corn in = 25 days
1 horse will consume it in = 25 x 16 days (Less horse, more days)
and 40 horses will consume it in = \(\frac { 25 x 16 }{ 40 }\) days (more horses, less days)
= 10 days

Question 5.
Solution:
By reading 18 pages a day, a book is finished in = 25 days
By reading 1 page a day, it will be finished = 25 x 18 days (Less page, more days)
and by reading 15 pages a day, it will be finished in = \(\frac { 25 x 18 }{ 15 }\) days (more pages, less days)
= 5 x 6 = 30 days

Question 6.
Solution:
Reeta types a document by typing 40 words a minute in = 24 minutes
She will type it by typing 1 word a minute in = 24 x 40 minutes (Less speed, more time)
Her friend will type it by typing 48 words 24 x 40 a minute in = \(\frac { 24 x 40 }{ 48 }\) minutes
(more speed, less time)
= 20 minutes

Question 7.
Solution:
With a speed of 45 km/h, a bus covers a distance in = 3 hours 20 minutes
= 3\(\frac { 1 }{ 3 }\) = \(\frac { 10 }{ 3 }\) hours
With a speed of 1 km/h it will cover the distance m = \(\frac { 10 x 45 }{ 3 }\) h
(Less speed, more time)
and with a speed of 36 km/h, it will cover the distance in
= \(\frac { 10 x 45 }{ 3 x 36 }\) hr (more speed, less time)
= \(\frac { 25 }{ 6 }\) h
= 4\(\frac { 1 }{ 6 }\) h
= 4 hr 10 minutes

Question 8.
Solution:
To make 240 tonnes of steel, material is sufficient in = 1 month or 30 days
To make 1 tonne of steel, it will be sufficient in = 30 x 240 days (Less steel, more days)
To make 240 + 60 = 300 tonnes of steel it will be sufficient in = \(\frac { 30 x 240 }{ 300 }\) days
= 24 days (more steel, less days)

Question 9.
Solution:
In the beginning, number of men = 210
After 12 days, more men employed = 70
Total men = 210 + 70 = 280
Total period = 60 days.
After 12 days, remaining period = 60 – 12 = 48 days
Now 210 men can build the house in = 48 days
and 1 man can build the house in = 48 x 210 days (less men, more days) .
280 men can build the house in = \(\frac { 48 x 210 }{ 280 }\) days
(more men, less days)
= 36 days

Question 10.
Solution:
In 25 days, the food is sufficient for = 630 men
In 1 day, the food will be sufficient for = 630 x 25 men (less days, more men)
and in 30 days, the food will be sufficient for = \(\frac { 630 x 25 }{ 30 }\) hr
(more days less men)
= 525 men
Number of men to be transfered = 630 – 525 = 105 men

Question 11.
Solution:
Number of men in the beginning = 120
Number of men died = 30
Remaining = 120 – 30 = 90 men
Total period = 200 days
No. of days passed = 5
Remaining period = 200 – 5 = 195
Now, The food lasts for 120 men for = 195 days
The food will last for 1 man for = 195 x 120 days (Less men, more days)
The food will last for 90 men for = \(\frac { 195 x 120 }{ 90 }\)
(more men less days)
= 65 x 4 = 260 days

Question 12.
Solution:
Period in the beginning = 28 days
No. of days passed = 4 days.
Remaining period = 28 – 4 = 24 days
The food is sufficient for 24 days for = 1200 soldiers
The food will be sufficient for 1 day for = 1200 x 24 soldiers (Less days, more men)
and the food will be sufficient for 32 days = \(\frac { 1200 x 24 }{ 32 }\)
= 900 soldiers (more days, less men)
No. of soldiers who left the fort = 1200 – 900 = 300 soldiers

Hope given RS Aggarwal Solutions Class 7 Chapter 9 Unitary Method Ex 9B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.