Category: CBSE Class 10

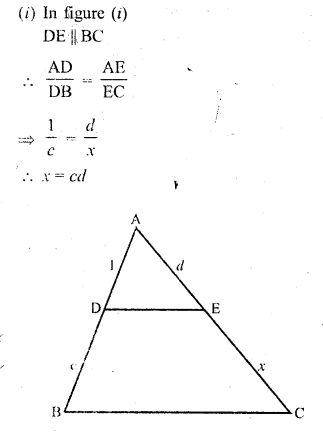
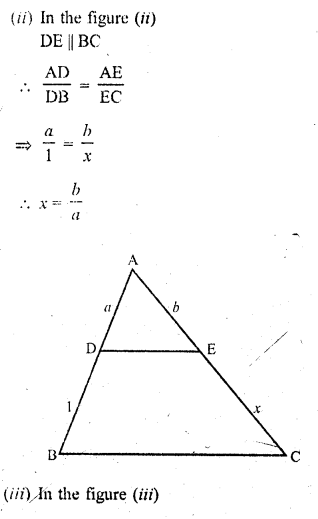
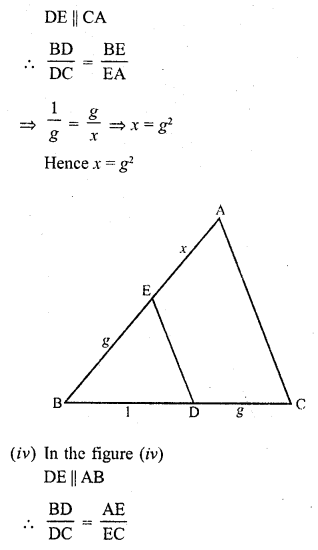
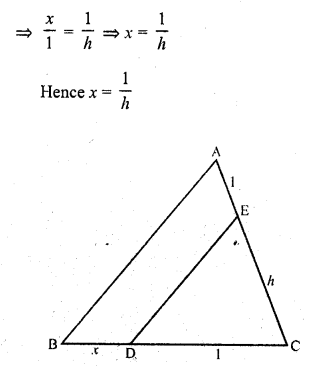
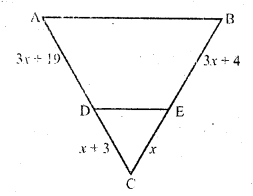
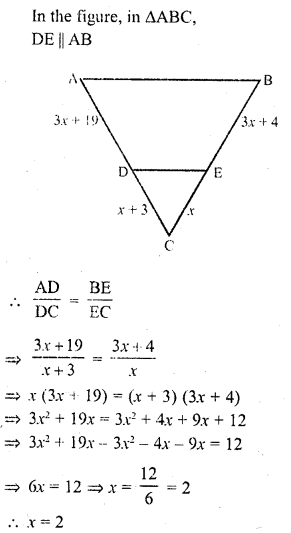
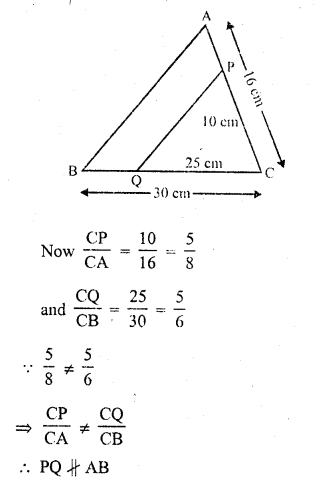
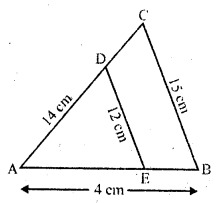
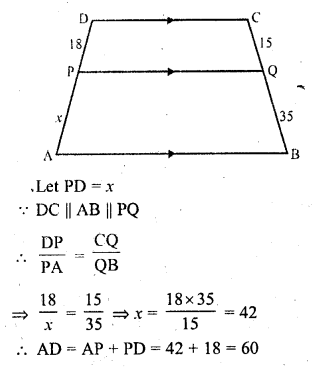
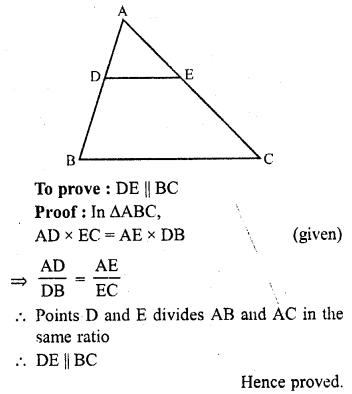
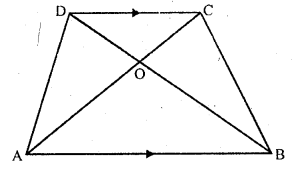
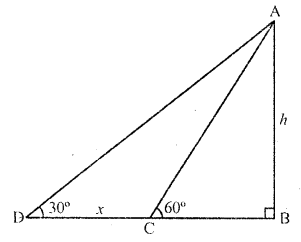
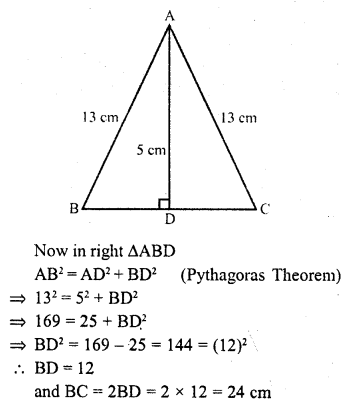
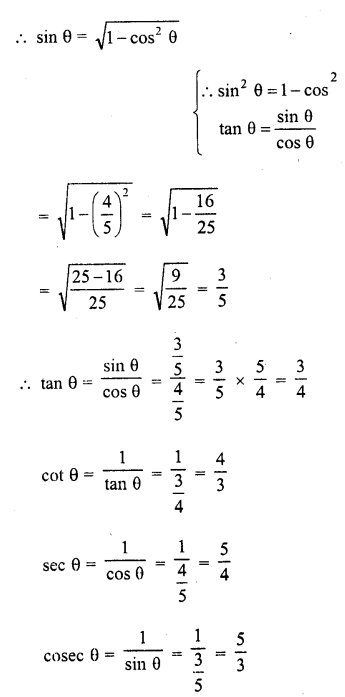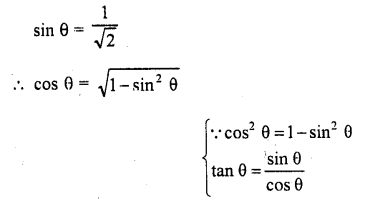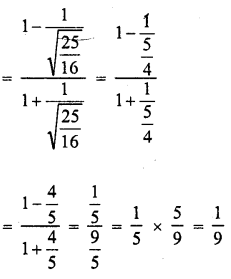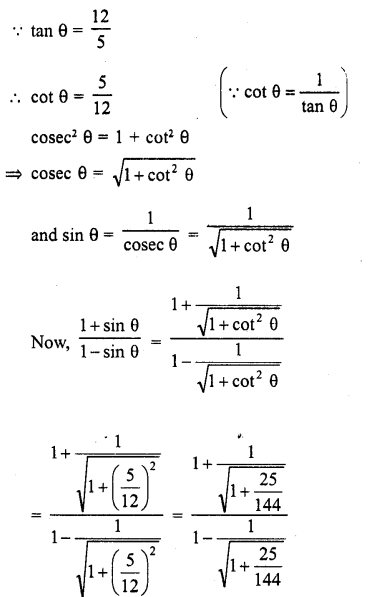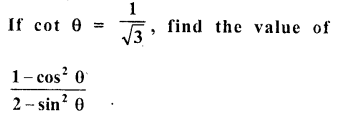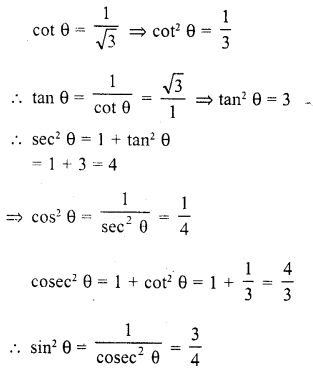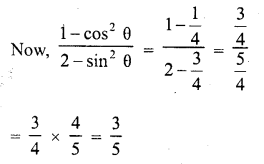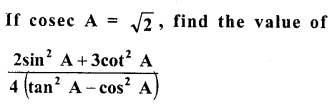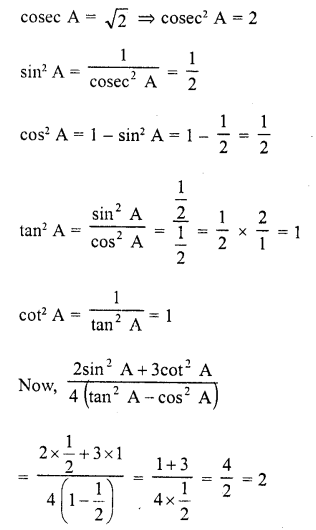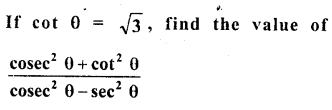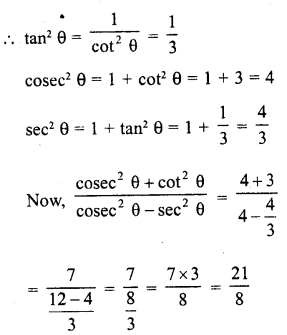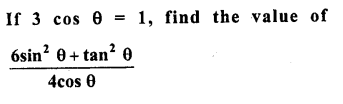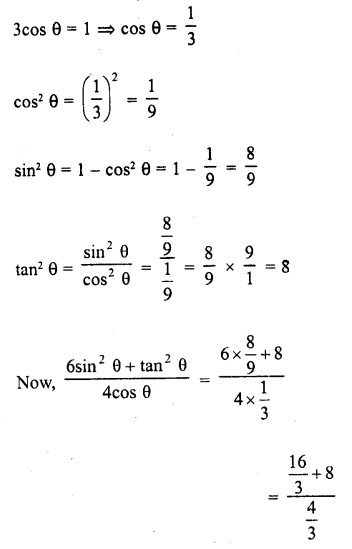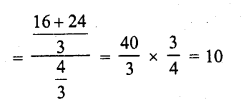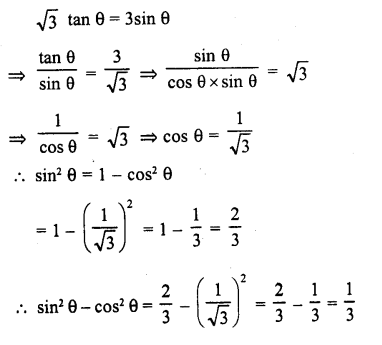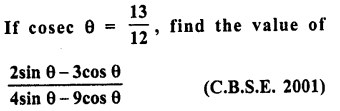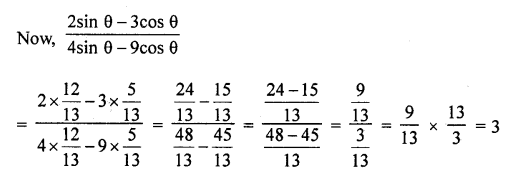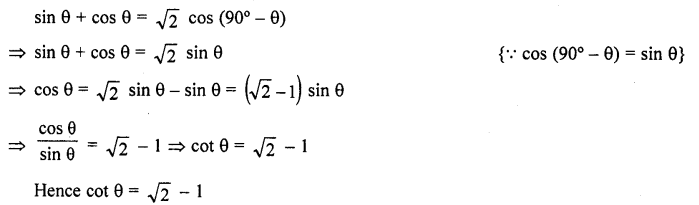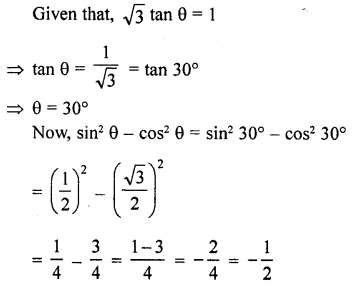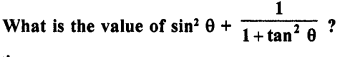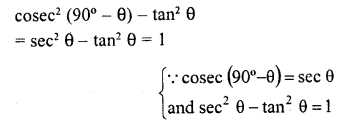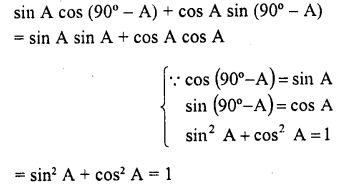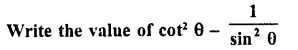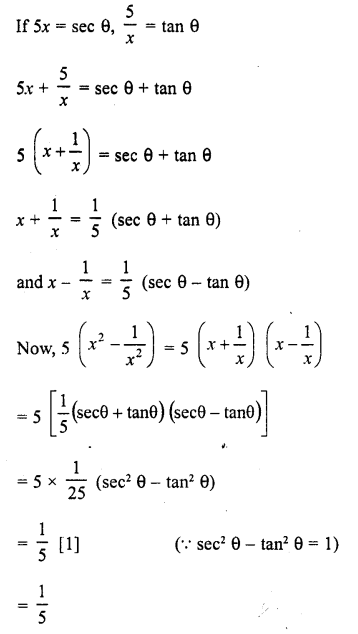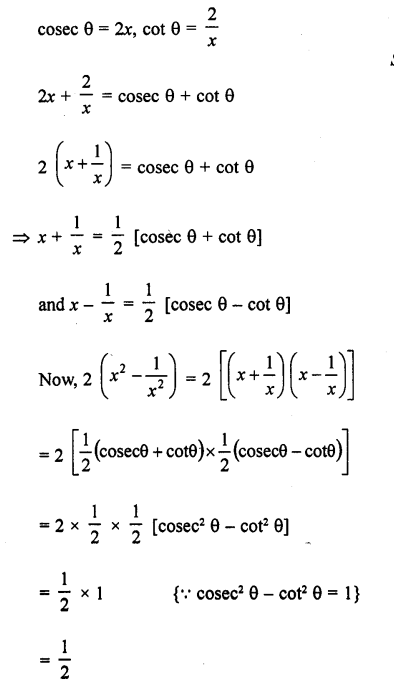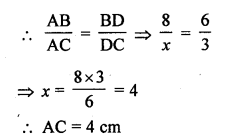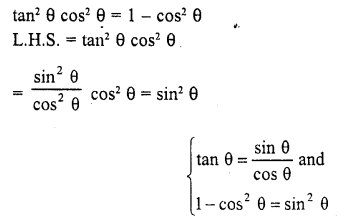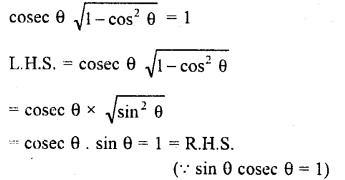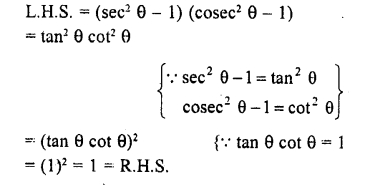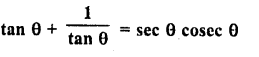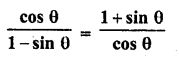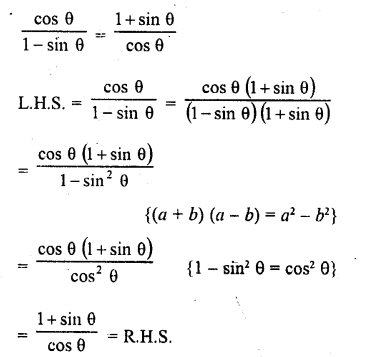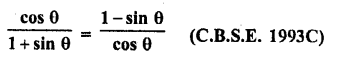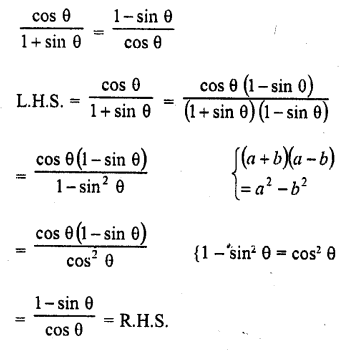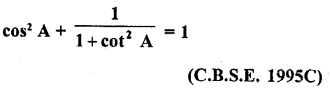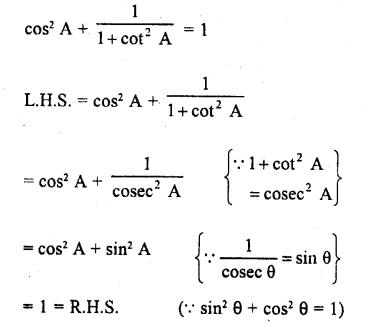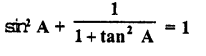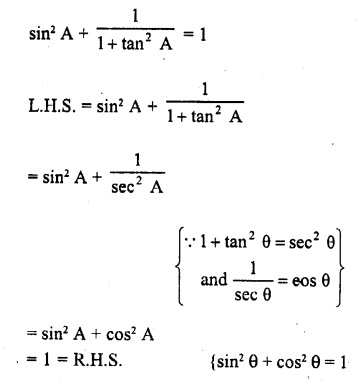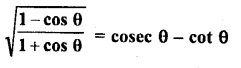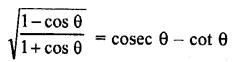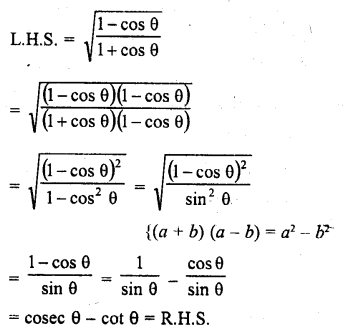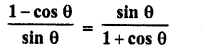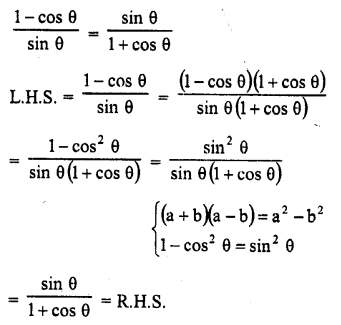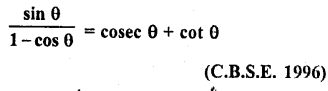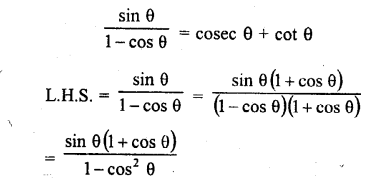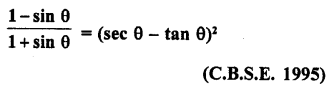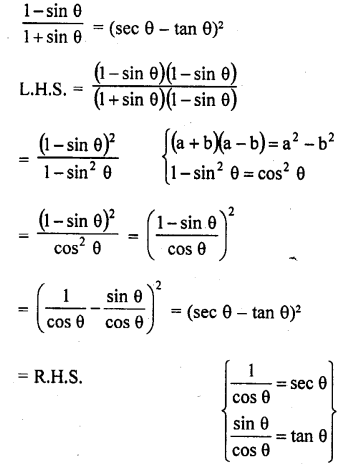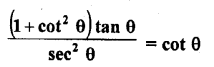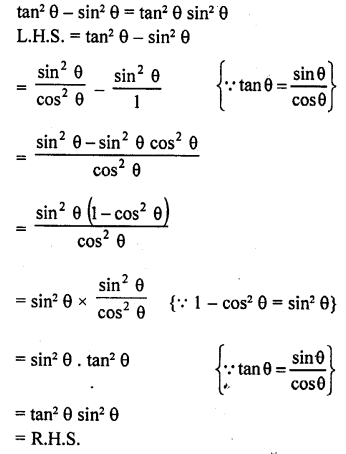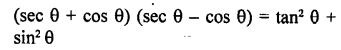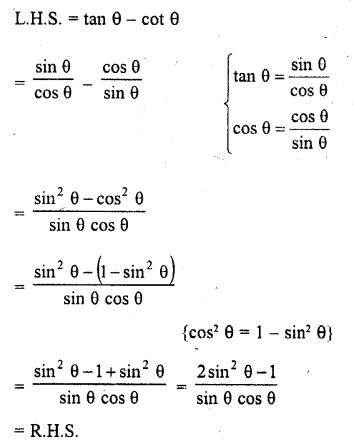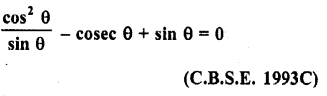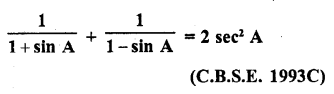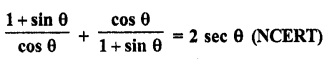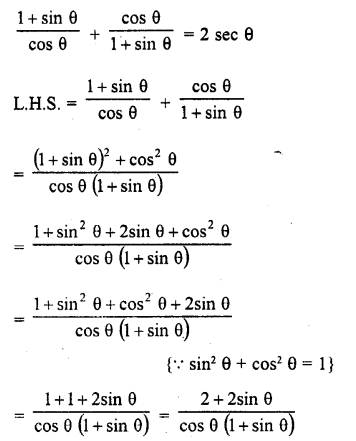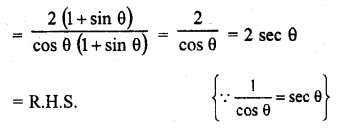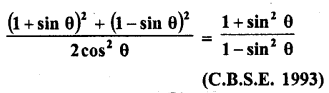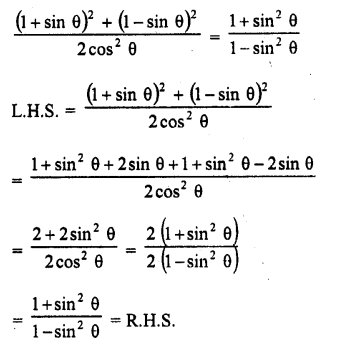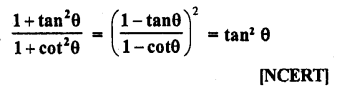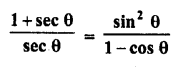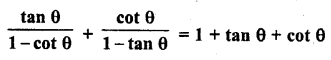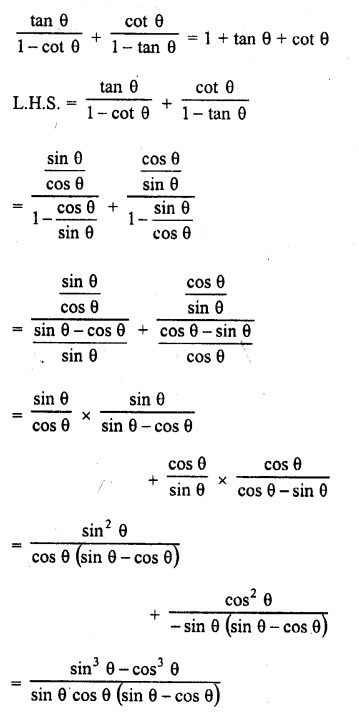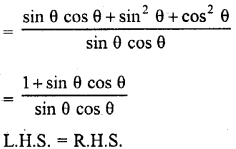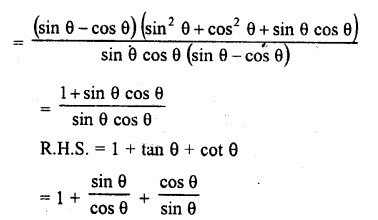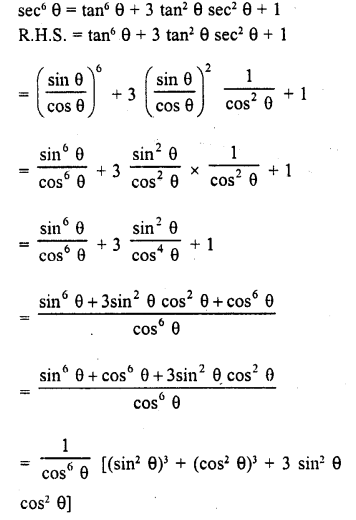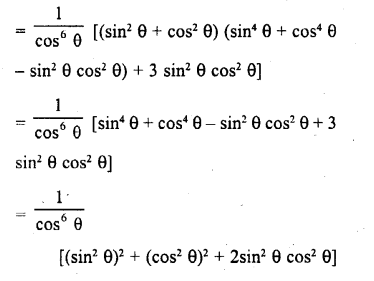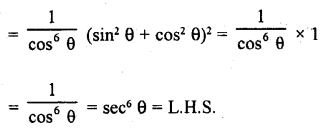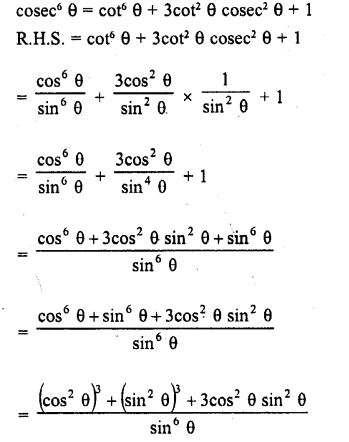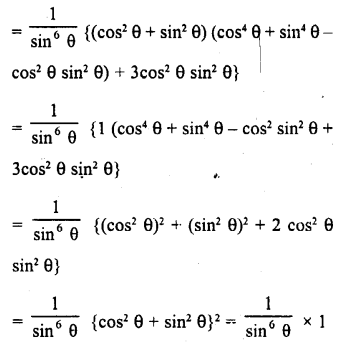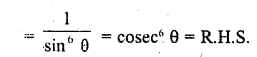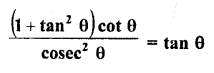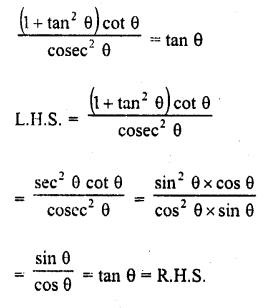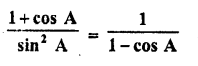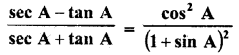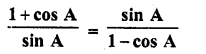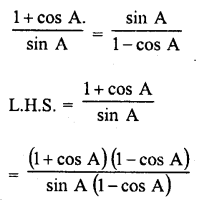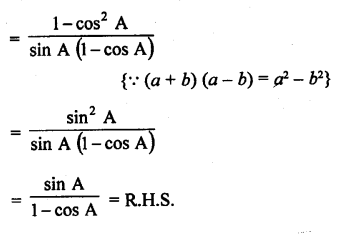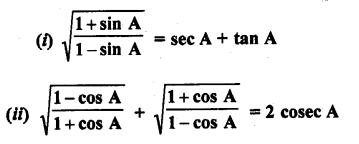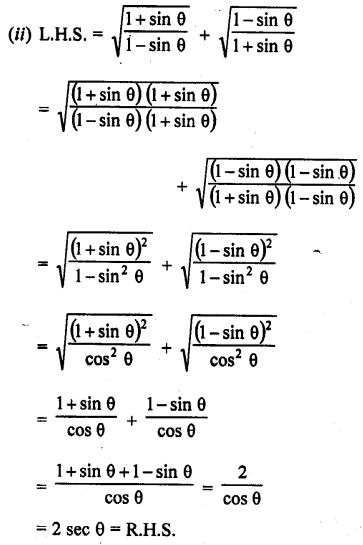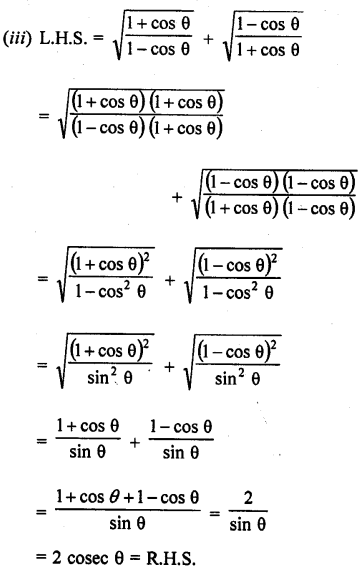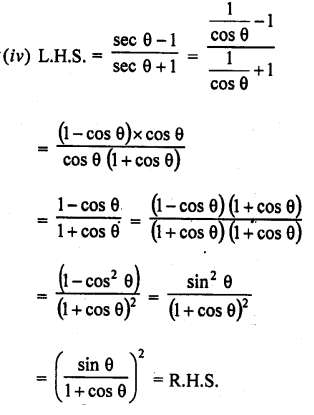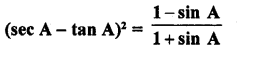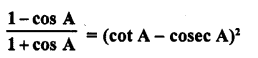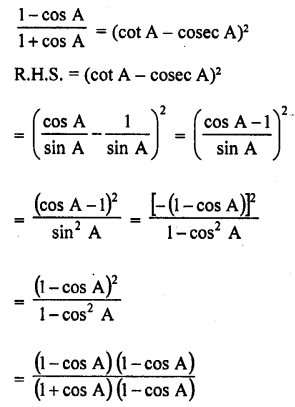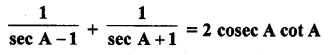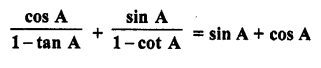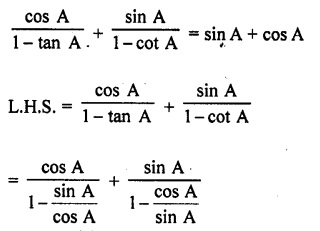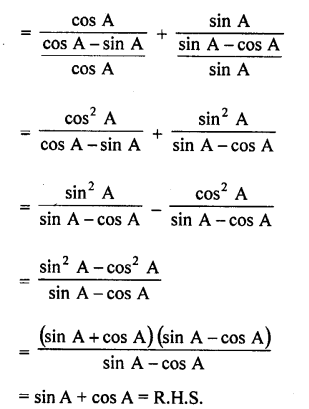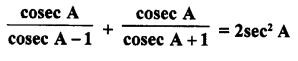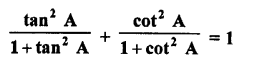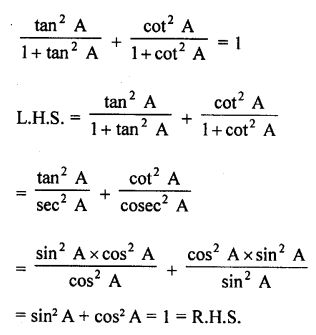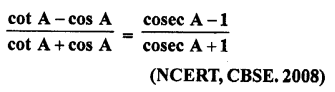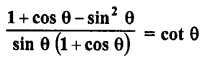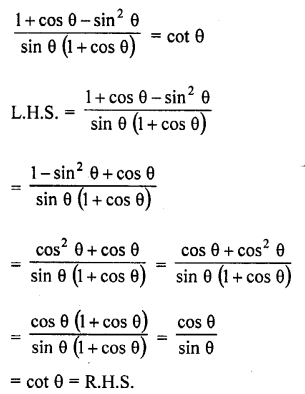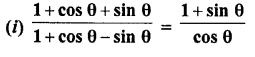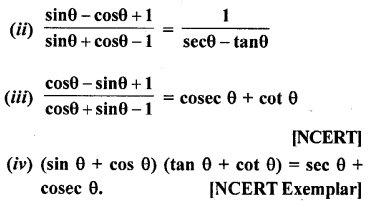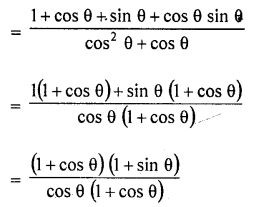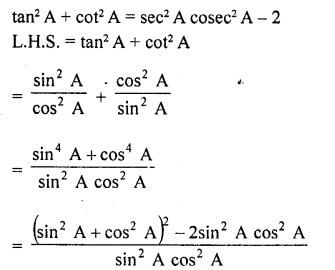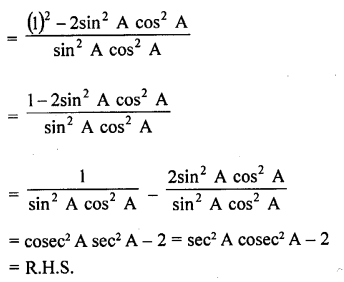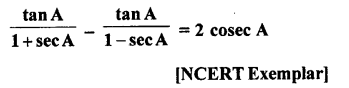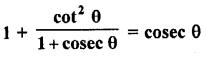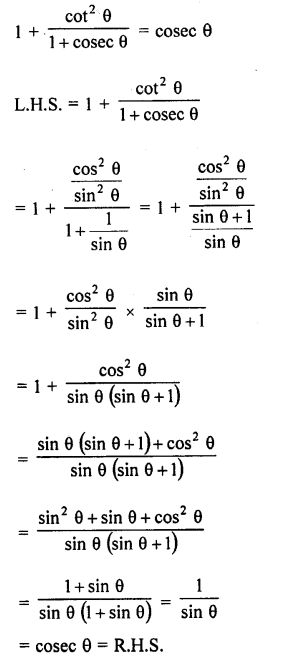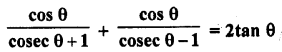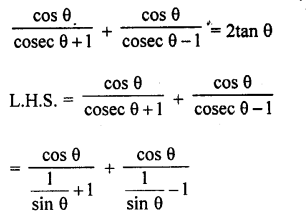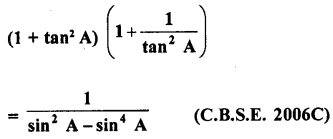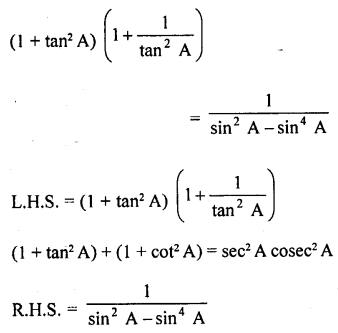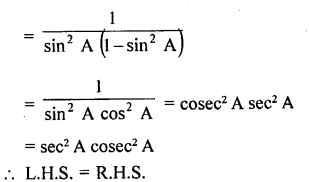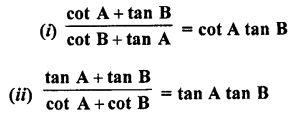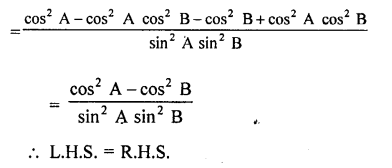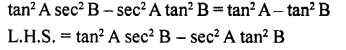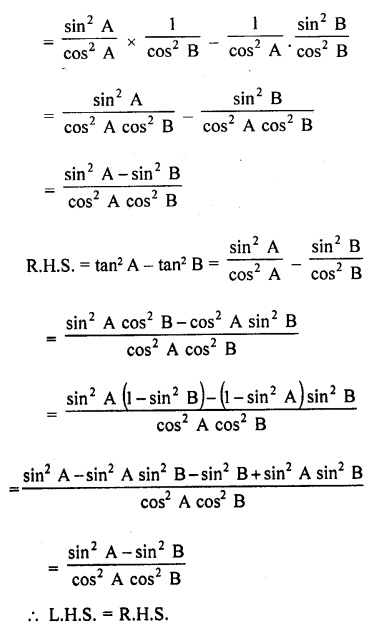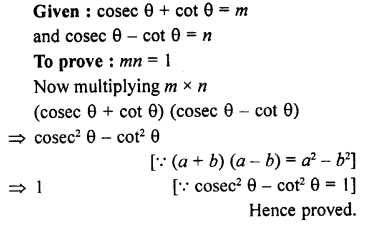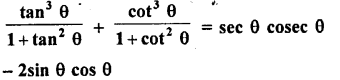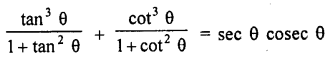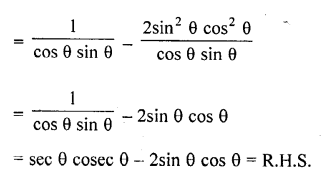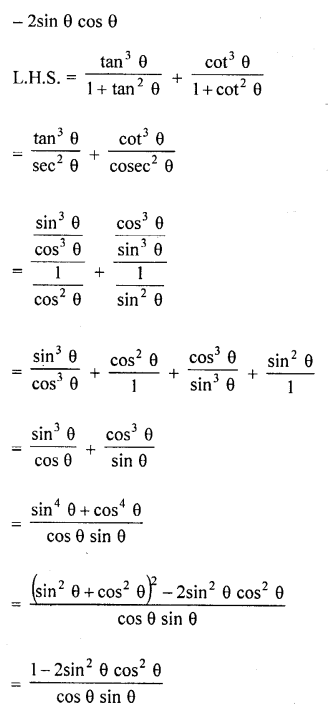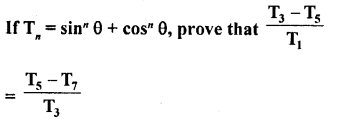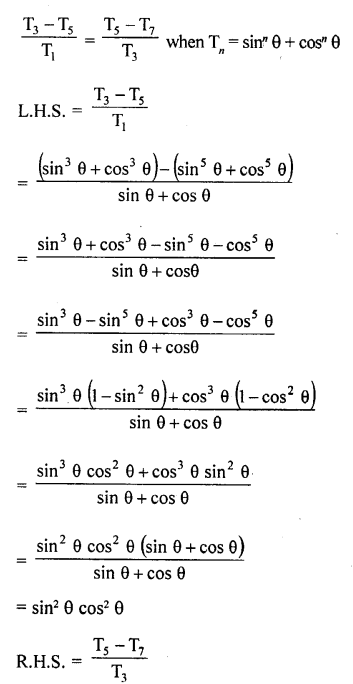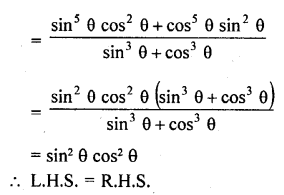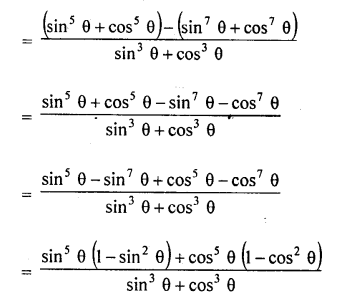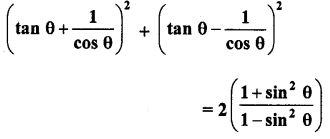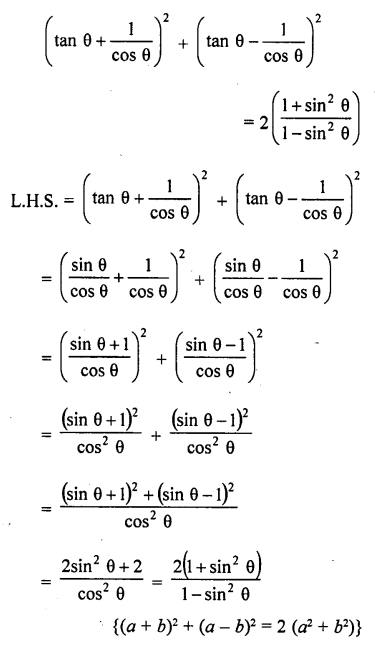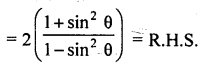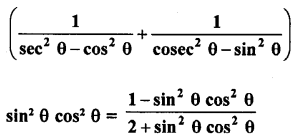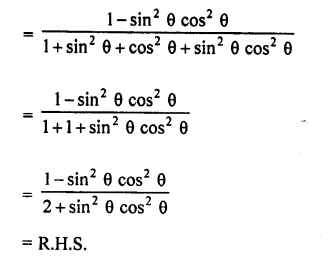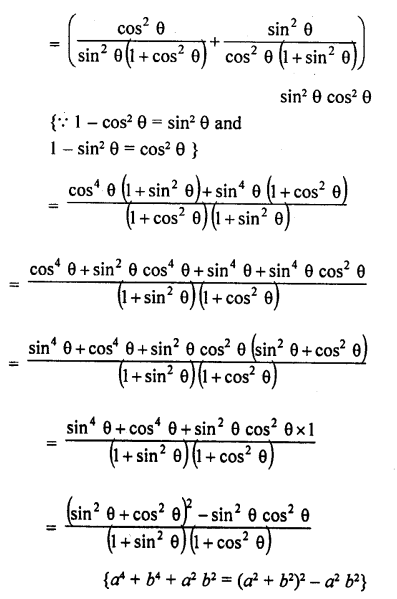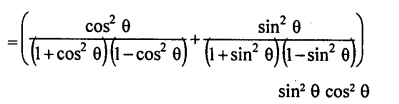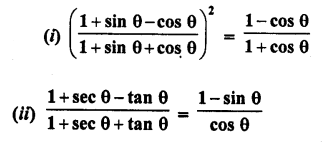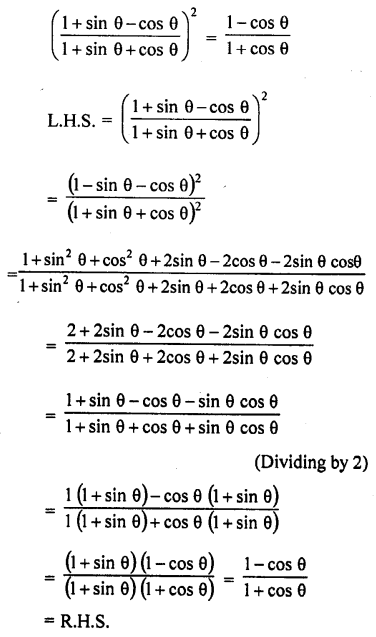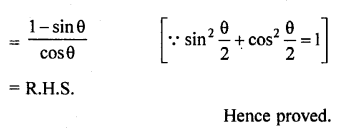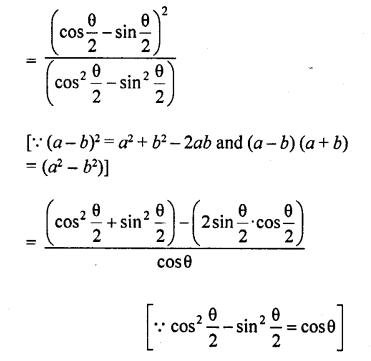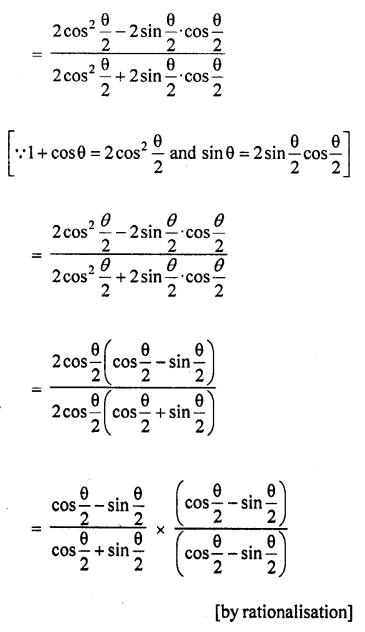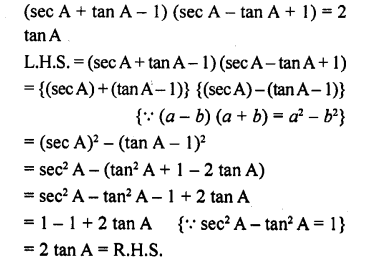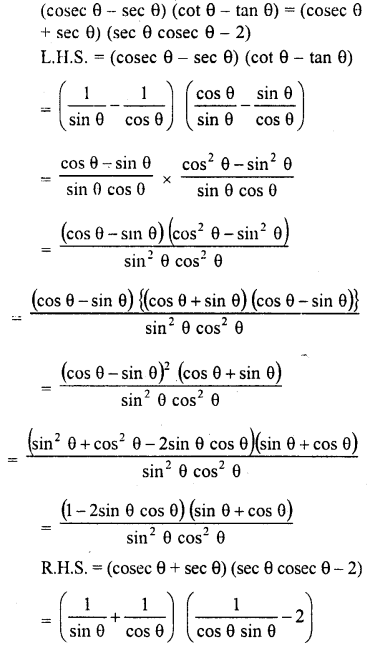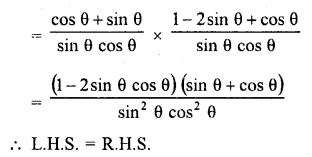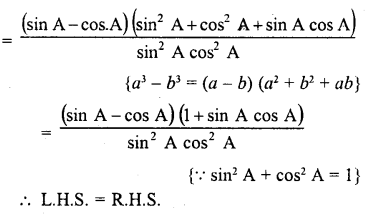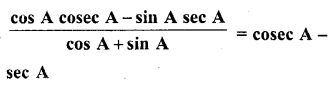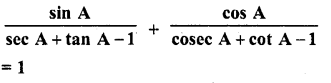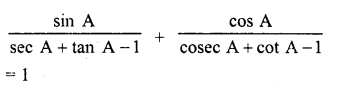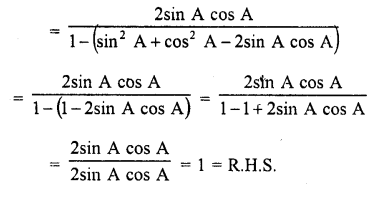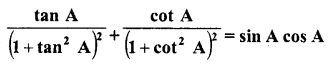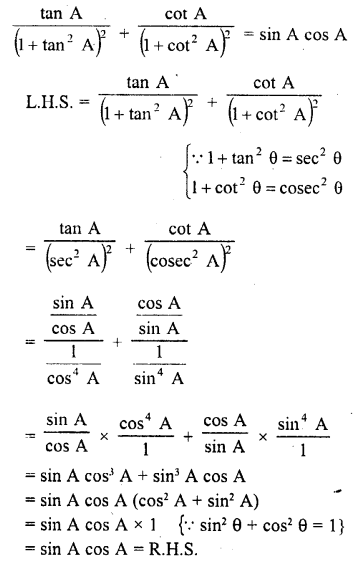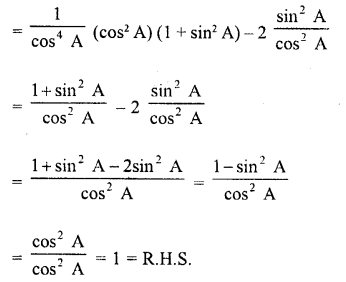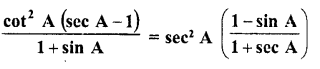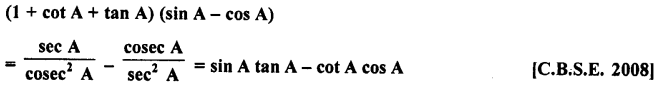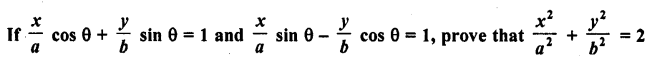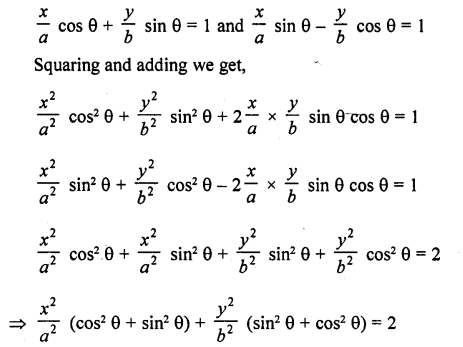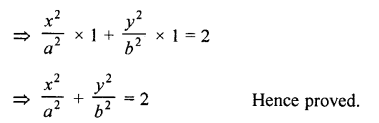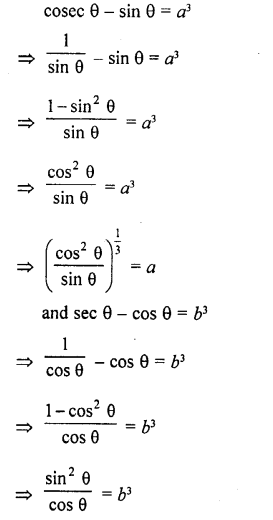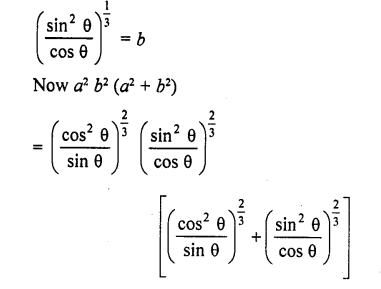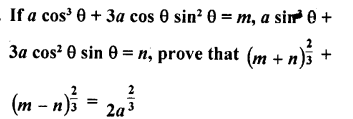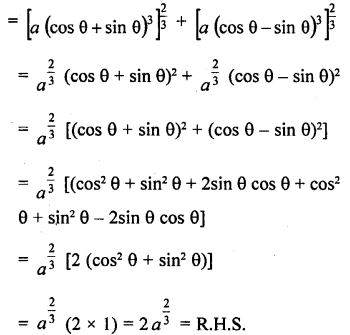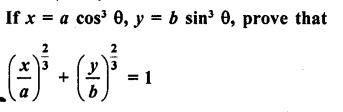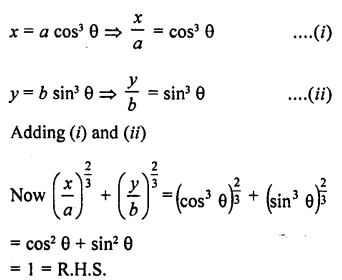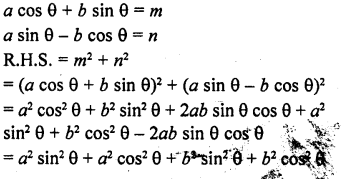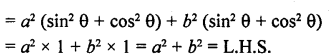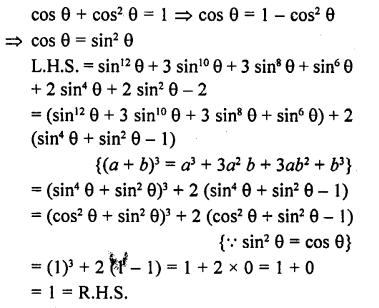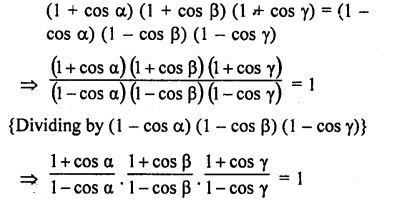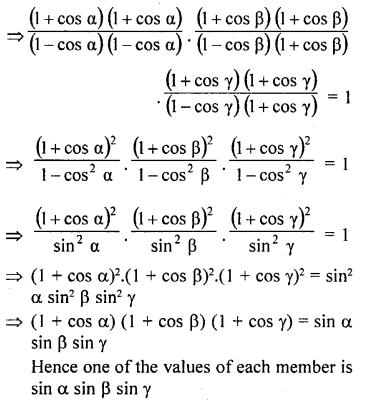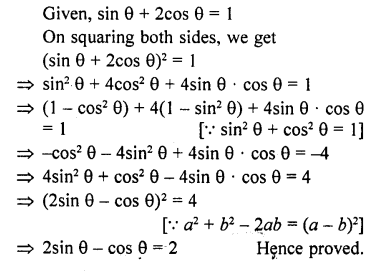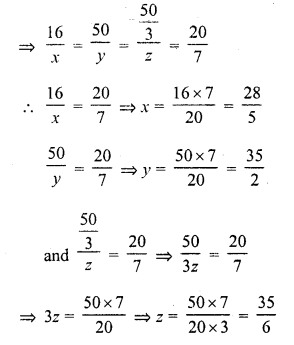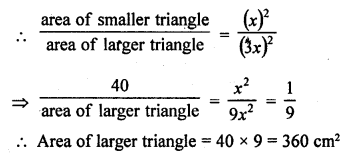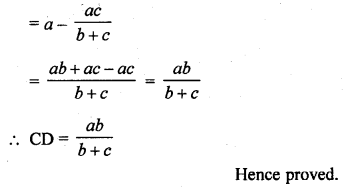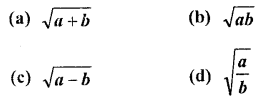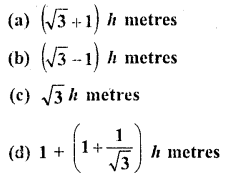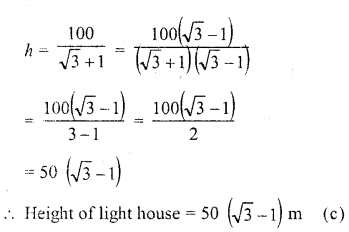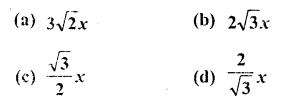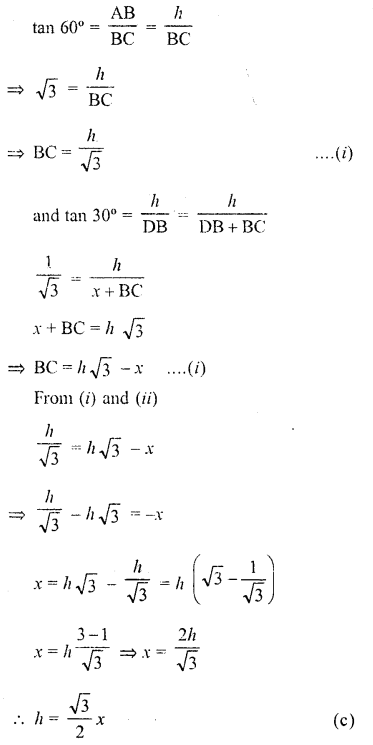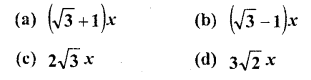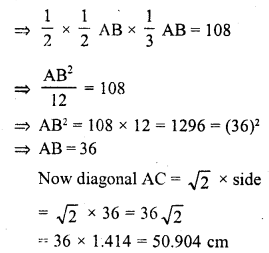RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios VSAQS
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios MCQS

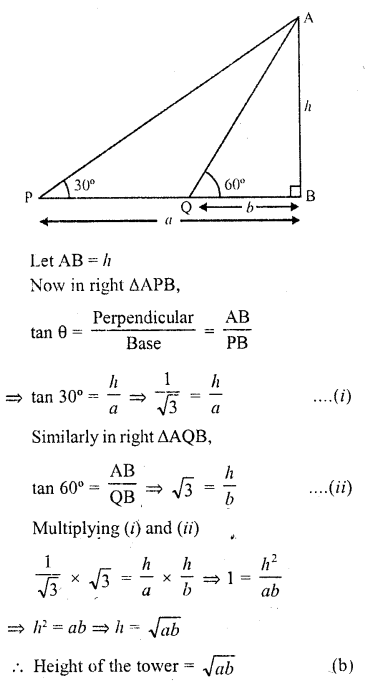
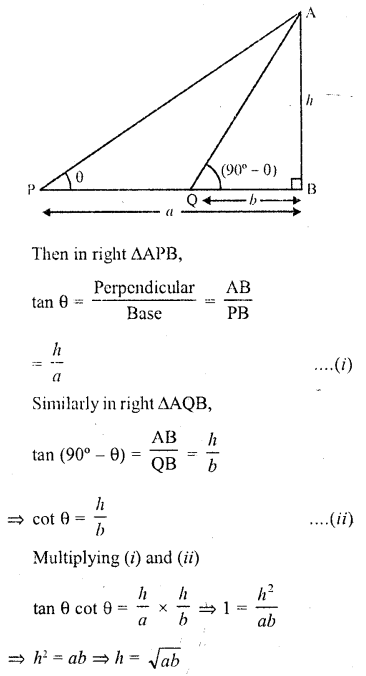
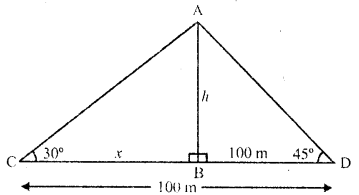
Question 1.
Evaluate the following :

Solution:

Question 2.
Evaluate the following :

Solution:

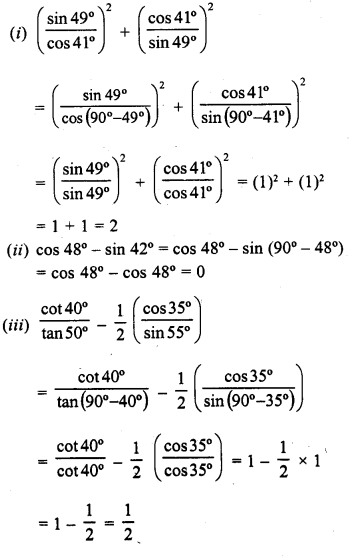
Question 3.
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
(i) sin 59° + cos 56°
(ii) tan 65° + cot 49“
(iii) sec 76° + cosec 52°
(iv) cos 78° + sec 78°
(v) cosec 54° + sin 72°
(vi) cot 85″ + cos 75°
(vii) sin 67° + cos 75°
Solution:
(i) sin 59° + cos 56°
= sin (90° – 31°) + cos (90° – 34°)
= cos 31° +sin 34°
(ii) tan 65° + cot 49°
= tan (90° – 25°) + cot (90° – 41°)
= cot 25° + tan 41°
(iii) sec 76° + cosec 52°
= sec (90° – 14°) + cosec (90 0 – 38°)
= cosec 14° + sec 38°
(iv) cos 78° + sec 78°
= cos (90° – 12°) + sec (90°- 12°)
= sin 12° + cosec 12°
(v) cosec 54° + sin 72°
= cosec (90° – 36°) + sin (90°-18°)
= sec 36° + cos 18°
(vi) cot 85° + cos 75°
= cot (90° – 5°) + cos (90° – 15°)
= tan 5° + sin 15°
(vii) sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°

Question 4.
Express cos 75° + cot 75° in terms of angles between 0° and 30°.
Solution:
cos 75° + cot 75° = cos (90° – 15°) + cot (90°-15°)
= sin 15° + tan 15°

Question 5.
If sin 3A = cos (A – 26°), where 3A is an acute angle, And the value of A.
Solution:
sin 3A = cos (A – 26°)
⇒ cos (90° – 3A) = cos (A – 26°)
Comparing,
90° – 3A = A – 26°
⇒ 90° + 26° = A + 3A ⇒ 4A = 116°

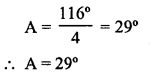
Question 6.
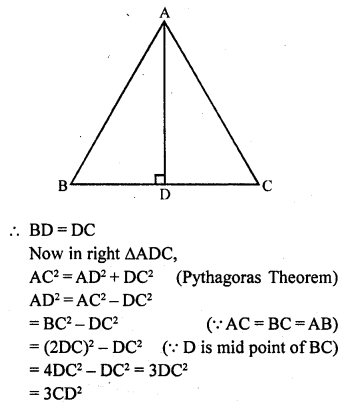
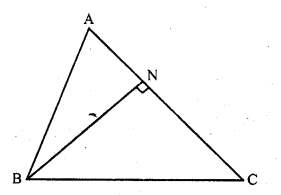
If A, B, C are the interior angles of a triangle ABC, prove

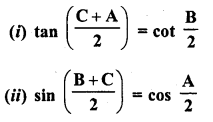
Solution:

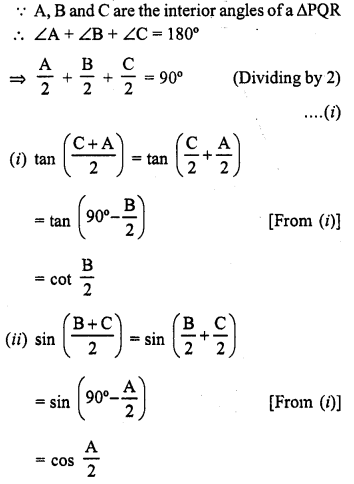
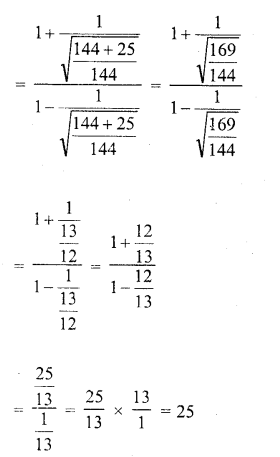
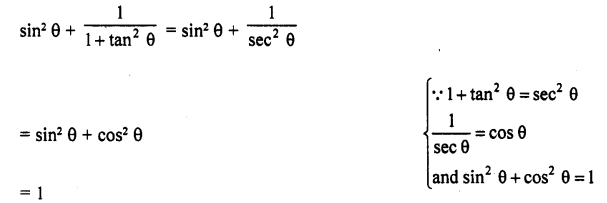
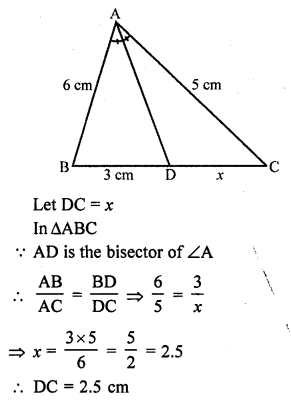
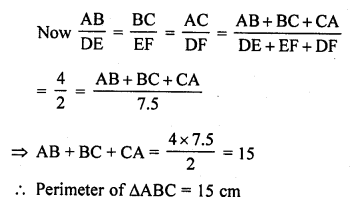
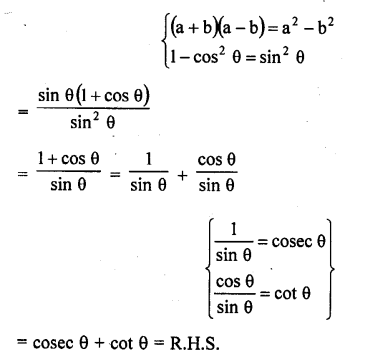
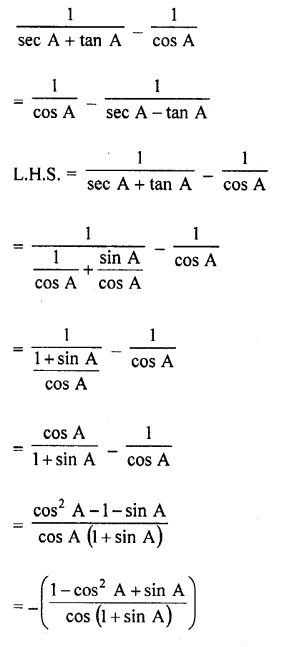
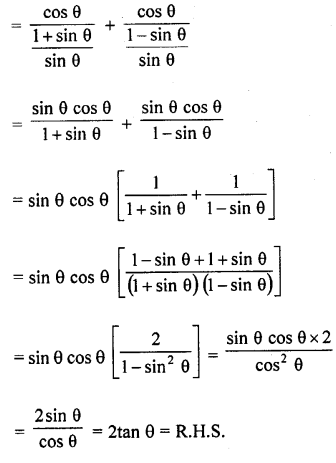
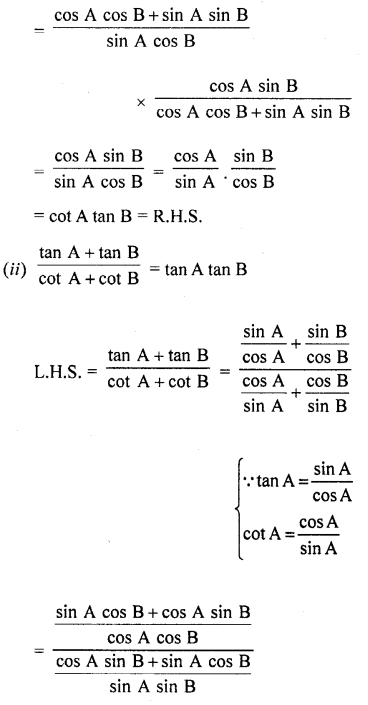
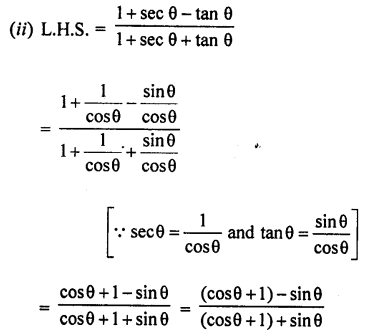
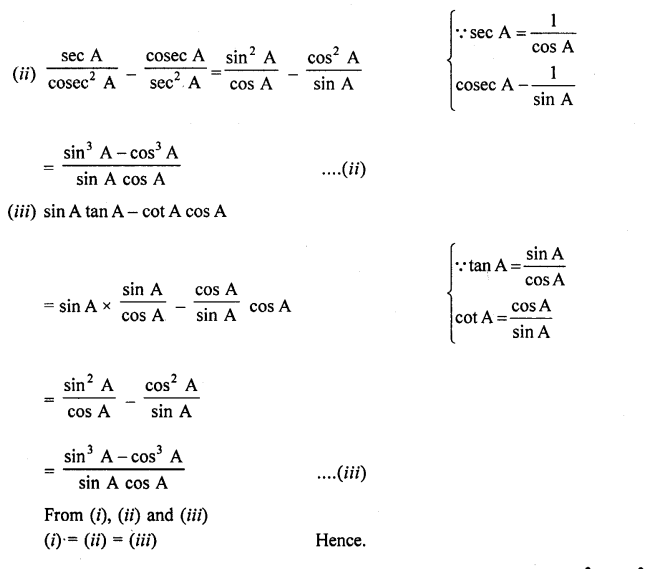
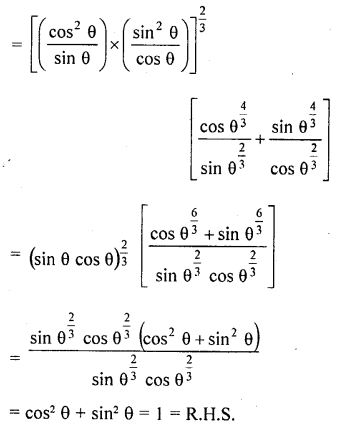
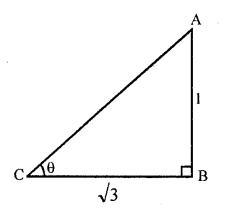
Question 7.
Prove that :

Solution:

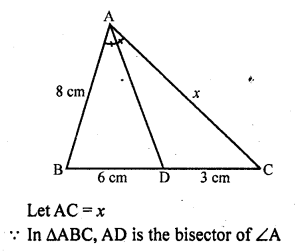
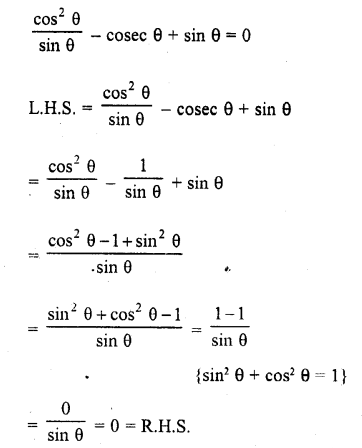
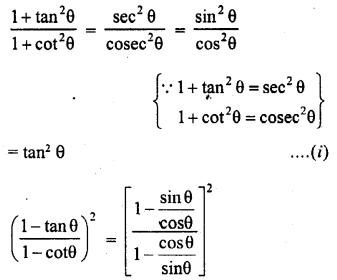
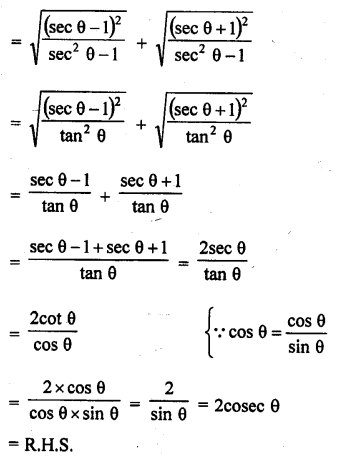
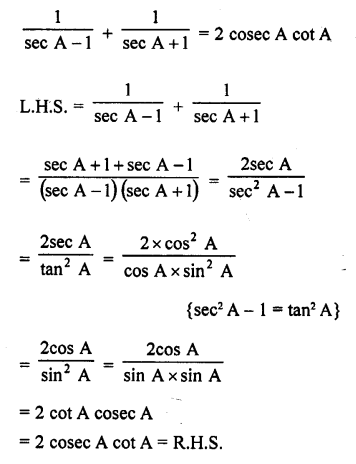
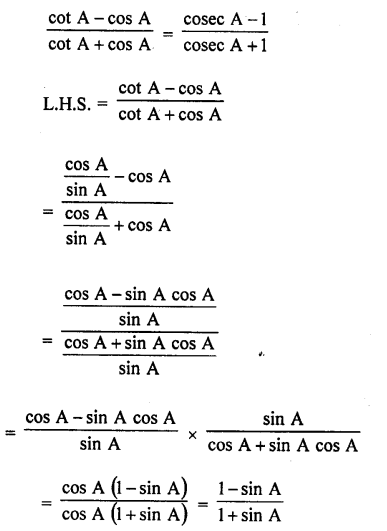
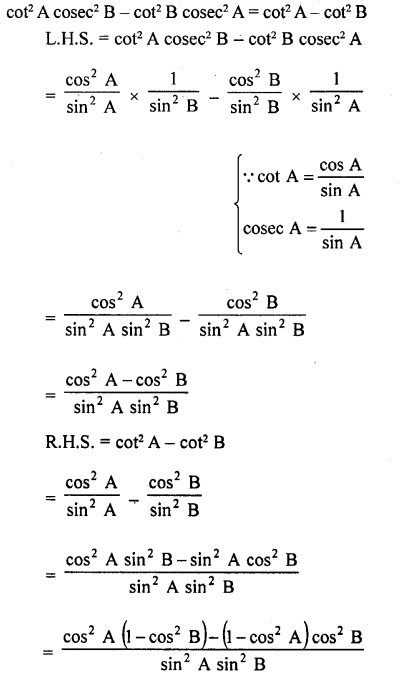
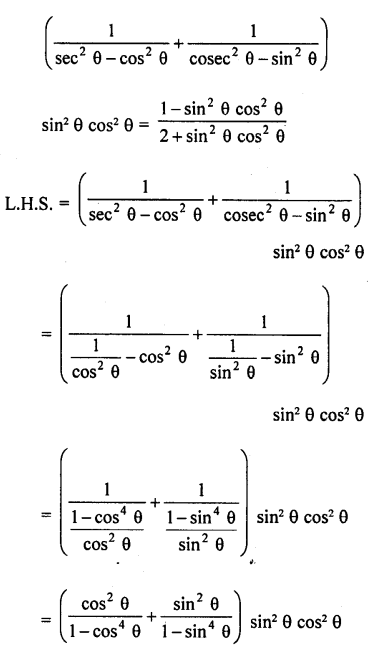
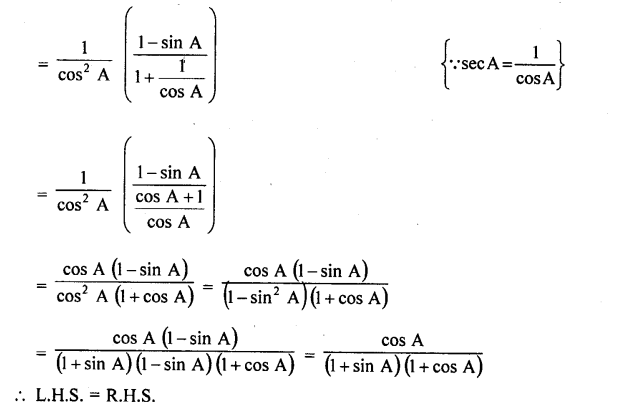
Question 8.
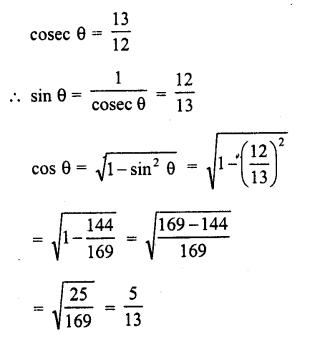
Prove the following :

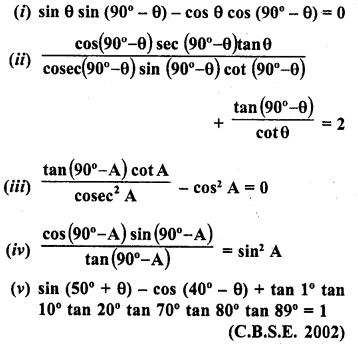
Solution:

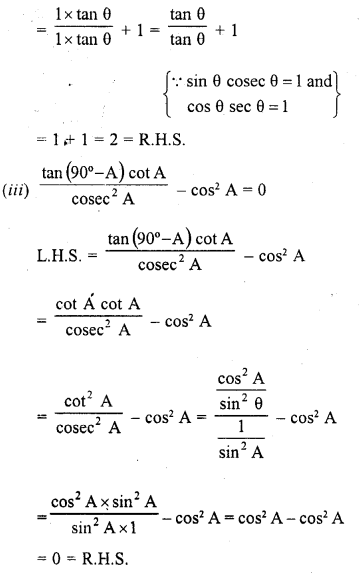
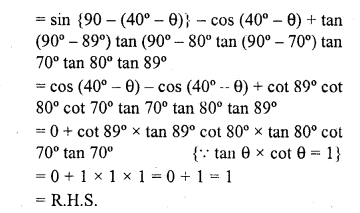
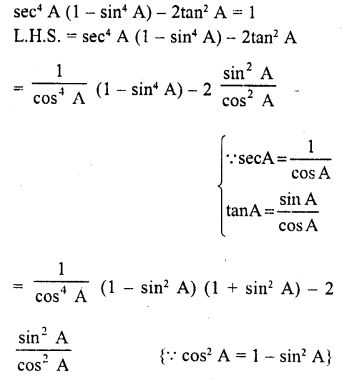
Question 9.
Evaluate :


Solution:

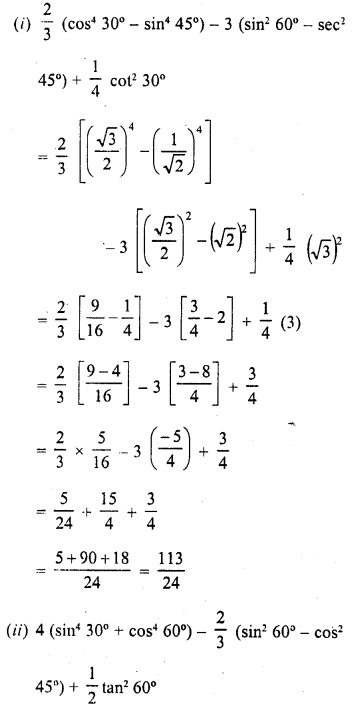
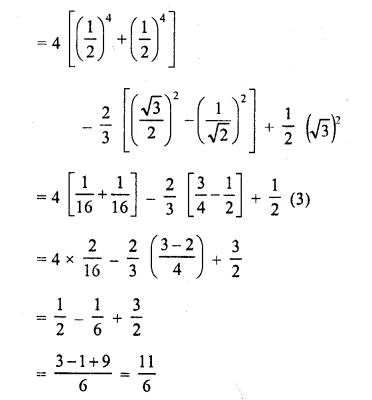
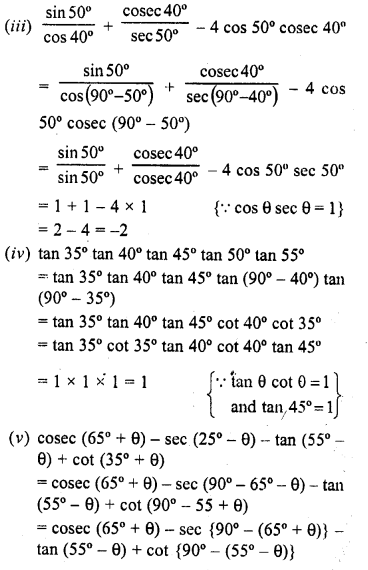
Question 10.
If sin θ= cos (θ – 45°), where θ and (θ – 45°) are acute angles, find the degree measure of θ.
Solution:

Question 11.
If A, B, C are the interior angles of a AABC, show that :
(i) \(sin\frac { B+C }{ 2 } cos\frac { A }{ 2 }\)
(ii) \(cos\frac { B+C }{ 2 } sin\frac { A }{ 2 }\)
Solution:

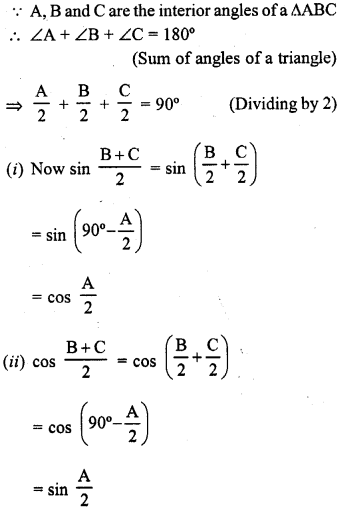
Question 12.
If 2θ + 45° and 30° – θ are acute angles, find the degree measures of θ satisfying sin (20 + 45°) = cos (30° – θ).
Solution:

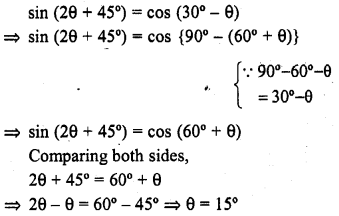
Question 13.
If θ is a positive acute angle such that sec θ = cosec 60°, And the value of 2 cos2 θ-1.
Solution:

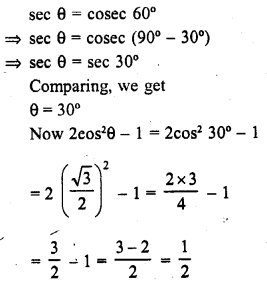
Question 14.
If cos 2 θ – sin 4 θ, where 2 θ and 4 θ are acute angles, find the value of θ.
Solution:

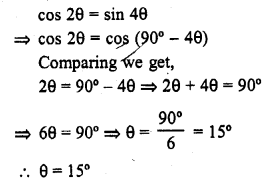
Question 15.
If sin 3 θ = cos (θ – 6°), where 3 θ and θ – 6° are acute angles, find the value of θ.
Solution:

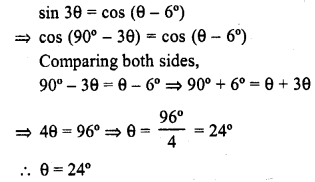
Question 16.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:

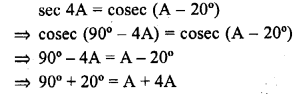
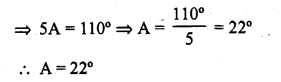
Question 17.
If sec 2A = cosec (A – 42°), where 2A is an acute angle, find the value of A. (C.B.S.E. 2008)
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1
• RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2
• RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS
• RD Sharma Class 10 Solutions Chapter 8 Circles MCQS

Question 1.
Fill in the blanks :
(i) The common point of a tangent and the circle is called ……….
(ii) A circle may have ………. parallel tangents.
(iii) A tangent to a circle intersects it in ……….. point(s).
(iv) A line intersecting a circle in two points is called a …………
(v) The angle between tangent at a point on a circle and the radius through the point is ………..
Solution:
(i) The common point of a tangent and the circle is called the point of contact.
(ii) A circle may have two parallel tangents.
(iii) A tangents to a circle intersects it in one point.
(iv) A line intersecting a circle in two points is called a secant.
(v) The angle between tangent at a point, on a circle and the radius through the point is 90°.

Question 2.
How many tangents can a circle have ?
Solution:
A circle can have infinitely many tangents.

Question 3.
O is the centre of a circle of radius 8 cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB.
Solution:
Radius OA = 8 cm, ST is the tangent to the circle at A and AB = 15 cm

OA ⊥ tangent TS
In right ∆OAB,
OB² = OA² + AB² (Pythagoras Theorem)
= (8)² + (15)² = 64 + 225 = 289 = (17)²
OB = 17 cm

Question 4.
If the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ = 24 cm and OQ = 25 cm. Find the radius of the circle.
Solution:
OP is the radius and TS is the tangent to the circle at P

OQ is a line
OP ⊥ tangent TS
In right ∆OPQ,
OQ² = OP² + PQ² (Pythagoras Theorem)
=> (25)² = OP² + (24)²
=> 625 = OP² + 576
=> OP² = 625 – 576 = 49
=> OP² = (7)²
OP = 7 cm
Hence radius of the circle is 7 cm

 

Hope given RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Question 1.
If cos θ = \(\frac { 4 }{ 5 }\) , find all other trigonometric ratios of angle θ
Solution:


Question 2.
If sin θ = \(\frac { 1 }{ \sqrt { 2 } }\) , find all other trigono­metric ratios of angle θ
Solution:

Question 3.
If tan θ = \(\frac { 1 }{ \sqrt { 2 } }\), find the value of \(\frac { { cosec }^{ 2 }-{ sec }^{ 2 } }{ { cosec }^{ 2 }+cot^{ 2 } }\) 
Solution:
<

Question 4.
If tan θ = \(\frac { 3 }{ 4 }\), find the value of \(\frac { 1-cosheta }{ 1+cosheta }\) 
 (C.B.S.E. 1995)
Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.
If \(\sqrt { 3 } \) tan θ = 3sin θ , find the value of sin² θ  – cos² θ .          (C.B.S.E. 2001)
Solution:

Question 11.

Solution:

Question 12.
If sin θ + cos θ = \(\sqrt { 2 } \)cos (90° – θ), find cot θ
Solution:

Question 13.
If 2sin² θ – cos² θ = 2, then find the value of θ. [NCERT Exemplar]
Solution:

Question 14.
If \(\sqrt { 3 } \) tan θ-1=0, find the value of sin² – cos² θ. [NCERT Exemplar]
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
Define an identity.
Solution:
An identity is an equation which is true for all values of the variable (s) involved.

Question 2.
What is the value of (1 – cos² θ) cosec² θ?
Solution:

Question 3.
What is the value of (1 + cot² θ) sin² θ ?
Solution:
(1 + cot² θ) sin² θ = cosec² sin² θ                           {1 + cot² θ = cosec² θ}
= (cosec θ sin θ)² = (l)² = 1                                      (∵ sin θ cosec θ=1)

Question 4.

Solution:

Question 5.
If sec θ + tan θ = x, write the value of sec θ – tan θ in terms of x.
Solution:
sec θ+ tan θ = x
We know that
sec² θ – tan² θ=1                                                                    .
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1                               {a² – b² = (a + b) (a – b)}
⇒  x (sec θ – tan θ) = 1
⇒  sec θ – tan θ = \(\frac { 1 }{ x }\)

Question 6.
If cosec θ – cot θ = α, write the value of cosec θ + cot α.
Solution:
cosec θ – cot θ = α
We know that,
cosec²  θ – cot²  θ=1
⇒  (cosec θ – cot θ) (cosec θ + cot θ) = 1
⇒  a (cosec θ + cot θ) = 1                                                {a² – b² = (a + b) (a – 6)}
⇒  cosec θ + cot θ = 1/α

Question 7.
Write the value of cosec² (90° – θ) – tan²θ
Solution:

Question 8.
Write the value of sin A cos (90° – A) + cos A sin (90° – A)
Solution:

Question 9.

Solution:

Question 10.
If x = a sin θ and y = b cos θ, what is the value of b²x² + a²y² ?
Solution:
x = a sin θ, y = b cos θ

Question 11.
If sin θ = \(\frac { 4 }{ 5 }\), What is the value of cot θ + cosec θ ?
Solution:

Question 12.
What is the value of 9 cot²  θ-9 cosec²  θ?
Solution:
9 cot²  θ – 9 cosec²  θ
= -(9cosec²  θ – 9cot²  θ)
= -9 (cosec²  θ – cot² θ) = -9 x 1
= -9                                                       {∵  cosec²  θ – cot² θ=1}

Question 13.

Solution:

Question 14.

Solution:

Question 15.
What is the value of (1 + tan² θ) (1 – sin θ) (1 + sin θ) ?
Solution:

Question 16.
If cos A = \(\frac { 7 }{ 25 }\), find the value of tan A +cot A. (C.B.S.E. 2008)
Solution:

Question 17.
If sin θ = \(\frac { 1 }{ 3 }\), then find the value of 2 cot² θ + 2. (C.B.S.E. 2009)
Solution:

Question 18.
If cos θ = \(\frac { 3 }{ 4 }\), then find the value of 9 tan² θ + 9.
Solution:

Question 19.
If sec²  θ (1 + sin θ) (1 – sin θ) = k, then find the value of k. (C.B.S.E. 2009)
Solution:

Question 20.
If cosec²  θ (1 + cos θ) (1 – cos θ) = λ, then find the value of λ.
Solution:
cosec²  θ (1 + cos θ) (1 – cos θ) = λ
⇒ cosec² θ (1 – cos² θ) = λ                      {(a + b) (a – b) = a¹ – b²)}
⇒  cosec² θ x sin θ = λ             (1 – cos² θ = sin² θ)
⇒ 1 = λ                                      (sin θ cosec θ=1)
∴ λ = 1

Question 21.
If sin² θ cos² θ (1 + tan² θ) (1 + cot² θ) = λ, then find the value of λ.
Solution:
sin² θ cos² θ (1+ tan² θ) (1 + cot² θ) = λ
sin² θ cos² θ (sec² θ) (cosec² θ) = λ

Question 22.


Solution:

Question 23.
If cosec θ = 2x and cot θ = \(\frac { 2 }{ x }\), find the value of 2 ( x² – \(\frac { 1 }{ x2 }\)           [CBSE 2010]
Solution:

Question 24.
Write ‘True’ or ‘False’ and justify your answer in each of the following:
(i) The value of sin θ is x + \(\frac { 1 }{ x }\), where ‘x’ is a positive real number.
(ii) cos θ = \(\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2ab }\) , where a and b are two lab distinct numbers such that ab > 0.
(iii) The value of cos² 23 – sin² 67 is positive.
(iv) The value of the expression sin 80° – cos 80° is negative.
(v) The value of sin θ + cos θ is always greater than 1.
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Mark the correct alternative in each of the following.
Question 1.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3
(b) 4 : 9
(c) 81 : 16
(d) 16 : 81
Solution:
(d) Triangles are similar and the ratio of their sides is 4 : 9
The ratio of the areas of two similar triangles are proportion to the square oT their corresponding sides
Ratio in their areas = (4)² : (9)² = 16 : 81

Question 2.
The areas of two similar triangles are in respectively 9 cm² and 16 cm². The ratio of their corresponding sides is
(a) 3 : 4
(b) 4 : 3
(c) 2 : 3
(d) 4 : 5
Solution:
(a) Ratio in the areas of two similar triangles = 9 cm² : 16 cm² = 9 : 16
The areas of similar triangles are proportional to the squares of their corresponding sides
Ratio in their corresponding sides = √\(\frac { 9 }{ 16 }\) = \(\frac { 3 }{ 4 }\) = 3 : 4

Question 3.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm² and 81 cm² respectively. If the longest side of larger ∆ABC be 36 cm, then. The longest side of the smaller triangle ∆DEF is :
(a) 20 cm
(b) 26 cm
(c) 27 cm
(d) 30 cm
Solution:
(c) Area of the larger triangle ABC = 144 cm²
and area of smaller ∆DEF = 81 cm²
Longest side of larger triangle = 36 cm
Let the longest side of smaller triangle = x cm
The ratio of the areas of two similar triangles is proportional to the squares of their corresponding sides

Question 4.
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangles ABC and BDE is :
(a) 2 : 1
(b) 1 : 2
(c) 4 : 1
(d) 1 : 4
Solution:
(c) ∆ABC and ∆BDE are equilateral triangles and D is the mid-point of PC
∆ABC and ∆BDE are both equilateral triangles

Question 5.
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
(a) 16 cm
(b) 12 cm
(c) 8 cm
(d) 4 cm
Solution:
(a)

Question 6.

(a) 2 : 5
(b) 4 : 25
(c) 4 : 15
(d) 8 : 125
Solution:
(b)

Question 7.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
Solution:
(c) In ∆ABC, XY || BC
AB = 4BX, YC = 2 cm

Question 8.
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
(a) 12 m
(b) 14 m
(c) 13 m
(d) 11 m
Solution:
(c) Let length of pole AB = 6 m
and of pole CD = 11 m
and distance between their foot = 12 m
i.e., BD = 12 m

Question 9.
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
(a) 1.1 cm
(b) 4 cm
(c) 4.4 cm
(d) 5.5 cm
Solution:
(c) In ∆ABC, DE || BC
AD : DB = 3 : 1, EA = 3.3 cm

Question 10.
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
(a) 35°
(b) 65°
(c) 75°
(d) 85°
Solution:
(c) In ∆ABC and ∆DEF,
∠A = ∠E = 40°
AB : ED = AC : EF, ∠F = 65°

Question 11.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:
(a) ∆ABC ~ ∆DEF
∠A = 47°, ∠E = 83°
∆ABC and ∆DEF are similar
∠A = ∠D, ∠B = ∠E and ∠C = ∠F
∠A = 47°
∠B = ∠E = 83°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
47° + 83° + ∠C = 180°
=> 130° + ∠C = 180°
=> ∠C = 180° – 130°
=> ∠C = 50°

Question 12.
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
(a) 1 : 4
(b) 1 : 2
(c) 2 : 3
(d) 4 : 5
Solution:
(a) D, E and F are the mid points of the sides. BC, CA and AB respectively of ∆ABC
DE, EF and FD are joined

Question 13.
In an equilateral triangle ABC, if AD ⊥ BC, then
(a) 2AB² = 3AD²
(b) 4AB² = 3AD²
(c) 3AB² = 4AD²
(d) 3AB² = 2AD²
Solution:
(c) In equilateral ∆ABC,
AD ⊥ BC

Question 14.
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD² =
(a) \(\frac { 3 }{ 2 }\) DC²
(b) 2 DC²
(c) 3 CD²
(d) 4 DC²
Solution:
(c) In equilateral ∆ABC, AD ⊥ BC
AD bisects BC at D

Question 15.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
(a) 11.3 cm
(b) 2.5 cm
(c) 3.5 cm
(d) None of these
Solution:
(b) In ∆ABC, AD is the bisector of ∠BAC
AB = 6 cm, AC = 5 cm, BD = 3 cm

Question 16.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
(a) 4 cm
(b) 6 cm
(c) 3 cm
(d) 8 cm
Solution:
(a) In ∆ABC, AD is the bisector of ∠BAC
AB = 8 cm, BD = 6 cm and DC = 3 cm

Question 17.
ABCD is a trapezium such that BC || AD and AB = 4 cm. If the diagonals AC and BD intersect at O such that \(\frac { AO }{ OC }\) = \(\frac { DO }{ OB }\) = \(\frac { 1 }{ 2 }\) , then BC =
(a) 7 cm
(b) 8 cm
(c) 9 cm
(d) 6 cm
Solution:
(b) In trapezium ABCD, BC || AD
AD = 4 cm, diagonals AC and BD intersect

=> x = 8
BC = 8 cm

Question 18.
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4 (AN² + CM²) =
(a) 4 AC²
(b) 5 AC²
(c) \(\frac { 5 }{ 4 }\) AC²
(d) 6 AC²
Solution:
(b) In right ∆ABC, ∠B = 90°
M and N are the mid points of AB and BC respectively

Question 19.
If in ∆ABC and ∆DEF, \(\frac { AB }{ DE }\) = \(\frac { BC }{ FD }\), then ∆ABC ~ ∆DEF when
(a) ∠A = ∠F
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠B = ∠E
Solution:
(c)

Question 20.

Solution:
(a)

Question 21.
∆ABC ~ ∆DEF, ar (∆ABC) = 9 cm², ar (∆DEF) = 16 cm². If BC = 2.1 cm, then the measure of EF is
(a) 2.8 cm
(b) 4.2 cm
(c) 2.5 cm
(d) 4.1 cm
Solution:
(a) ∆ABC ~ ∆DEF
ar (∆ABC) = 9 cm², ar (∆DEF) =16 cm²,
BC = 2.1 cm
∆ABC ~ ∆DEF

Question 22.
The length of the hypotenuse of an isosceles right triangle whose one side is 4√2 cm is
(a) 12 cm
(b) 8 cm
(c) 8√2 cm
(d) 12√2 cm
Solution:
(b) In isosceles right ∆ABC

∠B = 90°, AB = BC = 4√2
AC = √2
equal side = √2 x 4√2 = 8 cm

Question 23.
A man goes 24 m due west and then 7 m due north. How far is he from the starting point ?
(a) 31 m
(b) 17 m
(c) 25 m
(d) 26 m
Solution:
(c) In the figure, O is starting point OA = 24 m and AB = 7 m

By Pythagoras Theorem
OB² = OA² + AB²
= (24)² + (7)² = 576 + 49 = 625 = (25)²
OB = 25 m

Question 24.
∆ABC ~ ∆DEF. If BC = 3 cm, EF = 4 cm and ar (∆ABC) = 54 cm², then ar (∆DEF)
(a) 108 cm²
(b) 96 cm²
(c) 48 cm²
(d) 100 cm²
Solution:
(b)

Question 25.
∆ABC ~ ∆PQR such that ar (∆ABC) = 4 ar (∆PQR). If BC = 12 cm, then QR =
(a) 9 cm
(b) 10 cm
(c) 6 cm
(d) 8 cm
Solution:
(c) ∆ABC ~ ∆PQR
ar (∆ABC) = 4ar (∆PQR), BC = 12 cm
∆ABC ~ ∆PQR

Question 26.
The areas of two similar triangles are 121 cm² and 64 cm² respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangles is
(a) 11 cm
(b) 8.8 cm
(c) 11.1 cm
(d) 8.1 cm
Solution:
(b) Areas of two similar triangles are 121 cm² and 64 cm²
Median of first triangle = 12.1 cm

In ∆ABC, area ∆DEF
AD and PS are their corresponding median
∆ABC ~ ∆DEF

Question 27.
In an equilateral triangle ABC if AD ⊥ BC, then AD² =
(a) CD²
(b) 2 CD²
(c) 3 CD²
(d) 4 CD²
Solution:
(c) In equilateral ∆ABC, AD ⊥ BC

Question 28.
In an equilateral triangle ABC if AD ⊥ BC, then
(a) 5 AB² = 4 AD²
(b) 3 AB² = 4 AD²
(c) 4 AB² = 3 AD²
(d) 2 AB² = 3 AD²
Solution:
(b) In equilateral ∆ABC, AD ⊥ BC

Question 29.
In an isosceles triangle ABC if AC = BC and AB² = 2 AC², then ∠C =
(a) 30°
(b) 45°
(c) 90°
(d) 60°
Solution:
(c) In isosceles ∆ABC, AC = BC

and AB2 = 2 AC² = AC² + AC²
= AC² + BC² ( AC = BC)
By converse of Pythagoras Theorem,
∠C = 90°

Question 30.
∆ABC is an isosceles triangle in which ∠C = 90°. If AC = 6 cm, then AB =
(a) 6√2 cm
(b) 6 cm
(c) 2√6 cm
(d) 4√2 cm
Solution:
(a) ∆ABC is an isosceles with ∠C= 90°

AC = BC
AC = 6 cm
AB² = AC² + BC² (Pythagoras Theorem)
(6)² + (6)² = 36 + 36 = 72 (AC = BC)
AB = √72 = √(36 x 2) = 6√2 cm

Question 31.
If in two triangles ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true ?
(a) \(\frac { BC }{ DF }\) = \(\frac { AC }{ DE }\)
(b) \(\frac { AB }{ DE }\) = \(\frac { BC }{ DF }\)
(c) \(\frac { AB }{ EF }\) = \(\frac { AC }{ DE }\)
(d) \(\frac { BC }{ DF }\) = \(\frac { AB }{ EF }\)
Solution:
(b) In two triangles ABC and DEF
∠A = ∠E, ∠B = ∠F

Question 32.
In the figure, the measures of ∠D and ∠F are respectively
(a) 50°, 40°
(b) 20°, 30°
(c) 40°, 50°
(d) 30°, 20°

Solution:
(b) In ∆ABC
∠A = 180° – (∠B + ∠C)

Question 33.
In the figure, the value of x for which DE || AB is
(a) 4
(b) 1
(c) 3
(d) 2

Solution:
(b)

Question 34.
In the figure, if ∠ADE = ∠ABC, then CE =
(a) 2
(b) 5
(c) \(\frac { 9 }{ 2 }\)
(c) 3

Solution:
(c) In the figure ∠ADE = ∠ABC
AB = 2, DB = 3, AE = 3
Let EC = x
∠ADE = ∠ABC
But these are corresponding angles DE || BC
∆ADE ~ ∆ABC

Question 35.
In the figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively
(a) 12, 10
(b) 14, 6
(c) 10, 7
(d) 16, 8

Solution:
(d) In the figure RS || DB || PQ
CP = PD = 11 cm DR = RA = 3 cm
In ∆ABD
RS || BD and AR = RD
RS = \(\frac { 1 }{ 2 }\) BD
y = \(\frac { 1 }{ 2 }\) x or x = 2y
Only 16, 8 is possible

Question 36.
In the figure, if PB || CF and DP || EF, then \(\frac { AD }{ DE }\) =
(a) \(\frac { 3 }{ 4 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 1 }{ 4 }\)
(d) \(\frac { 2 }{ 3 }\)

Solution:
(b) In the figure, PB || CF, DP || EF
AB = 2 cm, AC = 8 cm
BC = AC – AB = 8 – 2 = 6 cm
In ∆ACF, BP || CF

\(\frac { AD }{ DE }\) = \(\frac { 1 }{ 3 }\)

Question 37.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
(a) 5√2
(b) 10√2
(c) \(\frac { 5 }{ \surd 2 }\)
(d) 10√3 [ICSE 2014]
Solution:
(b)

AB² = OA² + OB² (Pythagoras Theorem)
AB² = 10² + 10²
AB² = 2 (10)²
AB = 10√2

Question 38.
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
(a) 100 m
(b) 120 m
(c) 25 m
(d) 200 m
Solution:
(a) Height of a stick = 20 m
and length of its shadow = 10 m
At the same time
Let height of tower = x m
and its shadow = 50 m
20 : x = 10 : 50
x x 10 = 20 x 50
=> x = \(\frac { 20 x 50 }{ 10 }\) = 100
Height of tower = 100 m

Question 39.
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is :
(a) 4 : 5
(b) 5 : 4
(c) 3 : 2
(d) 5 : 7
Solution:
(a) The corresponding angles of two isosceles triangles are equal These are similar Ratio in their areas = 16 : 25
The ratio of areas of similar triangles are proportion to the squares of their corresponding altitudes (heights)
Ratio in their altitudes = \(\surd \frac { 16 }{ 25 } =\frac { 4 }{ 5 }\)
= i.e., 4 : 5

Question 40.
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ~ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
(a) 7.5 cm
(b) 15 cm
(c) 22.5 cm
(d) 30 cm
Solution:
(b) ∆DEF ~ ∆ABC
AB = 3 cm, BC = 2 cm, CA = 2.5 cm, EF = 4 cm
∆s are similar

Question 41.
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then :
(a) BC = CY
(b) BC = BY
(c) BC ≠ CY
(d) BC ≠ BY
Solution:
(a) In ∆ABC, XY || BC
BY is the bisector of ∠XYC

∠XYB = ∠CXB ….(i)
XY || BC
∠XYB = ∠XBC (Alternate angles) ……….(ii)
From (i) and (ii)
∠CYB = ∠YBC
BC = CY

Question 42.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
(a) \(\frac { 13 }{ 2 }\) cm
(b) \(\frac { 60 }{ 13 }\) cm
(c) \(\frac { 13 }{ 60 }\) cm
(d) \(\frac { 2\surd 15 }{ 13 }\) cm
Solution:
(b) In ∆ABC,
∠A = 90°, AB = 5 cm, AC = 12 cm

Question 43.
In a ∆ABC, perpendicular AD from A on BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
(a) ∆ABC is isosceles
(b) ∆ABC is equilateral
(c) AC = 2 AB
(d) ∆ABC is right-angled at A
Solution:
(d) In ∆ABC, AD ⊥ BC
BD = 8 cm, DC = 2 cm, AD = 4 cm

In right ∆ACD,
AC² = AD² + CD² (Pythagoras Theorem)
= (4)² + (2)² = 16 + 4 = 20
and in right ∆ABD,
AB² = AD² + DB²
= (4)² + (8)2 = 16 + 64 = 80
and BC² = (BD + DC)² = (8 + 2 )² = (10)² = 100
AB² + AC² = 80 + 20 = 100 = BC²
∆ABC is a right triangle whose ∠A = 90°

Question 44.
In a ∆ABC, point D is on side AB and point G is on side AC, such that BCED is a trapezium. If DE : BC = 3:5, then Area (∆ADE) : Area (BCED) =
(a) 3 : 4
(b) 9 : 16
(c) 3 : 5
(d) 9 : 25
Solution:
(b)

In ∆ABC, D and E are points on the side AB and AC respectively, such that BCED is a trapezium DE : BC = 3 : 5
In ∆ABC, DE || BC
∆ADE ~ ∆ABC

Question 45.
If ABC is an isosceles triangle and D is a point on BC such that AD ⊥ BC, then
(a) AB² – AD² = BD.DC
(b) AB² – AD² = BD² – DC²
(c) AB² + AD² = BD.DC
(d) AB² + AD² = BD² – DC²
Solution:
(a) If ∆ABC, AB = AC
D is a point on BC such that

AD ⊥ BC
AD bisects BC at D
In right ∆ABD,
AB² = AD² + BD²
AB² – AD² = BD² = BD x BD = BD x DC (BD = DC)

Question 46.
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then , \(\frac { BD }{ DC }\) =
(a) \(\left( \frac { AB }{ AC } \right) ^{ 2 }\)
(b) \(\frac { AB }{ AC }\)
(c) \(\left( \frac { AB }{ AD } \right) ^{ 2 }\)
(d) \(\frac { AB }{ AD }\)
Solution:
(a) In right angled ∆ABC, ∠A = 90°
AD ⊥ BC

Question 47.
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB² + BC² + CA² =
(a) 2 BE²
(b) 3 BE²
(c) 4 BE²
(d) 6 BE²
Solution:
(c) ∆ABC is an equilateral triangle
BE ⊥ AC

Question 48.
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
(a) AQ² + CP² = 2 (AC² + PQ²)
(b) 2 (AQ² + CP²) = AC² + PQ²
(c) AQ² + CP² = AC² + PQ²
(d) AQ + CP = \(\frac { 1 }{ 2 }\) (AC + PQ)
Solution:
(c) In right ∆ABC, ∠B = 90°
P and Q are points on AB and BC respectively
AQ, CP and PQ are joined

In right ∆ABC,
AC² = AB² + BC² ….(i)
(Pythagoras Theorem)
Similarly in right ∆PBQ,
PQ² = PB² + BQ² ………(ii)
In right ∆ABQ
AQ² = AB² + BQ² ….(iii)
and in right ∆CPB,
CP² = PB² + BC² ….(iv)
Adding (iii) and (iv)
AQ² + CP² = AB² + BQ² + PB² + BC²
= AB² + BC² + BQ² + PB²
= AC² + PQ2 {From (i) and (ii)}

Question 49.
If ∆ABC ~ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
(a) 18 cm
(b) 20 cm
(c) 12 cm
(d) 15 cm
Solution:
(d) ∆ABC ~ ∆DEF
DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm

Question 50.
If ∆ABC ~ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
(a) 36 cm
(b) 30 cm
(c) 34 cm
(d) 35 cm
Solution:
(d) ∆ABC ~ ∆DEF
AB = 9.1 cm and DE = 6.5 cm
Perimeter of ∆DEF = 25 cm

Question 51.
In an isosceles triangle ABC, if AB = AC = 25 cm and BC = 14 cm, then the measure of altitude from A on BC is
(a) 20 cm
(b) 22 cm
(c) 18 cm
(d) 24 cm
Solution:
(d) ∆ABC is an isosceles triangle in which AB = AC = 25 cm, BC = 14 cm

From A, draw AD ⊥ BC
D is mid-point of BC
BD = \(\frac { 1 }{ 2 }\) BC = \(\frac { 1 }{ 2 }\) x 14 = 7 cm
Now in right ∆ABD
AD² = AB² – BD²
= (25)² – (7)² = 625 – 49 = 576 = (24)²
AD = 24 cm

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Prove the following trigonometric identities :
Question 1.
(1 – cos² A) cosec² A = 1
Solution:
(1 – cos² A) cosec² A = 1
L.H.S. = (1 – cos² A) cosec² A = sin² A cosec² A  (∵ 1 – cos² A = sin² A)
= (sin A cosec A)² = (l)² = 1 = R.H.S.  {sin A cosec A = 1 }

Question 2.
(1 + cot² A) sin² A = 1
Solution:
(1 + cot² A) sin² A = 1
L.H.S. = (1 + cot² A) (sin² A)
= cosec² A sin² A {1 + cot² A = cosec² A}
= [cosec A sin A]²
= (1)²= 1 = R.H.S. (∵ sin A cosec A = 1

Question 3.
tan² θ cos²  θ = 1- cos²  θ
Solution:

Question 4.

Solution:

Question 5.
(sec² θ – 1) (cosec² θ – 1) = 1
Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.
tan²  θ – sin²  θ = tan²  θ sin² θ
Solution:

Question 17.
(sec θ + cos θ ) (sec θ – cos θ ) = tan²  θ + sin² θ
Solution:

Question 18.
(cosec θ + sin θ) (cosec θ – sin θ) = cot² θ + cos² θ
Solution:

Question 19.
sec A (1 – sin A) (sec A + tan A) = 1 (C.B.S.E. 1993)
Solution:

Question 20.
(cosec A – sin A) (sec A – cos A) (tan A + cot A) = 1
Solution:

Question 21.
(1 + tan²  θ) (1 – sin θ) (1 + sin θ) = 1
Solution:

Question 22.
sin² A cot² A + cos² A tan² A = 1 (C.B.S.E. 1992C)
Solution:

Question 23.

Solution:

Question 24.

Solution:

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Question 31.
sec⁶ θ= tan⁶  θ + 3 tan²  θ sec²  θ + 1
Solution:

Question 32.
cosec⁶  θ = cot⁶  θ+ 3cot²θ cosec²  θ + 1
Solution:

Question 33.

Solution:

Question 34.

Solution:

Question 35.

Solution:

Question 36.

Solution:

Question 37.

Solution:

Question 38.

Solution:

Question 39.

Solution:

Question 40.

Solution:

Question 41.

Solution:

Question 42.

Solution:

Question 43.

Solution:

Question 44.

Solution:

Question 45.

Solution:

Question 46.

Solution:

Question 47.


Solution:

Question 48.

Solution:

Question 49.
tan² A + cot² A = sec² A cosec² A – 2
Solution:

Question 50.

Solution:

Question 51.

Solution:

Question 52.

Solution:

Question 53.

Solution:

Question 54.
sin² A cos² B – cos² A sin² B = sin² A – sin² B.
Solution:
L.H.S. = sin² A cos² B – cos² A sin² B
= sin² A (1 – sin² B) – (1 – sin² A) sin² B
= sin² A – sin² A sin² B – sin² B + sin² A sin² B
= sin² A – sin² B
Hence, L.H.S. = R.H.S.

Question 55.

Solution:

Question 56.
cot² A cosec² B – cot² B cosec² A = cot² A – cot² B
Solution:

Question 57.
tan² A sec² B – sec² A tan² B = tan² A – tan² B
Solution:

Prove the following identities: (58-75)
Question 58.
If x = a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x¹ – y² = a² – b¹. [C.B.S.E. 2001, 20O2C]
Solution:
x – a sec θ + b tan θ
y = a tan θ + b sec θ
Squaring and subtracting, we get
x²-y² = {a sec θ + b tan θ)² – (a tan θ + b sec θ)²
= (a² sec² θ + b² tan²  θ + 2ab sec θ x tan θ) – (a² tan²  θ + b² sec²  θ + 2ab tan θ sec θ)
= a² sec² θ + b tan²  θ + lab tan θ sec θ – a² tan²  θ – b² sec²  θ – 2ab sec θ tan θ
= a² (sec² θ – tan²  θ) + b² (tan²  θ – sec²  θ)
= a² (sec² θ – tan²  θ) – b² (sec²  θ – tan²  θ)
=  a² x 1-b² x 1 =a²-b² = R.H.S.

Question 59.
If 3 sin θ + 5 cos θ = 5, prove that 5 sin θ – 3 cos θ = ±3
Solutioon:

Question 60.
If cosec θ + cot θ = mand cosec θ – cot θ = n,prove that mn= 1
Solution:

Question 61.

Solution:

Question 62.

Solution:

Question 63.

Solution:

Question 64.

Solution:

Question 65.

Solution:

Question 66.
(sec A + tan A – 1) (sec A – tan A + 1) = 2 tan A
Solution:

Question 67.
(1 + cot A – cosec A) (1 + tan A + sec A) = 2
Solution:

Question 68.
(cosec θ – sec θ) (cot θ – tan θ) = (cosec θ + sec θ) (sec θ cosec θ-2)
Solution:

Question 69.
(sec A – cosec A) (1 + tan A + cot A) = tan A sec A – cot A cosec A
Solution:

Question 70.

Solution:

Question 71.

Solution:

Question 72.

Solution:

Question 73.
sec⁴ A (1 – sin⁴ A) – 2tan² A = 1
Solution:

Question 74.

Solution:

Question 75.

Solution:

Question 76.

Solution:

Question 77.
If cosec θ – sin θ = a³, sec θ – cos θ = b³, prove that a²b² (a² + b²) = 1
Solution:

Question 78.

Solution:

Question 79.

Solution:

Question 80.
If a cos θ + b sin θ = m and a sin θ – b cos θ = n, prove that a² + b² = m² + n² 
Solution:

Question 81.
If cos A + cos² A = 1, prove that sin² A + sin⁴ A = 1
Solution:
cos A + cos² A = 1
⇒ cos A = 1 – cos² A
⇒cos A = sin² A
Now, sin² A + sin⁴ A = sin² A + (sin² A)²
= cos A + cos² A = 1 = R.H.S.

Question 82.
If cos θ + cos²  θ = 1, prove that
sin¹² θ + 3 sin¹⁰  θ + 3 sin⁸  θ + sin⁶  θ + 2 sin⁴  θ + 2 sin²  θ-2 = 1
Solution:

Question 83.
Given that :
(1 + cos α) (1 + cos β) (1 + cos γ) = (1 – cos α) (l – cos β) (1 – cos γ)
Show that one of the values of each member of this equality is sin α sin β sin γ
Solution:

Question 84.

Solution:

Question 85.

Solution:

Question 86.
If sin θ + 2cos θ = 1 prove that 2sin θ – cos θ = 2. [NCERT Exemplar]
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
State basic proportionality theorem and its converse.
Solution:
Basic Proportionality Theorem : If a line is drawn parallel to one side of a triangle intersects the other two sides in distinct points, then the other two sides are divided in the same ratio.
Conversely : In a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side of the triangle.

Question 2.
In the adjoining figure, find AC.

Solution:

Question 3.
In the adjoining figure, if AD is the bisector of ∠A, what is AC ?

Solution:
In the figure, AD is the angle bisector of ∠A of ∆ABC
AB = 6 cm, BC = 3 cm, DC = 2 cm

Question 4.
State AAA similarity criterion.
Solution:
If in two triangles, corresponding angles are respectively equal then the triangles are similar.

Question 5.
State SSS similarity criterion.
Solution:
If in two triangles, corresponding sides are in the same ratio, then the two triangles are similar.

Question 6.
State SAS similarity criterion.
Solution:
If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio, then the triangles are similar.

Question 7.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
Solution:
In ∆ABC, DE || BC

Question 8.
In the figure given below, DE || BC. If AD = 2.4 cm, DB = 3.6 cm and AC = 5 cm. Find AE.
Solution:
In ∆ABC, DE || BC
AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm

x = 2
AE = 2 cm

Question 9.
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR ?
Solution:
∆ABC ~ ∆PQR
Area of ∆ABC : area of ∆PQR = 9 : 16
BC = 4.5 cm
Let QR = A
The area of two similar triangles are in the ratio of the squares of their corresponding sides

Question 10.
The areas of two similar triangles are 169 cm² and 121 cm² respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle ?
Solution:
Let ∆ABC be the larger triangle and ∆PQR
be the smaller triangle and their longest sides be BC and QR respectively
Area of ∆ABC = 169 cm²
area of ∆PQR = 121 cm²
BC = 26 cm
Let QR = x cm
∆ABC ~ ∆PQR

Question 11.
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C ?
Solution:
∆ABC ~ ∆DEF
Their corresponding angles are equal ∠A = ∠D, ∠B = ∠E and ∠C = ∠F
But ∠A = 57°

Question 12.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas ?
Solution:
Let ∆ABC ~ ∆PQR
and let AL ⊥ BC and PM ⊥ QR

Question 13.

Solution:

Question 14.
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
Solution:

Question 15.
State Pythagoras Theorem and its converse.
Solution:
In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Conversely : If in a triangle, the square of one side is equal to the sum of squares of the remaining two sides, then the angle opposite to the first side is a right angle.

Question 16.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus. (C.B.S.E. 2008)
Solution:
In rhombus ABCD, BD = 30 cm, AC = 40 cm

Question 17.
In figure, PQ || BC and AP : PB = 1 : 2.

Solution:
In ∆ABC, PQ || BC
∆APQ ~ ∆ABC
But AP : PB = 1 : 2
The ratio of the areas of two similar triangles are proportional to the square of their corresponding sides

Question 18.
In the figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR. [CBSE 2010]

Solution:
In ∆PQR, ST || QR and PT = 2 cm, TR = 4 cm
PR = PT + TR = 2 + 4 = 6 cm

Question 19.
In the figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC. [CBSE 2010]

Solution:
In the given figure, AK = 10 cm, BC = 3.5 cm, HK = 7 cm

Question 20.
In the figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

Solution:
In the given figure,
DE || BC
BC = 8 cm, AB = 6 cm and DA = 1.5 cm

Question 21.
In the figure, DE || BC and AD = \(\frac { 1 }{ 2 }\) BD. If BC = 4.5 cm, find DE. [CBSE 2010]

Solution:
In the given figure,
DE || BC

Question 22.
In the figure, ∠M = ∠N = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

Solution:
In the figure, ∠M = ∠N = 46°
∠M = a, PN = x, MN = b, NK = c
∠M = ∠N = 46°
But there are corresponding angle
PN || ML
∆PKN ~ ∆LKM

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Question 1.
In each of the figures. [(i) – (iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segments are marked. Find the value of x in each of the following:


Solution:

Question 2.
What values of x will make DE || AB In the figure

Solution:

Question 3.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB ?
Solution:
In ∆ABC, P and Q are the points on two sides CA and CB respectively
CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm

Question 4.
In the figure, DE || CB. Determine AC and AE.

Solution:

Question 5.
In the figure, given that ∆ABC ~ ∆PQR and quad ABCD ~ quad PQRS. Determine the values of x, y, z in each case.



Solution:

Question 6.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
Solution:
In ∆ABC, P and Q are points on AB and AC respectively such that PQ || BC AP = 4 cm, PB = 6 cm, PQ = 3 cm

Question 7.
In each of the following figures, you find two triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.



Solution:
(i) In figure (i)
Let in ∆ABC, AB = 4.6, BC = 10, CA = 8
and in ∆DEF, DE = 2.3, EF = 5 and FD = 4

Question 8.
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm. state whether MN || QR.
Solution:
In ∆PQR, P and Q are points on PQ and PR such that
PM = 15 cm, NR = 8 cm PQ = 25 cm
and PR = 20 cm PN = PR – NR = 20 – 8 = 12 cm

Question 9.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
Solution:
In ∆ABC, P and Q are points on the sides AB and AC such that PQ || BC and AP = 3 cm, PQ = 5 cm, AC = 8 cm

8x = 24
=> x = 3
AQ = 3 cm

Question 10.
In the figure, ∆AMB ~ ∆CMD; determine MD in terms of x, y and z.

Solution:

Question 11.
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
Solution:
In ∆ABC, AD is the bisector of ∠A meeting BC in D
AB = 18 cm, AC = 15 cm and BC = 22 cm

Question 12.
In the figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.

Solution:

Question 13.
In the figure, AB || DC
(i) ∆DMU ~ ∆BMV
(ii) DM x BV = BM x DU

Solution:
Given : In the figure,
ABCD is a trapezium in which

Question 14.
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
Solution:
In trapezium ABCD,
AB || DC
P and Q are points on AD and BC respectively such that
PQ || BC PD = 18, BQ = 35, QC = 15

Question 15.
In ∆ABC, D and E are points on sides AB and AC respectively such that AD x EC = AE x DB. Prove that DE || BC.
Solution:
Given : In ∆ABC,
D and E are points on sides AB and AC respectively and AD x EC = AE x DB

Question 16.
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that \(\frac { area(\triangle OCD) }{ area(\triangle OAB) } =\frac { 1 }{ 9 }\) , if AB = 3CD
Solution:
Given: ABCD is a trapezium in which AB || DC and diagonals AC and BD intersect each other at O.


Hence proved.

Question 17.
Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm², determine the area of the larger triangle.
Solution:
Let the corresponding sides of two triangles are 2x : 3x
The ratio of the areas of two similar triangles is the ratio of the squares of their corresponding sides

Question 18.
The areas of two similar triangles are 36 cm² and 100 cm². If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
Solution:
Area of smaller triangle = 36 cm²
and area of larger triangle = 100 cm²
One side of smaller triangle = 3 cm
Let the corresponding side of larger triangle = x
∆s are similar

Question 19.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm², find the area of the larger triangle.
Solution:
The corresponding sides of two similar triangles are in the ratio 1 : 3
Let their sides be x, 3x
Area of the smaller triangle is 40 cm²
Triangles are similar

Question 20.
In the figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.

Solution:
Given : In the figure,
PA, QB, RC and SD are perpendiculars on l
AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm

Hence PQ = 8 cm, QR = 12 cm and RS = 16 cm

Question 21.
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segments are marked in each figure. Determine x, y, z in each case.

Solution:
(i) In figure (i)
In ∆ABC, ∠B = 90°
BD ⊥ AC
∆ABD ~ ∆CBD

Question 22.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
Solution:
Given : In an equilateral ∆ABC,
AD ⊥ BC
To prove : 3AB² = 4AD²
Proof : The altitude of an equilateral triangle bisects the opposite side

Question 23.
In ∆ABC, AD and BE are altitudes. Prove that :

Solution:
Given : In ∆ABC,
AD ⊥ BC and BE ⊥ AC

Question 24.
The diagonals of quadrilateral ABCD intersect at O. Prove that

Solution:
Given : ABCD is quadrilateral in which diagonals AC and BD intersect each other atO


= \(\frac { BO }{ DO }\) {From (i)}
Hence proved.

Question 25.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AB = c, prove that:
(i) BD = \(\frac { ac }{ b + c }\)
(ii) DC = \(\frac { ab }{ b + c }\)
Solution:
Given: In ∆ABC
AD is the bisector of ∠A
AB = c, BC = a, CA = b

Question 26.
There is a staircase as shown in the figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

Solution:
There are 4 steps in staircase AB
Taking first step,
In ∆ALP

Question 27.
In ∆ABC, ∠A = 60°. Prove that BC² = AB² + AC² – AB.AC.
Solution:


= AB² + AC² – AB.AC.
Hence proved.

Question 28.
In ∆ABC, ∠C is an obtuse angle, AD ⊥ BC and AB² = AC² + 3BC². Prove that BC = CD.
Solution:
Given : In ∆ABC, ∠C is an obtuse angle AD ⊥ BC and AB² = AC² + 3BC²
To prove : BC = CD

Question 29.
A point D is on the side BC of an equilateral triangle ABC such that DC = \(\frac { 1 }{ 4 }\) BC. Prove that AD² = 13 CD²
Solution:
Given : In the equilateral ∆ABC,
D is a point on BC such that DC = \(\frac { 1 }{ 4 }\) BC

Question 30.
In ∆ABC, if BD ⊥ AC and BC² = 2 AC.CD, then prove that AB = AC.
Solution:
Given : In ∆ABC,
BD ⊥ AC
BC² = 2 AC.CD

Question 31.
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC² + BD² = AD² + BC².
Solution:
Given : In quadrilateral ABCD,
∠A + ∠D = 90°
AC and BD are joined
To prove: AC² + BD² = AD² + BC²

Question 32.
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC² = 2 AC.CD.
Solution:
Given: In ∆ABC,
AB = AC
BD ⊥ AC

Question 33.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM² + BN² = DM² + DN².
Solution:
Given : In rectangle ABCD,
BD is the diagonal
AM ⊥ BD and CN ⊥ BD

Question 34.
In ∆ABC, AD is median. Prove that AB² + AC² = 2AD² + 2DC².
Solution:
Given : In ∆ABC, AD is the median of BC
To prove : AB² + AC² = 2AD² + 2DC²

Question 35.
In ∆ABC, ∠ABC = 135°. Prove that: AC² = AB² + BC² + 4 ar (∆ABC).
Solution:
Given : In ∆ABC, ∠ABC = 135°,


Hence proved.

Question 36.
In a quadrilateral ABCD, ∠B = 90°. If AD² = AB² + BC² + CD², then prove that ∠ACD = 90°.
Solution:
Given : In quadrilateral ABCD, ∠B = 90° and AD² = AB² + BC² + CD²

Question 37.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN² = AN.NC, prove that ∠B = 90°.
Solution:
Given : In ∆ABC, BN ⊥ AC and BN² = AN.NC
To prove : ∠B = 90°

Question 38.
Nazima is fly Ashing in a stream. The tip of her Ashing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out ? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

Solution:
Height of the rod from stream level = 1.8 m
and of string from the point under the tip of rod = 2.4 m
Let the length of string = x
x² = (1.8)² + (2.4)² = 3.24 + 5.76 = 9.00 = (3.0)²
x = 3.0
Length of string = 3 m
Rate of pulling the string = 5 cm per second
Distance covered in 12 seconds = 5 x 12 = 60 cm.
At this stage, length of string = 3.0 – 0.6 = 2.4 m
Height = 1.8 m
Let base = y then
(2.4)² = y² + (1.8)²
=> 5.76 = y² + 3.24
=> y² = 5.76 – 3.24 = 2.52
y = 1.59
and distance from her = 1.59 + 1.2 = 2.79 m

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1
• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS
• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS

Mark the correct alternative in each of the following :
Question 1.
The ratio of the length of a rod and its shadow is 1 : \(\sqrt { 3 } \) The angle of elevation of the sum is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution:
Let AB be rod and BC be its shadow
So that AB : BC = 1 : \(\sqrt { 3 } \)
Let θ be the angle of elevation

Question 2.
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60?, the height of the tower is

Solution:
Let AB be the tower and a point P at a distance of 100 m from its foot, angle of elevation of the top of the tower is 60°

Let height of the tower = h

Question 3.
If the altitude of the sun is at 60?, then the height of the vertical tower that will cast a shadow of length 30 m is

Solution:
Let AB be tower and a point P distance of 30 m from its foot of the tower which form an angle of elevation pf the sun of 60°

Question 4.
If the angles of elevation of a tower from two points distance a and b (a > b) from its foot and in the same straight line from it are 30? and 60?, then the height of the tower is

Solution:
Let AB be the tower and P and Q are such points that PB = a, QB = b and angles of elevation at P and Q are 30° and 60° respectively

Question 5.
If the anglr of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with It are complementary, then the height of the tower is

Solution:
Let AB be the tower and P and Q are two points such that PB = a and QB = b and angles of elevation are θ and (90° – θ)
Let height of tower = h

Question 6.
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is

Solution:
Let AB be light house and P and Q are two ships on its opposite sides which form angle of elevation of A as 45° and 30° respectively AB = h
Let PB = x and QB = y

Question 7.
The angle of elevation of the top of a tower stahding on a horizontal plane from a point A is a. After walking a distance d towards the foot of the tower the angle of elevation is found to be p. The height of the tower is

Solution:
Let AB be the tower and C is a point such that the angle of elevation of A is a. After walking towards the foot B of the tower, at D the angle of elevation is p Let h be the height of the tower and DB = x Now in right AACB,

Question 8.
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
(a) 12 m
(b) 10 in
(c) 8 m
(d) 6 m
Solution:
Let AB and CD be two poles
AB = 20 m, CD = 14 m
A and C are joined by a wire
CE || DB and angle of elevation of A is 30° Class 10 Solutions Chapter 12 Heights and Distances MCQS – 9.png
Let CE = DB = x and AC = l

Question 9.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
(a) 25 m
(b) 50 in
(c) 75 m
(d) 100 m
Solution:
Let AB be the tower and CD be cliff Angle of elevation of A is equal to the angle of depression of B at C
Let angle be Q and CD = 25 m

Question 10.
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart, the height of the light house is

Solution:
Let AB be the light house C and D are two ships whose angles of depression on A are 30° and 45° respectively

Question 11.
if the angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°, then the height of the cloud above the lake, is
(a) 200 m
(b) 500 m
(c) 30 m
(d) 400 m
Solution:
Let C be the cloud and R is its reflection in the lake
L is a point 200 m above the lake. Such that
LM = 200 m
Angle of elevation of C with L is 30° and angle of depression of R is 60°

Let height of cloud CB = h
∴ BR = h and NB = LM = 200 m
∴ CN = (h – 200) m and NR = (h + 200) m

Question 12.
The height of a tower is 100 m. When the angle of elevation of the sun changes from 30° to 45°, the shadow of the tower becomes x metres less. The value of x is

Solution:
Let AB be tower and AB = 100 m and angles of elevation of A at C and D are 30° and 45° respectively and CD = x
Let BD =y

Question 13.
Two persons are a metres apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is

Solution:
Let AB and CD are two persons standing ‘a’ metres apart
M is the mid-point of BD and from M, the angles of elevation of A and C are complementary

Question 14.
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
(a) It tan (45° + θ)
(b) h cot (45° – θ)
(c) h tan (45° – θ)
(d) h cot (45° + θ)
Solution:
Let C is the cloud and R is its reflection in the lake
From the lake, ‘7’ m aboves it, E is point
where angle of elevation of C is θ
and angle of depression of reflection is 45°

Question 15.
A lower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is

Solution:
Let CD is the tower and A is a point such that the angle of elevation of C is 30°
B is and their point h m high of A and angle of depressio of D is 60°

Question 16.
It is found that on walking x metres towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60° . The height of the chimney is

Solution:
In the figure, AB is chimney and CB and DB are its shadow

Question 17.
The length of the shadow of a tower standing on level ground is found to be 2.v metres longer when the sun’s elevation is 30° than when it was 45° . The height of the tower in metres is

Solution:
AB is a tower
BD and BC are its shadows and CD = 2x

Question 18.
Two poles are ‘a’ metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is


Solution:
Let height of pole CD = h
and AB = 2h, BD = a
M is mid-point of BD

Question 19.
The tops of two poles of height 16 m and 10 m are connected by a wire of length l metres. If the wire makes an angle of 30° with the horizontal, then l =
(a) 26
(b) 16
(c) 12
(d) 10
Solution:
Let AB and CD are two poles AB = 10 m and CD = 16 m

Question 20.
If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
(a) 1.5 m
(b) 2 m
(c) 2.5 m
(d) 2.8 m
Solution:
Let AB is girls and CD is lamp-post AB = 1.5
which casts her shadow EB

Question 21.
The length of shadow of a tower on the plane ground is \(\sqrt { 3 } \) times the height of the tower. The angle of elevation of sun is
(a) 45°
(b) 30°
(c) 60°
(d) 90° [CBSE 2012]
Solution:
Let AB be tower and BC be its shadow
∴Let AB = x

Question 22.
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
(a) 25 \(\sqrt { 3 } \)
(b) 50 \(\sqrt { 3 } \)
(c) 75 \(\sqrt { 3 } \)
(d) 150 [CBSE 2013]
Solution:
AB is a tower and AB = 75 m
From A, the angle of depression of a car C
on the ground is 30°

Question 23.
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is

Solution:
Let AB is a wall and AC is the ladder 15 m long which makes an angle of 60° with the ground
∴In ∆ABC, ∠B = 90°
Let height of wall AB = h

Question 24.
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
(a) 50\(\sqrt { 3 } \)
(b) 150 \(\sqrt { 3 } \)
(c) 150 \(\sqrt { 3 } \)
(d) 75
Solution:
Let AB be the tower of height 150 m
C is car and angle of depression is 30°

Question 25.
If the hei8ht of a vertical pole is \(\sqrt { 3 } \) times the length of its shadow on the ground, then the angle of elevation of the sun at that time is
(a) 30°
(b) 60°
(c) 45°
(d) 75° [CBSE 2014]
Solution:
Let AB be a vertical pole and let its shadow be BC

Question 26.
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45°. Then the height of the tower (in metres) is

Solution:
Let AB be tower and C is a point on the ground 50 m away

Question 27.
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is

Solution:
Suppose AB is the ladder of length x m
∴ OA = 2m, ∠OAB = 60°

Hope given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Question 1.
If the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is a right-angled triangle. (C.B.S.E. 1992)
Solution:
We know that if the square of the hypotenuse (longest side) is equal to the sum of squares of other two sides then it is right triangle
Now the sides of a triangle are 3 cm, 4 cm and 6 cm
(Longest side)² = (6)² = 36
and sum of two smaller sides = (3)² + (4)² = 9 + 16 = 25
36 ≠ 25
It is not a right-angled triangle

Question 2.
The sides of certain triangles are given below. Determine which of them are right triangles :
(i) a = 1 cm, b = 24 cm and c = 25 cm
(ii) a = 9 cm, b = 16 cm and c = 18 cm
(iii) a = 1.6 cm, b = 3.8 cm and c = 4 cm
(iv) a = 8 cm, b = 10 cm and c = 6 cm (C.B.S.E. 1992)
Solution:
We know that if the square of hypotenuse is equal to the sum of squares of other two sides, then it is a right triangle
(i) Sides of a triangle are a = 7 cm, b = 5.24 cm and c = 25 cm
(Longest side)² = (25)² = 625
Sum of square of shorter sides = (7)² + (24)² = 49 + 576 = 625
625 = 625
This is right triangle
(ii) Sides of the triangle are a = 9 cm, b = 16 cm, c = 18 cm
(Longest side)² = (18)² = 324
and sum of squares of shorter sides = (9)² + (16)² = 81 + 256 = 337
324 ≠ 337
It is not a right-angled triangle
(iii) Sides of the triangle are a = 1.6 cm, 6 = 3.8 cm, c = 4 cm
(Longest side)² = (4)² =16
Sum of squares of shorter two sides + (1.6)² + (3.8)² = 2.56 + 14.44 = 17.00
16 ≠ 17
It is not a right triangle
(iv) Sides of the triangle are a = 8 cm, b = 10 cm, c = 6 cm
(Longest side)² = (10)² = 100
Sum of squares of shorter sides = (8)² + (6)² = 64 + 36 = 100
100 = 100
It is a right triangle

Question 3.
A man goes 15 metres due west and then 8 metres due north. How far is he from the starting point ?
Solution:
Let a man starts from O, the starting point to west 15 m at A and then from A, 8 m due north at B
Join OB

Now in right ∆OAB
OB² = OA² + AB² (Pythagoras Theorem)
OB² = (15)² + (8)² = 225 + 64 = 289 = (17)²
OB = 17
The man is 17 m away from the starting point

Question 4.
A ladder 17 m long reaches a window of a building 15 m above the ground. Find the distance of the foot of the ladder from the building.
Solution:
Length of ladder = 17 m
Height of window = 15 m

Let the distance of the foot of ladder from the building = x
Using Pythagoras Theorem
AC² = AB² + BC²
=> (17)² = (15)² + x²
=> 289 = 225 + x²
=> x² = 289 – 225
=> x² = 64 = (8)²
x = 8
Distance of the foot of the ladder from the building = 8m

Question 5.
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops. (C.B.S.E. 1996C, 2002C)
Solution:
Two poles AB and CD which are 6 m and 11 m long respectively are standing oh the ground 12 m apart

Draw AE || BD so that AE = BD = 12 m and ED = AB = 6 m
Then CE = CD – ED = 11 – 6 = 5 m
Now in right ∆ACE
Using Pythagoras Theorem,
AC² = AE² + EC² = (12)² + (5)² = 144 + 25 = 169 = (13)²
AC = 13
Distance between their tops = 13 m

Question 6.
In an isosceles triangle ABC, AB = AC = 25 cm, BC = 14 cm. Calculate the altitude from A on BC. (C.B.S.E. 1994)
Solution:
∆ABC is an isosceles triangle in which AB = AC = 25 cm .
AD ⊥ BC BC = 14 cm

Perpendicular AD bisects the base i.e . BD = DC = 7 cm
Let perpendicular AD = x
In right ∆ABD,
AB² = AD² + BD² (Pythagoras Theorem)
=> (25)² = AD² + (7)²
=> 625 = AD² + 49
=> AD² = 625 – 49
=> AD² = 576 = (24)²
=> AD = 24
Perpendicular AD = 24 cm

Question 7.
The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its tip reach ?
Solution:
In first case,
The foot of the ladder are 6 m away from the wall and its top reaches window 8 m high
Let AC be ladder and BC = 6 m, AB = 8 m

Now in right ∆ABC,
Using Pythagoras Theorem
AC² = BC² + AB² = (6)² + (8)² = 36 + 64 = 100 = (10)²
AC = 10 m
In second case,
ED = AC = 10 m
BD = 8 m, let ED = x
ED² = BD² + EB²
=> (10)² = (8)² + x²
=> 100 = 64 + x²
=> x² = 100 – 64 = 36 = (6)²
x = 6
Height of the ladder on the wall = 6 m

Question 8.
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, find the distance between their tops.
Solution:
Let CD and AB be two poles which are 12 m apart
AB = 14 m, CD = 9 m and BD = 12 m
From C, draw CE || DB
CB = DB = 12 m
EB = CD = 9 m
and AE = 14 – 9 = 5 m

Now in right ∆ACE,
AC² = AE² + CE² (Pythagoras Theorem)
= (5)² + (12)²
= 25 + 144 = 169 = (13)²
AC = 13
Distance between their tops = 13 m

Question 9.
Using Pythagoras theorem, determine the length of AD in terms of b and c shown in the figure. (C.B.S.E. 1997C)

Solution:
In right ∆ABC, ∠A = 90°
AB = c, AC = b
AD ⊥ BC

Question 10.
A triangle has sides 5 cm, 12 cm and 13 cm. Find the length to one decimal place, of the perpendicular from the opposite vertex to the side whose length is 13 cm. (C.B.S.E. 1992C)
Solution:
A triangle has sides 5 cm, 12 cm and 13 cm
(Longest side)² = (13)² = 169
Sum of squares of shorter sides = (5)² + (12)² = 25 + 144= 169
169 = 169
It is a right triangle whose hypotenuse is 13 cm

BD = 4.6 cm

Question 11.
ABCD is a square, F is the mid point of AB. BE is one third of BC. If the area of ∆FBE = 108 cm² find the length of AC. (C.B.S.E. 1995)
Solution:
In square ABCD, F is mid point of AB i.e.,

Question 12.
In an isosceles triangle ABC, if AB = AC = 13 cm and the altitude from A on BC is 5 cm, find BC. (C.B.S.E. 2000)
Solution:
In ∆ABC, AB = AC
AD ⊥ BC
AB = AC = 13 cm, AD = 5 cm
AD ⊥ BC
AD bisects BC at D
BD = \(\frac { 1 }{ 2 }\) BC
=> BC = 2BD

Question 13.
In a ∆ABC, AB = BC = CA = 2a and AD ⊥ BC. Prove that
(i) AD = a √3
(ii) area (∆ABC) = √3 a² (C.B.S.E. 1991)
Solution:
In ∆ABC, AB = BC = AC = 2a
AD ⊥ BC
AD bisects BC at D
BD = DC = \(\frac { 1 }{ 2 }\) BC = a

Question 14.
The lengths of the diagonals of a rhombus are 24 cm and 10 cm. Find each side of the rhombus. (C.B.S.E. 1993C)
Solution:
ABCD is a rhombus whose diagonals AC = 24 cm and BD = 10 cm
The diagonals of a rhombus bisect eachother at right angles

AO = OC = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = OD = \(\frac { 10 }{ 2 }\) = 5 cm
Now in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
(12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm

Question 15.
Each side of a rhombus is 10 cm. If one of its diagonals is 16 cm, find the length of the other diagonal.
Solution:
In rhombus ABCD, diagonals AC and BD bisect eachother at O at right angles
Each side = 10 cm and one diagonal AC = 16 cm

AO = OC = \(\frac { 16 }{ 2 }\) = 8 cm
Now in right angled triangle AOB,
AB² = AO² + OB² (Pythagoras Theorem)
(10)² = (8)² + (BO)²
=> 100 = 64 + BO²
=> BO² = 100 – 64 = 36 = (6)²
BO = 6
BD = 2BO = 2 x 6 = 12 cm

Question 16.
Calculate the height of an equilateral triangle each of whose sides measures 12 cm.
Solution:
Each side of the equilateral ∆ABC = 12 cm
AD ⊥ BC which bisects BC at D


BD = DC = \(\frac { 12 }{ 2 }\) = 6 cm

Question 17.
In the figure, ∠B < 90° and segment AD ⊥ BC. Show that:
(i) b² = h² + a² + x² – 2ax
(ii) b² = a² + c² – 2ax

Solution:
Given : In ∆ABC, ∠B < 90°
AD ⊥ BC
AD = c, BC = a, CA = b AD = h, BD = x, DC = a – x
To prove: (i) b² = h² + a² + x² – 2ax
(ii) b² = a² + c² – 2ax
Proof: (i) In right ∆ADC, AC² = AD² + DC² (Pythagoras Theorem)
=> b² = h² + (a – x)² = h² + a² + x² – 2ax
(ii) Similarly in right ∆ADB
AB² = AD² + BD²
c² = h² + x² ….(i)
b² = h² + a² + x² – 2ax = h² + x² + a² – 2ax
= c² + a² – 2ax {From (i)}
= a² + c² – 2ax
Hence proved.

Question 18.
In an equilateral ∆ABC, AD ⊥ BC, prove that AD² = 3 BD². (C.B.S.E. 2002C)
Solution:
Given : ∆ABC is an equilateral in which AB = BC = CA .
AD ⊥ BC

Question 19.
∆ABD is a right triangle right-angled at A and AC ⊥ BD. Show that
(i) AB² = BC.BD
(ii) AC² = BC.DC
(iii) AD² = BD.CD
(iv) \(\frac { { AB }^{ 2 } }{ { AC }^{ 2 } }\) = \(\frac { BD }{ DC }\) [NCERT]
Solution:
In ∆ABD, ∠A = 90°
AC ⊥ BD

Question 20.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut ?
Solution:
Let AB be the vertical pole whose height = 18 m

Question 21.
Determine whether the triangle having sides (a – 1) cm, 2 √a cm and (a + 1) cm is a right angled triangle. [CBSE 2010]
Solution:
Sides of a triangle are (a – 1) cm, 2 √a cm and (a + 1) cm
Let AB = (a – 1) cm BC = (a + 1) cm
and AC = 2 √a

Question 22.
In an acute-angled triangle, express a median in terms of its sides.
Solution:
In acute angled ∆ABC,
AD is median and AL ⊥ BC
Using result of theorem, sum of the squares of any two sides is equal to the twice the square of half of the third side together with twice the square of the median which bisects the third side

Question 23.
In right-angled triangle ABC in which ∠C = 90°, if D is the mid point of BC, prove that AB² = 4AD² – 3AC².
Solution:
Given : In right ∆ABC, ∠C = 90°
D is mid point of BC

Question 24.
In the figure, D is the mid-point of side BC and AE ⊥ BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that :


Solution:

Question 25.
In ∆ABC, ∠A is obtuse, PB x AC and QC x AB. Prove that:
(i) AB x AQ = AC x AP
(ii) BC² = (AC x CP + AB x BQ)
Solution:
Given : In ∆ABC, ∠A is an obtuse angle PB x AC and QC x AB on producing them

Question 26.
In a right ∆ABC right-angled at C, if D is the mid-point of BC, prove that BC² = 4 (AD² – AC²).
Solution:
Given : In ∆ABC, ∠C = 90°
D is mid-point of BC
AD is joined

=> 4AD² = 4AC² + BC²
=> BC² = 4AD² – 4AC²
=> BC² = 4 (AD² – AC²)
Hence proved.

Question 27.
In a quadrilateral ABCD, ∠B = 90°, AD² = AB² + BC² + CD², prove that ∠ACD = 90°.
Solution:
Given : ABCD is a quadrilateral in which ∠B = 90° and AD² = AB² + BC² + CD²
To prove : ∠ACD = 90°
Construction : Join AC

proof : In right ∆ABC, ∠B = 90°
AC² = AB² + BC² ….(i) (Pythagoras Theorem)
But AD² = AB² + BC² + CD² (given)
=> AD² = AC² + CD² {From (i)}
∆ACD is a right angle with right angle ACD
Hence proved.

Question 28.
An aeroplane leaves an airport and flies due north at a speed of 1000 km/hr. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km/ hr. How far apart will be the two planes after 1\(\frac { 1 }{ 2 }\) hours?
Solution:

Speed of the first plane = 1000 km/hr
Distance travelled in 1\(\frac { 1 }{ 2 }\) hour due north = 1000 x \(\frac { 3 }{ 2 }\) = 1500 km
Speed of the second plane = 1200 km/hr
Distance travelled in 1\(\frac { 1 }{ 2 }\) hours due west

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances Ex 12.1
• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS
• RD Sharma Class 10 Solutions Chapter 12 Heights and Distances MCQS

Answer each of the following questions either in one word or one sentence or per requirement of the questions :
Question 1.
The height of a tower is 10 m. What is the length of its shadow when Sun’s altitude is 45° ?
Solution:
Let AB be the tower and BC is its shadow
Height of AB = 10 m
Let length of BC = x
Angle of elevation of A at C is 45°

Question 2.
If the ratio of the height of a angle tower and the length of 7 its shadow is \(\sqrt { 3 } \) : 1, what is the of elevation of the Sun?
Solution:
Ratio in the height of a tower and its shadow = \(\sqrt { 3 } \) : 1

Question 3.
What is the angle of elevation of the Sun when the length of the shadow of a vertical pole is equal to its height ?
Solution:
Let height of a vertical pole = h
Then its shadow = x

Question 4.
From a point on the ground, 20 m away from the foot of a vertical tower, the angle of elevation of the top of the tower is 60°, what is the height of the tower ?
Solution:
Let AB be the tower and the angles of elevation of its top from a point C on the ground is 60° and BC = 20 m
Let height of the tower AB = h

Question 5.
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line, with it are complementary, find the height of the tower.
Solution:
Let CD be the tower and let the angles of elevation of the top C of the tower from two points A and B are θ and (90° – θ) as the angles are complementary

Let height of the tower CD = h
and AD = 9 m, BD = 4 m

Question 6.
In the figure, what are the angles of depression from the observing positions O₁ and O₂ of the object at A ?
Solution:
In the given figure, draw XY || ABC from O₁,O₂ (by joinging them)
∵∠AO₁C = 60°
∠AO₁O₂ = 90° – 60° = 30°
Similarly,
∵∠O₂ AB = 45°
∠XO₂A = ∠O₂AB = 45° (alternate angles)
Hence angles of depression are 30° and 45°

Question 7.
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x : y. [CBSE2015]
Solution:
Let AB and CD be two towers which are apart from each other at a distance of BD and M is mid point of BD.
Angles of elevation are 30° and 60°

Question 8.
The angle of elevation of the top of a tower at a point on the ground is 30°. What will be the angle of elevation, if the height of the tower is tripled?     [CBSE 2015]
Solution:
Let AB be the tower and apgle of elevation of A at C is 30°

Question 9.
AB is a pole of height 6 m standing at a point B and CD is a ladder inclined at angle of 60° to the horizontal and reaches upto a point D of pole. If AD = 2.54 m, find the length of the ladder. (Use \(\sqrt { 3 } \)  = 1.73)       [CBSE 2016]
Solution:
BD = AB – AD = 6 – 2.54 = 3.46 m

Question 10.
An observer, 1.7 m tall, is 20\(\sqrt { 3 } \) m away from a tower. The angle of elevation from the eye of an observer to the top of tower is 30°. Find the height of the tower. [CBSE 2016]
Solution:

Question 11.
An observer, 1.5 m tall, is 28.5 m away from a 30 m high tower. Determine the angle of elevation of the top-of the tower from the eye of the observer. [CBSE 2017]
Solution:

Here, AE = 28.5 m
ED = BC = 28.5 m
In ΔADE,
tan ∠ADE = \(\frac { 28.5 }{ 28.5 }\)
= ∠ADE = tan^-1(1) – 45°
∴ The angle of elevation at the top of the tower from the eye of the observer is 45°.

Hope given RD Sharma Class 10 Solutions Chapter 12 Heights and Distances VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.