Category: CBSE Class 10

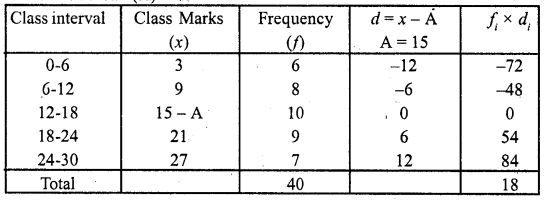
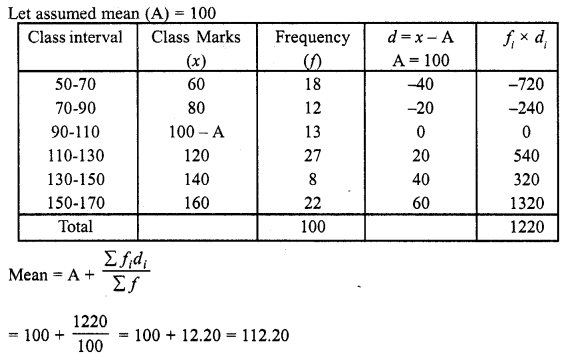
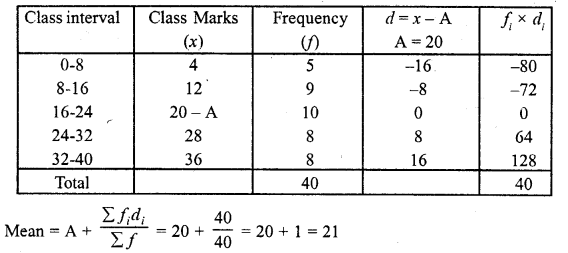
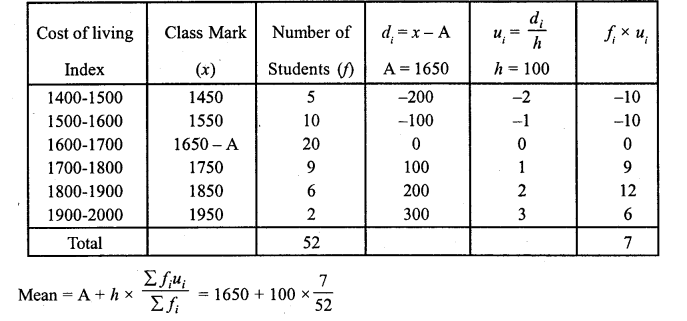
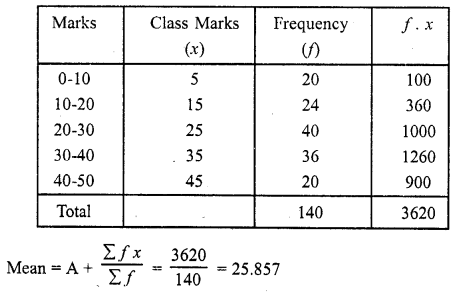
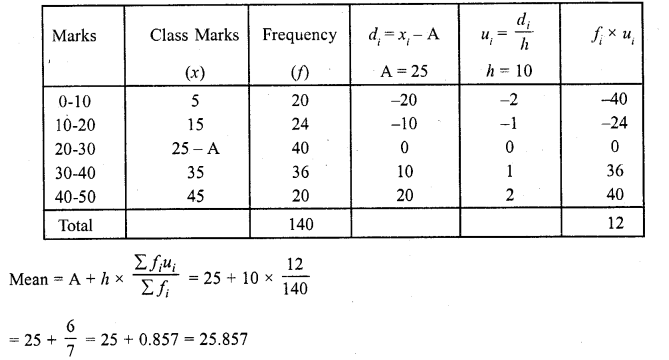
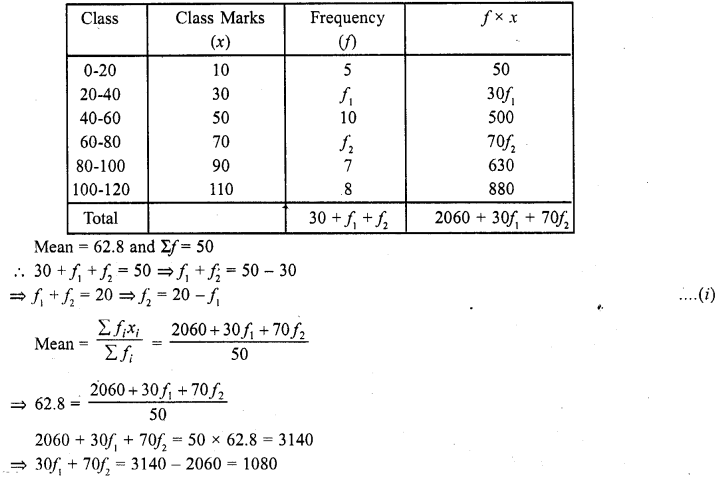
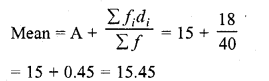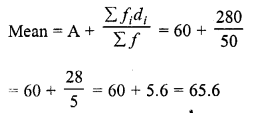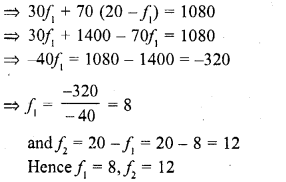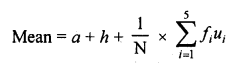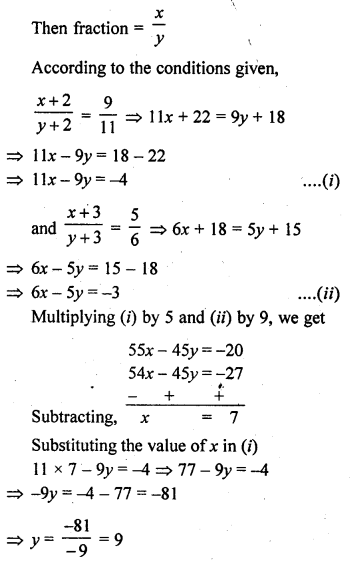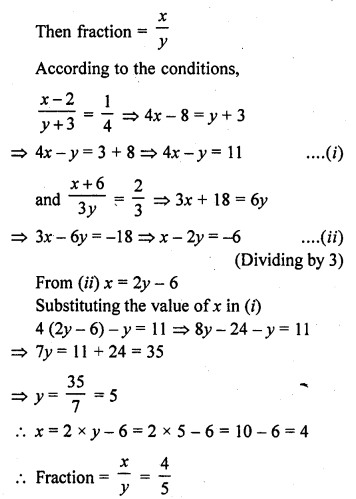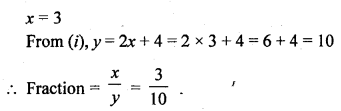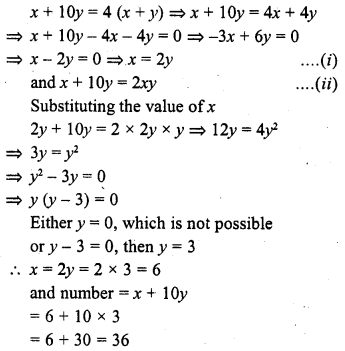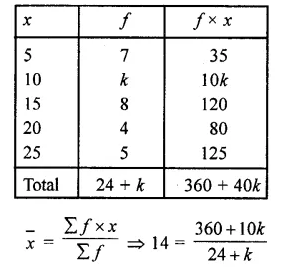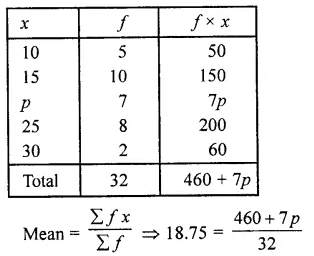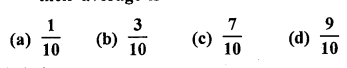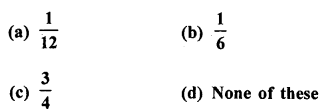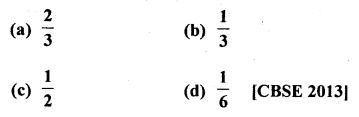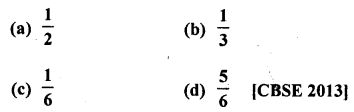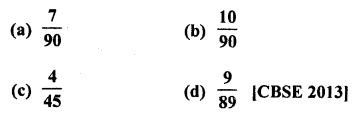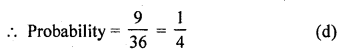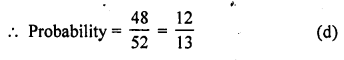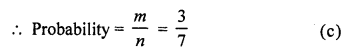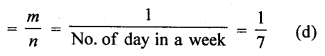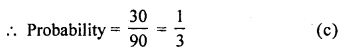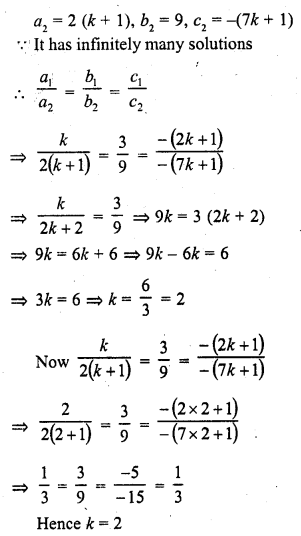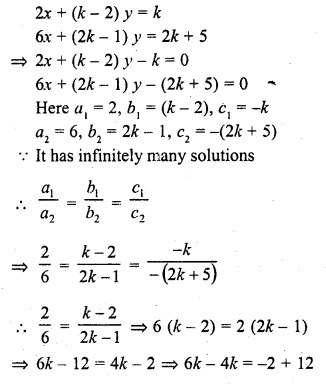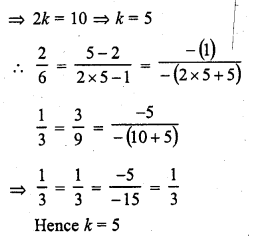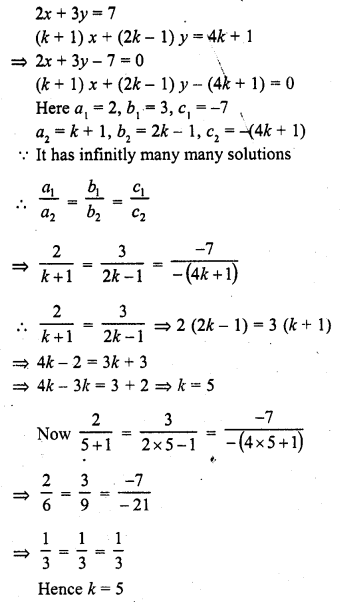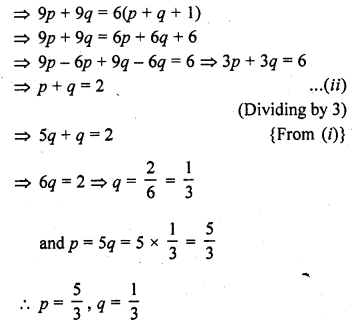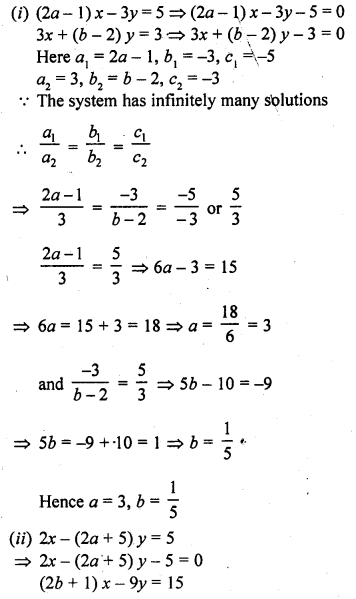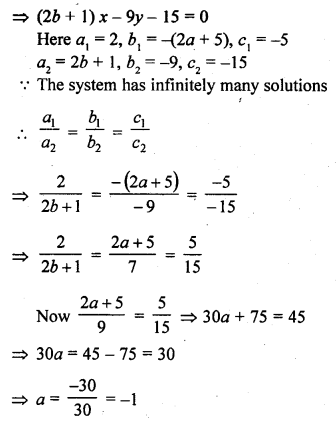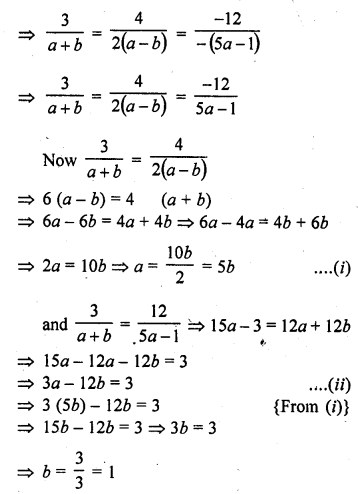RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

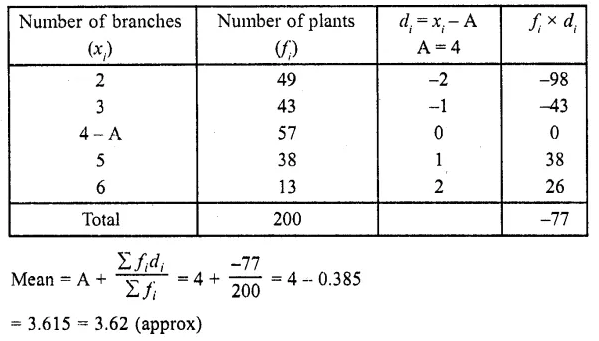
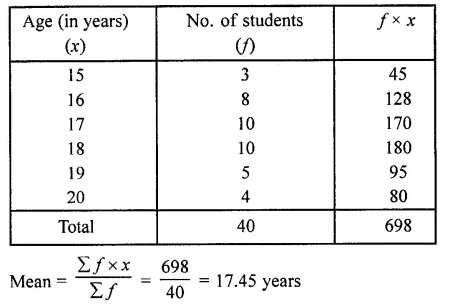
Question 1.
Following are the lives in hours of 15 pieces of the components of aircraft engine. Find the median :
715, 724, 725, 710, 729, 745, 694, 699, 696, 712, 734, 728, 716, 705, 719
Solution:
Arranging in ascending order, we get
694, 696, 699, 705, 710, 712, 715, 716, 719, 724, 725, 728, 729, 734, 745 Here N = 15 which is odd

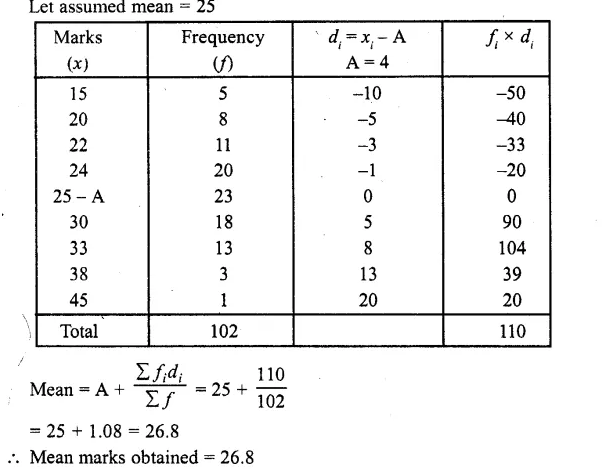
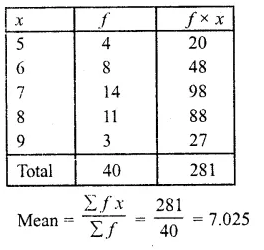
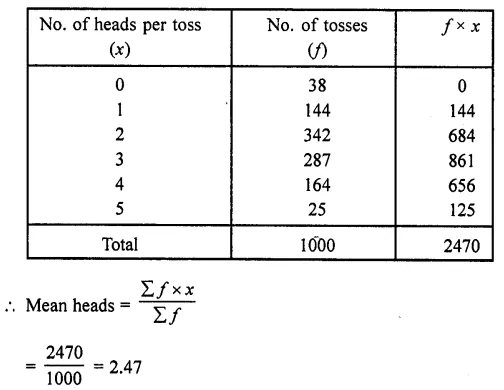
Question 2.
The following is the distribution of height of students of a certain class in a certain city :

Find the median height.
Solution:
Arranging the classes in exclusive form and then forming its cumulative frequency table as given

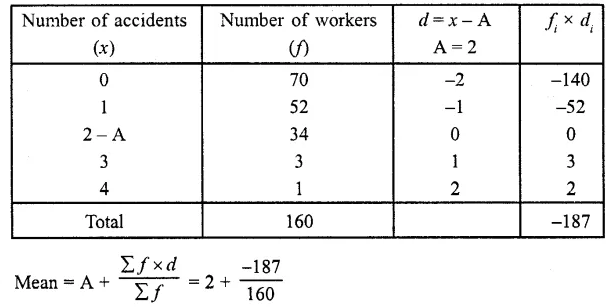
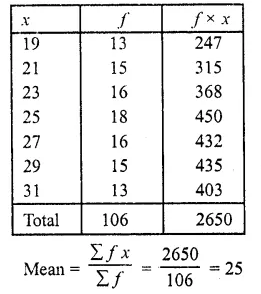
Question 3.
Following is the distribution of I.Q. of 100 students. Find the median I.Q.

Solution:
Arranging the classes in exclusive form and then forming it in cumulative frequency table as shown below :

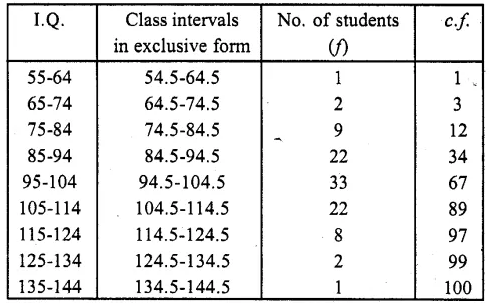
Here N = 100
∴ \(\frac { N }{ 2 }\) = \(\frac { 100 }{ 2 }\) = 50
∴ Corresponding median class is = 94.5-104.5
l = 94.5, f= 33, F = 34 and h = 10

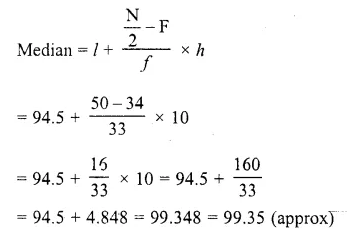
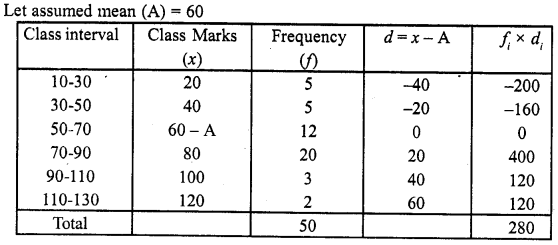
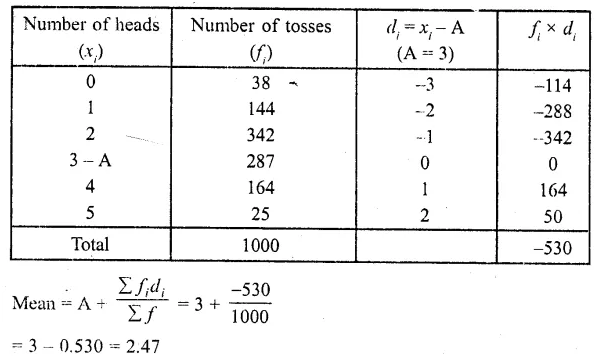
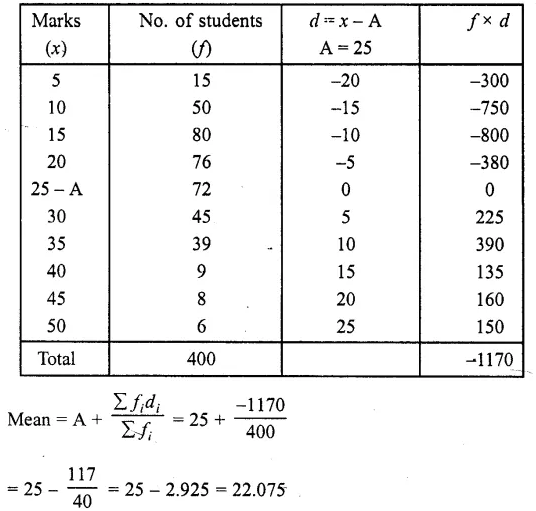
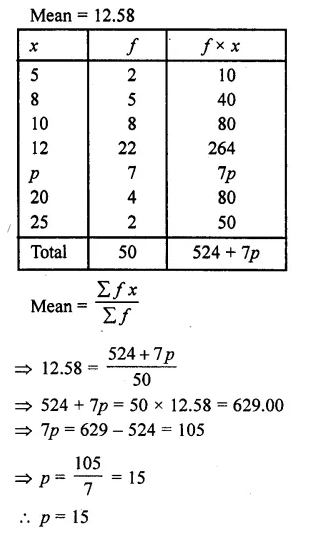
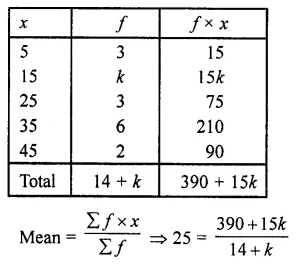
Question 4.
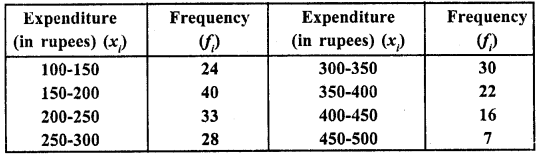
Calculate the median from the following data :

Solution:
Writing the given data in cumulative frequency table as shown

Question 5.
Calculate the median from the following data :

Solution:

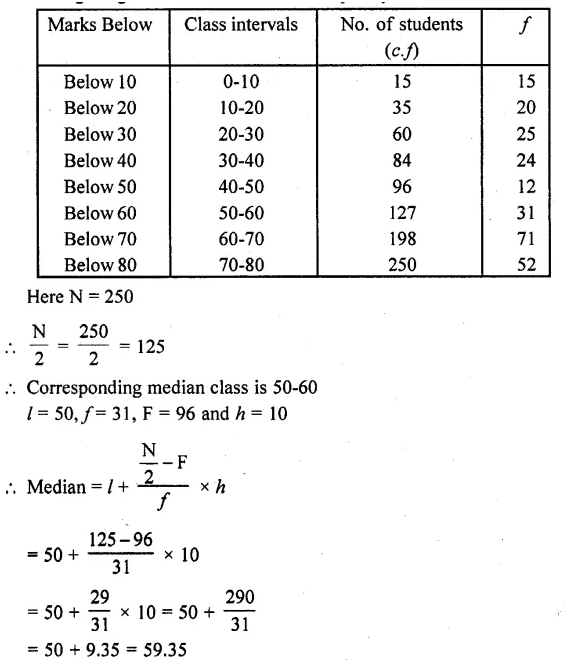
Question 6.
Calculate the missing frequency from the following distribution, it being given that the median of the distribution

Solution:
Median = 24, let p be the missing frequency.

Question 7.
The following table gives the frequency distribution of married women by age at marriage:

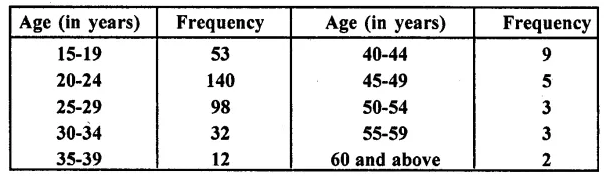
Calculate the median and interpret the results.
Solution:
Writing classes in exclusive form,

Question 8.
The following table gives the distribution of the life time of 400 neon lamps :

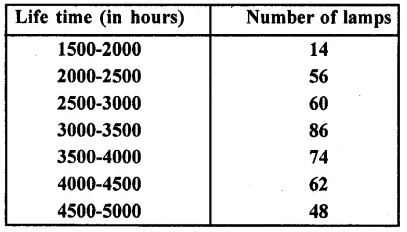
Find the median life.
Solution:

= 3000 + 406.98 = 3406.98

Question 9.
The distribution below gives the weight of 30 students in a class. Find the median weight of students :

Solution:
Here  N =30 ,\(\frac { N }{ 2 }\) = \(\frac { 30 }{ 2 }\) which  lies in the class 55 – 60 ( ∵ 13 < 15 < 19)

Question 10.
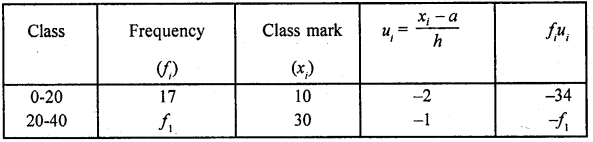
Find the missing frequencies and the median for the following distribution if the mean is 1.46.

Solution:
Mean = 1.46, N= 200
Let p₁ and p₂ be the missing frequencies

⇒ p₁+ 2p₂= 292 – 140 = 152
114-p₂ + 2p₂= 152
⇒ p₂ = 152- 114 = 38
∴ p₁= 114-p₂= 114-38 = 76
Hence missing frequencies are 76 and 38
Median = Here \(\frac { N }{ 2 }\) = \(\frac { 200 }{ 2 }\) = 100
∴ cf of 2nd class is 46 + 76 = 122
∴ Median = 1

Question 11.
An incomplete distribution is given below :

You are given that the median value is 46 and the total number of items is 230.
(i) Using the median formula fill up missing frequencies.
(ii) Calculate the AM of the completed distribution.
Solution:
Let p₁, and p₂ be the missing frequencies
Median = 46 and N = 230

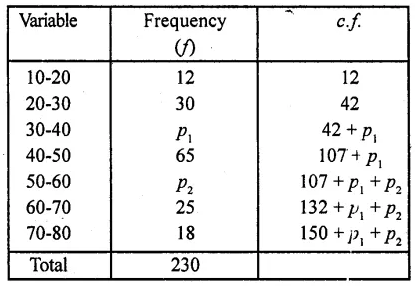
∴ 150 + p₁ + p₂ = 230

⇒ p₁+p₂ = 230 – 150 = 80
∴ p₂ = 80-p₁ ….(i)
∵ Median = 46 which lies in the class 40-50
∴ I = 40, f= 65, F = 42 +p₁, h = 10

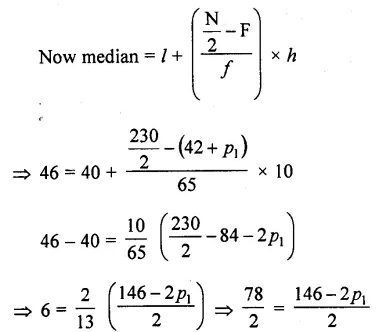
⇒ 39 = 73 – p₁
⇒ p₁ = 73 -39 = 34
∴ p₂ – 80 – p₁ = 80 – 34 = 46
Hence missing frequencies are 34, and 46
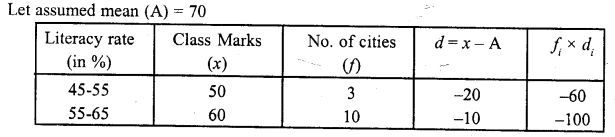
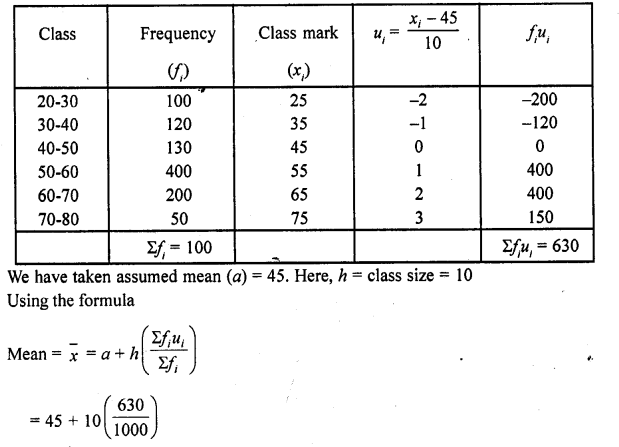
Mean Let assumed mean (A) = 45

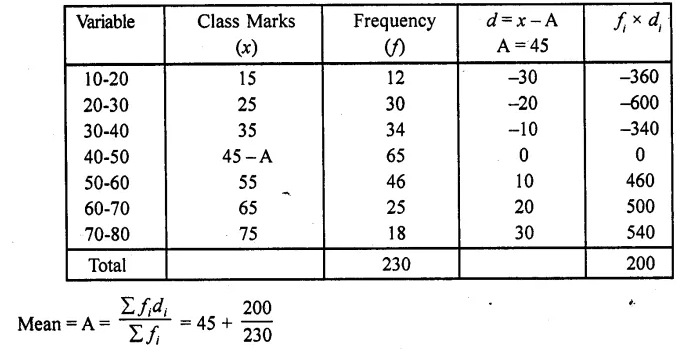
= 45 + 0.8695
= 45 + 0.87
= 45.87

Question 12.
If the median of the following frequency distribution is 28.5 find the missing frequencies:

Solution:
Mean = 28.5 , N = 60

17 = 25 -f₁
⇒ f₁= 25 -17 = 8
and f₂ = 15-f₁ = 15-8 = 7
Hence missing frequencies are 8 and 7

Question 13.
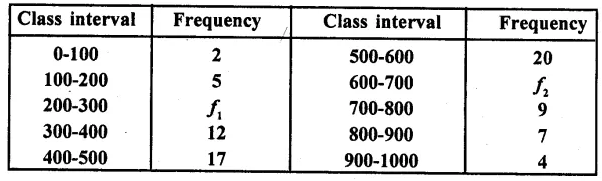
The median of the following data is 525. Find the missing frequency, if it is given that there are 100 observations in the data:

Solution:
Median = 525, N = 100

⇒ 525 – 500 = (14 -f₁) x 5
⇒ 25 = 70- 5f₁
⇒ 5f₁ = 70 – 25 = 45
⇒ f₁ = \(\frac { 45 }{ 5 }\) = 9
and f₂ = 24 – f₁ = 24 – 9 = 15
Hence f₁ = 9, f₂ = 15

Question 14.
If the median of the following data is 32.5, find the missing frequencies.

Solution:
Mean = 32.5 and N= 40

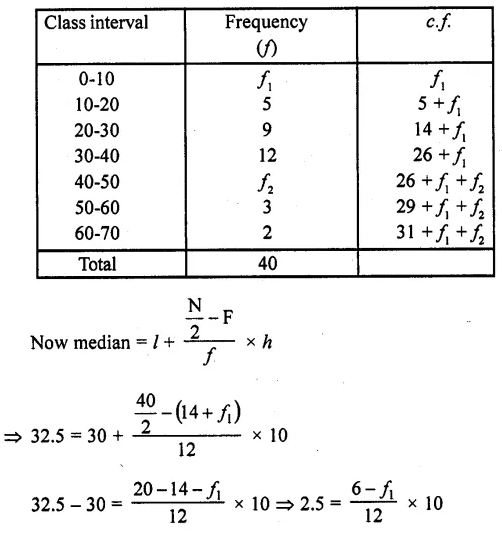
⇒ 2.5 x 12 = 60 – 10f₁
⇒ 30 = 60 – 10f₁
⇒ 10f₁ = 60-30 = 30
⇒ f₁ = \(\frac { 30 }{ 10 }\) =3
∴ f₂ = 9 – f₁ = 9-3 = 6
Hence f₁ = 3, f₂= 6

Question 15.
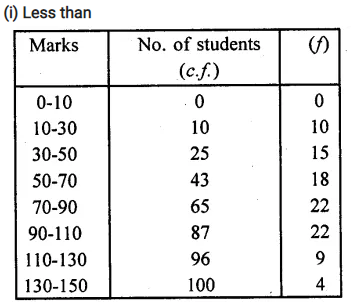
Compute the median for each of the following data:

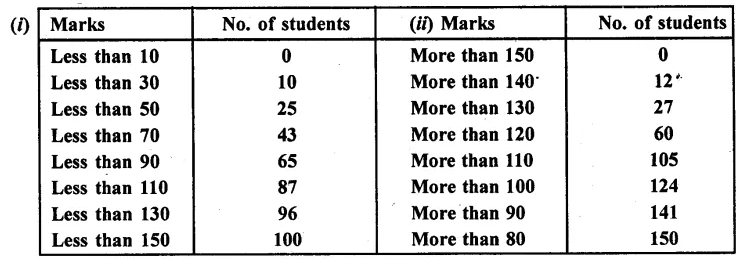
Solution:

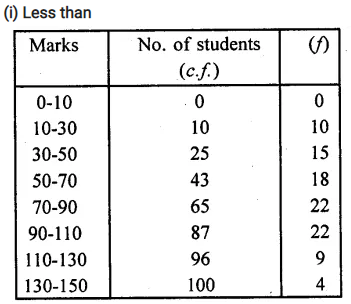
Here N= 100=
∴ \(\frac { N }{ 2 }\) = \(\frac { 100 }{ 2}\) = 50 which lies in the class 70-90 (∵ 50 < 65 and > 43)
∴ l = 70, F =43 , f = 22 ,h = 20

(ii) Greater than

N = 150, \(\frac { N }{ 2 }\) = \(\frac { 150 }{ 2 }\) = 75 which lies in the class 110-120 (∵ 75 > 105 and 75 > 60)
∴ l = 110, F = 60 , f=45, h= 10

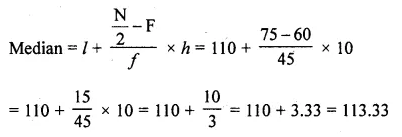
Question 16.
A survey regarding the height (in cm) of 51 girls of class X of a school was conducted and
the following data was obtained.

Find the median height.
Solution:

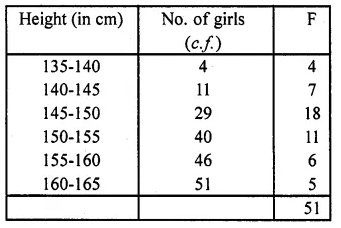
Here \(\frac { N }{ 2 }\) = \(\frac { 51 }{ 2 }\) = 25.5 or 26 which lies in the class 145-150
l= 145, F= 11, f= 18, h= 5

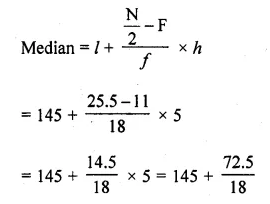
= 145 + 4.03 = 149.03

Question 17.
A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are only given to persons having age 18 years onward but less than 60 years.

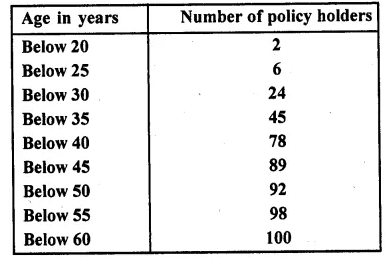
Solution:

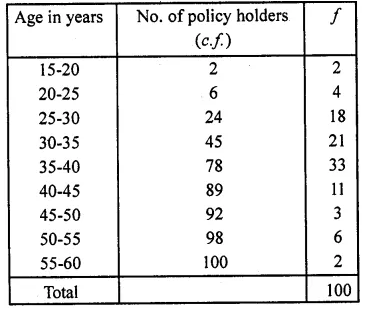
Here N = 100, \(\frac { N }{ 2 }\) = \(\frac { 100 }{ 2 }\) = 50 which lies in the class 35-40 ( ∵ 45 > 50> 78)
l = 35, F = 45, f= 33, h = 5

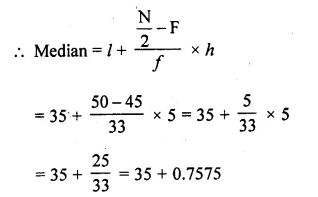
= 35 + 0.76 = 35.76

Question 18.
The lengths of 40 leaves of a plant are measured correct to the nearest millimetre, and the data obtained is represented in the following table:

Find the mean length of leaf.
Solution:

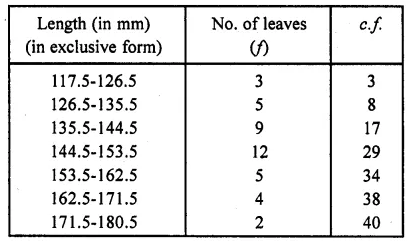
N = 40, \(\frac { N }{ 2 }\) = \(\frac { 40 }{ 2 }\) = 20 which lies in the class 144.5-153.5 as 17 < 20 < 29
∴ l= 144.5, F= 17, f= 12, h = 9

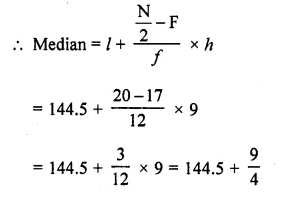
= 144.5 + 2.25 = 146.75

Question 19.
An incomplete distribution is given as follows :

You are given that the median value is 35 and the sum of all the frequencies is 170. Using the median formula, fill up the missing frequencies.
Solution:
Median = 25 and ∑f= N = 170
Let p₁ and p₂ be two missing frequencies

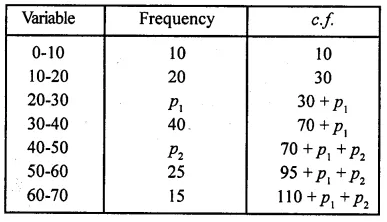
∴ 110 + p₁ +p₂ = 170
⇒ p₁+ p₂ = 170 – 110 = 60
Here N = 170, \(\frac { N }{ 2 }\) = \(\frac { 170 }{ 2 }\) = 85
∴ Median = 35 which lies in the class 30-40
Here l = 30, f= 40, F = 30 + p₁ and h = 10

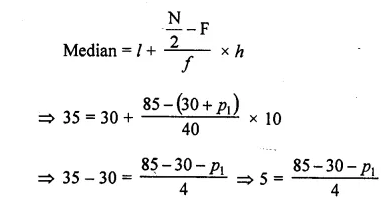
20 = 55 – p₁
⇒ p₁ = 55 – 20 = 35
But p₁+ p₂ = 60
∴ p₂ = 60 -p₁ = 60 – 35 = 25
Hence missing frequencies are 35 and 25

Question 20.
The median of the distribution given below is 14.4. Find the values of x and y, if the total frequency is 20.

Solution:

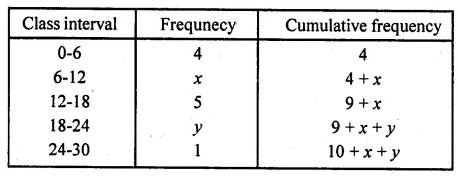
It is given that n = 20
So, 10 + x + y – 20, i.e., x+y= 10 …(i)
It is also given that median = 14.4
Which lies in the class interval 12-18
So, l = 12, f= 5, cf = 4 + x, h = 6
Using the formula,

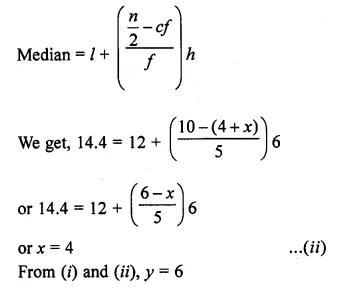
Question 21.
The median of the following data is SO. Find the values of p and q, if the sum of all the frequencies is 90.

Solution:

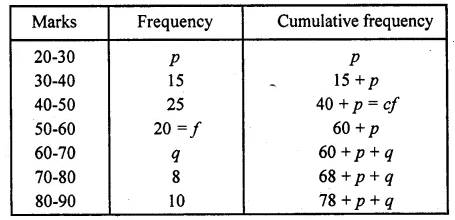
Given, N = 90
∴ \(\frac { N }{ 2 }\) = \(\frac { 90 }{ 2 }\) = 45
Which lies in the interval 50-60
Lower limit, l = 50, f= 20, cf= 40 + p, h = 10

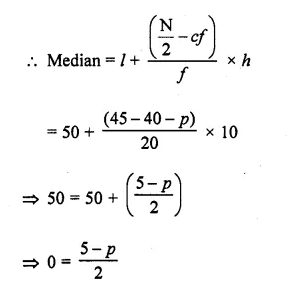
∴ P = 5
Also, 78 +p + q = 90
⇒ 78 + 5 + q = 90
⇒ q = 90-83
∴ q = 7

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
Points A and B are 70 km. a part on a highway. A car starts from A and another car starts from B simultaneously. If they travel in the same direction, they meet in 7 hours, but if they travel towards each other, they meets in one hour. Find the speed of the two cars. (C.B.S.E. 2002)
Solution:
Distance between two points A and B = 70 km
Let speed of first car starting from A = x km/hr
and speed of second car starting from B =y km/hr
When these start in the some direction, they meet after 7 hours
Distance travelled by the first car = 7x km
and by second car = 7y km

When these travel in opposite direction, they meet after 1 hour then distance travelled by first car = x km
and by second car = y km
x + y = 70 ….(ii)
Adding (i) and (ii)
2x = 80
=> x = 40
and subtracting (i) from (ii)
2y = 60
=> y = 30
Speed of first car = 40 km/hr
and speed of second car = 30 km/hr

Question 2.
A sailor goes 8 km downstream in 40 minutes and returns in 1 hour. Determine the speed of the sailor in still water and the speed of the current. (C.B.S.E. 1997)
Solution:
Let the speed of sailor in still water = x km/ hr
and speed of water = y km/hr
Distance covered = 8 km

Question 3.
The boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours, it can go 40 km upstream and 55 km downstream. Determine the speed of stream and that of the boat in still water.
Solution:
Let the speed of stream = y km/hr
and speed of boat = x km/hr
Speed of boat downstream = (x + y) km/hr
In first case, and up stream = (x – y) km/hr
Upstream distance = 30 km
and down distance = 44 km
Total time taken = 10 hrs
In second case,
upstream distance = 40 km
and downstream distance = 55 km
Total time taken = 13 hrs

Question 4.
A boat goes 24 km upstream and 28 km downstream in 6 hrs. It goes 30 km upstream and 21 km downstream in 6\(\frac { 1 }{ 2 }\) hrs. Find the speed of the boat in still water and also speed of the stream.
Solution:
Let the speed of boat = x km/hr
and speed of stream = y km/hr
In first case,
Distance covered upstream = 24 km
and down stream = 28 km
Total time taken = 6 hours
In second case,
Distance covered upstream = 30 km
and downstream = 21 km
Total time taken = 6\(\frac { 1 }{ 2 }\) = \(\frac { 13 }{ 2 }\) hrs.

Question 5.
A man walks a certain distance with a certain speed. If he walks 1/2 km an hour faster, he takes 1 hour less. But, if he walks 1 km an hour slower, he takes 3 more hours. Find the distance covered by the man and his original rate of walking.
Solution:
Let the distance = x km
and let certain speed = y km/hr

Question 6.
A person rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream. [NCERT Exemplar]
Solution:
Let the speed of the stream be v km/h
Given that, a person rowing in still water = 5 km/h
The speed of a person rowing in downstream = (5 + v) km/h
and the speed of a person Has rowing in upstream = (5 – v) km/h
Now, the person taken time to cover 40 km downstream,

Question 7.
Ramesh travels 760 km to his home partly by train and partly by car. He takes 8 hours if he travels 160 km. by train and the rest by car. He takes 12 minutes more if the travels 240 km by train and the rest by car. Find the speed of the train and car respectively.
Solution:
Total distance = 769 km
Let the speed of train = x km/hr
and speed of car = y km/hr
Time taken = 8 hours
In first case, distance travelled by train = 160 km
and rest distance 760 – 160 = 600 km by car
Time taken

Question 8.
A man travels 600 km partly by train and partly by car. If the covers 400 km by train and the rest by car, it takes him 6 hours and 30 minutes. But, if he travels 200 km by train and the rest by car, he takes half an hour longer. Find the speed of the train and that of the car. (C.B.S.E. 2001)
Solution:
Total journey = 600 km
Let the speed of train. = x km/hr
and speed of car = y km/hr
In first case,
Journey by train = 400 km
Journey by car = 600 – 400 = 200 km

Question 9.
Places A and B are 80 km apart from each other on a highway. A car starts from A and other from B at the same time. If they move in the same direction, they meet in 8 hours and if they move in opposite directions, they meet in 1 hour and 20 minutes. Find the speeds of the cars. [CBSE 2002]
Solution:
Distance between A and B = 80 km
One car starts from A and other from B in the same direction and they meet after 8 hours
Let the speed of the first car = x km/hr
and speed of second car = y km/hr
Distance travelled by the first car = 8x km
and by the second car = 8y km
8x – 8y = 80
=> x – y = 10 ….(i)
When the two cars move in opposite direction, they

Question 10.
A boat goes 12 km upstream and 40 km downstream in 8 hours. It can go 16 km upstream and 32 km downstream in the same time. Find the speed of the boat in still water and the speed of the steam. [CBSE 1999C]
Solution:
Let the speed of boat = x km/hr
and speed of stream = y km/hr
=> Speed of the boat upstream = (x – y) km/hr
and speed of boat down stream = x + y km/ hr



Hence speed of boat = 6 km/hr and speed streams = 2 km/hr

Question 11.
Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution:
Total distance = 300 km
Let the speed of train = x km/hr
and speed of bus = y km/hr
In first case,
Distance travelled by train = 60 km
and distance by bus = 300 – 60 = 240
and total time taken = 4 hrs

Question 12.
Ritu can row downstream 20 km in 2 hours and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
Solution:
Let the speed of rowing in still water = x km/hr
and speed of current of water = y km/hr
Speed of downstream = (x + y) km/hr
and speed of upstream = (x – y) km/hr

Speed of rowing = 6 km/hr and speed of current = 4 km/hr

Question 13.
A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream. [NCERT Exemplar]
Solution:
Let the speed of the motorboat in still water and the speed of the stream are u km/h and v km/h, respectively.
Then, a motorboat speed in downstream = (u + v) km/h
and a motorboat speed in upstream = (u – v) km/h
Motorboat has taken time to travel 30 km upstream,

Question 14.
Abdul travelled 300 km by train and 200 km by taxi, it took him 5 hours 30 minutes. But it he travels 260 km by train and 240 km by taxi he takes 6 minutes longer. Find the speed of the train and that of the taxi. (CBSE 2006C)
Solution:
Let the speed of train = x km/hr
and speed of taxi = y km/hr
In first case,

Question 15.
A train covered a certain distance at a uniform speed. If the train could have been 10 km/hr. faster, it would have taken 2 hours less than the Scheduled time. And, if the train were slower by 10 km/ hr ; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solution:
Let the speed of the train = x km/hr
and time taken = y hours
Distance = speed x time = x x y = xy km
In the first case,
Speed = (x + 10) km/hr
Time = (y – 2) hours
Distance = (x + 10) (y – 2) = xy
=> xy – 2x+ 10y – 20 = xy
=> -2x + 10y – 20 = 0
=> x – 5y + 10 = 0 ……….(i)
In second case,
Speed of the train = (x – 10) km/hr
and time = (y + 3) hours
Distance = (x – 10) (y + 3) = xy
=> xy + 3x – 10y – 30 = xy
=> 3x – 10y – 30 = 0 ………(ii)
Multiplying (i) by 2 and (ii) by 1

Question 16.
Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of two cars ?
Solution:
Distance between A and B places = 100 km
Let the speed of first car (starting from A) = x km/hr
and speed of second car (starting from B) = y km/hr
In first case, when the cars travel in the same direction
Time when they meet = 5 hours
Distance travelled by first car in 5 hours = 5x km
and by second car = 5y = 5y km
5x – 5y = 100
=> x – y = 20 …(i)
In second case, when the cars travel in the opposite direction
Time when they meet = 1 hour
Distance travelled by first case = x x 1 = x km
and by second car = y x 1 = y km
x + y = 100 ……..(i)
Adding (i) and (ii)
2x = 120 => x = 60
Subtracting (i) from (ii)
2y = 80 => y = 40
Speed of first car = 60 km/hr and speed of second car = 40 km/hr

Question 17.
While covering a distance of 30 km. Ajeet takes 2 hours more than Amit. If Ajeet doubles his speed, he would take 1 hour less than Amit. Find their speeds of walking.
Solution:
Total distance = 30 km
Let speed of Ajeet = x km/hr
and speed of Amit = y km/hr
Now according to the condition,

Speed of Ajeet = 5 km/hr and speed of Amit = 7.5 km/hr

Question 18.
A takes 3 hours more than B to walk a distance of 30 km. But if A doubles his pace (speed) he is ahead of B by 1\(\frac { 1 }{ 2 }\) hours. Find their speeds.
Solution:
Let speed of A = x km/hr
and speed of B = y km/hr
Total distance in first case,
\(\frac { 30 }{ x }\) – \(\frac { 30 }{ y }\) = 3

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
A father is three times as old as his son. After twelve years, his age will be twice as that of his son then. Find their present ages. (C.B.S.E. 1992)
Solution:
Let present age of father = x
and that of son = y
According to the conditions,
x = 3y ….(i)
After 12 years,
Age of father = x + 12
and age of son = y + 12
x + 12 = 2(y + 12)
x + 12 = 2y + 24
=> 3y + 12 = 2y + 24 {From (i)}
=> 3y – 2y = 24 – 12
=> y = 12
x = 3y = 3 x 12 = 36
Hence present age of father = 36 years and age of son = 12 years

Question 2.
Ten years later, A will be twice as old as B and five years ago, A was three times as old as B. What are the present ages of A and B ? (C.B.S.E. 1992)
Solution:
Let present age of A = x years
and age of B = y years
10 years later
A’s age will be = x + 10
and B’s age will be = y + 10
x + 10 = 2(y + 10)
=> x + 10 = 2y + 20
=> x – 2y = 20 – 10
=> x – 2y = 10 ….(i)
5 years ago,
A’s age was = x – 5 years
and B’s age was = y – 5 years
x – 5 = 3 (y – 5)
=> x – 5 = 3y – 15
=> x – 3y = 5 – 15 = -10 ….(ii)
Subtracting (ii) from (i) we get
y = 20
and x – 2 x 20 = 10
=> x = 40 + 10 = 50
A’s present age = 50 years
and B’s present age = 20 years

Question 3.
Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu ?
Solution:
Let present age of Nuri = x years
and age of Sonu = y years
5 years ago,
age of Nuri = (x – 5) years
and age of Sonu = (y – 5) years
x – 5 = 3 (y – 5) = 3y – 15
=> x = 3y – 15 + 5
=> x = 3y – 10 ….(i)
10 years later,
age of Nuri = x + 10
and age of Sonu = y + 10
x + 10 = 2 (y + 10) = 2y + 20
=> x = 2y + 20 – 10 = 2y+ 10 ….(ii)
From (i) and (ii)
3y – 10 = 2y + 10 => 3y – 2y = 10 + 10
=> y = 20
x = 3y – 10 [from (i)]
x = 3 x 20 – 10 = 60 – 10 = 50 years
and age of Sonu = 20 years

Question 4.
Six years hence a man’s age will be three times the age of his son and three years ago, he was nine times as old as his son. Find their present ages. (C.B.S.E. 1994)
Solution:
Let present age of a man = x years
and age of his son = y years
6 years hence,
age of the man = x + 6
and age of his son = y + 6
x + 6 = 3 (y + 6)
=> x + 6 = 3y + 18
=> x – 3y = 18 – 6 = 12
=> x – 3y = 12 ….(i)
3 years ago,
the age of the man = x – 3
and age of his son = y – 3
x – 3 = 9 (y – 3)
=> x – 3 = 9y – 27
=> x – 9y = -27 + 3
=> x – 9y = -24 ….(ii)
Subtracting (ii) from (i),
6y = 36
=> y = 6
From (i), x – 3 x 6 = 12
=> x – 18 = 12
=> x = 12 + 18 = 30
Present age of man = 30 years
and age of his son = 6 years

Question 5.
Ten years ago, a father was twelve times as old as his son and ten years hence, he will be twice as old as his son will be then. Find their present ages. (C.B.S.E. 1994)
Solution:
Let present age of father = x years
and age of his son = y years
10 years ago,
Father’s age = x – 10
and son’s age = y – 10
x – 10 = 12(y – 10)
=> x – 10 = 12y – 120
=> x – 12y = -120 + 10 = -110
=> x – 12y = -110 ….(i)
10 years hence,
Father’s age = x + 10
and his son’s age = y + 10
10y = 120
y = 12
From (ii), x – 2y = 10
x – 2 x 10 = 10
=> x – 24 = 10
=> x = 10 + 24
=> x = 34
Present age of father = 34 years
and age of his son = 12 years

Question 6.
The present age of a father is three years more than three times the age of the son. Three years hence father’s age will be 10 years more than twice the age of the son. Determine their present ages. (C.B.S.E. 1994C)
Solution:
Let present age of father = x years
and age of his son = y years
x = 3y + 3 …….(i)
3 years hence,
Father’s age = (x + 3)
and his son’s age = (y + 3)
x + 3 = 2 (y + 3) + 10 = 2y + 6 + 10
x + 3 = 2y + 16
=> x = 2y + 16 – 3 = 2y + 13 ….(ii)
From (i) and (ii)
3y + 3 = 2y + 13
=> 3y – 2y = 13 – 3
=> y = 10
and x = 3y + 3 = 3 x 10 + 3 = 30 + 3 = 33
Present age of father = 33 years
and age of his son = 10 years

Question 7.
A father is three times as old’as his son. In 12 years time, he will be twice as old as his son. Find the present ages of father and the son. (C.B.S.E. 1992, 1996)
Solution:
Let present age of father = x years
and age of son = y years
x = 3y ………(i)
12 years hence,
Father’s age = x + 12
and son’s age = y + 12
(x + 12) = 2 (y + 12)
=> x + 12 = 2y + 24
=> x = 2y + 24 – 12 = 2y + 12 ….(ii)
From (i) and (ii)
3y = 2y + 12
=> 3y – 2y = 12
=> y = 12
x = 3y = 3 x 12 = 36
Present age of father = 36 years and
age of son = 12 years

Question 8.
Father’s age is three times the sum of ages of his two children. After 5 years his age will be twice the sum of ages of two children. Find the age of father. (C.B.S.E. 2003)
Solution:
Let father’s present age = x years
and sum of ages of his two children = y
then x = 3y
=> y = \(\frac { 1 }{ 3 }\) x ….(i)
After 5 years,
Age of father = x + 5
and sum of age of two children = y + 2 x 5 = y + 10
(x + 5) = 2(y + 10)
x + 5 = 2y + 20
=> x = 2y + 20 – 5
x = 2y + 15 ….(ii)
From (i)
x = 2 x \(\frac { 1 }{ 3 }\) x + 15
=> x = \(\frac { 2 }{ 3 }\) x + 15
=> x – \(\frac { 1 }{ 3 }\) x = 15
=> \(\frac { 1 }{ 3 }\) x = 15
=> x = 15 x 3 =45
Age of father = 45 years

Question 9.
Two years ago, a father was five times as old as his son. Two years later, his age will be 8 more than three times the age of the son. Find the present ages of father and son. (C.B.S.E. 2004)
Solution:
Let present age of father = x years
and age of his son = y years
2 years ago,
age of father = x – 2
and age of son = y – 2
x – 2 = 5(y – 2)
=> x – 2 = 5y – 10
=> x = 5y – 10 + 2
=> x = 5y – 8 ………(i)
2 years later,
age of father = x + 2
and age of son = y + 2
x + 2 = 3 (y + 2) + 8
=> x + 2 = 3y + 6 + 8
=> x = 3y + 14 – 2 = 3y + 12 ….(ii)
From,(i) and (ii)
5y – 8 = 3y + 12
=> 5y – 3y = 12 + 8
=> 2y = 20
=> y = 10
From (i)
x = 5y – 8 = 5 x 10 – 8 = 50 – 8 = 42
Present age of father = 42 years
and age of son = 10 years

Question 10.
A is elder to B by 2 years. A’s father F is twice as old as A and B is twice as old as his sister S. If the ages of the father and sister differ by 40 years, find the age of A. (C.B.S.E. 1992C)
Solution:
Let age of A = x years
and age of B = y years
According to the conditions,
x = y + 2
=> y = x – 2 ….(i)
Age of A’s’ father = 2x
Age of B’s sisters = \(\frac { y }{ 2 }\)
2x – 2y = 40
4x – y = 80 ….(ii)
4x – (x – 2) = 80
=> 4x – x + 2 = 80
3x = 80 – 2 = 78
x = 26
A’s age = 26 years

Question 11.
The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju as tiwce as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Solution:
Let age of Ani = x years
and age of Biju = y years
x – y = 3 ….(i)
Ani’s father Dharam’s age = 2x
and Cathy’s age = \(\frac { 1 }{ 2 }\) y
But 2x – \(\frac { 1 }{ 2 }\) y = 30
=> 4x – y = 60 ….(ii)
Subtracting,
3x = 57
x = 19
and 4x – y = 60
=> 4 x 19 – y = 60
=> 76 – y = 60
=> 76 – 60 = y
=> y = 16
Anil’s age = 19 years
and Biju’s age = 16 years

Question 12.
Two years ago, Salim was thrice as old as his daughter and six years later, he will be four years older than twice her age. How old are they now? [NCERT Exemplar]
Solution:
Let Salim and his daughter’s age be x and y year respectively.
Now, by first condition,
Two years ago, Salim was thrice as old as his daughter.
i. e., x – 2 = 3(y – 2)
=> x – 2 = 3y – 6
=> x – 3y = -4 …(i)
and by second condition,
six years later, Salim will be four years older than twice her age.
x + 6 = 2(y + 6) + 4
=> x + 6 = 2y + 12 + 4
=> x – 2y = 16 – 6
=>x – 2y = 10 …(ii)
On subtracting Eq. (i) from Eq. (ii), we get
y = 14
Put the value of y in Eq. (ii), we get
x – 2 x 14 = 10
=> x = 10 + 28
=> x = 38
Hence, Salim and his daughter’s age are 38 years and 14 years, respectively.

Question 13.
The age of the father is twice the sum of the ages of his two children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father. [NCERT Exemplar]
Solution:
Let the present age (in year) of father and his two children be x, y and z year, respectively.
Now by given condition, x = 2(y + z) …(i)
and after 20 years,
(x + 20) = (y + 20) + (z + 20)
=> y + z + 40 = x + 20
=> y + z = x – 20
On putting the value of (y + z) in Eq. (i) and we get the present age of father
=> x = 2 (x – 20)
x = 2x – 40
=> x = 40
Hence, the father’s age is 40 years.

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
The following table gives the distribution of total household expenditure (in rupees) of manual workers in a city.

Find the average expenditure ( in rupees ) per household.
Solution:

Question 2.
A survey was conducted by a group of students as a part of their environment awareness programme, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.

Which method did you use for finding the mean, and why ?
Solution:
Let assumed mean (A) = 7

Question 3.
Consider the following distribution of daily wages of 50 workers of a facotry.

Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:

= 150 – 4.80 = 145.20
Mean daily wages per worker = Rs. 145.20

Question 4.
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method.

Find the mean of each of the following frequency distribution (5 – 14)
Solution:

Hence heart beats per minute = 75.9

Question 5.
Find the mean of each the following frequency distributions : (5 – 14)

Solution:
Let Assumed mean (A) =15

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:
Let assumed mean = 20

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.
For the following distribution, calculate mean using all suitable methods.

Solution:
Let assumed mean (A) = 12.5

Question 16.
The weekly observation on cost of living index in a certain city for the year 2004 – 2005 arc given below. Compute the weekly cost of living index.

Solution:
Let assumed mean (A)= 1650

= 1650 + 13.46 = 1663.46

Question 17.
The following table shows the marks scored by 140 students in an examination of a certain paper:

Calculate the average marks by using all the three methods: direct method, assumed mean deviation and shortcut method.
Solution:
(i) Direct Method :

(ii) Shortcut Method:

Question 18.
The mean of the following frequency distribution is 62.8 and the sum of all the frequencies is 50. Compute the missing frequency / and (C.B.S.E. 2004)

Solution:

Question 19.
The following distribution shows the daily pocket allowance given to the children of a multistory building. The average pocket allowance is Rs. 18.00. Find out the missing frequency.

Solution:

⇒ 752 + 20p = 792 + 18p
⇒ 20p- 18p = 792 – 752
⇒2p = 40
⇒p = \(\frac { 40 }{ 2 }\)
Hence missing frequency = 20

Question 20.
If the mean of the following distribution is 27, find the value of p.

Solution:
Mean = 27

⇒ 27 (43 +p) = 1245 + 15p
⇒ 1161 + 21p = 1245 + 15p
⇒ 27p -15p= 1245 – 1161
⇒ 12p = 84
⇒ p = \(\frac { 84 }{ 12 }\)
Hence p = 1

Question 21.
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose ?
Solution:
We shall apply the assumed mean deviation method
Let assumed mean (A) = 57
We shall choose the method of assumed mean deviation :

= 57 + 3 x \(\frac { 25 }{ 100 }\)
= 57 + \(\frac { 3 }{ 16 }\)
= 57 + 0.1875 = 57.1875 = 57.19

Question 22.
The table below shows the daily expenditure on food of 25 households in a locality

Solution:
Let assumed mean (A) = 225

∴ Mean expenditure on food = Rs. 211

Question 23.
To find out the concentration of S02 in the air (in parts per million, i.e., ppm), the data was collected for 30 localities in a certain city and is presented below :

Find the mean concentration of S02 in the air.
Solution:
Let assumed mean (A) = 0.10


= 0.10 – 0.00133 = 0.09867 = 0.099 (approx)

Question 24.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days student was absent.

Solution:

∴ Mean number of days a students was absent = 12.475

Question 25.
The following table gives the literacy rate (in percentage) of 3§ cities. Find the mean

Solution:

Question 26.
The following is the cummulative frequency distribution (of less than type) of 1000 persons each of age 20 years and above. Determine the mean age.[NCERT Exemplar]

Solution:
First, we make the frequency distribution of the given data and then proceed to calculate mean by computing class marks (x_i), u_i’s and f_iu_i‘s as follows:

= 45 + 6.3 = 51.3
Thus, the mean age is 51.3 years.

Question 27.
If the mean of the following frequency distribution is 18, find the missing frequency.

Solution:

Question 28.
Find the missing frequencies in the following distribution, if the sum of the frequencies is 120 and the mean is 50.

Solution:


⇒ 4+ f₂ -f₁ = 0
⇒ -f₂+ f₁ = 4 ……..(ii)
On adding Eqs. (i) and (ii), we get
⇒ 2f₁ = 56
⇒ f₁= 28
Put the value of f₁ in Eq. (i), we get
f₂ = 52-28
⇒ f₂ = 24
Hence, f₁ = 28 and f₂ = 24

Question 29.
The daily income of a sample of 50 employees are tabulated as follows:

Find the mean daily income of employees. [NCERT Exemplar]
Solution:
Since, given data is not continuous, so we subtract 0.5 from the lower limit and add 0.5 in the upper limit of each class.
Now we first, find the class mark xt of each class and then proceed as follows:

∴ Assumed mean, a = 300.5
Class width, h = 200
and total observation, N = 50
By step deviation method,

= 300.5 + 200 x \(\frac { 1 }{ 50 }\) x 14
= 300.5 + 56 = 356.5

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
The numerator of a fraction is 4 less than the denominator. If the numerator is decreased by 2 and denominator is increased by 1, then the denominator is eight times the numerator. Find the fraction. (C.B.S.E. 1990)
Solution:
Let numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x}{ y}\)
According to the conditions,
y – x = 4 ….(i)
and 8 (x – 2) = y + 1
=> 8x – 16 – y + 1
=> 8x – y = 1 + 16
=> 8x – y= 17 ….(ii)
Adding (i) and (ii)
7x = 21 => x = 3
y – 3 = 4
=> y = 4 + 3 = 7
Hence fraction = \(\frac { x}{ y}\)

Question 2.
A fraction becomes \(\frac { 9 }{ 11 }\) if 2 is added to both numerator and the denominator. If 3 is added to both the numerator and the denominator, it becomes \(\frac { 5 }{ 6 }\). Find the fraction. (C.B.S.E. 1990)
Solution:
Let the numerator of a fraction = x
and denominator = y

Fraction = \(\frac { x}{ y}\) = \(\frac { 7 }{ 9 }\)

Question 3.
A fraction becomes \(\frac { 1 }{ 3 }\) if 1 is subtracted from both its numerator and denominator. If 1 is added to both the numerator and denominator, it becomes \(\frac { 1 }{ 2 }\). Find the fraction. (C.B.S.E. 1993C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Question 4.
If we add 1 to the numerator and subtract 1 from the denominator, a fraction becomes 1. It also becomes \(\frac { 1 }{ 2 }\) if we only add 1 to the denominator. What is the fraction.
Solution:
Let numerator of a fraction = x
and denominator = y

Question 5.
The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(\frac { 1 }{ 2 }\). Find the fraction. (C.B.S.E. 2006C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Fraction = \(\frac { x}{ y}\) = \(\frac { 5 }{ 7 }\)

Question 6.
When 3 is added to the denominator and 2 is subtracted from the numerator a fraction becomes \(\frac { 1 }{ 4 }\). And, when 6 is added to numerator and the denominator is multiplied by 3, it becomes \(\frac { 2 }{ 3 }\). Find the fraction.
Solution:
Let numerator of a fraction = x
and denominator = y

Question 7.
The sum of a numerator and denominator of a fraction is 18. If the denominator is increased by 2, the fraction reduces to \(\frac { 1 }{ 3 }\). Find the fraction. (C.B.S.E. 1997C)
Solution:
Let the numerator of a fractrion = x
and denominator = y

Question 8.
If 2 is added to the numerator of a fraction, it reduces to \(\frac { 1 }{ 2 }\) and if 1 is subtracted from the denominator, it 1 reduces to \(\frac { 1 }{ 3 }\). Find the fraction. (C.B.S.E. 1997C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Question 9.
The sum of the numerator and denominator of a fraction is 4 more than twice the numerator. If the numerator and denominator are increased by 3, they are in the ratio 2 : 3. Determine the fraction (C.B.S.E. 2001C)
Solution:
Let the numerator of a fraction = x
and denominator = y

Question 10.
If the numerator of a fraction is multiplied by 2 and the denominator is reduced by 5 the fraction becomes \(\frac { 6 }{ 5 }\). And, if the denominator is doubled and the numerator is increased by 8, the fraction becomes \(\frac { 2 }{ 5 }\). Find the fraction.
Solution:
Let the numerator of fraction = x
and denominator = y

Question 11.
The sum of the numerator and denominator of a fraction is 3 less than twice the denominator. If the numerator and denominator are decreased by 1, the numerator becomes half the denominator. Determine the fraction. (C.B.S.E. 2001C)
Solution:
Let the numerator of a fraction = x
and denominator = y
Then fraction = \(\frac { x }{ y }\)
According to the conditions given,
x + y = 2y – 3
=> x + y – 2y = -3

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
The. number of telephone calls received at an exchange per interval for 250 successive one-minute intervals are given in the following frequency table:

Compute the mean number of calls per interval.
Solution:
Let assumed mean (A) = 4

Hence mean number of calls per interval = 3.54

Question 2.
Five coins were simultaneously tossed 1000 times, and at each toss the number of heads was observed. The number of tosses during which 0, 1, 2, 3, 4, and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss

Solution:
Let assumed means (A) = 3

Hence mean number of tosses per head = 2.47

Question 3.
The following table gives the number of branches and number of plants in the garden of a school.

Calculate the average number of branches per plant.
Solution:
Let assumed mean (A) = 4

∴Mean number of branches per plant = 3.62

Question 4.
The following table gives the number of children of 150 families in a village

Find the average number of children per family.
Solution:
Let assumed mean (A) = 3

= 3 – 0.65 = 2.35
Hence mean number of children per family = 2.35

Question 5.
The marks obtained out of 50, by 102 students in a Physics test are given in the frequency table below:

Find the average number of marks.
Solution:

Question 6.
The number of students absent in a class were recorded every day for 120 days and the

Solution:
Let assumed mean = 3

= 3 + 0.525 = 3.525 = 3.53 (approx)

Question 7.
In the first proof reading of a book containing 300 pages the following distribution of misprints was obtained:

Find the average number of misprints per page.
Solution:
Let assumed mean (A) = 2

= 2 – 127 = 0.73
∴ Average of number of misprints per page = 0.73

Question 8.
The following distribution gives the number of accidents met by 160 workers in a factory during a month.

Find the average number of accidents per worker.
Solution:
Let assumed mean = 2

= 2 – 1.168 = 2 – 1.17 = 0.83 (approx)
∴ Average number of accidents per worker = 0.83

Question 9.
Find the mean from the following frequency distribution of marks at a test in statistics

Solution:
Let assumed mean = 25

∴Average of marked obtained per student = 22.075

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
The sum of two numbers is 8. If their sum is four times their difference, find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 8 ….(i)
and x + y = 4 (x – y)
=> 4 (x – y) = 8
=> x – y = 2 ….(ii)
Adding (i) and (ii),
2x = 10 => x = 5
Subtracting (ii) from (i),
2y = 6 => y = 3
Numbers are 5, 3

Question 2.
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits, the result is 45. What is the number ?
Solution:
Let unit’s digit = x
and ten’s digit = y
Number = x + 10y
Now according to the condition
x + y = 13 ….(i)
Number after interchanging their digits,
y + 10x
Now y + 10x – x – 10y = 45
9x – 9y = 45
=> x – y = 5
x – y = 5 ….(ii)
Adding (i) and (ii),
2x = 18 => x = 9
subtracting 8
2y = 8 => y = 4
Number = x + 10y = 9 + 4 x 10 = 9 + 40 = 49

Question 3.
A number consists of two digits whose sum is five. When the digits are reversed, the number becomes greater by nine. Find the number.
Solution:
Let units digit = x
and ten’s digit = y
Number = x + 10y
and number by reversing their digits = y+ 10x
Now according to the conditions,
x + y = 5 ….(i)
and y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9x – y = 1 ….(ii)
(Dividing by 9)
Adding we get:
2x = 6 => x = 3
and subtracting,
2y = 4 => y = 2
Number = x + 10y = 3 + 10 x 2 = 3 + 20 = 23

Question 4.
The sum of digits of a two digit number is 15. The number obtained by reversing the order of digits of the given number exceeds the given number by 9. Find the given number. (C.B.S.E. 2004)
Solution:
Let the ones digit = x
and tens digit = y
Number = x + 10y
and number by reversing the order of digits = y +10x
According to the conditions,
x + y = 15 ….(i)
y + 10x = x + 10y + 9
=> y + 10x – x – 10y = 9
=> 9x – 9y = 9
=>x – y = 1 ……..(ii)
(Dividing by 9)
Adding (i) and (ii)
2x = 16
x = 8
and subtracting, 2y = 14 => y = 7
Number = x + 10y = 8 + 10 x 7 = 8 + 70 = 78

Question 5.
The sum of a two-digit number and the number formed by reversing the order of digits is 66. If the two digits differ by 2, find the number. How many such numbers are there ? [NCERT]
Solution:
Sum of two-digit number and number formed by reversing its digits = 66
Let units digit = x
Then tens digit = x + 2
Number = x + 10 (x + 2) = x + 10x + 20 = 11x + 20
and by reversing its digits
Unit digit = x + 2
and tens digit = x
Number = x + 2 + 10x = 11x + 2
11x + 20 + 11x + 2 = 66
=> 22x + 22 = 66
=> 22x = 66 – 22 = 44
=> x = 2
Number = 11x + 20 = 11 x 2 + 20 = 22 + 20 = 42
and number by reversing its digits will be 11x + 2 = 11 x 2 + 2 = 22 + 2 = 24
Hence numbers are 42 and 24

Question 6.
The sum of two numbers is 1000 and the difference between their squares is 256000. Find the numbers.
Solution:
Let first number = x
and second number = y
x + y = 1000 ……..(i)

Question 7.
The sum of a two digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number. (C.B.S.E. 2002)
Solution:
Let the unit’s digit of the number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits, the new number will be = y +10x
According to the condition,
x + 10y + y + 10x = 99
=> 11x + 11y = 99
=> x + y = 9 ….(i)
and x – y = 3 ….(ii)
Adding we get,
2x = 12
x = 6
and subtracting, 2y = 6
y= 3
Number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 8.
A two-digit number is 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let the unit digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the order of digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y)
=> x + 10y = 4x + 4y
=> 4x + 4y – x – 10y = 0
=> 3x – 6y = 0
=> x – 2y = 0
=> x = 2y ….(ii)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> – 9x + 9y = -18
=> x – y = 2 ….(ii)
(Dividing by – 9)
=> 2y – y = 2 {From (i}
=> y = 2
x = 2y = 2 x 2 = 4
Number = x + 10y = 4 + 10 x 2 = 4 + 20 = 24

Question 9.
A two-digit number is 3 more than 4 times the sum of its digits. If 18 is added to the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let unit digit of the number = x
and ten’s digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x + 10y = 4 (x + y) + 3
=> x + 10y = 4x + 4y + 3
=> x + 10y – 4x – 4y = 3
=> -3x + 6y = 3
=> x – 2y = -1 ….(i)
(Dividing by -3)
and x + 10y + 18 = y + 10x
=> x + 10y – y – 10x = -18
=> -9x + 9y = -18
=>x – y = 2 ….(ii)
(Dividing by 9)
Subtracting (i) from (ii)
y = 3
x – 3 = 2
=>x = 2 + 3 = 5 {From (ii)}
Number = x + 10y = 5 + 10 x 3 = 5 + 30 = 35

Question 10.
A two digit number is 4 more than 6 times the sum of its digits. If 18 is subtracted from the number, the digits are reversed. Find the number. (C.B.S.E. 2001C)
Solution:
Let units digit of the number = x
and ten’s digit = y
then number = x + 10y
The number by reversing the digits = y+ 10x
According to the condition given,
x + 10y = 6 (x + y) + 4
=> x + 10y = 6x + 6y + 4
=> x + 10y – 6x – 6y = 4
=> -5x + 4y = 4 ….(i)
and x + 10y – 18 = y + 10x
=> x + 10y – y – 10x = 18
=> -9x + 9y = 18
=> x – y = -2 ….(ii)
(Dividing by 9)
=> x = y – 2
Substituting in (i),
-5 (y – 2) + 4y = 4
-5y + 10 + 4y = 4
-y = 4 – 10 = – 6
y = 6
Number = x + 10y = 4 + 10 x 6 = 4 + 60 = 64

Question 11.
A two-digit number is 4 times the sum of its digits and twice the product of the digits. Find-the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
According to the conditions given,

Question 12.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digits interchange their places. Find the number. (C.B.S.E. 2005)
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after interchanging its digits = y + 10x
According to the conditions,
xy = 20

Question 13.
The difference between two pumbers is 26 and one number is three times the other. Find them.
Solution:
Let first number = x
and second number = y
x – y = 26 ……….(i)
x = 3y ….(ii)
Substituting the value of x in (i)
3y – y = 26
=> 2y = 26
=>y = 13
x = 3y = 3 x 13 = 39
Numbers are 39, 13

Question 14.
The sum of the digits o,f a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
Solution:
Let the units digit of the number = x
and tens digit number = y
Number = x + 10y
and the number by reversing the order of the digits = y + 10x
According to the condition;
x + y = 9 …..(i)
9 (x + 10y) = 2 (y + 10x)
=> 9x + 90y = 2y + 20x
=> 9x + 90y – 2y – 20x = 0
=> -11x + 88y = 0
=> x – 8y = 0 (Dividing by -11)
=> x = 8y
Substituting the value of x in (i)
8y + y = 9
=> 9y = 9
=> y= 1
x = 8y = 1 x 8 = 8
Number = x + 10y = 8 + 10 x 1 = 8 + 10 = 18

Question 15.
Seven times a two-digit number is equal to four times the number obtained by reversing the digits. If the difference between the digits is 3. Find the number.
Solution:
Let the units digit of the number = x
and tens digit = y
Number = x + 10y
and number after reversing the digits = y + 10x
According to the conditions,
x – y = 3 ….(i)
and 7 (x + 10y) = 4 (y + 10x)
=> 7x + 70y = 4y + 40x
=> 7x + 70y – 4y – 40x = 0
=> -33x + 66y = 0
=> x – 2y = 0 (Dividing by -33)
=> x = 2y
Substituting the value of x in (i),
2y – y = 3 => y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 16.
Two numbers are in the ratio 5 : 6. If 8 is subtracted from each of the numbers, the ratio becomes 4 : 5. Find the numbers. [NCERT Exemplar]
Solution:
Let the two numbers be x and y.
Then, by the first condition, ratio of these two numbers = 5 : 6
x : y = 5 : 6

Question 17.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number. [NCERT Exemplar]
Solution:
Let the two-digit number = 10x + y
Case I : Multiplying the sum of the digits by 8 and then subtracting 5 = two-digit number
=> 8 x (x + y) – 5 = 10x + y

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.2
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.3
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.4
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.5
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.6
• RD Sharma Class 10 Solutions Chapter 15 Statistics Ex VSAQS
• RD Sharma Class 10 Solutions Chapter 15 Statistics MCQS

Question 1.
Calculate the mean for the following distribution :

X	5	6	7	8	9
f	4	8	14	11	3

Solution:

Question 2.
Find the mean of the following data:

X	19	21	23	25	27	29	31
f	13	15	16	18	16	15	13

Solution:

Question 3.
If the mean of the following data is 20.6. Find the value of p. (C.B.S.E. 1997)

X	10	15	p	25	35
y	3	10	25	7	5

 Solution:

Question 4.
If the mean of the following data is 15, find p. (C.B.S.E. 1992C)

X	5	10	15	20	25
f	6	P	6	10	5

Solution:

Question 5.
Find the value of p for the following distribution whose mean is 16.6.

X	8	12	15	P	20	25	30
f	12	16	20	24	16	8	4

Solution:
Mean = 16.6

Question 6.
Find the missing value of p for the following distribution whose mean is 12.58. (C.B.S.E. 1992C)

X	5	8	10	12	P	20	25
f	2	5	8	22	7	4	2

Solution:

Question 7.
Find the missing frequency (p) for the following distribution whose mean is 7.68.

X	3	5	7	9	11	13
f	6	8	15	P	8	4

 Solution:

Question 8.
The following table gives the number of boys of a particular age in a class of 40 students. Calculate the mean age of the students

Age (in years)	15	16	17	18	19	20
No. of students	3	8	10	10	5	4

Solution:

Question 9.
Candidates of four schools appear in a mathematics test. The data were as follows :

Schools	No. of Candidates	Average Score
I	60	75
II	48	80
III	Not available	55
IV	40	50

If the average score of the candidates of all the four schools is 66, find the number of candidates that appeared from school III.
Solution:

Question 10.
Five coins were simultaneously tossed 1000 times and at each toss the number of heads were observed. The number of tosses during which 0, 1, 2, 3, 4 and 5 heads were obtained are shown in the table below. Find the mean number of heads per toss.

No. of heads per toss	No. of tosses
0	38
1	144
2	342
3	287
4	164
5	25
Total	1000

 Solution:

Question 11.
The arithmetic mean of the following data is 14, find the value of k. (C.B.S.E. 2002C)

X	5	10	15	20	25
f	7	k	8	4	5

Solution:
Mean=14

⇒ 14 (24 + k) = 360 + 10k
⇒ 336 + 14k = 360 + 10k
⇒ 14k- 10k- 360 -336 24
⇒ 4k = 24
⇒ k= \(\frac { 24 }{ 4 }\) = 6 4
Hence k = 6

Question 12.
The arithmetic mean of the following data is 25, find the value of k. (C.B.S.E. 2001)

X	5	15	25	35	45
f	3	k	3	6	2

Solution:
Mean =25

⇒ 25 (14 + k) = 390 + 15k
⇒ 350 + 25k= 390 + 15k
⇒ 25k- 15k = 390 -350
⇒ 10k = 40 ⇒ k = \(\frac { 40 }{ 10 }\) = 4
Hence k = 4

Question 13.
If the mean of the following data is 18.75. Find the value of p.

X	10	15	P	25	30
f	5	10	7	8	2

Solution:

⇒ 460 + 7p = 32 (18.75)
⇒ 460 + 7p = 600
⇒ 7p = 600 – 460 = 140
⇒ p =  \(\frac { 140 }{ 7 }\) = 20
∴ p = 20

Question 14.
Find the value of p, if the mean of the following distribution is 20.

X	15	17	19	20 + p	23
f	2	3	4	5p	6

Solution:

⇒ 5p² + 100p + 295 = 20 (15 + 5p)
⇒ 5p² + 100p + 295 = 300 + 100p
⇒ 5p² + 100p – 100p = 300 – 295
⇒  5p² = 5 ⇒  p²  =  \(\frac { 5 }{ 5 }\)  = 1
⇒ P= ±1
P = -1 i s not possible
∴ p= 1

Question 15.
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 50.

Solution:

Hope given RD Sharma Class 10 Solutions Chapter 15 Statistics Ex 15.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
5 pens and 6 pencils together cost ₹ 9 and 3 pens and 2 pencils cost ₹ 5. Find the cost of 1 pen and 1 pencil. (C.B.S.E. 1991)
Solution:
Let cost of 1 pen = ₹ x
and cost of 1 pencil = ₹ y
According to the conditions,
5x + 6y = 9 ….(i)
3x + 2y = 5 …(ii)
Multiplying (i) by 1 and (ii) by 3, we get

Cost of one pen = ₹ \(\frac { 3 }{ 2 }\)
and cost of one pencil = ₹ \(\frac { 1 }{ 4 }\)

Question 2.
7 audio cassettes and 3 video cassettes cost ₹ 1110, while 5 audio cassettes and 4 video cassettes cost ₹ 1350. Find the cost of an audio cassette and a video cassette. (C.B.S.E. 1992)
Solution:
Let the cost of 1 audio cassette = ₹ x
and cost of 1 video cassette = ₹ y
According to the condition,
7x + 3y= 1110 ….(i)
5x + 4y = 1350 ….(ii)
Multiplying (i) by 4 and (ii) by 3,

Question 3.
Reena has pens and pencils which together are 40 in number. If she has 5 more pencils and 5 less pens, then number of pencils would become 4 times the number of pens. Find,.the original number of pens and pencils. (C.B.S.E 1992C)
Solution:
Let number of pens = x
and number of pencils = y
x + y = 40 ….(i)
In second case,
number of pens = x – 5
and number of pencils = y + 5
(y + 5) = 4 (x – 5) => y + 5 = 4x – 20
4x – y = 5 + 20 => 4x – y = 25 ….(ii)
Adding (i) and (ii)
5x = 65 => x = 13 [From (i) ]
13 + y = 40 => y = 40 – 13 = 27
Hence number of pens = 13
and number of pencils = 27

Question 4.
4 tables and 3 chairs, together, cost ₹ 2,250 and 3 tables and 4 chairs cost ₹ 1950. Find the cost of 2 chairs and 1 table.
Solution:
Let cost of 1 table = ₹ x
and cost of 1 chair = ₹ y
According to the conditions,
4x + 3y = 2250 ….(i)
3x + 4y= 1950 ….(ii)
Multiplying (i) by 4 and (ii) by 3, we get

Question 5.
3 bags and 4 pens together cost ₹ 257 whereas 4 bags and 3 pens together cost ₹ 324. Find the total cost of 1 bag and 10 pens. (C.B.S.E. 1996)
Solution:
Let cost of 1 bag = ₹ x
and cost of 1 pen = ₹ y
According to the conditions,
3x + 4y = 257 ….(i)
4x + 3y = 324 ….(ii)
Multiplying (i) by 3 and (ii) by 4, we get

Question 6.
5 books and 7 pens together cost ₹ 79 whereas 7 books and 5 pens together cost ₹ 77. Find the cost of 1 book and 2 pens. (C.B.S.E. 1996)
Solution:
Let the cost 1 book = ₹ x
and cost of 1 pen = ₹ y
Now according to the conditions,
5x + 7y = 79 ….(i)
7x + 5y = 77 ….(ii)
Multiplying (i) by 5 and (ii) by 7, we get

Substituting the value of x in (i)
5 x 6 + 7y = 79
=> 30 + 7y = 79
=> 7y = 79 – 30 = 49
y = 7
Cost of 1 book and 2 pens = 6 + 2 x 7 = 6 + 14 = 20

Question 7.
Jamila sold a table and a chair for ₹ 1050, thereby making a profit of 10% on a table and 25% on the chair. If she had taken profit of 25% on the table and 10% on the chair she would have got ₹ 1065. Find the cost price of each. [NCERT Exemplar]
Solution:
Let the cost price of the table be ₹ x
and the cost price of the chair by ₹ y.
The selling price of the table, when it is sold at a profit of 10%

110x + 125y = 105000
and 125x + 110y = 106500
On adding and subtracting these equations, we get
235x + 235y = 211500
and 15x – 15y= 1500
i.e., x + y = 900 …(iii)
and x – y = 100 …(iv)
Solving equation (iii) and (iv), we get
2x = 1000
x = 500
500 + y = 900
=> y = 900 – 500
y = 400
x = 500, y = 400
So, the cost price of the table is ₹ 500 and the cost price of the chair is ₹ 400.

Question 8.
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received ₹ 1860 as annual interest. However, had she interchanged the amount of investment in the two schemes, she would have received 720 more as annual interest. How much money did she invest in each scheme?
[NCERT Exemplar]
Solution:
Let the amount of investments in schemes A and B be ₹ x and ₹ y, respectively.
Case I:
Interest at the rate of 8% per annum on scheme A + Interest at the rate of 9% per annum on scheme B = Total amount received

Case II:
Interest at the rate of 9% per annum on scheme A + Interest at the rate of 8% per annum on scheme B = ₹ 20 more as annual interest

Question 9.
The coach of a cricket team buys 7 bats and 6 balls for ₹ 3800. Later, he buys 3 bats and 5 balls for ₹ 1750. Find the cost of each bat and each ball.
Solution:
Let cost of 1 bat = ₹ x
and cost of 1 ball = ₹ y
According to the conditions,
7x + 6y = 3800 ….(i)
3x + 5y = 1750 ….(ii)
Multiplying (i) by 5 and (ii) by 6, we get

Question 10.
A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for seven days, while Susy paid ₹ 21 for the book she kept for five days. Find the fixed charge and the charge for each extra day;
Solution:
Let the fixed charge for the book = ₹ x
and let extra charge for each day = ₹ y
According to the given conditions,
x + 4y = 27 ….(i)
x + 2y = 21 ….(ii)
Subtracting,
2y = 6 => y = 3
Substituting the value of y in (i)
x + 4 x 3 = 27
=> x + 12 = 27
=> x = 27 – 12 = 15
Amount of fixed charge = ₹ 15
and charges for each extra day = ₹ 3

Question 11.
The cost of 4 pens and 4 pencil boxes is ₹ 100. Three times the cost of a pen is ₹ 15 more than the cost of a pencil box. Form the pair of linear equations for the above situation. Find the cost of a pen and pencil box. [NCERT Exemplar]
Solution:
Let the cost of a pen be ₹ x and the cost of a pencil box be ₹ y.
Then, by given condition,
4x + 4y = 100 => x + y = 25 …(i)
and 3x = y + 15
=> 3x – y = 15 …(ii)
On adding Eqs. (i) and (ii), we get
4x = 40 => x = 10
By substituting x = 10, in Eq. (i) we get
y = 25 – 10 = 15
Hence, the cost of a pen and a pencil box are ₹ 10 and ₹ 15, respectively.

Question 12.
One says, “Give me a hundred, friend! I shall then become twice as rich as you.” The other replies, “If you give me ten, I shall be six times as rich as you.” Tell me what is the amount of their respective capital?
Solution:
Let the amount of first person = ₹ x
and amount of second = ₹ y
According to the first condition,
x + 100 = 2 (y- 100)
=> x + 100 = 2y – 200
=> x – 2y = -200 – 100
=> x – 2y = -300 …….(i)
According to the second condition,
6(x – 10) = (y + 10)
6x – 60 = y + 10
6x – y = 10 + 60
6x – y = 70 ….(ii)
Multiplying (i) by 1 and (ii) by 2, we get


Hence first person has money = ₹ 40 and second person has = ₹ 170

Question 13.
A and B each have a certain number of mangoes. A says to B, “if you give 30 of your mangoes, I will have twice as many as left with you.” B replies, “if you give me 10, I will have thrice as many left with you.” How many mangoes does each have ?
Solution:
Let A has mangoes = x
and B has mangoes = y
According to the first condition,
x + 30 = 2 (y – 30)
x + 30 = 2y – 60
x – 2y = -60 – 30
=> x – 2y = -90 ….(i)
and according to the second condition
3 (x – 10) = (y + 10)
=> 3x – 30 = y + 10
=> 3x – y = 10 + 30
=> 3x – y = 40 ….(ii)
From (i) x = -90 + 2y Substituting in (i)
3 (-90 + 2y) – y = 40
– 270 + 6y – y = 40
=> 5y = 40 + 270 = 310
=> y = 62
and x = – 90 + 2y = – 90 + 2 x 62 = 124 – 90 = 34
A has mangoes = 34
and B has mangoes = 62

Question 14.
Vijay had some bananas, and he divided them into two lots A and B. He sold first lot at the rate of ₹ 2 for 3 bananas and the second lot at the rate of ₹ 1 per banana and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per banana and the second lot at the rate of ₹ 4 per five bananas, his total collection would have been ₹ 460. Find the total number of bananas he had. [NCERT Exemplar]
Solution:
Let the number of bananas in lots A and B be x and y, respectively.
Case I:
Cost of the first lot at the rate of ₹ 2 for 3 bananas + Cost of the second lot at the rate of ₹ 1 per banana = Amount received
=> \(\frac { 2 }{ 3 }\) x + y = 400
=> 2x + 3y= 1200 …(i)
Case II:
Cost of the first lot at the rate of ₹ 1 per banana + Cost of the second lot at the rate of ₹ 4 for 5 bananas = Amount received
=> x + \(\frac { 4 }{ 5 }\) y = 460
=> 5x + 4y = 2300 …(ii)
On multiplying in the Eq. (i) by 4 and Eq. (ii) by 3 and then subtracting them, we get,

Now, putting the value of x in Eq. (i), we get,
2 x 300 + 3y = 1200
=> 600 + 3y = 1200
=> 3y = 1200 – 600
=> 3y = 600
=> y = 200
Total number of bananas = Number of bananas in lot A + Number of bananas in lot B
= x + y
= 300 + 200 = 500
Hence, he had 500 bananas.

Question 15.
On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains ₹ 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss. He gains ₹ 1500 on the transaction. Find the actual prices of T.V. and fridge.
Solution:
Let the price of T.V. = ₹ x
and price of Fridge = ₹ y
According to first condition,


\(\frac { y }{ 10 }\) = 2000 – 1000 = 1000
=> y = 10 x 1000 = 10000
Hence price of T.V. = ₹ 20000 and of fridge = ₹ 10000

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

In each of the following systems of equations determine whether the system has a unique solution, no solution or infinitely many solutions. In case there is a unique solution, find it : (1 – 4)
Question 1.
x – 3y = 3
3x – 9y = 2 (C.B.S.E. 1994)
Solution:

Question 2.
2x + y = 5
4x + 2y = 10 (C.B.S.E. 1995C)
Solution:

Question 3.
3x – 5y = 20
6x – 10y = 40 (C.B.S.E. 1993)
Solution:

Question 4.
x – 2y = 8
5x – 10y = 10 (C.B.S.E. 1993)
Solution:

Find the value of k for which the following system of equations has a unique solution: (5 – 8)
Question 5.
kx + 2y = 5
3x + y = 1 (C.B.S.E. 1990C, 92C)
Solution:

Question 6.
4x + ky + 8 = 0
2x + 2y + 2 = 0 [NCERT]
Solution:

Question 7.
4x – 5y = k
2x – 3y = 12
Solution:

Question 8.
x + 2y = 3
5x + ky + 7 = 0
Solution:

Find the value of k for which each of the following systems of equations have infinitely many solution : (9 – 19)
Question 9.
2x + 3y – 5 = 0
6x + ky – 15 = 0 (C.B.S.E. 1991)
Solution:

Question 10.
4x + 5y = 3
kx + 15y = 9 (C.B.S.E. 1990C)
Solution:

Question 11.
kx – 2y + 6 = 0
4x – 3y + 9 = 0
Solution:

Question 12.
8x + 5y = 9
kx + 10y = 18 (C.B.S.E. 1999)
Solution:

Question 13.
2x – 3y = 7
(k + 2) x + (2k + 1) y = 3 (2k – 1) (C.B.S.E. 1999)
Solution:

Question 14.
2x + 3y = 2
(k + 2)x + (2k + 1) y = 2 (k – 1) (C.B.S.E. 2000, 2003)
Solution:

Question 15.
x + (k + 1) y = 4
(k + 1) x + 9y = 5k + 2 (C.B.S.E. 2000C)
Solution:

Question 16.
kx + 3y = 2k + 1
2(k+ 1) x + 9y = 7k + 1 (C.B.S.E. 2000C)
Solution:

Question 17.
2x + (k – 2) y = k
6x + (2k – 1) y = 2k + 5 (C.B.S.E. 2000C)
Solution:

Question 18.
2x + 3y = 7
(k + 1) x + (2k – 1)y = 4k + 1 (C.B.S.E. 2001)
Solution:

Question 19.
2x + 3y = k
(k – 1) x + (k + 2) y = 3k (C.B.S.E. 2001)
Solution:

Find the value of k for which the following system of equations has no solution : (20 – 25) :
Question 20.
kx – 5y = 2
6x + 2y = 1 (C.B.S.E. 1994C)
Solution:

Question 21.
x + 2y = 0
2x + ky = 5 (C.B.S.E. 1993C)
Solution:

Question 22.
3x – 4y + 7 = 0
kx + 3y – 5 = 0 (C.B.S.E. 1996)
Solution:

Question 23.
2x – ky + 3 = 0
3x + 2y – 1 = 0 (C.B.S.E. 1996)
Solution:

Question 24.
2x + ky = 11
5x – 7y = 5 (C.B.S.E. 1995)
Solution:

Question 25.
kx + 3y = 3
12x + ky = 6
Solution:

Question 26.
For what value of k, the following system of equations will be inconsistant ?
4x + 6y = 11
2x + ky = 1 (C.B.S.E. 1994C)
Solution:

Question 27.
For what value of a, the system of equations
αx + 3y = α – 3
12x + αy = α
will have no solution. (C.B.S.E. 2003)
Solution:

Question 28.
Find the value of k for which the system
kx + 2y = 5
3x + y = 1
has (i) a unique solution, and (ii) no solution.
Solution:

k = 6

Question 29.
Prove that there is a value of c (≠ 0) for which the system
6x + 3y = c – 3
12x + cy = c
has infinitely many solutions. Find this value.
Solution:

Question 30.
Find the values of k for which the system
2x + k y = 1
3x – 5y = 7
will have (i) a unique solution, and (ii) no solution.
Is there a value of k for which the system has infinitely many solutions?
Solution:

Question 31.
For what value of k, the following system of equations will represent the coincident lines ?
x + 2y + 7 = 0
2x + ky + 14 = 0 (C.B.S.E. 1992)
Solution:

Question 32.
Obtain the condition for the following system of linear equations to have a unique solution
ax + by = c
lx + my = n (C.B.S.E. 1991C)
Solution:

Question 33.
Determine the values of a and b so that the following system of linear equations have infinitely many solutions ?
(2a – 1) x + 3y – 5 = 0
3x + (b – 1) y – 2 = 0 (C.B.S.E. 2001C)
Solution:

Question 34.
Find the values of a and b for which the following system of linear equations has infinite number of solutions :
2x – 3y = 7
(a + b) x – (a + b – 3) y = 4a + b (C.B.S.E. 2002)
Solution:

Question 35.
Find the values of p and q for which the following system of linear equations has infinite number of solutions:
2x + 3y = 9
(p + q) x + (2p – q) y = 3 (p + q + 1)
Solution:

Question 36.
Find the value of a and b for which the following system of equations has infinitely many solutions :
(i) (2a – 1) x – 3y = 5
3x + (b – 2) y = 3 (C.B.S.E. 2002C)
(ii) 2x – (2a + 5) y = 5
(2b + 1) x – 9y = 15 (C.B.S.E. 2002C)
(iii) (a – 1) x + 3y = 2
6x + (1 – 2b) y = 6 (C.B.S.E. 2002C)
(iv) 3x + 4y = 12
(a + b) x + 2 (a – b) y = 5a – 1 (C.B.S.E. 2002C)
(v) 2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
(vi) 2x + 3y – 7 = 0 [CBSE 2010]
(a – 1) x + (a + 1) y = (3a – 1)
(vii) 2x + 3y = 7
(a – 1) x + (a + 2) y = 3a [CBSE 2010]
(viii) x + 2y = 1
(a – b) x + (a + b) y = a + b – 2 [NCERT Exemplar]
(ix) 2x + 3y = 7
2ax + ay = 28 – by [NCERT Exemplar]
Solution:

Question 37.
For which value(s) of λ, do the pair of linear equations λx + y = λ² and x + λy = 1 have
(i) no solution ?
(ii) infinitely many solutions ?
(iii) a unique solutions ? [NCERT Exemplar]
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.