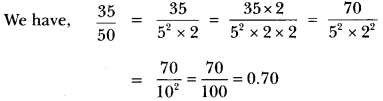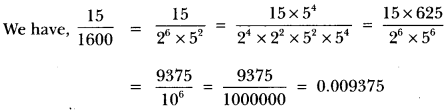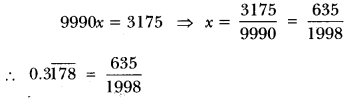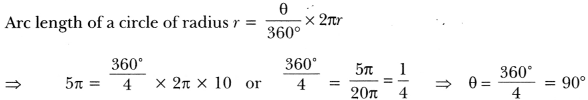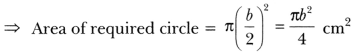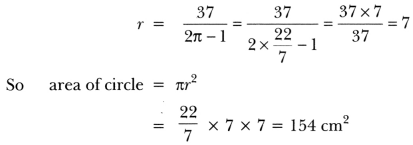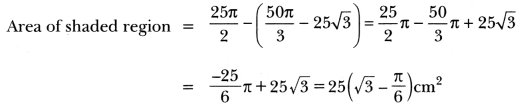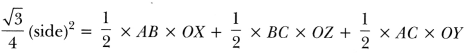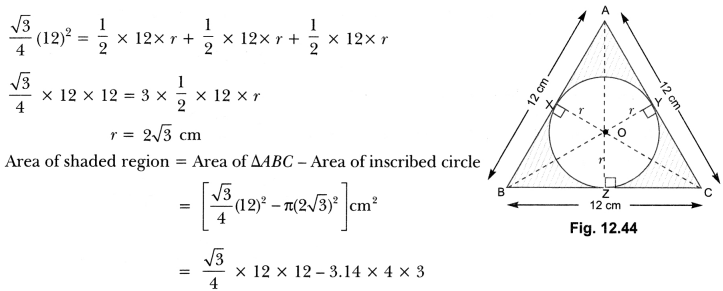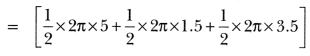Category: CBSE Class 10

Here we are providing Dust of Snow Extra Questions and Answers Class 10 English First Flight, Extra Questions for Class 10 English was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-english/

Dust of Snow Extra Questions and Answers Class 10 English First Flight

Dust of Snow Extra Questions and Answers Short Answer Type

Dust Of Snow Extra Questions Question 1.
How did the crow change the poet’s mood?
Answer:
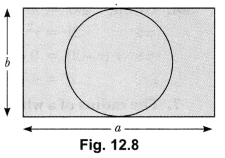
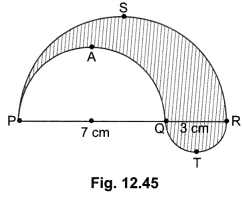
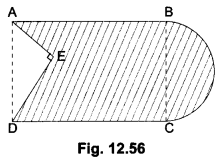
The poet was going somewhere in a snowy morning. He was upset. All the trees were covered with snow dust. A crow sitting on a hemlock tree shook the tree in such a way that some dust of snow fell on the poet. This changed his mood and he became happy and relaxed.

Dust Of Snow Class 10 Extra Questions Question 2.
What was the reaction of the poet when the dust of snow fell on him?
Answer:
Normally, people thought both crow and hemlock tree are auspicious. But when the dust of snow from hemlock tree fell on poet, he took it in other way. He was depressed and sorrowful but the moment the crow shook the hemlock tree and dust of snow fell on him, he felt unburdened and relieved.

Dust Of Snow Extra Question Answer Question 3.
How does the poet react to crow and hemlock tree?
Answer:
Crow and hemlock tree are considered inauspicious in the west. They are generally taken /is bad omen. But the poet did not take them in negative way. They saved his day. His negative outlook changed to the positive one.

Dust Of Snow Class 10 Extra Questions And Answers Question 4.
What made the poet change his mood?
Answer:
A crow on the hemlock tree shook down the dust of snow on the poet. The falling dust of snow on the poet has changed his mood.

Extra Questions Of Dust Of Snow Question 5.
Why does the poet feel that he has saved some part of the day?
Answer:
Crow shook down the dust of snow on the poet. Both crow and hemlock tree are considered inauspicious. The falling of dust of snow from hemlock tree is bad omen. But the poet took it in a positive way. He found himself relieved from sorrow after this incident. Now he could use his entire day in a fruitful way.

Dust Of Snow Important Questions Question 6.
Simple moment proves to be very significant and saves rest of the day of poet from being wasted. Explain on the basis of the poem ‘Dust of Snow”.
Answer:
‘Dust of Snow’ is a beautiful poem written by Robert Frost. This poem conveys that even a simple moment has a large significance. The poet mentioned crow and hemlock tree in this poem. Crow signifies his depressive and sorrowful mood and hemlock tree is a poisonous tree. Both these signify that the poet was not in a good mood and so he describes the dark, depressive and bitter side of nature to present his similar mood.

The poet says that once he was in a sad, depressive mood and was sitting under a hemlock tree. A crow, sitting on the same tree, shook off the dust of snow, small particles of snow that remained on the surface after the snowfall, on the poet. This simple action changed the poet’s mood. He realised that he had just wasted a part of his day repenting and being lost in sorrow. But the change in his mood made him realise that he should utilize the rest of the day in some useful activity. His sorrow was washed away by the light shower of dust of snow. His spirit was revived and he got ready to utilize the rest of the day.

Dust Of Snow Class 10 Questions And Answers Question 7.
The poet was sad and depressed. But one comical incident lifts his spirits. He is full of joy and happiness again. Based on your reading of the poem, write a paragraph on the topic – Happiness is relative.
Answer:
No one is always happy. It is just a passing phase of one’s life. It varies from time to time and place to place. It depends on certain people who you are close to. There are times when we are extremely happy or sorrowful. In most circumstances, our happiness is decided l>y certain moments in our life. Some light moments can really enliven our mood. The actions of our friends can make us happy or sometimes sorrowful. We must also realize that on every cloud there is a silver lining. This means that every sorrowful moment is followed by a period of joy and happiness.

Dust Of Snow Question Answer Question 8.
What do the ‘Hemlock’ tree and ‘Crow’ represent? What does the dust of snow metaphorically stand for ?
Answer:
The poet was going somewhere in a snowy morning. He was upset. All the trees were covered with snow dust. A crow sitting on a hemlock tree shook the tree in such a way that some dust of snow fell on the poet. This changed his mood and he became happy and relaxed.

Dust Of Snow Short Question Answer Question 9.
Narrate a similar experience of your life when nature intervened and changed your mood. Discuss.
Answer:
Normally, people thought both crow and hemlock tree are auspicious. But when the dust of snow from hemlock tree fell on poet, he took it in other way. He was depressed and sorrowful but the moment the crow shook the hemlock tree and dust of snow fell on him, he felt unburdened and relieved.

Dust Of Snow Extra Questions And Answers Question 10.
What is a “Dust of Snow”? What does the poet say has changed his mood? How has the poet’s mood changed?
Answer:
A ‘Dust of Snow” means the fine particles of snow. This ‘Dust of Snow” changed the poet’s mood. The poet’s mood changed from that of dismay to joy. He was holding the day in regret when this dust of snow fell on him and this simple little thing brought him some joy.

Class 10 Dust Of Snow Extra Questions Question 11.
How does Frost present nature in this poem? The following questions may help you to think of an answer.
(i) What are the birds that are usually named in poems? Do you think a crow is often mentioned in poems? What images come to your mind when you think of a crow?
(ii) Again, what is “a hemlock tree”? Why doesn’t the poet write about a more ‘beautiful’ tree such as
a maple, or an oak, or a pine?
(iii) What do the ‘crow’ and ‘hemlock’ represent—joy or sorrow? What does the dust of snow that the crow shakes off a hemlock tree stand for?
Answer:
Robert Frost has represented nature in quite an unconventional manner. While in other nature poems we come across birds such as nightingales or sparrows, Frost has used a crow in this poem. A crow can be associated with something dark, black, and foreboding. That is why, other poets usually mention singing nightingales or beautiful white doves in their poems.

Also, the poet has written about a hemlock tree, which is a poisonous tree. He has not written about a more beautiful tree such as a maple, an oak or a pine tree because these trees symbolize beauty and happiness. Robert Frost wanted to symbolize the feelings of sadness and regret, which is why he has used a hemlock tree.

The crow and the hemlock tree represent sorrow. The dust of snow that is shaken off the hemlock tree by the crow stands for joy that Robert Frost experiences. He has, therefore, used an unconventional tree and bird in order to contrast them with joy in the form of snow.

Class 10 English Dust Of Snow Extra Questions Question 12
Have there been times when you felt depressed or hopeless? Have you experienced a similar moment that changed your mood that day?
Answer:
The teacher may encourage the students to narrate any incident that changed their mood e.g. a sight of dead animal, a scene of accident, treatment of some animals on the way, a funeral procession, etc.

Dust of Snow Extra Questions and Answers Reference to Context

Read the stanza and answer the questions that follow:

Question 1.
The way a crow
Shook down on me
The dust of snow
From a hemlock tree.

(i) Name the poem and poet.
(ii) Where was the crow?
(iii) What did the crow do?
(iv) What does a “hemlock tree’ represent?
Answer:
(i) These lines have been taken from the poem “Dust of Snow” composed by Robert Frost.
(ii) The crow was on the hemlock tree.
(iii) The crow shook the tree is such a way that the dust of snow fell on the poet.
(iv) A hemlock tree is a poisonous tree. It is not considered auspicious. It represents sorrow.

Question 2.
Has given my heart
A change of mood
And saved some part
Of a day I had rued.

(i) Who is ‘I’ in these lines
(ii) What changed the mood of the poet?
(iii) What did the poet decide?
(iv) What was the mood of the poet before and after the incident?
Answer:
(i) ‘I’is the poet himself here.
(ii) The poet’s mood changed when the dust of snow from the hemlock tree fell down on the poet.
(iii) The poet decided to save rest of the day so that there is no harm or sorrow for him.
(iv) The poet was in depressive mood before the incident and after the incident the poet was in enjoyable mood.

Here we are providing The Thief’s Story Extra Questions and Answers Class 10 English Footprints Without Feet, Extra Questions for Class 10 English was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-english/

The Thief’s Story Extra Questions and Answers Class 10 English Footprints Without Feet

The Thief’s Story Extra Questions and Answers Short Answer Type

The Thief’s Story Extra Questions Question 1.
When and how did Hari Singh meet Anil?
Answer:
Hari Singh met Anil when he was watching a wrestling match. Hari Singh tried to befriend Anil.

The Thief Story Extra Questions Question 2.
How did Hari Singh succeed in his profession?
Answer:
He would frequently change his name to dupe the police. He would find out a kind and simple person for his target. He could wait until he had a favourable chance.

The Thief Story Class 10 Extra Questions Question 3.
Why did Hari Singh change his name every month?
Answer:
Hari Singh was a fifteen year old boy who introduces himself to Anil as Hari Singh. He was an experienced thief. He changed his name every month for his own safety from the police and his former employers.

The Thief Story Extra Question Answer Question 4.
Why did Anil agree to feed Hari Singh?
Answer:
Anil needed a helping hand who could cook for him. When Hari Singh said that he could copk well, Anil agreed to feed him.

Extra Questions Of The Thief Story Question 5.
How did the thief realise that Anil knew that he was robbed?
Answer:
When Anil gave him a fifty-rupees note it was still damp. The damp note was telling the whole story. Hari Singh knew that Anil was intelligent enough to understand what had happened in the rainy night.

The Thief’s Story Class 10 Extra Questions And Answers Question 6.
Why was it not easy for the thief to rob Anil?
Answer:
It was not easy for the thief to rob Anil as he was the most trusting person he had ever seen. The thief knew that it was easy to rob a greedy man because he could afford to be robbed. But to rob a careless man like Anil sometimes gave no pleasure of the work as he even did not notice that he had been robbed.

Thief Story Extra Questions Question 7.
What was the thief s reaction when he took Anil’s money?
Answer:
As the thief got the money he quickly crawled out of the room. When he was on the road, he began to run. He had the notes at his waist, held them by the string of his pyjamas. Later on he slowed down to walk and counted the notes. He thought that with those 600 rupees he could lead a luxurious life like an oil-rich Arab at least for a week.

The Thiefs Story Extra Questions Question 8.
How, according to Hari Singh, would the greedy man, the rich man and the poor man react. when they had lost their goods?
Answer:
Hari Singh had made a study of men’s faces when they had lost their goods. According to the thief, on losing their goods a greedy man’s face would show fear, the rich man’s face would show anger and the poor man’s face would show acceptance.

Thief’s Story Extra Questions Question 9.
How did Hari Singh know that Anil had forgiven him?
Answer:
It seems Anil knew about theft but neither his lips nor his eyes showed anything. He gave him fifty rupees and told him that now he would be paid regularly. He informed him that he would teach him to write sentences. It shows that Anil had forgiven him.

The Thief Story Extra Questions And Answers Question 10.
Why did the thief smile without any effect towards the end of the story?
Answer:
The thief smiled at Anil towards the end of the story in his most appealing way. But unlike as on previous occasions, this smile was natural and from the innermost comer of his heart. Being spontaneous, the smile was “without any effect”.

Class 10 The Thief Story Extra Questions Question 11.
Who does ‘I’ refer to in this story?
Answer:
In this story, T refers to the thief.

The Thief Story Short Question Answer Question 12.
What is he “a fairly successful hand” at?
Answer:
He is “a fairly successful hand” at stealing and robbing people.

Thief Story Class 10 Extra Questions Question 13.
What does he get from Anil in return for his work?
Answer:
When Hari asks Anil if he could work for him, Anil replies that he could not pay him. Finally, they reach an agreement that if he would cook, then Anil would feed him. However, Anil soon found out that he did not know how to cook. So, he taught him how to cook and later, how to write his name. He promised he would teach him how to write whole sentences and also how to add numbers. Apart from this, when Hari went out to buy the day’s supplies, he would make a profit of a rupee a day.

The Thief Story Class 10 Important Questions Question 14.
How does the thief think Anil will react to the theft?
Answer:
The thief thinks that on discovering the theft, Anil’s face would show a touch of sadness. The sadness would not be for the loss of money, but for the loss of trust.

Class 10 English The Thief Story Extra Questions Question 15.
What does he say about the different reactions of people when they are robbed?
Answer:
In his short career as a thief, he has studied reactions of so many people when they are robbed off their belongings. He has Observed that the greedy people showed fear; the rich showed anger and the poor people showed acceptance.

Question 16.
Does Anil realize that he has been robbed?
Answer:
Yes, Anil has realized that he has been robbed. He knew this probably because all the notes were wet and damp because of rain. However, he did not say anything to the thief and behaved normally.

The Thief’s Story Extra Questions and Answers Long Answer Type

Question 1.
“Everyone must have a chance to reform”. How did Anil worked upon these values and succeeded?
Answer:
Hari Singh had all the sharp wickedness to rob a person. He knew how to rob and whom to rob. He chose Anil for his purpose because the later was simple and easy, to approach. But when Anil started teaching him how to write words and then sentences and adding numbers, a good man in Hari Singh started dreaming of a life full of honestly and dignity. He got the chance to rob, he robed but the dream of being educated did not let him go. He returned to be educated.

Question 2.
‘Money cannot make a man as much as education can’. Elucidate this statement.
Answer:
Hari Singh had all the sharp wickedness to rob a person. He knew hdw to rob and whom to rob. He chose Anil for his purpose because the later was simple and easy, to approach. But when Anil started teaching him how to write words and then sentences and adding numbers, a good man in Hari Singh started dreaming of a life full of honestly and dignity. He got the chance to rob, he robed but the dream of being educated did not let him go. He returned to be educated.

Question 3.
“Love, trust and compassion transformed Hari Singh”. Explain with reference to the story “The Thief s story”.
Answer:
It is love and sympathy which has transformed Hari Singh into a respectable person. Anil Singh’s job was to write for a magazine. His income was not regular. He led an easygoing life. Anil can easily understand that he had been robbed when he found the notes wet. Anil does not react but rather offers him fifty rupees in the morning. Initially also Anil promised Hari Singh to teach him cooking as well as to write sentences. It was thus good action of Anil that helped Hari Singh to forget about the money and gave more importance to education.

Question 4.
How did Hari Singh happen to stay with Anil? How did he stay with Anil before he tried to rob him?
Answer:
Though Hari Singh was only fifteen years old yet he was a seasoned and successful thief. He met Anil at a wrestling match. He decided to rob him. He got himself introduced to Anil. He lied that he could cook. Anil allowed Hari Singh to stay with him. He would not pay but feed him. Anil did not turn him away though he cooked hopeless food. Anil promised to teach Hari Singh to cook as well as to write.

Due to lack of a regular income, Anil did not pay him any money. Hari Singh prepared the morning tea. He cheated Anil in the shopping and made about a rupee a day. Anil trusted him completely though he knew everything. It was quite difficult to rob Anil, a trusting and careless person. Anyhow he tried to rob him because his thievish nature urged him to do so.

Question 5.
Why did. Hari Singh decide to return stolen money? What light does it throw on his character?
Answer:
After stealing the money Hari Singh rushed to the railway station to catch 10.30 Express to Lucknow. But for some inexplicable reason he did not board the train. He decided to return to the man whom he had robbed. He sat down in the shelter of the Clock Tower and began to reflect upon his life. Suddenly he realised that Anil was helping him to learn reading and writing and that could change his life once and for all.

In his further mediation he made up his mind to return.It shows Hari Singh was grateful to Anil for helping him learn read and write. It also shows that deep in heart he had a- desire to change the course of his life. He wanted to give up theft and wanted to lead a life of a respectable person.

Question 6.
If you were Anil, would you have pardoned the thief? If Yes/No why?
Answer:
Once Hari Singh, a seasonal thief met Anil at a wrestling match. He gave Anil an artificial smile and asked for work in case he could feed him. Anil agreed but on every purchase Hari Singh made a profit. One day Hari Singh stole Anil’s money which was kept-under the mattress and left for the station. But the train left. In between, a good sense prevailed on Hari Singh. He slipped the money under the mattress and slept.

After tea, Anil gave Hari Singh a fifty rupee not and promised to pay him regularly. The note was still wet. Anil understood everything but did not expose the thief s doing. If I had been Anil, I would have pardoned him and traced the reasons for his thievish nature. I would give him an opportunity to mend his ways after serving a warning on the thief.

Question 7.
“A thief in Hari Singh changed into a good human being”. How far was Anil’s considerate nature responsible for this transformation?
Answer:
Hari Singh was an experienced thief who had robbed many people at such a tender age of fifteen years.’ He joined Anil as a cook with a motive of stealing money. But Anil was a kind and considerate person. He employed Hari Singh and taught him how to cook. He trusted him like his younger brother. He was always sympathetic towards him. Hari Singh found it was very difficult to rob such a good human being. He stole money but his conscience did not allow him to run away. He came back and became a . good human being. There was a change in his heart. Thus, it was Anil’s considerate nature which was responsible for this transformation.

Question 8.
What are Hari Singh’s reactions to the prospect of receiving an education? Do they change over time? (Hint’, compare, for example, the thought: “I knew that once I could write like an educated man there would be no limit to what I could not achieve” with these later thought: ‘Whole sentences, I knew, cloud one day bring me more than a few hundred rupees. It was a simple matter to steal—and sometimes just as simple to be caught. But to be a really big man, a clever and respected man, was something else.”)
What makes him return to Anil?
Answer:
When Anil offered to educate him, he thought of it as a bright career prospect for him. Hari knew that once he learnt to read and write, he would achieve more because the motivation behind it was robbing people and becoming a more cunning cheat. But soon Hari Singh’sf reaction to the prospect of receiving education changed and there was a change in his heayt. Probably because he got influenced by the calm in Anil’s life.

Now he also wanted to earn respect and developed a desire to be part of the civilized society. Although, both of them depended on irregular sources of income, but Anil seems to be more satisfied. This motivation was enough for him to return to Anil.

Question 9.
Why does not Anil hand the thief over to the police? Do you think most people would have done so? In what ways is Anil different from such employers?
Answer:
Anil does not hand over the thief to the police because he realized that Hari has already learnt a lesson and he has changed for the better now. Otherwise he would have never put the money back in its place. Though Anil knew how Hari cheated him of a rupee while buying the daily supplies but he never made it obvious in front of him.

Anil wants to give Hari one more chance to mend his ways and thus forgives him. Hari’s case is such that nobody would have forgiven him and straightway handed him over to the police. But Anil is a little different from such employers because he is modest in nature and does not want another person to suffer without giving him a chance to become a better person.

Question 10.
Do you think people like Anil and Hari Singh are found only in fiction, or are there such people in real life?
Answer:
I don’t think that people like Anil and Hari Singh are found only in fiction. There are such people in real life also. Although they are rare in today’s society but yes, they do exist. The first reaction of people, if someone is caught stealing, is that they will try to punish him and then hand him over to the police. But it should be realized that humans are bound to make errors but that shouldn’t let them loose a chance to rectify their mistake and change for good. At least a chance to reform should be given to that person. This is the only way to bring anyone to right path rather than punishing severely and thus making him a criminal forever.

Question 11.
Do you think there is a significant detail in the story that Anil is a struggling writer? Does this explain his behavior in any way?
Answer:
Hari Singh’s observation about Anil having irregular income and Anil’s statement about his sale of a book to a publisher indicates that he is a struggling writer. He lives life according to the amount of money he gets at a given time. When he has the money he enjoys eating out with his friends. When he is having less money then he even doesn’t pay salary to Hari Singh. This shows that he easily makes adjustments in his life without letting anything bother him.

Question 12.
Have you met anyone like Hari Singh? Can you think and imagine the circumstances that can turn a fifteen years old boy into a thief?
Answer:
Yes I know of a boy who was spoilt. His father was a driver and his mother was doing household work in various houses. He was sent to school but he started stealing something or the other from the student’s bags. So he was turned out of the school. He was beaten many times by his parents but he did not give up stealing. One day he ran from his house. After seven months he came back home. Difficulties faced by him made him a changed boy. He rejoined the school and is doing well with his studies.

I think the circumstances that can turn a fifteen year old boy into a thief may vary from person to person. But poverty, lack of education, unemployment, lack of food, negligence of parents and lack of pocket money, bad company and various allurements to buy something or others when there is no sufficient money may be some of the reasons for this.

Question 13.
Where is the story set? (You can get clues from the names of the persons and places mentioned in it). Which languages or languages are spoken in these places? Do you think the characters in the story spoke to each other in English?
Answer:
I think the story is set in old Delhi. Names like Hari Singh and Anil are very common in Delhi. The name (Jumna sweet shop’ indicates that the city must be on the bank of river yamuna. We find small residential houses in markets over the shops in old Delhi. Anil lived in such a house. The old Delhi railway station is adjacent to old Delhi Farm where Hari Singh decided to take Lucknow Express. His house must be very close to the railway station as he went there on foot. These clues from the story suggest that this story is set in old Delhi only. Hindi is spoken in old Delhi. No, the characters do not speak to each other in English.

Here we are providing The Proposal Extra Questions and Answers Class 10 English First Flight, Extra Questions for Class 10 English was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-english/

The Proposal Extra Questions and Answers Class 10 English First Flight

The Proposal Extra Questions and Answers Very Short Answer Type

The Proposal Class 10 Extra Questions Question 1.
Why did Lomov visit Chubukov?
Answer:
Lomov visited Chubukov’s house to propose to Natalaya.

The Proposal Class 10 Extra Questions And Answers Question 2.
What does Chubukov suspect?
Answer:
Chubukov suspects that Lomov has come to borrow money from him.

The Proposal Extra Questions And Answers Question 3.
What does Lomov think about Natalaya?
Answer:
He thinks that Natalaya is an excellent housekeeper, not bad looking, and well-educated.

The Proposal Short Questions And Answers Question 4.
How old was Lomov?
Answer:
Lomov was already thirty-five years old.

The Proposal Class 10 Questions And Answers Question 5.
Where was the Oxen Meadows situated?
Answer:
Oxen Meadows were wedged in between Chubukov’s Birchwoods and the Burnt Marsh.

The Proposal Question Answer Question 6.
What does Natalaya guess on seeing Lomov?
Answer:
She thinks that he is perhaps going to a ball for dancing.

The Proposal Extra Questions Question 7.
Why is Lomov not able to answer properly?
Answer:
Lomov is nervous and confused as he is going to propose to Natalya, so he is not able to answer properly.

The Proposal Class 10 Important Questions Question 8.
What does Natalaya say about Oxen Meadows?
Answer:
Natalaya says that Oxen Meadows belong to her.

Proposal Extra Questions Question 9.
What does Lomov say on his part?
Answer:
Lomov says that Natalaya can see from the documents.

Extra Questions Of The Proposal Question 10.
Who is a land grabber?
Answer:
A land grabber is a person who grabs the land of others.

Proposal Class 10 Extra Questions Question 11.
What threatening was given by Lomov?
Answer:
Lomov told him to go to the court for a decision.

The Proposal Extra Question Answer Question 12.
What is the last threatening to Lomov?
Answer:
Chubukov warned Lomov never to set foot in his house again.

Class 10 The Proposal Extra Questions Question 13.
What was felt by Lomov?
Answer:
Lomov felt heart-palpitation.

The Proposal Questions And Answers Question 14.
How does Chubukov behave in the end?
Answer:
Chubukov gives Lomov’s hand into Natalaya’s hands and advises them for a kiss.

Extra Questions From The Proposal Question 15.
Write down the final advice of Chubukov?
Answer:
Chubukov advised Natalaya and Lomov to start their family bliss.

The Proposal Extra Questions and Answers Short Answer Type

Question 1.
What is the play “The Proposal”?
Answer:
The play “The Proposal’ is about Lomov’s visit to his neighbor’s Chubukov house. Lomov is wearing a formal dress. He has come with the intention of making a marriage proposal to Chubukov’s daughter, Natalaya.

Question 2.
What does Lomov think when he is alone?
Answer:
Lomov thinks that Natalaya is an excellent housekeeper, not bad looking, well educated. It is impossible for him not to marry. In the first place, he is already thirty-five. He ought to lead a quiet and regular life. He suffers from palpitations. He is excitable and always getting upset. There are some other problems too which trouble him.

Question 3.
Why does Lomov wish to propose to Natalaya?
Answer:
Lomov wishes to propose to Natalaya because he feels she is an excellent housekeeper, not bad looking, and is also well-educated. Moreover he feels that he is already thirty-five, which is a critical age and he ought to lead a regular and settled life.

Question 4.
Justify, in brief, the title of the play “The Proposal”.
Answer:
The title of the play “The Proposal” is apt. Lomov comes to Chubukov’s house to propose to his daughter. He talks to Chubukov about his intention and the old man is very happy to have Lomov as the husband of this ageing daughter. When Natalaya comes and there begins an argument. It reminds us of a married couple.

Question 5.
Who is Lomov? Why does he visit Chubukov?
Answer:
Lomov was a young wealthy landowner and an unmarried man of thirty-five. He was anxious to get married as he had already reached a critical age. So he decided to propose Natalaya, a girl of twenty-five years old. He visited Chubukov to ask for his daughter Natalaya’s hand in marriage.

Question 6.
How does Natalaya react when she comes to know that Lomov had come to propose for her hand?
Answer:
When she knows that Lomov came to propose to her, she starts weeping. She calls her father to bring him back at once. He has gone out after the quarrel. She also accuses Chubukov that he drove Lomov out. She becomes hysterical.

Question 7.
What makes Chubukov misunderstand the purpose of Lomov’s visit?
Answer:
Chubukov misunderstands that Lomov has come to borrow money. He does not reveal his purpose of coming directly instead he says that he has come to trouble him with a request for help.

The Proposal Extra Questions and Answers Long Answer Type

Question 1.
Neighbours must have a cordial relationship that Lomov and Natalaya do not have. Describe/ Justify/ Explain the first fight between them.
Answer:
Neighbours must have a cordial relationship but in the case of Lomov and Natalaya, it was different. Lomov and Natalaya were rich people. They were wealthy people and had a competition between them on the subject of wealth. Both were neighbours. Lomov, at a critical age of thirty-five, thought that he had to marry and found Natalaya not bad looking, an excellent housekeeper. So he decided to propose to her.

Lomov, in a well-dressed manner, wearing coat and gloves, one evening went to Chubukov’s house. Chubukov was Natalaya’s father. When he came there and said that he wanted a help, the help which could only be done by him. Chubukov, for first time suspected that he had come for asking money. But after a long struggling and shivering, Lomov uncovers his need. He had come to propose to Natalaya. Chubukov was mistaken and he was filled with extreme joy and called Natalaya. Lomov asked then, whether Natalaya would agree for it or not. Then, Chubukov said that, she would be ready to accept it because she was a lovesick cat.

When Natalaya arrived, she actually did not know that Lomov had come to propose to her. They started talking and when they were talking about land, Lomov stated “Our Oxen Meadows”. Then Natalaya said, “Our Oxen Meadows”, it is not your Oxen Meadows’, it is their. Lomov did not agree. But Natalaya initiated a heated argument. By arguing with each other, they did not solve any problem. They got trapped in a long argument just because of their lack of tolerance towards each other and their desire to keep their pride. Neighbours must have a cordial relationship which Lomov and Natalaya do not have.

Question 2.
Anton Chekov has used humour and exaggeration in the play to comment on courtship in his times. Illustrate with examples from the lesson, “The Proposal”. Also mention the values, you think, any healthy relationship requires.
OR
The principle ‘forgive and forget’ helps a lot is maintaining cordial relations with our neighbours. Do you think Chubukov conveys this message in the play “The Proposal’.
Answer:
Lomov and Natalaya meet for a serious purpose , i.e., to talk about marriage that decides the progress of one’s life as a member of the conventionally established society. But the purpose of their meeting gets lost on two consecutive occasions because Lomov’s faith in the values of his society disrupts his approach to the topic of marriage. He learns that the girl and her father like him, but, instead of proposing to marry her and discussing how their marriage should be organised, he goes on to talk about properties, relations, family histories, and pets, draws them into an unnecessary argument, and antagonises both of them.

Finally, Chubukov marries Lomov and Natasha by force before another problem crops up. Thus the play ends in a comic note, just because the couple gets together with their father to celebrate their marriage while the dispute over the pets is still continuing. For any healthy relationship there should be mutual understanding and respect. Quarreling over trivial issues like dog cannot guarantee longevity of a relationship.

Question 3.
Is Natalaya really a lovesick cat as called by her father? If it is so, why does she quarrel with Lomov?
Answer:
Natalaya was a young unmarried girl of twenty five years. She lived in the neighbourhood of Lomov, a young unmarried man. She was an excellent housekeeper and was not bad looking. She wanted love in her life. Her father called her a lovesick cat. Lomov said that she was well educated, but she did not seem to be so.

She was very quarrelsome and abusive by nature. She began a bitter quarrel with Lomov over a piece of land that had little value. She said that those meadows were not much worth to her but she could not stand unfairness. But when she learnt that Lomov had come to propose to her, she forgot all fairness and unfairness.

She began to wail over the lost chance. She forced her father to call him back. But in no time, she started quarrelling with him again. It was on their dogs. Both claimed their respective dogs to be of a superior breed.

Question 4.
What type of person is Natalaya? Give two examples to show her quarrelsome nature.
Answer:
Natalaya is also rather hypocritical, and she is obstinate and argumentative. When Natalaya first
enters the room, she greets Lomov with warmth and is very gracious as she permits him to smoke and compliments him upon his appearance. However, when Lomov speaks of “my meadows,” she abruptly interrupts and contradicts him. An argument then ensures over who own what land.

Even when Lomov offers them to her as a gift, she continues to insist upon her ownership of them in the first place, reigniting the argument until Lomov leaves. When her father finally reveals to Natalaya that Lomov has actually come to propose marriage; she is infuriated, blaming her father for causing the neighbour to depart.

Question 5.
The principle ‘Forgive and Forget’ helps a lot in maintaining cordial relations with our neighbours. Do you think the author proves this message in the play “The Proposal”?
Answer:
Life is a journey which is often compared to the roller coaster ride. It means life is full of ifs and buts and ups and down. But the path of life can be smoothened by virtues of our actions, attitudes and behaviour. And the principle of forgive and forget comes from these virtues. Letting go of anger and bitterness can work wonders both for our attitude and for our health.

Anger may spoil anything like poison. One cannot afford to remain wallowing in the marsh of anger’or sad feelings. Life has to move on and if one wants to get ahead one has to imbibe “forgive and forget”. Only sensitive and great people can follow this gospel.

In the present play “The Proposal” we find that Lomov visits the house of Chubukov with a proposal to marry his daughter Natalaya. Chubukov’s joy knows no bound to hear this. But in course of their common talk, they pick up nonsensical issue and stand fighting and abusing each other.

Even Natalaya also jumps into the ring of verbal quarrel. When things become normal after the sudden departure of Lomov, Natalaya comes to know about the proposal, She asks her father to call Lomov back. When he comes back this time he and Natalaya starts abusing each other and have heated oral fight over dogs. But in the end, they compromise, they forget their issue and forgive each other. The proposal changes into marriage. Hence we see that the principle helped them unite.

Question 6.
What does Chubukov at first suspect that Lomov had come for? Is he sincere when he later
says, “And I’ve always loved you, my angel, as if you were my own son”? Find reasons for your answer from the play.
Answer:
Chubukov has often helped Lomov with money whenever he requested for it. So he thinks and suspects that Lomov will ask for money. But this time the case is different. He requests a proposal to get Natalaya’s hand for marriage. Since long, Chubukov wanted match for his daughter. Finding fact in his favour, Chubukov changes and uses sweet words and becomes ready for the match.

Question 7.
Chubukov says of Natalaya, “… as if she won’t consent! She’s in love; egad, she’s like a lovesick cat…” Would you agree? Find reasons for your answer.
Answer:
In reality Natalaya has got the fittest age for the marriage. She wants a life partner. On the other hand, Chubukov also desires that his daughter should be married. Lomov is the most suitable match in every respect. In order to say something outwardly, Chubukov happens to pour out these words. It is an acceptable fact that Natalaya loves Lomov from the core of her heart.

Question 8.
(i) Find all the words and expressions in the play that the characters use to speak about
each other, and the accusations and insults they hurl at each other. (For example, Lomov in the end calls Chubukov an intriguer; but earlier, Chubukov has himself called Lomov a “malicious, doublefaced intriguer. Again, Lomov begins by describing Natalaya as “an excellent housekeeper, not bad looking, well-educated.)
(ii) Then think of five adjectives or adjectival expressions of your own to describe each character in the play.
(iii) Can you now imagine what these characters will quarrel about next?
Answer:
(i) There are so many words and expressions that the characters use, to accuse and insult each other.
Some can be given as under. Chubukov calls Lomov: pettifogger, lunatic, drunkard, guzzling gambler, backbiters, villain, scarecrow, blind hen, stuffed-sausage, wizen-faced frump, turnip ghost. Lomov calls Chubukov and his family members: hump-backed, grabber.

(ii) Adjectival expression: Some of the adjectives can be thought as under: proud, industrious, treasure, darling, love, decent, well-educated, sensible and lovable, etc.

(iii) Natalaya, the daughter of Chubukov has got hand of Lomov. Both embrace and kiss each other. Chubukov blesses them to start a family. But like a lie, a Quarrel can be done on any issue.

The Proposal Extra Questions and Answers Reference to Context

Read the following passages and answer the questions that follow:

Question 1.
Chubukov: We just get along somehow, my angel, thanks to your prayers, and so on. Sit down, please do… Now you know, you shouldn’t forget all about your neighbours, my darling. Me dear fellow, why are you so formal in your get-up! Evening dress, gloves, and so on. Can you be going anywhere, my treasure?
(i) Who is the speaker?
(ii) Who do ‘my darling’ and ‘my Angel’ refer to?
(iii) Do you think Chubukov means all the nice words he speaks?
(iv) What is antonym of‘formal’?
Answer:
(i) Chubukov is the speaker of these lines.
(ii) ‘My darling’ and ‘ my angel’ refer to Lomov.
(iii) Not at all, he is a bit hypocritical and shows excess hospitality to Lomov.
(iv) ‘informal’.

Question 2.
Lomov: Well, you see, it’s like this. (Takes his arm) I’ve come to you, honoured Stepan Stepanovitch, to trouble you with a request. Not once or twice have I already had the privilege of applying to you for help, and you have always, so to speak… I must ask your pardon, I am getting excited. I shall drink some water, honoured Stepan Stepanovitch.
(i) Who is the speaker?
(ii) What was he hoping for?
(iii) Why is he so excited?
(iv) Pick out the word from the passage that means the same as ‘opportunity’.
Answer:
(i) Lomov is the speaker of these lines.
(ii) He was hoping for marriage proposal for Natalaya.
(iii) He is excited because he had to propose to his daughter, Natalaya.
(iv) ‘privilege’.

Question 3.
Chubukov: [Interrupting] Me dear fellow… I’m so glad, and so on… Yes, indeed, and all that sort of thing. [Embraces and kisses Lomov] I’ve been hoping for it for a long time. It’s been my continual desire. [Sheds a tear] And I’ve always loved you, my angel, as if you were my own son. May god give you both—His help and His love and so on, and so much hope… What am I behaving in this idiotic way for? I’m off my balance with joy, absolutely off my balance! Oh, with all my soul… I’ll go and call Natasha, and all that.
(i) Who is the speaker?
(ii) What was he hoping for?
(iii) Why is he excited?
(iv) What does the speaker wish for the listener?
Answer:
(i) Chubukov is the speaker of these lines.
(ii) Chubukov was hoping for the marriage proposal for his daughter from Lomov.
(iii) Chubukov is excited because Lomov had come with marriage proposal for his daughter.
(iv) Chubukov wishes for Lomov that God may give him His help and His love.

Question 4.
Lomov: It’s cold… I’m trembling all over, just as if I’d got an examination before me. The great thing is, I must have my mind made up. If I give myself time to think, to hesitate, to talk a lot, to look for an ideal, or for real love, then I’ll never get married. Brr… It’s cold! Natalaya Stepanovna is an excellent housekeeper, not bad-looking, well-educated. What more do I want? But I’m getting a noise in my ears from excitement.
(i) Who is the speaker?
(ii) Who is feeling cold her?
(iii) Why did he feel cold?
(iv) Pick out the word from passage that means the same as ‘to decide’.
Answer:
(i) Lomov is the speaker of these lines.
(ii) Lomov is feeling cold here.
(iii) He feels cold as he has come to propose Natalaya. He is not sure how she would react.
(iv) ‘Mind made up’ means to decide.

Question 5.
Natalya: Then smoke. Here are the matches. The weather is splendid now, but yesterday it was so wet that the workmen didn’t do anything all day. How much hay have you stacked? Just think, I felt greedy and had a whole field cut, and now I’m not at all pleased about it because I’m afraid my hay may rot. I ought to have waited a bit. But what’s this? Why, you’re in evening dress! Well, I never! Are you going to a ball or what? Though I must say you look better… Tell me, why are you got up like that?
(i) Who is speaking these words and to whom?
(ii) Why is she not pleased?
(iii) What does she offer him?
(iv) Pick out the word from the passage that means the same as ‘managed in a pile’.
Answer:
(i) Natalaya is speaking these words to Lomov.
(ii) Natalaya is not pleased because she thinks her hay might rot. She had a whole field cut and hay stacked but unfortunately it had rained the previous day.
(iii) She offers him a cigarette to smoke.
(iv) ‘stacked’.

Question 6.
Lomov: I shall try to be brief. You must know, honoured Natalaya Stepanovna, that I have long, since my childhood, in fact had the privilege of knowing your family. My late aunt and her husband, from whom, as you know, I inherited my land, always had the greatest respect for your father and your late mother. The Lomovs and the Chubukovs have always had the most friendly, and I might almost say the most affectionate, regard for each other. And, as you know, my land is a near neighbour of yours. You will remember that my Oxen Meadows touch your birchwoods.
(i) Who is the speaker?
(ii) Who is being addressed?
(iii) What type of relations they had in the past?
(iv) What is common between the Lomovs and Chubukovs?
Answer:
(i) Lomov is the speaker of these lines.
(ii) Lomov is being addressed to Natalaya.
(iii) They had good relations in the past. Both the families had respect and affection for each other.
(iv) Lomov’s Oxen Meadows touch Chubukov’s birchwoods.

Question 7.
Lomov: …Oxep Meadows, it’s true, were once the subject of dispute, but now everybody knows that they are mine. There’s nothing to argue about. You see my aunt’s grandmother gave the free use of these Meadows in perpetuity to the peasants of your father’s grandfather, in return for which they were to make bricks for her. The peasants belonging to your father’s grandfather had the free use of the Meadows for forty years, and had got into the habit of regarding them as their own, when it happened that.
(i) Who is the speaker of these lines?
(ii) What are they arguing about?
(iii) Who gave the Meadows and to whom?
(iv) What were they supposed to do?
Answer:
(i) Lomov is the speaker of these lines.
(ii) They are arguing about the ownership of the Oxen Meadows.
(iii) The Oxen Meadows were given by Lomov’s aunt’s grandmother to the peasants belonging to Chubukov’s father.
(iv) They were supposed to make bricks for her aunty.

Question 8.
Natalya: No you’re simply joking, or making fun of me. What a surprise! We’ve had the land for nearly three hundred years, and then we’re suddenly told that it isn’t ours! Ivan Vassilevitch, I can hardly believe my own ears. These Meadows aren’t worth much to me. They only come to five dessiatins, and are worth perhaps 300 roubles, but I can’t stand unfairness. Say what you will, I can’t stand unfairness.(Page 148)
(i) Who is the speaker? Who is being addressed?
(ii) How much are the Meadows worth.
(iii) What does she find ‘unfair’?
(iv) Pick out the word from the passage that means opposite to ‘gradually’.
Answer:
(i) Natalaya is the speaker. She is speaking to Lomov.
(ii) The Meadows are worth 300 roubles.
(iii) Natalaya finds Lomov claim that Oxen Meadows are his as unfair.
(iv) ‘suddenly’.

Question 9.
Natalya: Ours! You can go on proving it for two days on end, you can go and put on fifteen caress jackets, but I tell you they’re ours, ours, ours! I don’t want anything of yours and I don’t want to give anything of mine. So there!
(i) Who is speaking these words and to whom?
(ii) What are they arguing over?
(iii) Pick out the word from the passage that means the same as “confirm”.
(iv) What does the speaker offer to prove two days on end?
Answer:
(i) Natalaya is speaking these words for Lomov.
(ii) They are arguing over the ownership of Oxen Meadows.
(iii) ‘prove’(PROVE)
(iv) The Natalya offer to prove for two days on end to ownership of oxen meadows.

Question 10.
Natalya: I can make you a present of them myself, because they’re mine! Your behaviour, Ivan Vassilevitch, is strange, to say the least! Up to this we have always thought of you as a good neighbour, a friend; last year we lent you our threshing-machine, although on that account we had to put off our own threshing till November, but you behave to us as if we were gypsies. Giving me my own land, indeed! No, really, that’s not at all neighbourly! In my opinion, it’s even impudent, if you want to know.
(i) Who is the speaker?
(ii) Who is being addressed?
(iii) What does the speaker offer?
(iv) What does the speaker remind the listener?
Answer:
(i) Natalaya is the speaker.
(ii) Natalaya is addressing Lomov.
(iii) She offers that she can give Lomov her Oxen Meadows as a gift.
(iv) She reminds Lomov that they were good friends and her family gave him their threshing machine last year.

Question 11.
Lomov: But, please, Stepan Stepanovitch, how can they be yours? Do be a reasonable man! My aunt’s grandmother gave the Meadows for the temporary and free use of your grandfather’s peasants. The peasants used the land for forty years and got accustomed to it as if it was their own, when it happened that…
(i) Who is the speaker?
(ii) Who is being addressed?
(iii) What do ‘They’ stand for?
(iv) Pick out the word from the passage that means the same as “familiar”.
Answer:
(i) Lomov is the speaker of these lines.
(ii) Lomov is addressing Chubukov.
(iii) ‘They’ refer to the ‘Meadows’. Each one is trying to prove that the Meadows belong to them.
(iv) ‘accustomed’.

Question 12.
Natalya: There’s some demon of contradiction in you today, Ivan Vassilevitch. First you pretend that the Meadows are yours; now, that Guess is better than Squeezer. I don’t like people who don’t say what they mean, because you know perfectly well that Squeezer is a hundred times better than your silly Guess. Why do you want to say he isn’t?
(i) What does Natalaya blame Lomov for?
(ii) What do Natalaya and Lomov first argue about?
(iii) Who are Guess and Squeezer?
(iv) Pick out the word from the passage that means the same as “opposition”.
Answer:
(i) Natalaya blames Lomov for opposing whatever she says.
(ii) Natalaya and Lomov first argue about the ownership of Oxen Meadows.
(iii) Guess and Squeezer are the names of their dogs.
(iv) ‘contradiction’.

Question 13.
Chubukov: It’s not true! My dear fellow, I’m very liable to lose my temper, and so, just because of that, let’s stop arguing. You started because everybody is always jealous of everybody else’s dogs. Yes, we’re all like that! You too, sir, aren’t blameless! You no sooner begin with this, that and the other, and all that… I remember everything!
(i) Who is the speaker of these lines?
(ii) Who give this advice to whom?
(iii) Who is not blameless? Why?
(iv) Pick out the synonym of innocent or guiltless’ from the passage.
Answer:
(i) Chubukov is the speaker of these lines.
(ii) Chubukov gives this advice to Lomov.
(iii) According the Chubukov, Lomov is not blameless because he had tried to prove that Guess, his dog is superior to Squeezer.
(iv) blameless.

Here we are providing Class 10 Civics Chapter 8 Extra Questions and Answers Challenges to Democracy was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-social-science/

Challenges to Democracy Class 10 Extra Questions Civics Chapter 8

Question 1.
Define challenge.
Answer:
A challenge is not just any problem. We usually call only those difficulties a challenge which are significant and which can be overcome. A challenge is difficulty that carries within it. Once we can overcome a challenge, we can go up to a higher level than before.

Question 2.
How many type of challenges does a Democracy face?
Answer:
Generally, democracy has to face three type of challenges.

1. Fundational challenge.
2. Challenge of expansion.
3. Challenge of deepening of democracy.

Question 3.
What are the foundational challenges of democracy in the modem world?
Answer:

• Making the transition to democracy and instituting Democratic government.
• this involves bringing down the Existent Non-Democratic regime, keeping military away from controlling government and establishing a sovereign and functional state.

Question 4.
Name some countries which facing challenges of expansion.
Answer:
India, USA, Ghana, Ireland Shri Lanka etc.

Question 5.
What is political reform or Democracy reform.
Answer:
Generally, all the suggestions or proposals about overcoming various challenges to democracy are called democracy reform or political reform.

Question 6.
It is possible to keep a list of political reforms?
Answer:

1. No, we cannot have a general list of political or democracy reforms because the challenges at national and state level may be different.
2. Such a list might lose its relevance after some time.

Question 7.
How can low help in political reform?
Answer:

• Law has an important but limited role to play in political reform, carefully Devised changes in low can help to discourage wrong political practices and encourage good ones.
• But legal constitutional changes by themselves cannot overcome challenges to democracy.

Question 8.
Who are mainly responsible for carrying out the political reforms?
Answer:
Democratic reforms are to be carried out mainly by political activists. Parties movement and political conscious citizens.

Question 9.
What should be our main concern to face challenges of Democracy?
Answer:

• Democratic reform are to be brought about principally through political practice. Therefore, the main focus of political reform should be on ways to strengthen Democratic practice.
• The most important concern should be to increase and improve the quality of political, by participation facing my ordinary citizens.

Question 10.
Which law are not very useful in politics?
Answer:

• Generally, laws that seek to ban something are not very successful in political.
• Laws that give political actor incentive to do things have more chances of working.

Question 11.
“Most of the established Democracies face the challenges of expansion”. Discuss.
Answer:

• Most of the established democracies face the challenges of expansion.
• This involves applying the basic principle of Democratic government across all the’ regions. Different social groups and various institutions.
• Ensuring greater power to local governments. Extension of federal principle to all the units of the Federation. Inclusion of women and minority groups, etc. Falls under this challenge.
• This also means that less and less decision should remain outside the arena of Democratic control. Most countries, including India and old democracies like the US, face this challenge.

Question 12.
Explain the challenge of deepening of democracy.
Answer:

The challenge of deepening of democracy is faced by every Democracy in one form or another, this involves strengthening of institutions and practices of democracy.

This should happen in such a way that people can. realize, their expectations of democracy but ordinary people have different expectations from democracy in different societies.

Therefore the challenge take different meaning and paths in different parts of the world.

In concrete terms It usually means strengthening those institutions that help People’s participation and control. This requires an attempt to bring down the control and influence of the rich and powerful people on decision making.

Question 13.
“The best laws are those which empower people to carry out Democratic reforms, explain.
Answer:
Any legal change must carefully look at what result it will on politics. Sometimes the results may be counter-productive. For example, many states have banned. People who have more than two children from contesting panchayat elections.

This has resulted in denial of Democratic opportunity to Manipur and women which was not intended.

Generally, laws that seek to ban something are not very successful in politics. Laws that give political actor incentive to do good things have more chances of working.

The best laws are those which empower people to carry out democratic reforms. The right to Information Act is good example of law that empowers the people to find out and act as watchdogs of democracy. Such a law helps to control corruption and supplements the existing laws that banned corruption. An imposed strict penalties.

Question 14.
What other qualification would you like to add to the existing definition of democracy In order to expand it.
Answer:

• The rulers elected by the people must take all the major decisions.
• Election must offer a choice and Fair Opportunity to the people to exchange the current rulers.
• This choice and opportunity should be available to all the people on an equal basis.
• The exercise of the choice must lead to government Limited by basic rules of the constitution and citizens rights.

Question 15.
What are the major challenges faced by Democracies in most countries of the world today.
Answer:

Following are the three main type of challenges faced by democracies.
1. Foundational challenges: This involves-

• Bringing down the non-Democratic regimes and keeping military away from controlling government.
• Establishing a sovereign and functional state.

2. Challenges of expansion: This involve-

• Applying the basic principle of Democratic government throughout the world.
• Ensuring greater power to local governments. Extension of federal principle and inclusion of women and minority groups.

3. Challenges of deepening democracy: This involves-

• Strengthening of the institutions and practices of democracy.
• Strengthening those institutions that help People’s participation and control.

Question 16.
Describe the role of citizens in democracy.
Answer:

• citizen play an important role in a Democracy as the exercise their rights and freedoms and get benefited from the Democratic setup of the country.
• They must be aware of their rights and duties and should be ever ready to perform their duties.
• They should be aware of the issues and problems facing the country.
• They must Cooperative in maintaining the law and law order in the country.
• People must consider others needs and interests. Also, they should be prepared to make ultimate sacrifice for the sake of Motherland.

Objective Type Question

Four choices are given to the following questions.
Choose the correct answer.

Question 1.
the foundational challenge of democracy involves.
(a) Making the transition to democracy and then instituting Democratic government.
(b) Ensuring greater power to local governments.
(c) Strengthening of the institutions and practices of democracy.
(d) Both B&C.
Answer:
(b) Ensuring greater power to local governments.

Question 2.
The challenge of expansion of democracy involves.
(a) Making the transition to democracy and then instituting Democratic government.
(b) Ensuring greater power to local governments.
(c) Strengthening of the institutions and practices of democracy.
(d) Both B&C.
Answer:
(b) Ensuring greater power to local governments.

Question 3.
The challenge of deepening of democracy involved.
(a) Bringing down the existing non- Democratic governments.
(b) Inclusion of women and minority groups.
(c) Strengthening of the institutions and practices of democracy.
(d) None of this.
Answer:
(c) Strengthening of the institutions and practices of democracy.

Question 4.
Which of the following countries facing the challenge of expansion?
(a) Myanmar.
(b) Belgium.
(c) Pakistan.
(d) India.
Answer:
(d) India.

Question 5.
Which of the following countries facing the foundational challenge of democracy?
(a) India.
(b) USA.
(c) Nepal
(d) Mexico.
Answer:
(c) Nepal

Question 6.
Which of the following countries facing the challenge of deepening of democracy?
(a) Pakistan,
(b) Chile
(c) China
(d) Sri Lanka.
Answers:
(a) Pakistan.

Extra Questions for Class 10 Social Science

Here we are providing Class 10 Civics Chapter 5 Extra Questions and Answers Popular Struggles and Movements was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-social-science/

Popular Struggles and Movements Class 10 Extra Questions Civics Chapter 5

Question 1.
Why did the king dismiss the parliament in 2005?
Answer:

• King Gyanendra was not ready to accept democratic rule in Nepal
• He took advantage of the weakness and unpopularity of the democratically elected government.
• In February 2005, he dismissed the then Prime Minister and dissolved the popular ejected parliament.

Question 2.
What is constitutional monarchy?
Answer:
In a constitutional monarchy, the constitutions acknowledges an elected representative as the head of the state.

Question 3.
Define absolute monarchy.
Answer:
The head of the state has absolute powers under absolute monarchy.

Question 4.
Who had the real powers in Nepal after it won democracy?
Answer:
The King was the formal head of the state but the elected representatives had the real powers to take and implement various decisions.

Question 5.
Why was water supply privatised in Bolivia?
Answer:
The World Bank pressurised the government to give up its contro of water supply.

Question 6.
Give one difference be ween a political party and a pressure group.
Answer:
Pressure groups are organisations that attempt to influence government policies. But unlike political parties, pressure groups do not aim to directly control or share political power. These organisations are formed when people with common occupation, interest, aspirations or opinions come together in order to achieve a common objective.

Question 7.
State one similarity and one difference between an interest group and people’s movement.
Answer:

• Like an interest group, a movement also attempts to influence group, nee politics rather than directly take part in electoral competition.
• But unlike the interest groups, movements have a loose organisation. Their decision making is more informal and flexible. They depend much more on spontaneous mass participation than an interest group.

Question 8.
Give some examples of people’s movement.
Answer:
Narmada Bachao Andolan, movement for right to information, anti liquor movement, women’s movement omnronmental movement etc.

Question 9.
Write the activities of NAPM.
Answer:

• National Alliance for People’s Movements (NAPM) is an organisation of organisations. Various movement groups struggling on specific issues are the members of this organisation.
• It coordinates the activities of a large number of peoples movement in our country.

Question 10.
Write a short note on ‘Kittiko- Hachchiko’ movement.
Answer:
In 1984 Karnataka government set up a company called Karnataka Pulpwood Limited. About 30,000 hectares of land was given virtually free to this company for 40 years. Much of this land was used by local farmers as grazing land for their cattle.

However the company began could be used plant eucalyptus trees in these lands, which could be used for making paper pulp. In 1987 a movement called Kittiko-Hachchiko (meaning, pluck and plant) started a non-violent protest, where people plucked the eucalyptus plants and planted saplings of trees that were useful to the people.

Question 11.
Describe different types of movement groups.
Answer:
A movement seeks to exert influence on the policies of the government. These movements can be of various types. Some movements are issue-specific movements that are concerned with only one issue. They work to achieve that single objective and have a very limited time frame. Some movements have more than one objective to deal with. They work to achieve the broader goal have a long time frame.

Example: The Nepalese movement for democracy worked for the specific objective of regaining the democracy in the country. The Narmada Bachao Andolan started with the issue of people that would be displaced with the construction of the dam on Narmada River. It took a general view as it became a wider movement and questioned all such dams and the people that would be displaced because of it.

Question 12.
Define pressure groups or interest groups.
Answer:
An interest group is a group that seeks to encourage or prevent changes in the country policies without getting elected. They either work to promote a particular policy of the government or protest against the policy of the government depending on their interests. Thus pressure groups or interest groups are those that represent the interests of a particular section of the society.

Example: There can be an interest group that promotes the interests of only the workers, employees or a particular caste group. Their main aim is the well being of their members or their particular section and not of the society in general.

Question 13.
What do you mean by Sectional interest groups?
Answer:

• Usually, interest groups seek to promote the interests of a particular section or group of society. Trade unions, business associations and professional (lawyers, doctors, teachers, etc.) bodies are some examples of this type,
• They are sectional because they represent a section of society: workers, employees, business persons, industrialists, followers of a religion, caste group, etc.
• Their principal concern is the betterment and well being of their members, not society in general “most of the movement are issue”.

Question 14.
Specific movement that seek to achieve a single objective within a limited time frame.” Explain.
Answer:
Most of the movements are issue-specific movements that seek to achieve a single objective within a limited time frame.

The Nepalese Movement for Democracy arose with the specific objective of reversing the king’s orders that led to suspension of democracy.

In India, Narmada Bachao Andolan is a good example of this kind of movement. The movement started with the specific issue of the people displaced by the creation of Sardar Sarovar dam on the Narmada river. Its objective was to stop the dam from being constructed. Gradually it became a wider movement that questioned all such big dams and the model of development that required such dams.

Movements of this kind tend to have a clear leadership and some organisation. But their active life is usually short.

Question 15.
Distinguish between sectional interest group and public interest group.
Answer:
An interest group is a group that seeks to encourage or prevent changes in the public policy without getting elected. They either work to promote a particular policy of the government or protest against the policy of the government depending on their interests. Sectional interest groups are those that represent the interests of a particular section of the society.

They aim for the betterment of their members only. A public interest group is one that represents the interest of the entire society in general. Their activities benefit all the members of the society and not just a particular section in the society.

Example: An interest group that seeks to promote the interests of only the employees or workers or a particular caste group is called a sectional interest group. Whereas, an interest group fighting against caste discrimination affects everybody who is suffering from such discrimination and is an example of a public interest group.

Question 16.
“Some movements are more general or generic movements that seek to achieve a broad goal in the very term.” Do you agree? Why?
Answer:
The single-issue movements can be contrasted with movements that are long term and involve more than one issue. The environmental movement and the women’s movement are classic examples of such movements. There is to one organisation that controls or guides such movements. Environmental movement is a label for a large number of organisations and issue-specific movements. All of these have separate organisation, independent leadership and often different views on policy-related matters.

Yet all of these share a broad objective and have a similar approach. That is why they are called a movement. Sometimes these broad movements have a loose umbrella organisation as well. For example, the National Alliance for Peoples Movements (NAPM) is an organisation of organisations. Various movement groups struggling on specific issues are constituents of this loose organisation which coordinates the activities of alarge number of peoples’ movements in our country.

Question 17.
“The relationship between political parties and pressure which coordinates the activities of a large number of country: groups can take different forms.” Elaborate.
Answer:
The relationship between political parties and pressure groups can take different forms, some direct and others very indirect:
In some instances, the pressure groups are either formed or led by the leaders of political parties or act as extended arms of political parties. For example, most trade unions and students’ organisations in India are either established by or of filiated to one or the other pressure groups are usually activists and leaders

Sometimes political parties grow out of movements’. For example, when the Assam movement led by students against the “foreigners’ came to an end, Gan Parishad. The roots of parties like the DMK and the AIADMK in Tamil Nadu can be traced to a long drawn social reform movement during the 1930 and 1940s.

In most cases the relationship between parties and interest or movement groups is not so direct. They often take positions that are opposed to each other. Yet they are in dialogue and negotiation. Movement groups have raised new issues that have been taken up by political parties. Most of the new leadership of political parties comes from interest or movement groups.

Question 18.
Describe Bolivia’s Water War.
Answer:
Bolivia is a poor country in Latin America. The World Bank pressurised the government to give up its control of municipal water supply. The government sold these rights for the city of Cochabamba to a multi-national company (MNC). The company immediately increased the price of water by four times. Many people received monthly water bill of ₹ 1000 in a country where average income is around ₹ 5000 a month. This led to a spontaneous popular protest.

In January 2000 a new alliance of labour, human rights and community leaders organised a successful four-day general strike in the city. The government agreed to negotiate and the strike was called off. Yet nothing happened. The police resorted to brutal repression when the agitation was started again in February. Another strike followed in April and the government imposed martial law. But the power of the people forced the officials of the MNC to flee the city and made the government concede to all the demands of the protesters. The contract with the MNC was cancelled and water supply was restored to the municipality at old This came to be known as Bolivia’s Water War.

Question 19.
What are public interest groups? What are their aims?
Answer:
Sometimes organisations are not about representing the interest of one section of society. They represent some common or general interest that needs to be defended. The numbers of the organisation may not benefit from the cause that the organisation represents. The Bolivian organisation FEDECOR is an example of that kind of an organisation. In the context of Nepal we noted the participation of human right organisation. These second type of groups are called promotional groups or public interest groups. They promote collective, rather than selective, good.

They aim to help groups other than their own members. For example a group fighting against bonded labour fight not for themselves but for those who are suffering under such bondage. In some instances the members of a public interest group may undertake activity that benefits them as well as others too. For example, BAMCEF (Backward and Minorities Community Employees Federation) is an organisation largely of government employees that campaigns against caste discrimination. Its principal concern is social justice and social equality for the entire society.

Question 20.
“Pressure groups and movements have deepened democracy.” Explain.
Answer:

• Pressure’ groups and movements have deepened democracy. Putting pressure on the rulers is not an unhealthy activity in a democracy as long as everyone gets this opportunity.
• Governments can often come under undue pressure from a small group of rich and powerful people.
• Public interest groups and movements perform a useful role of countering this undue influence and reminding the government of the needs and concerns of ordinary citizens.
• Even the sectional interest groups play a valuable role. Where different groups function actively, no one single group can achieve dominance ovfer society.
• If one group brings pressure on government to make policies in its favour, another will bring counter pressure not to make policies in the way the first group desires.
• The government gets to hear about what different sections of the population want This leads to a rough balance of power and accommodation of conflicting interests.

Multiple Choice Questions

Four choices are given to the following questions.
Choose the correct answer.

Question 1.
When was King Birendra Killed?
(a) 2000
(b) 2001
(c) 2002
(d) 2005
Answer:
(b) 2001

Question 2.
Who became the king of Nepal after the death of King Birendra?
(a) King Deependra
(b) King Narendra
(c) King Vikram
(d) King Gyanendra
Answer:
(d) King Gyanendra

Question 3.
When did King Gyanendra dissolve the popularly elected parliament?
(a) February 2005
(b) June 2005
(c) March 2006
(d) May 2005
Answer:
(a) February 2005

Question 4.
What was the aim of the movement of April 2006 in Nepal?
(a) Restoration of Monarchy
(b) Restoration of Autocracy
(c) Restoration of Democracy
(d) None of these
Answer:
(c) Restoration of Democracy

Question 5.
Who led the movement of April 2006 in Nepal?
(a) Seven Party Alliance
(b) Two-Party Alliance
(c) NCP
(d) Congress
Answer:
(a) Seven Party Alliance

Question 6.
Who became the new Prime Minister of Nepal?
(a) S.p. Thapa
(b) D.B. Gurung
(c) B.N.Jha
(d) G.P. Koirala
Answer:
(d) G.P. Koirala

Question 7.
Bolivia is a country of
(а) Asia
(б) Europe
(c) Latin Amercia
(d) Affrica
Answer:
(c) Latin Amercia

Question 8.
After privatization, the price of water in Bolivia was raised by:
(a) Two times
(b) Four times
(c) Six times
(d) Ten times
Answer:
(b) Four times

Question 9.
“Kittiko-Hachchiko” movement was started in Karnataka in:
(a) 1985
(b) 1986
(c) 1987
(d) 1980
Answer:
(d) 1980

Question 10.
The protest against water privatization in Bolivia was led by:
(a) Fedecor
(b) NCP (Maoist)
(c) Congress
(d) BJP
Answer:
(a) Fedecor

Question 11.
Socialist Party came to power in Bolivia in:
(a) 2001
(b) 2004
(c) 2005
(d) 2006
Answer:
(d) 2006

Question 12.
Organisations that attempt to influence government policies are called:
(a) Pressure group
(b) Political Parties
(c) Social group
(d) None of these
Answer:
(a) Pressure group

Question 13.
These groups who promote collective rather than selective good are called:
(a) Sectional interest group
(b) Public Interest group
(c) Pressure group
(d) Interest group
Answer:
(b) Public Interest group.

Extra Questions for Class 10 Social Science

Here we are providing Class 10 Economics Chapter 1 Extra Questions and Answers Development was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-social-science/

Development Class 10 Extra Questions Economics Chapter 1

Question 1.
What do you mean by economic development?
Answer:
Economic development is meant a process whereby the real per capita income of the country increases over a long period of time along with improvement in the material welfare.

Question 2.
What do you mean by sustained development?
Answer:
Sustained development is the development which takes care of the needs of the present generation without compromising with the needs of the future generations.

Question 3.
Name the three sectors of economy?
Answer:

1. Primary sector,
2. Secondary sector,
3. Territory sector.

Question 4.
Point out the main activities that constitute the Primary sector.
Answer:
The primary sector is constituted by the following activities-

• Agriculture,
• Fishing,
• Mining,
• Hunting,
• Forestry,
• Logging etc.

Question 5.
What is meant by the Secondary sector?
Answer:
Secondary sector constitutes the sectors that are dependent on the primary goods. In other words, preparing goods from the primary goods are the secondary activities. For example, making bread from wheat is a secondary activity. The sectors engaged in these type of activities are known as the secondary sectors.

Question 6.
What is mixed economy?
Answer:
Mixed Economy is the economy that has the characteristics of both capitalist economy as well as socialistic economy.

Question 7.
What is meant by consumption?
Answer:
Taking and using the goods and services by the people is consumption.

Question 8.
What do you mean by production of services?
Answer:
The production of services refers to the activities such as transportation, medical treatment, postal services, courier telephone services, washing of clothes etc.

Question 9.
What is meant by the territary activities?
Answer:
The territary activities are the support services, these are the activities which link the producers and consumers. Banking, Insurance, retail stores, communication, teaching, all are the examples of the territary activities.

Question 10.
Which of the countries are considered as developed countries?
Answer:
Developed countries are those countries where the per capita income is high. These are the countries where people are less engaged in primary activities. U. S. A, U. K., Canada, Japan are some of the examples of this type of countries.

Question 11.
Define national income?
Answer:
National income may be defined as the total value of all the goods and services produced within a country plus the income that is coming from abroad.

Question 12.
What is per capita income?
Answer:
Per capita income is the total national income that is divided by total population.

Question 13.
Which are low-income countries?
Answer:
Countries with S 825 and less per capita income are called low-income countries.

Question 14.
What is Body Mass Index (BMI)?
Answer:
The BMI is an index which helps us calculate whether the adults are nourished or undernourished.

Question 15.
What is meant by renewable resources?
Answer:
Resources which can be renewed are called renewable resources. Groundwater is an example of renewable resource.

Question 16.
What is reserve/production ratio?
Answer:
Reserve/production ratio is one through which one is able to know the number of years that the reserves will last if production and use continue at current rates.

Question 17.
What do you mean by the term economic development
Answer:
Economic development is the system of earning and spending well in order to raise the living standards. Economic development in fact is the progress that a country makes in the field of economy. If in a particular country the people earn higher income and are able to satisfy all their needs, it is said that the country is a developed country and its economy is developed economy.

On the other hand, where people are not able to earn a higher income and are not able to get all the facilities requires for their satisfaction, then we say that such an economy is a developing economy.

Question 18.
Point out the main features of the mixed economy?
Answer:
The main features of the mixed economy are the following

• It is a combination of free-market economy and government planned economy.
• In this type of economy production activities are carried out by individuals as well as by the government.
• In this type of economy, the prices of goods and services produced by individuals are decided by market forces but the goods produced by the government are decided by the government itself.
• The involvement of the government in production level ensures the welfare of the people rather than the profit.

Question 19.
(i) Why do different persons have different notions of development? Which of the following explanations is more important and why?
(a) Because people are different.
(b) Because life situations of persons are different.

(ii) Do the following two statements mean the same? Justify your answer.
(a) People have different developmental goals.
(b) People have conflicting developmental goals.

(iii) Give some examples where factors other than income are important aspects of our lives.
(iv) Explain some of the important ideas of the above section in your own words?
Answer:
(i) Because people are different, that is why they have different notions of development. At times, they have conflicting nations of development.

(ii) The two statements are different. People have different developmental goals. Our development goals may be different than what may be the goal of my Neighbour. It is also possible that people with different goals may have conflicting developmental goals.

(iii) In addition to the factor of income, there are numerous other factors which are important in our lives. Some such examples are

• level of health care,
• level of education,

(iv) Development is what everyone seeks. It is because of the developmental goals that we are able to seek facilities and goals. Indeed, different as we are, we have different goals as well. At times, our developmental goals clash with each other.

Question 20.
(i) Give three examples where an average is used for comparing situations.
(ii) Why do you think average income is an important criterion for development? Explain.
(iii) Besides size of per capita income, what other property of income is important in comparing two Or more societies?
(iv) Suppose records shows that the average income in a country has been increasing over a period. From this, can we conclude that all sections of the economy have become better? Illustrate your answer with an example.
(v) From the text, find out the per capita income level of middle-income countries as per WDR- 2006.
(vi) Write a paragraph on your notion of what should India do, or achieve, to become a developed country.
countries.
Answer:
(i) Average is used in

• calculating the monthly income of citizens;
• in calculating the monthly expenditure of four individuals,
• in calculating the life expectancy of a fixed number of Individuals

As the average income increases, this indicates that there is a consequent development in respect of income.

The size of import and export is also an important component for comparing the two or more countries.

Not so; there may be more income obtained by the business class, and less for the salaried oiie, though the average income may increase.

Not so; there may be more income obtained by the business class, and less for the salaried one, though the average income may increase.

Students may do it with the help of the teachers.
Students may do it with the help of the teachers: Hints

• More educational facilities in the rural areas.
• More health facilities in the rural areas.

Question 21.
(i) Look at data in Table A and B. Is Punjab as ahead of Bihar in literacy rate etc. as it is in terms of per capita income?
(ii) Think of other examples where collective provision of goods and services is cheaper than individual provision.
(iii) Does availability of good health and educational facilities depend only on amount of money spent by the government on these facilities? What other factors could be relevant? ‘
(iv) In Tamil Nadu, 75% of the people living in rural areas use a ration shop, whereas in Jharkhand only 8% of rural people do so. Where would people be better off and why?

Answer:
(i) Yes, Punjab is ahead of Bihar in literacy rate (Punjab 70%, Bihar 47%) as it is in per capita income (Punjab ₹ 26000/- Bihar ₹ 5700/-)

(ii) Students may do it with the help of their teachers.

(iii) Though money can buy facilities, yet money alone is not the sole factor. The other factors which can buy goods and services may include literacy and health rates.

(iv) Ration shops do help people obtain basic necessities at reasonable rates. What needs to be done is efficient working system.

Question 22.
(a) Is crude oil essential for the development process in a country? Discuss.
(b) India does not have enough reserves to meet its present needs. It has to import crude oil. What problems do you anticipate for the country looking at the above, situation?
Answer:
(a) Crude oil helps in generating energy and in transportation. These help in the developmental process of a country.

(b) India imports crude oil and spends a lot of foreign exchange. The rise in the prices of crude oil leads to inflation.

Question 23.
Assume that there are only four families each in two countries. Study the table on the right carefully and answer the questions that follows
(a) Fill in the blanks in a way that both country X and country Y have the same average income.
(b) Now say, which country is better off and why.

Country X is better of: because there is almost an equal average income (or equitable distribution of income) of the four families. But in country Y there is a lot of difference in the income of the four families. Family D has seven times more income than the income of family A, more than 8 times of family B, and about six times more of family C.

Question 24.
Describe the different factors of production?
Answer:
The main factors of production are the different factors of production include the factors that are essential for the production of goods and services. These factors are in fact the resources that are essential in order to carry out various economic activities. In economic terms, these factors are called inputs of factors of production.

These are the factors which help in production of commodities. These are also known as resources. These factors of production or the resources are owned by the individuals, Community government or
by the combination of any two or all the three of them.

The main factors of production are as follows Land :

• It is used for getting all the natural resources. It is the land that provides us with wood, crop, cotton, tea, or other things to Promote our industries.
• Moreover, we also need land to establish industries and factories.
• Land is also required to make the the living places for workers.
• Hence it is the most important factor and resource without which we even cannot imagine about economic development.

Labour: It is also one of the most significant factors of production. Without labour the economic activities cannot take form. All physical and manual efforts of mankind which are used in production or earning money are called labour.

Capital: It is that part of wealth which has been produced by man in his past and which is being used in production nf other goods and services presently. Capital is very essential for production. because without capital one would not be able to buy land or raw material. Neither the labour would be a available without money. Hence without money, no production activity will occur.

Question 24.
Distinguish Between Developed and Developing Economies.
Answer:
manual efforts of mankind which are used in production or earning money are called labour.
Capital: It is that part of wealth which has been produced by man in his past and which is being used in production of other goods and services presently.

Capital is very essential for production because without capital one would not be able to buy land or raw material. Neither the labour would be a available without money. Hence without money no production activity will occur.

Developed	Developing Economics
1. The standard of living of the people in this type of economy is very high.	In this type of economy the standard of the people is comparatively low.
2. Per capita income in this economy is very high.	Per capita income is quite is low.
3.The countries with this type of economy is very developed in industrial sector.	Countries with this type of economy are not so developed in industrial sector.
4. In this type of economy people are engaged more and more in secondary and terriatry kind of economic activities.	Here people are dependent more and more on the primary sector.
5. The per capita income of this type of economy is $10000 or even more. (2004)	The per capita income in this type of economy is $ 825 only or even less. (2004).

Question 25.
Distinguish between Economic and Non-economic activities.
Answer:

Economic activities	Non-economic activities
1. It includes all the activities which give money in return.	In this type of activity, money is not paid.
2. Teaching in schools, selling vegetables, providing legal services are the examples of economic activities.	Painting for hobby, teaching as providing social services, watching movies are examples of non-economic activities.
3. These type of activities play a direct role in the development of a nation.	These type of activities also plays a role in the development of the nation, but indirectly.
4. Economic activities are productive type.	These activities represent consumption.
5. Economic activities are included in national income.	These are not included in national income.

Question 26.
How do you find out undernourishment among the adults?
Answer:
One way to find out if adults are undernourished is to calculate what nutrition scientists call Body Mass Index (BMI). This is easy to calculate. Take the weight of the person in kg. Then take the height in metres. Divide the weight by the square of the height.

If this figure is less than 18.5 then the person would be considered undernourished. However, if this BMI is more than 3 then a person is overweight. This criterion is not applicable to growing children. This also indicates that such a person’s economics background is not sufficient enough to obtain nourishment diet.

Objective Type Questions

Fill in the blanks

Question 1.
The proven reserves (bn tonnes) of crude oil of the World is ………………………. . (137.3,133.7)
Answer:
(137.3)

Question 2.
The reserve/production ratio in terms of years with regard to crude oil is in the world is ……………………… . (93.4, 43.0)
Answer:
(43)

Question 3.
India’s HDI (2004) rank in the 177 countries is ……………………… .
Answer:(126, 137)
(126)

Question 4.
Life Expectancy at birth in India (2004) is ……………………… .(64, 74)
Answer:
(64)

Question 5.
Literacy rate for 15+ years population (2004) in India is ……………………… . (48,60)
Answer:
(60).

Extra Questions for Class 10 Social Science

Here we are providing Class 10 History Chapter 8 Extra Questions and Answers Novels Society and History was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-social-science/

Novels Society and History Class 10 Extra Questions History Chapter 8

Question 1.
Who forned the new readership for novels in the 18th century?
Answer:
Lower middle-class people such as shopkeepers and clerks, the traditional aristocrats formed new readership for novels.

Question 2.
Who used to collect the popular Scottish ballads?
Answer:
Walter Scott.

Question 3.
What is Dickens’ Oliver Twist about?
Answer:
Oliver Twist is about a poor orphan who lived with petty criminals.

Question 4.
Who is Hardy’s hero in his Mayor of Casterbridge?
Answer:
A grain merchant, Michael Henchard.

Question 5.
When women began writing novels, what did some people feel?
Answer:
When women began writing novels, some people felt that women would neglect their traditional role as wives and mothers.

Question 6.
Under what name Sarah Woolsey wrote?
Answer:
Susan Coolidge.

Question 7.
What type of adventurer Robinson Crusoe was?
Answer:
Robinson Crusoe was a typical adventurer; he made inferior creatures his slaves.

Question 8.
Who was the novelist who wrote Chandrakanta?
Answer:
Devaki Nandan Khatri.

Question 9.
Who wrote Durgeshnandni?
Answer:
Bankim Chandra Chattopadhyay.

Novelist	Novel
Samuel Richardson	Pamela (letters)
Henry Fielding	Tom Jones
Charles Dickens	Pickwick Papers, Hard Times Oliver Twist
Homas hardy	Mayor of Caster bridge
Emile Zola	Germinal
Jane Austen	Pride and Prejudice
Charlotte Bronte	Jane Eyre
Stevenson	Treasure Island
Rudyard Kipling	Jungle Book
Helen Jackson	Romana
Susan Coolidge	What Katydid
Daniel Defoe	Robinson Crusoe
Chandu Menon	Indulekha
Goldsmith	Vicar of Wakefield
Sriniwas Das	Pratibha Guru
Premchand	Sewdsadan.

Question 10.
Who wrote Padmarag?
Answer:
Rokeya Hossein (1880-1932).

Question 11.
Name the book Pothari Kunjambu wrote?
Answer:
Saraswativiayan.

Question 12.
Mention Bhudeb Mulchopaadhyay’s novel.
Answer:
Anguriya Binimoy: It was the first historical novel written in Bengal.

Question 13.
What is Dickens novel Hard Times about?
Answer:
Charles Dickens novel Hard Times (1854) describes Coketown, a fictitious industrial town, as a grim place full of machinery, smoking chimneys, rivers polluted purple and buildings that all looked the same. Here workers are known as ‘hands’ as if they had no identity other than as operators of machines. Dickens criticised not just the greed for profits but also the ideas that reduced human beings into simple instruments of production.

Question 14.
What is Germinal all about?
Answer:
Emile Zola’s Germinal (1995) on the life of a young miner in France explores in harsh detail the grim conditions of miners’ live. It ends on a note of despair: the strike the hero lead fails, his co-workers turn against him, and hopes are shattered.

Question 15.
How did the novels explore the world of women?
Answer:
Women got more leisure to read as well as write novels. And novels began exploring the world of women their emotions and identities, their experiences and problems. Many novels were about domestic life-a theme about which women were allowed to speak with authority. They drew upon their experience, wrote about family life and earned public recognition.

Question 16.
Give example as to how the novelists portrayed colonial people.
Answer:
In most of the novels written by the Westerners, the colonial people were seen as primitive and barbaric, less than human, and colonial rule was considered necessary to civilise them, to make them fully human. It was only later, in the twentieth century, that writers like Joseph Conrad (1857-1924) wrote novels that showed the darker side of colonial occupation.

Question 17.
“Bharatendu Harishchandra is described as the pioneer of modern Hindi literature in north India.” Substantiate.
Answer:
In north India Bharatendu Harishchandra, the pioneer of modern Hindi literature encouraged many members of his circle of poets and writers to recreate and translate novels from other languages. Many novels were actually translated and adapted from English and Bengali under his influence.

Question 18.
How did Chandu Menon portray a woman and a man in his novel, Indulekha?
Answer:
Chandu Menon portrayed Indulekha as a woman of breathtaking beauty, high intellectual abilities, artistic talent, and with an education in English and Sanskrit. Madhavan, the hero of the novel, was also presented in ideal colours.

He was a member of the newly English-educated class of Nayars from the University of Madras. He was also a ‘first-rate Sanskrit scholar’. He dressed in western clothes. But, at the same time, he kept a long tuft of hair, according to the Nayar custom.

Question 19.
How has the novel become a popular medium of entertainment among the middle class?
Answer:
As elsewhere in the world in India too, the novel became a popular medium of entertainment among the middle class. The circulation of printed books allowed people to amuse themselves in new ways. Picture books, translations from other languages popular songs sometimes composed on contemporary events, stories in newspapers and magazines-all these offered new forms of entertainment. Within this new culture of print, novels soon” became immensely popular.

Question 20.
Do you think that reading a novel was like daydreaming?
Answer:
Novels give silent reading. In general, they encouraged reading alone and in silence. Individuals sitting at home or travelling in trains enjoyed them. Even in a crowded room, the novel offered a special world of imagination into which the reader could slip, and be all alone. In this, reading a novel was like daydreaming.

Question 21.
Explain what is meant by the following types of novels:
Epistolary novel
Serialised novel
For each type, name one writer who wrote in that style.
Answer:
Epistolary novel: The epistolary novel, used the private and personal form of letters to tell its story. Samuel Richardson’s Pamela, written in the eighteenth century, told much of its story through an exchange of letters between two lovers. These letters tell the reader of the hidden conducts in the heroine’s mind.

Serialised novel: A format in which the story is published in instalments, each part in a new issue of a journal. Example: Charles Dickens’s Pickwick Papers were published in a magazine from 1836.

Question 22.
Write about two important characteristics of the early Hindi novel.
Answer:

1. Earlier, the novels from other languages were translated in Hindi.
2. Original early Hindi novels such as ‘Pariksha-Guru’ were highly moralising, so they flopped.

Question 23.
Taking note of Hardy’s novels, explain as to how did he depict the traditional rural community life and its problems.
Answer:
The nineteenth-century British novelist Thomas Hardy, for instance, wrote about traditional rural communities of England that were last vanishing This was actually a time when large farmers fenced off land, bought machines and employed labourers to produce for the market. The old rural culture with its independent farmers was dying out. We get a sense of this change in Hardy’s Mayor of Casterbridge (1886).

It is about Michael Henchard, a successful grain merchant, who becomes the mayor of the farming town of Casterbridge. He is an independent-minded man who follows his own style in conducting business. He can also be both unpredictably generous and cruel with his employees.

Consequently, he is no match for his manager and rival Donald Farfrae who runs his business on efficient managerial lines and is well regarded for he is smooth and even-tempered with everyone. Thus Hardy mourns the loss of the more personalised world that is disappearing, even as he is aware of its problems and the advantages of the new order.

Question 24.
How does Jane Austen portray the world of women and the genteel tural society in her novel?
Answer:
The novels of Jane Austen give us a glimpse of the world of women in gentel rural society in early-nineteenth-century Britain. They make us think about a society which encouraged women to look for ‘good’ marriages and find wealthy or propertied husbands.

The first sentence of Jane Austen’s Pride and Prejudice states: ‘It is a truth universally acknowledged that a single man in possession of a good fortune, must be in want of a wife.’ This observation allows us to see the behaviour of the main characters, who are preoccupied with marriage and money, as typifying Austen’s society. But women novelists did not simply popularise the domestic role of women. In Charlotte Bronte’s Jane Eyre (1874), young Jane is shown independent and assertive.

Question 25.
Explain with example that from 1920s, there were novels depicting the lives of peasants and low caste people in Bengal.
Answer:
From the 1920s in Bengal too a new kind of novel emerged that depicted the lives of peasants and ‘low’ castes. Advaita Malia Burman’s (1914-51) Titash Ekti Nadir Naam (1956) is an epic about the Mall as, a community of fisherfolk who live off fishing in the river Tishta. The novel is about three generations of the Mallas, about their recurring tragedies and the story of Ananta, a child born of parents who were tragically separated after their wedding night.

Ananta leaves the community to get educated in the city. The novel describes the community life of the Mallas in great detail, their Holi and Kali Puja festivals, boat races, Bhatia songs, their relationships of friendship and animosity with the peasants and the oppression of the upper castes.

Question 26.
What do you known about Basheer, a novelist in Malayalam?
Answer:
Vaikkom Muhammad Basheer (1908-96), was one of the early Muslim writers to gain wide renown as a novelist in Malayalam.
Basheer had little formal education. Most of his works were based on his own rich personal experience rather than on books from the past. When he was in class five at school, Basheer left home to take part in the Salt Satyagraha.

Later he spent years wandering in different parts or India and travelling even to Arabia, working in a ship, living with Sufis and Hindu sanyasis, and training as a wrestler. Basheer’s short novels and stories were written in the ordinary language of conversation. With wonderful humour, Basheer’s novels spoke about details from the everyday life of Muslim households. He also brought into Malayalam writing themes which were considered very unusual at that time – poverty, insanity and life in prisons.

Question 27.
Do you agree that Premchand’s novels are filled with all kinds of powerful characters? Give examples.
Answer:
Premchand’s novels, for instance, are filled with all kinds of powerful characters drawn from all levels of society. In his novels, you meet aristocrats and landlords, middle-level Peasants and landless labourers, middle-class professionals and people from the margins of society.

The women characters are strong individuals especially those who come from the lower classes and are not modernised. Unlike many of his contemporaries, Premchand rejected the nostalgic obsession with ancient history. Instead, his novels look towards the future without forgetting the importance.

Drawn from various strata of society, Premchand’s characters create a community based on democratic values. The central character of his novel Rangbhoomi (The Arena), Surdas, is a visually impaired beggar from a so-called ‘untouchable’ caste. The very act of choosing such a person as the ‘hero’ of a novel is significant. Godan (The Gift of Cow), published in 1936, remains Premchand’s best-known work.

It is an epic of the Indian peasantry. The novel tells the moving story of Hori and his wife Dhania, a peasant couple. Landlords, moneylenders, priests and colonial bureaucrats all those who hold power in society form a network of oppression, rob their land and make them into landless labourers Yet Hori and Dhania retain their dignity to the end.

Objective Type Questions

1. Choose the most appropriate alternative:

Question 1.
One of the following was not written by Premchand
(a) Indulekha
(b) Godan
(c) Rangbhoomi
(d) Sewasadan
Answer:
(a) Indulekha

Question 2.
Jane Austen wrote the following:
(a) Pride and Prejudice
(b) Jane Eyre
(c) Hard Times
(d) Mayor of Casterbridge
Answer:
(a) Pride and Prejudice

Question 3.
The following is not the novel written by Charles Dickens:
(a) Hard Times
(b) Oliver Twist
(c) Great Expectations
(d) Jungle Book
Answer:
(d) Jungle Book

Question 4.
Robinson Crusoe was written by:
(a) Henry Fielding
(b) Charles Dickens
(c) Daniel Defoe
(d) Thomas Hardy
Answer:
(c) Daniel Defoe.

2. Choose true (✓) or false (✗) in the following:

Question 1.
Thomas Hardy wrote Tess
Answer:
(✓)

Question 2.
Premchand was the author of Indulekha.
Answer:
(✗)

Question 3.
am Tolstoy wrote War and Peace.
Answer:
(✓)

Question 4.
Charlotte He Bronte’s novel was Jane Eyre.
Answer:
(✓).

Extra Questions for Class 10 Social Science

Here we are providing Real Numbers Class 10 Extra Questions Maths Chapter 1 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/

Extra Questions for Class 10 Maths Real Numbers with Answers Solutions

Extra Questions for Class 10 Maths Chapter 1 Real Numbers with Solutions Answers

Real Numbers Class 10 Extra Questions Very Short Answer Type

Real Numbers Class 10 Extra Questions Question 1.
What is the HCF of the smallest composite number and the smallest prime number?
Solution:
Smallest composite number = 4
Smallest prime number = 2
So, HCF (4, 2) = 2

Class 10 Maths Chapter 1 Extra Questions Question 2.
The decimal representation of \(\frac{6}{1250}\) will terminate after how many places of decimal?
Solution:

This representation will terminate after 4 decimal places.

Extra Questions For Class 10 Maths Chapter 1 Question 3.
If HCF of a and b is 12 and product of these numbers is 1800. Then what is LCM of these numbers?
Solution:
Product of two numbers = Product of their LCM and HCF
⇒ 1800 = 12 × LCM
⇒ LCM = \(\frac{1800}{12}\) = 150.

Class 10 Real Numbers Extra Questions Question 4.
What is the HCF of 3³ × 5 and 3² × 5²?
Solution:
HCF of 3³ × 5 and 3² × 5² = 3² × 5 = 45

Real Numbers Class 10 Extra Questions With Answers Question 5.
if a is an odd number, b is not divisible by 3 and LCM of a and b is P, what is the LCM of 3a and 2b?
Solution:
6P

Extra Questions On Real Numbers Class 10 Question 6.
If P is prime number then, what is the LCM of P, P², P³?
Solution:
P³

Extra Questions Of Real Numbers Class 10 Question 7.
Two positive integers p and q can be expressed as p = ab² and q = a²b, a and b are prime numbers. What is the LCM of p and q?
Solution:
a²h²

Class 10 Maths Ch 1 Extra Questions Question 8.
A number N when divided by 14 gives the remainder 5. What is the remainder when the same
number is divided by 7?
Solution:
5, because 14 is multiple of 7.
Therefore, remainder in both cases are same.

Real Numbers Extra Questions Question 9.
Examine whether \(\frac{17}{30}\) is a terminating decimal or not.
Solution:

Since the denominator has 3 as its factor.
∴ \(\frac{17}{30}\) is a non4ermznatlng decimal.

Real Numbers Class 10 Important Questions With Solutions Question 10.
What are the possible values of remainder r, when a positive integer a is divided by 3?
Solution:
According to Euclid’s division lemma
a = 3q + r, where O r < 3 and r is an integer.
Therefore, the values of r can be 0, 1 or 2.

Chapter 1 Maths Class 10 Extra Questions Question 11.
A rational number in its decimal expansion is 1.7351. What can you say about the prime factors of q when this number is expressed in the form \(\frac{p}{q}\) ? Give reason.
Solution:
As 1.7351 is a terminating decimal number, so q must be of the form 2^m 5ⁿ, where in, n are natural numbers.

Real Numbers Class 10 Important Questions With Solutions 2021 Question 12.
Without actually performing the long division, find \(\frac{987}{10500}\) will have terminating or non.terminating repeating decimal expansion. Give reason for your answer.
Solution:
\(\frac{987}{10500}\) = \(\frac{47}{500}\) and 500 = 2² × 5³, so it has terminating decimal expansion.

Real Numbers Class 10 Extra Questions Short Answer Type 1

Maths Class 10 Chapter 1 Extra Questions Question 1.
Can the number 4ⁿ, n be a natural number, end with the digit 0? Give reason.
Solution:
if 4ⁿ ends with 0, then it must have 5 as a factor. But, (4)ⁿ = (2²)ⁿ = 2²ⁿ i.e., the only prime factor
of 4ⁿ is 2. Also, we know from the fundamental theorem of arithmetic that the prime factorization of each number is unique.
∴ 4ⁿ can never end with 0.

Real Numbers Class 10 Extra Questions 2021 Question 2.
Write whether the square of any positive integer can be of the form 3m + 2, where m is a natural number. Justify your answer.
Solution:
No, because any positive integer can be written as 3q, 3q + 1, 3q + 2, therefore, square will be
9q² = 3m, 9q² + 6q + 1 = 3(3q²+ 2q) + 1 = 3m + 1,
9q² + 12q + 4 = 3(3q²+ 4q + 1) + 1 = 3m + 1.

Real Numbers Extra Questions For Class 10th Question 3.
Can two numbers have 18 as their HCF and 380 as their LCM? Give reason.
Solution:
No, because here HCF (18) does not divide LCM (380).

Ch 1 Maths Class 10 Extra Questions Question 4.
Write a rational number between √3 and √5.
Solution:
A rational number between √3 and √5 is √3.24 = 1.8 = \(\frac{18}{10}\) = \(\frac{9}{5}\)

Ncert Class 10 Maths Chapter 1 Extra Questions Question 5.
The product of two consecutive integers is divisible by 2. Is this statement true or false? Give reason.
Solution:
True, because n(n + 1) will always be even, as one out of the n or n+ 1 must be even.

Class 10 Maths Real Numbers Extra Questions Question 6.
Explain why 3 × 5 × 7 + 7 is a composite number.
Solution:
3 × 5 × 7 + 7 = 7(3 × 5 + 1) = 7 × 16, which has more than two factors.

Class 10 Maths Extra Questions Chapter 1 Question 7.
What is the least number that is divisible by all the numbers from 1 to 10?
Solution:
Required number = LCM of 1, 2, 3, … 10 = 2520

Class 10th Maths Chapter 1 Extra Questions Question 8.
Find the sum \(0 . \overline{68}\) + \(0 . \overline{73}\).
Solution:

Chapter 1 Class 10 Maths Extra Questions Question 9.
“The product of three consecutive positive integers is divisible by 6”. Is this statement true or false? Justify your answer.
Solution:
True, because n(n + 1) (n + 2) will always be divisible by 6, as at least one of the factors will be divisible by 2 and at least one of the factors will be divisible by 3.

Real Numbers Class 10 Extra Questions Short Answer Type 2

Question 1.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:
For the maximum number of columns, we have to find the HCF of 616 and 32.
Now, since 616 > 32, we apply division lemma to 616 and 32.
We have, 616 = 32 × 19 + 8
Here, remainder 8 ≠ O. So, we again apply division lemma to 32 and 8.
We have, 32 = 8 × 4 + O
Here, remainder is zero. So, HCF (616, 32) = 8
Hence, maximum number of columns is 8.

Question 2.
Find the LCM and HCF of 12, 15 and 21 by applying the prime factorisation method.
Solution:
The prime factors of 12, 15 and 21 are
12 2² × 3, 15 = 3 × 5 and 21 = 3 × 7
Therefore, the HCF of these integers is 3.
2², 3¹, 5¹ and 7¹ and are the greatest powers involved in the prime factors of 12, 15 and 21.
So, LCM (12, 15, 21) = 2² × 3¹ × 5¹ × 7¹ = 420.

Question 3.
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(1) 26 and 91 (ii) 198 and 144
Solution:
(i) We have, 26 = 2 × 13 and 91 = 7 × 13
Thus, LCM (26, 91) = 2 × 7 × 13 = 182
HCF (26, 91) = 13
Now, LCM (26, 91) × HCF (26, 91) = 182 × 13 = 2366
and Product of the two numbers = 26 × 91 = 2366
Hence, LCM × HCF = Product of two numbers.

(ii) 144 = 24 × 32 and 198 = 2 × 32 × 11
∴ LCM(198,144)2⁴ × 3² × 11 = 1584
HCF(198, 144) = 2 × 3² = 18
Now, LCM (198, 144) × HCF (198, 144) = 1584 × 18 = 28512
and product of 198 and 144 = 28512
Thus, product of LCM (198, 144) and HCF (198, 144)
= Product of 198 and 144.

Question 4.
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start from the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solution:
To find the time after which they meet again at the starting point, we have to find LCM of 18 and 12 minutes. We have

Therefore, LCM of 18 and 12 = 2² × 3² = 36
So, they will meet again at the starting point after 36 minutes.

Question 5.
Write down the decimal expansiwns of the following numbers:
(i) \(\frac{35}{50}\) (ii) \(\frac{15}{1600}\)
Solution:
(i)

(ii)

Question 6.
Express the number \(0.3 \overline{178}\) in the form of rational number \(\frac{a}{b}\)
Solution:
Let x = \(0.3 \overline{178}\)
then x = 0.3178178178 … … (1)
10x = 3.178178178 … …(ii)
10000x = 3178.178178… …(iii)
On subtracting (ii) from (iii), we get

Question 7.
If n is an odd positive integer, show that (n² – 1) is divisible by 8.
Solution:
We know that an odd positive integer n is of the form (4q + 1) or (4 + 3) for some integer q.
Case – I When n = (4q + 1)
In this case n² – 1 = (4q + 1)²1 = 16q² + 8q = 8q(2q + 1)
which is clearly divisible by 8.

Case – II When n = (4q + 3)
In this case, we have
n2² = (4q + 3)² – 1 = 16q² + 24q + 8 = 8(2q²+ 3q + 1)
which is clearly divisible by 8.
Hence (n² – 1) is divisible by 8.

Question 8.
The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one
number is 280, then find the other number.
Solution:
Let HCF of the numbers hex then according to question LCM of the number will be 14x
And x + 14 = 600 ⇒ 15x = 600 ⇒ x = 40
Then HCF = 40 and LCM = 14 × 40 = 560
∵ LCM × HCF = Product of the numbers
560 × 40 = 280 × Second number Second number = \(\frac{560 \times 40}{280}\) = 80
Then other number is 80

Question 9.
Find the value of x, y and z in the given factor tree. Can the value of ‘x’ be found without finding the value of ‘y’ and ‘z’? If yes, explain.

Solution:
z = 2 × 17 = 34; y = 34 × 2 = 68 and x = 2 × 68 = 136
Yes, value of x can be found without finding value of y or z as
x = 2 × 2 × 2 × 17 which arc prime 1tctors of x.

Question 10.
Show that any positive odd integer is of the form 6q + 1 or 6q + S or 6q + 5 where q is some integer.
Solution:
Let a he any positive odd integer and h = 6. Then, by Euclid’s algorithm, a = 6q + r, for some
integer q ≥ O and O ≤ r < 6.
i.e., the possible remainders are 0, 1, 2, 3, 4, 5.
1’hus,a canbeoftheform6q,or6q + I,or6q + 2,orßq + 3,ör6q + 4,
or 6q + 5, where q is some quotient.
Since a. is odd integer, so a cannot be of the form , or + 2, or 6q + 4, (since they are even).
Thus, a is of the form 6q + 1, 6q + 3, or 6q + 5, where q is some integer.
Hence, any odd positive integer is of the form 6q + 1 or 6q -1- 3 or 6q + 5, where q is sorne integer.

Question 11.
The decimal expansions of some real numbers are given below. In each case, decide whether they are rational or not. If they are rational, write it in the form \(\frac{p}{q}\). What can you say about the prime factors of q?
(i) 0.140140014000140000… (ii) \(0 . \overline{16}\)
Solution:
(i) We have, 0.140140014000140000… a non-terminating and non-repeating decimal expansion. So it is irrational. It cannot be written in the form of \(\frac{p}{q}\)

(ii) We have, \(0 . \overline{16}\) a non-terminating but repeating decimal expansion. So it is rational.
Let x = \(0 . \overline{16}\)
Then, x = 0.1616… (i)
100×16.1616… ..(ii)
On subtracting (i) from (ii), we get
100x – x = 16.1616 – 0.1616
⇒ 99x = 16 ⇒ x = \(\frac{16}{99}\) = \(\frac{p}{q}\)
The denominator (q) has factors other than 2 or 5.

Real Numbers Class 10 Extra Questions Long Answer Type 1

Question 1.
Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solution:
Let a be an arbitrary positive integer.
Then by Euclid’s division algorithm, corresponding to the positive integers a and 3 there exist
non-negative integers q and r such that
a = 3q + r where 0 ≤ r <3
a² = 9q² + 6qr + r² ….(i) 0 ≤ r <3

Case – I: When r = 0 [putting in (i)]
a² = 9q² = 3(3q²) = 3m where m = 3q²

Case – II: r = 1
a² = 9q²+6q + 1 = 3(3q² + 2q)+ 1 = 3m + 1 where m = 3q² + 2q

Case – III: r = 2
a² = 9q² + 12 + 4 = 3(3q² + 4q + 1) + 1 = 3m + 1 where m = (3q² + 4q + 1)
Hence, square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

Question 2.
Show that one and only one out of n, n + 2, n + 4 is divisible by 3, where n is any positive integer.
Solution:
Let q be the quotient and r be the remainder when n is divided by 3.
Therefore, n = 3q + r, where r = 0, 1, 2
n = 3q or n = 3q + 1 or n = 3q + 2
Case (i) if n = 3q, then n is divisible by 3, n + 2 and n +. 4 arc not divisible by 3.
Case (ii) if 71 = 3q + 1 then n + 2 = 3q + 3 = 3(q + 1), which is divisible by 3 and
n + 4 = 3q + 5, which is not divisible by 3.
So, only (n + 2) is divisible by 3.
Case (iii) If n = 3q + 2, then n + 2 = 3q + 4, which is not divisible by 3 and
(n + 4) = 3q + 6 = 3(q + 2), which is divisible by 3.
So, only (n + 4) is divisible by 3.
Hence one and only one out of n, (n + 2), (n + 4), is divisible by 3.

Question 3.
Use Euclid’s division algorithm to find the HCF of:
(i) 960and432
(ii) 4052 and 12576.
Solution:
(j) Since 960 > 432, we apply the division lemma to 960 and 432.
We have, 960 = 432 × 2 + 96
Since the remainder 96 ≠ 0, so we apply the division lemma to 432 and 96.
We have, 432 = 96 × 4 + 48
Again remainder 48 ≠ 0 so we again apply division lemma to 96 and 48.
We have, 96 = 48 × 2 + O
The remainder has now become zero. So our procedure stops.
Since the divisor at this stage is 48.
Hence, HOE of 960 and 432 is 48.
i.e., HCF (960, 432) = 4H

(ii) Since 12576 > 4052, we apply the division lemma to 12576 and 4052, to get
12576 = 4052 × 3 + 420
Since the remainder 420 ≠ 0, we apply the division lemma to 4052 and 420, to get
4052 = 420 × 9 + 272
We consider the new divisor 420 and the new remainder 272, and apply the division lemma to get
420 = 272 × 1 + 148
We consider the new divisor 272 and the new remainder 148, and apply the division lemma to get
272 = 148 × 1 + 124
We consider the new divisor 148 and the new remainder 124, and apply the division lemma to get
148 = 124 × 1 + 24
We consider the new divisor 124 and the new remainder 24, and apply the division lemma to get
124 = 24 × 5 + 4
We consider the new divisor 24 and the new remainder 4, and apply the division lemma to get
24 = 4 × 6 + O
The remainder has now become zero, so our procedure stops. Since the divisor at this stage is 4, the HCF of 12576 and 4052 is 4.

Question 4.
Using prime factorisation method, find the HCF and LCM of 30, 72 and 432. Also show that HCF × LCM ≠ Product of the three numbers.
Solution:
Given members = 30, 72, 432 .
30 = 2 × 3 × 5; 7² = 2³ × 3² and 432 = 2⁴ × 3³
Here, 2’ and 31 are the smallest powers of the common factors 2 and 3 respectively.
So, HCF (30, 72, 432) = 2¹ × 3¹ = 2× 3 = 6
Again, 2, 33 and 51 arc the greatest powers of the prime factors 2, 3 and 5 respectively.
So, LCM (30, 72, 432) = 2⁴ × 3³ × 5¹ = 2160
HCF × LCM = 6 × 2160 = 12960
Product of numbers = 30 × 72 × 432 = 933120 .
Therefore, HCF × LCM ≠ Product of the numbers.

Question 5.
Prove that √7 is an irrational number.
Solution:
Let us assume, to the contrary, that √7 is a rational number.
Then, there exist co-prime positive integers and such that
√7 = \(\frac{a}{b}\) , b ≠ 0
So, a = √7 b
Squaring both sides, we have
a² = 7b² …… (i)
⇒ 7 divides a² ⇒ 7 divides a
So, we can write
a = 7c (where c is an integer)
Putting the value of a = 7c in (i), we have
49c² = 7b² 7² = b²
It means 7 divides b² and so 7 divides b.
So, 7 is a common factor of both a and b which is a contradiction.
So, our assumption that √7 is rational is wrong.
Hence, we conclude that √7 is an irrational number.

Question 6.
Show that 5 – √3 is an irrational number.
Solution:
Let us assume that 5 – √3 is rational.
So, 5 – √3 may be written as
5 – √3 = \(\frac{p}{q}\), where p and q are integers, having no common factor except 1 and q ≠ 0.
⇒ 5 – \(\frac{p}{q}\) = √3 ⇒ √3 = \(\frac{5 q-p}{q}\)
Since \(\frac{5 q-p}{q}\) is a rational number as p and q are integers.
∴ √3 is also a rational number which is a contradiction.
Thus, our assumption is wrong.
Hence, 5 – √3 is an irrational number.

Question 7.
Using Euclid’s division algorithm, find whether the pair of numbers 847,2160 are co-prime or not.
Solution:
Since 2160 > 847 we apply the division lemma to 2160 and 847
we have, 2160 847 × 2 + 466
Since remainder 466 ≠ 0. So, we apply the division lemma to 847 and 466
847 = 466 × 1+ 381
Again remainder 381 ≠ 0. So we again apply the division lemma to 466 and 381.
466 = 381 × 1 + 85
Again remainder 85 ≠0. So, we again apply the division lemma to 381 and 85
381 = 85 × 4 + 41
Again remainder 41 ≠ 0. So, we again apply the division lemma to 85 and 41.
85 = 41 × 2 + 3
Again remainder 3 ≠ 0. So, we again apply the division lemma to 4 1 and 3.
41 = 3 × 13 + 2
Again remainder 2 ≠ 0. So, we again apply the division lemma to 3 and 2.
3 = 2 × 1 + 1
Again remainder 1 ≠ 0. So, we apply division lemma to 2 and 1
2 = 1 × 2 + 0
The remainder now becomes O. So, our procedure stops.
Since the divisor at this stage is 1.
Hence, HCF of 847 and 2160 is 1 and numbers are co-prime.

Question 8.
Check whether 6ⁿ can end with the digit O for any natural number n.
Solution:
If the number 6ⁿ, for any n, were to end with the digit zero, then h would bc divisible by 5. That is, the prime factorisation of 6ⁿ would contain the prime 5. But 6ⁿ = (2 × 3)ⁿ = 2ⁿ × 3ⁿ So the primes in factorisation of 6ⁿ are 2 and 3. So the uniqueness of the Fundamental Theorem of Arithmetic guarantees that (here are no other primes except 2 and 3 in the factorisation of 6ⁿ. So there is no natural number n for which 6” ends with digit zero.

Real Numbers Class 10 Extra Questions HOTS

Question 1.
Show that there is iw positive integer n for which \(\sqrt{n-1}\) + \(\sqrt{n+1}\) is rational.
Solution:
Let there be a positive integer n for which \(\sqrt{n-1}\) + \(\sqrt{n+1}\) be rational number.

⇒ \(\sqrt{n-1}\) is also perfect. square of positive integer From (A) and (B)
\(\sqrt{n+1}\) and \(\sqrt{n-1}\) are perfect squares of positive integer. It contradict the fact that two perfect
squares differ at least by 3.
Hence, there is no positive integer n for which\(\sqrt{n-1}\) + \(\sqrt{n+1}\) is rational.

Question 2.
Let a, b, e, k be rational numbers such that k is not a perfect cube. if a + bk^1/2 + ck^2/3 then prove that a = b, c = 0.
Solution:


This is impossible as k^2/3 is irrational and \(\frac{a}{c}\) is rational.
∴ a³ – k²c³ ≠ 0
Hence, c = 0
Substituting c = 0 in b² – ac = 0, we get b = 0
Substituting b = 0 and c = 0 in a + bk^1/3 + ck^2/3= 0, we get a = 0
Hence, a = b = c = 0
Question 3.
Find the largest positive integer that will divide 398, 436 and 542 leaving remainders 7, 11 and 15 respectively.
Solution:
It is given that on dividing 398 by the required number, there is a remainder of 7. This means that 398 – 7 = 391 is exactly divisible by the required timber In other words, required number is a factor of 391.
Similarly, required positive integer is a Íctor of 436 – 11 = 425 and 542 – 15 = 527
Clearly, the required number is the HCF of 391, 425 and 527.
Using the factor tree, we get the prime factorisations of 391, 425 and 527 as follows:
391 = 17 × 23, 425 52 × 17 and 527 17 × 31
∴ HCF of 391, 425, and 527 is 17.
Hence, the required number = 17.

Here we are providing Triangles Class 10 Extra Questions Maths Chapter 6 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers.  https://ncertmcq.com/extra-questions-for-class-10-maths/

Extra Questions for Class 10 Maths Triangles with Answers Solutions

Extra Questions for Class 10 Maths Chapter 6 Triangles with Solutions Answers

Triangles Class 10 Extra Questions Very Short Answer Type

Triangles Class 10 Extra Questions Question 1.
Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
Solution:
Since the perimeters and two sides are proportional
∴ The third side is proportional to the corresponding third side.
i.e., The two triangles will be similar by SSS criterion.

Triangles Extra Questions Class 10 Question 2.
A and B are respectively the points on the sides PQ and PR of a ∆PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm, and PB = 4 cm. Is AB || QR? Give reason.
Solution:

Class 10 Triangles Extra Questions Question 3.
If ∆ABC ~ ∆QRP, \(\frac { ar(∆ABC) }{ ar(∆PQR) } \) = \(\frac{9}{4}\), AB = 18 cm and BC = 15 cm, then find the length of PR.
Solution:

Triangles Class 10 Important Questions Question 4.
If it is given that ∆ABC ~ ∆PQR with \(\frac{BC}{QR}\) = \(\frac{1}{3}\), then find \(\frac { ar(∆PQR) }{ ar(∆ABC) } \)
Solution:

Class 10 Triangles Important Questions With Solutions Pdf Question 5.
∆DEF ~ ∆ABC, if DE : AB = 2 : 3 and ar(∆DEF) is equal to 44 square units. Find the area (∆ABC).
Solution:

Triangle Class 10 Extra Questions Question 6.
Is the triangle with sides 12 cm, 16 cm and 18 cm a right triangle? Give reason.
Solution:
Here, 12²+ 16² = 144 + 256 = 400 ≠ 18²
∴ The given triangle is not a right triangle.

Triangles Class 10 Extra Questions Short Answer Type 1

Questions On Similarity Of Triangles Class 10 Question 1.
In triangles PQR and TSM, ∠P = 55°, ∠Q = 25°, ∠M = 100°, and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
Solution:
Şince, ∠R = 180° – (∠P + ∠Q)
= 180° – (55° + 25°) = 100° = ∠M
∠Q = ∠S = 25° (Given)
∆QPR ~ ∆STM
i.e., . ∆QPR is not similar to ∆TSM.

Extra Questions On Triangles Class 10 Question 2.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 63°, then the measures of ∠C = 70°. Is it true? Give reason.
Solution:
Since ∆ABC ~ ∆DEF
∴ ∠A = ∠D = 47°
∠B = ∠E = 63°
∴ ∠C = 180° – (∠A + ∠B) = 180° – (47° + 63°) = 70°
∴ Given statement is true.

Class 10 Maths Chapter 6 Extra Questions Question 3.
Let ∆ABC ~ ∆DEF and their areas be respectively 64 cm² and 121 cm². If EF = 15.4 cm, find BC.
Solution:

Extra Questions Of Triangles Class 10 Question 4.
ABC is an isosceles triangle right-angled at C. Prove that AB² = 2AC².
Solution:
∆ABC is right-angled at C.
∴ AB² = AC² + BC² [By Pythagoras theorem]
⇒ AB² = AC² + AC²
[∵ AC = BC]
⇒ AB² = 2AC²

Class 10 Maths Triangles Extra Questions Question 5.
Sides of triangle are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse.
(i) 7cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
Solution:
(i) Let a = 7 cm, b = 24 cm and c = 25 cm.
Here, largest side, c = 25 cm
We have, a² + b² = (7)² + (24)² = 49 + 576 = 625 = c² [∵c = 25]
So, the triangle is a right triangle.
Hence, c is the hypotenuse of right triangle.

(ii) Let a = 3 cm, b = 8 cm and c = 6 cm
Here, largest side, b = 8 cm
We have, a² + c² = (3)² + (6)² = 9 + 36 = 45 ≠ b²
So, the triangle is not a right triangle.

Triangles Chapter Class 10 Extra Questions Question 6.
If triangle ABC is similar to triangle DEF such that 2AB = DE and BC = 8 cm. Then find the length of EF.
Solution:
∆ABC ~ ∆DEF (Given)

Triangles Class 10 Important Questions With Solutions Question 7.
If the ratio of the perimeter of two similar triangles is 4 : 25, then find the ratio of the areas of the similar triangles.
Solution:
∵ Ratio of perimeter of 2 ∆’s = 4 : 25
∵ Ratio of corresponding sides of the two ∆’s = 4 : 25
Now, the ratio of area of 2 ∆’s = Ratio of square of its corresponding sides.
= \(\frac{(4)^{2}}{(25)^{2}}\) = \(\frac{16}{625}\)

Class 10 Triangle Extra Questions Question 8.
In an isosceles ∆ABC, if AC = BC and AB² = 2AC², then find ∠C.
Solution:

AB² = 2AC² (Given)
AB² = AC² + AC²
AB² = AC² + BC² (∵ AC = BC)
Hence AB is the hypotenuse and ∆ABC is a right angle A.
So, ∠C = 90°

Class 10 Triangles Important Questions Question 9.
The length of the diagonals of a rhombus are 16 cm and 12 cm. Find the length of side of the rhombus.

Solution:
∵ The diagonals of rhombus bisect each other at 90°.
∴ In the right angle ∆BOC
BO = 8 cm
CO = 6 cm
∴ By Pythagoras Theorem
BC² = BO² + CO² = 64 + 36
BC² = 100
BC = 10 cm

Triangles Important Questions Class 10 Question 10.
A man goes 24 m towards West and then 10 m towards North. How far is he from the starting point?
Solution:

By Pythagoras Theorem
AC² = AB² + BC² = (24)² + (10)²
AC² = 676
AC = 26 m
∴ The man is 26 m away from the starting point.

Question 11.
∆ABC ~ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, what is the perimeter of ∆ABC?
Solution:
Since ∆ABC ~ ∆DEF.

Question 12.
∆ABC ~ ∆PQR; if area of ∆ABC = 81 cm², area of ∆PQR = 169 cm² and AC = 7.2 cm, find the length of PR.
Solution:
Since ∆ABC ~ ∆PQR

Triangles Class 10 Extra Questions Short Answer Type 2

Question 1.
In Fig. 7.10, DE || BC. If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, find the value of x.
Solution:

In ∆ABC, we have
DE || BC,
∴ \(\frac{A D}{D B}\) = \(\frac{A E}{E C}\) [By Basic Proportionality Theorem]
⇒ \(\frac{x}{x-2}\) = \(\frac{x+2}{x-1}\)
⇒ x(x – 1) = (x – 2) (x + 2)
⇒ x² – x = x² – 4
⇒ x = 4

Question 2.
E and F are points on the sides PQ and PR respectively of a ∆PQR. Show that EF ||QR if PQ = 1.28 cm, PR= 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.
Solution:

We have, PQ = 1.28 cm, PR = 2.56 cm
PE = 0.18 cm, PF = 0.36 cm
Now, EQ = PQ-PE = 1.28 – 0.18 = 1.10 cm and
FR = PR – PF = 2.56 – 0.36 = 2.20 cm

Therefore, EF || QR [By the converse of Basic Proportionality Theorem]

Question 3.
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Let AB be a vertical pole of length 6m and BC be its shadow and DE be tower and EF be its shadow. Join AC and DF.
Now, in ∆ABC and ∆DEF, we have

h = 42 Hence, height of tower, DE = 42m

Question 4.
In Fig. 7.13, if LM || CB and LN || CD, prove that \(\frac{A M}{A B}=\frac{A N}{A D}\)
Solution:

Firstly, in ∆ABC, we have
LM || CB (Given)
Therefore, by Basic Proportionality Theorem, we have

Question 5.
In Fig. 7.14, DE || OQ and DF || OR Show that EF || QR.
Solution:
In ΔPOQ, we have
DE || OQ (Given)

[Applying the converse of Basic Proportionality Theorem in ∆PQR]

Question 6.
Using converse of Basic Proportionality Theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Solution:

Given: ∆ABC in which D and E are the mid-points of sides AB and AC respectively.
To prove: DE || BC
Proof: Since D and E are the mid-points of AB and AC respectively
∴ AD = DB and AE = EC

DB EC Therefore, DE || BC (By the converse of Basic Proportionality Theorem)

Question 7.
State which pairs of triangles in the following figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form.

Solution:
(i) In ∆ABC and ∆QRP, we have


∆NML is not similar to ∆PQR.

Question 8.
In Fig. 7.17, \(\frac{A O}{O C}\) = \(\frac{B O}{O D}\) = \(\frac{1}{2}\) and AB = 5cm. Find the value of DC.
Solution:

⇒ DC = 10 cm.

Question 9.
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ∆ABE ~ ∆CFB.
Solution:

In ∆ABE and ∆CFB, we have
∠AEB = ∠CBF (Alternate angles)
∠A = ∠C (Opposite angles of a parallelogram)
∴ ∆ABE ~ ∆CFB (By AA criterion of similarity)

Question 10.
S and T are points on sides PR and QR of ∆PQR such that ∠P = ∠RTS. Show that ∆RPQ ~ ∆RTS.
Solution:

In ∆RPQ and ∆RTS, we have
∠RPQ = ∠RTS (Given)
∠PRQ = ∠TRS = ∠R (Common)
∴ ∆RPQ ~ ∆RTS (By AA criterion of similarity)

Question 11.
In Fig. 7.20, ABC and AMP are two right triangles right-angled at B and M respectively. Prove that:
(i) ∆ABC ~ ∆AMP
(ii) \(\frac{C A}{P A}\) = \(\frac{B C}{M P}\)
Solution:

(i) In ∆ABC and ∆AMP, we have
∠ABC = ∠AMP = 90° (Given)
And, ∠BAC = ∠MAP (Common angle)
∴ ∆ABC ~ ∆AMP (By AA criterion of similarity)

(ii) As ∆ABC ~ ∆AMP (Proved above)
∴ \(\frac{C A}{P A}\) = \(\frac{B C}{M P}\) (Sides of similar triangles are proportional)

Question 12.
D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA² = CB.CD.
Solution:

Question 13.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution:

Let ABC be an equilateral triangle of side 2a units.
We draw AD ⊥ BC. Then D is the mid-point of BC.
⇒ \(\frac{B C}{2}\) = \(\frac{2 a}{2}\) = a
Now, ABD is a right triangle right-angled at D.
⇒ AB² = AD² + BD² [By Pythagoras Theorem]
⇒ (2a)² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
⇒ AD = √3a
Hence, each altitude = √3a unit.

Question 14.
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1 \(\frac{1}{2}\) hours?
Solution:

Let the first aeroplane starts from O and goes upto A towards north where

(Distance = Speed × Time)
Again let second aeroplane starts from O at the same time and goes upto B towards west where
OB = 1200 × \(\frac{3}{2}\) = 1800 km
Now, we have to find AB.
In right angled ∆ABO, we have
AB² = OA² + OB² [By using Pythagoras Theorem]
⇒ AB² = (1500)² + (1800)²
⇒ AB² = 2250000 + 3240000
⇒ AB² = 5490000
∴ AB = 100 √549 = 100 × 23.4307 = 2343.07 km.

Question 15.
In the given Fig. 7.24, ∆ABC and ADBC are on the same base BC. If AD intersects BC at 0. Prove
that \(\frac { ar(∆ABC) }{ ar(∆DBC) }\) = \(\frac{AO}{DO}\)
Solution:
Given: ∆ABC and ∆DBC are on the same base BC and AD intersects BC at O.

Question 16.
In Fig. 7.25, AB || PQ || CD , AB = x units, CD = y units and PQ = z units. Prove that \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\).
Solution:

In ∆ADB and ∆PDQ,
Since AB || PQ
∠ABQ = ∠PQD (Corresponding ∠’s)
∠ADB = ∠PDQ (Common)
By AA-Similarity
ΔADB ~ ΔPDQ

Question 17.
In Fig. 7.26, if ∆ABC ~ ∆DEF and their sides are of lengths (in cm) as marked along with them, then find the lengths of the sides of each triangle.
Solution:
∆ABC ~ ∆DEF (Given)

⇒ 4x – 2 = 18
⇒ x = 5
∴ AB = 2 × 5 – 1 = 9, BC = 2 × 5 + 2 = 12
CA = 3 × 5 = 15, DE = 18, EF = 3 × 5 + 9 = 24
and FD = 6 × 5 = 30
Hence, AB = 9 cm, BC = 12 cm, CA = 15 cm
DE = 18 cm, EF = 24 cm, FD = 30 cm

Question 18.
In ΔABC, it is given that \(\frac{A B}{A C}\) = \(\frac{B D}{D C}\) . If ∠B = 70° and ∠C = 50° then find ∠BAD.
Solution:

In ∆ABC
∵ ∠A + ∠B + 2C = 180° (Angle sum property)
∠A + 70° + 50° = 180°
⇒ ∠A = 180° – 120°
⇒ ∠A = 60°
∵ \(\frac{A B}{A C}\) = \(\frac{B D}{D C}\) (Given)
∴ ∠1 = ∠2
[Because if a line through one vertex of a triangle divides the opposite sides in the ratio of the other two sides, then the line bisects the angle at the vertex.]
But ∠1 + ∠2 = 60° …(ii)
From (i) and (ii) we get,
2∠1 = 60°
⇒ ∠1 = \(\frac{60°}{2}\) = 30°
Hence, ∠BAD = 30°

Question 19.
If the diagonals of a quadrilateral divide each other proportionally, prove that it is a trapezium.
Solution:

AB || DC
⇒ In quad ABCD, AB || DC
⇒ ABCD is a trapezium.

Question 20.
In the given Fig. 7.29, \(\frac{P S}{S Q}\) = \(\frac{P T}{T R}\) and ∠PST = ∠PRQ. Prove that PQR is an isosceles triangle.
Solution:

Given: \(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\) and ∠PST = ∠PRQ
To Prove: PQR is isosceles triangle.
Proof: \(\frac{PS}{SQ}\) = \(\frac{PT}{TR}\)
By converse of BPT we get
ST || QR
∴ ∠PST = ∠PQR (Corresponding angles) ….(i)
But, ∠PST = ∠PRQ (Given) ….(ii)
From equation (i) and (ii)
∠PQR = ∠PRQ
⇒ PR = PQ
So, ∆PQR is an isosceles triangle.

Question 21.
The diagonals of a trapezium ABCD in which AB || DC, intersect at O. If AB = 2CD, then find the ratio of areas of triangles AOB and COD.
Solution:

In ∆AOB and ∆COD
∠COD = ∠AOB (Vertically opposite angles)
∠CAB = ∠DCA (Alternate angles)
∆AOB ~ ∆COD (By AA-Similarity)
By area theorem

Hence, ar(∆AOB) : ar(∆COD) = 4 : 1.

Question 22.
In the given Fig. 7.31, find the value of x in terms of a, b and c.
Solution:
In ∆LMK and ∆PNK
We have, ∠M = ∠N = 50° and ∠K = ∠K (Common)
∴ ∆LMK ~ ∆PNK (AA – Similarity)

Question 23.
In the given Fig. 7.32, CD || LA and DE || AC. Find the length of CL, if BE = 4 cm and EC = 2 cm.
Solution:

Question 24.
In the given Fig. 7.33, AB = AC. E is a point on CB produced. If AD is perpendicular to BC and EF perpendicular to AC, prove that ∆ABD is similar to ∆ECF.
Solution:

AB = AC (Given)
⇒ ∠ABC = ∠ACB (Equal sides have equal opposite angles)
Now, in ∆ABD and ∆ECF
∠ABD = ∠ECF (Proved above)
∠ADB = ∠EFC (Each 90°)
So, ∆ABD ~ ∆ECF (AA – Similarity)

Triangles Class 10 Extra Questions Long Answer Type

Question 1.
Using Basic Proportionality Theorem, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Solution:

Given: A ∆ABC in which D is the mid-point of AB and DE is drawn parallel to BC, which meets AC at E.
To prove: AE = EC
Proof: In ∆ABC, DE || BC
∴ By Basic Proportionality Theorem, we have
\(\frac{A D}{D B}\) = \(\frac{A E}{E C}\) …(i)
Now, since D is the mid-point of AB
⇒ AD = BD …(ii)
From (i) and (ii), we have
\(\frac{A D}{D B}\) = \(\frac{A E}{E C}\)
⇒ 1 = \(\frac{A E}{E C}\)
Hence, E is the mid-point of AC.

Question 2.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac{A O}{B O}\) = \(\frac{C O}{D O}\).
Solution:
Given: ABCD is a trapezium, in which AB || DC and its diagonals intersect each other at point O.

Question 3.
If AD and PM are medians of triangles ABC and PQR respectively, where ∆ABC ~ ∆PQR, prove that \(\frac{A B}{P Q}\) = \(\frac{A D}{P M}\)
Solution:
In ΔABD and ΔPQM we have
∠B = ∠Q (∵ ∆ABC ~ ∆PQR) …(i)

Question 4.
In Fig. 7.37, ABCD is a trapezium with AB || DC. If ∆AED is similar to ΔBEC, prove that AD = BC.
Solution:
In ∆EDC and ∆EBA we have
∠1 = ∠2 [Alternate angles]
∠3 = ∠4 [Alternate angles]
∠CED = ∠AEB [Vertically opposite angles]
∴ ∆EDC ~ ∆EBA [By AA criterion of similarity]

Question 5.
Prove that the area of an equilateral triangle described on a side of a right-angled isosceles triangle is half the area of the equilateral triangle described on its hypotenuse.
Solution:

Given: A ∆ABC in which ∠ABC = 90° and AB = BC.
∆ABD and ΔCAE are equilateral triangles.
To Prove: ar(∆ABD) = \(\frac {1}{2}\) × ar(∆CAE)
Proof: Let AB = BC = x units.
∴ hyp. CA = √x² + √x² = x√2 units.
Each of the ABD and ∆CAE being equilateral has each angle equal to 60°.
∴ ∆АВD ~ ∆CAE
But, the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

Question 6.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:

Given: Two triangles ABC and DEF, such that
∆ABC ~ ∆DEF and area (∆ABC) = area (∆DEF)
To prove: ∆ABC ≅ ∆DEF
Proof: ∆ABC ~ ∆DEF
⇒ ∠A = ∠D, ∠B = ∠E, ∠C = ∠F

AB = DE, BC = EF, AC = DF
∆ABC ≅ ∆DEF (By SSS criterion of congruency)

Question 7.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
Let ∆ABC and ∆PQR be two similar triangles. AD and PM are the medians of ∆ABC and ∆PQR respectively.

Question 8.
In Fig. 7.41,0 is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF²
Solution:

Join OA, OB and OC.
(i) In right ∆’s OFA, ODB and OEC, we have
OA² = AF² + OF² …(i)
OB² = BD² + OD² …(ii)
and C² = CE² + OE²
Adding (i), (ii) and (iii), we have
⇒ 0A² + OB² + OC² = AF² + BD² + CE² + OF² + OD² + OE²
⇒ 0A² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²

(ii) We have, OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
⇒ (OA² – OE²) + (OB² – OF²) – (OC² – OD²) = AF² + BD² + CE²
⇒ AE² + CD² + BF² = AP² + BD² + CE²
[Using Pythagoras Theorem in ∆AOE, ∆BOF and ∆COD]

Question 9.
The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3CD (see Fig. 7.42). Prove that 2AB² = 2AC² + BC²
Solution:

We have, DB = 3CD
Now,
BC = BD + CD
⇒ BC = 3CD + CD = 4CD (Given DB = 3CD)
∴ CD = \(\frac{1}{4}\) BC
and DB = 3CD = \(\frac{1}{4}\)BC
Now, in right-angled triangle ABD using Pythagoras Theorem we have
AB² = AD² + DB² …(i)
Again, in right-angled triangle ∆ADC, we have
AC² = AD² + CD² …(ii)
Subtracting (ii) from (i), we have
AB² – AC² = DB² – CD²

∴ 2AB² – 2AC² = BC²
⇒ 2AB² = 2AC² + BC²

Question 10.
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:

Let ABC be an equilateral triangle and let AD ⊥ BC.
∴ BD = DC
Now, in right-angled triangle ADB, we have
AB² = AD² + BD² [Using Pythagoras Theorem]

Question 11.
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7.44 DE || BC and BD = CE. Prove that ∆ABC is an isosceles triangle.

Solution:
Given: A triangle ABC in which a line parallel to side BC intersects other two sides AB and AC at D and E respectively.

⇒ AB = AC (As DB = EC)
∴ ∆ABC is an isosceles triangle.

Question 12.
In Fig. 7.46, ABD is a triangle right-angled at A and AC ⊥ BD Show that
(i) AB² = BC. BD
(ii) AD² = BD.CD
(iii) AC² = BC.DC
Solution:
Given: ABD is a triangle right-angled at A and AC ⊥ BD.

To prove: (i) AB² = BC .BD
(ii) AD² = BD.CD
(iii) AC² = BC . DC
Proof: (i) In ∆ACB and ∆DAB, we have
∠ACB = ∠DAB = 90°
∠ABC = ∠DBA = ∠B [Common]
∴ ∆ACB ~ ∆DAB [By AA criterion of similarity]
\(\frac{BC}{AB}=\frac{AB}{DB}\)
⇒ AB² = BC.BD

(ii) In ∆ACD and ∆BAD, we have
∠ACD = ∠BAD = 90°
∠CDA = ∠BDA = ∠D [Common]
∴ ∆ACD ~ ∆BAD [By AA criterion of similarity]
\(\frac{AD}{BD}=\frac{CD}{AD}\)
⇒ AD² = BD.CD

(iii) We have ∆ACB – ∆DAB
⇒ ∆ВСА ~ ∆ВAD …(i)
and ∆ACD ~ ∆BAD …(ii)
From (i) and (ii), we have
∆ВСА ~ ∆АСD
\(\frac{B C}{A C}=\frac{A C}{D C}\)
AC² = BC . DC

Question 13.
Prove that ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides. Using the above result do the following: Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution:
Given: Two triangles ABC and PQR such that ∆ABC ~ ∆PQR


Second Part:

In ∆AOB and ∆COD we have
∠AOB = ∠COD (Vertically opposite angles) and
∠OAB = ∠OCD (Alternate angles)
∆AOB ~ ∆COD (By AA criterion of similarity]

Hence, the ratio of areas of ∆AOB and ∆COD 4 : 1.

Question 14.
Prove that, in a right triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
Using the above, do the following:
Prove that, in a ∆ABC if AD is perpendicular to BC, then AB² + CD² = AC² + BD².
Solution:

Given: A right triangle ABC right-angled at B.
To Prove: AC² = AB² + BC²
Construction: Draw BD ⊥ AC
Proof: In ∆ADB and ∆ABC
∠A = ∠A (Common)
∠ADB = ∠ABC (Both 90°)
∴ ∆ADB ~ ∆ABC (AA similarity criterion)

Adding (i) and (ii), we get
AD. AC + CD . AC = AB² + BC²
or, AC (AD + CD) = AB² + BC²
or, AC . AC = AB² + BC²
or, AC² = AB² +BC²

Second Part:
In Fig. 7.50, As AD ⊥ BC
Therefore, ∠ADB = ∠ADC = 90°
By Pythagoras Theorem, we have
AB² = AD² + BD² …..(i)
AC² = AD² + DC² …..(ii)
Subtracting (ii) from (i)
AB² – AC² = AD² + BD² – (AD² + DC²)
⇒ AB² – AC² = BD² – DC² = AB² + DC² = BD² + AC²

Question 15.
In a triangle, if the square on one side is equal to the sum of the squares on the other two sides, prove that the angle opposite to the first side is a right angle. Use the above theorem to find the measure of ∠PKR in Fig. 7.51.

Solution:
Given: A triangle ABC in which AC² = AB² + BC²
To Prove: ∠B = 90°.
Construction: We construct a ∆PQR right-angled at Q such that PQ = AB and QR = BC
Proof: Now, from ∆PQR, we have,

Question 16.
ABC is a triangle in which AB = AC and D is a point on AC such that BC² = AC × CD. Prove that BD = BC.
Solution:
Given: ∆ABC in which AB = AC and D is a point on the side AC such that BC² = AC × CD
To prove: BD = BC
Construction: Join BD
Proof: We have,

Question 17.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:
Let ABCD be a square and ABCE and ∆ACF have been drawn on side BC and the diagonal AC respectively.

Question 18.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE² + BD² = AB² + DE².
Solution:

In right angled ΔACE and ΔDCB, we have
AE² = AC² + CE² (Pythagoras Theorem) …(i)
and BD² = DC² + BC²… (ii)
Adding (i) and (ii), we have
AE² + BD² = AC² + CE² + DC² + BC²
AE² + BD² = (AC² + BC²) + (DC² + CE²)
AE² + BD² = AB² + DE²
[∵ AC² + BC² = AB² in right-angled triangle ABC and DC² + EC² = DE² in right-angled triangle CDE.]

Triangles Class 10 Extra Questions HOTS

Question 1.
In Fig. 7.57, ΔFEC ≅ ΔGDB and ∠1 = ∠2. Prove that ΔADE ~ ∆ABC.
Solution:
Since ΔFEC ≅ ΔGDB

Question 2.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ∆ABC ~ ∆PQR.
Solution:
Given: In ∆ABC and ∆PQR, AD and PM are their medians respectively

To prove: ∆ABC ~ ∆PQR
Construction: Produce AD to E such that AD = DE and produce PM to N such that PM = MN. Join BE, CE, QN, RN.
Proof: Quadrilateral ABEC and PQNR are ||^gm because their diagonals bisect each other at D and M respectively.
⇒ BE = AC and QN = PR


∆ABC ~ ∆PQR (By SAS criterion of similarity)

Question 3.
In Fig. 7.59, P is the mid-point of BC and Q is the mid-point of AP. If BQ when produced meets AC at R, prove that RA = \(\frac{1}{3}\) CA.
Solution:

Given: In ∆ABC, P is the mid-point of BC, Q is the mid-point of AP such that BQ produced meets AC at R.
To prove: RA = \(\frac{1}{3}\) CA
Construction: Draw PS || BR, meeting AC at S.
Proof: In ABCR, P is the mid-point of BC and PS || BR.
∴ S is the mid-point of CR.
⇒ CS = SR ….(i)
In ∆APS, Q is the mid-point of AP and QR ||PS
∴ R is the mid-point of AS.
∴ AR = RS …(ii)
From (i) and (ii), we get
AR = RS = SC
⇒ AC = AR + RS + SC = 3 AR
⇒ AR = \(\frac{1}{3}\)AC = \(\frac{1}{3}\)CA

Question 4.
In Fig. 7.60, ABC and DBC are two triangles on the same base BC. If ar(∆ABC) AO AD intersects BC at O, show that \(\frac { ar(∆ABC) }{ ar(∆DBC) }\) = \(\frac{AO}{DO}\)

Solution:
Given: Two triangles ∆ABC and ADBC which stand on the same base but on opposite sides of BC.

Question 5.
Two poles of height a metres and b metres are p metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given \(\frac{a b}{a+b}\) metres.
Solution:
Let AB and CD be two poles of height a and b metres respectively such that the poles are p metres
apart i.e., AC = p metres.
Suppose the lines AD and BC meet at O such that OL = h metres.
Let CL = x and LA = y. Then, x + y = p.
In ∆ABC and ALOC, we have
∠CAB = ∠CLO [Each equal to 90°)
∠C = ∠C [Common]
∴ ∆ABC ~ ∆LOC [By AA criterion of similarity]

Hence, the height of the intersection of the lines joining the top of each pole to the foot of the opposite pole is \(\frac{a b}{a+b}\) metres.

Question 6.
In an equilateral triangle ABC, D is a point on side BC such that BD = \(\frac{1}{3}\) BC. Prove that 9AD² = 7AB².
Solution:

Given: An equilateral triangle ABC and D be a point on BC such that
BD = \(\frac{1}{3}\) BC.
To Prove: 9AD² = 7AB²
Construction: Draw AE ⊥ BC. Join AD.
DE Proof: ∆ABC is an equilateral triangle and AE ⊥ BC
BE = EC
Thus, we have
BD = \(\frac{1}{3}\) BC and DC = \(\frac{2}{3}\) BC and BE = EC = \(\frac{1}{2\) BC
In ∆AEB
AE² + BE² = AB² [Using Pythagoras Theorem]
AE² = AB² – BE²
AD² – DE² = AB² – BE² [∵ In ∆AED, AD² = AE² + DE²]
AD² = AB² – BE² + DE²

9AD² = 9AB² – 2AB² [∵ AB = BC]
9AD² = 7AB²

Question 7.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced to E. Prove that EL = 2BL.
Solution:
In ∆BMC and ∆EMD, we have
MC = MD [∵ M is the mid-point of CD]
∠CMB = ∠DME [Vertically opposite angles]
and ∠MBC = ∠MED [Alternate angles]
So, by AAS criterion of congruence, we have
∆BMC ≅ ∆EMD
⇒ BC = DE [CPCT]
Also, BC = AD [∵ ABCD is a parallelogram]
Now, in ∆AEL and ∆CBL, we have
∠ALE = ∠CLB [Vertically opposite angles]
∠EAL = ∠BCL [Alternate angles]
So, by AA criterion of similarity of triangles, we have
∆AEL ~ ∆CBL

In this page, we are providing Life Processes Class 10 Extra Questions and Answers Science Chapter 6 pdf download. NCERT Extra Questions for Class 10 Science Chapter 6 Life Processes with Answers will help to score more marks in your CBSE Board Exams. https://ncertmcq.com/extra-questions-for-class-10-science/

Class 10 Science Chapter 6 Extra Questions and Answers Life Processes

Extra Questions for Class 10 Science Chapter 6 Life Processes with Answers Solutions

Extra Questions for Class 10 Science Chapter 6 Very Short Answer Type

Life Processes Class 10 Extra Questions Question 1.
What will happen to a plant if its xylem is removed?  [CBSE 2009]
Answer:
Xylem helps in the transport of water and minerals to the various parts of the plant. If xylem is removed it would ultimately lead to the death of the plant.

Life Processes Class 10 Extra Questions With Answers Question 2.
Name the green dot like structures in some cells observed by a student when a leaf peel was viewed under a microscope. What is the green colour due to?  [CBSE 2010]
Answer:
The green dots like structures seen are the chloroplasts. The green colour is due to the pigment called chlorophyll.

Life Processes Extra Questions Question 3.
Give one reason why multicellular organisms require special organs for exchange of gases between their body and their environment.  [CBSE 2010]
Answer:
Simple diffusion is not sufficient for the exchange of gases in multicellular organisms as all their cells are not in direct contact with the environment. So, they require special organs for exchange of gases between their body and their environment.

Extra Questions Of Life Processes Class 10 Question 4.
What process in plants is known as transpiration?  [CBSE 2008]
Answer:
The loss of water in the form of vapour from the aerial parts of the plant is known as transpiration.

Class 10 Science Chapter 6 Extra Questions Question 5.
What is osmoregulation?  [CBSE 2006]
Answer:
The maintenance of optimum concentration of water and salts (electrolytes) in the body fluids is called as osmoregulation.

Life Process Extra Question Answer Question 6.
Why is carbon dioxide mostly transported in dissolved form?
Answer:
Carbon dioxide is mostly transported in the dissolved form as it is more soluble in water.

Life Processes Class 10 Extra Questions Pdf Question 7.
When we breathe out, why does the air passage not collapse?  [CBSE 2014]
Answer:
Rings of cartilage present on trachea prevent it from collapsing during the passage of air.

Class 10 Life Processes Extra Questions Question 8.
Herbivores have longer small intestine while carnivores have shorter small intestine. Give reason.  [CBSE 2014]
Answer:
Herbivores have a longer small intestine compared to the carnivores to allow time for the cellulose present in the grass to get digested.

Extra Questions On Life Processes Class 10 Question 9.
Mention the respiratory unit of lungs and excretory unit of kidneys.  [CBSE 2014]
Answer:
The respiratory unit of lungs are alveoli and excretory unit of kidneys are nephrons.

Class 10 Science Ch 6 Extra Questions Question 10.
Some organisms derive nutrition from plants or animals without killing them. What are these organisms called? Write one example.  [CBSE 2014]
Answer:
They are called parasites, e.g. Cuscuta and tapeworm are the parasites of plants and animals respectively.

Important Questions For Class 10 Science Chapter 6 Life Processes Question 11.
What are the major constituents of urine?  [CBSE 2008]
Answer:
Urine is an aqueous solution of water, urea, chloride, sodium, potassium, creatinine and other dissolved ions, inorganic and organic compounds (proteins, hormones, and metabolites).

Chapter 6 Science Class 10 Extra Questions Question 12.
Where does the urine produced by the kidneys get stored?  [CBSE 2006]
Answer:
Urinary bladder.

Extra Questions Life Processes Class 10 Question 13.
How does transpiration help in upward transport of substances?  [CBSE 2008]
Answer:
Transpiration creates a suction pressure which pulls up water along with the minerals through the xylem.

Life Processes Class 10 Extra Questions And Answers Question 14.
When the right atrium contract, blood flows from it to which part of the heart?  [CBSE 2007]
Answer:
Right ventricle.

Ch 6 Science Class 10 Extra Question Question 15.
State the functions of the following:
(i) Blood
(ii) WBC  [CBSE 2011, 2012]
Answer:
Function of RBC – To carry oxygen to various parts of the body.
Function of WBC – To protect the body against both infectious diseases and foreign invaders.

Extra Questions For Class 10 Science Chapter 6 Question 16.
Write the functions of the two upper chambers of the human heart.  [CBSE 2011]
Answer:
The right atrium receives deoxygenated blood from various parts of the body through the vena cava.
The left atrium receives the oxygenated blood from the lungs through the pulmonary artery.

Ncert Class 10 Science Chapter 6 Extra Questions Question 17.
Leakage of blood from vessels reduces the efficiency of pumping system. How is the leakage prevented? [CBSE 2010, 2011]
Answer:
Leakage is prevented by the blood platelets present in the blood which help in clotting the blood at the site of injury.

Class 10 Life Process Extra Questions Question 18.
Which mechanism plays an important role in transportation of water in plants
(i) During daytime
(ii) At night?  [CBSE 2011, 2012]
Answer:
During daytime – Transpiration; At Night – Root pressure.

Extra Questions Of Chapter 6 Science Class 10 Question 19.
Why are valves present in heart and the veins?   [CBSE 2010,2011]
Answer:
Valves present in the heart does not allow the blood to flow backwards when the atria or ventricles contracts. Valves are present in the veins to prevent the back flow of blood in the veins as it travels at very slow rate in the veins.

Extra Questions for Class 10 Science Chapter 6 Short Answer Type I

Class 10 Science Life Process Extra Questions Question 1.
How are the fats digested in our bodies? Where does this process take place?  [CBSE 2011]
Answer:
Bile juice produced by the liver breaks down the large fat globules into smaller globules by the process of emulsification. These small globules are then digested by the fat digesting enzymes. This process takes place in the small intestine.

Extra Questions From Life Processes Class 10 Question 2.
State the function of the epiglottis.  [CBSE 2004]
Answer:
Epiglottis covers the opening of the wind pipe (the glottis) and prevents the entry of food into the wind pipe during swallowing.

Extra Questions For Class 10 Science Life Processes Question 3.
The breathing cycle is rhythmic, whereas exchange of gases is a continuous process. Comment upon this statement.
Answer:
Some volume of air called as residual volume is left behind in the lungs even after forceful breathing out of air. This helps to provide sufficient time for oxygen to be absorbed and for carbon dioxide to be released. Even in the absence of continuous breathing, the exchange of these gases is continuous. Hence, breathing cycle is rhythmic, whereas exchange of gases is a continuous process.

Class 10 Chapter 6 Science Extra Questions Question 4.
What are the end products formed during fermentation in yeast? Under what condition a similar process takes place in our body that lead to muscle cramps?  [CBSE 2010]
Answer:
The end products formed during fermentation in yeast are ethanol and carbon dioxide. A similar process occurs in the muscles and produces lactic acid during anaerobic respiration in the muscles. Accumulation of lactic acid in the muscle cells lead to muscular cramps.

Extra Questions Of Chapter Life Processes Class 10 Question 5.
Give Reasons:
(a) Rings of cartilage are present in the trachea.
(b) Lungs always contain a residual volume of air.  [CBSE 2013]
Answer:
(a) The walls of trachea have rings of cartilage on them which prevent it from collapsing.
(b) The volume of air left behind in the lungs even after forceful breathing out of air is called as residual volume. This helps to provide sufficient time for oxygen to be absorbed and for the carbon dioxide to be released.

Question 6.
State in brief the role of lungs in the exchange of gases.  [CBSE 2012]
Answer:
Lungs have alveoli which provide a larger surface for exchange of gases and are richly supplied with blood vessels to enable faster exchange. So, lungs help in providing oxygen to various tissues of the body and removal of carbon dioxide from the body.

Question 7.
What is the basic unit of kidney called? Why is it composed of very thin blood capillaries?  [CBSE 2015]
Answer:
The basic unit of kidney is called nephron. It is composed of a cluster of very thin blood capillaries as they help in filtration of blood and remove the nitrogenous wastes from the body in the form of urine.

Question 8.
How does the plant get rid of excretory products?  [CBSE 2009]
Answer:
Excess oxygen and carbon dioxide removed through stomata.
Plant waste products are also removed by:

• Storage in cellular vacuoles
• Storage in leaves that fall off
• Storing as resins and gums in old xylem
• By excreting into the soil around them.

Question 9.
Tabulate two differences between renal artery and renal vein. [CBSE 2009]
Answer:
Renal Artery

1. Blood in renal artery contains glucose, oxygen and cellular waste products.
2. It takes blood towards the kidney.

Renal Vein:

1. Blood in renal vein is filtered, and is free from cellular waste and any other impurities.
2. It takes blood away from the kidney towards the heart.

Question 10.
(a) What is the main toxic waste that kidney filters from the blood?
(b) Name any two substances which are selectively reabsorbed from the tubules of a nephron.  [CBSE 2010, 2012]
Answer:
(a) Urea is the main excretory product removed by the kidneys of human beings.
(b) The substances selectively reabsorbed by the kidneys are water, glucose, electrolytes, etc.

Question 11.
What is excretion? How do unicellular organisms remove their wastes?  [CBSE 2012]
Answer:
Removal of metabolic wastes from the body is called as excretion. Many unicellular organisms remove metabolic wastes from the body surface into the surrounding water by simple diffusion.

Question 12.
Write a function of (a) blood vessels (b) blood platelets.  [CBSE 2008]
Answer:
(a) Blood vessels help in carrying blood to various parts of the body.
(b) Blood platelets help in the clotting of blood at the point of injury to prevent non-stop bleeding.

Question 13.
How are water and minerals absorbed by the plant?  [CBSE 2010]
Answer:
The water and minerals in the soil are absorbed by plants with the help of root hairs present on their roots. Root hairs provide a larger surface area for absorption.

Question 14.
What are capillaries? Sate the function performed by them.  [CBSE 2012]
Answer:
The capillaries are one-cell thick, small blood vessels which help in the exchange of materials between the blood and the surrounding tissues.

Question 15.
Mention the two main components of the transport system in plants. State one function of each one of these components.  [CBSE 2010, 2011]
Answer:
The two main components of the transport system in the plants are xylem and phloem. Xylem helps to transport water and minerals to various parts of the plant. Phloem helps to carry food from leaves to the various parts of the plant.

Question 16.
During one cycle how many times does blood go to the heart of fish and why?  [CBSE 2010]
Answer:
The blood passes only once through the heart in one cycle in fishes because the two-chambered heart of the fishes pump the blood to gills for oxygenation. The blood from gills is then directly passed to the various parts of the body in the fishes.

Question 17.
What would be the consequences of deficiency of haemoglobin in our bodies?  [CBSE 2012]
Answer:
Haemoglobin helps in transport of oxygen to the body parts. Deficiency of haemoglobin will affect transport of oxygen and the person will suffer from improper metabolism, weakness, fatigue and pain.

Question 18.
Name the following:
(а) The process in plants that links light energy with chemical energy.
(b) Organisms that can prepare their own food.
(c) The cell organelle where photosynthesis occurs.
(d) Cells that surround a stomatal pore.
(e) Organisms that cannot prepare their own food.
(f) An enzyme secreted from gastric glands in stomach that acts on proteins. [NCERT Exemplar]
Answer:
(a) Photosynthesis
(b) Autotrophs
(c) Chloroplast
(d) Guard cells
(e) Heterotrophs
(f) Pepsin

Question 19.
“All plants give out oxygen during the day and carbon dioxide during night”. Do you agree with this statement? Give reason.  [NCERT Exemplar]
Answer:
The rate of photosynthesis is higher than the rate of respiration during the daytime, so the net result is the evolution of oxygen. In the absence of photosynthesis at night, only respiration occurs in the plants so carbon dioxide is released at night.

Question 20.
How do the guard cells regulate opening and closing of stomatal pores?  [NCERT Exemplar]
Answer:
The entry of water into the guard cells of the stomata causes an increase in turgor pressure in the guard cells which leads to opening of the stomata. The loss of water from the guard cells results in their shrinking and closes the stomata.

Question 21.
Two green plants are kept separately in oxygen free containers, one in the dark and the other in continuous light. Which one will live longer? Give reasons.  [NCERT Exemplar]
Answer:
Plant kept in continuous light will perform photosynthesis and release oxygen for its respiration. Hence, it will live longer than the plant kept in the dark.

Question 22.
If a plant is releasing carbon dioxide and taking in oxygen during the day, does it mean that there is no photosynthesis occurring? Justify your answer.  [NCERT Exemplar]
Answer:
During the day time the plants take in carbon dioxide and release oxygen as a by product of photosynthesis. Release of carbon dioxide and taking in air during the daytime means that either the rate of photosynthesis is too low or its not occurring at all.

Question 23.
Why do fishes die when taken out of water? [NCERT Exemplar]
Answer:
Fishes take water from mouth and send it to the gills which are richly supplied with blood capillaries for absorbing the oxygen dissolved in water. But the fishes cannot absorb gaseous oxygen, so they die soon after they are taken out of water.

Question 24.
Is ‘nutrition’ a necessity for an organism? Discuss.  [NCERT Exemplar]
Answer:
Nutrition (food) is a necessity for an organism as

• It provides energy for the various metabolic processes in the body.
• It is essential for the growth and repair of various cells and tissues.
• It helps to provide resistance against various diseases.

Question 25.
What would happen if green plants disappear from the Earth?  [NCERT Exemplar]
Answer:
The green plants are the source of energy for the entire organisms on the Earth. Herbivores depend directly on the plants while the carnivores and omnivores depend either directly or indirectly on plants. So, all the organisms will die due to starvation if all the green plants disappear from the Earth.

Question 26.
Leaves of a healthy potted plant were coated with vaseline. Will this plant remain healthy for long? Give reasons for your answer.  [NCERT Exemplar]
Answer:
This plant will not remain healthy for a long time because the stomata will get blocked, so plant

• Will not get carbon dioxide for photosynthesis.
• Will not get oxygen for respiration.
• Will not be able to do transpiration which will in turn affect the upward transport of water and minerals.

Extra Questions for Class 10 Science Chapter 6 Short Answer Type II

Question 1.
(a) Explain why the rate of photosynthesis is low both at lower and higher temperatures.
(b) Is green light most or least useful in photosynthesis and why?  [CBSE 2005]
Answer:
(a) The reactions occurring during the process of photosynthesis is under the control of enzymes, which work under an optimum range of temperature only. The very high temperatures as well as very low temperatures decrease the activity of the enzymes. So, the rate of photosynthesis is low both at lower and higher temperatures.
(b) Chlorophyll does not absorb the green light, so the green light is least useful in photosynthesis.

Question 2.
Draw a well labelled diagram of stomata. List two functions of stomata.  [CBSE 2011]
Answer:
The function of stomata are:
(a) Help in the exchange of gases like carbon dioxide and oxygen from the leaves of the plants.
(b) Help in the transport of water, minerals and food materials in plants by transpiration.
(c) Transpiration occurring through stomata on leaves helps in cooling of leaf surface.

Question 3.
Explain how the products of photosynthesis and other substances are translocated in plants?  [CBSE 2015]
Answer:
Translocation is the transport of soluble products of photosynthesis through phloem. Sucrose is transferred into sieve tubes of phloem via the companion cells using energy from ATP. This increases the osmotic pressure inside the sieve tubes which causes movement of water into the sieve tubes from the adjacent xylem. This pressure helps in translocation of material in the phloem to tissues which have less pressure.

Question 4.
Write three events which occur during the process of photosynthesis.  [CBSE 2015]
Answer:
The three events which occur during photosynthesis are:

1. Absorption of light energy of chlorophyll.
2. Conversion of light energy to chemical energy + splitting of water molecules into hydrogen and oxygen.
3. Reduction of carbon dioxide to carbohydrates.

Question 5.
Explain why the transportation of materials is necessary in animals?  [CBSE 2014]
Answer:
The transportation system is necessary to transport the various nutrients and gases to and from the various parts of the body. It also helps in removing the wastes from the body of the organisms. The various life processes are maintained and carried out due to an efficient transport system in animals.

Question 6.
Plants absorb water from the soil. Explain how does the water reach the tree top?  [CBSE 2014]
Answer:
There are two ways for the transport of water in plants:
(а) By root pressure: The cells of root in contact with soil actively take up ions which creates a difference in ion concentration between the root and the soil. Water moves into the root from the soil to eliminate this difference, creating a column of water that is steadily pushed upwards.

(b) By transpiration pull: Loss of water from stomata by transpiration gets replaced by the xylem vessels in the leaf which creates a suction to pull water from the xylem cells of the roots. This strategy is used during day time and helps to transport water to the highest points of the plant body.

Question 7.
State the function of the following in the alimentary canal.
(a) Liver
(b) Gallbladder
(c) Villi   [CBSE2014]
Answer:
(a) Liver: Helps in detoxification of harmful chemicals. Produces bile juice which helps in digestion of fats.
(b) Gall bladder: Helps in the storage of bile juice released from the liver.
(c) Villi: Helps to increase the surface area of the small intestine and aid in absorption of the digested nutrients.

Question 8.
(a) How does exchange of respiratory gases—oxygen and carbon dioxide take place between tissues and blood in human beings?
(b) Name the respiratory pigment in humans. Where is it found?  [CBSE 2014]
Answer:
(a) The arteries have oxygenated blood having oxygen at higher pressure to that present in the tissues. Carbon dioxide is present at a higher pressure inside the tissues. The oxygen is thus exchanged at the tissue surface with carbon dioxide in order to supply oxygen to the tissues of the body.

(b) Haemoglobin is the respiratory pigment in humans which is present in the red blood cells.

Question 9.
Explain giving any three reasons the significance of transpiration in plants.   [CBSE 2014]
Answer:
The significance of transpiration is:

1. Absorption and upward movement of water and minerals.
2. It also helps in temperature regulation by cooling the leaf surface.
3. It helps to maintain the shape and size of the cells.

Question 10.
Mention the pathway of urine starting from the organ of its formation. Name four substances which are reabsorbed from the initial filtrate in the tubular part of the nephron.  [CBSE 2014]
Answer:
The urine formed in the kidney moves through the ureters to the urinary bladder. Ureters takes urine into the urinary bladder where it is stored until it is released through the urethra. Release of urine is under nervous control.

Glucose, amino acids, salts and water are reabsorbed from the initial filtrate in the tubular part of the nephron.

Question 11.
Major amount of water is selectively reabsorbed by the tubular part of nephron. On what factor does the amount of water reabsorbed depends?  [CBSE 2010, 2011, 2012]
Answer:
The amount of water reabsorbed by the tubular part of nephron depends on two factors:

1. The amount of nitrogenous and other excretory wastes present in the body.
2. The amount of excess water present in the body.

Question 12.
State the functions of
(a) Renal artery
(b) kidney
(c) urinary bladder.  [CBSE 2012]
Answer:
(a) Renal artery: It brings blood having nitrogenous wastes to nephrons for filtration.
(b) Kidney: It help to filter the nitrogenous and other wastes from the blood.
(c) Urinary bladder: Stores urine until it is eliminated.

Question 13.
(a) Write the important functions of the structural and functional unit of kidney.
(b) Write any one function of an artificial kidney.  [CBSE 2011]
Answer:
(a) The structural and functional units of kidney are the nephrons which help in filtration, reabsorption and secretion. They help to eliminate the wastes from the body.

(b) Artificial kidneys help to remove the harmful nitrogenous wastes from the body of a patient whose kidneys are not functioning properly.

Question 14.
How is urine produced?  [CBSE 2011]
Answer:
The urine formation involves three steps:
(a) Glomerular filtration: Nitrogenous wastes, glucose water, amino acid are filtered from the blood in blood capillaries into Bowman Capsule of the nephrons.

(b) Selective reasbsorption: Some substances in the initial filtrate, such as glucose, amino acids, salts and a major amount of water are selectively reabsorbed back by capillaries surrounding the nephrons.

(c) Tubular secretion: Some ions like K⁺, H⁺, etc. are secreted into the tubule which opens up into the collecting duct.

Question 15.
Blood does not clot in the blood vessels. Give reasons.  [CBSE 2009]
Answer:
Blood does not clot inside the blood vessels because the chemical which causes the blood to clot in the cut area gets activated only when it comes in contact with air (oxygen actually) to form the clotting substance. The chemical for clotting of blood is released by the blood platelets.

Question 16.
What is translocation? How does it take place in plants?  [CBSE 2011]
Answer:
Translocation is the movement of materials from leaves to other tissues throughout the plant by the phloem. During translocation, sucrose is transferred into sieve tubes of phloem via the companion cells using energy from ATP. This increases the osmotic pressure inside the sieve tubes which causes movement of water into the sieve tubes from the adjacent xylem. This pressure helps in translocation of material in the phloem to tissues which have less pressure.

Question 17.
(a) Transport of food in plants require living tissues and energy. Justify this statement.
(b) Name the components of food that are transported by the living tissues.  [CBSE 2012]
Answer:
(a) The energy in the form of ATP is required both during loading of sucrose in the sieve tubes at the leaf surface and during uploading of the sucrose at the site which needs sucrose for its metabolic activities. So, it can be said that transport of food in plants require living tissues i.e., phloem and energy in the form of ATP.

(b) The components of food transported by the phloem are sugars, hormones, and minerals elements dissolved in water.

Question 18.
What are the adaptations of leaf for photosynthesis?  [NCERT Exemplar]
Answer:
The various adaptations in leaf for photosynthesis are:

• Leaves have expanded portion to provide large surface area for maximum light absorption.
• Leaves are arranged at right angles to the light source in a way that causes overlapping.
• The extensive network of veins helps in quick transport of substances in leaf.
• Easy gaseous exchange is facilitated by the presence of stomata on the leaves.
• The chloroplasts are more in number on the upper surface of leaves.

Question 19.
Why is small intestine in herbivores longer than in carnivores?  [NCERT Exemplar]
Answer:
Herbivores have a longer small intestine compared to the carnivores to allow time for the cellulose present in the grass to get digested. Cellulose takes longer time to get digested. Animals have shorter small intestine as they are not able to digest cellulose.

Question 20.
What will happen if mucus is not secreted by the gastric glands?  [NCERT Exemplar]
Answer:
Mucus forms the lining of the stomach and protects it from the action of hydrochloric acid released by the gastric glands of stomach. If mucus is not secreted then acidity and ulcers may be caused due to erosion of the inner lining of the stomach by the acid.

Question 21.
What is the significance of emulsification of fats?  [NCERT Exemplar]
Answer:
The large globules of fats are broken down into smaller fat globules by the action of bile salts present in the bile juice. This is called emulsification and it increases the efficiency of the fat digesting enzymes that can digest the smaller fat globules.

Question 22.
Why does absorption of digested food occur mainly in the small intestine?  [NCERT Exemplar]
Answer:
Maximum absorption occurs in small intestine because

• The process of digestion gets completed in the small intestine by intestinal juice.
• Finger-like projections called villi provide larger surface area for absorption.
• The villi are richly supplied with blood vessels to enable easy absorption into the bloodstream.

Question 23.

Group (A)	Group (B)
(a) Autotrophic nutrition	(i) Leech
(b) Heterotrophic nutrition	(ii) Paramecium
(c) Parasitic nutrition	(iii) Deer
(d) Digestion in food vaceolus	(iv) Green plants

Answer:
(a) (iv)
(b) (iii)
(c) (i)
(d) (ii)

Question 24.
Why is the rate of breathing in aquatic organisms much faster than in terrestrial organisms?  [NCERT Exemplar]
Answer:
Aquatic animals use the oxygen dissolved in water. They breathe at a faster rate since the amount of dissolved oxygen is fairly low compared to the amount of oxygen in the air.

Question 25.
In each of the following situations what happens to the rate of photosynthesis?  [NCERT Exemplar]
(a) Cloudy days
(b) No rainfall in the area
(c) Good manuring in the area
(d) Stomata get blocked due to dust
Answer:
(a) Decreases
(b) Decreases
(c) Increases
(d) Decreases

Question 26.
Name the energy currency in the living organisms. When and where is it produced?  [NCERT Exemplar]
Answer:
The energy currency in the cells is Adenosine triphosphate (ATP). It is produced in mitochondria during respiration and in chloroplasts during photosynthesis in plants.

Question 27.
What is common for Cuscuta, ticks and leeches?  [NCERT Exemplar]
Answer:
Cuscuta, ticks and leeches are parasites which obtain their nutrition from plants and animals without killing them.

Question 28.
Explain the role of mouth in digestion of food.  [NCERT Exemplar]
Answer:
The mouth plays an important role in digestion because

• The teeth present in the mouth crush the food into small pieces.
• Tongue helps in thorough mixing of food with saliva and to swallow the food.
• Saliva secreted in mouth contains an enzyme called salivary amylase which helps to break down the starch into maltose.

Question 29.
What are the functions of gastric glands present in the wall of the stomach?
Answer:
The functions of gastric glands present in the wall of the stomach are:

1. Produce pepsin enzyme that digests proteins.
2. Secrete mucus which protects the inner lining of stomach from the action of acids.

Extra Questions for Class 10 Science Chapter 6 Long Answer Type

Question 1.
How is oxygen and carbon dioxide transported in the human beings?  [CBSE All India 2008]
Answer:
At the alveolar surface, the oxygen diffuses out from the alveoli to the capillaries which surround the alveoli. The oxygenated blood is transported from the lungs to the heart which pumps it to the various parts of the body to supply it to various tissues.

At the tissue surface, the oxygen from the blood diffuses out into the tissues and carbon dioxide which is at higher concentration in the tissues, diffuses out into the capillaries. The capillaries transport the carbon dioxide rich blood from tissues to the alveoli where carbon dioxide diffuses out into the alveoli and oxygen enters into the capillaries to be transported to the tissues.

Question 2.
(a) State reason for the following:
(i) Herbivores need a longer small intestine while carnivores have shorter small intestine.
(ii) The lungs are designed in human beings to maximise the area for exchange of gases.
(b) The rate of breathing in aquatic organisms is much faster than that seen in terrestrial organisms.  [CBSE 2014]
Answer:
(a) (i) The cellulose present in the grasses takes a longer time to digest. So, the herbivores have a longer small intestine than the carnivores.
(ii) The alveoli present in the lungs provide a larger surface area for the exchange of gases in the lungs.

(b) Aquatic organisms breathe at a faster rate since the amount of dissolved oxygen is fairly low compared to the amount of oxygen in the air.

Question 3.
Draw a diagram of excretory unit of human kidney and label the following:
(a) Bowman’s capsule
(b) Glomerulus
(c) Collecting duct
(d) Renal artery  [CBSE 2011, 2012]
Answer:

Question 4.
Explain how deoxygenated blood travels from body to lung for purification. Draw well labelled diagram in support of your answer.  [CBSE 2011]
Answer:
The deoxygenated blood from the various parts of the body is collected by the veins which transport the blood to the heart through the vena cava. Vena cava pours the deoxygenated blood in the right atrium of the heart. The right atrium contracts and the blood moves into the right ventricle. On contraction of the right ventricle the deoxygenated blood is transported to the lungs through the pulmonary artery for purification.

Schematic representation of transport and exchange of oxygen and carbon dioxide

Question 5.
Draw the sectional view of human heart and label the following parts given below:
(a) Chamber where oxygenated blood from lungs is collected
(b) Largest blood vessel in the body
(c) Muscular wall separating right and left chambers
(d) Blood vessel that carries blood from heart to the lungs  [CBSE 2010]
OR
(a) Part which receives deoxygenated blood from vena cava
(b) Part which sends deoxygenated blood to lung through pulmonary artery
(c) Part which receives oxygenated blood from lungs
(d) Part which sends oxygenated blood to all parts of the body through aorta  [CBSE 2012]
OR
(a) the chamber of heart that pumps out deoxygenated blood
(b) the blood vessel that carries away oxygenated blood from the heart
(c) the blood vessel that receives deoxygenated blood from the lower part of our body  [CBSE 2010, 2011, 2012]
Answer:

(а) Chamber where oxygenated blood from lungs is collected – Left atrium
(b) Largest blood vessel in the body – Aorta
(c) Muscular wall separating right and left chambers – Septum
(d) Blood vessel that carries blood from heart to the lungs – Pulmonary artery
OR
(а) Part which receives deoxygenated blood from vena cava – Right atrium
(b) Part which sends deoxygenated blood to lung through pulmonary artery – Right Ventricle
(c) Part which receives oxygenated blood from lungs – Left atrium
(d) Part which sends oxygenated blood to all parts of the body through aorta – Left Ventricle
OR
(а) the chamber of heart that pumps out deoxygenated blood – Right Ventricle
(b) the blood vessel that carries away oxygenated blood from the heart – Aorta
(c) the blood vessel that receives deoxygenated blood from the lower part of our body – Inferior Vena cava

Question 6.
Explain the process of nutrition in Amoeba.  [NCERT Exemplar]
Answer:
Nutrition in Amoeba:
Temporary finger-like extensions of the cell surface called pseudopodia are used by Amoeba to engulf food. Pseudopodia fuse over the food particle forming a food-vacuole in which complex substances are broken down into simpler ones and diffuse into the cytoplasm. The remaining undigested material moves to the surface of the cell and gets thrown out.

Question 7.
Describe the alimentary canal of man.  [NCERT Exemplar]
Answer:
Mouth: Helps in intake of whole food.
Teeth: Helps in chewing and grinding of food.
Tongue: Helps in tasting food + rolling food + swallowing food.

Salivary glands: Secrete saliva and mucus. The enzyme called salivary amylase is present in saliva which breaks down the complex starch into sugar.

Oesophagus (food pipe): Food moves towards stomach through oesophagus by rhythmic contraction of its muscles called as peristaltic movements or peristalsis.

Stomach: Muscular walls of stomach help in mixing food thoroughly with digestive juices. Stomach has gastric glands which secrete gastric juice containing pepsin for digestion of proteins, hydrochloric acid for creating acidic medium and mucus to protect inner lining of stomach from acid.

Small Intestine: Digestive juices like pancreatic juice, bile juice and the intestinal juices are secreted in the small intestine to help to complete the process of digestion. After digestion, the nutrients are absorbed by the villi present in the walls of the small intestine.

Large intestine: The unabsorbed food is sent into the large intestine where more villi absorb water from this material and remove the wastes through the anus by egestion. The exit of this waste material is regulated by the anal sphincter.

Question 8.
Explain the process of breathing in man.  [NCERT Exemplar]
Answer:
Air enters the body after getting filtered by fine hairs and mucus in the nostrils.
The air then passes through trachea (present in throat) into the lungs. The trachea divide into bronchi which enter the lungs and divide further into bronchioles which finally terminate in balloon-like structures called alveoli which have a rich supply of blood vessels and help in exchange of gases.

During inhalation (breathing in), the volume of the chest cavity becomes larger as the ribs get lifted and diaphragm gets flattened. Air gets sucked into the lungs and fills the expanded alveoli. The blood brings carbon dioxide from the rest of the body to the alveoli and exchanges it for oxygen to be transported to all the cells in the body.

During exhalation (breathing out), the volume of the chest cavity becomes smaller as the ribs get relaxed and diaphragm moves upward (relaxes). Air rich in carbon dioxide gets pushed out of the lungs to come out through the nostrils.

Question 9.
Explain the importance of soil for plant growth.
Answer:
Soil is important for the plant growth as it helps in the

• Anchoring the plant.
• Acts as a source of water and minerals for the plants.
• Ensures availability of oxygen for respiration of root cells.
• Microbes living in symbiotic association are found in the soil which helps to provide nitrogen for the plants.

Life Processes HOTS Questions With Answers

Question 1.
Which part of visible the spectrum is mostly ineffective in the process of photosynthesis? Why?
Answer:
The green part of the visible spectrum is mostly ineffective in the process of photosynthesis because chlorophyll involved in the process does not absorb green light. The green component of the visible spectrum gets reflected by the chlorophyll due to which the leaves appear green.

Question 2.
What difference would be seen in the small intestine of a grass eating animal and a flesh eating animal?
Answer:
The grass eating animal would have a longer small intestine than a flesh eating animal as the cellulose present in the grass takes a longer time to get digested.

Question 3.
The gall bladder of a patient is removed when a stone was observed in the gall bladder. Which kind of nutrient in the diet should be absent from the diet given to the patient?
Answer:
The gall bladder release bile juice which helps in the digestion of fats in the human beings. So, the patient should be advised a diet free from fats during the treatment process, as the digestion of fats will be most affected due to removal of gall bladder.

Question 4.
Stomata of desert plants remain closed during the daytime. Then how do they take up carbon dioxide and perform photosynthesis?  [CBSE 2010, 2012]
Answer:
The stomata of the desert plants open during the night time and absorb carbon dioxide to use it during the daytime for performing photosynthesis.

Question 5.
How do carbohydrates, proteins and fats get digested in human beings?
Answer:
An enzyme called salivary amylase is present in the saliva produced in the mouth. Salivary amylase helps in the breakdown of carbohydrates into maltose in the mouth.

The proteins get digested initially by the pepsin enzyme in the stomach and then by the enzymes present in the pancreatic juice secreted into the small intestine. The fats are broken down into small globules by the bile salts present in the bile juice secreted into the small intestine. This helps in increasing the efficiency of fat digesting enzymes.

The intestinal juice secreted by the walls of the small intestine help to complete the digestion of carbohydrates into glucose/monosaccharide, digestion of proteins into amino acids and the digestion of fats into fatty acids and glycerol.

Extra Questions for Class 10 Science Chapter 6 Value Based Questions

Question 1.
Raksha planted many plants in her home garden as she knew that the plants help to purify air. To get purified air in her room she kept some of the plants in a closed room, it leaves turned pale in colour after some days.
(a) Define photosynthesis. What are the conditions necessary for photosynthesis?
(b) What are the values shown by Raksha?
(c) What can be the most probable reason which resulted in the pale leaves?
Answer:
(a) The process by which the autotrophs synthesise their own food is called as photosynthesis.
Photosynthesis,occurs in the presence of carbon dioxide, water, chlorophyll and sunlight.
(b) The values shown by Raksha are intelligence, environment friendly, scientific temper, creative thinking.

Question 2.
Ayush experienced muscular cramps during the training session for his upcoming cricket match. His coach advised him a schedule of aerobic exercises to overcome this problem. Ayush followed his coach’s advice and did not experience any muscular cramps during the game. Based on this, answer the following questions:
(а) What was the reason for the muscular cramps?
(b) What was the effect of aerobic exercises?
(c) What are the values shown by Ayush?
Answer:
(a) The muscular cramps were caused as the muscles produced lactic acid during anaerobic respiration in the muscle cells. The accumulation of lactic acid caused the cramps.

(b) Aerobic exercises helped in providing enough oxygen for the various muscle cells so that they had a more supply of oxygen.

(c) Values shown by Ayush are respect for his coach, responsibility, hard work and patience.

Question 3.
Anshika noticed that one of the plants in her garden had wrinkled and drooping leaves. She went to the garden and felt the soil below the plant which was too dry. She immediately made provisions for watering the plant and made a daily schedule for watering it every day. Within a few days the plant revived and became green and healthy. On the basis of this text, answer the following questions:
(a) How is water transported up into the plants?
(b) What is the role of the leaves and the roots in such transport?
(c) What are the values shown by Anshika?
Answer:
(a) Water is transported up into the plants with the help of xylem. The movement of water in the xylem occurs due to transpiration and root pressure.

(b) Roots absorb water through their root hairs. Leaves have stomata through which transpiration occurs and pulls up the water through the xylem to the top of the plant.

(c) The values shown by Anshika are: Love for nature, scientific aptitude, awareness, care

Question 4.
Sameer went to a forest and observed the villagers collecting reins and gums from the plants. He asked the villagers about the use of the resins and gums. They told him that they will be used in making the paints and varnishes for furniture. He learnt the technique of collecting resins from the villagers and enjoyed the activity with the villagers by helping them in collection.
On the basis of the text, answer the following questions:
(а) Why are resins and gums released by plants?
(b) What are the ways in which plants get rid of their waste products?
(c) What are the values shown by Sameer?
Answer:
(a) Resins and gums are the excretory products of the plants.
(b) Plants remove excess oxygen and carbon dioxide through stomata, excess water by transpiration through stomata and other waste products by storage in cellular vacuoles, leaves that fall off, storage as resins and gums in old xylem or by excreting into the soil around them.
(c) Values shown by Sameer are: Care of the environment, scientific attitude, helpfulness, curiosity.

Here we are providing Areas Related to Circles Class 10 Extra Questions Maths Chapter 12 with Answers Solutions, Extra Questions for Class 10 Maths was designed by subject expert teachers. https://ncertmcq.com/extra-questions-for-class-10-maths/

Extra Questions for Class 10 Maths Areas Related to Circles with Answers Solutions

Extra Questions for Class 10 Maths Chapter 12 Areas Related to Circles with Solutions Answers

Areas Related to Circles Class 10 Extra Questions Very Short Answer Type

Area Related To Circle Class 10 Extra Questions With Solutions Question 1.
Find the area of a square inscribed in a circle of diameter p cm.

Solution:
Diagonal of the square = p cm
∴ p² = side² + side²
⇒ p² = 2side²
or side² = \(\frac{p^{2}}{2}\) cm² = area of the square

Areas Related To Circles Class 10 Extra Questions Question 2.
Find the area of the circle inscribed in a square of side a cm.

Solution:
Diameter of the circle = a

Areas Related To Circles Extra Questions Question 3.
Find the area of a sector of a circle whose radius is and length of the arc is l.
Solution:
Area ola sector ola circle with radius r

Area Related To Circle Class 10 Extra Questions Question 4.
Find the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal.
Solution:

Areas Related To Circles Class 10 Extra Questions With Answers Question 5.
A square inscribed in a circle of diameter d and another square is circumscribing the circle. Show that the area of the outer square is twice the area of the inner square.

Solution:
Side of outer square = d {Fig. 12.5]
∴ Its area = d
Diagonal of inner square = d
∴ Side = \(\frac{d}{\sqrt{2}}\)
⇒ Area = \(\frac{d^{2}}{2}\)
Area of outer square = 2 × Area of inner square.

Class 10 Maths Chapter 12 Extra Questions Question 6.
If circumference and the area of a circle are numerically equal, find the diameter of the circle.
Solution:
Given, 2πr = πr²
⇒ 2r = r²
⇒ r(r – 2) = 0 or r = 2
i.e. d = 4 units

Area Related To Circles Extra Questions Question 7.
The radius of a wheel is 0.25 m. Find the number of revolutions it will make to travel a distance of 11 km.
Solution:

Area Related To Circle Class 10 Extra Questions With Solutions Pdf Question 8.
If the perimeter of a semi-circular protractor is 36 cm, find its diameter.
Solution:
Perimeter of a semicircular protractor = Perimeter of a semicircle
= (2r + πr) cm
⇒ 2r + πr = 36
⇒ r\(\left(2+\frac{22}{7}\right)\) = 36
⇒ r = 7cm
Diameter 2r = 2 × 7 = 14 cm.

Area Related To Circle Class 10 Extra Questions Pdf Question 9.
If the diameter of a semicircular protractor is 14 cm, then find its perimeter.
Solution:
Perimeter of a semicircle = πr + 2r
= \(\frac{22}{7}\) × 7 + 2 × 7 = 22 + 14 = 36cm

Areas Related to Circles Class 10 Extra Questions Short Answer Type 1

Area Related To Circle Class 10 Important Questions With Solutions Question 1.
If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?

Solution:
Let radius of the circle be r units.
Then, diagonal of the square = 2r

Area Related To Circle Difficult Questions Question 2.
What is the area of the largest triangle that is inscribed in a semi circle of radius r unit?
Solution:

Area of largest ∆ABC = \(\frac{1}{2}\) × AB × CD
\(\frac{1}{2}\) × 2r × r = r² sq. units

Extra Questions Of Area Related To Circles Class 10 Question 3.
What is the angle subtended at the centre of a circle of radius 10 cm by an arc of length 5π cm?
Solution:

Areas Related To Circles Class 10 Important Questions Question 4.
What is the area of the largest circle that can be drawn inside a 4 rectangle of length a cm and breadth b cm (a > b)?

Solution:
Diameter of the largest circle that can be inscribed in the given b
rectangle = b cm
∴ Radius = \(\frac{b}{2}\) cm

Ch 12 Maths Class 10 Extra Questions Question 5.
Difference between the circumference and radius of a circle is 37 cm. Find the area of circle.
Solution:
Given 2π r – r = 37
or r (2π – 1) = 37

Extra Questions For Class 10 Maths Areas Related To Circles Question 6.
The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having area equal to the sum of the areas of the two circles.
Solution:
Let r be the radius of required circle. Then, we have
πr² = π(8)² + π(6)²
⇒ πr² = 64π + 36π
⇒ πr² = 100π
∴ r² = \(\frac{100 \pi}{\pi}\) = 100
⇒ r = 10cm
Hence, radius of required circle is 10 cm.

Class 10 Areas Related To Circles Extra Questions Question 7.
The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has circumference equal to the sum of the circumferences of the two circles.
Solution:
Let R be the radius of required circle. Then, we have
2πR = 2π(19) + 2π (9)
⇒ 2πR = 2π (19 + 9)
⇒ R = \(\frac{2 \pi \times 28}{2 \pi}\) = 28
⇒ R = 28 cm
Hence, the radius of required circle is 28 cm.

Area Related To Circle Extra Questions Question 8.
Find the area of a circle whose circumference is 22 cm.
Solution:
Let r be the radius of the circle. Then,
Circumference = 22 cm

Class 10 Maths Ch 12 Extra Questions Question 9.
The area of a circular playground is 22176 m². Find the cost of fencing this ground at the rate of ₹50 per m.
Solution:
Area of circular playground = 22176 m²
πr² = 22176
⇒ \(\frac{22}{7}\) r² = 2176
⇒ \(\frac{22176 \times 7}{22}\)
⇒ r = 84 m
∴ Circumference of the playground =2πr = 2 × \(\frac{22}{7}\) × 84 = 44 × 12 = 528 m .
∴ Cost of fencing this ground = ₹ 528 × 50 = ₹ 26400.

Class 10 Area Related To Circles Extra Questions Question 10.
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
Solution:
We know that

Important Questions Of Area Related To Circle Class 10 Question 11.
Find the area of a quadrant of a circle whose circumference is 22 cm.
Solution:
Let r be the radius of circle, then circumference = 22 cm

Chapter 12 Maths Class 10 Extra Questions Question 12.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Solution:
Since the minute hand rotates through 6° in one minute, therefore, area swept by the minute hand in one minute is the area of a sector of angle 6° in a circle of radius 14 cm.

Extra Questions On Areas Related To Circles Question 13.
To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)
Solution:
We have, r = 16.5 km and 0 = 80°
∴ Area of the sea over which the ships are warned =

Areas Related to Circles Class 10 Extra Questions Short Answer Type 2

Area Related To Circles Class 10 Extra Questions Question 1.
If the perimeter of a semicircular protractor is 66 cm, find the diameter of the protractor
(Take π = \(\frac{22}{7}\)).
Solution:
Let the radius of the protractor be r сm. Then,
Perimeter = 66 cm
= πr + 2r = 66 [∴ Perimeter of a semicircle = πr + 2r]

Extra Questions Areas Related To Circles Class 10 Question 2.
The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius of the circle.
Solution:
Let the radius of the circle be r сm. Then,
Diameter = 2r cm and Circumference = 2πr cm
According to question,
Circumference = Diameter + 16.8
⇒ 2πr = 2r + 16.8
⇒ 2 × \(\frac{22}{7}\) × r = 2r + 16.8
⇒ 44r = 14r + 16.8 × 7
⇒ 44r – 14r = 117.6 or 30r = 117.6
⇒ r = \(\frac{117.6}{30}\) = 3.92
Hence, radius = 3.92 cm.

Question 3.
A race track is in the form of a ring whose inner circumference is 352 m, and the outer circumference is 396 m. Find the width of the track.
Solution:
Let the outer and inner radii of the ring be R m and r m respectively. Then,
2πR = 396 and 2πr = 352

Hence, width of the track = (R – r) m = (63 – 56) m = 7 m

Question 4.
The inner circumference of a circular track [Fig. 12.10] is 220 m. The track is 7 m wide everywhere. Calculate the cost of putting up a fence along the outer circle at the rate of ₹2 per metre.
Solution:

Let the inner and outer radii of the circular track berm and R m respectively. Then,
Inner circumference = 2πr = 220 m

Since the track is 7 m wide everywhere. Therefore,
R = Outer radius = r + 7 = (35 + 7)m = 42 m
∴ Outer circumference = 2πR = 2 × \(\frac{22}{7}\) × 42m = 264m
Rate of fencing = ₹ 2 per metre
∴ Total cost of fencing = (Circumference × Rate) = ₹(264 × 2) = ₹ 528

Question 5.
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?
Solution:
The diameter of a wheel = 80 cm.
radius of the wheel = 40 cm.
Now, distance travelled in one complete revolution of wheel = 2π × 40 = 80π
Since, speed of the car is 66 km/h
So, distance travelled in 10 minutes = \(\frac{66 \times 100000 \times 10}{60}\)
= 11 × 100000 cm = 1100000 cm.
So, Number of complete revolutions in 10 minutes

Question 6.
An umbrella has 8 ribs which are equally spaced (Fig. 12.11). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

Solution:
We have, r = 45 cm

Question 7.
A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (Fig. 12.12). Find (i) the area of that part of the field in which the horse can graze;
(ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use π = 3.14)

Solution:
Let the horse be tied at point O and the length of the rope is OH (Fig. 12.13).
Thus, (i) the area of the part of the field in which the horse can graze
= Area of the quadrant of a circle (OAHB)

(ii) Now r = 10 m and


Increase in the grazing area
= (78.5 – 19.625) m²
= 58.875 m²

Question 8.
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115o. Find the total area cleaned at each sweep of the blades.
Solution:
We have, r = 25 cm and θ = 115°.
∴ Total area cleaned at each sweep of the blades
= 2 × (Area of the sector having radius 25 cm and angle θ = 115°).

Question 9.
In Fig. 12.15, sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area
of the shaded region.
Solution:
Let A₁ and A₂ be the areas of sectors OAB and OCD respectively. Then, A, = Area of a sector of angle 30° in a circle of radius 7 cm.

Question 10.
The minute hand of a clock is 10 cm long. Find the area of the face of the clock described by the minute hand between 9 AM and 9.35 AM.
Solution:
We have,
Angle described by the minute hand in one minute = 6°
∴ Angle described by the minute hand in 35 minutes = (6 × 35)° = 210°
Area swept by the minute hand in 35 minutes = Area of a sector of a circle of radius 10 cm

Question 11.
Find the area of the sector of a circle with radius 4 cm and of angle 30°. Also, find the area of the corresponding major sector. (Use π = 3.14)
Solution:

Area of the sector OAPB = \(\frac{\theta}{360^{\circ}} \times \pi r^{2}\)
\(\frac{30^{\circ}}{360^{\circ}}\) × 3.14 × 4 × 4 cm²
= \(\frac{12.56}{3}\)cm²
= 4.19 cm² (approx.)
Area of the corresponding major sector = πr² – Area of sector OAPB
= (3.14 × 4 × 4 – 4.19)cm² = (50.24 – 4.19) cm²
= 46.05 cm² = 46.1 cm² (approx.)

Question 12.
A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle. (Use π = 3.14 and √3 = 1.73)
Solution:
We have, r = 15 cm and θ = 60°
Given segment is APB

Now, area of major segment = Area of circle – Area of minor segment
= π(15)² – 20.44 = 3.14 × 225 – 20.44
= 706.5 – 20.44 = 686.06 cm

Question 13.
A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle. (Use π = 3.14 and √3 = 1.73)
Solution:
We have, r = 12 cm and θ = 120°
Given segment is APB
Now, area of the corresponding segment of circle
= Area of the minor segment

Question 14.
A round table cover has six equal designs as shown in Fig. 12.19. If the radius of the cover is 28 cm?, find the cost of making the designs at the rate of ₹ = 0.35 per cm². (Use √3 = 1.7)
Solution:
Area of one design = Area of the sector OAPB – Area of ΔAOB

Area of 6 such designs = 77.47 × 6 = 464.8 cm²
Hence, cost of making such designs = ₹ 162.69

Question 15.
Find the area of the shaded region in Fig. 12.20, if PQ = 24 cm, PR = 7 cm and O is the centre of the circle.
Solution:

Here, ROQ is the diameter of given circle, therefore ∠RPQ = 90°
Now, in right angled ΔPRQ, we have
RQ² = RP² + PQ² (by Pythagoras Theorem)
RQ² = (7)² + (24)² = 49 + 576 = 625
RQ = \(\sqrt{625}\) = 25 cm
Therefore, radius r = \(\frac{25}{2}\) cm
Now, area of shaded region
= Area of the semi-circle – Area of ARPQ

Question 16.
Find the area of the shaded region in Fig. 12.21, if radii of the two concentric circles with centre 0 are 7 cm and 14 cm respectively and ∠AOC = 40°.
Solution:
Area of shaded region
= Area of sector AOC – Area of sector OBD

Question 17.
Find the area of the shaded region in Fig. 12.22, if ABCD is a square of side 14 cm and APD and BPC are semicircles.
Solution:
We have, radius of semicircles = 7 cm
∴ Area of shaded region
= Area of square ABCD – Area of semi-circles (APD +BPC)

Question 18.
Find the area of the shaded region in Fig. 12.23, where a circular arc of radius 6 cm has been drawn with vertex 0 of an equilateral triangle OAB of side 12 cm as centre.
Solution:
We have, radius of circular region
= 6 cm and each side of ΔOAB = 12 cm.
∴ Area of the circular portion
= Area of circle – Area of the sector

Quesiton 19.
From each corner of a square of side 4 cm, a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. 12.24. Find the area of the remaining portion of the square.
Solution:
We have, the side of the square ABCD = 4 cm
Area of the square ABCD = (4)² = 16 cm²
Since, each quadrant of a circle has radius 1 cm.
∴ The sum of the areas of four quadrants

Question 20.
In Fig. 12.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touches externally two of the remaining three circles. Find the area of the shaded region.

Solution:
We have, each side of square ABCD = 14 cm
∴ Area of square ABCD = (14²)cm² = 196 cm²
Now, radius of each quadrant of circle,
r = \(\frac{14}{2}\) = 7 cm
∴ The sum of the area of the four quadrants at the four corners of the square

Now, area of shaded portion
= Area of square ABCD – The sum of the areas of four quadrants at the four corners of the square
= (196 – 154) cm² = 42 cm²

Question 21.
On a square handkerchief, nine circular designs, each of radius 7 cm are made (see Fig. 12.26). Find the area of the remaining portion of the handkerchief.

Solution:
Total area of circular design = 9 × Area of one circular design
= 9 × π × (7)²
= 9 × \(\frac{22}{7}\) × 7 × 7 = 1386 cm²
Now, each side of square ABCD = 3 × diameter of circular design
= 3 × 14 = 42 cm
∴ Area of square ABCD = (42)² = 1764 cm²
∴ Area of the remaining portion of handkerchief
= Area of square ABCD – Total area of circular design
= (1764 – 1386) cm = 378 cm²

Question 22.
In Fig. 12.27, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB, (ii) shaded region.
OR
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.
Solution:

Question 23.
In Fig. 12.28, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14).
Solution:
We have,
Radius of quadrant

= 200 × 3.14 – 400 = 628 – 400 = 228 cm²

Question 24.
Calculate the area of the designed region in Fig. 12.29, which is common between the two quadrants of circles of radius, 8 cm each.
Solution:
Here, radius of each quadrant ABPD and BQDC = 8 cm

Question 25.
In the given Fig. 12.30, find the area of the shaded region.
Solution:

Clearly, diameter of the circle
= Diagonal BD of rectangle ABCD
Now, BD

Let r be the radius of the circle. Then, r = \(\left(\frac{10}{2}\right)\)cm = 5 cm
Hence, area of the shaded region = Area of the circle – Area of rectangle ABCD
= πr² – l × b = (3.14 × 5 × 5) – (8 × 6)
= (78.50 – 48) cm² = 30.50 cm²

Question 26.
A square park has each side of 100 m. At each corner of the park, there is a flower bed in the form of a quadrant of radius 14 m as shown in Fig. 12.31. Find the area of the remaining part of the park.
Solution:

We have,
Area of 4 quadrants of a circle of radius 14 m

Area of square park having side 100 m long
= (100 × 100) m² = 10,000 m².
Hence, area of the remaining part of the park
= Area of square – Area of 4 quadrants at each corner
= (10,000 – 616) m² = 9384 m²

Question 27.
Find the area of the shaded region in Fig. 12.32, where ABCD is a square of side 14 cm each.

Solution:
Area of square ABCD = 14 × 14 cm² = 196 cm²
Diameter of each circle = \(\frac{14}{2}\) cm = 7 cm
So, radius of each circle = \(\frac{7}{2}\) cm

∴ Area of shaded region = Area of square – Area of 4 circles
= (196 – 154) cm² = 42 cm²

Question 28.
In Fig. 12.33, ABCD is a trapezium of area 24.5 sq. cm. In it, AD || BC, ∠DAB = 90°, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of the shaded region. [Take π = \(\frac{22}{7}\)
Solution:

Area of trapezium = 24.5 cm²
\(\frac{1}{2}\)[AD + BC] AB = 24.5
\(\frac{1}{2}\)[10 + 4] × AB = 24.5
AB = 3.5 cm ⇒ r = 3.5 cm
Area of quadrant = \(\frac{1}{4}\)πr²
.025 × \(\frac{22}{7}\) × 3.5 × 3.5 = 9.625 cm²
The area of shaded region = 24.5 – 9.625 = 14.875 cm²

Question 29.
In Fig. 12.34, O is the centre of a circle such that diameter AB = 13 cm and AC = 12 cm. BC is joined. Find the area of the shaded region. (Take π = 3.14)
Solution:

In ΔABC, ∠ACB = 90° (Angle in the semicircle)
∴BC² + AC² = AB²
∴ BC² = AB² – AC²
= 169 – 144 = 25
∴ BC = 5 cm
Area of the shaded region = Area of semicircle – Area of right ΔABC

Question 30.
In Fig. 12.35, are shown two arcs PAQ and PBQ. Arc PAQ is a part of circle with centre 0 and radius OP while arc PBQ is a semi-circle drawn on PQ as diameter with centre M.
If OP = PQ = 10 cm show that area of shaded region is \(25\left(\sqrt{3}-\frac{\pi}{6}\right)\)cm².
Solution:
Since OP = PQ = QO
⇒ ΔPOQ is an equilateral triangle
∴ ∠POQ = 60°
Area of segment PAQM

Areas Related to Circles Class 10 Extra Questions Long Answer Type

Question 1.
PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semicircles are drawn on PQ and QS as diameters is shown in Fig. 12.36. Find the perimeter and area of the shaded region.

Solution:
We have,
PS = Diameter of a circle of radius 6 cm = 12 cm
∴ PQ = QR = RS = \(\frac{12}{3}\) = 4 cm
Fig. 12.36 QS = QR + RS = (4 + 4) cm = 8 cm
Hence, required perimeter
= Arc of semicircle of radius 6 cm + Arc of semi circle of radius 4 cm + Arc of semi-circle of radius 2 cm
= (π × 6 + π × 4 + π × 2) cm = 12π cm = 12 × = \(\frac{22}{7}\) = \(\frac{264}{7}\) = 37.71 cm.
Required area = Area of semicircle with PS as diameter + Area of semicircle with PQ as diameter – Area of semi-circle with QS as diameter

Question 2.
Figure 12.37 depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.
Solution:

Question 3.
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days.
Solution:
In 2 days, the short hand will complete 4 rounds.
Distance moved by its tip = 4 (Circumference of a circle of radius 4 cm)

Question 4.
Fig. 12.38, depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) the distance around the track along its inner edge.
(ii) the area of the track.
Solution:

Here, we have
OE = O’G = 30 m
AE = CG = 10 m
OA = O’C = (30 + 10) m = 40 m
AC = EG = FH = BD = 106 m

(i) The distance around the track along its inner edge
= EG + FH + 2 × (circumference of the semicircle of radius OE = 30cm)

(ii) Area of the track = Area of the shaded region
= Area of rectangle AEGC + Area of rectangle BFHD + 2 (Area of the semicircle of radius 40 m – Area of the semicircle with radius 30 m)

Question 5.
The area of an equilateral triangle ABC is 17320.5 cm. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.39). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)
Solution:

Let each side of the equilateral triangle be x cm. Then,
Area of equilateral triangle ABC = 17320.5 cm (Given)

Question 6.
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.40. Find the area of the design.
Solution:
Here, ∆ABC is an equilateral triangle. Let O be the circumcentre of circumcircle.
Radius, r = 32 cm.
Now, area of circle = πr²

Question 7.
In Fig. 12.41, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
Solution:

Question 8.
In Fig. 12.42 ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
Solution:
In ∆ABC, we have

Hence, area of the shaded region = Area of the semi-circle BQC – Area of the segment BPC
= (154 – 56)cm² = 98cm²

Question 9.
In Fig 12.43, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use π = 3.14 and √3 = 1.73]

Solution:
Construction:
Join OA, OB and OC
Draw OZ ⊥ BC, OX ⊥ AB and OY ⊥ AC.
Let the radius of the circle be r сm.
Area of ∆ABC = Area of ∆AOB + Area of ∆BOC + Area of ∆AOC


= 1.73 × 3 × 12 – 3.14 × 4 × 3
= 62.28 – 37.68 = 24.6 cm²

Question 10.
In Fig. 12.45, PSR, RTQ and PAQ are three semicircles of diameters 10 cm, 3 cm and 7 cm respectively. Find the perimeter of the shaded region. [Use π = 3.14]
Solution:

Radius of semicircle PSR = \(\frac{1}{2}\) × 10 cm = 5 cm
Radius of semicircle RTQ = \(\frac{1}{2}\) × 3 cm = 1.5 cm
Radius of semicircle PAQ = \(\frac{1}{2}\) × 7 em = 3.5 cm
Perimeter of shaded region = Circumference of semicircle PSR + Circumference of semicircle RTQ + Circumference of semicircle PAQ.

= π[5 + 1.5 + 3.5]= 3.14 × 10 = 31.4cm

Question 11.
An elastic belt is placed around the rim of a pulley of radius 5 cm. (Fig. 12.46). From one point C on the belt, the elastic belt is pulled directly away from the centre O of the pulley until it is at P, 10 cm from the point O. Find the length of the belt that is still in contact with the pulley. Also find the shaded area. (Use π = 3.14 and √3 = 1.73)
Solution:

PA = 5√3 cm = BP [Tangents from an external point are equal]

Question 12.
In Fig. 12.47, a sector OAP of a circle with centre O, containing ∠θ. AB is perpendicular to the radius OA and meets OP produced at B. Prove that the perimeter of shaded region is

Solution:

Question 13.
Find the area of the shaded region in Fig. 12.48, where APD, AQB, BRC , CSD are semi-circles of diameter 14 cm, 3.5 cm, 7 cm and 3.5 cm respectively. (Use π = \(\frac{22}{7}\) )
Solution:

Question 14.
A chord PQ of a circle of radius 10 cm subtends an angle of 60° at the 14 cmcentre of circle. Find the area of major and minor segments of the Fig. 12.48 circle.
Solution:
Area of minor segment
= Area of minor sector having angle 60° at centre – area of equilateral ∆OPQ

Question 15.
In the given figure, ∆ABC is a right-angled triangle in which ∠A is 90°. Semicircles are drawn on AB, AC and BC as diameters. Find the area of the shaded region.
Solution:
∵ ABC is right angled triangle

Question 16.
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region.
Solution:
In right angle triangle ABC

Areas Related to Circles Class 10 Extra Questions HOTS

Question 1.
Two circles touch internally. The sum of their areas is 116 ncmo and distance between their centres is 6 cm. Find the radii of the circles.
Solution:

Let R and r be the radii of the circles [Fig. 12.52].
Then, according to question,
⇒ πR² +πr² = 116π
⇒ R² + r² = 116 …..(i)
Distance between the centres = 6 cm
⇒ OO’ = 6 cm
⇒ R – s = 6 …(ii)
Now, (R + r)² + (R – 1)² = 2(R² + m²)
Using the equation (i) and (ii), we get
(R + r)² + 36 = 2 × 116
= (R + r)² = (2 x 116 – 36) = 196
= R + r = 14 …..(iii)
Solving (ii) and (iii), we get R = 10 and r = 4
Hence, radii of the given circles are 10 cm and 4 cm respectively.

Question 2.
A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel.
Solution:
Let the radius of the wheel be r сm.

∴ Diameter = 2r cm = (2 × 35) cm = 70 cm
Hence, the diameter of the wheel is 70 cm.

Question 3.
Find the area of the shaded design of Fig. 12.53, where ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter (use π = 3.14).

Solution:

Let us mark the four unshaded regions as I, II, III and IV (Fig. 12.53).
Area of I + Area of III
= Area of ABCD – Areas of two semicircles of radius 5 cm each

= (100 – 3.14 × 25) cm² = (100 – 78.5) cm² = 21.5 cm²
Similarly, Area of II + Area of IV = 21.5 cm²
So, Area of the shaded design
= Area of ABCD – Area of (I + II + III + IV)
= (100 – 2 × 21.5) cm²
= (100 – 43) cm² = 57 cm²

Question 4.
A copper wire, when bent in the form of a square, encloses an area of 484 cm². If the same wire is bent in the form of a circle, find the area enclosed by it.
Solution:
We have, Area of the square = a² = 484 cm²
∴ Side of the square = √1484 cm = 22 cm
So, Perimeter of the square = 4 (side) = (4 × 22) cm = 88 cm
Let r be the radius of the circle. Then, according to question,
Circumference of the circle = Perimeter of the square

Question 5.
Two circles touch externally. The sum of their areas is 130 r sq. cm and the distance between their centres is 14 cm. Find the radii of the circles.
Solution:

If two circles touch externally, then the distance between their centres is equal to the sum of their radii.
Let the radii of the two circles be r, cm and r² cm respectively [Fig. 12.55).
Let C, and C, be the centres of the given circles. Then,
C₁C₂ = r₁ +r₂
= 14 = r₁ +r₂
[∵ C₁C₂ = 14 cm given]
= r₁ +r₂ = 14
It is given that the sum of the areas of two circles is equal to 130 n cm²

Solving (i) and (iv), we get r₁ = 11 cm and r₂ = 3 cm.
Hence, the radii of the two circles are 11 cm and 3 cm.

Question 6.
In Fig. 12.56, from a rectangular region ABCD with A
AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside the region. Find the area of the shaded region. [Use π = 3.14]

Solution:
Area of shaded region
= Area of rectangle – Area of triangle + Area of semicircle. In right ∆ADE.
AD² = AE² + DE²

Area of rectangle = AB × BC = 20 × 15 = 300 cm²
Area of shaded region = 300 + 88.31 – 54 = 334.31 cm²

Question 7.
In the given Fig. 12.58, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O’ are centres of the circles. Find the area of shaded region.

Solution:
Area of shaded region
= Area of square + Area of 2 major sectors having angle 270° at centre

Question 8.
In the given Fig. 12.59, ABCD is a rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
Solution:

Area of shaded region
Area of shaded region
= Area of rectangle – Area of semicircle
=(l × b) – \(\frac{1}{2}\) × π × r²
= (21 × 14) – \(\frac{1}{2}\) × π × 7 × 7
= 294 – \(\frac{1}{2}\) × \(\frac{22}{7}\) × 7 × 7
= 294 – 77 = 217 cm²
Now, perimeter of shaded region = 2l + b + circumference of semicircle i.e.; πr
= 2 × 21 + 14 + \(\frac{22}{7}\) × 7
= 56 + 22 = 78 cm