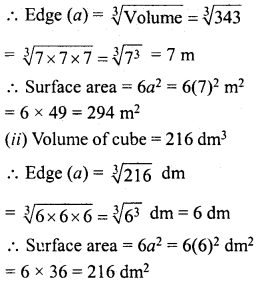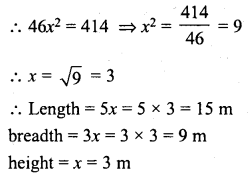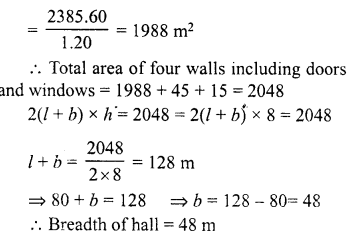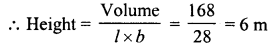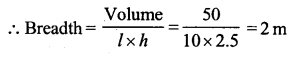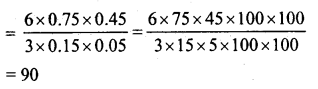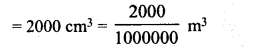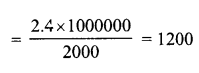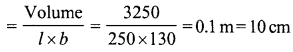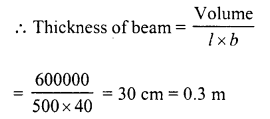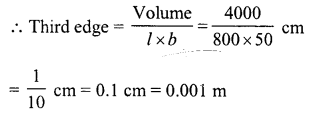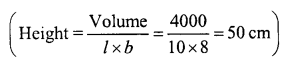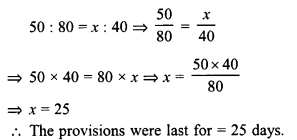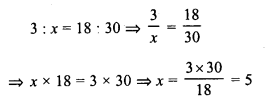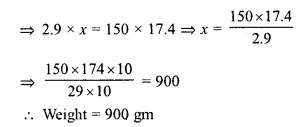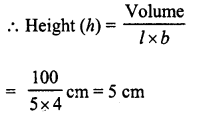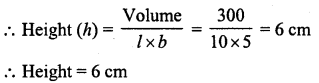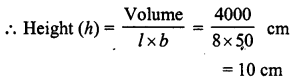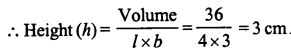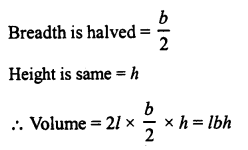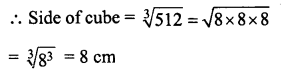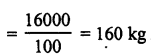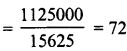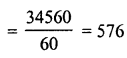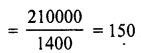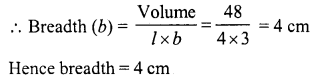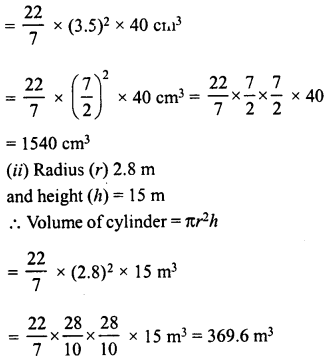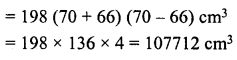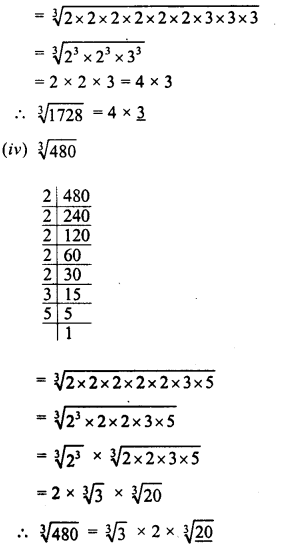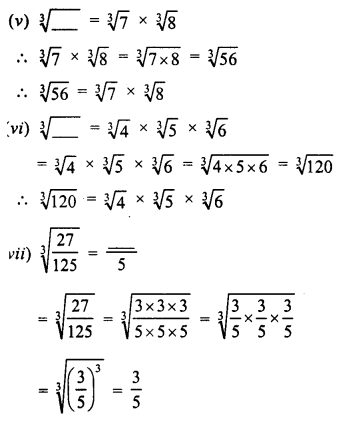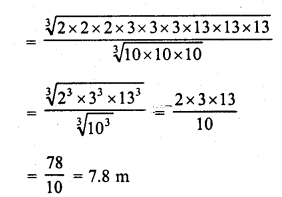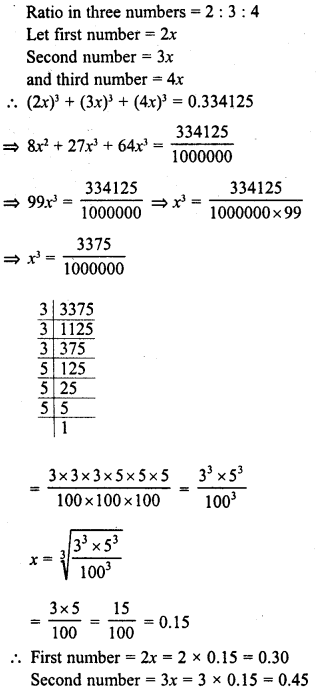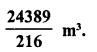RD Sharma Class 8 Solutions Chapter 21 Mensuration II (Volumes and Surface Areas of a Cubiod and a Cube) Ex 21.4
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4
Other Exercises
- RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1
- RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2
- RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
- RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4
Question 1.
Find the length of the longest rod that can be placed in a room 12 m long, 9 m broad and 8 m high.
Solution:
Length of room (l) = 12m
Breadth (b) = 9 m
Height (h) = 8 m
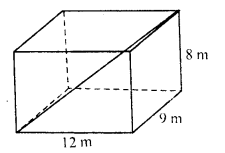
Longest rod to be kept in the room
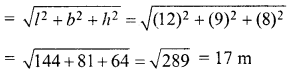
Question 2.
If V is the volume of the cuboid of dimensions a, b, c and S its the surface area then prove that
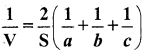
Solution:
∵ a, b, c are the dimensions of a cuboid
∴ Volume (V) = abc
Surface area (S) = 2(ab + bc + ca)
Now

Question 3.
The areas of three adjacent faces of a cuboid are .v, y and z. If the volume is V1 prove that V2 = xyz.
Solution:
Let length of cuboid = l
Breadth = b
and height = h
Volume = Ibh
∴ x = lb,y = bh and z = hl
Now x.y.z = lb.bh.hl
= l2 b2 h2 = (Ibh)2 = V2
∴ V2 = xyz Hence proved
Question 4.
A rectangular water reservoir contains 105 m3 of water. Find the depth of the water in the reservoir if its base measures 12 m by 3.5 m.
Solution:
Volume of the water in reservoir = 105 m2
Length (l)= 12 m
and breadth (b) = 3.5 m
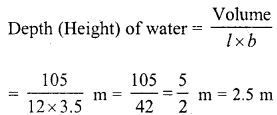
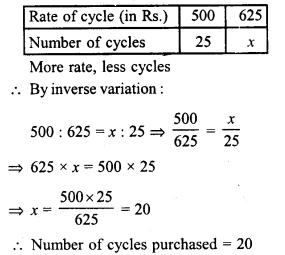
Question 5.
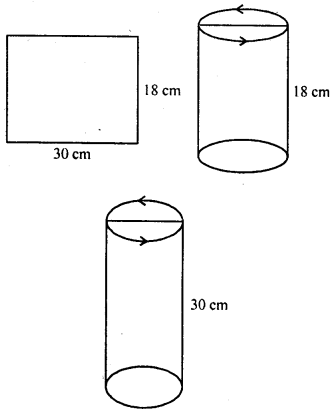
Cubes A, B, C having edges 18 cm, 24 cm and 30 cm respectively are melted and moulded into a new cube D. Find the edge of the bigger cube D.
Solution:
Edge of cube A = 18 cm
∴ Volume = a2 = (18)3 cm3 = 5832 cm3
Edge of cube B = 24 cm
∴ Volume = (24)3 = 13824 cm3
Edge of cube C = 30 cm
∴Volume = (30)3 = 27000 cm3
Volume of A, B, C cubes
= 5832+ 138-24+ 27000 = 46656 cm3
Volume of cube D = 46656 cm3
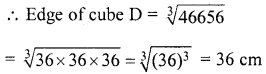
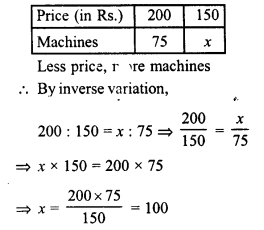
Question 6.
The breadth of a room is twice its height, one half of its length and the volume of the room is 512 cu.dm. Find its dimensions.
Solution:
Volume of room = 512 cu.dm
Let height of the room (h) = x
Then breadth (b) = 2x
and length (l) = 2x x 2 = 4x.
∴ Volume = l x b x h = 4x x 2x x x = 8×3
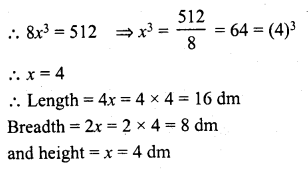
Question 7.
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of Rs 5 per metre sheet, sheet being 2 m wide.
Solution:
Length of iron tank (l) = 12 m
Breadth (b) = 9 m
Depth (h) = 4 m
∴ Surface area of the tank = 2(l x b + b x h + h x l)
= 2(12 x 9 + 9 x 4 + 4 x 12) m2
= 2(108 + 36 + 48) = 2 x 192 m2
= 384 m2
Width of sheet used = 2 m

Question 8.
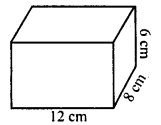
A tank open at the top is made of iron sheet 4 m wide. If the dimensions of the tank are 12 m x 8 m x 6 m, find the cost of iron sheet at Rs 17.50 per metre.
Solution:
Dimensions of the open iron tank = 12mx 8m.x 6m
∴ Surface area (without top)
= 2(1 x b) x h + lb
= 2(12 + 8) x 6+12 x 8m2
= 2 x 20 x 6 + 96 = 240 + 96 m2 = 336 m2
Width of sheet used = 4 m
∴ Length of sheet = \(\frac { Area }{ b }\) = \(\frac { 336 }{ 4 }\) m = 84 m b 4
Rate of sheet = Rs 17.50 per m.
∴ Total cost = Rs 17.50 x 84 = Rs 1470
Question 9.
Three equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the new cuboid to that of the sum of the surface areas of the three cubes.
Solution:
Let edge of each equal cubes = x
Then, surface area of one cube = 6x2
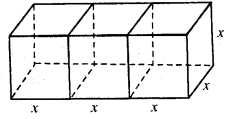
and surface area of three cubes = 3 x 6x2 = 18x2
By placing the cubes in a row,
The length of newly formed cuboid (l) = 3x
Breadth (b) = x
and height (h) = x
∴ Surface area of the cuboid so formed
Question 10.
The dimensions of a room are 12.5 m by 9 m by 7 m. There are 2 doors and 4 windows in the room; each door measures 2.5 m by 1.2 m and each window 1.5 m by 1 m. Find the cost of painting the walls at Rs 3.50 per square metre.
Solution:
Dimensions of a room = 12.5 m x 9 m x 7 m
∴ Total surface area of the walls = 2(1 + b) x h = 2(12.5 + 9) x 7 m2
= 2 x 21.5 x 7 = 301 0 m2
Area of 2 doors = 2 x (2.5 x 1.2) m2 = 2 x 3.00 = 6 m2
Area of 4 windows = 4 x (1.5 x 1) m2
4 x 1.5 = 6 m2
∴ Remaining area of the walls = 301 -(6 + 6) m2
= 301 – 12 = 289 m2
∴ Rate of painting the walls = Rs 3.50 per m2
∴ Total cost = Rs 3.50 x 289 = Rs 1011.50
Question 11.
A field is 150 m long and 100 m wide. A plot (outside the field) 50 m long and 30 m wide is dug to a depth of 8 m and the earth taken out from the plot is spread evenly in the field. By how much the level of field is raised ?
Solution:
Length of the plot (l) = 50 m
Width (b) = 30 m
and depth (h) = 8 m
∴ Volume of the earth dug out = l x b x h = 50 x 30 x 8 = 12000 m3
Length of the field = 150 m
and breadth = 100 m
∴ Height of the earth spread out on the field
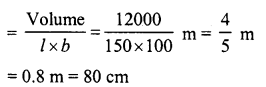
Question 12.
Two cubes, each of volume 512 cm3 are joined end to end, find the surface area of the resulting cuboid.
Solution:
Volume of each cube = 512 cm3
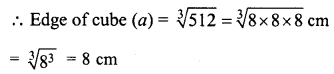
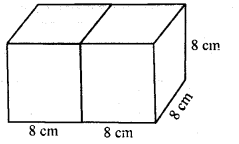
Now by joining the two equal cubes of side 8 cm, the length of so formed cuboid (l)
= 2 x 8 = 16 cm
Breadth (b) = 8 cm
and height (h) = 8 cm
∴ Surface area = 2( l x b + b x h + h x l)
= 2(16 X 8 + 8 X 8 + 8X16) cm2
= 2(128 + 64 + 128) cm2
= 2 x 320 = 640 cm2
Question 13.
Three cubes whose edges measure 3 cm, 4 cm and 5 cm respectively are melted to form a new cube. Find the surface area of the new cube formed.
Solution:
Edge of first cube = 3 cm
∴ Volume = a3 = (3)3 27 cm3
Edge of second cube = 4 cm
∴Volume = a3 = (4)3 = 64 cm3
Edge of third cube = 5 cm
∴ Volume = a3 = (5)3 = 125 cm3
Volume of three cubes together = 27 + 64+ 125 = 216 cm3
∴ Volume of the new cube = 216 cm3
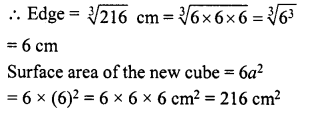
Question 14.
The cost of preparing the’walls of a room 12 m long at the rate of Rs 1.35 per square metre is Rs 340.20 and the cost of matting the floor at 85 paise per square metre is Rs 91.80. Find the height of the room.
Solution:
Length of the room (l) = 12 m
Rate of matting the floor = 85 paise per m2
Total cost of matting = Rs 91.80

Question 15.
The length of a hall is 18 m and width 12 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the wall.
Solution:
Length of hall (l) = 18 m
and breadth (b) = 12 m
∴ Area of floor = l x b = 18 x 12 = 216 m2
and area of roof = 216 m2
Total area of floor and roof
= (216 + 216) m2 = 432 m2
∴ Area of four walls = 432 m2
But area of 4 walls = 2(l + b) x h
∴ 2h (l + b) = 432
⇒ 2h (18 + 12) = 432
⇒ 2h x 30 = 432 432
⇒ h = \(\frac { 432 }{ 60 }\) = 7.2m
∴ Height of the wall = 7.2 m
Question 16.
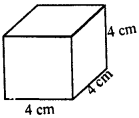
A metal cube of edge 12 cm is melted and formed into three smaller cubes. If the edges of the two smaller cubes are 6 cm and 8 cm, find the edge of the third smaller cube.
Solution:
Edge of metal bigger cube = 12 cm
∴ Volume = (12)3 = 1728 cm3
∴ Sum of volumes of 3 smaller cubes = 1728 cm3
Edge of first smaller cube = 6 cm
∴ Volume = (6)3 = 216 cm3
Edge of second smaller cube = 8 cm
∴ Volume = (8)3 = 512 cm3
Sum of volumes of two smaller cubes = 216+ 512 = 728 cm3
∴ Volume of third smaller cube = 1728-728 cm3 = 1000 cm3
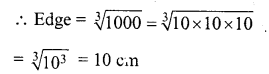
Question 17.
The dimensions of a cinema hall are 100 m, 50 m and 18 m. How many persons can sit in the hall if each person requires 150 m3 of air ?
Solution:
Length of cinema hall (l) = 100 m
Breadth (b) = 50 m
and height (h) = 18 m
∴ Volume of air of the hall = l x b x h
= 100 x 50 x 18 m3
= 90000 m3
Each person requires air = 150 m3
∴ Number of persons = \(\frac { 90000 }{ 150 }\)= 600
Question 18.
The external dimensions of a closed wooden box are 48 cm, 36 cm, 30 cm. The box is made of 1.5 cm thick wood. How many bricks of size 6 cm x 3 cm x 0.75 cm can be put in this box ?
Solution:
Outer dimensions of a closed wooden box = 48 cm x 36 cm x 30 cm
Thickness of wood = 1.5 cm.
∴ Inner length (l) = 48 – 2 x 1.5 cm = 48 – 3 = 45 cm
Breadth(b) = 36-2 x 1.5 = 36-3 = 33 cm
Height (h) = 30 – 2 x 1.5 = 30 – 3 = 27 cm
∴ Volume of inner box = l x b x h = 45 x 33 x 27 cm3 = 40095 cm3
Volume of one brick of size 6 cm x 3 cm x 0.75 cm
= 6 x 3 x 0.75 = 6 x 3 x \(\frac { 3 }{ 4 }\) cm3 = \(\frac { 27 }{ 2 }\) cm3
∴ Number of bricks = \(\frac { 40095 x 2 }{ 27 }\)
= 1485 x 2 = 2970 bricks
Question 19.
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost of covering it with sheet of paper at the rates of Rs 8 and Rs 9.50 per m2 is Rs 1,248. Find the dimensions of the box.
Solution:
Ratio in the dimensions of a box =2:3:4
Difference in total cost = Rs 1,248
Difference in rates = Rs 9.50 – Rs 8 = Rs 1.50
Let length (l) = 2x
Then breadth (b) = 3x
and height (h) = 4x
∴ Surface area = 2 (l x b + b x h + h x l)
= 2(2x 3x + 3x x 4x + 4x x 2x)
= 2(6x2 + 12x2 + 8 x2) = 2 x 26x2 = 52x2
First rate of paper = Rs 9.50 per m2
and second rate = 8.00 per m2
∴ First cost = Rs 52x2 x 9.50
and second cost = Rs 52x2 x 8
∴ 52x2 x 9.50 – 52x2 x 8= 1248
⇒ 52x2 (9.50 – 8) = 1248
⇒ 52x2(1.50) = 1248
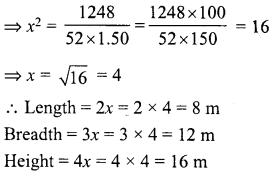
Hope given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.