Category: CBSE Class 9

On this page, you will find Heron’s Formula Class 9 Notes Maths Chapter 7 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 7 Heron’s Formula will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 7 Notes Heron’s Formula

Heron’s Formula Class 9 Notes Understanding the Lesson

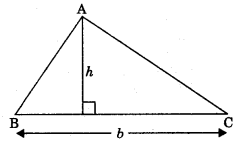
1. Area of triangle with base ‘b’ and altitude ‘h’ is
Area = \(\frac{1}{2}\)(b x h)

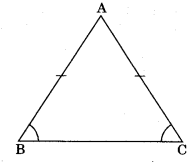
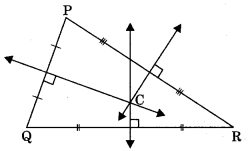
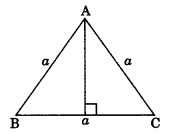
2. Area of an isosceles triangle with equal sides ‘a’ each and third side b is
Area \(=\frac{b}{4} \sqrt{4 a^{2}-b^{2}}\)

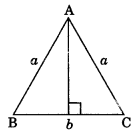
3. Area of an equilateral triangle with side ‘a’ each is
Area=\(\frac{\sqrt{3}}{4} a^{2}\)

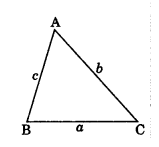
4. Area of a triangle by Heron’s formula when sides a, b and c are given is
Area = \(\sqrt{s(s-a)(s-b)(s-c)}\)
Where s = semi-perimeter = \frac{a+b+c}{2}

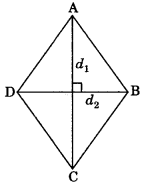
5. Area of rhombus
Area= \(\frac{1}{2} d_{1} \times d_{2}\)
where d₁ and d₂ are the lengths of its diagonals.

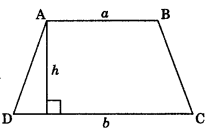
6. Area of trapezium
Area=\(\frac{1}{2}\) (a+b) h
where a and b are parallel sides and h is distance between two parallel sides.

On this page, you will find Coordinate Geometry Class 9 Notes Maths Chapter 6 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 6 Coordinate Geometry will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 6 Notes Coordinate Geometry

Coordinate Geometry Class 9 Notes Understanding the Lesson

Rene Descartes was a French mathematician. He introduced an idea of Carterian Coordinate System for describing the position of a point in a plane. The idea which has given rise to an important branch of Mathematics known as Coordinate Geometry.

1. Cartesian coordinate system: A system which describe the position of a point in a plane is called Cartesian system.

2. Cartesian coordinate axis: Let us draw a horizontal line XX’ and a vertical line YY’ in a plane. Both the lines intersect each other at 90°, then the plane is divided into four parts.

The lines XX’ and YY’ are called axes i.e., XX’ is the x-axis and YY’ is y-axis.

3. Origin: The point where both the axis intersect each other is known as origin.

4. Quadrant
When XX’ and YY’ intersect each other then the plane is divided into four parts. These parts are called quadrants. The plane is known as Cartesian plane or XY plane.

5. Coordinate Geometry: It is a branch of geometry in which geometric problems are solved through algebra by using coordinate system.

6. Cartesian Coordinate (Rectangular Coordinate) System

In this system, the position of a point P is determined by knowing the distances from two perpendicular lines passing through the fixed point O is called origin.
The position of the point P from origin on x-axis is called x-coordinate and the position of P from origin on y-axis is called y-coordinate.

Abscissa: The distance of a point P from y-axis is called abscissa.

Ordinate: The distance of a point P from x-axis is called its ordinate.

Abscissa and ordinate together determine the position of a point in a plane, and it is called coordinates of the point. If a and b are respectively abscissa and ordinate, then the coordinates are (a, b).

Note:

• In first quadrant values of x and y are both positive.
• In second quadrant value of x is negative whereas the value of y is positive.
• In third quadrant value of x and y both are negative.
• In fourth quadrant, the value of x is positive and value ofy is negative.
• Perpendicular distance of a point from x-axis = (+)y-coordinate.
• Perpendicular distance of a point from y-axis = (+)x-coordinate.
• A point which lies on x-axis has coordinates of the form (a, 0).
• A point which lies on y-axis has coordinates of the form (0, b).
• Distance of a point P(x, y) from origin 0(0, 0) =\(\sqrt{x^{2}+y^{2}}\)
  e.g., distance of a point A(4,5) from origin, OA = \(\sqrt{4^{2}+5^{2}}\)
  \(=\sqrt{16+25}=\sqrt{41}\)units

On this page, you will find Triangles Class 9 Notes Maths Chapter 5 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 5 Lines and Angles will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 5 Notes Triangles

Triangles Class 9 Notes Understanding the Lesson

Two geometric figures are said to be congruent if they have exactly the same shape and size.
Note: Congruent means equal in all respect. When one figure is kept over another then it should superimpose on the other to cover it exactly.

If a 500-rupee note is placed over another 500-rupee note then they cover each other.
If 5-rupee coin is placed over another 5-rupee coin of same year, then they cover each other completely.
Congruence of line segments: Two line segments are congruent if they are of the same length. Length of AB = length of CD

Hence, \(\overline{\mathrm{AB}} \cong \overline{\mathrm{CD}}\)

Congruence of angles: Two angles are congruent if they have equal degree measures.

Hence, \(\angle \mathrm{ABC} \cong \angle \mathrm{CDE}\)

Congruence of squares: Two squares are said to be congruent, if they have equal sides.
Hence,

Note: Congruent plane figures are equal in area.

Congruence of circles: Two circles are congruent if they have equal radii.
Hence, Circle C₁ ≅ Circle C₂

Congruent Polygons
Two polygons are said to be congruent if they are the same size and shape. For existence of congruency,
(a) their corresponding angles are equal, and
(b) their corresponding sides are equal.

Congruence Triangles
Two triangles are congruent if they will have exactly the same three sides and three angles.

Axiom 7,1: SAS (Side-Angle-Side) Congruence rule: Two triangles are said to be congruent if two sides and the included angle of one triangle are equal to A D
the two sides and the included angle of the other.

In ΔABC and ΔDEF,
AB = DE
∠ABC = ∠DEF
BC = EF
ΔABC ≅ ΔDEF (by SAS)

Theorem 7.1: ASA (Angle-Side-Angle)
Congruence rule: Two triangles are said to be congruent, if two angles and the included side of one triangle are equal to two angles and the included side of other triangle.
In Δ ABC and Δ DEF,
∠ABC = ∠DEF
BC = EF
∠ACB = ∠DFE
∴ΔABC = ΔDEF (by ASA)

Given: AABC and ADEF in which
∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF
To Prove: ΔABC = ΔDEF
Proof: There are three cases arises for primary two congruence of the two triangles.

Case I: Let AB = DE
In ΔABC and ΔDEF,
AB = DE (assumed)
∠ABC = ∠DEF (given)
BC = EF (given)
So ΔABC ≅ ΔDEF (by SAS congruency)

Case II: Let AB > DE. So we can take a point P on AB such that PB = DE.
Now in ΔPBC and ΔDEF
PB = DE (by construction)
∠PBC = ∠DEF (given)
BC = EF (given)
∴ ΔPBC ≅ ΔDEF (by SAS Congruency)
∠PCB = ∠DFE …(1) (by CPCT)
∴ ∠ACB = ∠DFE …(2)
From eqn (1) and (2),
∠PCB = ∠ACB
which is not possible. This is only possible if point P coincides with A.
Hence AB = DE (PB=AB)
So ΔABC = ΔDEF (by SAS congruency)

Case III: If AB < DE, so we take a point Q on DE such that QE = AB
Now in ΔABC and ΔQEF,
AB = QE (by construction)
∠ABC = ∠QEF (given)
BC = EF (given)
Hence ΔABC = ΔQEF (by SAS congruency)
∠ACB = ∠QFE (by CPCT)
But ∠ACB = ∠DFE
Hence ∠QFE = ∠DFE
which is only possible if point Q coincides with D.
∴ AB = DE
Hence ΔABC ≅ ΔDEF (by SAS congruency)

Corollary: AAS (Angle-Angle-Side) congruence rule:
Two triangles are said to be congruent if two angles and one side of one triangle is equal to two angles and one side of another triangle.
In A ABC and A DEF,
∠ACB = ∠DFE . ∠ABC – ∠DEF
AB = DE
∴ ΔABC = ΔDEF (by AAS)

Given: ΔABC and ΔDEF
In which ∠A = ∠D, ∠B = ∠E
and BC = EF
To Prove: ΔABC ≅ ΔDEF
Proof: In ΔABC and ΔDEF
∠1 = ∠4 … (1) (given)
and ∠2 = ∠3 … (2) (given)
Adding eqn. (1) and (2),
∠1 + ∠2 = ∠3 + ∠4
⇒ 180° – (∠1 + ∠2) = 180° – (∠3 + ∠4) (by angle sum property)
∠ACB = ∠DFE
Hence ΔABC ≅ ΔDEF

Theorem 7.2 Angle opposite to equal sides of an isosceles triangle are equal.
If AB = AC, then
∠ABC = ∠ACB
Given: ABC is a triangle in which
AB = AC
To Prove: ∠B = ∠C


Construction:
Draw AD angle bisector of ∠A.
Proof: In ΔBAD and ΔCAD,
AB = AC (given)
∠BAD = ∠CAD (by construction)
AD = AD (common)
.∴ΔBAD = ΔCAD (by SAS)
Hence ∠B = ∠C (by CPCT)

Theorem 7.3. The sides opposite to equal angles of a triangle are equal.
Given: ΔABC in which ∠B = ∠C
To Prove: AB = AC
Construction:
Draw AD bisector of ∠A which meets BC at D.
Proof: In ΔBAD and ΔCAD,
∠B = ∠C
∠BAD – ∠CAD
AD = AD
∴ΔBAD ≅ ΔCAD
Hence AB – AC
Theorem SSS (Side-Side-Side)

Congruence rule: Two triangles are said to be congruent if all sides (three) of one triangle are equal to the all sides (three sides) of another triangles then the two triangle are congruent.
In Δ ABC and Δ DEF,
AB = DF
BC = EF
AC = DE
ΔABC ≅ΔDEF

Theorem 7.5: RHS (Right angle-Hypotenuse-Side)
Congruence rule: If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of another triangle, their the two triangles are congruent.

In ΔABC and ΔDEF,
∠ABC = ∠DEF
AC = DF
AB = DE
∴ ΔABC ≅ ΔDEF (by R.H.S)

Inequalities in a Triangle
Theorem 7.6: If two sides of a triangle are unequal, the angle opposite to the longer side is greater.
∠ABC > ∠BAC
∴ AC > BC
Given: ΔABC in which
AC > AB
To Prove:
∠ABC > ∠ACB

Construction:
Take a point D on AC such that AD = AB and join BD.
Proof: In Δ ABD,
AB – AD (by construction)
∴  ∠1 = ∠2 …(1) (Angle opposite to equal sides are equal)
∠2 > ∠3 ……..(2)  ∠1 is exterior angle of ΔBCD)

From eqn. (1) and (2),
∠1 > ∠3
Hence ∠ABC > ∠ACB.

Theorem 7.7: In a triangle, side opposite to greater angle is longer.
If ∠ABC > ∠BAC
∴ AC > BC
Given: Δ ABC in which
∠ABC > ∠ACB
To Prove: AC > AB

Proof: Here three cases arises.

• AC = AB
• AC < AB
• AC < AC

Case I: If AC = AB
∠ABC – ∠ACB (Angle opposite to equal sides are equal)
But ∠ABC > ∠ACB (given)
This is a contradiction.
Hence AC ≠AB
∴ AC > AB

Case II: AC < AB
∠ACB > ∠ABC (Angle opposite to longer side is greater)
This is contradiction of given hypothesis.
Hence only one possibility is left.
i.e. AC > AB (It must be true)
Hence AC > AB

Theorem 7.8: The sum of any two sides of a triangle is greater than the third side.
(i) AB + AC > BC
(ii) AB + BC > AC
(iii) BC + AC > AB
Given: ΔABC
Prove that:
(i) AB + BC > AC
(ii) AB + AC > BC
(iii) AC + BC > BC

Construction: BA produce to D such that AD = AC. Join CD.
Proof: In ΔACD,
AC = AD (by construction)
∠2 = ∠1 (Angle opposite to equal sides are equal)
∠2 + ∠3 > ∠1 (∠2 + ∠3 = ∠BCD)
Hence ∠BCD > ∠BDC

Hence BD > BC
⇒ AB + AC > BC (AD = AC by construction)
Similarly, AB + BC > AC
and AC + BC > AB

Median of a triangle: A line segment which joins the mid-point of the side to the opposite vertex. AD is median. D is the mid-point of BC.

Centroid: The point of intersection of all three medians of a triangle is known as its centroid.
Note: Centroid G divides the medians in the ratio 2: 1, i.e., AG : GD = 2: 1

Altitude: Perpendicular drawn from a vertex to the opposite side.

Orthocentre: The point at which all the three altitudes intersect each other is known as orthocentre.

Incentre: The point at which the bisectors of internal angles of a triangle intersect each other is called incentre.

Circumcentre: The point at which perpendicular bisectors of the sides of a triangle intersect each other is called circumcentre.

On this page, you will find Lines and Angles Class 9 Notes Maths Chapter 4 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 4 Lines and Angles will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 4 Notes Lines and Angles

Lines and Angles Class 9 Notes Understanding the Lesson

Point: A point is a dot made by a sharp pen or pencil. It is represented by capital letter.

Line: A straight and endless path on both the directions is called a line.

 

Line segment: A line segment is a straight path between two points.

Ray: A ray is a straight path which goes forever in one direction.

Collinear points: If three or more than three points lie on the same line, then they are called collinear points.

Non-collinear points: If three or more than three points does not lie on the same line, then they are called non-collinear points.

Angle: The space between two straight lines that diverge from a common point or between two planes that extend from a common line.

Types of Angles
1. Acute angle: An angle between 0° and 90° is called acute angle.

2. Right angle: An angle which is equal to 90° is called right angle.

3. Obtuse angle: An angle which is more than 90° but less than 180° is called obtuse angle.

4. Straight angle: An angle whose measure is 180° is called straight angle.

5. Reflex angle: An angle whose measure is between 180° and 360° is called reflex angle.

6. Complete angle: An angle which is equal to 360° is called complete angle

Pairs of Angles

1.Complementary angles: Two angles are said to be complementary if the sum of their degree measure is 90°.

For example, pair of complementary angles are 35° and 55°.

2. Supplementary angles: Two angles are said to be supplementary if the sum of their degree measure is 180°.
∠AOC + ∠BOC = 180°

3. Bisector of angle: A ray which divides an angle into two equal parts is called bisector of the angle.
∠AOC = ∠BOC

4. Adjacent angles: Two angles are said to be adjacent angles if

• They have a common vertex (O)
• They have a common arm (OC)
• and their non-common arms are on either side of common arm (OA and OB).
  ∠AOB = ∠AOC +∠BOC

5. Linear pair: Two adjacent angles are said to be linear pair if their sum is equal to 180°.

∠AOC + ∠BOC = 180°
Axiom 6.1: If a ray stands on a line, then the sum of two adjacent angles so formed is 180°.
Axiom 6.2: If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.

6. Vertically opposite angles: Vertically opposite angles are those angles which are opposite to each other (or not adjacent) when two lines cross each other.

Theorem 6.1: If two lines intersect each other, then the vertically opposite angles are equal.
To prove: If lines AB and CD mutually intersect at point O, then
(a) ∠AOC = ∠BOD (Vertically opposite angles)
(b) ∠AOD = ∠BOC

Proof: Lines AB intersect CD at O.
∠1 + ∠2 = 180° (Linear pair)
∠2 + ∠3 = 180° (Linear pair)
From eqn. (1) and (2), ∠1 + ∠2 = ∠2 + ∠3
⇒ ∠1 = ∠3 ⇒ ∠AOD = ∠BOC
Similarly, ∠AOC = ∠BOD

Parallel Lines
If distance between two lines is the same at each and every point on two lines, then two lines are said to be parallel.
If lines l and m do not intersect each other at any point then l || m.

Transversal line: A line is said to be transversal which intersect two or more lines at distinct points.

1. Corresponding angles: Pair of angles having different vertex but lying on same side of the transversal are called corresponding angles. Note that in each pair one is interior and other is exterior angle.

• ∠1 and ∠2
• ∠3 and ∠4
• ∠5 and ∠6
• ∠1 and ∠8

These angles are pair of corresponding angles.

2. Alternate interior angles: Pair of angles having distinct vertices and lying can either side of the transversal are called alternate interior angles.

• ∠1 and ∠2
• ∠3 and ∠4

These angles are alternate interior angles

3. Consecutive interior angles: Pair of interior angles of same side of transversal line.

• ∠1 and ∠2
• ∠2 and ∠4

These angles are consecutive interior angles or co-interior angles

Axiom 6.3: If two parallel lines are intersected by a transversal then each pair of corresponding angles are equal.
If AB || CD, then

• ∠PEB = ∠EFD
• ∠PEA = ∠EFC
• ∠BEF = ∠DFQ
• ∠AEF = ∠CFQ

Theorem 6.2: If two parallel lines are intersected by a transversal then pair of alternate interior angles are equal.
If AB || CD, then ?

• ∠AEF = ∠EFD
• ∠BEF = ∠CFE

 

Theorem 6.3: If two parallel lines are intersected by a transversal then the ! sum of consecutive interior angles of same side of transversal is equal to 180°. If AB || CD then
(i) ∠BEF + ∠DFE = 180°
(ii) ∠AEF + ∠CFE = 180°

Axiom 6.4: If two lines are intersected by a transversal and a pair of corresponding angles are equal, then two lines are parallel.
(i) If ∠PEB = ∠EFD (corresponding angles), then AB || CD

Theorem 6.4: If two lines intersected by a transversal and a pair of alternate interior angles are equal, then two lines are parallel. If ∠AEF = ∠EFD (alternate interior angles), then AB || CD.

Theorem 6.5: If two lines are intersected by a transversal and the sum of consecutive interior angles of same side of transversal is equal to 180°, the lines are parallel. If ∠AEF + ∠CFE = 180°, then AB || CD.

Theorem 6.6: Lines which are parallel to the same line are parallel to each other.
If AB || EF and CD || EF then AB || CD

 

 

Theorem 6.7: The sum of the angles of a triangle is equal to 180°.
Given: ΔABC
To prove: ∠A + ∠B + ∠C = 180°
Construction: Draw DE || BC
Proof: DE || BC
then ∠1 = ∠4 …(1) (alternate interior angles)
∠2 = ∠5 …(2) (alternate interior angles)
Adding equations (1) and (2),
∠1 + ∠2 = ∠4 +∠5
Adding ∠3 on both sides,
∠1 +∠2 + ∠3 = ∠3 + ∠4 + ∠5
⇒ ∠A + ∠B + ∠C = 180° (Sum of angles at a point on same side of a line is 180°)

Theorem 6.8: If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
Given: AABC in which, side BC is produced to D.
To Prove: ∠ACD = ∠BAC + ∠ABC
Proof: ∠ACD + ∠ACB = 180° …(1) (Linear pair)
∠ABC + ∠ACB + ∠BAC = 180° …(2)
From eqn. (1) and (2), ∠ACD + ∠ACB
= ∠ABC + ∠ACB + ∠BAC
= ∠ACD = ∠ABC + ∠BAC

 

On this page, you will find Introduction to Euclid’s Geometry Class 9 Notes Maths Chapter 3 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 3 Introduction to Euclid’s Geometry will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 3 Notes Introduction to Euclid’s Geometry

Introduction to Euclid’s Geometry Class 9 Notes Understanding the Lesson

1. The word ‘geometry is derived from the Greek Word ‘Geo’ means Earth and ‘matrein’ means to measure,

2. In India the excavations of Harappa and Mohenjo-daro show the industrially civilisation (about 300 BCE) made use of geometry.

3. Sulbasutras were the manuals of geometrical constructions in (800 BCE to 500 BCE)

4. The Sriyantra (given in Atharvaveda) which consist 9 interwoven isosceles triangles. These triangles are arranged in such a way that they produce 43 subsidiary triangles.

5. Thales was a great mathematician who gives the proof and statement that a circle is bisected by its diameter.

6. Thales famous pupil was Pythagoaras (572 BCE). He and his group developed the theory of geometry to a great extent.

7. Euclid was a teacher of mathematics at Alexandria in Egypt collect all the famous work and arranged it in his famous treatise called ‘Elements’. He divided the elements in thirteen chapters which are each called a book. These books influenced the whole worlds to understand geometry.

Definitions which are given by Euclid

• Point-, a point is that which has no part.
• Line: A line is breadthless length.
• The ends of a line are points.
• Straight line: It is a line which lies evenly with the points on itself.
• Surface: A surface is that which has length and breadth only.
• Edge: The edges of a surface are lines.
• Plane surface: A plane surface is a surface which lies evenly with the straight lines on itself

If we study these definitions, we find the some of terms like part, length, breadth, evenly, etc. need to be further described clearly. Euclid assumed certain properties, which were not to be proved. Euclid’s assumptions are universal truths,

• Axiom: The basic facts which are taken for granted without proofs are called axiom.
• Statement: A sentence which is either true or false but both is called a statement.
• Theorem: A statement which requires proof.

Euclid’s Axioms

• Things which are equal to the same thing are equal to one another.
• If equals are added to equals, the wholes are equal.
• If equals are subtracted from equals the remainders are equal.
• Things which coincide with one another are equal to one another.
• The whole is greater than the part.
• Things which are double of the same things are equal to one another.
• Things which are halves of the same things are equal to one another.

Collinear points: Three or more points are said to be collinear, if they all lie in the same line.

Plane: A plane is a flat, two dimensional surface that extends infinitely in all directions. Intersecting lines: Two lines land m are said to be intersecting lines if l and m have only one point common.

Playfair Axiom: Two intersecting lines cannot both be parallel to a same line.

Plane figure: A figure that exist in a plane is called a plane figure.

Note:

• Common notions often called axioms.
• Postulates were the assumptions that are specific for geometry.

Axiom 5.1: There is a unique line that passes through two distinct points.

1. Through a given point infinitely many lines can be drawn.

2. A line contains infinitely many points.

Euclid’s five postulates
Postulate 1: A straight line may be drawn from any one point to any other point.
Note: This postulate tells us that one and only one (unique) line passes through two distinct points.

Postulate 2: A terminated line can be produced indefinitely.
This postulate tells us that a line segment can be extended on either side to form a line.

Postulate 3: A circle can be drawn with any centre and any radius.

Postulates 4: All right angles are equal to one another.

Postulate 5: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.

Example: Sum of ∠1 and ∠2 is less than 180°. Therefore, the lines AB and CD will enventually intersect on the left side of PQ. Nowadays, axioms and postulates are used in same sense.

 

Note: The statements that were proved are called propositions or theorems.
I Euclid deduced 465 propositions in a logical chain by using his axioms,

Theorem 5.1
Two distinct lines can not have more than one point in common,
Proof: Let us suppose that two lines l and m intersect in two distinct points say P and Q. Therefore two lines passing through two distinct points P and Q. But our assumption clashes with the axiom that only one line can pass through two distinct points. So, the assumption was wrong that we started with, that two lines can pass through two distinct points is wrong. Hence two distinct lines can passe through one common point.

On this page, you will find Atoms and Molecules Class 9 Notes Science Chapter 3 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 3 Atoms and Molecules will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 3 Notes Atoms and Molecules

Atoms and Molecules Class 9 Notes Understanding the Lesson

1. The structure of matter has been a subject of speculation from a very early time. The ancient Indian and Greek philosophers regarded matter to be discontinuous and made up of infinitely small particles. Around the same period, Greek philosopher, Democritus, suggested that if we go on dividing matter into smaller parts, a stage would be reached when particles obtained cannot be divided further. He called these particles ‘Atoms’ meaning indivisible.

2. After Democritu’s death, little more was done with atomic theory until the end of the 18th century, when Antoine Lavoisier introduced modern chemistry to the world. He put forward two important laws of chemical combination which formed the basis of Dalton’s atomic theory which were published in 1808.

3. Laws of Chemical Combination: Whenever reactants react together to form the products or the elements combine together to form a compound, they do so according to certain laws. These laws are called “Laws of Chemical Combination”.

4. Laws of Conservation of Mass: Law of Conservation of Mass states that mass can neither be created nor destroyed in a chemical reaction.

5. Law of Constant Proportions: This law was stated by Proust as “In a chemical substance, the elements are always present in definite proportion by mass”. For example: In a compound such as water, the ratio of the mass of hydrogen to the mass of oxygen is always 1: 8, whatever the source of water. Thus, if 9 g of water is decomposed, 1 g of hydrogen and 8 g of oxygen are always obtained.

6. As the law of constant proportions is true, it helps us to calculate the percentage of any element in the given compound, using the following expression:

7. Dalton’s Atomic Theory : On the basis of laws of chemical combination, John Dalton, proposed that behaviour of matter could be explained using an atomic theory.

8. Postulates of Dalton’s Atomic Theory

• All matter is made of very tiny particles called atoms.
• Atoms are indivisible particles, which cannot be created or destroyed in a chemical reaction.
• Atoms of a given element are identical in mass and chemical properties.
• Atoms of different elements have different masses and chemical properties.
• Atoms combine in the ratio of small whole numbers to form compounds.
• The relative number and kinds of atoms are constant in a given compound.

9. Limitations of Dalton’s Atomic Theory

• It failed to explain how atoms of different elements differ from each other i.e., it did not tell anything about internal structure of the atom.
• It could not explain how and why atoms of different elements combine with each other to form compound- atoms or molecules.
• It failed to explain the nature of forces that hold together different atoms in a molecule.
• It did not make any distinction between ultimate particle of an element that takes part in reaction (atom) and ultimate particle that has independent existence (molecule).

Question 10.
Atom
Answer:
An atom is defined as the smallest particle of an element which may not be capable of free existence. However, it is the smallest particle that takes part in a chemical reaction.

Question 11.
How big are atoms?
Answer:
Atoms are very small, they are smaller than anything that we can imagine or compare with more than millions of atoms when stacked would make a layer barely as thick as a thin sheet of paper.

Atoms are very small in size. The size of an atom is expressed in terms of atomic radius. Atomic radius is measured in nanometers (nm).
\(1 \mathrm{nm}=\frac{1}{10^{9}} \mathrm{m}=10^{-9} \mathrm{m}\)

Radii of most of the atoms are the order of 0.1 nm or 10_1° m. For example, atomic radius of hydrogen is
0. 037 nm while that of gold atom is 0.144 nm.

Question 12.
Symbols used to represent atoms of different elements
Answer:
Daltons suggested symbols for the atoms of different elements. He was the first scientist to use the symbols for elements in a quantitative sense. When he used symbol for an element he meant a definite quantity of that element, that is, one atom of the element.

Question 13.
Modern Symbols of Elements
Answer:
1. The symbol of an element is the “first letter and another letter” of the English or Latin name of the element. However, in all cases, the first letter is always capital and the other letter (if added) is always a small letter.
For example: Hydrogen is represented by ‘H’, oxygen by ‘O’, carbon by ‘C’ etc.

2. The necessity of adding another letter arises only in case of elements whose names start with the same
letter. However, the other letter added is not always the second letter of the name. Further, the other – letter added may be a letter from the Latin name of the element.

For example: Carbon, Calcium, Cobalt, Chlorine and Copper all start with the first letter ‘C’ Hence carbon is represented by C and calcium is represented by Ca, cobalt by Co, chlorine by Cl and copper by Cu

Element	Symbol	Element	Symbol	Element	Symbol
Aluminium	A1	Copper	Cu	Nitrogen	N
Argon	Ar	Fluorine	F	Oxygen	O
Barium	Ba	Gold	Au	Potassium	K
Boron	B	Hydrogen	H	Silicon	Si
Bromine	Br	Iodine	I	Silver	Ag
Calcium	Ca	Iron	Fe	Sodium	Na
Carbon	C	Lead	Pb	Sulphur	S
Chlorine	Cl	Magnesium	Mg	Uranium	U
Cobalt	CO	Neon	Ne	Zinc	Zn

Question 14.
Atomic Mass
Answer:
The atomic mass of an element is the relative mass of its atoms as compared with the mass of an atom of carbon -12 isotope taken as 12 units.
\(\text { Atomic mass }=\frac{\text { Mass of } 1 \text { atom of the element }}{\frac{1}{12} \text { of the mass of an atom of Carbon-12 }}\)

Since atomic masses are relative masses, they are pure numbers and are often given without units. In case of most of the elements, all the atoms of the elements do not have same relative mass. The atoms of an element having different relative masses are called isotopes. For example: Chlorine contains two types of atoms having relative masses 35 u and 37 u and their relative abundance is 3:1.
\(\text { Atomic mass of chlorine }=\frac{35 \times 3+37 \times 1}{4}=35.5 \mathrm{u}\)

Question 15.
What is a Molecule?
Answer:
A molecule can be defined as the smallest particle of an element or a compound that is capable of an independent existence and shows all the properties of that substance.

Question 16.
Molecule of an element
Answer:
Molecule of an element means one, two or more atoms of the same element existing as one species in the free state.
(i) Monoatomic molecules: Noble gases like helium, neon, etc., exist as single atom. Hence, their molecules are monoatomic.

(ii) Diatomic molecules: For example, in a molecule of hydrogen, two atoms of hydrogen exist together. Its molecule is, therefore, represented by H₂, i.e., it is a diatomic molecule.

(iii) Triatomic molecules: For example, in a molecule of ozone, three atoms of oxygen exist together as one species. Hence, it is triatomic with formula O₂

(iv) Tetratomic molecules: For example; Phosphorus P₄ is a triatomic molecule.

Molecules containing more than four atoms are generally called polyatomic.

The number of atoms present in one molecule of the substance is called its atomicity.

Molecules of a compound: Atoms of different elements join together in definite proportion to form molecules of compounds. For example, H₂O represents the molecule of a compound in which two atoms of hydrogen are combined with one atom of oxygen, or hydrogen and oxygen are combined in the fixed proportion, i.e., 1 : 8 by mass.

Molecular mass: The molecular mass of a substance (an element or a compound) may be defined as the average relative mass of a molecule of the substance as compared with mass of an atom of carbon (C-12 isotope) taken as 12 u.
\(\text { Molecular mass }=\frac{\text { Mass of } 1 \text { molecule of the substance }}{\frac{1}{12} \text { of the mass of an atom of } \mathrm{C}-12}\)

For example, molecular mass of CO₂ is 12 x 1+ 16 x 2 = 44.
Formula mass: Formula mass of an ionic compound is obtained by adding atomic masses of all the atoms in a formula unit of the compound.
For example, formula mass of potassium chloride (KCl)
= Atomic mass of potassium + atomic mass of chlorine
= 39 + 35.5
= 74.5

Question 17.
What is an ion?
Answer:
An atom or a group of atoms which contains positive or negative charge are called ions.

• A positively charged ion called ‘cation’.
• A negatively charged ion is called ‘anion’.
• The ions consisting of only single atoms are called monoatomic ions.
• The ions consisting of a group of atoms is called polyatomic ion.

Question 18.
Writing chemical formula
Answer:
Chemical formula of a compound represents the actual number of atoms of different elements present in one molecule of the compound. For example, chemical formula of water is H₂O.

Valency is defined as the combining capacity of the element. It is equal to the number of hydrogen atoms or number of chlorine atoms or double the number of oxygen atoms with which one atom of the element combines.

For example, valency of oxygen is 2. This means that one atom of oxygen can combine with two atoms of hydrogen. Hence, the formula of the compound formed is H₂O.

Rules for writing the chemical formula

• Formula of compound is given by writing the symbols of constituent elements side by side.
• Symbol of the more metallic element is written first in the formula.
• Number of atoms of each of the constituent elements present in the molecule is indicated by subscript.
• When either of the ions or both the ions are polyatomic and their valency is more than 1, we enclose the polyatomic ions in brackets. No brackets are riecessary if the valencies of polyatomic ions are 1.
• While writing formula of a compound if the valency numbers have a highest common factor [H.C.F.], divide the valency numbers by H.C.F. to get a simple ratio between the combining elements.

The simplest compounds, which are made up of two different elements are called binary compounds and formula can be written by criss crossing the valencies of elements present in a molecule of the compound. Formula of the compound can be derived by following steps

Step – 1: Write the constituent elements and their valencies as shown.

Step – 2: Reduce the valency numerals to the simplest whole numbers by dividing by some common factor, if any

Step – 3: Criss-cross the reduced valency numerals and write them as subscripts at the bottom right-hand side of the symbols.

The subscript 1 is not written. Thus, the formula of the compound is CO₂.

Mole concept: A mole of particles (atoms, ions or molecules) is defined as that amount of the substance which contains the same number of particles as there are C-12 atoms in 12 g, i.e., 0.012 kg of C-12 isotope.

Te number of particles (atoms, molecules or ions) present in 1 mole of any substance is fixed, with a value 6.022 x 10²³. This number is called avogadro’s number. Avogadro’s number (N_A or N₀) = 6.022 x 10²³

The volume occupied by one mole of molecules of a gaseous substance is called molar volume or gram molecular volume.

Class 9 Science Chapter 3 Notes Important Terms

Element: A chemical substance that cannot be decomposed by chemical means into simpler parts. It contains same kind of atoms. There are 118 elements known, out of which 94 are natural.

Compound: When two or more atoms of different elements chemically combine, the molecule of a compound is obtained. The examples of some compounds are water, ammonia, sugar, etc.

Molar mass: Molar mass is the sum of the atomic masses of the elements present in a molecule. It is obtained by multiplying the atomic mass of each element by the number of its atoms and adding them together.

Ion: Any atom or molecule which has a resultant electric charge due to loss or gain of valence electrons.

Valency: It is the capacity of atoms of a given element that tend to combine with, or replace atoms of hydrogen. In HCl gas, valency of chlorine is 1.

Atomicity: It corresponds to the number of atoms present in a given molecule of an element. For example, ozone (O₃) has an atomicity of 3 and benzene (C₆H₆) has an atomicity of 12.

Mole: [Historically the word ‘mole’ was introduced about hundred years back by Wilhelm Ostwald. He derived this word from the Latin word ‘moles’ meaning ‘ heap or a pile’]. A mole is the amount of a substance that contains as many elementary entities (atoms, molecules or other particles) as there are atoms in exactly 0.012 kg of the carbon-12 isotope.

On this page, you will find Polynomials Class 9 Notes Maths Chapter 2 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 2 Polynomials will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 2 Notes Polynomials

Polynomials Class 9 Notes Understanding the Lesson

1. An expression which is the combination of constants and variables and are connected by some or all the operations addition, subtraction, multiplication and division is known as an algebraic expression.
Example: 7 + 9x – 2x² + \(\frac{5}{6}\) xy

2. Constant: Which has fixed numerical value.
Example: 7, -4, \(\frac{3}{4}\) , n etc.

3. Variable: A symbol which has no fixed numerical value is known as a variable.
Example: 2x, 5x²

4. Terms: These are the parts of an algebraic expression which are separated by operations, like addition or subtraction are known as terms.
Example: In the expression 5x³ + 9x² + 7x – 3, terms are 5x³, 9x², 7x and -3

5. Polynomial: An algebraic expression of which variables have non-negative integral powers is called a polynomial.
Example:
(a) 5x² + 7x + 3
(b) 9y³ – 7y² + 3y + 7

6. Coefficient: A coefficient is the numerical value in a term.
Note: If a term has no coefficient, the coefficient is an unwritten 1.
Example: 5x³ – 7x² – x + 3

7. Degree of a polynomial (in one variable): The highest power of the variable is called the degree of the polynomial.
Example: 5x + 4 is a polynomial in x of degree 1.

8. Degree of a polynomial in two or more variables: The highest sum of powers of variables is called the degree of the polynomial.
Example: 7x³ + 2x²y² – 3ry + 8

9. Degree of polynomial = 4 (Sum of the powers of variables x and y )

10. Types of Polynomial

(i) Linear polynomial: A polynomial of degree one is called a linear polynomial.
Example: 2x + 3 is a linear polynomial in x.

(ii) Quadratic polynomial: A polynomial of degree 2 is called a quadratic polynomial.
Example: 5x² – 7x + 4 is a quadratic polynomial.

(iii) Cubic polynomial: A polynomial of degree 3 is called a cubic polynomial.
Example: 3x³ + 7x² – 4x + 9 is a cubic polynomial.

(iv) Biquadratic polynomial: A polynomial of degree 4 is called a biquadratic polynomial.
Example: 7x⁴ – 2x³ + 4x + 9 is a biquadratic polynomial.

11. Number of Terms in a Polynomial
Categories of the polynomial according to their terms:

(i) Moflomil A polynomial which has only one non-zero term is called a monomial.
Example: 7, 4x, \(\frac{4}{5}\) xy, 7x²y³z⁵, all are monomials.

(ii) Binomial: A polynomial which has only two non-zero terms is called binomial.
Example: 2x + 7, 9x² + 3, 3x²yz + 4x³y³z², all are binomials.

(iii) Trinomial: A polynomial which has only three non-zero terms is called a trinomial.
Example: 5x² + lx + 9, 5xy + 7xy² + 3x³yz, all are trinomials.

(iv) Constant polynomial: A polynomial which has only one term and that is a constant is called a constant polynomial.
Example: \(\frac{-3}{4}\), 7, 5 all are constant polynomials. 4
Note: The degree of constant non-zero polynomial is zero.

(v) Zero polynomial. A polynomial which has only one term i.e., 0 is called a zero polynomial.
Note: Degree of a zero polynomial is not defined.

12. Value of a Polynomial

Value of a polynomial is obtained, when variable of a given polynomial is interchanged or replaced by a ; constant.    Let p(x) is a polynomial then value of polynomial at x = a is p(a).
Zero or root of a polynomial: A zero or root of a polynomial is the value of that variable for which value of polynomial p(x) becomes zero i.e., p(x) = 0.
Let p(x) be the polynomial and x – a.
If p(a) = 0 then real value a is called zero of a polynomial.

13. Remainder Theorem
Let p(x) be a polynomial of degree ≥ 1 and a be any real number. If p(x) is divided by the linear polynomial x-a, then the remainder is p(a).

Proof: Let p(x) be any polynomial of degree greater than or equal to 1. When p(x) is divided by x – a, the quotient is q(x) and remainder is r(x).
i.e.,p(x) = (x-a) q(x) + r(x)
Since degree of x – a is 1 and the degree of r(x) is less than the degree of x – a so the degree of r(x) = 0.
It: means r(x) is a constant, say r.
Therefore, for every value of x,  r(x) = r
then   p(x) = (x-a) q(x) + r
When x = a, then  p(a) = (a – a) q(x) + r ⇒ p(a) = r

14. Factor Theorem
If p(x) is a polynomial of degree greater than or equal to 1 and a be any real number, then

• x – a is a factor of p(x) i.e., p(x) – (x-a) q(x) which shows x – a is a factor of p(x)
• Since x – a is a factor of p(x)
  p(x) = (x-a)g(x) for same polynomial g(x). In this case,p(a) = (a-a) g (a) = 0

15. Factorisation of the Polynomial ax² + bx + c by Splitting the Middle Term
Let           p(x) = ax² + bx + c
and factor of polynomial p(x) = (px + q) and (rx + s)
then   ax² + bx + c = (px + q) (rx + s) = prx² + (ps +qr)x+ qs
Comparing the coefficient of x² on both sides
a = pr …………. (1)
Comparing the coefficient of x
b =ps + qr …………. (2)
and comparing the constant terms
c = qs ……………..(3)
which shows that b is the sum of two numbers ps + qr.
Product of two numbers ps x qr =pr x qs = ac
So for factors ax² + bx + c, we should write b as sum of two numbers whose product is ac.
Example: Factorise 6x² + 17x + 5
Here,  b = p + q = 17
and   ac = 6 x 5 = 30 (= pq)
then we get factors of 30,      1 x 30, 2 x 15, 3 x 10, 5 x 6,
Among above factors of 30, the sum of 2 and 15 is 17
i.e.,p + q = 2 + 15 = 17
∴ 6x² + 17x + 5 = 6x² + (2 + 15)x + 5 = 6x² + 2x + 15x + 5
= 2x(3x + 1) + 5(3x + 1) = (3x + 1) (2x + 5)

16. Algebraic Indentities

On this page, you will find Is Matter Around Us Pure Class 9 Notes Science Chapter 2 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 2 Is Matter Around Us Pure will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 2 Notes Is Matter Around Us Pure

Is Matter Around Us Pure Class 9 Notes Understanding the Lesson

1. Pure substance: A pure substance is defined as a material which contains only one kind of atoms or molecules. In pure substance all the constituting particles have the same chemical nature. Thus, a pure substance con¬sists of a single type of particles.

2. Pure substances are always homogeneous.

• Element: A pure substance which is made up of only one kind of atom.
• Compound: A pure substance which is made up of only one kind of molecules.

3. Mixtures: It is a form of matter in which two or more elements or compounds combine physically in any proportion by weight.

4. Types of Mixtures

• Homogeneous mixture: A mixture which has same composition throughout. Solutions are homogeneous mixtures. For example, air, sea water, grass, vinegar, etc.
• Heterogeneous mixture: A mixture which has different compositions in different parts. For example, sand, mud, iron filings, sulphur, etc.

5. Characteristics of Mixture

• Mixture may be homogeneous and heterogeneous.
• Mixture does not have a fixed melting point.
• In a mixture, the different constituents combine physically in any proportion by mass.
• The constituents of a mixture do not loose their identical property.
• Usually, no energy change take place during the formation of a mixture.

6. Solution
It is a homogeneous mixture of two or more non-reacting substances.

7. Solvent is the substance in which a solute is dissolved.

8. On the basis of the size of particles, solutions can be classified as:

• True solution
• Colloidal solution
• Suspension

9. True Solution : A homogeneous system in which the particle size is less than 1 nm. For example, sugar solution.

10. Properties of True Solution

• A solution is a homogeneous mixture.
• The particles of a solution are smaller than 1 nm in diameter. So, they cannot be seen by the naked eye.
• Because of very small particle size, they do not scatter a beam of light passing through the solution. So, the path of light is not visible in a solution.
• The solute particles cannot be separated from the mixture by the process of filtration. The solute particles do not settle down when left undisturbed that is, a solution is stable.

11. Concentration of solution
There are two methods for expressing the concentration of solution.
Saturated solution: A solution in which no more of solute can be dissolved at a given temperature is called a saturated solution.
(i) Mass by Mass percentage of a Solution =\(\frac{\text { Mass of solute }}{\text { Mass of solution }} \times 100\)

(ii) Mass by Volume percentage of a Solution \(=\frac{\text { Mass of solute }}{\text { Volume of solution }} \times 100\)

12. Unsaturated solution: A solution in which more of the solute can be dissolved at a given temperature is called an unsaturated solution.
Suspension

13. A suspension: is a heterogeneous mixture in which one substance having particle size greater than 100 nm in diameter is spread throughout another substance. For example, muddy water, dust storm, aluminium paint, etc.

14. Properties of Suspension

• A suspension is a heterogeneous mixture.
• The particles of a suspension do not pass through a filter paper. Hence, it is possible to separate them by ordinary filtration.
• The particles of a suspension settle down when a suspension is left undisturbed. Thus, a suspension is unstable.
• The particles of suspension can be seen with naked eyes or with the help of a simple microscope.
• The size of particle in a suspension is greater than 100 nm in diameter.
• A suspension is not transparent to light.

15. Colloidal solutions
A solution in which the size of particles lies in between those of true solutions and suspensions are called colloidal solutions or colloids.
Colloidal solution is heterogeneous in nature and consists of two phases:

• Dispersed phase: It is the component present in small proportion and consists of particles of colloidal dimensions (1 nm to 100 nm).
• Dispersion medium: The solvent like medium in which colloidal particles are dispersed is called dispersion medium.

16. Properties of Colloidal Solutions

(i) Heterogeneous Nature: A colloidal solution is heterogeneous in nature. It consists of two phases— dispersed phase and dispersion medium.

(ii) Filtrability: The size of the colloidal particles is less than the pores of a filter paper,, and, therefore, they easily pass through a filter paper. Colloidal particles, however, cannot pass through the parchment paper or an animal membrane or ultra-filter.

(iii) Tyndall Effect: When a strong beam of light is passed through a colloidal solution placed in a dark place, the path of the beam gets illuminated by a bluish light. This phenomenon is called Tyndall effect. The phenomenon is due to scattering of light by the colloidal particles. The same phenomenon is noticed when a beam of sunlight enters a dark room through a small slit, due to scattering of light by dust particles in the air.

(iv) Visibility: Colloidal particles are too small to be seen by the naked eye. They, however, scatter light and become visible when viewed through an ultramicroscope.

(v) Brownian Movement: When colloidal particles are seen under an ultramicroscope, the particles are found to be in constant motion in zig-zag path in all possible directions. This zig-zag motion of colloidal particles is called Brownian movement. The movement of the particles is due to the collisions with the molecules of the dispersion medium.

(vi) Diffusion: Colloidal particles diffuse from a region of higher concentration to that of lower concentration. However, because of their bigger sizes colloidal particles move slowly and hence diffuse at a slower rate.

(vii) Sedimentation or Settling: Under the influence of gravity, the solute particles tend to settle down very slowly. This rate of settling down or sedimentation can be accelerated by the use of high speed centrifuge called ultracentrifuge.

17. Common methods for the separation mixtures are:

(a) Filtration: Filtration is the process of separating solids that are suspended in liquids by pouring the mixture into a filter funnel. As the liquid passes through the filter, the solid particles remain behind on the filter.

(b) Distillation: Distillation is the process of heating a liquid to form vapour and then cooling the vapour to get back the liquid. This is a method by which a mixture containing volatile substances can be separated into its components.

(c) Sublimation: This is the process of conversion of a solid directly into vapour on heating. Substances showing this property are called sublimate, e.g., iodine, naphthalene, camphor. This method is used to separate a sublimate from non-sublimate substances.

(d) Crystallisation: It is the process of separating solids having different solubilities in a particular solvent.

(e) Magnetic separation: This process is based upon the fact that a magnet attracts magnetic components from a mixture of magnetic and non-magnetic substances. The non-magnetic substance remains unaffected. Thus, it can be used to separate magnetic components from non-magnetic components.

(f) Atmolysis: This method is based upon rates of diffusion of gases and used for their separation from a gaseous mixture.

18. Physical Change: A temporary change which includes change in the shape, size, physical states and appearance of a substance,but not its chemical composition is known as physical change. Physical change is temporary and reversible. Chemical composition of the substance remains the same.
Examples:

• Heating of sulphur
• Sublimation of camphor
• Drying of wet clothes
• Breaking of glass

19. Chemical Change: A permanent change in which the chemical substance loses its own characteristics and composition and gives one or more new substances is called a chemical change. Chemical change is generally permanent and irreversible. Chemical change gives one or more new substances as products.
Examples

• Rusting of iron
• Digestion of food
• Burning of wood
• Ripening of fruit

20. Types of Pure Substances

1. Element: An element is defined as the simplest form or the basic form of a pure substance which can neither be broken into nor built up from simpler substances by any physical or chemical changes.

Properties of metals

• They have a lustre (shine).
• They have silvery-grey or golden-yellow colour.
• They conduct heat and electricity.
• They are ductile (can be drawn into wires).
• They are malleable (can be hammered into thin sheets).
• They are sonorous (make a ringing sound when hit).
  Examples of metals: Gold, silver, copper, iron, etc.

Properties of non-metals:

• They are poor conductors of heat and electricity.
• They are not lustrous, sonorous or malleable.
• They display a variety of colours.
  Examples of non-metals: Hydrogen, oxygen, iodine, bromine, chlorine, etc.
  Metalloids: Elements having certain properties of metals and non-metals are called metalloids.
  Examples: Arsenic, germanium, antimony and bismuth.

2. Compound: A compound is a substance composed of two or more elements, chemically combined with one another in a fixed proportion. For example: Water is compound of hydrogen and oxygen elements and these elements are present in water in the ratio of
1 : 8 by mass.
Characteristics of compound:

• In a compound constituents are presents in definite proportion by mass.
• The properties of the compound are different from the properties of the constituents (elements) that make up the compound.
• The constituents of a compound cannot be separated by simple physical processes.
• A compound has a fixed melting point and boiling point.
• A compound is always homogeneous in nature.

Difference between mixture and compound

Mixture	Compound
1. In a mixture, the constituents can be present in any proportion by mass. Thus, a mixture does not have any definite formula.	1. In a compound, constituents are present in  definite proportion by mass. A compound has a definite formula.
2. A mixture shows the properties of its constituents.	2. The properties of a compound are different from the properties of its constituent elements.
3. A mixture can be separated into its constituents by physical methods such as distillation, sublimation, filtration, etc.	3. The constituent of a compound can be separated only by chemical methods.
4. Formation of a mixture is not accompanied by much energy change.	4. Formation of a compound is generally accompanied by the evolution of energy in the form of heat or light.
5. A mixture does not have a fixed melting point and boiling point.	5. A compound has fixed melting point and boiling point.
6. A mixture may be homogeneous or heterogeneous.	6. A compound is always homogeneous.

Class 9 Science Chapter 2 Notes Important Terms

1. Matter is defined as anything that has weight and occupies space.

2. Intermolecular force is the force of attraction between the consituent particles of matter.

3. Alloys are mixtures of two or more metals or a metal and a non-metal and cannot be separated into their components by physical methods.

4. Solution is a homogeneous mixture of two or more substances. The major component of a solution is called the solvent, and the minor, the solute.

5. Colloids are heterogeneous mixtures in which the particle size is too small to be seen with the naked eyes, but is big enough to scatter light.

On this page, you will find Matter in Our Surroundings Class 9 Notes Science Chapter 1 Pdf free download. CBSE NCERT Class 9 Science Notes Chapter 1 Matter in Our Surroundings will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Science Chapter 1 Notes Matter in Our Surroundings

Matter in Our Surroundings Class 9 Notes Understanding the Lesson

1. Matter is everything around you. Everything in this universe is made up of material which in scientific term is called matter.

2. Matter can be defined as anything that occupies space possesses mass, offers resistance and can be felt by one or more of our senses.

3. Examples: Water, air, plant, animal, stones, clouds, etc.
Matter is classified on the basis of their physical and chemical nature.

• Physical classification: On the basis of physical properties, matter has been classified as solid, liquid and gas.
• Chemical classification: On the basis of chemical composition, matter has been classified as element, compound and mixture.

4. Properties of Matter

• Matter is made up of small particles.
• Particles of matter have space between them.
• Particles of matter are continuously moving.
• Particles of matter attract each other because of force of attraction.

5. States of Matter
This classification is done on the basis of arrangement among particles, energy of particles and the distance between the particles.
(i) Solids:

• They have fixed shape and definite volume.
• They have small interparticle distances.
• They are incompressible.
• They are rigid.
• They have high density and do not diffuse.
• They have strong intermolecular forces of attraction.
• Their constituent particles are very closely packed.
• Their kinetic energy is very less.
  Examples: Sugar, salt, etc.

(ii) Liquids:

• They do not have fixed shape but have fixed volume.
• Their interparticle distances are larger than solids.
• They are almost incompressible.
• They have low density than solids.
• Their interparticle forces of attraction are weaker than solids.
• Their constituent particles are less closely packed.
• They assume the shape of the portion of the container they occupy.
• They can flow and thus can be called fluids.
• The kinetic energy of particles is more than that of solids.
• Examples: Milk, water, etc.

(iii) Gases:

• They have neither fixed shape nor fixed volume.
• Their interparticle distances are largest among the three states of matter.
• They have high compressibility.
• They have least density and diffuse.
• Their interparticle forces of attraction are weakest.
• Their constituent particles are free to move about.
• They can expand to occupy larger volume.
• They are also called vapour.
• The particles of gases have maximum kinetic energy.
• Examples: H₂, N₂, CO₂ etc.

6. Interchange of States of Matter

• Matter can be changed from one state to another state.
• Most of the metals, which are solid change into liquid on heating and then into vapour on further heating.
• The change of state of matter depends on:
  (i) Temperature
  (ii) Pressure

7. Effect of Change of Temperature

8. The temperature effect on heating a solid varies depending on the nature of the solid and the conditions required for bringing the change.

9. Generally on heating, temperature of substances increases. But during state transformation, temperature remains same.

10. On heating: The kinetic energy of particles increases which overcomes the force of attraction between the particles thereby solid melts and is converted to a liquid.

11. Melting point: It is the temperature at which a solid changes to a liquid at atomospheric pressure.

12. Different substances have different melting points.

13. Higher the melting point means large forces of attraction between the particles.

14. Melting point of ice is 273.16 K.

15. The process of melting is also known as fusion.

16. Melting point is characteristic propertyof a substance.

17. Latent heat: The hidden heat which breaks the force of attraction between the molecule is called latent heat.

18. It is the heat supplied to a substance during the change of its state.

19. It is the heat energy hidden in the bulk of matter.

20. Latent heat of fusion: Amount of heat energy required to convert 1 kg of a solid into a liquid at atmospheric pressure at its melting point is known as latent heat of fusion of a substance.

21. A solid having stronger interparticle forces has greater latent heat of fusion.

22. Latent heat of fusion of water is 333.7 kJ/kg.

23. Boiling point: The temperature at which a liquid starts boiling at atmospheric pressure is known as its boiling point.

24. A liquid having weaker interparticle forces has lower boiling point and is more volatile.

25. Latent heat of vapourisation: The amount of heat energy required to convert 1 kg of a liquid into a gas at atmospheric pressure at its boiling point is known as latent heat of vapourisation of the substance.

26. Latent heat of vapourisation of water is 2259 kJ/kg. Thus 1 kg of water in the form of steam at 373 K has 2259 kJ more energy than 1 kg of water at 373 K.

27. Condensation: The change of state from gas to liquid is called condensation.

28. The condensation process is reverse of vapourisation.

29. Freezing: The change of state from liquid to solid is called freezing.

30. Freezing is the reverse of melting or fusion.

31. Sublimation: Sublimation involves direct conversion of a solid into the gaseous state on heating and vice-versa.

32. Dry ice sublimes at -78 °C (195 K).

33. Camphor, ammonium chloride, iodine and naphthalene are some substances which undergo sublimation.

34. Effect of Change of Pressure

In the gaseous state, the interparticle spaces are very large and attractive forces between the particles are negligible. Because of large interparticle space, gases are highly compressible. When pressure is applied on a gas, enclosed in a cylinder, its molecules move closer and the gas undergoes appreciable compression. As the molecules move closer, the attractive forces between the molecules increase. At a sufficiently high pressure, the gas changes into liquid.

(i) Solid CO₂ is stored under high pressure. At a pressure of 1 atmosphere, solid CO₂ changes directly into gas without passing through the liquid state. Solid CO₂ is known as dry ice. Thus, we can conclude that we can liquefy gas by applying pressure and reducing temperature.

(ii) Change in volume from gaseous state to liquid state is very large whereas change in volume from liquid state to solid state is very small (negligible). This is due to the reason that in liquid the interparticle spaces are very small in a liquid.

(iii) Atmospheric pressure: The pressure exerted by the atmosphere or air is called atmospheric pressure. It decreases with increase in height.

(iv) Atmosphere (atm) is a unit of pressure.

(v) The SI unit of pressure is pascal (pa).
1 atm = 1.01 x 10⁵pa
1 bar = 1 x 10⁵ pa 1
bar = 1.01 atm.

(vi) Evaporation: The phenomenon of change of a liquid into vapour at any temperature below its boiling point is called evaporation.

(vii) Particles of matter possess kinetic energy. At a particular temperature, in a sample of liquid all the particles do not have same kinetic energy. There is a small fraction of molecule which has enough kinetic energy to overcome the attractive forces of other particles. If such a particle happens to come near the surface, it escapes into vapour state and evaporation takes place.

35. Factors Affecting the Rate of evaporation

(i) Surface area: Evaporation is a surface phenomenon, i.e., only the particles on the surface of the liquid gets converted into vapour. Thus, greater is the surface area, more is the rate of evaporation. For example, clothes dry faster when they are well spread out.

(ii) Increase in temperature: The rate of evaporation increases with increase in temperature. At higher temperature greater number of particles have enough kinetic energy to escape into the vapour state. For example, clothes dry faster in summer than in winter.

(iii) Decrease in humidity: The amount of water vapour present in air is referred to as humidity. The air cannot hold more than a definite amount of water vapour at a given temperature. If the humidity is more, the rate of evaporation decreases. For example, clothes do not dry easily during rainy season because the rate of evaporation is less due to high moisture content in the air.

(iv) Increase in the speed of the wind: With the increase in wind speed, the particles of water vapour move away with the wind, decreasing the amount of water vapour in the surrounding. For example, wet clothes dry faster on a windy day.

(v) Nature of liquid: Different liquids have different rates of evaporation. A liquid having weaker interparticle attractive forces evaporates at a faster rate because less energy is required to overcome the attractive forces. For example, acetone evaporates faster than water.

(vi) Evaporation causes cooling: Only the liquid particles having high kinetic energy leave the surface of the liquid and get converted into vapour. As a result, the average kinetic energy of the remaining particles of the liquid decreases and hence the temperature falls. Thus, evaporation causes cooling.

Class 9 Science Chapter 1 Notes Important Terms

Melting Point: It is the temperature at which a solid changes into liquid at atmospheric pressure.

Freezing point: The temperature at which a liquid freezes to become a solid at atmospheric pressure is called the freezing point.

Boiling point: The temperature at which a liquid starts boiling at atmospheric pressure is called its boiling point.

Latent heat of vapourisation: The amount of heat energy that is required to change 1 kg of liquid into vapour at atmospheric pressure at its boiling point is called latent heat of vapourisation.

Condensation: The process of changing a gas (or vapour) to a liquid by cooling is called condensation. Sublimation: Sublimation involves direct conversion of a solid into the gaseous state on heating and vice-versa.

Latent heat: The hidden heat which breaks the force of attraction between the molecules is known as latent heat.

Latent heat of fusion: The heat of energy required to convert 1 kg of a solid into liquid at atmospheric pressure, as its melting point, is known as latent heat of fusion.

Boiling: Boiling is a bulk phenomenon. Particles from the bulk (whole) of the liquid change into vapour state.

Evaporation: Evaporation is a surface phenomenon. Particles from the surface gain enough energy to overcome the force of attraction present in the liquid and change into vapour state.

On this page, you will find Number Systems Class 9 Notes Maths Chapter 1 Pdf free download. CBSE NCERT Class 9 Maths Notes Chapter 1 Number Systems will seemingly help them to revise the important concepts in less time.

CBSE Class 9 Maths Chapter 1 Notes Number Systems

Number Systems Class 9 Notes Understanding the Lesson

1. Number: A number is a mathematical object which is used in counting and measuring.

2. Number system: A number system defines a set of values used to represent a quantity.

3. Natural numbers: A set of counting numbers is called the natural numbers.
N = {1,2, 3, 4, 5,…}
These are infinite in number. Here first natural number is 1 whereas there is no last natural number.

4. Whole numbers: A set of natural numbers including zero is called the whole numbers.
W = {0, 1, 2, 3, 4, 5,…}

Note: All natural numbers are whole numbers but all whole numbers are not natural numbers.
Integers: A set of all whole numbers including negative of all the natural numbers.
Z = {…, – 7, – 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, 5, 6, 7, …}

5. Rational Numbers
A number is called rational number if it can be expressed in the form of \(\frac{p}{q}\), where p and q are integers and q≠ 0.
Example: \(\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{7}{9}, \text { etc. }\)

Note:

• Every fractional number and integer is a rational number because they can be expressed in the form\(\frac{p}{q}\)
• Between two rational numbers, infinite number of rational numbers can be possible. A rational number between two rational numbers a and b can be found as \(\frac{1}{2}\)(a + b)by using mean method.
• The sum, difference and product of the rational numbers is always a rational number.
• The quotient of a division of one rational number by a non-zero rational number is a rational number.

6. Types of Rational Numbers
1. The natural numbers form a subset of the integers.
2. Natural numbers with zero are referred to as non-negative integers.
3. The natural numbers without zero are known as positive integers.
4. When negative of a positive integer is added to the corresponding positive integer then it produces 0.

• Terminating decimal: It has a finite number of digits after the decimal point.
  \(\frac{3}{8}\)=0.375
• Non-terminating recurring decimal or repeating decimal: It has a digit or group of digits after the decimal point that repeat endlessly.
  

7. Irrational Numbers
Those numbers which cannot be expressed in the form of \(\frac{p}{q}\), where p and q are integers and
q ≠0. They neither terminate nor do they repeat. They are also known as non-terminating non-repeating numbers. Example: \(\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}, \sqrt{13}, \sqrt{\frac{7}{3}}, \ldots 5+\sqrt{7}\) are irrational numbers.
An irrational number between two rational numbers a and b can be found as the square root of their product \(\sqrt{a b}\)

Note:

• Euler’s number ‘e’ is an irrational whose first few digits are 2.71828….
• The sum, difference, multiplication and division of irrational numbers are not always irrational.
• Rational number and irrational number can be represented on a number line.
• Irrational numbers like \(\sqrt{2}, \sqrt{3}, \sqrt{5}\) etc. can be represented on a number line by using Pythagoras theorem.

8. Number line: A number line is a line which represent all the numbers. It is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point.

9. Real Numbers”
The union of the set of rational numbers and the set of irrational numbers.
A group of rational or irrational numbers is called real numbers. It can be represented on a number line.

10. Successive Magnification

• Let us suppose we locate 4.46 on the number line. We know 4.46 lies between 4 and 5.
• Now let us divide the portion between 4 and 5 into 10 equal parts and represent 4.1, 4.2, 4.3, …, 4.9.
• We know that 4.46 lies between 4.4 and 4.5 so further divide the portion into 10 equal parts, then these points will represent 4.41, 4.42, 4.43, …, 4.49 on number line. Thus we can locate the given number 4.46 on the number line.

NCERT Class 9 Maths Notes Pdf free download provided gives you an overview of the respective chapter and prepared in a manner that every concept is covered as per the syllabus guidelines. NCERT Notes for Class 9 Maths Standard are very effective for students to have last minute quick revision. Download the required study material from the resources available here and score higher grades in your exams.

CBSE Class 9 Maths Notes

1. Number Systems Class 9 Notes
2. Polynomials Class 9 Notes
3. Introduction to Euclid’s Geometry Class 9 Notes
4. Lines and Angles Class 9 Notes
5. Triangles Class 9 Notes
6. Coordinate Geometry Class 9 Notes
7. Heron’s Formula Class 9 Notes
8. Linear Equations in Two Variables Class 9 Notes
9. Quadrilaterals Class 9 Notes
10. Areas of Parallelograms and Triangles Class 9 Notes
11. Circles Class 9 Notes
12. Constructions Class 9 Notes
13. Surface Areas and Volumes Class 9 Notes
14. Statistics Class 9 Notes
15. Probability Class 9 Notes

We believe the information shared regarding the NCERT Notes for Class 9 Maths & Study Material has aided in your preparation. If you need any further assistance do leave us a comment and we will get back to you at the earliest possible. Stay tuned to our site for more information on Class 9th Maths Notes, Study Materials, and other preparation related stuff.