Category: CBSE Class 9

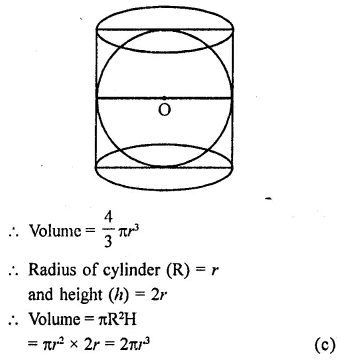
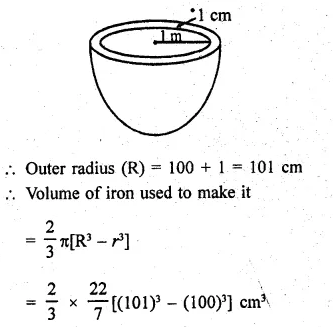
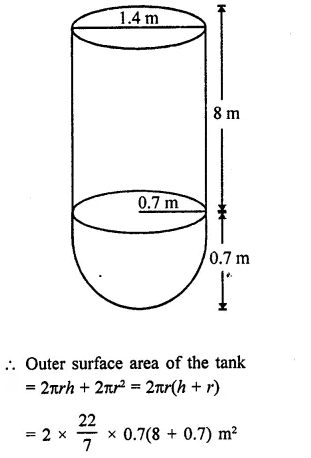
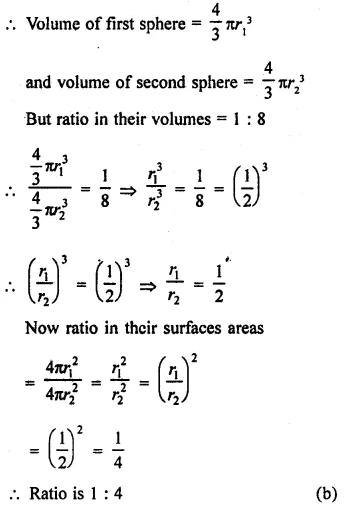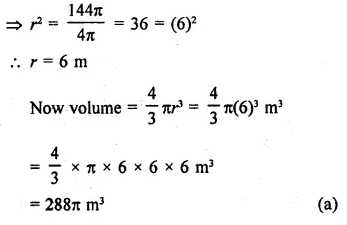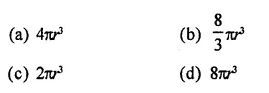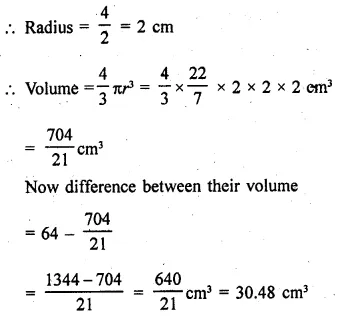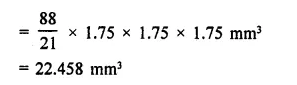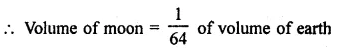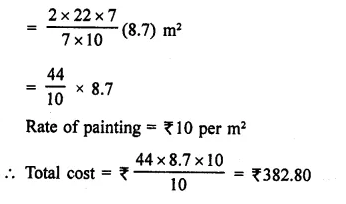RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1
• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.2
• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data MCQS

Question 1.
Define cumulative frequency distribution.
Solution:
Cumulative frequency : In a discrete frequency distribution, the cumulative frequency of a particular value of the variable is the total of all the frequencies of the values of the variable which are less than or equal to the particular value.

Question 2.
Explain the difference between a frequency distribution and a cumulative frequency distribution.
Solution:
The number of times an observation occurs in the given data, is called frequency of the
observation while a cumulative frequency of a particular value of the variable is the total of all the frequencies of the values of the variable which are less than or equal to the particular value.

Question 3.
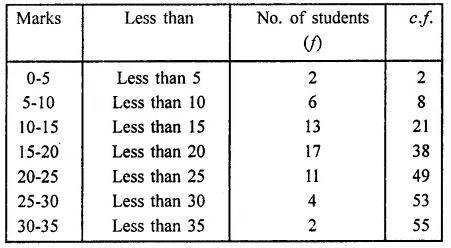
The marks scored by 55 students in a test are given below:

Prepare a cumulative frequency table.
Solution:
Cumulative frequency table is given below:

Question 4.
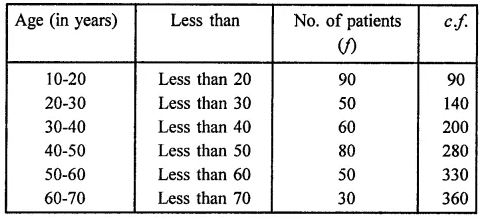
Following are the ages of 360 patients getting medical treatment in a hospital on a day:

Construct a cumulative frequency distribution.
Solution:
Cumulative frequency distribution table (less than) is given below:

Question 5.
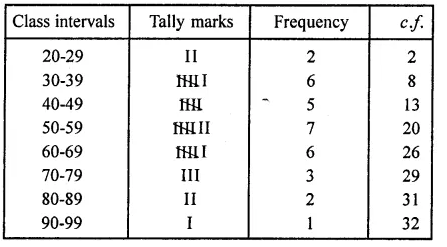
The water bills (in rupees) of 32 houses in a certain street for the period 1.1.98 to 31.3.98 are given below:
56, 43, 32, 38, 56, 24, 68, 85, 52, 47, 35, 58, 63, 74, 27, 84, 69, 35, 44, 75, 55, 30, 54, 65, 45, 67, 95, 72, 43, 65, 35, 59.
Tabulate the data and present the data as a cumulative frequency table using 70-79 as one of the class intervals.
Solution:
Highest bill = 95 Lowest bill = 24
Range = 95 – 24 = 71
Cumulative frequency table is given below:

Question 6.
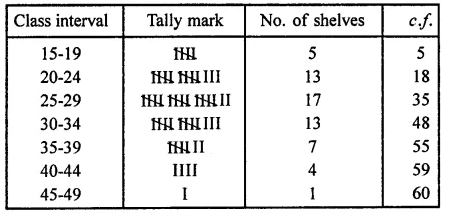
The number of books in different shelves of a library are as follows:
30, 32, 28, 24, 20, 25, 38, 37, 40, 45, 16, 20, 19, 24, 27, 30, 32, 34, 35, 42, 27, 28, 19, 34,
38, 39, 42, 29, 24, 27, 22, 29, 31, 19, 27, 25, 28, 23, 24, 32, 34, 18, 27, 25, 37, 31, 24, 23,
43, 32, 28, 31, 24, 23, 26, 36, 32, 29, 28, 21.
Prepare a cumulative frequency distribution table using 45-49 as the last class interval.
Solution:
Greatest number = 43
Lowest number =16
Range = 43 – 16 = 27
Cumulative frequency table is given below:

Question 7.
Given below are the cumulative frequencies showing the weights of 685 students of a school. Prepare a frequency distribution table.

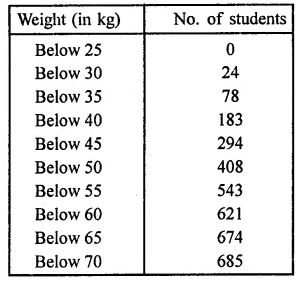
Solution:
The frequency table of the given cumulative frequency is given below:

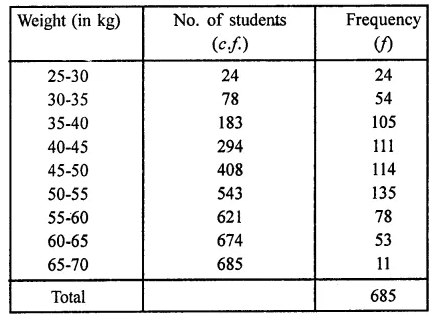
Question 8.
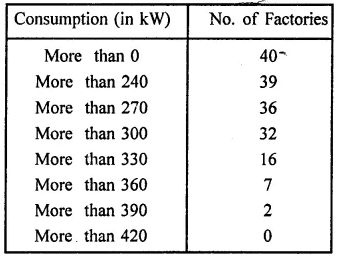
The following cumulative frequency distribution table shows the daily electricity consumption (in kW) of 40 factories in an industrial state:

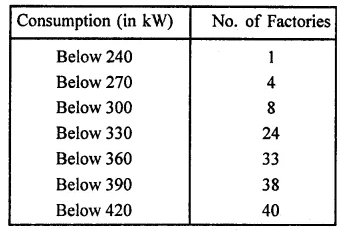
(i) Represent this as a frequency distribution table.
(ii) Prepare a cumulative frequency table.
Solution:
(i) The frequency distribution table is given below:

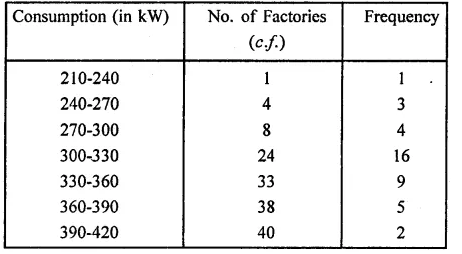
(ii) Now cumulative frequency table (more then)

Question 9.
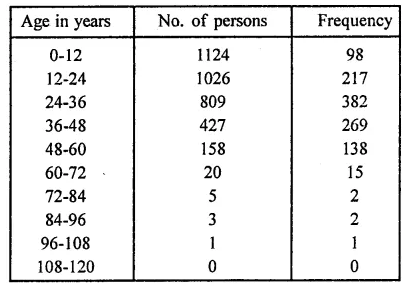
Given below is a cumulative frequency distribution table showing the ages of people living in a locality.

Prepare a frequency distribution table.
Solution:
Frequency distribution table is given below:

Hope given RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 25 Data Handling III (Pictorial Representation of Data as Pie Charts or Circle Graphs) Ex 25.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 25 Data Handling III Ex 25.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 25 Data Handling III Ex 25.1
• RD Sharma Class 8 Solutions Chapter 25 Data Handling III Ex 25.2

Question 1.
The number of hours, spent by a school boy on different activities in a working day, is given below:

Present the information in the form of a pie-chart .
Solution:
Total = 24

Now we draw a circle and divide it in the sectors having above central angles as shown in the figure.

Question 2.
Employees of a company have been categorized according to their religions as given below:

Draw a pie-chart to represent the above information.
Solution:
Total =1080

Now draw a circle and divided it into sectors having the above central angles as shown in the figure.

Question 3.
In one day the sales (in rupees) of different items of a baker’s shop are given below :

Draw pie-chart representing the above sales.
Solution:
Total = 480


Now draw a circle and divide it into sectors having the above central angles as shown in the figure.

Question 4.
The following data shows the expenditure of a person on different items during a month. Represent the data by a pie-chart.

Solution:
Total = 10800

Now we draw a circle and divide it into sector having the above central angles as shown in figure.

Question 5.
The percentages of various categories of workers in a state are given in the following table:

Present the information in the form of a pie-chart.
Solution:
Total = 100

Now, we draw a circle and divide it into sectors having the above central angles as shown in the figure.

Question 6.
The following table shows the expenditure incurred by a publisher in publishing a book:

Present the above data in the form of a pie-chart.
Solution:
Total = 100% = 100

Now, we draw a circle and divide it into sectors having the above central angles as shown in the figure

Question 7.
Percentage of the different products of a village in a particular district are given below. Draw a pie-chart representing this information.

Solution:
Total = 100

Now, we draw a circle and divided it into sectors having the above central angles as shown in the figure.

Question 8.
Draw a pie-diagram for the following data of expenditure pattern in a family.

Solution:
Total =100


Now we draw a circle and divide it into sectors having the above central angles as shown in the figure.

Question 9.
Draw a pie-diagram of the areas of continents cf the world given in the following table :

Solution:
Total = 133.3

Now, we draw a circle and divide it into sectors having the above given central angles as shown in the figure.

Question 10.
The following data gives the amount spent of the construction of a house. Draw a pie diagram.

Solution:
Total = 300 (in thousands)

Now, we draw a circle and divide it into sectors having the above given central angles as shown in the figure.

Question 11.
The following table shows how a student spends his pocket money during the course of a month. Represent it by a pie-diagram.

Solution:
Total expenditure = 100


Now, we draw a circle and divide it into sectors having the above given central angles as shown in the figure.

Question 12.
Represent the following data by a pie-diagram :

Solution:
1. For family A
Total = 10000

Now, we draw a circle and divide it in sectors having the above central angles as shown in the figure.
(2) For family B
Total = 11680

Now, we draw a circle and divide it into sectors having the above central angles as shown in the figure.

Question 13.
Following data gives the break up of the cost of production of a book:

Draw a pie – diagram depicting the above information.
Solution:
Total = 100

Now, we draw a circle and divide it into sectors of above central angles as shown in the figure.

Question 14.
Represent the following data with the help of pie-diagram.

Solution:
Total = 6000 tons

Now, we draw a circle and divide it into sectors having the above central angles as shown in the figure.

Question 15.
Draw a pie-diagram representing the relative frequencies (expressed as percentage) of the eight classes as given below :
12.6,18.2,17.5,20.3,2.8,4.2,9.8,14.7
Solution:
Total =100

Now, we draw a circle and divide it into sectors having the above central angles as shown in the figure given.

Question 16.
Following is the break up of the expenditure of a family on different items of consumption :

Draw a a pie – diagram to represent the above data.
Solution:
Total = Rs. 3000

Now, we draw a circle and divide it into sectors having the above central angles as shown in the figure.

Question 17.
Draw a pie-diagram for the following data of the investment pattern in five year plan :

Solution:
Total = 100


Now, we draw a circle and divide it into sectors having the above central angles as shown in the figure.

Hope given RD Sharma Class 8 Solutions Chapter 25 Data Handling III Ex 25.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS

Mark the correct alternative in each of the following:
Question 1.
In a sphere, the number of faces is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
Number of faces of a sphere is 1 (a)

Question 2.
The total surface area of a hemisphere of radius r is
(a) πr²
(b) 2πr²
(c) 3πr²
(d) 4πr²
Solution:
Total surface area of a hemisphere is 37πr² (c)

Question 3.
The ratio of the total surface area of a sphere and a hemisphere of same radius is
(a) 2 : 1
(b) 3 : 2
(c) 4 : 1
(d) 4 : 3
Solution:
Total surface area of a sphere = 4πr²
and total surface area of a hemisphere = 3m²
∴ Ratio 4πr²: 3πr²
= 4 : 3 (d)

Question 4.
A sphere and a cube are of the same height. The ratio of their volumes is
(a) 3 :4
(b) 21 : 11
(c) 4 : 3
(d) 11 : 21
Solution:
Let r be the height of a sphere and cube

Question 5.
The largest sphere is cut off from a cube of side 6 cm. The volume of the sphere will be
(a) 27π cm³
(b) 36π cm³
(c) 108π cm³
(d) 12π cm³
Solution:
Side of cube = 6 cm
∴ Diameter of sphere cut off from it = 6 cm

Question 6.
A cylmderical rod whose height is 8 times of its radius is melted and recast into spherical balls of same radius. The number of balls will be
(a) 4
(b) 3
(c) 6
(d) 8
Solution:
Let r be the radius of a cylindrical rod = r
Then its height (h) = 8r
Volume = πr²h = πr² x 8r = 8πr³
Radius of spherical ball = r

Question 7.
If the ratio of volumes of two spheres is 1 : 8, then the ratio of their surface areas is
(a) 1 : 2
(b) 1 : 4
(c) 1 : 8
(d) 1 : 16
Solution:
Let r₁ and r₂ be the radius of two spheres

Question 8.
If the surface area of a sphere is 144π m² then its volume (in. m3) is
(a) 288π
(b) 316π
(c) 300π
(d) 188π
Solution:
Surface area of a sphere = 144π m²
Let r be the radius, then
4πr² = 144π

Question 9.
If a solid sphere of radius 10 cm is moulded into 8 spherical solid balls of equal radius, then the surface area of each ball (in sq. cm) is
(a) 100π
(b) 75π
(c) 60π
(d) 50π
Solution:
Radius of a sphere (r) = 10 cm

Question 10.
If a sphere is inscribed in a cube, then the ratio of the volume of the sphere to the volume of the cube is
(a) π : 2
(b) π : 3
(c) π : 4
(d) π : 6
Solution:
Let side of a cube = a
Then volume of cube = a³
The diameter of inscribed sphere = a

Question 11.
If a solid sphere of radius r is melted and cast into the shape of a solid cone of height r, then the radius of the base of the cone is
(a) 2r
(b) 3r
(c) r
(d) 4r
Solution:
Radius of a sphere = r

Question 12.
A sphere is placed inside a right circular cylinder so as to touch the top, base and lateral surface of the cylinder. If the radius of the sphere is r, then the volume of the cylinder is

Solution:
Radius of sphere = r

Question 13.
The ratio between the volume of a sphere and volume of a circumscribing right circular cylinder is
(a) 2 : 1
(b) 1 : 1
(c) 2 : 3
(d) 1 : 2
Solution:
Let r be the radius of the sphere, then 4
Volume = \(\frac { 4 }{ 3 }\)πr³
Diameter of circumscribed cylinder = 2r
∴ Radius = r
and height (h) = 2r

Question 14.
A cone and a hemisphere have equal bases and equal volumes the ratio of their heights is
(a) 1 : 2
(b) 2 : 1
(c) 4 : 1
(d) \(\sqrt { 2 } \) : 1
Solution:
Let radius of hemisphere and a cone be r

Question 15.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is
(a) 1 : 2 : 3
(b) 2 : 1 : 3
(c) 2 : 3 : 1
(d) 3 : 2 : 1
Solution:
∵ Bases of a cone, hemisphere and a cylinder are same
Let radius of each = r
and height of each = r

Hope given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS

Question 1.
Find the surface area of a sphere of radius 14 cm.
Solution:
Radius of a sphere (r) = 14 cm
∴ Surface area = 4πr² = 4 x \(\frac { 22 }{ 7 }\) x 14 x 14 cm²
= 2464 cm³

Question 2.
Find the total surface afea of a hemisphere of radius 10 cm.
Solution:
Radius of hemisphere (r) = 10 cm
∴ Total surface area = 3πr²

Question 3.
Find the radius of a sphere whose surface area is 154 cm².
Solution:
Surface area of a sphere = 154 cm²

Question 4.
The hollow sphere, in which the circus motor cyclist performs his stunts, has a diameter of 7 m. Find the area available to the motor cyclist for riding.
Solution:
Diameter of hollow sphere = 7 m

Question 5.
Find the volume of a sphere whose surface area is 154 cm².
Solution:
Surface area of a sphere = 154 cm²

Question 6.
How many spherical bullets can be made out of a solid cube of lead whose edge measures 44 cm, each bullet being 4 cm in diameter?
Solution:
Edge of a solid cube = 44 cm
∴ Volume = a² = (44)² cm²
= 44 × 44 × 44 cm³
Diameter of a spherical bullet = 4 cm

Question 7.
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
Solution:
Radius of a sphere (R) = 2r

Question 8.
If a hollow sphere of intefnal and external diameters 4 cm and 8 cm respectively melted into a cone of base diameter 8 cm, then find the height of the cone.
Solution:
Internal diameter of a hollow sphere = 4cm
∴ Internal radius = \(\frac { 4 }{ 2 }\) = 2 cm
Similarly the outer radius (R) = \(\frac { 8 }{ 2 }\) = 4 cm
∴ Volume of melted used in hollow sphere

Question 9.
The surface area of a sphere of radius 5 cm is five times the area of the curved surface of a cone of radius 4 cm. Find the height of the cone.
Solution:
Radius of a sphere (r) = 5 cm
∴ Surface area = 4πr²
= 4π x 5 x 5 = 100π cm²
Radius of cone (r₁) = 4 cm

Question 10.
If a sphere is inscribed in a cube, find the ratio of the volume of cube to the volume of the sphere.
Solution:
Let edge of a cube = a
Then its volume = a³
∵ A sphere is inscribed in the cube
∴ Diameter of sphere = a

Hope given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS

Question 1.
Find the volume of a sphere whose radius is
(i) 2 cm
(ii) 3.5 cm
(iii) 10.5 cm
Solution:
(i) Radius of sphere (r) = 2 cm

Question 2.
Find the volume of a sphere whose diameter is,
(i) 14 cm
(ii) 3.5 dm
(iii) 2.1 m
Solution:
(i) Diameter of a sphere = 14 cm

Question 3.
A hemspherical tank has inner radius of 2.8 m. Find its capacity in litres.
Solution:
Radius of hemispherical tank (r) = 2.8 m

Question 4.
A hemispherical bowl is made of steel 0.25 cm thick. The inside radius of the bowl is 5 cm. Find the volume of steel used in making the bowl.
Solution:
Thickness of steel = 0.25 cm = \(\frac { 1 }{ 4 }\)cm
Inside radius of the hemispherical bowl (r) = 5 cm
∴ Outer radius (R) = 5 + 0.25 = 5.25 cm
∴ Volume of the steel used = \(\frac { 1 }{ 4 }\)π(R³ – r³)

Question 5.
How many bullets can be made out of a cube of lead, whose edge measures 22 cm, each bullet being 2 cm in diameter?
Solution:
Edge of cube (r) = 22 cm
∴ Volume = a³ = (22)³ cm³
= 22 x 22 x 22 = 10648 cm³
Diameter of a bullet = 2 cm

Question 6.
A shopkeeper has one laddoo of radius 5 cm. With the same material how many laddoos of radius 2.5 cm can be made?
Solution:
Radius of bigger laddoo (R) = 5 cm

Question 7.
A spherical ball of lead 3 cm in diameter is melted and recast into three spherical balls. It the diameters of two balls be \(\frac { 3 }{ 2 }\) cm and 2 cm, find the diameter of the third ball.
Solution:
Diameter of a spherical ball of lead = 3 cm

Question 8.
A sphere of radius 5 cm is immersed in water filled in a cylinder, the level of water rises \(\frac { 5 }{ 3 }\) cm. Find the radius of the cylinder.
Solution:
Radius of sphere (r1) = 5 cm

Level of water rises in the cylinder after immersing the sphere in it
∴ Height of water level = \(\frac { 5 }{ 3 }\) cm
Let r be radius of the cylinder, then Volume of water = Volume of the sphere

Question 9.
If the radius of a sphere is doubled, what is the ratio of the volumes of the first sphere to that of the second sphere?
Solution:
Let r2 be the radius of the given sphere
then volume = \(\frac { 4 }{ 3 }\) πr³
By doubling the radius the radius of the new sphere = 2r

Question 10.
A vessel in the form of a hemispherical bowl is full of water. Its contents are emptied in a right circular cylinder. The internal radii of the bowl and the cylinder are 3.5 cm and 7 cm respectively. Find the height to which the water will rise in the cylinder.
Solution:
Radius of hemispherical bowl (r) = 3.5 cm

Question 11.
A cylinder whose height is two thirds of its diameter, has the same volume as a sphere of radius 4 cm. Calculate the radius of the base of the cylinder.
Solution:
Radius of a sphere (r) = 4 cm

Question 12.
A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of water in the cylinder.
Solution:
Radius of hemispherical bowl (r) = 6 cm

Question 13.
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross-section. If the length of the wire is 108 m, find its diameter.
Solution:
Diameter of a copper sphere = 18 cm

Question 14.
The diameter of a sphere is 6 cm. It is melted and drawn into a wire of diameter 0.2 cm. Find the length of the wire.
Solution:
Diameter of a sphere = 6 cm

Question 15.
The radius of the internal and external surfaces of a hollow spherical shell are 3 cm and 5 cm respectively. If it is melted and recast into a solid cylinder of height 2 \(\frac { 2 }{ 3 }\) cm. Find the diameter of the cylinder.
Solution:
Internal radius of the hollow spherical shell (r) = 3 cm
and external radius (R) = 5 cm

Question 16.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Solution:
Radius of hemisphere (r) = 7 cm

Question 17.
A hollow sphere of internal and external radius 2 cm and 4 cm respectively is melted into a cone of base radius 4 cm. Find the height and slant height of the cone.
Solution:
Internal radius of a hollow sphere (r) = 2 cm
and external radius (R) = 4 cm
∴ Volume of the metal used

Question 18.
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones each of radius 3.5 cm and height 3 cm. Find how many cones are obtained.
Solution:
Radius of a metallic sphere (R) = 10.5 cm

Question 19.
A cone and a hemisphere have equal bases and equal volumes. Find the ratio Of their heights.
Solution:
Let r be the radius and h be the height of the cone, hemisphere

Question 20.
The largest sphere is carved out of a cube of side 10.5 cm. Find the volume of the sphere.
Solution:
By carving a largest sphere out of the cube, the diameter of the sphere = 10.5

Question 21.
A cube, of side 4 cm, contains a sphere touching its sides. Find the volume of the gap in between.
Solution:
Side of cube = 4 cm
∴ Volume = (side)³ = 4x4x4 = 64 cm³
Diameter of the largest sphere touching its sides = 4 cm

Question 22.
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1m, then find the volume of the iron used to make the tank. (NCERT)
Solution:
Thickness of hemispherical tank = 1 cm
Inner radius (r) = 1 m = 100 cm

Question 23.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule? (NCERT)
Solution:
Diameter of a medicine spherical capsule = 3.5 mm

Question 24.
The diameter of the moon is approximately one fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon? (NCERT)
Solution:

Question 25.
A cone and a hemisphere have equal bases and equal volumes. Find the ratio in their heights.
Solution:
Let r be the radius of cone and hemisphere and let h be the height of the cone then

Question 26.
A cylindrical tub of radius 16 cm contains water to a depth of 30 cm. A spherical iron ball is dropped into the tub and thus level of water is raised by 9 cm. What is the radius of the ball?
Solution:
Radius of cylinderical tub (r) = 16 cm
Height of water in it (h) = 30 cm

Question 27.
A cylinder of radius 12 cm contains water to a depth of 20 cm. A spherical iron ball is dropped into the cylinder and thus the level of water is raised by 6.75 cm. Find the radius of the ball. (Use π = 22/7).
Solution:
Radius of cylinder (r) = 12 cm
Depth of water in it (h) = 20 cm
By dropping a ball, the water level rose by 6.75 cm

Question 28.
A cylindrical jar of radius 6 cm contains oil. Iron spheres each of radius 1.5 cm are immersed in the oil. How many spheres are necessary to raise the level of the oil by two centimetres?
Solution:
Radius of cylinderical jar (r) = 6 cm
Level of oil in it (h) = 2 cm

Question 29.
A measuring jar of internal diameter 10 cm is partially filled with water. Four equal spherical balls of diameter 2 cm eacfy are dropped in it and they sink down in water completely. What will be the change in the level of water in the jar?
Solution:
Diameter of measuring jar = 10 cm

Now after swing the ball in the water of jar Let volume of water raised, by h cm

Question 30.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2:3.
Solution:
∵ Bases and heights of a cones hemisphere and a cylinder are equal
Let r be the radius and h be their heights

Question 31.
A cylinderical tub of radius 12 cm contains water to a depth of 20 cm. A spherical form ball is dropped into the tub and thus the level of water is raised by 6.75 cm. What is the radius of the ball?
Solution:
Radius of the cylinderical tub (r) = 12 cm
Depth of water in it (h) = 20 cm
By dropping a spherical ball in it, the water raised by 6.75 cm

Question 32.
A sphere, a cylinder and a cone have the same diameter. The height of the cylinder and also the cone are equal to the diameter of the sphere. Find the ratio of their volumes.
Solution:
Diameter of a sphere, cylinder and a cone are equal
Let each as diameter = 2r
Then radius of each = r
Height of cylinder = diameter = 2r
and height of cone = 2r
Now volume of sphere = \(\frac { 4 }{ 3 }\)πr³
Volume of cylinder = πr²h

Hope given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS

Question 1.
Find the surface area of a sphere of radius.
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
Solution:
In a sphere,
(i) Radius (r) = 10.5 cm
Surface area = 4πr²

Question 2.
Find the surface area of a sphere of diameter
(i) 14 cm
(ii) 21 cm
(iii) 3.5 cm
Solution:
(i) Diameter of a sphere = 14 cm
Radius (r) = \(\frac { 14 }{ 2 }\) = 7 cm

Question 3.
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm. [Use π = 3.14]
Solution:
(i) Radius of hemisphere = 10 cm
∴ Total surface area of hemisphere = 2πr²
= 2 x 3.14 x 10 x 10 cm²
= 628 cm²
(ii) Total surface area of solid hemisphere
= 3πr² = 3 x 3.14 x 10 x 10 cm²
= 942 cm²

Question 4.
The surface area of a sphere in 5544 cm², find the diameter.
Solution:
Let r be the radius of a sphere, then Surface area = 4πr²

Question 5.
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹4 per 100 cm². [NCERT]
Solution:
Inner diameter of a hemispherical bowl = 10.5 cm

Question 6.
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of painting it at the rate of ₹2 per sq. m.
Solution:
Radius of dome (hemispherical) = 63 dm
Area of curved surface

Question 7.
Assuming the earth to be a sphere of radius 6370 km, how many square kilometres is area of the land, if three-fourth of the earth’s surface is covered by water?
Solution:
Radius of earth (sphere) = 6370 km
Water on the earth = \(\frac { 3 }{ 4 }\) % total area

Question 8.
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved surface area of the shape if the length of the shape be 7 cm.
Solution:
Total height of the so formed shape = 7 cm

Question 9.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Solution:
Diameter of moon = \(\frac { 1 }{ 4 }\) of diameter of earth
Let radius of earth = r km
Then radius of moon = \(\frac { 1 }{ 4 }\) r km
Now surface area of earth = 4πr²

Question 10.
A hemi-spherical dome of a building needs to be painted. If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is ₹5 per 100 cm². [NCERT]
Solution:
Circumference of the base of dome (r) = 17.6 m

Question 11.
A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 16 cm and its height is 15 cm. Find the cost of painting the toy at ₹7 per 100 cm².
Solution:
Diameter of toy = 16 cm
Radius (r) = \(\frac { 16 }{ 2 }\) = 8 cm
Height of conical part (h) = 15 cm

Question 12.
A storage tank consists of a circular cylinder with a hemisphere adjoined on either end. If the external diameter of the cylinder be 1.4 m and its length be 8 m, find the cost of painting it on the outside at the rate of ₹10 per m².
Solution:
Diameter of the tank = 1.4 m
∴ Radius (r) = \(\frac { 1.4 }{ 2 }\) m = 0.7 m
and height of cylindrical portion = 8m

Question 13.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in the figure. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm². [NCERT]

Solution:
Diameter of each spheres = 21 cm
∴ Radius (R) = \(\frac { 21 }{ 2 }\) cm
Radius of each cylinder (r) = 1.5 cm
and height (h) = 7 cm

Now surface area of one sphere = 4πR²

Hope given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Mark the correct alternative in each of the following:
Question 1.
The number of surfaces of a cone has, is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
Number of surfaces of a cone are 2 (b)

Question 2.
The area of the curved surface of a cone of radius 2r and slant height \(\frac { 1 }{ 2 }\), is

Solution:
Radius of a cone = 2r

Question 3.
The total surface area of a cone of radius \(\frac { r }{ 2 }\) and length 2l, is

Solution:

Question 4.
A solid cylinder is melted and cast into a cone of same radius. The heights of the cone and cylinder are in the ratio
(a) 9 : 1
(b) 1 : 9
(c) 3 : 1
(d) 1 : 3
Solution:
Let r be the radius and h be the height of cylinder, then volume = πr²h
Now volume of cone = πr²h
r is the radius

Question 5.
If the radius of the base of a right circular cone is 3r and its height is equal to the radius of the base, then its volume is

Solution:
Radius of the base of a cone (R) = 3r
and height (H) = 3r

Question 6.
If the volumes of two cones are in the ratio 1 : 4 and their diameters are in the ratio 4 : 5, then the ratio of their heights, is
(a) 1 : 5
(b) 5 : 4
(c) 5 : 16
(d) 25 : 64
Solution:
Ratio in the volumes of two cones =1:4
and ratio in their diameter = 4:5
Let h₁, h₂ be their heights

Question 7.
The curved surface area of one cone is twice that of the other while the slant height of the latter is twice that of the former. The ratio of their radii is
(a) 2 : 1
(b) 4 : 1
(c) 8 : 1
(d) 1 : 1
Solution:
Let r be the radius and l be the slant height
∴ Curved surface area of first cone = πr₁l₁
and let curved surface area of second cone = πr₂l₂

Question 8.
If the height and radius of a cone of volume V are doubled, then the volume of the cone, is
(a) 3V
(b) 4V
(c) 6V
(d) 8V
Solution:
Let r and h be the radius and height of a cone, then

Question 9.
The ratio of the volume of a right circular cylinder and a right circular cone of the same base and height, is
(a) 1 : 3
(b) 3 : 1
(c) 4 : 3
(d) 3 : 4
Solution:
Let r be the radius and h be the height of a right circular cylinder and a right circular cone, and V₁ and V₂ are their volumes, the V₁ =  πr²h and

Question 10.
A right cylinder and a right circular cone have the same radius and same volumes. The ratio of the height of the cylinder to that of the cone is
(a) 3 : 5
(b) 2 : 5
(c) 3 : 1
(d) 1 : 3
Solution:
Let r be the radius of cylinder and cone and volumes are equal
and h₁, and h₂ be their have h₂ is respectively

Question 11.
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, the ratio of their curved surface areas, is
(a) 4 : 5
(b) 25 : 16
(c) 16 : 25
(d) 5 : 4
Solution:
∵ Diameters of two cones are equal
∴ Their radii are also be equal
Let r be their radius of each cone,
and ratio in their slant heights = 5:4
Let slant height of first cone (h₁) = 5x
Then height of second cone (h₂) = 4x

Question 12.
If the heights of two cones are in the ratio of 1 : 4 and the radii of their bases are in the ratio 4 : 1, then the ratio of their volumes is
(a) 1 : 2
(b) 2 : 3
(c) 3 : 4
(d) 4 : 1
Solution:
Ratio in the heights of two cones =1 : 4
and ratio in their radii of their bases = 4 : 1
Let height of the first cone = x
and height of the second cone = 4x
Radius of the first cone = 4y
and radius of the second cone = y

Question 13.
The slant height of a cone is increased by 10%. If the radius remains the same, the curved surface area is increased by
(a) 10%
(b) 12.1%
(c) 20%
(d) 21%
Solution:
Let r be radius and l be the slant height of a cone, then curved surface area = πrl
If slant height is increased by 10%, then

Question 14.
The height of a solid cone is 12 cm and the area of the circular base is 6471 cm². A plane parallel to the base of the cone cuts through the cone 9 cm above the vertex of the cone, the area of the base of the new cone so formed is
(a) 9π cm²
(b) 16π cm²
(c) 25π cm²
(d) 36π cm²
Solution:
Height of a solid cone (h) = 12 cm
Area of circular base = 64π cm²

Question 15.
If the base radius and the height of a right circular cone are increased by 20%, then the percentage increase in volume is approximately
(a) 60
(b) 68
(c) 73
(d) 78
Solution:
In first case,
Let r be radius and h be height, in volume

Question 16.
If h, S and V denote respectively the height, curved surface area and volume of a right circular cone, then 3πVh³ – S2h² + 9V² is equal to
(a) 8
(b) 0
(c) 4π
(d) 32π²
Solution:
h = height, S = curved surface area
V = volume of a cone
Let r be the radius of the cone, then

Question 17.
If a cone is cut into two parts by a horizontal plane passing through the mid¬point of its axis, the ratio of the volumes of upper and lower part is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 7
(d) 1 : 8
Solution:
∴ ∆PDC ~ ∆PBA (AA axiom)
and O’ is mid point of PO

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.