Category: CBSE Class 9

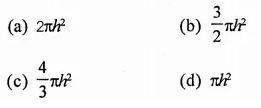
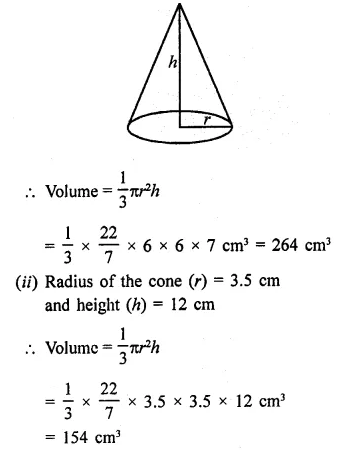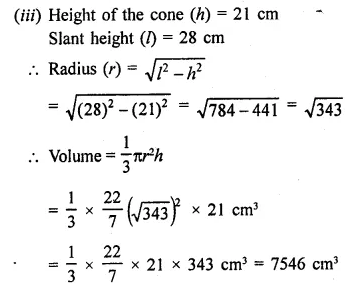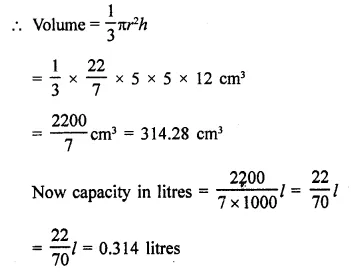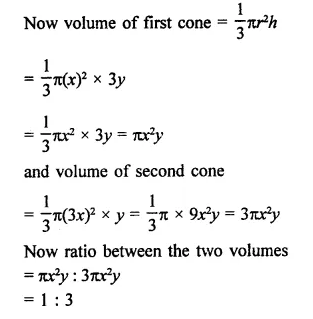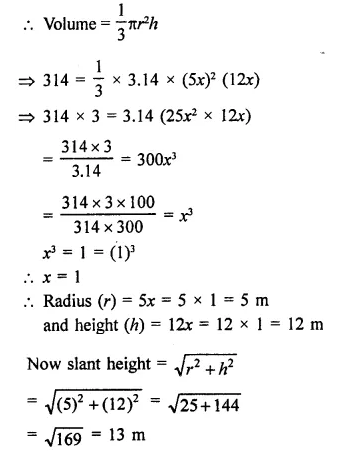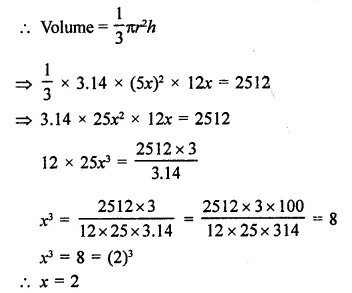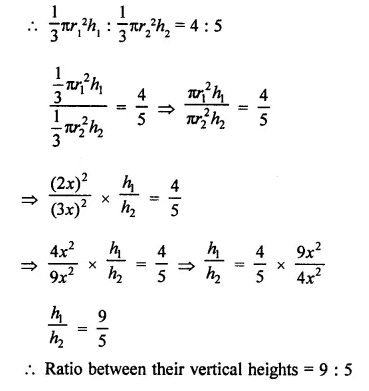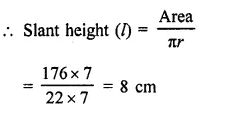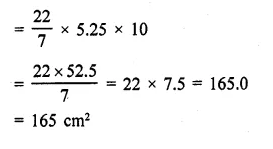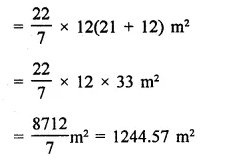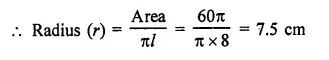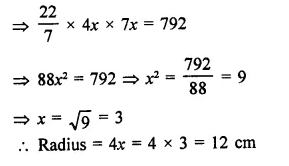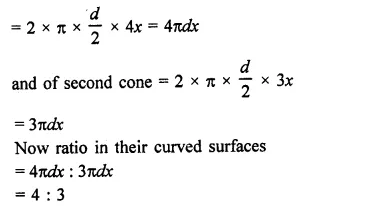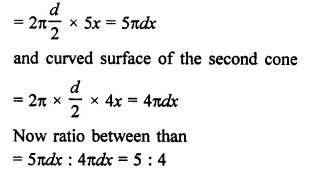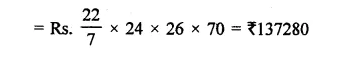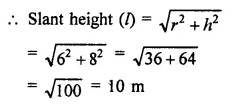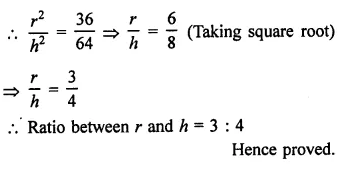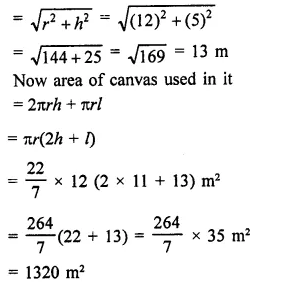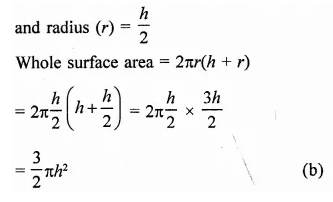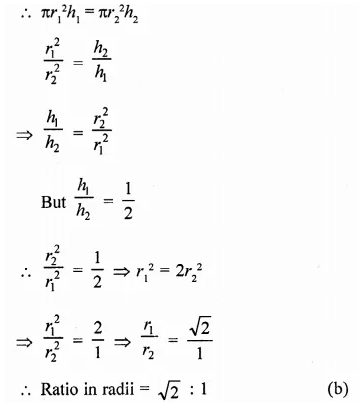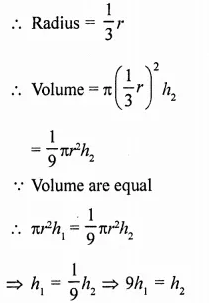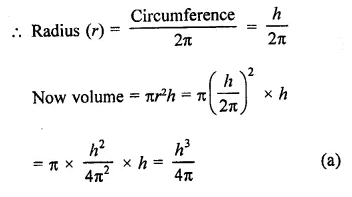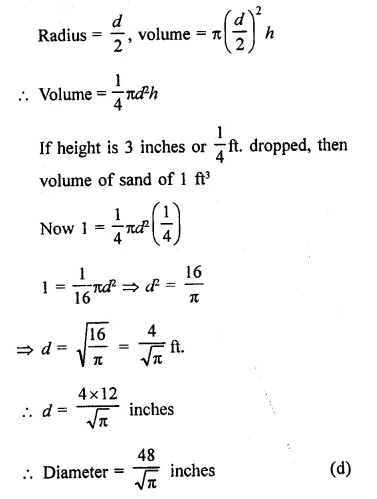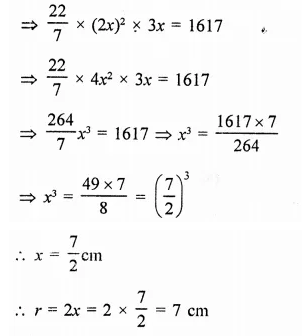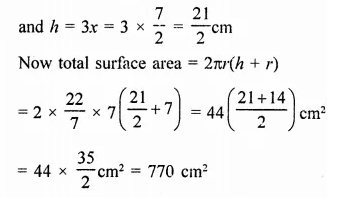RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

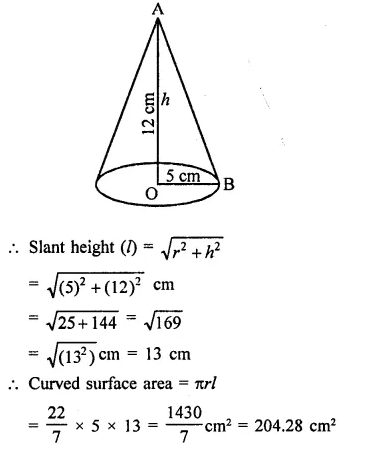
Question 1.
The height of a cone is 15 cm. If its volume is 500π cm³, then find the radius of its base.
Solution:
Volume of cone = 500π cm³
and height (h) = 15 cm

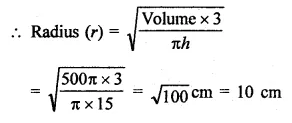
Question 2.
If the volume of a right circular cone of height 9 cm is 48π cm³, find the diameter of its base.
Solution:
Volume of a cone = 48π cm³
Height (h) = 9 cm

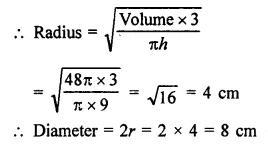
Question 3.
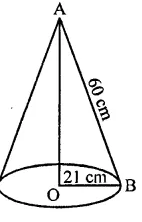
If the height and slant height of a cone are 21 cm and 28 cm respectively. Find its volume.
Solution:
Height of a cone (h) = 21 cm
and slant height (l) = 28 cm

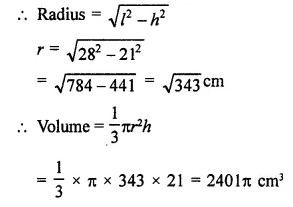
Question 4.
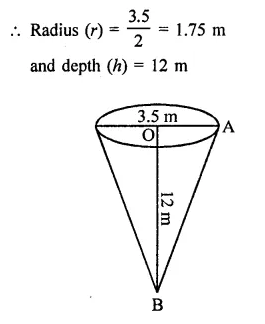
The height of a conical vessel is 3.5 cm. If its capacity is 3.3 litres of milk. Find the diameter of its base.
Solution:
Capacity of conical vessel = 3.3 litres
Volume = 3.3 m³
= 3.3 x 1000 = 3300 cm²

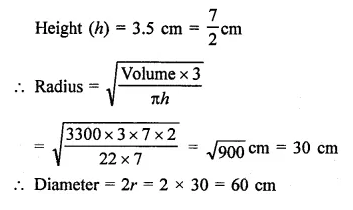
Question 5.
If the radius and slant height of a cone are in the ratio 7 : 13 and its curved surface area is 286 cm2, find its radius.
Solution:
Two ratio in radius and slant height of a cone = 7 : 13
Let radius (r) = 7x
and slant height (1) = 13x
Curved surface area = πrl

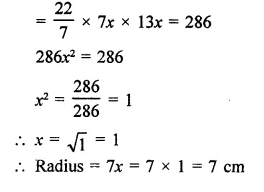
Question 6.
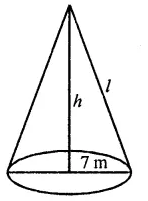
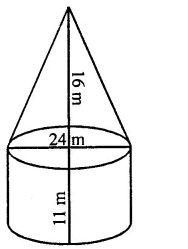
Find the area of canvas required for a conical tent of height 24 m and base radius 7 m.
Solution:
Base radius of the closed cone (r) = 7 cm
and vertical height (h) = 24 cm

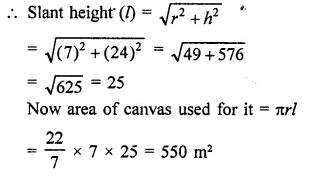
Question 7.
Find the area of metal sheet required in making a closed hollow cone of base radius 7 cm and height 24 cm. making a closed hollow cone of base radius 7 cm and height 24 cm.
Solution:
Base radius of the closed cone (r) = 7 cm
and vertical height (h) = 24 cm

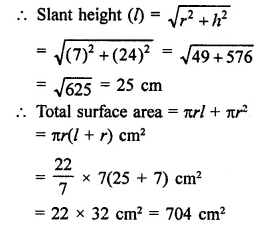
Question 8.
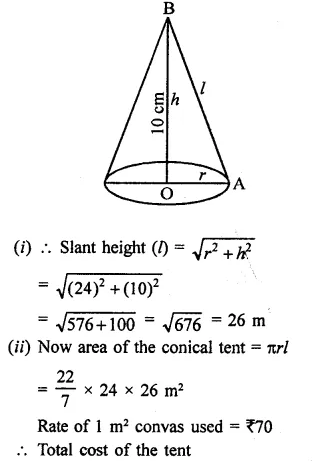
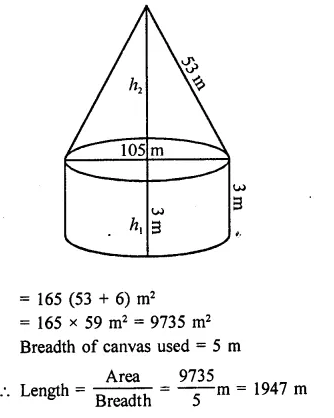
Find the length of cloth used in making a conical pandal of height 100 m and base radius 240 m, if the cloth is 100π m wide.
Solution:
Height of conical pandal (A) = 100 m
Base radius (r) = 240 m

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Question 1.
Find the volume of a right circular cone with:
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm
(iii) height 21 cm and slant height 28 cm. [NCERT]
Solution:
(i) Radius of a cone (r) = 6 cm
and height (h) = 7 cm

Question 2.
Find the capacity in litres of a conical vessel with:
(i) radius 7 cm, slant height 25 cm,
(ii) height 12 cm, slant height 13 cm. [NCERT]
Solution:
(i) Radius of the conical vessel (r) = 7 cm
Slant height (h) = 25 cm

Question 3.
Two cones have their heights in the ratio 1 : 3 and the radii of their bases in the ratio 3:1. Find the ratio of their volumes.
Solution:
Ratio in the heights of two cones =1:3
and ratio in their radii = 3: 1
Let radius of first cone (r₁) = x
and of second cone (r₂) = 3x
and height of first cone (h₁) = 3y
and of second cone (h₂)

Question 4.
The radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cubic metre, find the slant height and the radius (Use π = 3.14).
Solution:
Ratio in the radius and height of a cone = 5 : 12
Volume = 314 cm³
Let radius (r) = 5x
and height (h) = 12x

Question 5.
The radius and height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the slant height and radius of the cone. (Use π = 3.14).
Solution:
Ratio in the radius and height of a right circular cone = 5 : 12
Volume = 2512 cm³
Let radius (r) = 5x
Then height (h) = 12x

Question 6.
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
Solution:
Ratio in volumes of two cones = 4:5
and ratio in radii = 2:3
Let radius of the first cone (r₁) = 2x
Then radius of second cone (r₂) = 3x
Let h₁, h₂ be their heights respectively

Question 7.
Ratio between their vertical heights = 9:5 7. A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
Solution:
Let r be the radius and h be the height of a cylinder and a cone, then
Volume of cylinder = πr²h

Question 8.
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
Solution:
Let r be the radius and h be the height of the cone, then
Volume = \(\frac { 1 }{ 3 }\) πr²h
By halving the radius and same height the

Question 9.
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use π = 3.14). [NCERT]
Solution:
Diameter of conical heap of wheat = 9 m

Question 10.
Find the weight of a solid cone whose base is of diameter 14 cm and vertical height 51 cm, supposing the material of which it is made weighs 10 grams per cubic cm.
Solution:
Diameter of the base of solid cone = 14 cm
and vertical height (h) = 51 cm

Question 11.
A right angled triangle of which the sides containing the right angle are 6.3 cm and 10 cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
Solution:
Length of sides of a right angled triangle are 6.3 cm and 10 cm
By turning around the longer side, a cone is formed in which radius (r) = 6.3 cm
and height (h) = 10 cm

Question 12.
Find the volume of the largest right circular cone that can be fitted in a cube whose edge is 14 cm.
Solution:
Side of cube = 14 cm ,
Radius of the largest cone that can be fitted

Question 13.
The volume of a right circular cone is 9856 cm³. If the diameter of the base is 28 cm, find:
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone. [NCERT]
Solution:
Volume of a right circular cone = 9856 cm³
Diameter of the base = 28 cm

Question 14.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres? [NCERT]
Solution:
Diameter of the top of the conical pit = 3.5 m

Question 15.
Monica has a piece of Canvas whose area is 551 m². She uses it to have a conical tent made, with a base radius of 7 m. Assuming that all the stitching margins and wastage incurred while cutting, amounts to approximately 1 m². Find the volume of the tent that can be made with it. [NCERT]
Solution:
Area of Canvas = 551 m²
Area of wastage = 1 m²
Actual area = 551 – 1 = 550 m²
Base radius of the conical tent = 7 m

Let l be the slant height and h be the vertical

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1
• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.2
• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data MCQS

Question 1.
What do you understand by the word ‘statistics’ in (i) singular form, (ii) plural forms.
Solution:
The word ‘statistics’ is used in both its singular as well as its plural senses.
In singular sense, statistics piay be defined as the science of collection, presentation, analysis and interpretation of numerical data.
In plural sense, statistics means numerical facts or observations collected with definite purpose.
For example, income and expenditure of persons in a particular locality, number of males and females in a particular town are statistics.

Question 2.
Describe some fundamental characteristics of statistics.
Solution:
Statistics in plural sense have the following characteristics:
(i) A single observation does not form statistics. Statistics are a sum total of observations.
(ii) Statistics are expressed quantitatively and not qualitatively.
(iii) Statistics are collected with a definite purpose.
(iv) Statistics in an experiment are comparable and can be classified into various groups.

Question 3.
What are (i) primary data? (ii) secondary data? Which of the two – the primary or the secondary data – is more reliable and why?
Solution:
(i) Primary data : When an investigator collects the data himself with a definite plan Or design in his mind, it is called primary data.
(ii) Secondary data : Data which are not originally collected rather obtained from the published or unpublished, sources are called secondary data.
Primary data are reliable and relevent because they are original in character and are collected by some individuals or by some institutions or by research bodies.

Question 4.
Why do we group data?
Solution:
When the number of observations is large, then arranging data in ascending or descending order is tedius job and it does not tell us much except minimum or maximum(s) of data. So, to make it easily understandable and clear, we tabulate data in the form of a table.

Question 5.
Explain the meaning of the following terms:
(i) variate
(ii) class intervals
(iii) class size
(iv) class mark
(v) frequency
(vi) class limits
(vii) true class limits.
Solution:
(i) Variate : The observations of a data are called variate.
(ii) Class intervals : When the presentations of data in classes, or groups, then groups are called classes or class intervals.
(iii) Class size : The difference between upper limit and lower limit is called class size.
(iv) Class mark : The mean of lower limit and upper limit is called class mark or mid value. Therefore class mark
= \(\frac { lower limit + upper limit }{ 2 }\)
(v) Frequency : The number of times an observation occurs in the given data, is called frequency of that observation.
(vi) Class limits : Every class has two limits : lower limit and upper limit.
(vii) True class limits : Whenever inclusive method is used, it is necessary tp make an adjustment to determine the correct class intervals, and to have continuity. If a-b is a class in inclusive method, then in order to change it into exclusive method, it becomes
a – \(\frac { h }{ 2 }\) – b + \(\frac { h }{ 2 }\) where h = \(\frac { 1 }{ 2 }\) [lower limit of a class – upper limit of previous class]

Question 6.
The ages of ten students of a group are given below. The ages have been recorded in years and months.
8-6, 9-0, 8-4, 9-3, 7-8, 8-11, 8-7, 9-2, 7¬10, 8-8
(i) What is the lowest age?
(ii) What is the highest age?
(iii) Determine the range?
Solution:
From the given data
(i) Lowest age is 7 years 8 months
(ii) The highest age is 9 years, 3 months
(iii) Range = Highest term – Lowest term
= 9 years 3 months – 7 years 8 months
= 1 years 7 months

Question 7.
The monthly pocket money of six friends is given below:
₹45, ₹30, ₹40, ₹50, ₹25, ₹45
(i) What is the highest pocket money?
(ii) What is the lowest pocket money?
(iii) What is the range?
(iv) Arrange the amounts of pocket money in ascending order.
Solution:
From the given data
(i) Highest pocket money = ₹50
(ii) Lowest pocket money = ₹25
(iii) Range = Highest term – Lowest term = ₹50-₹25 = ₹25
(iv) In ascending order : ₹25, ₹30, ₹40, ₹45, ₹45, ₹50

Question 8.
Write the class-size in each of the following:
(i) 0-4,5-9,10-14
(ii) 10-19, 20-29, 30-39
(iii) 100-120, 120-140, 160-180
(iv) 0-0.25, 0.25-0.50, 0.50-0.75
(v) 5-5,01, 5.01-5.02, 5.02-5.03
Solution:
(i) In 0-4, 5-9, 10-14
0-4 means from 0 to 4, similarly 5-9 means 5 to 9 and 10-14 means 10 to 14
class-size is 5
(ii) In 10-19, 20-29, 30-39
Here 10-19, means 10 to 19, 20-29 means 20 to 29 and 30-39 means 30 to 39
Class-size = 10
(iii) 100-120, 120-140, 160-180
Here 100-120, 120-140, 160-180
Then 120 – 100 = 20, 140 – 120 = 20, 180 – 160 = 20 is class-size = 20
(iv) 0-0.25, 0.25-0.50, 0.50-0.75
Here 0.25 – 0 = 0.25, 0.50 – 0.25 = 0.25 and 0.75 – 0.50 = 0.25
∴ Class-size = 0.25
(v) 5-5.01, 5.01-5.02, 5.02-5.03
Here 5.01 – 5 = 0.01, 5.02 – 5.01 = 0.01 and 5.03 – 5.02 = 0.01
∴ Class-size = 0.01

Question 9.
The final marks in mathematics of 30 students are as follows:
53, 61, 48, 60, 78, 68, 55, 100, 67, 90
75, 88, 77, 37, 84, 58, 60, 48, 62, 56
44, 58, 52, 64, 98, 59, 70, 39, 50, 60
(i) Arrange these marks in the ascending order,30 to 39 one group, 40 to 49 second group, etc.
Now answer the following:
(ii) What is the highest score?
(iii) What is the lowest score?
(iv) What is the range?
(v) If 40 is the pass mark how many have failed?
(vi) How many have scored 75 or more?
(vii) Which observations between 50 and 60 have not actually appeared?
(viii)How many have scored less than 50?
Solution:
(i) Arranging in ascending order:
37, 39, 44, 48, 48, 50, 52, 53, 55, 56, 58, 58, 59, 60, 60, 60, 61, 62, 64, 67, 68, 70, 75, 77, 78, 84, 88, 90, 98, 100

(ii) Highest score =100
(iii) Lowest score = 37
(iv) Range =  Highest score – Lowest score = 100 – 37 = 63
(v) If 40 is marks, then the number of students who failed = 2
(vi) No. of students who scored 75 or more = 8
(vii) Between 50 and 60, the scores which are missing 51, 54, 57
(viii) Number of students who scored less then 50 = 2 + 3 = 5

Question 10.
The weights of new born babies (in kg) in a hospital on a particular day are as follows:
2.3, 2.2, 2.1, 2.7, 2.6, 3.0, 2.5, 2.9, 2.8, 3.1, 2.5, 2.8, 2.7, 2.9, 2.4
(i) Rearrange the weights in descending order.
(ii) Determine the highest weight.
(iii) Determine the lowest weight.
(iv) Determine the range.
(v) How many babies were bom on that day?
(vi) How many babies weigh below 2.5 kg?
(vii) How many babies weigh more than 2.8 kg?
(viii)How many babies weigh 2.8 kg?
Solution:
(i) Weights in descending order are
3.1, 3.0, 2.9, 2.9, 2.8, 2.8, 2.7, 2.7, 2.6, 2.5, 2.5, 2.4, 2.3, 2.2, 2.1
(ii) Highest weight = 3.1
(iii) Lowest weight = 2.1
(iv) Range = Highest weight – Lowest wight = 3.1 – 2.1 = 1.0
(v) No. of babies who bom = 15
(vi) No. of babies whose weights are below 2.5 kg = 4
(vii) No. of babies whose weight are more than 2.8 kg = 4.
(viii) No. of babies whose weight is 2.8 kg = 2

Question 11.
The number of runs scored by a cricket player in 25 innings are as follows:
26, 35, 94, 48, 82, 105, 53, 0, 39, 42, 71, 0, 64, 15, 34, 67, 0, 42, 124, 84, 54, 48, 139, 64, 47.
(i) Rearrange these runs in ascending order.
(ii) Determine the player, is highest score.
(ii) How many times did the player not score a run?
(iv) How many centuries did he score?
(v) How many times did he score more than 50 runs?
Solution:
(i) Arranging in ascending order
0, 0, 0, 15, 26, 34, 35, 39, 42, 42, 47, 48, 48, 53, 54, 64, 64, 67, 71, 82, 84, 94, 105, 124, 139
(ii) Highest score is 139
(iii) 3 times when his score is 0
(iv) No. of times, he made century = 3
(v) No. of times his score more then 50 runs = 12

Question 12.
The class size of a distribution is 25 and the first class-interval is 200-224. There are seven class-intervals.
(i) Write the class-intervals.
(ii) Write the class-marks of each interval
Solution:
Class size = 25
First class is 200-224
∴ Number of class = 7
∴ Class interval will be
(i) 200-224, 225-249, 250-274, 275-299, 300-324, 325-349, 350-374

Question 13.
Write the class size and class limits in each of the following:
(i) 104, 114, 124, 134, 144, 154 and 164
(ii) 47, 52, 57, 62, 67, 72, 77, 82, 87, 92, 97 and 102
(iii) 12.5, 17.5, 22.5, 27.5, 32.5, 37.5, 42.5, 47.5
Solution:
(i) 104, 114, 124, 134, 144, 154 and 164
Here class size = 114 – 104 = 10
Here in first class, 104 – \(\frac { 10 }{ 2 }\)
= 104 – 5 = 99 and 104 + 5 = 109
∴ Class will be 99-109
In this way other classes will be 109-119, 119-129, 129-139, 139-149, 149-159, 159¬169
(ii) In 47, 52, 57, 62, 67, 72, 77, 82, 87, 92, 97, 102
Here class size = 52 – 47 = 5
∴ In first class, 47 – \(\frac { 5 }{ 2 }\) and 47 + \(\frac { 5 }{ 2 }\)
= 44.5-49.5
In this way other classes will be = 49.5-54.5, 54.5-59.5, 59.5-64.5, 64.5-69.5,69.5-74.5, 74.5-79.5, 79.5-84.5, 84.5-89.5, 89.5-94.5,94.5-99.5, 99.5-104.5 070 12.5, 17.5, 22.5, 27.5, 32.5, 37.5, 42.5, 47.5
Here class interval (size) = 17.5 – 12.5 = 5
In the class = 12.5 – \(\frac { 5 }{ 2 }\) , 12.5 + \(\frac { 5 }{ 2 }\)
⇒ 12.5 – 2.5, 12.5 + 2.5
⇒ 10, 15
∴ First class will be 10-15
In this way other classes 15-20, 20-25, 25-30, 30-35, 35-40, 40-45, 45-50

Question 14.
Following data gives the number of children in 41 families:
1, 2, 6, 5, 1, 5, 1, 3, 2, 6, 2, 3, 4, 2, 0, 0, 4, 4, 3, 2, 2, 0, 0, 1, 2, 2, 4, 3, 2, 1, 0, 5, 1, 2, 4, 3, 4, 1, 6, 2, 2.
Represent it in the form of a frequency distribution.
Solution:
Frequency distribution table is given below:

Question 15.
The marks scored by 40 students of class IX in mathematics are given below:
81, 55, 68, 79, 85, 43, 29, 68, 54, 73, 47, 35, 72, 64, 95, 44, 50, 77, 64, 35, 79, 52, 45, 54, 70, 83, 62, 64, 72, 92, 84, 76, 63, 43, 54, 38, 73, 68, 52, 54.
Prepare a frequency distribution with class size of 10 marks.
Solution:
Maximum marks = 95,
minimum marks = 29,
range = 95 – 29 = 66
Frequency distribution is given below

Question 16.
The heights (in cm) of 30 students of class IX are given below:155, 158, 154, 158, 160, 148, 149, 150, 153, 159, 161, 148, 157, 153, 157, 162, 159, 151, 154, 156, 152, 156, 160, 152, 147, 155, 163, 155, 157, 153.
Prepare a frequency distribution table with 160-164 as one of the class intervals.
Solution:
Maximum height = 163 cm,
minimum height = 147 cm,
range 163 – 147 = 16
Frequency distribution of the given data is given below

Question 17.
The monthly wages of 30 workers in a factory are given below:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 836, 878,840, 868, 890, 806, 840, 890.
Represent the data in the form of a frequency distribution with class size 10.
Solution:
Highest wage = ₹890,
lower wage = ₹804,
range = 890 – 804 = 86
Frequency distribution table is given below

Question 18.
The daily maximum temperatures (in degree Celsius) recorded in a certain city during the month of November are as follows:
25.8, 24.5, 25.6, 20.7, 21.8, 20.5, 20.6, 20.9, 22.3, 22.7, 23.1, 22.8, 22.9, 21.7, 21.3, 20.5, 20.9, 23.1, 22.4, 21.5, 22.7, 22.8, 22.0, 23.9, 24.7, 22.8, 23.8, 24.6, 23.9, 21.1
Represent them as a frequency distribution table with class size 1°C.
Solution:
Maximum temperature = 25.8
Minimum temperature = 20.5
Range = 25.8 – 20.5 = 5.3
Frequency distribution table is given below:

Question 19.
Construct a frequency table with equal class intervals from the following data on the monthly wages (in rupees) of 28 labourers working in a factory, taking* one of the class intervals as 210-230 (230 not included):
220, 268, 258, 242, 210, 268, 272, 242, 311, 290, 300, 320, 319, 304, 302, 318, 306, 292, 254, 278, 210, 240, 280, 316, 306, 215, 256, 236.
Solution:
Maximum wages = ₹320
Minimum wages = ₹210
Range = 320 – 210 = 110
Required frequency table is given below:

Question 20.
The blood groups of 30 students of class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O
Represent this data in the form of a frequency distribution table. Find out which is the most common and which is the rarest blood group among these students. (NCERT)
Solution:
Frequency distribution table is given below:

Question 21.
Three coins were tossed 30 times. Each time the number of heads occuring was noted down as follow:
0 1 2 2 1 2 3 1 3 0
1 3 1 1 2 2 0 1 2 1
3 0 0 1 1 2 3 2 2 0
Prepare a frequency distribution table for the data given above. (NCERT)
Solution:
Frequency distribution table is given below:

Question 22.
Thirty children were asked about the number of hours they watched T.V. programmes in the previous week. The results were found as follows:
1 6 2 35 12 5 8 4 8
10 3 4 12 2 8 15 1 17 6
3 2 8 5 9 6 8 7 14 12
(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class intervals as 5-10.
(ii) How many children watched television for 15 or more hours a week? (NCERT)
Solution:
Highest number of hours = 17
Lowest number of hours = 1
(i) The frequency table is given below:

(ii) No. of children watching T.V. for 15 or more hours a week = 2

Question 23.
The daily minimum temperatures in degrees Celsius recorded in a certain Arctic region are as follows:
-12.5, -10.8, -18.6, -8.4, -10.8, -4.2, -4.8, -6.7, -13.2, -11.8, -2.3, 1.2, 2.6, 0, 2.4, 0, 3.2, 2.7, 3.4, 0, -2.4, -2.4, 0, 3.2, 2.7, 3.4, 0, -2.4, -5.8, -8.9, -14.6, -12.3, -11.5,-7.8,-2.9.
Represent them as frequency distribution table taking -19.9 to -15 as the first class interval.
Solution:
Maximum temperature = -18.6
Minimum temperature = 3.4
Range = 3.4 – (-18.6) = 3.4 + 18.6 = 22
The required frequency distribution table is given below:

Hope given RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Question 1.
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
Solution:
Radius of the base of the cone = 21 cm
and slant height (l) = 60 cm

Question 2.
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
Solution:
Radius of the base of a cone = 5 cm
Vertical height (h) = 12 cm

Question 3.
The radius of a cone is 7 cm and area of curved surface is 176 cm2. Find the slant height.
Solution:
Curved surface area of a cone = 176 cm²
and radius (r) = 1 cm²

Question 4.
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
Solution:
Height of the cone (h) = 21 cm
Slant height (l) = 28 cm
∴ l² = r² + h²
⇒ r² = l²– h² = (28)² – (21 )²
⇒ 784 – 441 = 343 …(i)
Now area of base = πr²
= \(\frac { 22 }{ 7 }\) x 343 [From (i)]
= 22 x 49 = 1078 cm²

Question 5.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
Solution:
Radius of base of cone (r) = 6 cm
and height (h) = 8 cm

Question 6.
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10 cm. [NCERT]
Solution:
Radius of base of a cone (r) = 5.25 cm
and slant height (l) = 10 cm
Curved surface area = πrl

Question 7.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m. [NCERT]
Solution:
Slant height of a cone (l) = 21 m
and diameter of its base = 24 m
∴ Radius (r) = \(\frac { 24 }{ 2 }\) = 12 m
Now total surface area = πr(l + r)

Question 8.
The area of the curved surface of a cone is 60π cm². If the slant height of the cone be 8 cm, find the radius of the base.
Solution:
Curved surface area of a cone = 6071 cm²
Slant height (l) = 8 cm

Question 9.
The curved surface area of a cone is 4070 cm² and its diameter is 70 cm. What is the slant height ? (Use π = 22/7).
Solution:
Surface area of a cone = 4070 cm²
Diameter of its base = 70 cm

Question 10.
The radius and slant height of a cone are in the ratio of 4 : 7. If its curved surface area is 792 cm², find its radius. (Use π = 22/7)
Solution:
Curved surface area of a cone = 792 cm²
Ratio in radius and slant height = 4:7
Let radius = 4x
Then slant height = 7x
∴ Curved surface area πrl = 792

Question 11.
A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps. [NCERT]
Solution:
Radius of the base of a conical cap (r) = 7 cm
and height (h) = 24 cm

Question 12.
Find the ratio of the curved surface areas of two cones if their diameters of the bases are equal and slant heights are in the ratio 4 : 3.
Solution:
Let diameters of each cone = d
Then radius (r) = \(\frac { d }{ 2 }\)
Ratio in their slant heights = 4 : 3
Let slant height of first cone = 4x
and height of second cone = 3x
Now curved surface area of the first cone = 2πrh

Question 13.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
Solution:
In two cones, curved surface of the first cone = 2 x curved surface of the second cone
Slant height of the second cone = 2 x slant height of first cone
Let r₁ and r₂ be the radii of the two cones
and let height of the first cone = h
Then height of second cone = 2h
∴ Curved surface of the first cone = 2πr₁h

Question 14.
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surfaces.
Solution:
Let diameter of one cone = d
and diameter of second cone = d
∴ Radius of the first cone (r) = \(\frac { d }{ 2 }\)
and of second cone (r₂) = \(\frac { d }{ 2 }\)
Ratio in their slant heights = 5:4
Let slant height of the first cone = 5x
Then that of second cone = 4x
Now curved surface of the first cone = 2πrh

Question 15.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find the radius of the base and total surface area of the cone. [NCERT]
Solution:
Area of curved surface of a cone = 308 cm²
and slant height (l) = 14 cm

Question 16.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per 100 m². [NCERT]
Solution:
Slant height of a cone (l) = 25 m

Question 17.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 m² canvas is Rs. 70, find the cost of the canvas required to make the tent. [NCERT]
Solution:
Height of conical tent (A) = 10 m
Radius of the base (r) = 24 m

Question 18.
The circumference of the base of a 10 m height conical tent is 44 metres. Calculate the length of canvas used in making the tent if width of canvas is 2 m. (Use π = 22/7)
Solution:
Circumference of the base of a conical tent = 44 m

Question 19.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assum that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use π = 3.14) [NCERT]
Solution:
Height of the conical tent (h) = 8 m
and radius of the base (r) = 6 m

Now curved surface area of the tent = πrl = 3.14 x 6 x 10 = 188.4 m
Width of tarpaulin used = 3 m
∴ Length = 188.4 , 3 = 62.8 m
Extra length required = 20 cm = 0.2 m
∴ Total length of tarpaulin = 62.8 + 0.2 = 63 m

Question 20.
A bus stop is barricated from the remaining part of the road, by using 50 hollow cones made of recycled card-board. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹12 per m², what will be the cost of painting these cones. (Use π = 3.14 and \(\sqrt { 1.04 } \) = 1.02) [NCERT]
Solution:
Diameter of the base of tent = 40 cm
∴ Radius of the base of cone (r) = \(\frac { 40 }{ 2 }\)

Question 21.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8 : 5, show that the radius of each is to the height of each as 3 : 4.
Solution:
Let radius of cylinder = r
and radius of cone = r
and let height of cylinder = h
and height of cone = h

Question 22.
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of the canvas required for the tent.
Solution:
Diameter of the cylindrical portion = 24 m 24
∴ Radius (r) = \(\frac { 24 }{ 2 }\) = 12 m
Height of cylindrical portion = 11 m
and total height = 16 m

∴ Height of conical portion = 16 – 11 = 5 m
∴ Slant height of the conical portion (l)

Question 23.
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
Solution:
Diameter of the cylindrical tent = 105 m

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Mark correct alternative in each of the following:
Question 1.
In a cylinder, if radius is doubled and height is halved, curved surface area will be
(a) halved
(b) doubled
(c) same
(d) four times
Solution:
Let radius of the first cylinder (r₁) = r
and height (h₁) = h
Surface area = 2πrh
If radius is doubled and height is halved

∴ Their surface area remain same (c)

Question 2.
Two cylindrical jars have their diameters in the ratio 3:1, but height 1:3. Then the ratio of their volumes is
(a) 1 : 4
(b) 1 : 3
(c) 3 : 1
(d) 2 : 5
Solution:
Sol. Ratio in the diameters of two cylinder = 3:1
and ratio in their heights = 1:3
Let radius of the first cylinder (r₁) = 3x
and radius of second (r₂) = x
and height of the first (h₁) = y
and height of the second (h₂) = 3y
Now volume of the first cylinder = πr²h
= π(3x)² x y = 9πx²y
and of second cylinder = π(x²) (3y)
∴ Ratio between then = 9πx²y : 3πx²y
= 3 : 1 (c)

Question 3.
The number of surfaces in right cylinder is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
The number of surfaces of a right cylinder is three. (c)

Question 4.
Vertical cross-section of a right circular cylinder is always a
(a) square
(b) rectangle
(c) rhombus
(d) trapezium
Solution:
The vertical cross-section of a right circular cylinder is always a rectangle. (b)

Question 5.
If r is the radius and h is height of the cylinder the volume will be

Solution:
Volume of a cylinder = πr²h (b)

Question 6.
The number of surfaces of a hollow cylindrical object is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
The number of surfaces of a hollow cylindrical object is 4. (d)

Question 7.
If the radius of a cylinder is doubled and the height remains same, the volume will be
(a) doubled
(b) halved
(c) same
(d) four times
Solution:
If r be the radius and h be the height, then volume = πr2h
If radius is doubled and height remain same,
the volume will be
= π(2r)²h = π x 4r²h
= 4πr²h = 4 x Volume
The volume is four times (d)

Question 8.
If the height of a cylinder is doubled and radius remains the same, then volume will be
(a) doubled
(b) halved
(c) same
(d) four times
Solution:
If r be the radius and h be the height, then volume of a cylinder = πr²h
If height is doubled and radius remain same, then volume = πr²(2h) = 2πr²h
∴ Its doubled (a)

Question 9.
In a cylinder, if radius is halved and height is doubled, the volume will be
(a) same
(b) doubled
(c) halved
(d) four times
Solution:
Let r be radius and h be height, then Volume = πr²h
If radius is halved and height is doubled

Question 10.
If the diameter of the base of a closed right circular cylinder be equal to its height h, then its whole surface area is

Solution:
Let diameter of the base of a cylinder (r) = h
Then its height (h) = h

Question 11.
A right circular cylindrical tunnel of diameter 2 m and length 40 m is to be constructed from a sheet of iron. The area of the iron sheet required in m², is
(a) 40π
(b) 80π
(c) 160π
(d) 200π
Solution:
Diameter of a cylindrical tunnel = 2 m
∴ Radius (r) = \(\frac { 2 }{ 2 }\) = 1m
and length (h) = 40 m
Curved surfae area = 2πrh = 2 x π x 1 x 40 = 80π (b)

Question 12.
Two circular cylinders of equal volume have their heights in the ratio 1 : 2. Ratio of their radii is

Solution:
Let r₁ and h₁ be the radius and height of the
first cylinder, then
Volume = πr₁²h₁
Similarly r₁ and h₂ are the radius and height of the second cylinder
∴ Volume = πr²h₂
But their volumes are equal,

Question 13.
The radius of a wire is decreased to one- third. If volume remains the same, the length will become
(a) 3 times
(b) 6 times
(c) 9 times
(d) 27 times
Solution:
In the first case, r and h1, be the radius and height of the cylindrical wire
∴ Volume = πr²h₁ …(i)
In second case, radius is decreased to one third

∴ In second case height is 9 times (c)

Question 14.
If the height of a cylinder is doubled, by what number must the radius of the base be multiplied so that the resulting cylinder has the same volume as the original cylinder?

Solution:
Let r be the radius and h be the height then volume = πr²h
If height is doubled and volume is same and let x be radius then πr²h = π(x)² x 2h

Question 15.
The volume of a cylinder of radius r is 1/4 of the volume of a rectangular box with a square base of side length x. If the cylinder and the box have equal heights, what is r in terms of x?

Solution:
Let r be the radius and h be the height, then volume = πr²h
This volume is \(\frac { 1 }{ 4 }\) of the volume of a rectangular box
∴ Volume of box = 4πr²h
Let side of base of box = x and height h,
then volume = x²h
∴ 4πr²h = x²h

Question 16.
The height ft of a cylinder equals the circumference of the cylinder. In terms of ft, what is the volume of the cylinder?

Solution:
In a cylinder,
h = circumference of the cylinder

Question 17.
A cylinder with radius r and height ft is closed on the top and bottom. Which of the following expressions represents the total surface area of this cylinder?
(a) 2πr(r + h)
(b) πr(r + 2h)
(c) πr(2r + h)
(d) 2πr² + h
Solution:
r is the radius of the base and ft is the height of a closed cylinder
Then total surface area = 2πr(r + h ) (a)

Question 18.
The height of sand in a cylindrical-shaped can drops 3 inches when 1 cubic foot of sand is poured out. What is the diameter, in inches, of the cylinder?

Solution:
Let h be the height and d be the diameter of a cylinder, then

Question 19.
Two steel sheets each of length a₁ and breadth a₂ are used to prepare the surfaces of two right circular cylinders – one having volume v₁ and height a₂ and other having volume v₂ and height a₁. Then,

Solution:
Length of each sheet = a₁
and breadth = a₂
Volume of cylinder = πr²h
In first case,
v₁ is volume and a₂ is the height

Question 20.
The altitude of a circualr cylinder is increased six times and the base area is decreased to one-ninth of its value. The factor by which the lateral surface of the cylinder increases, is

Solution:
In first case,
Let r be the radius and h be the height of the cylinder. Then,
∴ Lateral surface area = 2πrh
In second case,

Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Question 1.
Write the number of surface of a right circular cylinder.
Solution:
Three, two circular and one curved.

Question 2.
Write the ratio of total surface area to the curved surface area of a cylinder of radius r and height h.
Solution:
∵ Radius = r
and height = h
∴ Curved surface area = 2πrh
and total surface area = 2πr(h + r)
∴ Ratio = 2πr(h + r) : 2πrh
= h + r : h

Question 3.
The ratio between the radius of the base and height of a cylinder is 2 : 3. If its volume is 1617 cm3, find the total surface area of the cylinder.
Solution:
Ratio in radius and height of the cylinder = 2 : 3
Let radius (r) = 2x
Then height (h) = 3x
∴ Volume = πr²h

Question 4.
If the radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3, then find the ratio of their volumes.
Solution:
Ratio of radii of two cylinder = 2:3
Let radius of first cylinder (r₁) = 2x
and second cylinder (r₂) = 3x
and ratio in their heights = 5:3
Let height of first cylinder (h₁) = 5y
and height of second (h₂) = 3y
∴ Volume of the first cylinder =πr²h
= π x (2x)² x 5y = 20πx²y
and volume of second cylinder = π(3x)2 x 3y = 27πx²y
Now ratio between then,
= 20πx²y: 21πx²y
= 20 : 27

Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.