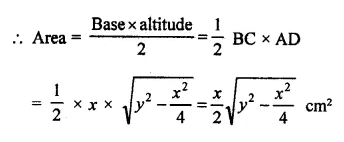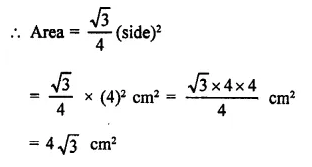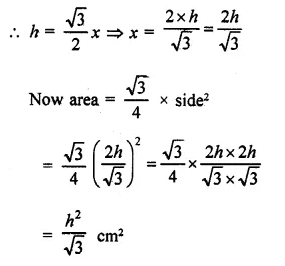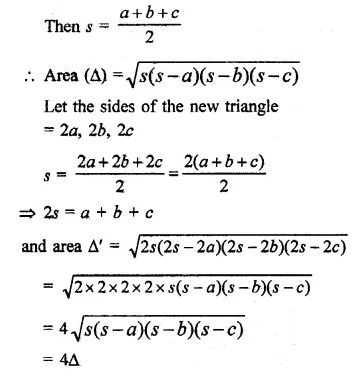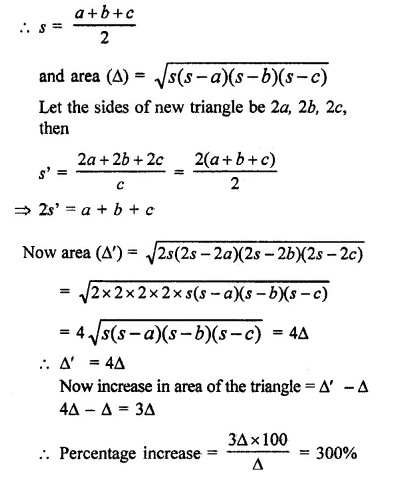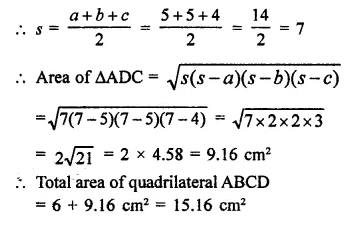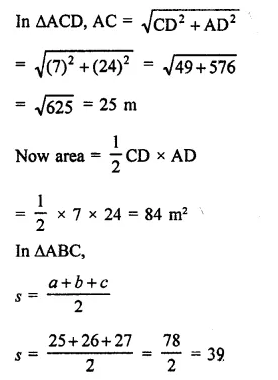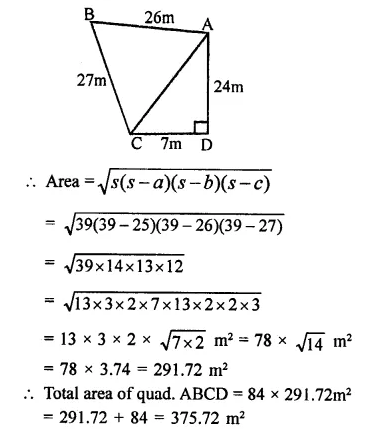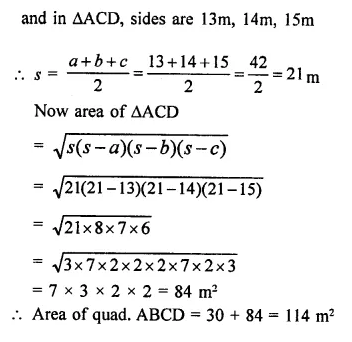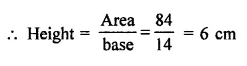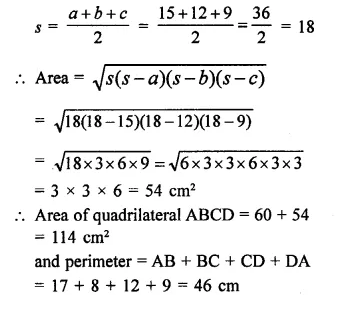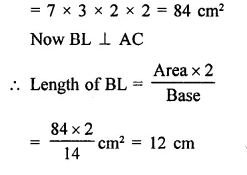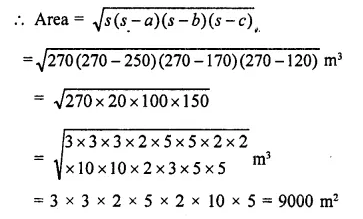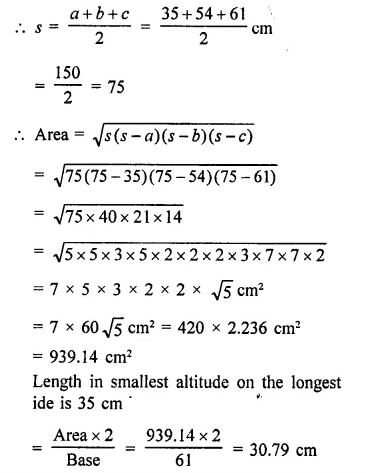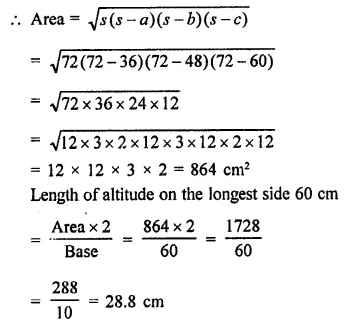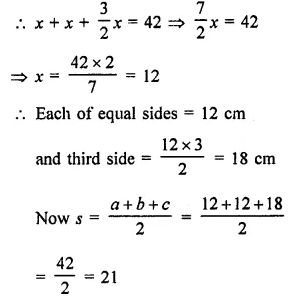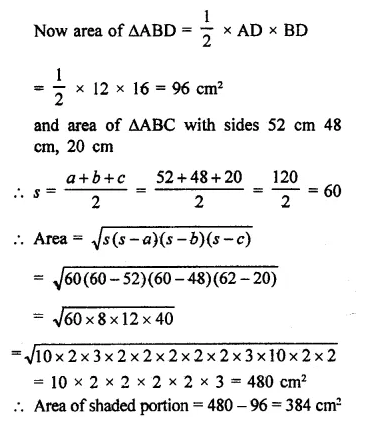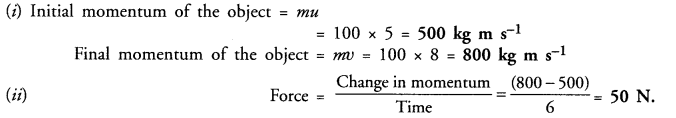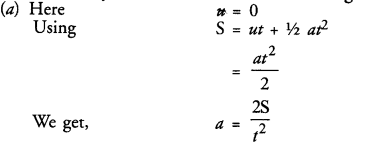Category: CBSE Class 9

RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1
• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2
• RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS
• RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

Mark the correct alternative in each of the following:
Question 1.
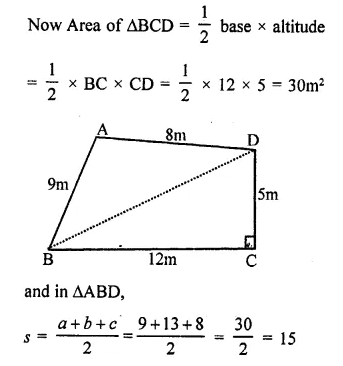
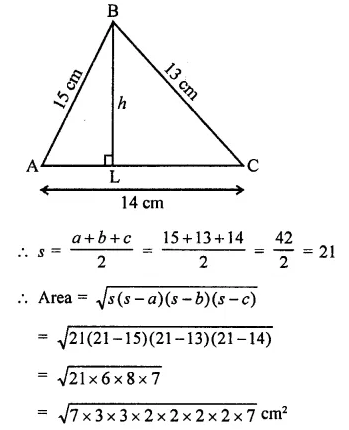
The sides of a triangle are 16 cm, 30 cm, 34 cm. Its area is
(a) 225 cm²
(b) 225\(\sqrt { 3 } \) cm²
(c) 225\(\sqrt { 2 } \) cm²
(d) 240 cm²
Solution:
Sides of triangle and 16 cm, 30 cm, 34 cm

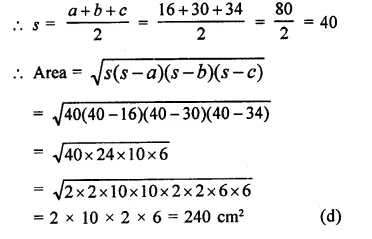
Question 2.
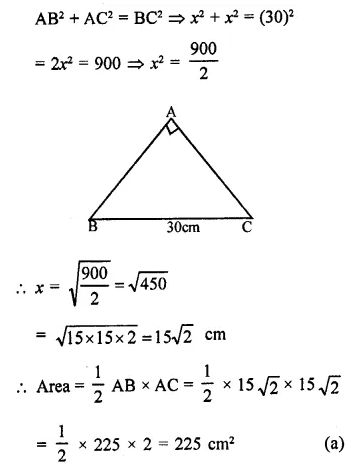
The base of an isosceles right triangle is 30 cm. Its area is
(a) 225 cm²
(b) 225\(\sqrt { 3 } \) cm²
(c) 225\(\sqrt { 2 } \) cm²
(d) 450 cm²
Solution:
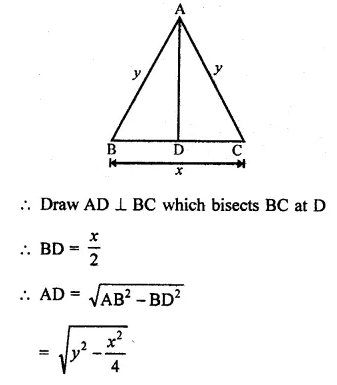
Base of isosceles triangle ∆ABC = 30cm
Let each of equal sides = x
Then AB = AC = x
Now in right ∆ABC,

Question 3.
The sides of a triangle are 7cm, 9cm and 14cm. Its area is
(a) 12\(\sqrt { 5 } \) cm²
(b) 12\(\sqrt { 3 } \) cm²
(c) 24 \(\sqrt { 5 } \) cm²
(d) 63 cm²
Solution:

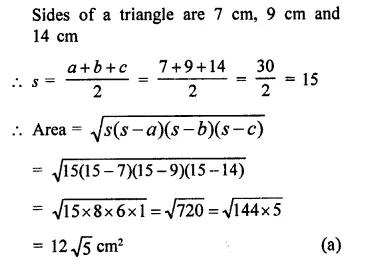
Question 4.
The sides of a triangular field are 325 m, 300 m and 125 m. Its area is
(a) 18750 m²
(b) 37500 m²
(c) 97500 m²
(d) 48750 m²
Solution:
Sides of a triangular field are 325m, 300m, 125m

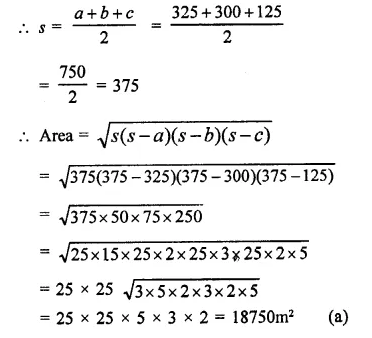
Question 5.
The sides of a triangle are 50 cm, 78 cm and 112 cm. The smallest altitude is
(a) 20 cm
(b) 30 cm
(c) 40 cm
(d) 50 cm
Solution:
The sides of a triangle are 50 cm, 78 cm, 112cm

Question 6.
The sides of a triangle are 11m, 60m and 61m. Altitude to the smallest side is
(a) 11m
(b) 66 m
(c) 50 m
(d) 60 m
Solution:
Sides of a triangle are 11m, 60m and 61m

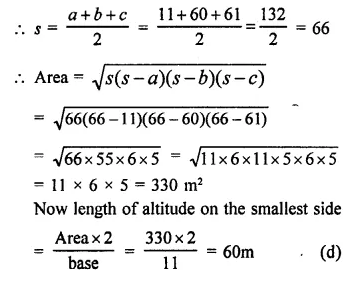
Question 7.
The sides of a triangle are 11 cm, 15 cm and 16 cm. The altitude to the largest side is

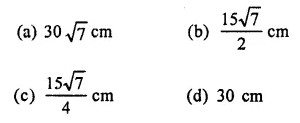
Solution:
Sides of a triangle are 11 cm, 15 cm, 16 cm

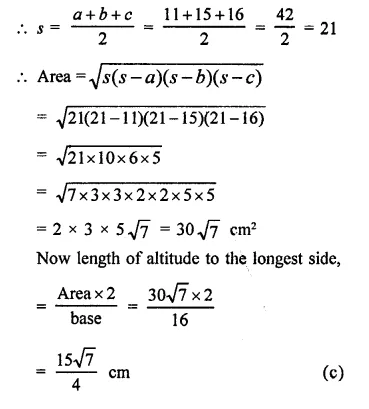
Question 8.
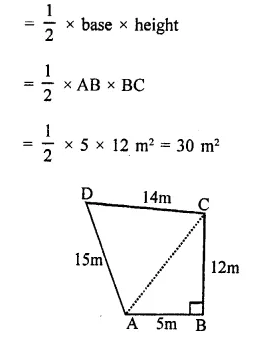
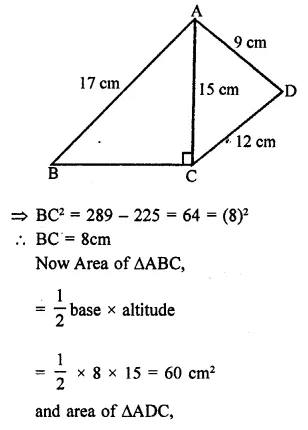
The base and hypotenuse of a right triangle are respectively 5cm and 13cm long. Its area is
(a) 25 cm²
(b) 28 cm²
(c) 30 cm²
(d) 40 cm²
Solution:
In a right triangle base = 5 cm
base hypotenuse = 13 cm

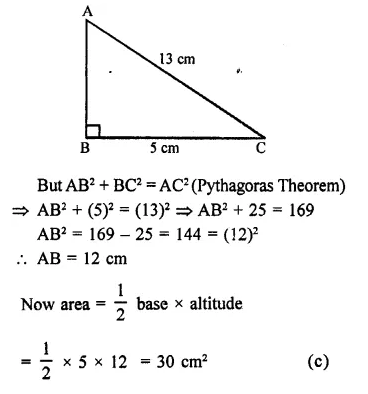
Question 9.
The length of each side of an equilateral triangle of area 4 \(\sqrt { 3 } \) cm², is

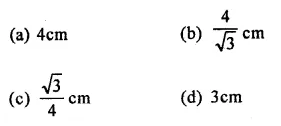
Solution:
Area of an equilateral triangle = 4\(\sqrt { 3 } \) cm²
Let each side be = a

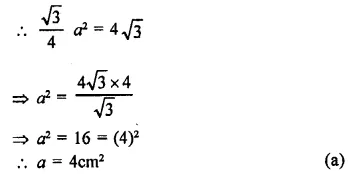
Question 10.
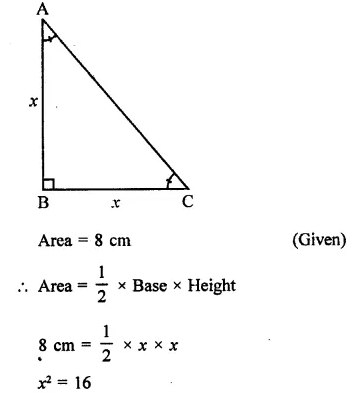
If the area of an isosceles right triangle is 8cm, what is the perimeter of the triangle.
(a) 8 + \(\sqrt { 2 } \) cm²
(b) 8 + 4\(\sqrt { 2 } \) cm²
(c) 4 + 8\(\sqrt { 2 } \) cm²
(b) 12\(\sqrt { 2 } \) cm²
Solution:
Let base = x
ABC an isosceles right triangle, which has 2 sides same
⇒ Height = x

Question 11.
The length of the sides of ∆ABC are consecutive integers. If ∆ABC has the same perimeter as an equilateral triangle with a side of length 9cm, what is the length of the shortest side of ∆ABC?
(a) 4
(b) 6
(c) 8
(d) 10
Solution:
Side of an equilateral triangle = 9 cm
Its perimeter = 3 x 9 = 27 cm
Now perimeter of ∆ABC = 27 cm
and let its sides be x, x + 1, x +2

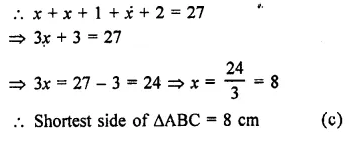
Question 12.
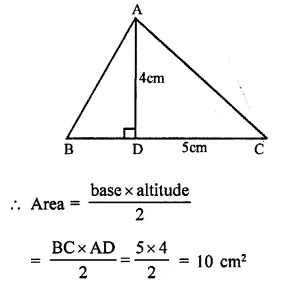
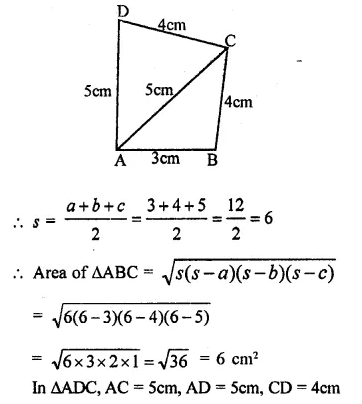
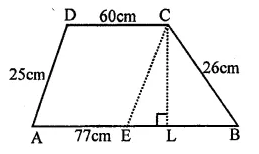
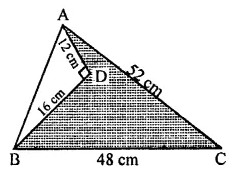
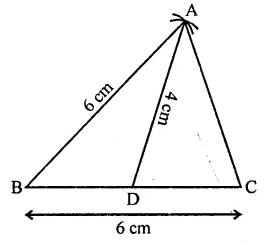
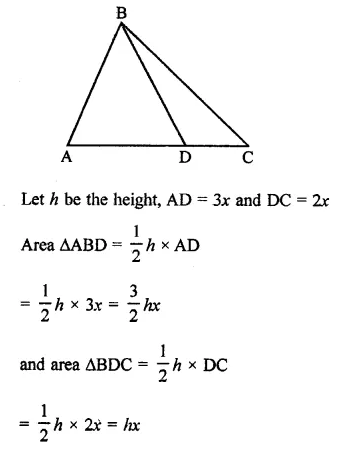
In the figure, the ratio of AD to DC is 3 to 2. If the area of ∆ABC is 40cm2, what is the area of ∆BDC?
(a) 16 cm²
(b) 24 cm²
(c) 30 cm²
(d) 36 cm²
Solution:
Ratio in AD : DC = 3:2
and area ∆ABC = 40 cm²

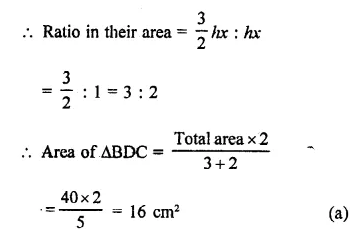
Question 13.
If the length of a median of an equilateral triangle is x cm, then its area is

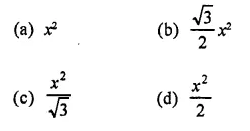
Solution:
∵ The median of an equilateral triangle is the perpendicular to the base also,
∴ Let side of the triangle = a

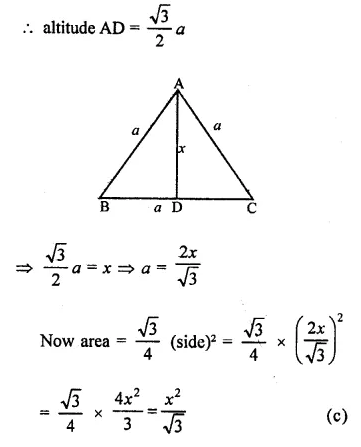
Question 14.
If every side of a triangle is doubled, then increase in the area of the triangle is
(a) 100\(\sqrt { 2 } \) %
(b) 200%
(c) 300%
(d) 400%
Solution:
Let the sides of the original triangle be a, b, c

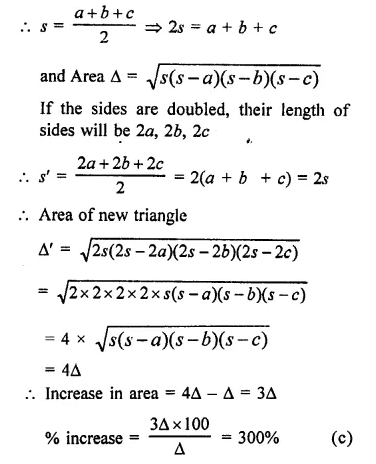
Question 15.
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is 1272 cm, then area of the triangle is

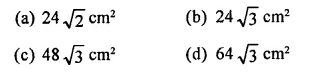
Solution:
A square and an equilateral triangle have equal perimeter

Hope given RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
In the figure, ∆ABC is an equilateral triangle. Find m ∠BEC.

Solution:
∵ ∆ABC is an equilateral triangle
∴ A = 60°
∵ ABEC is a cyclic quadrilateral
∴ ∠A + ∠E = 180° (Sum of opposite angles)
⇒ 60° + ∠E = 180°
⇒ ∠E = 180° – 60° = 120°
∴ m ∠BEC = 120°

Question 2.
In the figure, ∆PQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.

Solution:
In the figure, ∆PQR is an isosceles PQ = PR
∠PQR = 35°
∴ ∠PRQ = 35°
But ∠PQR + ∠PRQ + ∠QPR = 180° (Sum of angles of a triangle)
⇒ 35° + 35° + ∠QPR = 180°
⇒ 70° + ∠QPR = 180°
∴ ∠QPR = 180° – 70° = 110°
∵ ∠QSR = ∠QPR (Angle in the same segment of circles)
∴ ∠QSR = 110°
But PQTR is a cyclic quadrilateral
∴ ∠QTR + ∠QPR = 180°
⇒ ∠QTR + 110° = 180°
⇒ ∠QTR = 180° -110° = 70°
Hence ∠QTR = 70°

Question 3.
In the figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

Solution:
In the figure, O is the centre of the circle ∠BOD =160°
ABCD is the cyclic quadrilateral
∵ Arc BAD subtends ∠BOD is the angle at the centre and ∠BCD is on the other part of the circle
∴ ∠BCD = \(\frac { 1 }{ 2 }\) ∠BOD
⇒ x = \(\frac { 1 }{ 2 }\) x 160° = 80°
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180°
⇒ y + x = 180°
⇒ y + 80° = 180°
⇒ y =180°- 80° = 100°
∴ x = 80°, y = 100°

Question 4.
In the figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

Solution:
In a circle, ABCD is a cyclic quadrilateral ∠BCD = 100° and ∠ABD = 70°
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180° (Sum of opposite angles)

⇒ ∠A + 100°= 180°
∠A = 180°- 100° = 80°
Now in ∆ABD,
∠A + ∠ABD + ∠ADB = 180°
⇒ 80° + 70° + ∠ADB = 180°
⇒ 150° +∠ADB = 180°
∴ ∠ADB = 180°- 150° = 30°
Hence ∠ADB = 30°

Question 5.
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.

Solution:
Given : ABCD is a cyclic quadrilateral in which AD || BC

To prove : ∠B = ∠C
Proof : ∵ AD || BC
∴ ∠A + ∠B = 180°
(Sum of cointerior angles)
But ∠A + ∠C = 180°
(Opposite angles of the cyclic quadrilateral)
∴ ∠A + ∠B = ∠A + ∠C
⇒ ∠B = ∠C
Hence ∠B = ∠C

Question 6.
In the figure, O is the centre of the circle. Find ∠CBD.

Solution:
Arc AC subtends ∠AOC at the centre and ∠APC at the remaining part of the circle

∴ ∠APC = \(\frac { 1 }{ 2 }\) ∠AOC
= \(\frac { 1 }{ 2 }\) x 100° = 50°
∵ APCB is a.cyclic quadrilateral,
∴ ∠APC + ∠ABC = 180°
⇒ 50° + ∠ABC = 180° ⇒ ∠ABC =180°- 50°
∴ ∠ABC =130°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ 130° + ∠CBD = 180°
⇒ ∠CBD = 180°- 130° = 50°
∴ ∠CBD = 50°

Question 7.
In the figure, AB and CD are diameiers of a circle with centre O. If ∠OBD = 50°, find ∠AOC.

Solution:
Two diameters AB and CD intersect each other at O. AC, CB and BD are joined

∠DBA = 50°
∠DBA and ∠DCA are in the same segment
∴ ∠DBA = ∠DCA = 50°
In ∆OAC, OA = OC (Radii of the circle)
∴ ∠OAC = ∠OCA = ∠DCA = 50°
and ∠OAC + ∠OCA + ∠AOC = 180° (Sum of angles of a triangle)
⇒ 50° + 50° + ∠AOC = 180°
⇒ 100° + ∠AOC = 180°
⇒ ∠AOC = 180° – 100° = 80°
Hence ∠AOC = 80°

Question 8.
On a semi circle with AB as diameter, a point C is taken so that m (∠CAB) = 30°. Find m (∠ACB) and m (∠ABC).
Solution:
A semicircle with AB as diameter

∠ CAB = 30°
∠ACB = 90° (Angle in a semi circle)
But ∠CAB + ∠ACB + ∠ABC = 180°
⇒ 30° + 90° + ∠ABC – 180°
⇒ 120° + ∠ABC = 180°
∴ ∠ABC = 180°- 120° = 60°
Hence m ∠ACB = 90°
and m ∠ABC = 60°

Question 9.
In a cyclic quadrilateral ABCD, if AB || CD and ∠B = 70°, find the remaining angles.
Solution:
In a cyclic quadrilateral ABCD, AB || CD and ∠B = 70°

∵ ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
⇒ 70° + ∠D = 180°
⇒ ∠D = 180°-70° = 110°
∵ AB || CD
∴ ∠A + ∠D = 180° (Sum of cointerior angles)
∠A+ 110°= 180°
⇒ ∠A= 180°- 110° = 70°
Similarly, ∠B + ∠C = 180°
⇒ 70° + ∠C- 180° ‘
⇒ ∠C = 180°-70°= 110°
∴ ∠A = 70°, ∠C = 110°, ∠D = 110°

Question 10.
In a cyclic quadrilateral ABCD, if m ∠A = 3(m ∠C). Find m ∠A.
Solution:
In cyclic quadrilateral ABCD, m ∠A = 3(m ∠C)

∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180°
⇒ 3 ∠C + ∠C = 180° ⇒ 4∠C = 180°
⇒ ∠C = \(\frac { { 180 }^{ \circ } }{ 4 }\)  = 45°
∴ ∠A = 3 x 45°= 135°
Hence m ∠A =135°

Question 11.
In the figure, O is the centre of the circle and ∠DAB = 50°. Calculate the values of x and y.

Solution:
In the figure, O is the centre of the circle ∠DAB = 50°
∵ ABCD is a cyclic quadrilateral
∴ ∠A + ∠C = 180°
⇒ 50° + y = 180°
⇒ y = 180° – 50° = 130°
In ∆OAB, OA = OB (Radii of the circle)
∴ ∠A = ∠OBA = 50°
∴ Ext. ∠DOB = ∠A + ∠OBA
x = 50° + 50° = 100°
∴ x= 100°, y= 130°

Question 12.
In the figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.

Solution:
In ∆ABC,
∠BAC + ∠ABC + ∠ACB = 180° (Sum of angles of a triangle)

60° + ∠ABC + 20° = 180°
∠ABC + 80° = 180°
∴ ∠ABC = 180° -80°= 100°
∵ ABCD is a cyclic quadrilateral,
∴ ∠ABC + ∠ADC = 180°
100° + ∠ADC = 180°
∴ ∠ADC = 180°- 100° = 80°

Question 13.
In the figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.

Solution:
In a circle, ∆ABC is an equilateral triangle

∴ ∠A = 60°
∵ ∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 60°
∵ BECD is a cyclic quadrilateral
∴ ∠BDC + ∠BEC = 180°
⇒ 60° + ∠BEC = 180°
⇒ ∠BEC = 180°-60°= 120°
Hence ∠BDC = 60° and ∠BEC = 120°

Question 14.
In the figure, O is the centre of the circle. If ∠CEA = 30°, find the values of x, y and z.

Solution:
∠AEC and ∠ADC are in the same segment
∴ ∠AEC = ∠ADC = 30°
∴ z = 30°
ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
⇒ x + z = 180°
⇒ x + 30° = 180°
⇒ x = 180° – 30° = 150°
Arc AC subtends ∠AOB at the centre and ∠ADC at the remaining part of the circle
∴ ∠AOC = 2∠D = 2 x 30° = 60°
∴ y = 60°
Hence x = 150°, y – 60° and z = 30°

Question 15.
In the figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.

Solution:
In the figure, two circles intersect each other at C and D
∠BAD = 78°, ∠DCF = x, ∠DEF = y
ABCD is a cyclic quadrilateral
∴ Ext. ∠DCF = its interior opposite ∠BAD
⇒ x = 78°
In cyclic quadrilateral CDEF,
∠DCF + ∠DEF = 180°
⇒ 78° + y = 180°
⇒ y = 180° – 78°
y = 102°
Hence x = 78°, and y- 102°

Question 16.
In a cyclic quadrilateral ABCD, if ∠A – ∠C = 60°, prove that the smaller of two is 60°.
Solution:
In cyclic quadrilateral ABCD,
∠A – ∠C = 60°
But ∠A + ∠C = 180° (Sum of opposite angles)

Adding, 2∠A = 240° ⇒ ∠A = \(\frac { { 62 }^{ \circ } }{ 2 }\)  = 120° and subtracting
2∠C = 120° ⇒ ∠C = \(\frac { { 120 }^{ \circ } }{ 2 }\)  = 60°
∴ Smaller angle of the two is 60°.

Question 17.
In the figure, ABCD is a cyclic quadrilateral. Find the value of x.

Solution:
∠CDE + ∠CDA = 180° (Linear pair)
⇒ 80° + ∠CDA = 180°
⇒ ∠CDA = 180° – 80° = 100°

In cyclic quadrilateral ABCD,
Ext. ∠ABF = Its interior opposite angle ∠CDA = 100°
∴ x = 100°

Question 18.
ABCD is a cyclic quadrilateral in which:
(i) BC || AD, ∠ADC =110° and ∠B AC = 50°. Find ∠DAC.
(ii) ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
(iii) ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.
Solution:
(i) In the figure,

ABCD is a cyclic quadrilateral and AD || BC, ∠ADC = 110°
∠BAC = 50°
∵ ∠B + ∠D = 180° (Sum of opposite angles)
⇒ ∠B + 110° = 180°
∴ ∠B = 180°- 110° = 70°
Now in ∆ABC,
∠CAB + ∠ABC + ∠BCA = 180° (Sum of angles of a triangle)
⇒ 50° + 70° + ∠BCA = 180°
⇒ 120° + ∠BCA = 180°
⇒ ∠BCA = 180° – 120° = 60°
But ∠DAC = ∠BCA (Alternate angles)
∴ ∠DAC = 60°
(ii) In cyclic quadrilateral ABCD,
Diagonals AC and BD are joined ∠DBC = 80°, ∠BAC = 40°

Arc DC subtends ∠DBC and ∠DAC in the same segment
∴ ∠DBC = ∠DAC = 80°
∴ ∠DAB = ∠DAC + ∠CAB = 80° + 40° = 120°
But ∠DAC + ∠BCD = 180° (Sum of opposite angles of a cyclic quad.)
⇒ 120° +∠BCD = 180°
⇒ ∠BCD = 180°- 120° = 60°
(iii) In the figure, ABCD is a cyclic quadrilateral BD is joined
∠BCD = 100°
and ∠ABD = 70°

∠A + ∠C = 180° (Sum of opposite angles of cyclic quad.)
∠A+ 100°= 180°
⇒ ∠A= 180°- 100°
∴ ∠A = 80°
Now in ∆ABD,
∠A + ∠ABD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 80° + 70° + ∠ADB = 180°
⇒ 150° +∠ADB = 180°
⇒ ∠ADB = 180°- 150° = 30°
∴ ∠ADB = 30°

Question 19.
Prove that the circles described on the four sides of a rhombus as diameter, pass through the point of intersection of its diagonals.
Solution:
Given : ABCD is a rhombus. Four circles are drawn on the sides AB, BC, CD and DA respectively

To prove : The circles pass through the point of intersection of the diagonals of the rhombus ABCD
Proof: ABCD is a rhombus whose diagonals AC and BD intersect each other at O
∵ The diagonals of a rhombus bisect each other at right angles
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
Now when ∠AOB = 90°
and a circle described on AB as diameter will pass through O
Similarly, the circles on BC, CD and DA as diameter, will also pass through O

Question 20.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that is diagonals are equal.
Solution:
Given : In cyclic quadrilateral ABCD, AB = CD
AC and BD are the diagonals

To prove : AC = BC
Proof: ∵ AB = CD
∴ arc AB = arc CD
Adding arc BC to both sides, then arc AB + arc BC = arc BC + arc CD
⇒ arc AC = arc BD
∴ AC = BD
Hence diagonal of the cyclic quadrilateral are equal.

Question 21.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
Solution:
Given : In ∆ABC, circles are drawn on sides AB and AC
To prove : Circles drawn on AB and AC intersect at D which lies on BC, the third side
Construction : Draw AD ⊥ BC

Proof: ∵ AD ⊥ BC
∴ ∠ADB = ∠ADC = 90°
So, the circles drawn on sides AB and AC as diameter will pass through D
Hence circles drawn on two sides of a triangle pass through D, which lies on the third side.

Question 22.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Solution:
In the figure, ABCD is a trapezium in which AD || BC and ∠B = 70°

∵ AD || BC
∴ ∠A + ∠B = 180° (Sum of cointerior angles)
⇒ ∠A + 70° = 180°
⇒ ∠A= 180°- 70° = 110°
∴ ∠A = 110°
But ∠A + ∠C = 180° and ∠B + ∠D = 180° (Sum of opposite angles of a cyclic quadrilateral)
∴ 110° + ∠C = 180°
⇒ ∠C = 180°- 110° = 70°
and 70° + ∠D = 180°
⇒ ∠D = 180° – 70° = 110°
∴ ∠A = 110°, ∠C = 70° and ∠D = 110°

Question 23.
In the figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.

Solution:
In the figure, ABCD is a cyclic quadrilateral whose diagonals AC and BD are drawn ∠DBC = 55° and ∠BAC = 45°

∵ ∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 45°
Now in ABCD,
∠DBC + ∠BDC + ∠BCD = 180° (Sum of angles of a triangle)
⇒ 55° + 45° + ∠BCD = 180°
⇒ 100° + ∠BCD = 180°
⇒ ∠BCD = 180° – 100° = 80°
Hence ∠BCD = 80°

Question 24.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Solution:
Given : ABCD is a cyclic quadrilateral

To prove : The perpendicular bisectors of the sides are concurrent
Proof : ∵ Each side of the cyclic quadrilateral is a chord of the circle and perpendicular of a chord passes through the centre of the circle
Hence the perpendicular bisectors of each side will pass through the centre O
Hence the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent

Question 25.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
Solution:
Given : ABCD is a cyclic rectangle and diagonals AC and BD intersect each other at O

To prove : O is the point of intersection is the centre of the circle.
Proof : Let O be the centre of the circle- circumscribing the rectangle ABCD
Since each angle of a rectangle is a right angle and AC is the chord of the circle
∴ AC will be the diameter of the circle Similarly, we can prove that diagonal BD is also the diameter of the circle
∴ The diameters of the circle pass through the centre
Hence the point of intersection of the diagonals of the rectangle is the centre of the circle.

Question 26.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that:
(i) AD || BC
(ii) EB = EC.
Solution:
Given : ABCD is a cyclic quadrilateral in which sides BA and CD are produced to meet at E and EA = ED

To prove :
(i) AD || BC
(ii) EB = EC
Proof: ∵ EA = ED
∴ In ∆EAD
∠EAD = ∠EDA (Angles opposite to equal sides)
In a cyclic quadrilateral ABCD,
Ext. ∠EAD = ∠C
Similarly Ext. ∠EDA = ∠B
∵ ∠EAD = ∠EDA
∴ ∠B = ∠C
Now in ∆EBC,
∵ ∠B = ∠C
∴ EC = EB (Sides opposite to equal sides)
and ∠EAD = ∠B
But these are corresponding angles
∴ AD || BC

Question 27.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Solution:
Given : A segment ACB shorter than a semicircle and an angle ∠ACB inscribed in it
To prove : ∠ACB < 90°
Construction : Join OA and OB

Proof : Arc ADB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle ∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB But ∠AOB > 180° (Reflex angle)
∴ ∠ACB > \(\frac { 1 }{ 2 }\) x [80°
⇒ ∠ACB > 90°

Question 28.
Prove that the angle in a segment greater than a semi-circle is less than a right angle
Solution:
Given : A segment ACB, greater than a semicircle with centre O and ∠ACB is described in it
To prove : ∠ACB < 90°
Construction : Join OA and OB

Proof : Arc ADB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle
∴ ∠ACB =\(\frac { 1 }{ 2 }\) ∠AOB
But ∠AOB < 180° (A straight angle) 1
∴ ∠ACB < \(\frac { 1 }{ 2 }\) x 180°
⇒ ∠ACB <90°
Hence ∠ACB < 90°

Question 29.
Prove that the line segment joining the mid-point of the hypotenuse of a rijght triangle to its opposite vertex is half of the hypotenuse.
Solution:
Given : In a right angled ∆ABC
∠B = 90°, D is the mid point of hypotenuse AC. DB is joined.
To prove : BD = \(\frac { 1 }{ 2 }\) AC
Construction : Draw a circle with centre D and AC as diameter

Proof: ∵ ∠ABC = 90°
∴ The circle drawn on AC as diameter will pass through B
∴ BD is the radius of the circle
But AC is the diameter of the circle and D is mid point of AC
∴ AD = DC = BD
∴ BD= \(\frac { 1 }{ 2 }\) AC

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1
• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2
• RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS
• RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

Question 1.
Find the area of a triangle whose base and altitude are 5 cm and 4 cm respectively.
Solution:
In ∆ABC,
Base BC = 5cm
Altitude AD = 4cm

Question 2.
Find the area of a triangle whose sides are 3 cm, 4 cm and 5 cm respectively.
Solution:
Sides of triangle are 3 cm, 4cm and 5cm

Question 3.
Find the area of an isosceles triangle having the base x cm and one side y cm.
Solution:
In isosceles ∆ABC,
AB = AC = y cm
BC = x cm

Question 4.
Find the area of an equilateral triangle having each side 4 cm.
Solution:
Each side of equilateral triangle (a) = 4cm

Question 5.
Find the area of an equilateral triangle having each side x cm.
Solution:

Question 6.
The perimeter of a triangular field is 144 m and the ratio of the sides is 3 : 4 : 5. Find the area of the field.
Solution:
Perimeter of the field = 144 m
Ratio in the sides = 3:4:5
Sum of ratios = 3 + 4 + 5 = 12

Question 7.
Find the area of an equilateral triangle having altitude h cm.
Solution:
Altitude of an equilateral triangle = h
Let side of equilateral triangle = x

Question 8.
Let ∆ be the area of a triangle. Find the area of a triangle whose each side is twice the side of the given triangle.
Solution:
Let a, b, c be the sides of the original triangle

Hence area of new triangle = 4 x area of original triangle.

Question 9.
If each side of a triangle is doubled, then find percentage increase in its area.
Solution:
Sides of original triangle be a, b, c

Question 10.
If each side of an equilateral triangle is tripled then what is the percentage increase in the area of the triangle?
Solution:
Let the sides of the original triangle be a, b, c and area ∆, then

Hope given RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1
• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2
• RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS
• RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

Question 1.
Find the area of a quadrilateral ABCD in which AB = 3cm, BC = 4cm, CD = 4cm, DA = 5cm and AC = 5cm (NCERT)
Solution:
In the quadrilateral, AC is the diagonal which divides the figure into two triangles
Now in ∆ABC, AB = 3 cm, BC = 4cm, AC = 5cm

Question 2.
The sides of a quadrangular field taken in order are 26 m, 27 m, 7 m and 24 m respectively. The angle contained by the last two sides is a right angle. Find its area.
Solution:
In quad. ABCD, AB = 26 m, BC = 27 m CD = 7m, DA = 24 m, ∠CDA = 90°
Join AC,

Question 3.
The sides of a quadrilateral taken in order are 5, 12, 14 and 15 metres respectively, and the angle contained by the first two sides is a right angle. Find its area.
Solution:
In quad. ABCD,
AB = 5m, BC = 12 m, CD = 14m,
DA = 15 m and ∠ABC = 90°
Join AC,
Now in right ∆ABC,
AC² = AB² + BC² = (5)² + (12)²
= 25 + 144 = 169 = (13)²
∴ AC = 13 m
Now area of right ∆ABC

Question 4.
A park, in shape of a quadrilateral ABCD, has ∠C = 90°, AB = 9m, BC = 12m, CD = 5m and AD = 8m. How much area does it occupy? (NCERT)
Solution:
In quadrilateral ABCD,
AB = 9m, BC = 12m, CD = 5m and
DA = 8m, ∠C = 90°
Join BD,
Now in right ∆BCD,
BD² = BC²+ CD² = (12)² + (5)²
= 144 + 25 = 169 = (13)²
∴ BD = 13m

Question 5.
Find the area of a rhombus whose perimeter is 80m and one of whose diagonal is 24m.
Solution:
Perimeter of rhombus ABCD = 80 m

Question 6.
A rhombus sheet whose perimeter = 32 m and whose one diagonal is 10 m long, is painted on both sides at the rate of ₹5 per m². Find the cost of painting.
Solution:
Perimeter of the rhombus shaped sheet = 32 m

∴ Length of each side = \(\frac { 32 }{ 4 }\) = 8m
and length of one diagonal AC = 10 m
In ∆ABC, sides are 8m, 8m, 10m

Question 7.
Find the area of a quadrilateral ABCD in which AD = 24 cm, ∠BAD = 90° and BCD forms an equilateral triangle whose each side is equal to 26 cm. (Take \(\sqrt { 3 } \) = 1.73 )
Solution:
In quadrilateral ABCD, AD = 24cm, ∠BAD = 90°

BCD is an equilateral triangle with side 26cm
In right ∆ABD,
BD² = AB²+ AD²
(26)² = AB² + (24)²
⇒ 676 = AB² + 576
AB² = 676 – 576 = 100 = (10)²
∴ AB = 10cm
Now area of right ∆ABD,

Question 8.
Find the area of a quadrilateral ABCD in which AB = 42cm, BC = 21cm, CD = 29 cm, DA = 34 cm and diagonal BD = 20 cm.
Solution:
In quadrilateral ABCD,
AB = 42 cm, BC = 21 cm, CD = 29cm DA = 34 cm, BD = 20 cm

Question 9.
The adjacent sides of a parallelogram ABCD measures 34 cm and 20 cm, and the diagonal AC measures 42 cm. Find the area of the parallelogram.
Solution:
In ||gm ABCD,
AB = 34cm, BC = 20 cm
and AC = 42 cm

∵ The diagonal of a parallelogram divides into two triangles equal in area,
Now area of ∆ABC,

Question 10.
Find the area of the blades of the magnetic compass shown in figure. (Take \(\sqrt { 11 } \) = 3.32).

Solution:
ABCD is a rhombus with each side 5cm and one diagonal 1cm
Diagonal BD divides into two equal triangles Now area of ∆ABD,

Question 11.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 13 cm, 14 cm and 15 cm and the parallelogram stands on the base 14 cm, find the height of the parallelogram.
Solution:
Area of a triangle with same base and area of a 11gm with equal sides of triangle are 13, 14, 15 cm

Question 12.
Two parallel sides of a trapezium are 60cm and 77 cm and other sides are 25 cm and 26 cm. Find the area of the trapezium.
Solution:
In trapezium ABCD, AB || DC

AB = 77cm, BC = 26 cm, CD 60cm DA = 25 cm
Through, C, draw CE || DA meeting AB at E
∴ AE = CD = 60 cm and EB = 77 – 60 = 17 cm,
CE = DA = 25 cm
Now area of ∆BCE, with sides 17 cm, 26 cm, 25 cm

Question 13.
Find the perimeter and area of the quadrilateral ABCD in which AB = 17 cm, AD = 9cm, CD = 12cm, ∠ACB = 90° and AC = 15cm.
Solution:
In right ΔABC, ∠ACB = 90°
AB² = AC² + BC²
(17)² = (15)²+ BC² = 289 = 225 + BC²

Question 14.
A hand fan is made by stitching 10 equal size triangular strips of two different types of paper as shown figure. The dimensions of equal strips are 25 cm, 25 cm and 14 cm. Find the area of each types of paper needed to make the hand fan.
Solution:
In the figure, a hand fan has 5 isosceles and triangle. With sides 25 cm, 25 cm and 14 cm each.

Hope given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1
• RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.2
• RD Sharma Class 9 Solutions Chapter 17 Constructions VSAQS
• RD Sharma Class 9 Solutions Chapter 17 Constructions MCQS

Question 1.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm.
Solution:
Sides of triangle are 120 cm, 150 cm, 200 cm

Question 2.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm.
Solution:
Sides of a triangle are 9 cpi, 12 cm, 15 cm

Question 3.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
Perimeter of a triangle = 42 cm
Two sides are 18 cm and 10 cm
Third side = 42 – (18 + 10)
= 42 – 28 = 14 cm

Question 4.
In a ∆ABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ∆ABC and hence its altitude on AC.
Solution:
Sides of triangle ABC are AB = 15 cm, BC = 13 cm, AC = 14 cm

Question 5.
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle. [NCERT]
Solution:
Perimeter of a triangle = 540 m
Ratio in sides = 25 : 17 : 12
Sum of ratios = 25 + 17 + 12 = 54

Question 6.
The perimeter of a triangle is 300 m. If its sides are in the ratio 3:5:7. Find the area of the triangle. [NCERT]
Solution:
Perimeter of a triangle = 300 m
Ratio in the sides = 3 : 5 : 7
∴ Sum of ratios = 3 + 5 + 7= 15

Question 7.
The perimeter of a triangular field is 240 dm. If two of its sides are 78 dm and 50 dm, find the length of the perpendicular on the side of length 50 dm from the opposite vertex.
Solution:
Perimeter of a triangular field = 240 dm
Two sides are 78 dm and 50 dm
∴ Third side = 240 – (78 + 50)
= 240 – 128 = 112 dm

Question 8.
A triangle has sides 35 cm, 54 cm and 61 cm long. Find its area. Also, find the smallest of its altitudes.
Solution:
Sides of a triangle are 35 cm, 54 cm, 61 cm

Question 9.
The lengths of the sides of a triangle are in the ratio 3:4:5 and its perimeter is 144 cm. Find the area of the triangle and the height corresponding to the longest side.
Solution:
Ratio in the sides of a triangle = 3:4:5

Question 10.
The perimeter of an isosceles triangle is 42 cm and its base is (3/2) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
Solution:
Perimeter of an isosceles triangle = 42 cm
Base = \(\frac { 3 }{ 2 }\) of its one of equal sides
Let each equal side = x, then 3
Base = \(\frac { 3 }{ 2 }\) x

Question 11.
Find the area of the shaded region in figure.

Solution:
In ∆ABC, AC = 52 cm, BC = 48 cm
and in right ∆ADC, ∠D = 90°
AD = 12 cm, BD = 16 cm
∴ AB²=AD² + BD² (Pythagoras Theorem)
(12)² + (16)² = 144 + 256 = 400 = (20)²
∴ AB = 20 cm

Hope given RD Sharma Class 9 Solutions Chapter 17 Constructions Ex 17.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
In the figure, O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

Solution:
Arc AB, subtends ∠AOB at the centre and ∠APB at the remaining part of the circle
∴∠AOB = 2∠APB = 2 x 50° = 100°
Join AB

∆AOB is an isosceles triangle in which
OA = OB
∴ ∠OAB = ∠OBA But ∠AOB = 100°
∴∠OAB + ∠OBA = 180° – 100° = 80°
⇒ 2∠OAB = 80°
80°
∴∠OAB = \(\frac { { 80 }^{ \circ } }{ 2 }\)  = 40°

Question 2.
In the figure, O is the centre of the circle. Find ∠BAC.

Solution:
In the circle with centre O
∠AOB = 80° and ∠AOC =110°
∴ ∠BOC = ∠AOB + ∠AOC
= 80°+ 110°= 190°
∴ Reflex ∠BOC = 360° – 190° = 170°
Now arc BEC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.

∴ ∠BOC = 2∠BAC
⇒ 170° = 2∠BAC
⇒ ∠BAC = \(\frac { { 170 }^{ \circ } }{ 2 }\) = 85°
∴ ∠BAC = 85°

Question 3.
If O is the centre of the circle, find the value of x in each of the following figures:



Solution:
(i) A circle with centre O
∠AOC = 135°
But ∠AOC + ∠COB = 180° (Linear pair)
⇒ 135° + ∠COB = 180°
⇒ ∠COB = 180°- 135° = 45°
Now arc BC subtends ∠BOC at the centre and ∠BPC at the remaining part of the circle
∴ ∠BOC = 2∠BPC
⇒ ∠BPC = \(\frac { 1 }{ 2 }\)∠BOC = \(\frac { 1 }{ 2 }\) x 45° = \(\frac { { 45 }^{ \circ } }{ 2 }\)
∴ ∠BPC = 22 \(\frac { 1 }{ 2 }\)° or x = 22 \(\frac { 1 }{ 2 }\)°
(ii) ∵ CD and AB are the diameters of the circle with centre O
∠ABC = 40°
But in ∆OBC,
OB = OC (Radii of the circle)
∠OCB = ∠OBC – 40°
Now in ABCD,
∠ODB + ∠OCB + ∠CBD = 180° (Angles of a triangle)
⇒ x + 40° + 90° = 180°
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
∴ x = 50°
(iii) In circle with centre O,
∠AOC = 120°, AB is produced to D
∵ ∠AOC = 120°
and ∠AOC + convex ∠AOC = 360°
⇒ 120° + convex ∠AOC = 360°
∴ Convex ∠AOC = 360° – 120° = 240°
∴ Arc APC Subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle
∴ ∠ABC = \(\frac { 1 }{ 2 }\)∠AOC = \(\frac { 1 }{ 2 }\)x 240° = 120°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ 120° + x = 180°
⇒ x = 180° – 120° = 60°
∴ x = 60°
(iv) A circle with centre O and ∠CBD = 65°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ ∠ABC + 65° = 180°
⇒ ∠ABC = 180°-65°= 115°
Now arc AEC subtends ∠x at the centre and ∠ABC at the remaining part of the circle
∴ ∠AOC = 2∠ABC
⇒ x = 2 x 115° = 230°
∴ x = 230°
(v) In circle with centre O
AB is chord of the circle, ∠OAB = 35°
In ∆OAB,
OA = OB (Radii of the circle)
∠OBA = ∠OAB = 35°
But in ∆OAB,
∠OAB + ∠OBA + ∠AOB = 180° (Angles of a triangle)
⇒ 35° + 35° + ∠AOB = 180°
⇒ 70° + ∠AOB = 180°
⇒ ∠AOB = 180°-70°= 110°
∴ Convex ∠AOB = 360° -110° = 250°
But arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴∠ACB = \(\frac { 1 }{ 2 }\)∠AOB
⇒ x = \(\frac { 1 }{ 2 }\) x 250° = 125°
∴ x= 125°
(vi) In the circle with centre O,
BOC is its diameter, ∠AOB = 60°
Arc AB subtends ∠AOB at the centre of the circle and ∠ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB
= \(\frac { 1 }{ 2 }\) x 60° = 30°
But in ∆OAC,
OC = OA (Radii of the circle)
∴ ∠OAC = ∠OCA = ∠ACB
⇒ x = 30°
(vii) In the circle, ∠BAC and ∠BDC are in the same segment
∴ ∠BDC = ∠BAC = 50°
Now in ABCD,
∠DBC + ∠BCD + ∠BDC = 180° (Angles of a triangle)
⇒ 70° + x + 50° = 180°
⇒ x + 120° = 180° ⇒ x = 180° – 120° = 60°
∴ x = 60°
(viii) In circle with centre O,
∠OBD = 40°
AB and CD are diameters of the circle
∠DBA and ∠ACD are in the same segment
∴ ∠ACD = ∠DBA = 40°
In AOAC, OA = OC (Radii of the circle)
∴ ∠OAC = ∠OCA = 40°
and ∠OAC + ∠OCA + ∠AOC = 180° (Angles in a triangle)
⇒ 40° + 40° + x = 180°
⇒ x + 80° = 180° ⇒ x = 180° – 80° = 100°
∴ x = 100°
(ix) In the circle, ABCD is a cyclic quadrilateral ∠ADB = 32°, ∠DAC = 28° and ∠ABD = 50°
∠ABD and ∠ACD are in the same segment of a circle
∴ ∠ABD = ∠ACD ⇒ ∠ACD = 50°
Similarly, ∠ADB = ∠ACB
⇒ ∠ACB = 32°
Now, ∠DCB = ∠ACD + ∠ACB
= 50° + 32° = 82°
∴ x = 82°
(x) In a circle,
∠BAC = 35°, ∠CBD = 65°
∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 35°
In ∆BCD,
∠BDC + ∠BCD + ∠CBD = 180° (Angles in a triangle)
⇒ 35° + x + 65° = 180°
⇒ x + 100° = 180°
⇒ x = 180° – 100° = 80°
∴ x = 80°
(xi) In the circle,
∠ABD and ∠ACD are in the same segment of a circle
∴ ∠ABD = ∠ACD = 40°
Now in ∆CPD,
∠CPD + ∠PCD + ∠PDC = 180° (Angles of a triangle)
110° + 40° + x = 180°
⇒ x + 150° = 180°
∴ x= 180°- 150° = 30°
(xii) In the circle, two diameters AC and BD intersect each other at O
∠BAC = 50°
In ∆OAB,
OA = OB (Radii of the circle)
∴ ∠OBA = ∠OAB = 52°
⇒ ∠ABD = 52°
But ∠ABD and ∠ACD are in the same segment of the circle
∴ ∠ABD = ∠ACD ⇒ 52° = x
∴ x = 52°

Question 4.
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A.
Solution:
Given : O is the circumcentre of ∆ABC.
OD ⊥ BC
OB is joined
To prove : ∠BOD = ∠A
Construction : Join OC.

Proof : Arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle
∴ ∠BOC = 2∠A …(i)
In right ∆OBD and ∆OCD Side OD = OD (Common)
Hyp. OB = OC (Radii of the circle)
∴ ∆OBD ≅ ∆OCD (RHS criterion)
∴ ∠BOD = ∠COD = \(\frac { 1 }{ 2 }\) ∠BOC
⇒ ∠BOC = 2∠BOD …(ii)
From (i) and (ii)
2∠BOD = 2∠A
∴∠BOD = ∠A

Question 5.
In the figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.

Solution:
Given : In the figure, a circle with centre O OB is the bisector of ∠ABC
To prove : AB = BC
Construction : Draw OL ⊥ AB and OM ⊥ BC

Proof: In ∆OLB and ∆OMB,
∠1 = ∠2 (Given)
∠L = ∠M (Each = 90°)
OB = OB (Common)
∴ ∆OLB ≅ ∆OMB (AAS criterion)
∴ OL = OM (c.p.c.t.)
But these are distance from the centre and chords equidistant from the centre are equal
∴ Chord BA = BC
Hence AB = BC

Question 6.
In the figure, O and O’ are centres of two circles intersecting at B and C. ACD is a straight line, find x.

Solution:
In the figure, two circles with centres O and O’ intersect each other at B and C.
ACD is a line, ∠AOB = 130°
Arc AB subtends ∠AOB at the centre O and ∠ACB at the remaining part of the circle.

∴ ∠ACB =\(\frac { 1 }{ 2 }\)∠AOB
= \(\frac { 1 }{ 2 }\) x 130° = 65°
But ∠ACB + ∠BCD = 180° (Linear pair)
⇒ 65° + ∠BCD = 180°
⇒ ∠BCD = 180°-65°= 115°
Now, arc BD subtends reflex ∠BO’D at the centre and ∠BCD at the remaining part of the circle
∴ ∠BO’D = 2∠BCD = 2 x 115° = 230°
But ∠BO’D + reflex ∠BO’D = 360° (Angles at a point)
⇒ x + 230° = 360°
⇒ x = 360° -230°= 130°
Hence x = 130°

Question 7.
In the figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.

Solution:
Arc AB subtend ∠ACB and ∠ADB in the same segment of a circle
∴ ∠ACB = ∠ADB = 40°
In ∆PDB,
∠DPB + ∠PBD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 120° + ∠PBD + 40° = 180°
⇒ 160° + ∠PBD = 180°
⇒ ∠PBD = 180° – 160° = 20°
⇒ ∠CBD = 20°

Question 8.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
A circle with centre O, a chord AB = radius of the circle C and D are points on the minor and major arcs of the circle

∴ ∠ACB and ∠ADB are formed Now in ∆AOB,
OA = OB = AB (∵ AB = radii of the circle)
∴ ∆AOB is an equilateral triangle,
∴ ∠AOB = 60°
Now arc AB subtends ∠AOB at the centre and ∠ADB at the remainder part of the circle.
∴ ∠ADB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\)x 60° = 30°
Now ACBD is a cyclic quadrilateral,
∴ ∠ADB + ∠ACB = 180° (Sum of opposite angles of cyclic quad.)
⇒ 30° + ∠ACB = 180°
⇒ ∠ACB = 180° – 30° = 150°
∴ ∠ACB = 150°
Hence angles are 150° and 30°

Question 9.
In the figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

Solution:
In circle with centre O and ∠AOC = 150°
But ∠AOC + reflex ∠AOC = 360°
∴ 150° + reflex ∠AOC = 360°
⇒ Reflex ∠AOC = 360° – 150° = 210°
Now arc AEC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.

Reflex ∠AOC = 2∠ABC
⇒ 210° = 2∠ABC
∴ ∠ABC = \(\frac { { 210 }^{ \circ } }{ 2 }\)  = 105°

Question 10.
In the figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
Solution:
Given : In circle, O is centre

To prove : ∠x = ∠y + ∠z
Proof : ∵ ∠3 and ∠4 are in the same segment of the circle
∴ ∠3 = ∠4 …(i)
∵ Arc AB subtends ∠AOB at the centre and ∠3 at the remaining part of the circle
∴ ∠x = 2∠3 = ∠3 + ∠3 = ∠3 + ∠4 (∵ ∠3 = ∠4) …(ii)
In ∆ACE,
Ext. ∠y = ∠3 + ∠1
(Ext. is equal to sum of its interior opposite angles)
⇒ ∠3 – ∠y – ∠1 …(ii)
From (i) and (ii),
∠x = ∠y – ∠1 + ∠4 …(iii)
Similarly in ∆ADF,
Ext. ∠4 = ∠1 + ∠z …(iv)
From (iii) and (iv)
∠x = ∠y-∠l + (∠1 + ∠z)
= ∠y – ∠1 + ∠1 + ∠z = ∠y + ∠z
Hence ∠x = ∠y + ∠z

Question 11.
In the figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.

Solution:
In the figure, O is the centre of the circle,
PQ is the diameter and ∠ROS = 40°
Now we have to find ∠RTS
Arc RS subtends ∠ROS at the centre and ∠RQS at the remaining part of the circle

∴ ∠RQS = \(\frac { 1 }{ 2 }\) ∠ROS
= \(\frac { 1 }{ 2 }\) x 40° = 20°
∵ ∠PRQ = 90° (Angle in a semi circle)
∴ ∠QRT = 180° – 90° = 90° (∵ PRT is a straight line)
Now in ∆RQT,
∠RQT + ∠QRT + ∠RTQ = 180° (Angles of a triangle)
⇒ 20° + 90° + ∠RTQ = 180°
⇒ ∠RTQ = 180° – 20° – 90° = 70° or ∠RTS = 70°
Hence ∠RTS = 70°

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Construct a ∆ABC in which BC = 3.6 cm, AB + AC = 4.8 cm and ∠B = 60°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.6 cm.
(ii) At B, draw a ray BX making an angle of 60° and cut off BE = 4.8 cm.
(iii) Join EC.
(iv) Draw perpendicular bisector of CE which intersects BE at A.
(v) Join AC.
∆ABC is the required triangle.

Question 2.
Construct a ∆ABC in which AB + AC = 5.6 cm, BC = 4.5 cm and ∠B = 45°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4.5 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = 5.6 cm and join CE.
(iii) Draw the perpendicular bisector of CE which intersects BE at A.
(iv) Join AC.
∆ABC is the required triangle.

Question 3.
Construct a AABC in which BC = 3.4 cm, AB – AC = 1.5 cm and ∠B = 45°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.4 cm.
(ii) At B, draw a ray BX making an angle of 45° and cut off BE = 1.5 cm.
(iii) Join EC.
(iv) Draw the perpendicular bisector of CE which intersects BE produced at A.
(v) Join AC.
∆ABC is the required triangle.

Question 4.
Using ruler and compasses only, construct a ∆ABC, given base BC = 7 cm, ∠ABC = 60° and AB + AC = 12 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 7 cm!
(ii) At B, draw a ray BX making an angle of 60° and cut off BE = 12 cm.
(iii) Join EC.
(iv) Draw the perpendicular bisector of EC which intersects BE at A.
(v) Join AC.
∆ABC is the required triangle.

Question 5.
Construct a right-angled triangle whose perimeter is equal to 10 cm and one acute angle equal to 60°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 10 cm.
(ii) At P, draw a ray PX making an angle of 90° and at Q, QY making an angle of 60°.
(iii) Draw the angle bisectors of ∠P and ∠Q meeting each other at A.
(iv) Draw the perpendicular bisectors of AP and AQ intersecting PQ at B and C respectively,
(v) Join AB and AC.
∆ABC is the required triangle.

Question 6.
Construct a triangle ABC such that BC = 6cm, AB = 6 cm and median AD = 4 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm and bisect it at D.
(ii) With centre B and radius 6 cm and with centre D and radius 4 cm, draw arcs intersecting each other at A.
(iii) Join AD and AB and AC.
Then ∆ABC is the required triangle.

Question 7.
Construct a right triangle ABC whose base BC is 6 cm and the sum of hypotenuse AC and other side AB is 10 cm.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm

(ii) At B, draw a ray BX making an angle of 90° and cut off BE = 10 cm.
(iii) Join EC and draw the perpendicular bisector of CE which intersects BE at A.
(iv) Join AC.
∆ABC is the required triangle.

Question 8.
Construct a triangle whose perimeter is 6.4 cm, and angles at the base are 60° and 45°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 6.4 cm.
(ii) At P draw a ray PX making an angle of 60° and at Q, a ray QY making an angle of 45°.
(iii) Draw the bisector of ∠P and ∠Q meeting each other at A.
(iv) Draw the perpendicular bisectors of PA and QA intersecting PQ at B and C respectively.
(v) Join AB and AC.
∆ABC is the required triangle.

Question 9.
Using ruler and compasses only, construct a ∆ABC, from the following data:
AB + BC + CA = 12 cm, ∠B = 45° and ∠C = 60°.
Solution:
Steps of construction :
(i) Draw a line segment PQ = 12 cm.
(ii) Draw ray PX at P making are angle of 45° and at Q, QY making an angle of 60°.
(Hi) Draw the angle bisectors of ∠P and ∠Q meeting each other at A.
(v) Draw the perpendicular bisector of AP and AQ intersecting PQ at B and C respectively.
(v) Join AB and AC.
∆ABC is the required triangle.

Question 10.
Construct a triangle XYZ in which ∠Y = 30° , ∠Z = 90° XY +YZ + ZX = 11
Solution:
Steps of construction :
(i) Draw a line segment PQ =11 cm.
(ii) At P, draw a ray PL making an angle of 30° and Q, draw another ray QM making an angle of 90°.
(iii) Draw the angle bisector of ∠P and ∠Q intersecting each other at X.
(iv) Draw the perpendicular bisector of XP and XQ. Which intersect PQ at Y and Z respectively.
(v) Join XY and XZ.
Then ∆XYZ is the required triangle

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
• RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3

Question 1.
Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC.
Solution:
Steps of construction :
(i) Draw an angle BAC.
(ii) Draw a line DF.
(iii) With centre A and D, draw arcs of equal radius which intersect AC at L and AB at M and DF at P.
(iv) Cut off PQ = LM and join DQ and produce it to E, then
∠EDF = ∠BAC.

Question 2.
Draw an obtuse angle. Bisect it. Measure each of the angles so obtained.
Solution:
Steps of construction :
(i) Draw an angle ABC which is an obtuse i.e. more than 90°.
(ii) With centre B and a suitable radius draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
ThenBD is die bisector of ∠ABC.
On measuring each part, we find each angle = 53°.

Question 3.
Using your protractor, draw an angle of measure 108°. With this angle as given, draw an angle of 54°.
Solution:
Steps of construction :
(i) With the help of protractor draw an angle ABC = 108°.
As 54° = \(\frac { 1 }{ 2 }\) x 108°
∴ We shall bisect it.

(ii) With centre B and a suitable radius, draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF, draw arcs intersecting each other at G
(iv) Join BG and produce it to D.
Then ∠DBC = 54°.

Question 4.
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Solution:
Steps of construction :
(i) Using protractor, draw a right angle ∆ABC.
i. e. ∠ABC = 90°.
(ii) With centre B and a suitable radius, draw an arc which meets BC at E and BA at F.
(iii) With centre E and F, draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC =\(\frac { 1 }{ 2 }\) x 90° = 45°.

Question 5.
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Solution:
Steps of construction :
(i) Draw a linear pair ∠DCA and ∠DCB.
(ii) Draw the bisectors of ∠DCA and ∠DCB. Forming ∠ECF on measuring we get ∠ECF = 90°.
Verification : ∵∠DCA + ∠DCB = 180°
⇒ \(\frac { 1 }{ 2 }\) ∠DCA + \(\frac { 1 }{ 2 }\) ∠DCB = 180° x \(\frac { 1 }{ 2 }\) = 90°
∴ ∠ECF = 90°
i.e. EC and FC are perpendicular to each other.

Question 6.
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line
Solution:
Steps of construction :
(i) Draw two lines AB and CD intersecting each other at O.
(ii) Draw the bisector of ∠AOD and also the bisector of ∠BOC. Which are OP and OQ respectively. We see that OP and OQ are in the same straight line.

Question 7.
Using ruler and compasses only, draw a right angle.
Solution:
Steps of construction :
(i) Draw a line segment BC.
(ii) With centre B and a suitable radius, draw an arc meeting BC at E.
(iii) With centre E and same radius, cut off arcs EF and FG.
(iv) Bisect arc FG at H.
(v) Join BH and produce it to A.
Then ∠ABC = 90°.

Question 8.
Using ruler and compasses only, draw an angle of measure 135°.
Solution:
Steps of construction :
(i) Draw a line DC and take a point B on it.
(ii) With centre B and a suitable radius draw an arc meeting BC at P.
(iii) With centre P, cut off arcs PQ, QR and RS.
(iv) Bisect as QR at T and join BT and produce it to E.
(v) Now bisect the arc KS at RL.
(vi) Join BL and produce it to A.
Now ∠ABC = 135°.

Question 9.
Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Solution:
Steps of construction :
(i) Draw an angle ABC = 12° with the help of protractor.
(ii) With centre B and a suitable radius, draw an arc EF.
(iii) With centre E and F, draw arcs intersecting
each other at G and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC = 72° x \(\frac { 1 }{ 2 }\) = 36°.
(iv) Again bisect ∠ABD in the same way then PB is the bisector of ∠ABD.
∴ ∠PBC = 36° + \(\frac { 1 }{ 2 }\) x 36°
= 36° + 18° = 54°
Hence ∠PBC = 54°

Question 10.
Construct the following angles at the initial point of a given ray and justify the construction:
(i) 45°
(ii) 90°
Solution:
(i) 45°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) With centre E, cut off equal arcs EF and FG.
(d) Bisect FG at H.
(e) Join BH and produce to X so that ∠XBC = 90°.
(f) Bisect ∠XBC so that ∠ABC = 45°.

(ii) 90°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E and with centre E cut off arcs from E, EF = FG
(c) Now bisect the arc EG at H.
(d) Join BH and produce it to A.
∴ ∠ABC = 90°.

Question 11.
Construct the angles of the following measurements:
(i) 30°
(ii) 75°
(iii) 105°
(iv) 135°
(v) 15°
(vi) 22 \(\frac { 1 }{ 2 }\)°
Solution:
(i) 30°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) Cut off arcs EF and bisect it at G.
So that ∠ABC = 30°.

(ii) 75°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF = FG from E.
(d) Bisect the arc FG at K and join BK so that ∠KBC = 90°.
(e) Now bisect arc HF at L and join BL and produce it to A so that ∠ABC = 75°.

(iii) 105°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) From E, cut off arc EF = FG and divide FG at H.
(d) Join BH meeting the arc at K.
(e) Now bisect the arc KG at L.
Join BL and produce it to A.
Then ∠ABC = 105°.

(iv) 135°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) From E, cut off EF = FG = GH.
(d) Bisect arc FG at K, and join them.
(e) Bisect arc KH at L.
(f) Join BL and produce it to A, then ∠ABC = 135°.

(v) 15°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF from E and bisect it at G. Then ∠GBC = 30°.
(d) Again bisect the arc EJ at H.
(e) Join BH and produce it to A.
Then ∠ABC = 15°.

(vi) 22 \(\frac { 1 }{ 2 }\)°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc and from E, cut off EF = FG
(c) Bisect FG at H so that ∠HBC = 90°.
(d) Now bisect ∠HBC at K. So that ∠YBC = 45°.
(e) Again bisect ∠YBC at J. So thttt ∠ABC = 22 \(\frac { 1 }{ 2 }\)°

Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.