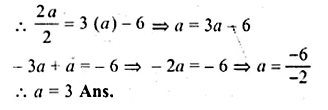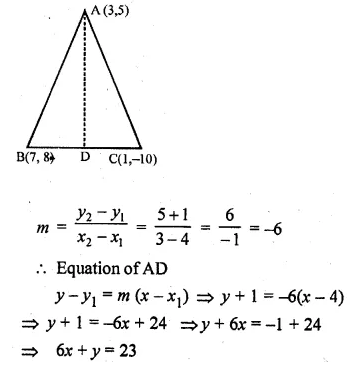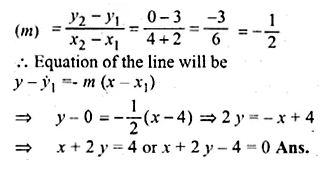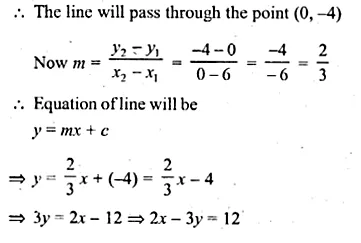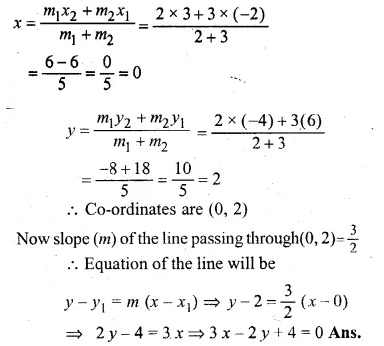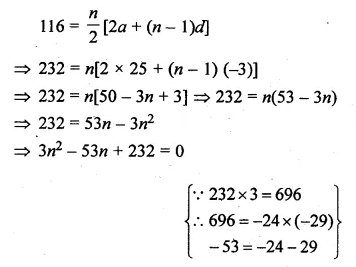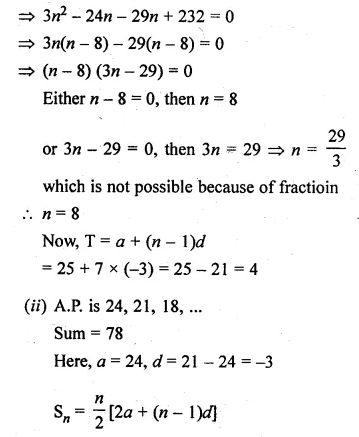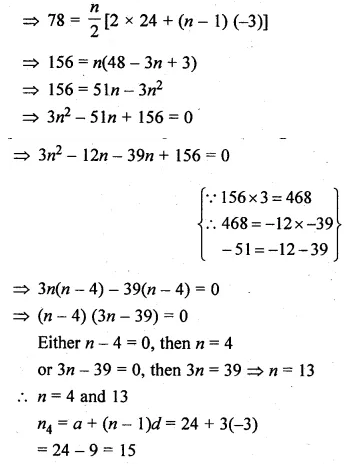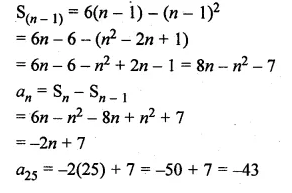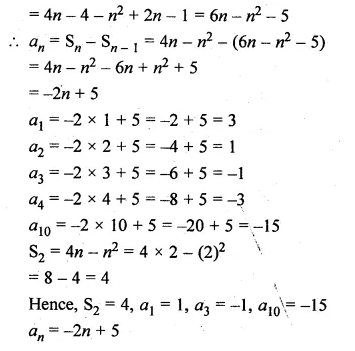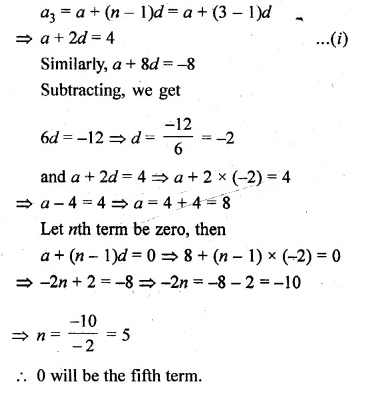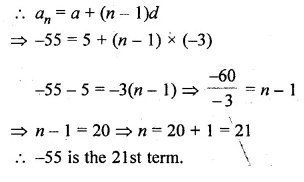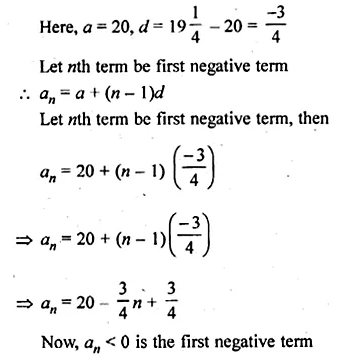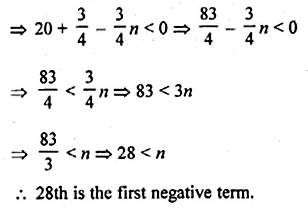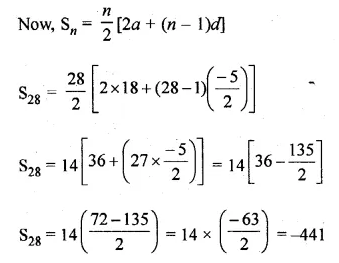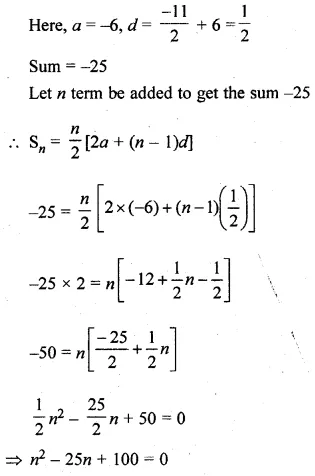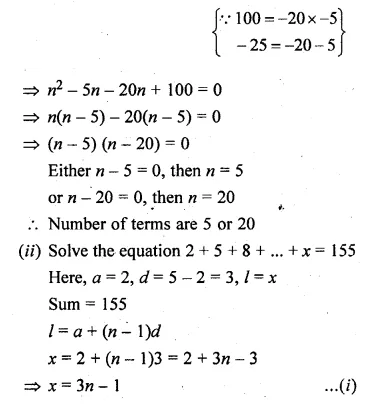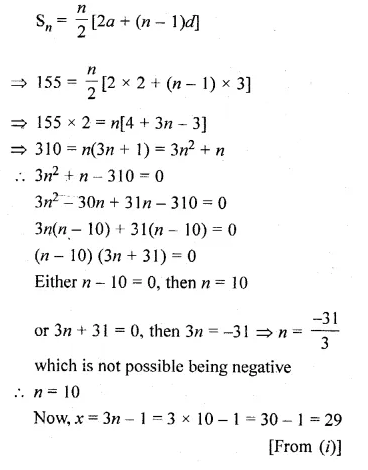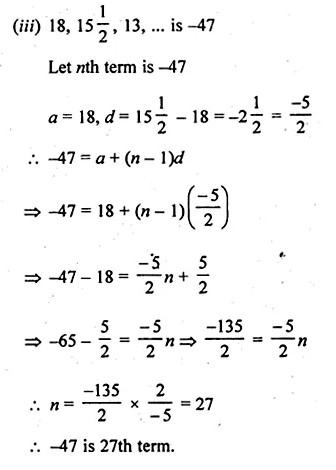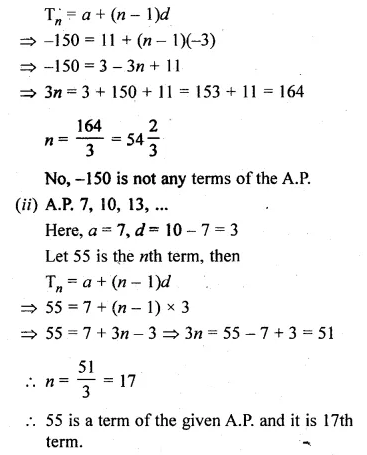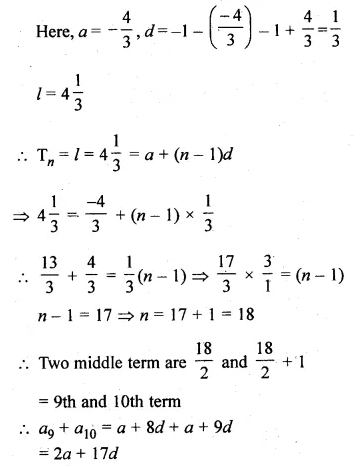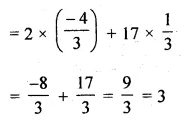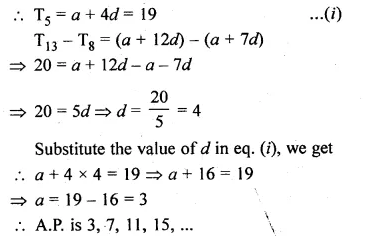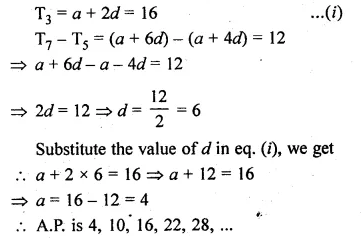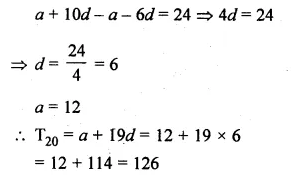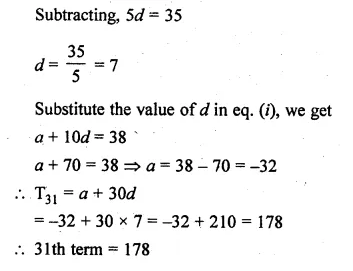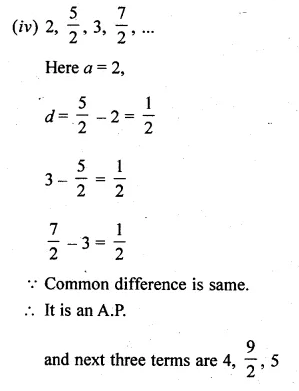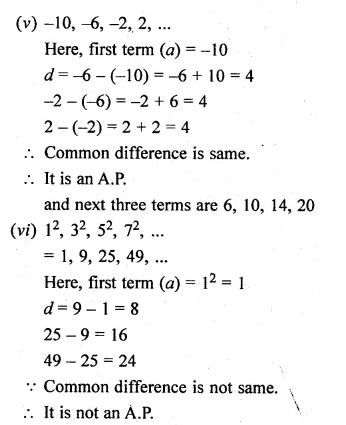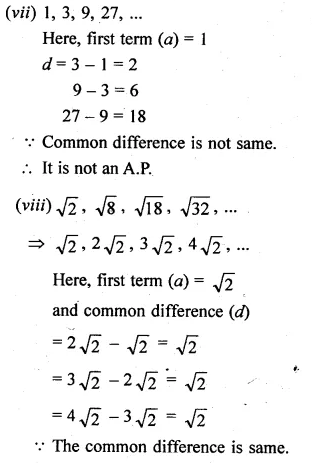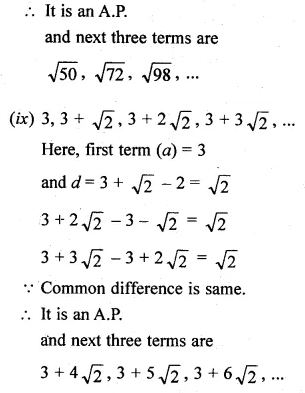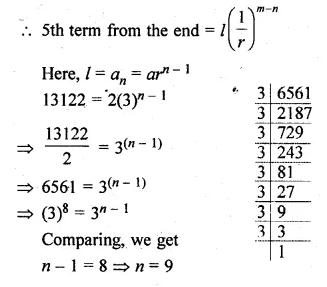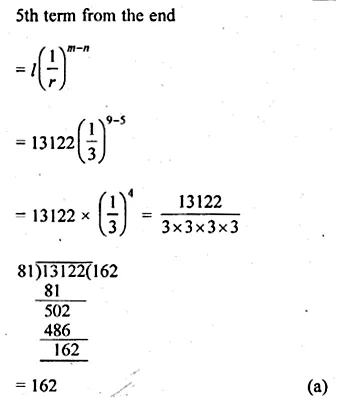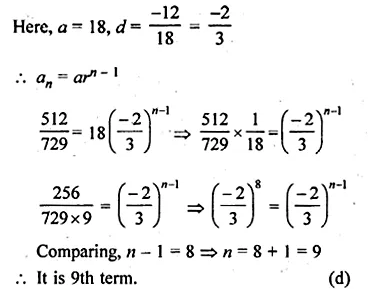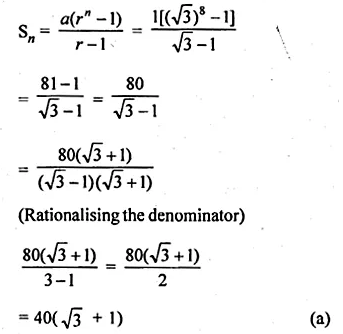Category: ICSE Class 10

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test

Question 1.
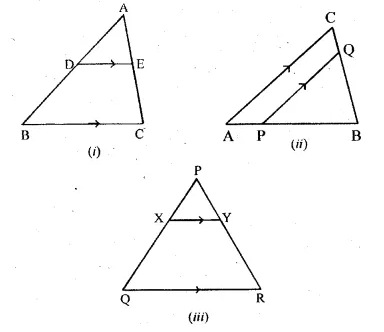
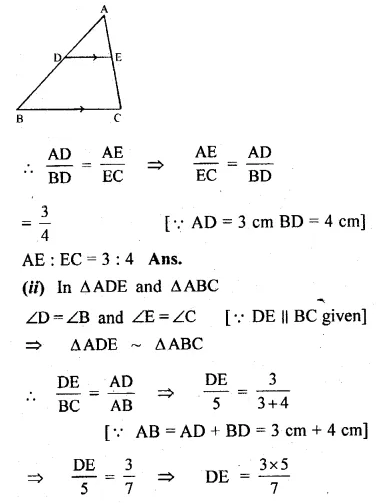
(a) In the figure (i) given below if DE || BG, AD = 3 cm, BD = 4 cm and BC = 5 cm. Find (i) AE : EC (ii) DE.
(b) In the figure (ii) given below, PQ || AC, AP = 4 cm, PB = 6 cm and BC = 8 cm. Find CQ and BQ.
(c) In the figure (iii) given below, if XY || QR, PX = 1 cm, QX = 3 cm, YR = 4.5 cm and QR = 9 cm, find PY and XY.

Solution:
(a) In the figure (i)
Given : DE || BC, AD = 3 cm, BD = 4 cm and BC = 5 cm.
To find (i) AE : EC and
(ii) DE Since DE || BC of ∆ABC

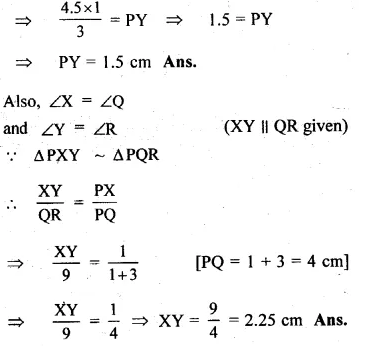
Question 2.
In the given figure, DE || BC.
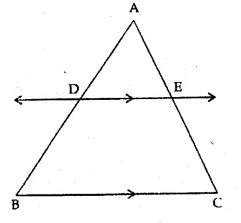
(i) If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, find the value of x.
(ii) If DB = x – 3, AB = 2x, EC = x – 2 and AC = 2x + 3, find the value of x.

Solution:
In the given figure, DE || BC
(i) AD = x, DB = x – 2, AE = x + 2, EC = x – 1
In ∆ABC,
∵DE || BC

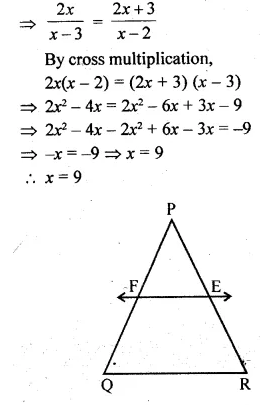
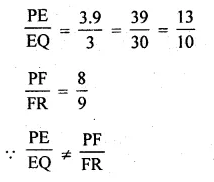
Question 3.
E and F are points on the sides PQ and PR respectively of a ∆PQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 8 cm and RF = 9 cm.
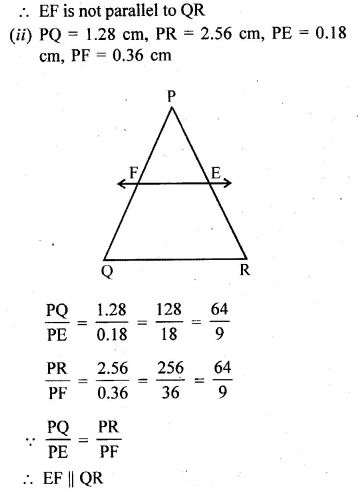
(ii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.
Solution:
(i) In ∆PQR, E and F are the points on the sides PQ and PR respectively
PE = 3.9 cm, EQ = 3 cm, PF = 8 cm,
RF = 9 cm
Is EF || QR ?

Question 4.
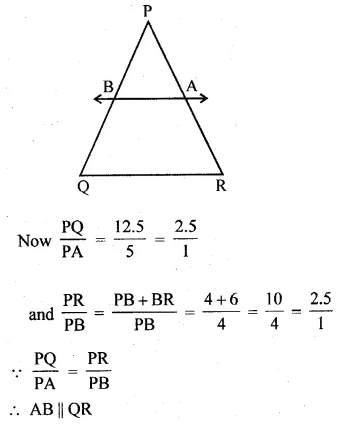
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
Solution:
In ∆PQR, A and B are points on the sides PQ and PR such that
PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm

Question 5.
(a) In figure (i) given below, DE || BC and BD = CE. Prove that ABC is an isosceles triangle.
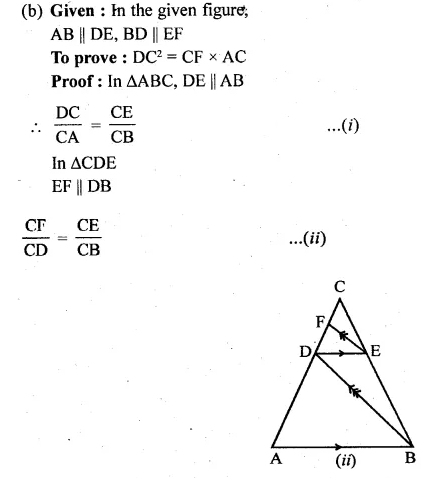
(b) In figure (ii) given below, AB || DE and BD || EF. Prove that DC² = CF x AC.
Solution:
(a) Given: In the figure,
DE || BC and BD = CE
To prove: ∆ABC is an isosceles triangle
Proof: In ∆ABC, DE || BC

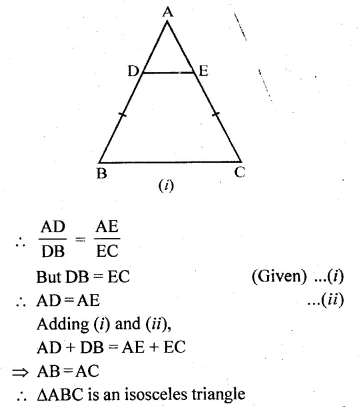
Question 6.
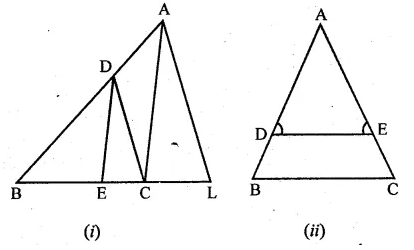
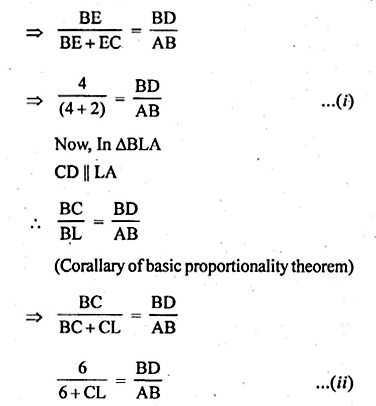
(a) In the figure (i) given below, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm.
(b) In the given figure, ∠D = ∠E and \(\frac { AD }{ BD } =\frac { AE }{ EC } \). Prove that BAC is an isosceles triangle.

Solution:
(a) Given : CD || LA and DE || AC
Length of BE = 4 cm
Length of EC = 2 cm
Now, in ∆BCA
DE || AC
\(\frac { BE }{ BC } =\frac { BD }{ BA } \)
(Corallary of basic proportionality theorem)

Question 7.
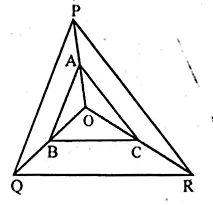
In the figure given below, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. show that BC || QR.

Solution:
In the given figure, A, B, C are points on
OP, OQ and OR respectively
and AB || PQ and AC || PR
To prove: BC || QR
Proof: In POQ,
AB || PQ

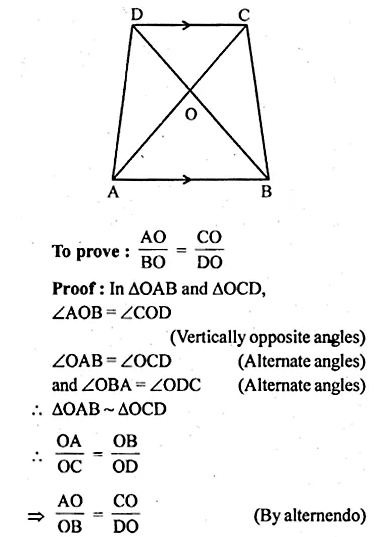
Question 8.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at O. Using Basic Proportionality theorem, prove that \(\frac { AO }{ BO } =\frac { CO }{ DO } \)
Solution:
Given : ABCD is a trapezium in which AB || DC
Its diagonals AC and BD intersect each other at O

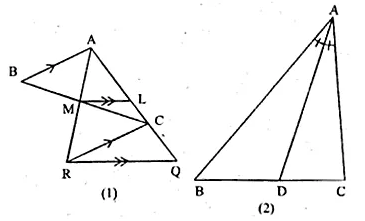
Question 9.
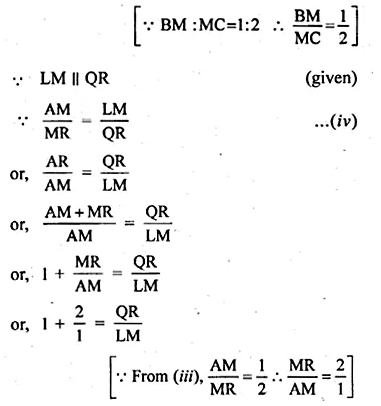
(a) In the figure (1) given below, AB || CR and LM || QR.
(i) Prove that \(\frac { BM }{ MC } =\frac { AL }{ LQ } \)
(ii) Calculate LM : QR, given that BM : MC = 1 : 2.
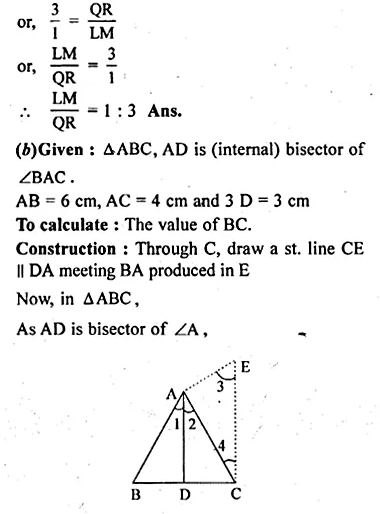
(b) In the figure (2) given below AD is bisector of ∠BAC. If AB = 6 cm, AC = 4 cm and BD = 3cm, find BC

Solution:
(a) Given: AB || CR and LM II QR.
Also BM : MC = 1:2
To Prove:
(i) \(\frac { BM }{ MC } =\frac { AL }{ LQ } \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
If A = \(\begin{bmatrix} 3 & \quad 5 \\ 4 & \quad -2 \end{bmatrix}\) and B = \(\left[ \begin{matrix} 2 \\ 4 \end{matrix} \right] \), is the product AB possible ? Give a reason. If yes, find AB.
Solution:
Yes, the product is possible because of
number of column in A = number of row in B
i.e., (2 x 2). (2 x 1) = (2 x 1) is the order of the matrix.

Question 2.
If A = \(\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}\),B = \(\begin{bmatrix} 1 & -1 \\ -3 & 2 \end{bmatrix}\), find AB and BA, Is AB = BA ?
Solution:
A = \(\begin{bmatrix} 2 & 5 \\ 1 & 3 \end{bmatrix}\),
B = \(\begin{bmatrix} 1 & -1 \\ -3 & 2 \end{bmatrix}\)

Question 3.
If P = \(\begin{bmatrix} 4 & 6 \\ 2 & -8 \end{bmatrix}\),Q = \(\begin{bmatrix} 2 & -3 \\ -1 & 1 \end{bmatrix}\)
Find 2PQ
Solution:
P = \(\begin{bmatrix} 4 & 6 \\ 2 & -8 \end{bmatrix}\),
Q = \(\begin{bmatrix} 2 & -3 \\ -1 & 1 \end{bmatrix}\)
\(2PQ=2\begin{bmatrix} 4 & \quad 6 \\ 2 & -8 \end{bmatrix}\times \begin{bmatrix} 2\quad & -3 \\ -1 & \quad 1 \end{bmatrix}\)

Question 4.
Given A = \(\begin{bmatrix} 1 & 1 \\ 8 & 3 \end{bmatrix}\) , evaluate A² – 4A
Solution:
A = \(\begin{bmatrix} 1 & 1 \\ 8 & 3 \end{bmatrix}\)
A² – 4A = \(\begin{bmatrix} 1 & \quad 1 \\ 8 & \quad 3 \end{bmatrix}\begin{bmatrix} 1\quad & 1 \\ 8\quad & 3 \end{bmatrix}-4\begin{bmatrix} 1\quad & 1 \\ 8\quad & 3 \end{bmatrix}\)

Question 5.
If A = \(\begin{bmatrix} 3 & \quad 7 \\ 2 & \quad 4 \end{bmatrix}\), B = \(\begin{bmatrix} 0 & \quad 2 \\ 5 & \quad 3 \end{bmatrix}\) and C = \(\begin{bmatrix} 1 & \quad -5 \\ -4 & \quad 6 \end{bmatrix}\)
Find AB – 5C
Solution:
A = \(\begin{bmatrix} 3 & \quad 7 \\ 2 & \quad 4 \end{bmatrix}\), B = \(\begin{bmatrix} 0 & \quad 2 \\ 5 & \quad 3 \end{bmatrix}\) and C = \(\begin{bmatrix} 1 & \quad -5 \\ -4 & \quad 6 \end{bmatrix}\)
AB = \(\begin{bmatrix} 3 & \quad 7 \\ 2 & \quad 4 \end{bmatrix}\)\(\begin{bmatrix} 0 & \quad 2 \\ 5 & \quad 3 \end{bmatrix}\)

Question 6.
If A = \(\begin{bmatrix} 1 & \quad 2 \\ 2 & \quad 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 2 & \quad 1 \\ 1 & \quad 2 \end{bmatrix}\), find A(BA)
Solution:
A = \(\begin{bmatrix} 1 & \quad 2 \\ 2 & \quad 1 \end{bmatrix}\)
B = \(\begin{bmatrix} 2 & \quad 1 \\ 1 & \quad 2 \end{bmatrix}\)

Question 7.
Given matrices:
A = \(\begin{bmatrix} 2 & \quad 1 \\ 4 & \quad 2 \end{bmatrix}\) and B = \(\begin{bmatrix} 3 & \quad 4 \\ -1 & \quad -2 \end{bmatrix}\), C = \(\begin{bmatrix} -3 & \quad 1 \\ 0 & \quad -2 \end{bmatrix}\)
Find the products of (i) ABC (ii) ACB and state whether they are equal.
Solution:
A = \(\begin{bmatrix} 2 & \quad 1 \\ 4 & \quad 2 \end{bmatrix}\)
B = \(\begin{bmatrix} 3 & \quad 4 \\ -1 & \quad -2 \end{bmatrix}\),
C = \(\begin{bmatrix} -3 & \quad 1 \\ 0 & \quad -2 \end{bmatrix}\)

Question 8.
Evaluate : \(\begin{bmatrix} 4\sin { { 30 }^{ o } } & \quad 2cos{ 60 }^{ o } \\ sin{ 90 }^{ o } & \quad 2cos{ 0 }^{ o } \end{bmatrix}\begin{bmatrix} 4 & 5 \\ 5 & 4 \end{bmatrix}\)
Solution:
\(\begin{bmatrix} 4\sin { { 30 }^{ o } } & \quad 2cos{ 60 }^{ o } \\ sin{ 90 }^{ o } & \quad 2cos{ 0 }^{ o } \end{bmatrix}\begin{bmatrix} 4 & 5 \\ 5 & 4 \end{bmatrix}\)
\(sin{ 30 }^{ o }=\frac { 1 }{ 2 } ,cos{ 60 }^{ o }=\frac { 1 }{ 2 } \)

Question 9.
If A = \(\begin{bmatrix} -1 & \quad 3 \\ 2 & \quad 4 \end{bmatrix}\), B = \(\begin{bmatrix} 2 & \quad -3 \\ -4 & \quad -6 \end{bmatrix}\) find the matrix AB + BA
Solution:
A = \(\begin{bmatrix} -1 & \quad 3 \\ 2 & \quad 4 \end{bmatrix}\),
B = \(\begin{bmatrix} 2 & \quad -3 \\ -4 & \quad -6 \end{bmatrix}\)
\(AB=\begin{bmatrix} -1 & \quad 3 \\ 2 & \quad 4 \end{bmatrix}\times \begin{bmatrix} 2 & \quad -3 \\ -4 & \quad -6 \end{bmatrix}\)

Question 10.
A = \(\begin{bmatrix} 1 & \quad 2 \\ 3 & \quad 4 \end{bmatrix}\) and B = \(\begin{bmatrix} 6 & \quad 1 \\ 1 & \quad 1 \end{bmatrix}\), C = \(\begin{bmatrix} -2 & \quad -3 \\ 0 & \quad 1 \end{bmatrix}\)
find each of the following and state if they are equal.
(i) CA + B
(ii) A + CB
Solution:
(i) CA + B
CA = \(\begin{bmatrix} -2 & \quad -3 \\ 0 & \quad 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & \quad 2 \\ 3 & \quad 4 \end{bmatrix}\)

Question 11.
If A = \(\begin{bmatrix} 1 & -2 \\ 2 & -1 \end{bmatrix}\) and B = \(\begin{bmatrix} 3 & 2 \\ -2 & 1 \end{bmatrix}\)
Find 2B – A²
Solution:
A = \(\begin{bmatrix} 1 & -2 \\ 2 & -1 \end{bmatrix}\)
B = \(\begin{bmatrix} 3 & 2 \\ -2 & 1 \end{bmatrix}\)
2B = \(2\begin{bmatrix} 3 & 2 \\ -2 & 1 \end{bmatrix}\)
= \(\begin{bmatrix} 6 & 4 \\ -4 & 2 \end{bmatrix}\)

Question 12.
If A = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) and B = \(\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}\), C = \(\begin{bmatrix} 5 & 1 \\ 7 & 4 \end{bmatrix}\), compute
(i) A(B + C)
(ii) (B + C)A
Solution:
(i) A(B + C)
A = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)
B = \(\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}\),
C = \(\begin{bmatrix} 5 & 1 \\ 7 & 4 \end{bmatrix}\)

Question 13.
If A = \(\begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}\) and B = \(\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix}\), C = \(\begin{bmatrix} 1 & 3 \\ 3 & 1 \end{bmatrix}\)
find the matrix C(B – A)
Solution:
A = \(\begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}\)
B = \(\begin{bmatrix} 2 & 1 \\ 3 & 2 \end{bmatrix}\),
C = \(\begin{bmatrix} 1 & 3 \\ 3 & 1 \end{bmatrix}\)

Question 14.
A = \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 2 & 3 \\ -1 & 0 \end{bmatrix}\)
Find A² + AB + B²
Solution:
Given that
A = \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix}\)
B = \(\begin{bmatrix} 2 & 3 \\ -1 & 0 \end{bmatrix}\)

Question 15.
If A = \(\begin{bmatrix} 2 & 1 \\ 0 & -2 \end{bmatrix}\) and B = \(\begin{bmatrix} 4 & 1 \\ -3 & -2 \end{bmatrix}\), C = \(\begin{bmatrix} -3 & 2 \\ -1 & 4 \end{bmatrix}\)
Find A² + AC – 5B
Solution:
A = \(\begin{bmatrix} 2 & 1 \\ 0 & -2 \end{bmatrix}\)
B = \(\begin{bmatrix} 4 & 1 \\ -3 & -2 \end{bmatrix}\),
C = \(\begin{bmatrix} -3 & 2 \\ -1 & 4 \end{bmatrix}\)

Question 16.
If A = \(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\), find A2 and A3.Also state that which of these is equal to A
Solution:
A = \(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)
A² = A x A = \(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\)

Question 17.
If X = \(\begin{bmatrix} 4 & 1 \\ -1 & 2 \end{bmatrix}\), show that 6X – X² = 9I Where I is the unit matrix.
Solution:
Given that
X = \(\begin{bmatrix} 4 & 1 \\ -1 & 2 \end{bmatrix}\)

Question 18.
Show that \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\) is a solution of the matrix equation X² – 2X – 3I = 0,Where I is the unit matrix of order 2
Solution:
Given
X² – 2X – 3I = 0
Solution = \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)
or
X = \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)
∴ X² = \(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)\(\begin{bmatrix} 1 & 2 \\ 2 & 1 \end{bmatrix}\)

Question 19.
Find the matrix X of order 2 × 2 which satisfies the equation
\(\begin{bmatrix} 3 & 7 \\ 2 & 4 \end{bmatrix}\begin{bmatrix} 0 & 2 \\ 5 & 3 \end{bmatrix}+2X=\begin{bmatrix} 1 & -5 \\ -4 & 6 \end{bmatrix}\)
Solution:
Given
\(\begin{bmatrix} 3 & 7 \\ 2 & 4 \end{bmatrix}\begin{bmatrix} 0 & 2 \\ 5 & 3 \end{bmatrix}+2X=\begin{bmatrix} 1 & -5 \\ -4 & 6 \end{bmatrix}\)

Question 20.
If A = \(\begin{bmatrix} 1 & 1 \\ x & x \end{bmatrix}\), find the value of x, so that A² – 0
Solution:
Given
A = \(\begin{bmatrix} 1 & 1 \\ x & x \end{bmatrix}\)
A² = \(\begin{bmatrix} 1 & 1 \\ x & x \end{bmatrix}\)\(\begin{bmatrix} 1 & 1 \\ x & x \end{bmatrix}\)

Question 21.
If \(\begin{bmatrix} 1 & 3 \\ 0 & 0 \end{bmatrix}\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} x \\ 0 \end{matrix} \right] \) Find the value of x
Solution:
\(\begin{bmatrix} 1 & 3 \\ 0 & 0 \end{bmatrix}\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} x \\ 0 \end{matrix} \right] \)
⇒ \(\begin{bmatrix} 2 & -3 \\ 0 & 0 \end{bmatrix}=\left[ \begin{matrix} x \\ 0 \end{matrix} \right] \)
⇒ \(\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} x \\ 0 \end{matrix} \right] \)
Comparing the corresponding elements
x = -1

Question 22.
(i) Find x and y if \(\begin{bmatrix} -3 & 2 \\ 0 & -5 \end{bmatrix}\left[ \begin{matrix} x \\ 2 \end{matrix} \right] =\left[ \begin{matrix} -5 \\ y \end{matrix} \right] \)
(ii) Find x and y if \(\begin{bmatrix} 2x & x \\ y & 3y \end{bmatrix}\left[ \begin{matrix} 3 \\ 2 \end{matrix} \right] =\left[ \begin{matrix} 16 \\ 9 \end{matrix} \right] \)
Solution:
(i) \(\begin{bmatrix} -3 & 2 \\ 0 & -5 \end{bmatrix}\left[ \begin{matrix} x \\ 2 \end{matrix} \right] =\left[ \begin{matrix} -5 \\ y \end{matrix} \right] \)
⇒ \(\begin{bmatrix} -3x & 4 \\ 0 & -10 \end{bmatrix}=\left[ \begin{matrix} -5 \\ y \end{matrix} \right] \)


Here x = 2, y = 1

Question 23.
Find x and y if
\(\begin{bmatrix} x+y & y \\ 2x & x-y \end{bmatrix}\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} 3 \\ 2 \end{matrix} \right] \)
Solution:
Given
\(\begin{bmatrix} x+y & y \\ 2x & x-y \end{bmatrix}\left[ \begin{matrix} 2 \\ -1 \end{matrix} \right] =\left[ \begin{matrix} 3 \\ 2 \end{matrix} \right] \)

Question 24.
If \(\begin{bmatrix} 1 & 2 \\ 3 & 3 \end{bmatrix}\begin{bmatrix} x & 0 \\ 0 & y \end{bmatrix}=\begin{bmatrix} x & 0 \\ 9 & 0 \end{bmatrix} \) find the values of x and y
Solution:
Given
\(\begin{bmatrix} 1 & 2 \\ 3 & 3 \end{bmatrix}\begin{bmatrix} x & 0 \\ 0 & y \end{bmatrix}=\begin{bmatrix} x & 0 \\ 9 & 0 \end{bmatrix} \)

Question 25.
If \(\begin{bmatrix} 3 & 4 \\ 2 & 5 \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\) write down the values of a,b,c and d
Solution:
Given
\(\begin{bmatrix} 3 & 4 \\ 2 & 5 \end{bmatrix}=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)

Comparing the corresponding elements
a = 3, b = 4, c = 2, d = 5

Question 26.
Find the value of x given that A² = B
Where A = \(\begin{bmatrix} 2 & 12 \\ 0 & 1 \end{bmatrix}\) and
B = \(\begin{bmatrix} 4 & x \\ 0 & 1 \end{bmatrix}\)
Solution:
A = \(\begin{bmatrix} 2 & 12 \\ 0 & 1 \end{bmatrix}\) and
B = \(\begin{bmatrix} 4 & x \\ 0 & 1 \end{bmatrix}\)
A² = B

Question 27.
If A = \(\begin{bmatrix} 2 & x \\ 0 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 4 & 36 \\ 0 & 1 \end{bmatrix}\), find the value of x, given that A² – B
Solution:
Given
A² = \(\begin{bmatrix} 2 & x \\ 0 & 1 \end{bmatrix}\)\(\begin{bmatrix} 2 & x \\ 0 & 1 \end{bmatrix}\)

Question 28.
If A = \(\begin{bmatrix} 3 & x \\ 0 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 9 & 16 \\ 0 & -y \end{bmatrix}\) find x and y when A² = B
Solution:
Given
A = \(\begin{bmatrix} 3 & x \\ 0 & 1 \end{bmatrix}\) and B = \(\begin{bmatrix} 9 & 16 \\ 0 & -y \end{bmatrix}\) find x and y when A² = B

Question 29.
Find x, y if \(\begin{bmatrix} -2 & 0 \\ 3 & 1 \end{bmatrix}\left[ \begin{matrix} -1 \\ 2x \end{matrix} \right] +3\left[ \begin{matrix} -2 \\ 1 \end{matrix} \right] =2\left[ \begin{matrix} y \\ 3 \end{matrix} \right] \)
Solution:
Given
\(\begin{bmatrix} -2 & 0 \\ 3 & 1 \end{bmatrix}\left[ \begin{matrix} -1 \\ 2x \end{matrix} \right] +3\left[ \begin{matrix} -2 \\ 1 \end{matrix} \right] =2\left[ \begin{matrix} y \\ 3 \end{matrix} \right] \)

Question 30.
If \(\begin{bmatrix} a & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 4 & 3 \\ -3 & 2 \end{bmatrix}=\begin{bmatrix} b & 11 \\ 4 & c \end{bmatrix} \) find a,b and c
Solution:
\(\begin{bmatrix} a & 1 \\ 1 & 0 \end{bmatrix}\begin{bmatrix} 4 & 3 \\ -3 & 2 \end{bmatrix}=\begin{bmatrix} b & 11 \\ 4 & c \end{bmatrix} \)
⇒ \(\begin{bmatrix} 4a-3 & 3a+2 \\ 4+0 & 3+0 \end{bmatrix}=\begin{bmatrix} b & 11 \\ 4 & c \end{bmatrix} \)

Question 31.
If A = \(\begin{bmatrix} 1 & 4 \\ 0 & -1 \end{bmatrix}\) ,B = \(\begin{bmatrix} 2 & x \\ 0 & -\frac { 1 }{ 2 } \end{bmatrix} \) find the value of x if AB = BA
Solution:
Given
AB = \(\begin{bmatrix} 1 & 4 \\ 0 & -1 \end{bmatrix}\)\(\begin{bmatrix} 2 & x \\ 0 & -\frac { 1 }{ 2 } \end{bmatrix} \)

Question 32.
If A = \(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\) find x and y so that A² – xA + yI
Solution:
Given
A² = \(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\)\(\begin{bmatrix} 2 & 3 \\ 1 & 2 \end{bmatrix}\)

Question 33.
If P = \(\begin{bmatrix} 2 & 6 \\ 3 & 9 \end{bmatrix}\), Q = \(\begin{bmatrix} 3 & x \\ y & 2 \end{bmatrix}\)
find x and y such that PQ = 0
Solution:
Given
P = \(\begin{bmatrix} 2 & 6 \\ 3 & 9 \end{bmatrix}\),
Q = \(\begin{bmatrix} 3 & x \\ y & 2 \end{bmatrix}\)

Question 34.
Let \(M\times \begin{bmatrix} 1 & 1 \\ 0 & 2 \end{bmatrix}=\left[ \begin{matrix} 1 & 2 \end{matrix} \right] \) where M is a matrix
(i) State the order of matrix M
(ii) Find the matrix M
Solution:
Given
(i) M is the order of 1 x 2
let M = [x y]

Question 35.
Given \(\begin{bmatrix} 2 & 1 \\ -3 & 4 \end{bmatrix}\) ,X = \(\left[ \begin{matrix} 7 \\ 6 \end{matrix} \right] \)
(i) the order of the matrix X
(ii) the matrix X
Solution:
We have
\(\begin{bmatrix} 2 & 1 \\ -3 & 4 \end{bmatrix}\) , X = \(\left[ \begin{matrix} 7 \\ 6 \end{matrix} \right] \)

Question 36.
Solve the matrix equation : \(\left[ \begin{matrix} 4 \\ 1 \end{matrix} \right] \) ,X = \(\begin{bmatrix} -4 & 8 \\ -1 & 2 \end{bmatrix}\)
Solution:
\(\left[ \begin{matrix} 4 \\ 1 \end{matrix} \right] \) , X = \(\begin{bmatrix} -4 & 8 \\ -1 & 2 \end{bmatrix}\)
Let matrix X = [x y]

Question 37.
(i) If A = \(\begin{bmatrix} 2 & -1 \\ -4 & 5 \end{bmatrix}\) and B = \(\left[ \begin{matrix} -3 \\ 2 \end{matrix} \right] \) find the matrix C such that AC = B
(ii) If A = \(\begin{bmatrix} 2 & -1 \\ -4 & 5 \end{bmatrix}\) and B = [0 -3] find the matrix C such that CA = B
Solution:
(i) given
A = \(\begin{bmatrix} 2 & -1 \\ -4 & 5 \end{bmatrix}\)
B = \(\left[ \begin{matrix} -3 \\ 2 \end{matrix} \right] \)

Question 38.
If A = \(\begin{bmatrix} 3 & -4 \\ -1 & 2 \end{bmatrix}\) , find matrix B such that BA = I,where I is unity matrix of order 2
Solution:
A = \(\begin{bmatrix} 3 & -4 \\ -1 & 2 \end{bmatrix}\)
BA = I, where I is unity matrix of order 2

Question 39.
If B = \(\begin{bmatrix} -4 & 2 \\ 5 & -1 \end{bmatrix}\) and C = \(\begin{bmatrix} 17 & -1 \\ 47 & -13 \end{bmatrix}\)
find the matrix A such that AB = C
Solution:
B = \(\begin{bmatrix} -4 & 2 \\ 5 & -1 \end{bmatrix}\)
C = \(\begin{bmatrix} 17 & -1 \\ 47 & -13 \end{bmatrix}\)
and AB = C

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Chapter Test

Question 1.
Find the slope of a line whose inclination is
(i) 45°
(ii) 30°
Solution:
(i) tan 45° = 1
(ii) tan 30° = \(\frac { 1 }{ \sqrt { 3 } } \)

Question 2.
Find the inclination of a line whose gradient is
(i) 1
(ii) √3
(iii) \(\frac { 1 }{ \sqrt { 3 } } \)
Solution:
(i) tan θ = 1 ⇒ θ = 45°
(ii) tan θ = √3 ⇒ θ = 60°
(iii) tan θ = \(\frac { 1 }{ \sqrt { 3 } } \) ⇒ θ = 30°

Question 3.
Find the equation of a straight line parallel 1 to x-axis which is at a distance
(i) 2 units above it
(ii) 3 units below it.
Solution:
(i) A line which is parallel to x-axis is y = a
⇒ y = 2
⇒ y – 2 = 0
(ii) A line which is parallel to x-axis is y = a
⇒ y = -3
⇒ y + 3 = 0

Question 4.
Find the equation of a straight line parallel to y-axis which is at a distance of:
(i) 3 units to the right
(ii) 2 units to the left.
Solution:
(i) The equation of line parallel to y-axis is at a distance of 3 units to the right is x = 3 ⇒ x – 3 = 0
(ii) The equation of line parallel to y-axis at a distance of 2 units to the left is x = -2 ⇒ x + 2 = 0

Question 5.
Find the equation of a straight line parallel to y-axis and passing through the point ( – 3, 5).
Solution:
The equation of the line parallel to y-axis passing through ( – 3, 5) to x = -3
⇒ x + 3 = 0

Question 6.
Find the equation of the a line whose
(i) slope = 3, y-intercept = – 5
(ii) slope = \(– \frac { 2 }{ 7 } \), y-intercept = 3
(iii) gradient = √3, y-intercept = \(– \frac { 4 }{ 3 } \)
(iv) inclination = 30°,y-intercept = 2
Solution:
Equation of a line whose slope and y-intercept is given is
y = mx + c
where m is the slope and c is the y-intercept
(i) y = mx + c
⇒ y = 3x + (-5)
⇒ y = 3x – 5

Question 7.
Find the slope and y-intercept of the following lines:
(i) x – 2y – 1 = 0
(ii) 4x – 5y – 9 = – 0
(iii) 3x +5y + 7 = 0
(iv) \(\frac { x }{ 3 } +\frac { y }{ 4 } =1\)
(v) y – 3 = 0
(vi) x – 3 = 0
Solution:
We know that in the equation
y = mx + c, m is the slope and c is the y-intercept.
Now using this, we find,

Question 8.
The equation of the line PQ is 3y – 3x + 7 = 0
(i) Write down the slope of the line PQ.
(ii) Calculate the angle that the line PQ makes with the positive direction of x-axis.
Solution:
Equation of line PQ is 3y – 3x + 7 = 0
Writing in form of y = mx + c

Question 9.
The given figure represents the line y = x + 1 and y = √3x – 1. Write down the angles which the lines make with the positive direction of the x-axis. Hence determine θ.

Solution:
Slope of the line y = x + 1 after comparing
it with y = mx + c, m = 1

Question 10.
Find the value of p, given that the line \(\frac { y }{ 2 } =x-p\) passes through the point ( – 4, 4) (1992).
Solution:
Equation of line is \(\frac { y }{ 2 } =x-p\)
It passes through the points (-4, 4)
It will satisfy the equation

Question 11.
Given that (a, 2a) lies on the line \(\frac { y }{ 2 } =3x-6\) find the value of a.
Solution:
∵ Point (a, 2a) lies on the line
\(\frac { y }{ 2 } =3x-6\)
∴this point will satisfy the equation

Question 12.
The graph of the equation y = mx + c passes through the points (1, 4) and ( – 2, – 5). Determine the values of m and c.
Solution:
Equation of the line is y = mx + c
∴ it passes through the points (1, 4)
∴ 4 = m x 1 + c
⇒ 4 = m + c
⇒ m + c = 4 … (i)
Again it passes through the point (-2, -5)
∴ 5 = m (-2) + c
⇒ 5 = -2 m + c
⇒ 2m – c = 5 …(ii)
Adding (i) and (ii)
3m = 9
⇒ m = 3
Substituting the value of m in (i)
3 + c = 4
⇒ c = 4 – 3 = 1
Hence m = 3, c = 1

Question 13.
Find the equation of the line passing through the point (2, – 5) and making an intercept of – 3 on the y-axis.
Solution:
∴ The line intersects y-axis making an intercept of -3
∴ the co-ordinates of point of intersection will be (0, -3)
Now the slope of line (m) = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)

Question 14.
Find the equation of a straight line passing through ( – 1, 2) and whose slope is \(\\ \frac { 2 }{ 5 } \).
Solution:
Equation of the line will be
\(y-{ y }_{ 1 }=m(x-{ x }_{ 1 }) \)
\(y-2=\frac { 2 }{ 5 } (x+1)\)
⇒ 5y – 10 = 2x + 2
⇒ 2x – 5y + 2 + 10 = 0
⇒ 2x – 5y + 12 = 0

Question 15.
Find the equation of a straight line whose inclination is 60° and which passes through the point (0, – 3).
Solution:
The equation of line whose slope is wand passes through a given point is
\(y-{ y }_{ 1 }=m(x-{ x }_{ 1 }) \)
Here m = tan 60° = √3 and point is (0, -3)
∴ y + 3 = √3 (x – 0)
⇒ y + 3 = √3x
⇒ √3x – y – 3 = 0

Question 16.
Find the gradient of a line passing through the following pairs of points.
(i) (0, – 2), (3, 4)
(ii) (3, – 7), ( – 1, 8)
Solution:
m = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } \)
Given
(i) (0, -2), (3, 4)
(ii) (3, -7), (-1, 8)

Question 17.
The coordinates of two points E and F are (0, 4) and (3, 7) respectively. Find :
(i) The gradient of EF
(ii) The equation of EF
(iii) The coordinates of the point where the line EF intersects the x-axis.
Solution:
Co-ordinates of points E (0, 4) and F (3, 7) are given, then
(i) The gradient of EF

Question 18.
Find the intercepts made by the line 2x – 3y + 12 = 0 on the co-ordinate axis.
Solution:
Putting y = 0, we will get the intercept made on x-axis,
2x – 3y + 12 = 0
⇒ 2x – 3 × 0 + 12 = 0
⇒ 2x – 0 + 2 = 0
⇒ 2x = -12
⇒ x = -6
and putting x = 0, we get the intercepts made on y-axis,
2x – 3y + 12 = 0
⇒ 2 × 0 – 3y + 12 = 0
⇒ -3y = -12
⇒ \(y= \frac { -12 }{ -3 } \) = 4

Question 19.
Find the equation of the line passing through the points P (5, 1) and Q (1, – 1). Hence, show that the points P, Q and R (11, 4) are collinear.
Solution:
The two given points are P (5, 1), Q(1, -1).
∴ Slope of the line (m)

Question 20.
Find the value of ‘a’ for which the following points A (a, 3), B (2,1) and C (5, a) are collinear. Hence find the equation of the line.
Solution:
Given That
A(a, 3), B (2, 1) and C (5, a) are collinear.
Slope of AB = Slope of BC

Question 21.
Use a graph paper for this question. The graph of a linear equation in x and y, passes through A ( – 1, – 1) and B (2, 5). From your graph, find the values of h and k, if the line passes through (h, 4) and (½, k). (2005)
Solution:
Points (h, 4) and (½, k) lie on the line passing
through A(-1, -1) and B(2, 5)

Question 22.
ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, – 4). Find
(i) the coordinates of A
(ii) the equation of the diagonal BD.
Solution:
Given that
ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, -4)

Question 23.
In ∆ABC, A (3, 5), B (7, 8) and C (1, – 10). Find the equation of the median through A.
Solution:
AD is median
⇒ D is mid point of BC
∴ D is \(\left( \frac { 7+1 }{ 2 } ,\frac { 8-10 }{ 2 } \right) \)
i.e (4, -1)
slope of AD

Question 24.
Find the equation of a line passing through the point ( – 2, 3) and having x-intercept 4 units. (2002)
Solution:
x-intercept = 4
∴ Co-ordinates of the point will be (4, 0)
Now slope of the line passing through the points (-2, 3) and (4, 0)

Question 25.
Find the equation of the line whose x-intercept is 6 and y-intercept is – 4.
Solution:
x-intercept = 6
∴ The line will pass through the point (6, 0)
y -intercept = -4 ⇒ c = -4

Question 26.
Write down the equation of the line whose gradient is \(\\ \frac { 1 }{ 2 } \) and which passes through P where P divides the line segment joining A ( – 2, 6) and B (3, – 4) in the ratio 2 : 3. (2001)
Solution:
P divides the line segment joining the points
A (-2, 6) and (3, -4) in the ratio 2 : 3
∴ Co-ordinates of P will be

Question 27.
Find the equation of the line passing through the point (1, 4) and intersecting the line x – 2y – 11 = 0 on the y-axis.
Solution:
line x – 2y – 11 = 0 passes through y-axis
x = 0,
Now substituting the value of x in the equation x – 2y – 11 = 0

Question 28.
Find the equation of the straight line containing the point (3, 2) and making positive equal intercepts on axes.
Solution:

Let the line containing the point P (3, 2)
passes through x-axis at A (x, 0) and y-axis at B (0, y)
OA = OB given
∴ x = y

Question 29.
Three vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2) find:
(i) the coordinates of the fourth vertex D.
(ii) length of diagonal BD.
(iii) equation of side AB of the parallelogram ABCD. (2015)
Solution:
Three vertices of a parallelogram ABCD taken in order are
A (3, 6), B (5, 10) and C (3, 2)
(i) We need to find the co-ordinates of D
We know that the diagonals of a parallelogram bisect each other
Let (x, y) be the co-ordinates of D

Question 30.
A and B arc two points on the x-axis and y-axis respectively. P (2, – 3) is the mid point of AB. Find the

(i) the co-ordinates of A and B.
(ii) the slope of the line AB.
(iii) the equation of the line AB. (2010)
Solution:
Points A and B are on x-axis and y-axis respectively
Let co-ordinates of A be (X, O) and of B be (O, Y)
P (2, -3) is the midpoint of AB

Question 31.
Find the equations of the diagonals of a rectangle whose sides are x = – 1, x = 2 , y = – 2 and y = 6.

Solution:
The equations of sides of a rectangle whose equations are
x₁ = -1, x₂ = 2, y₁ = -2, y₂ = 6.
These lines form a rectangle when they intersect at A, B, C, D respectively
Co-ordinates of A, B, C and D will be
(-1, -2), (2, -2), (2, 6) and (-1, 6) respectively.
AC and BD are its diagonals
(i) Slope of the diagonal AC

Question 32.
Find the equation of a straight line passing through the origin and through the point of intersection of the lines 5x + 1y – 3 and 2x – 3y = 7
Solution:
5x + 7y = 3 …(i)
2x – 3 y = 7 …(ii)
Multiply (i) by 3 and (ii) by 7,
15x + 21y = 9
14x – 21y = 49
Adding we get,

Question 33.
Point A (3, – 2) on reflection in the x-axis is mapped as A’ and point B on reflection in the y-axis is mapped onto B’ ( – 4, 3).
(i) Write down the co-ordinates of A’ and B.
(ii) Find the slope of the line A’B, hence find its inclination.
Solution:
A’ is the image of A (3, -2) on reflection in the x-axis.
∴ Co-ordinates of A’ will be (3, 2)
Again B’ (- 4, 3) in the image of A’, when reflected in the y-axis
∴ Co-ordinates of B will be (4, 3)
(ii) Slope of the line joining, the points A’ (3, 2) and B (4, 3)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 12 Equation of a Straight Line Ex 12.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the sum of the following A.P.s :
(i) 2, 7, 12, … to 10 terms
(ii) \(\frac { 1 }{ 15 } ,\frac { 1 }{ 12 } ,\frac { 1 }{ 10 } ,… \) t0 11 terms
Solution:
(i) 2, 7, 12, … to 10 terms
Here a = 2, d = 7 – 2 = 5 and n = 10

Question 2.
How many terms of the A.P. 27, 24, 21, …, should be taken so that their sum is zero?
Solution:
A.P. = 27, 24, 21,…
a = 27
d = 24 – 27 = -3
S_n =0
Let n terms be there in A.P.

Question 3.
Find the sums given below :
(i) 34 + 32 + 30 + … + 10
(ii) – 5 + ( – 8) + ( – 11) + … + ( – 230)
Solution:
(i) 34 + 32 + 30 + … + 10
Here, a = 34, d = 32 – 34 = -2, l = 10
T_n = a + (n – 1)d
10 = 34 + (n – 1)(-2)
-24 = -2 (n – 1)

Question 4.
In an A.P. (with usual notations) :
(i) given a = 5, d = 3, a_n = 50, find n and S_n
(ii) given a = 7, a₁₃ = 35, find d and S₁₃
(iii) given d = 5, S₉ = 75, find a and a₉
(iv) given a = 8, a_n = 62, S_n = 210, find n and d
(v) given a = 3, n = 8, S = 192, find d.
Solution:
(i) a = 5, d = 3, a_n = 50
a_n = a + (n – 1 )d
50 = 5 + (n – 1) x 3
⇒ 50 – 5 = 3(n – 1)

Question 5.
(i) The first term of an A.P. is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.
(ii) The sum of first 15 terms of an A.P. is 750 and its first term is 15. Find its 20th term.
Solution:
(i) First term of an A.P. (a) = 5
Last term (l) = 45
Sum = 400
l = a + (n – 1 )d
45 = 5 + (n – 1)d
⇒ (n – 1)d = 45 – 5 = 40 …(i)

Question 6.
The first and the last terms of an A.P. are 17 and 350 respectively. If the common difference is 9, how many terms are there and what is their sum?
Solution:
First term of an A.P. (a) = 17
and last term (l) = 350
d= 9
l = T_n = a + (n – 1 )d

Question 7.
Solve for x : 1 + 4 + 7 + 10 + … + x = 287.
Solution:
1 + 4 + 7 + 10 + .. . + x = 287
Here, a = 1, d = 4 – 1 = 3, n = x
l = x = a = (n – 1)d = 1 + (n – 1) x 3

Question 8.
(i) How many terms of the A.P. 25, 22, 19, … are needed to give the sum 116 ? Also find the last term.
(ii) How many terms of the A.P. 24, 21, 18, … must be taken so that the sum is 78 ? Explain the double answer.
Solution:
(i) A.P. is 25, 22, 19, …
Sum = 116
Here, a = 25, d = 22 – 25 = -3
Let number of terms be n, then

Question 9.
Find the sum of first 22 terms, of an A.P. in which d = 7 and a₂₂ is 149.
Solution:
Sum of first 22 terms of an A.P. whose d = 7
a₂₂ = 149 and n = 22

Question 10.
(i) Find the sum of first 51 terms of the A.P. whose second and third terms are 14 and 18 respectively.
(ii) If the third term of an A.P. is 1 and 6th term is – 11, find the sum of its first 32 terms.
Solution:
Sum of first 51 terms of an A.P. in which
T₂ = 14, T₃ = 18

Question 11.
If the sum of first 6 terms of an A.P. is 36 and that of the first 16 terms is 256, find the sum of first 10 terms.
Solution:
S₆ = 36
S₁₆ = 256

Question 12.
Show that a₁, a₂, a₃, … form an A.P. where a_n is defined as a_n = 3 + 4n. Also find the sum of first 15 terms.
Solution:
a_n = 3 + 4n
a₁ = 3 + 4 x 1 = 3 + 4 = 7
a₂ = 3 + 4 x 2 = 3 + 8 = 11
a₃ = 3 + 4 x 3 = 3 + 12 = 15
a₄ = 3 + 4 x 4 = 3 + 16 = 19
and so on Here, a = 1 and d = 11 – 7 = 4

Question 13.
(i) If a_n = 3 – 4n, show that a₁, a₂, a₃, … form an A.P. Also find S₂₀.
(ii) Find the common difference of an A.P. whose first term is 5 and the sum of first four terms is half the sum of next four terms.
Solution:
(i) a_n = 3 – 4n
a₁ = 3 – 4 x 1 = 3 – 4 = -1
a₂ = 3 – 4 x 2 = 3 – 8 = -5
a₃ = 3 – 4 x 3 = 3 – 12 = -9
a₄ = 3 – 4 x 4 = 3 – 16 = -13 and so on
Here, a = -1, d = -5 – ( -1) = -5 + 1 = -4

Question 14.
The sum of first n terms of an A.P. whose first term is 8 and the common difference is 20 equal to the sum of first 2n terms of another A.P. whose first term is – 30 and the common difference is 8. Find n.
Solution:
In an A.P.
S_n = S_2n
For the first A.P. a = 8, d = 20
and for second A.P. a = -30, d = 8

Question 15.
The sum of first six terms of an arithmetic progression is 42. The ratio of the 10th term to the 30th term is \(\\ \frac { 1 }{ 3 } \). Calculate the first and the thirteenth term.
Solution:
T₁₀ : T₃₀ = 1 : 3, S₆ = 42
Let a be the first term and d be a common difference, then

Question 16.
In an A.P., the sum of its first n terms is 6n – n². Find is 25th term.
Solution:
S_n = 6n – n²
T₂₅ = ?

Question 17.
If the sum of first n terms of an A.P. is 4n – n², what is the first term (i. e. S₁)? What is the sum of the first two terms? What is the second term? Also, find the 3rd term, the 10th term, and the nth terms?
Solution:
S_n = 4n – n²
S_n – 1 = 4(n – 1) – (n – 1)²
= 4n – 4 – (n² – 2n + 1)

Question 18.
If S_n denotes the sum of first n terms of an A.P., prove that S₃₀ = 3(S₂₀ – S₁₀).
Solution:
S_n denotes the sum of first n terms of an A.P.
To prove: S₃₀ = 3(S₂₀ – S₁₀)

Question 19.
(i) Find the sum of first 1000 positive integers.
(ii) Find the sum of first 15 multiples of 8.
Solution:
(i) Sum of first 1000 positive integers
i. e., 1 + 2 + 3+ 4 + … + 1000
Here, a = 1, d = 1, n = 1000

Question 20.
(i) Find the sum of all two digit natural numbers which are divisible by 4.
(ii) Find the sum of all natural numbers between 100 and 200 which are divisible by 4.
(iii) Find the sum of all multiples of 9 lying between 300 and 700.
(iv) Find the sum of all natural numbers less than 100 which are divisible by 6.
Solution:
(i) Sum of two digit natural numbers which are divisible by 4
which are 12, 16, 20, 24, …, 96
Here, a = 12, d = 16 – 12 = 4, l = 96

Question 21.
(i) Find the sum of all two digit odd positive numbers.
(ii) Find the sum of all 3-digit natural numbers which are divisible by 7.
(iii) Find the sum of all two digit numbers which when divided by 7 yield 1 as the
Solution:
(i) Sum of all two-digit odd positive numbers which are 11, 13, 15, …, 99
Here, a = 11, d = 2, l = 99

Question 22.
A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows : Rs 200 for the first day, Rs 250 for the second day, Rs 300 for the third day, etc., the penalty for each succeeding day being Rs 50 more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work for 30 days ?
Solution:
Penalty for
First day = Rs 200
Second day = Rs 250
Third day = Rs 300

Question 23.
Kanika was given her pocket money on 1st Jan, 2016. She puts Rs 1 on Day 1, Rs 2 on Day 2, Rs 3 on Day 3, and continued on doing so till the end of the month, from this money into her piggy bank. She also spent Rs 204 of her pocket money, and was found that at the end of the month she still has Rs 100 with her. How much money was her pocket money for the month ?
Solution:
Pocket money for Jan. 2016
Out of her pocket money, Kanika puts
Rs 1 on the first day i.e., 1 Jan.
Rs 2 on second Jan
Rs 3 on third Jan
Rs 31 on 31st Jan

Question 24.
Yasmeen saves Rs 32 during the first month, Rs 36 in the second month and Rs 40 in the third month. If she continues to save in this manner, in how many months will she save Rs 2000?
Solution:
Savings for the first month = Rs 32
For the second month = Rs 36
For the third month = Rs 40
Total savings for the period = Rs 2000

Question 25.
The students of a school decided to beautify the school on the Annual Day by fixing colourful flags on the straight passage of the school. They have 27 flags to be fixed at intervals of every 2 m. The flags are stored at the position of the middle most flag. Ruchi was given the responsibility of placing the flags. Ruchi kept her books where the flags were stored. She could carry only one flag at a time. How much distance did she cover in completing this job and returning back to collect her books ? What is the maximum distance she travelled carrying a flag ?
Solution:
Total number of flags = 27
To fixed after every = 2 m
The flag is stored at the middlemost flag

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
Given that M = \(\begin{bmatrix} 2 & 0 \\ 1 & 2 \end{bmatrix} \) and N = \(\begin{bmatrix} 2 & 0 \\ -1 & 2 \end{bmatrix}\),find M + 2N
Solution:
M = \(\begin{bmatrix} 2 & 0 \\ 1 & 2 \end{bmatrix} \)
N = \(\begin{bmatrix} 2 & 0 \\ -1 & 2 \end{bmatrix}\)

Question 2.
If A = \(\begin{bmatrix} 2 & 0 \\ -3 & 1 \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & 1 \\ -2 & 3 \end{bmatrix} \)
find 2A – 3B
Solution:
A = \(\begin{bmatrix} 2 & 0 \\ -3 & 1 \end{bmatrix} \)
B = \(\begin{bmatrix} 0 & 1 \\ -2 & 3 \end{bmatrix} \)

Question 3.
If A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 2 \\ 3 & 1 \end{bmatrix} \)
Compute 3A + 4B
Solution:
A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \)
B = \(\begin{bmatrix} 1 & 2 \\ 3 & 1 \end{bmatrix} \)

Question 4.
Given A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -4 & -1 \\ -3 & -2 \end{bmatrix} \)
(i) find the matrix 2A + B
(ii) find a matrix C such that C + B = \(\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \)
Solution:
A = \(\begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix} \)
B = \(\begin{bmatrix} -4 & -1 \\ -3 & -2 \end{bmatrix} \)

Question 5.
A = \(\begin{bmatrix} 1 & 2 \\ -2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & -1 \\ 1 & 2 \end{bmatrix} \) , C = \(\begin{bmatrix} 0 & 3 \\ 2 & -1 \end{bmatrix} \)
Find A + 2B – 3C
Solution:
A = \(\begin{bmatrix} 1 & 2 \\ -2 & 3 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & -1 \\ 1 & 2 \end{bmatrix} \) , C = \(\begin{bmatrix} 0 & 3 \\ 2 & -1 \end{bmatrix} \)
∴ A + 2B – 3C

Question 6.
If A = \(\begin{bmatrix} 0 & -1 \\ 1 & 2 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 2 \\ -1 & 1 \end{bmatrix} \)
Find the matrix X if :
(i) 3A + X = B
(ii) X – 3B = 2A
Solution:
A = \(\begin{bmatrix} 0 & -1 \\ 1 & 2 \end{bmatrix} \)
B = \(\begin{bmatrix} 1 & 2 \\ -1 & 1 \end{bmatrix} \)
(i) 3A + X = B
⇒ X = B – 3A

Question 7.
Solve the matrix equation
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-3X=\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}\)
Solution:
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-3X=\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}\)
\(\begin{bmatrix} 2 & 1 \\ 5 & 0 \end{bmatrix}-\begin{bmatrix} -7 & 4 \\ 2 & 6 \end{bmatrix}=3X\)

Question 8.
If \(\begin{bmatrix} 1 & \quad 4 \\ -2 & \quad 3 \end{bmatrix}+2M=3\begin{bmatrix} 3 & \quad 2 \\ 0 & -3 \end{bmatrix}\), find the matrix M
Solution:
\(\begin{bmatrix} 1 & \quad 4 \\ -2 & \quad 3 \end{bmatrix}+2M=3\begin{bmatrix} 3 & \quad 2 \\ 0 & -3 \end{bmatrix}\)
2M =

Question 9.
A = \(\begin{bmatrix} 2 & -6 \\ 2 & 0 \end{bmatrix} \) and B = \(\begin{bmatrix} -3 & 2 \\ 4 & 0 \end{bmatrix} \) , C = \(\begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix} \)
Find the matrix X such that A + 2X = 2B + C
Solution:
A = \(\begin{bmatrix} 2 & -6 \\ 2 & 0 \end{bmatrix} \) and B = \(\begin{bmatrix} -3 & 2 \\ 4 & 0 \end{bmatrix} \) , C = \(\begin{bmatrix} 4 & 0 \\ 0 & 2 \end{bmatrix} \)
let X = \(\begin{bmatrix} x & y \\ z & t \end{bmatrix}\)

Question 10.
Find X and Y if X + Y = \(\begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix}\) and X – Y = \(\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}\)
Solution:
X + Y = \(\begin{bmatrix} 7 & 0 \\ 2 & 5 \end{bmatrix}\)…..(i)
X – Y = \(\begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}\)…….(ii)

Question 11.
If \(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\) Find the values of x and y
Solution:
\(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\)
\(\begin{bmatrix} 6 & 8 \\ 10 & 2x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} 7 & 0 \\ 10 & 5 \end{bmatrix}\)

Question 12.
If \(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\) Find the values of x and y
Solution:
\(2\begin{bmatrix} 3 & 4 \\ 5 & x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\)
\(\begin{bmatrix} 6 & 8 \\ 10 & 2x \end{bmatrix}+\begin{bmatrix} 1 & y \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} z & 0 \\ 10 & 5 \end{bmatrix}\)

Question 13.
If \(\begin{bmatrix} 5 & 2 \\ -1 & \quad y+1 \end{bmatrix}-2\begin{bmatrix} 1 & 2x-1 \\ 3 & -2 \end{bmatrix}=\begin{bmatrix} 3 & -8 \\ -7 & 2 \end{bmatrix}\) Find the values of x and y
Solution:
\(\begin{bmatrix} 5 & 2 \\ -1 & \quad y+1 \end{bmatrix}-2\begin{bmatrix} 1 & 2x-1 \\ 3 & -2 \end{bmatrix}=\begin{bmatrix} 3 & -8 \\ -7 & 2 \end{bmatrix}\)

Question 14.
If \(\begin{bmatrix} a & \quad 3 \\ 4 & \quad 2 \end{bmatrix}+\begin{bmatrix} 2 & \quad b \\ 1 & -2 \end{bmatrix}-\begin{bmatrix} 1\quad & 1 \\ -2\quad & c \end{bmatrix}=\begin{bmatrix} 5 & 0 \\ 7 & 3 \end{bmatrix}\)
Find the value of a,b and c
Solution:
\(\begin{bmatrix} a & \quad 3 \\ 4 & \quad 2 \end{bmatrix}+\begin{bmatrix} 2 & \quad b \\ 1 & -2 \end{bmatrix}-\begin{bmatrix} 1\quad & 1 \\ -2\quad & c \end{bmatrix}=\begin{bmatrix} 5 & 0 \\ 7 & 3 \end{bmatrix}\)

Question 15.
If A = \(\begin{bmatrix} 2 & a \\ -3 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & 3 \\ 7 & b \end{bmatrix} \) , C = \(\begin{bmatrix} c & 9 \\ -1 & -11 \end{bmatrix} \) and 5A + 2B = C, find the values of a,b,c
Solution:
A = \(\begin{bmatrix} 2 & a \\ -3 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} -2 & 3 \\ 7 & b \end{bmatrix} \) , C = \(\begin{bmatrix} c & 9 \\ -1 & -11 \end{bmatrix} \)
and 5A + 2B = C

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

 

Question 1.
Write the first four terms of the A.P. when its first term is – 5 and the common difference is – 3.
Solution:
First 4 term of A.P. whose first term (a) = -5
and common difference (d) = -3
= -5, -8, -11, -14

Question 2.
Verify that each of the following lists of numbers is an A.P., and the write its next three terms :
(i) \(0,\frac { 1 }{ 4 } ,\frac { 1 }{ 2 } ,\frac { 3 }{ 4 } ,… \)
(ii) \(5,\frac { 14 }{ 3 } ,\frac { 13 }{ 3 } ,4,… \)
Solution:
(i) \(0,\frac { 1 }{ 4 } ,\frac { 1 }{ 2 } ,\frac { 3 }{ 4 } ,… \)
Here a = 0, d = \(\\ \frac { 1 }{ 4 } \)

Question 3.
The nth term of an A.P. is 6n + 2. Find the common difference.
Solution:
T_n of an A.P. = 6n + 2 .
T₁ = 6 x 1 + 2 = 6 + 2 = 8
T₂ = 6 x 2 + 2 = 12 + 2 = 14
T₃ = 6 x 3 + 2 = 18 + 2 = 20
d = 14 – 8 = 6

Question 4.
Show that the list of numbers 9, 12, 15, 18, … form an A.P. Find its 16th term and the nth.
Solution:
9, 12, 15, 18, …
Here, a = 9, d = 12 – 9 = 3
or 15 – 12 = 3
or 18 – 15 = 3
Yes, it form an A.P.

Question 5.
Find the 6th term from the end of the A.P. 17, 14, 11, …, – 40.
Solution:
6th term from the end of
A.P. = 17, 14, 11, …… 40
Here, a = 17, d = -3, l = -40
l = a + (n – 1 )d

Question 6.
If the 8th term of an A.P. is 31 and the 15th term is 16 more than its 11th term, then find the A.P.
Solution:
In an A.P.
a₈ = 31, a₁₅ = a₁₁ + 16
Let a be the first term and d be a common difference, then

Question 7.
The 17th term of anA.P. is 5 more than twice its 8th term. If the 11th term of the A.P. is 43, then find the wth term.
Solution:
In an A.P.
a₁₇ = 2 x a₈ + 5
a₁₁ = 43, find a_n
Let a be the first term and d be the common

Question 8.
The 19th term of an A.P. is equal to three times its 6th term. If its 9th term is 19, find the A.P.
Solution:
In an A.P.
a₁₉ = 3 x a₆ and a₉ = 19
Let a be the first term and d be the common
difference, then

Question 9.
If the 3rd and the 9th terms of an A.P. are 4 and – 8 respectively, then which term of this A.P. is zero?
Solution:
In an A.P.
a₃ = 4, a₉ = -8, which term of A.P. will be zero
Let a be the first term and d be a common difference, then

Question 10.
Which term of the list of numbers 5, 2, – 1, – 4, … is – 55?
Solution:
A.P. is 5, 2, -1, – 4, …
Which term of A.P. is -55
Let it be nth term
Here, a = 5, d = 2 – 5 = -3

Question 11.
The 24th term of an A.P. is twice its 10th term. Show that its 72nd term is four times its 15th term.
Solution:
In an A.P.
24th term = 2 x 10th term
To show that 72nd term = 4 x 15th term
Let a be the first term and d be a common difference, then

Question 12.
Which term of the list of numbers \(20,19\frac { 1 }{ 4 } ,18\frac { 1 }{ 2 } ,17\frac { 3 }{ 4 } ,..\) is the first negative term?
Solution:
In A.P., which is the first negative term
\(20,19\frac { 1 }{ 4 } ,18\frac { 1 }{ 2 } ,17\frac { 3 }{ 4 } ,..\)

Question 13.
If the pth term of an A.P. is q and the qth term is p, show that its nth term is (p + q – n)
Solution:
In an A.P.
pth term = q
qth term = p
Show that (p + q – n) is nth term
Let a be the first term and d be the common

Question 14.
How many three digit numbers are divisible by 9?
Solution:
3-digit numbers which are divisible by 9 are 108, 117, 126, 135, …, 999
Here, a = 108, d = 9 and l = 999

Question 15.
The sum of three numbers in A.P. is – 3 and the product is 8. Find the numbers.
Solution:
Sum of three numbers of an A.P. = -3
and their product = 8
Let the numbers be
a – d, a, a + d, then
a – d + a + a + d = -3

Question 16.
The angles of a quadrilateral are in A.P. If the greatest angle is double of the smallest angle, find all the four angles.
Solution:
Angles of a quadrilateral are in A.P.
Greatest angle is double of the smallest
Let the smallest angle of the quadrilateral is
a + 3d…..(i)

Question 17.
The nth term of an A.P. cannot be n² + n + 1. Justify your answer.
Solution:
nth term of an A.P. can’t be n² + n + 1
Giving some different values to n such as 1, 2, 3, 4, …
we find then

Question 18.
Find the sum of first 20 terms of an A.P. whose nth term is 15 – 4n.
Solution:
Giving some different values such as 1 to 20
We get,

Question 19.
Find the sum :
\(18+15\frac { 1 }{ 2 } +13+…+\left( -49\frac { 1 }{ 2 } \right) \)
Solution:
Find the sum
\(18+15\frac { 1 }{ 2 } +13+…+\left( -49\frac { 1 }{ 2 } \right) \)

Question 20.
(i) How many terms of the A.P. – 6,\(– \frac { 11 }{ 2 } \) – 5,… make the sum – 25?
(ii) Solve the equation 2 + 5 + 8 + … + x = 155.
Solution:
(i) Sum = -25
A.P. = -6, \(– \frac { 11 }{ 2 } \) -5,…

Question 21.
If the third term of an A.P. is 5 and the ratio of its 6th term to the 10th term is 7 : 13, then find the sum of first 20 terms of this A.P.
Solution:
3rd term of an A.P. = 5
Ratio in 6th term and 10th term = 7 : 13
Find S₂₀
Let a be the first term and d be the common difference

Question 22.
In an A.P., the first term is 2 and the last term is 29. If the sum of the terms is 155, then find the common difference of the A.P.
Solution:
In an A.P.
First term (a) = 2
Last term (l) = 29
Sum of terms = 155

Question 23.
The sum of first 14 terms of an A.P. is 1505 and its first term is 10. Find its 25th term.
Solution:
Sum of first 14 terms = 1505
First term (a) = 10
Find 25th term

Question 24.
Find the number of terms of the A.P. – 12, – 9, – 6, …, 21. If 1 is added to each term of this A.P., then find the sum of all terms of the A.P. thus obtained.
Solution:
A.P. -12, -9, -6,…, 21
If 1 is added to each term, find the sum of there terms

Question 25.
The sum of first n term of an A.P. is 3n² + 4n. Find the 25th term of this A.P.
Solution:
S_n = 3n² + 4n
S_n – 1 = 3(n – 1)² + 4(n – 1)

Question 26.
In an A.P., the sum of first 10 terms is – 150 and the sum of next 10 terms is – 550. Find the A.P.
Solution:
In an A.P.
Sum of first 10 terms = -150
Sum of next 10 terms = -550, A.P. = ?
Sum of first 10 terms = -150

Question 27.
The sum of first m terms of an A.P. is 4m² – m. If its nth term is 107, find the value of n. Also find the 21 st term of this A.P.
Solution:
S_m = 4m² – m
S_n = 4n² – n

Question 28.
If the sum of first p, q and r terms of an A.P. are a, b and c respectively, prove that
\(\frac { a }{ p } (q-r)+\frac { b }{ q } (r-p)+\frac { c }{ r } (p-q)=0 \)
Solution:
Let the first term of A.P. be A and common difference be d.
Sum of the first p terms is

Question 29.
A sum of Rs 700 is to be used to give 7 cash prizes to students of a school for their overall academic performance. If each prize is Rs 20 less than its preceding prize, find the value of each of the prizes.
What is the importance of an academic prise in students life? (Value Based)
Solution:
Total sum = Rs 700
Cash prizes to 7 students = 7 prize
Each prize is Rs 20 less than its preceding prize
d = -20, d = -20, n = 7

Question 30.
Find the geometric progression whose 4th term is 54 and 7th term is 1458.
Solution:
In a G.P.
a₄ = 54
a₇ = 1458
Let a be the first term and r be the common difference

Question 31.
The fourth term of a G.P. is the square of its second term and the first term is – 3. Find its 7th term.
Solution:
In G.P.
a₄ = (a₂)², a₁ = -3
Let a be the first term and r be the common ratio

Question 32.
If the 4th, 10th and 16th terms of a G.P. are x, y and z respectively, prove that x, y and z are in G.P.
Solution:
In a G.P.
a₄ = x, a₁₀ = y, a₁₆ = z
Show that x, y, z are in G.P.
Let a be the first term and r be the common ratio, then

Question 33.
The original cost of a machine is Rs 10000. If the annual depreciation is 10%, after how many years will it be valued at Rs 6561 ?
Solution:
Original cost of machine = Rs 10000
Since, machine depreciates at the rate of 10%
on reducing the balance,
Value of machine after one year

Question 34.
How many terms of the G.P. \(3,\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } \),are needed to give the sum \(\\ \frac { 3069 }{ 512 } \) ?
Solution:
G.P. \(3,\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } \)
S_n = \(\\ \frac { 3069 }{ 512 } \)

Question 35.
Find the sum of first n terms of the series : 3 + 33 + 333 + …
Solution:
Series is
3 + 33 + 333 + … n terms
= 3[1 + 11 + 111 +…n terms]

Question 36.
Find the sum of the series 7 + 7.7 + 7.77 + 7.777 + … to 50 terms.
Solution:
The given sequence is 7, 7.7, 7.77, 7.777,…
Required sum = S₅₀
= 7 + 7.7 + 7.77 + … 50 terms
= 7(1 + 1.1 + 1. 11 + … 50 terms)

Question 37.
The inventor of chessboard was a very clever man. He asked the king, h reward of one grain of wheat for the first square, 2 grains for the second, 4 grains for the third, and so on, doubling the number of the grains for each subsequent square. How many grains would have to be given?
Solution:
In a chessboard, there are 8 x 8 = 64 squares
If a man put 1 grain in first square,
2 grains in second square,
4 grains in third square
and goes on upto the last square, i.e. 64th square
Therefore, 1 + 2 + 4 + 8 + 16 + … 64 terms
Here, a = 1, r = 2 and n = 64

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Ex 11
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula Chapter Test

Choose the correct answer from the given four options (1 to 12) :

Question 1.
The points A (9, 0), B (9, 6), C ( – 9, 6) and D ( – 9, 0) are the vertices of a
(a) rectangle
(b) square
(c) rhombus
(d) trapezium
Solution:
A (9, 0), B (9, 6), C (-9, 6), D (-9, 0)
AB² = (x₂ – x₁)² + (y₂ – y₁)²

Question 2.
The mid-point of the line segment joining the points A ( – 2, 8) and B ( – 6, – 4) is
(a) ( – 4, – 6)
(b) (2, 6)
(c) ( – 4, 2)
(d) (4, 2)
Solution:
Mid-point of the line segment joining the points A (-2, 8), B (-6, -4)

Question 3.
If \(P\left( \frac { a }{ 3 } ,4 \right) \) segment joining the points Q ( – 6, 5) and R ( – 2, 3), then the value of a is
(a) – 4
(b) – 6
(c) 12
(d) – 12
Solution:
\(P\left( \frac { a }{ 3 } ,4 \right) \) is mid-point of the line segment
joining the points Q (-6, 5) and R (-2, 3)

Question 4.
If the end points of a diameter of a circle are A ( – 2, 3) and B (4, – 5), then the coordinates of its centre are
(a) (2, – 2)
(b) (1, – 1)
(c) ( – 1, 1)
(d) ( – 2, 2)
Solution:
End points of a diameter of a circle are (-2, 3) and B (4,-5)
then co-ordinates of the centre of the circle
= \(\left( \frac { -2+4 }{ 2 } ,\frac { 3-5 }{ 2 } \right) or\left( \frac { 2 }{ 2 } ,\frac { -2 }{ 2 } \right) \)
= (1, -1) (b)

Question 5.
If one end of a diameter of a circle is (2, 3) and the centre is ( – 2, 5), then the other end is
(a) ( – 6, 7)
(b) (6, – 7)
(c) (0, 8)
(d) (0, 4)
Solution:
One end of a diameter of a circle is (2, 3) and centre is (-2, 5)
Let (x, y) be the other end of the diameter

Question 6.
If the mid-point of the line segment joining the points P (a, b – 2) and Q ( – 2, 4) is R (2, – 3), then the values of a and b are
(a) a = 4, b = – 5
(b) a = 6, b = 8
(c) a = 6, b = – 8
(d) a = – 6, b = 8
Solution:
the mid-point of the line segment joining the
points P (a, b – 2) and Q (-2, 4) is R (2, -3)

Question 7.
The point which lies on the perpendicular bisector of the line segment joining the points A ( – 2, – 5) and B (2, 5) is
(a) (0, 0)
(b) (0, 2)
(c) (2, 0)
(d) ( – 2, 0)
Solution:
the line segment joining the points A (-2, -5) and B (2, -5), has mid-point
= \(\left( \frac { -2+2 }{ 2 } ,\frac { -5+5 }{ 2 } \right) \) = (0, 0)
(0, 0) lies on the perpendicular bisector of AB. (a)

Question 8.
The coordinates of the point which is equidistant from the three vertices of ∆AOB (shown in the given figure) are
(a) (x, y)
(b) (y, x)
(c) \(\left( \frac { x }{ 2 } ,\frac { y }{ 2 } \right) \)
(d) \(\left( \frac { y }{ 2 } ,\frac { x }{ 2 } \right) \)

Solution:
In the given figure, vertices of a ∆OAB are (0, 0), (0, 2y) and (2x, 0)
The point which is equidistant from O, A and B is the mid-point of AB.
∴ Coordinates are \(\left( \frac { 0+2x }{ 2 } ,\frac { 2y+0 }{ 2 } \right) \) or (x, y) (a)

Question 9.
The fourth vertex D of a parallelogram ABCD whose three vertices are A ( – 2, 3), B (6, 7) and C (8, 3) is
(a) (0, 1)
(b) (0, – 1)
(c) ( – 1, 0)
(d) (1, 0)
Solution:
ABCD is a ||gm whose vertices A (-2, 3), B (6, 7) and C (8, 3).
The fourth vertex D will be the point on which diagonals AC and BD
bisect each other at O.

Question 10.
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, – 5) is the mid-point of PQ, then the coordinates of P and Q are, respectively
(a) (0, – 5) and (2, 0)
(b) (0, 10) and ( – 4, 0)
(c) (0, 4) and ( – 10, 0)
(d) (0, – 10) and (4, 0)
Solution:
A line intersects y-axis at P and x-axis a Q.
R (2, -5) is the mid-point

Question 11.
The points which divides the line segment joining the points (7, – 6) and (3, 4) in the ratio 1 : 2 internally lies in the
(a) Ist quadrant
(b) IInd quadrant
(c) IIIrd quadrant
(d) IVth quadrant
Solution:
A point divides line segment joining the points
A (7, -6) and B (3, 4) in the ratio 1 : 2 internally.

Let (x, y) divides it in the ratio 1 : 2

Question 12.
The centroid of the triangle whose vertices are (3, – 7), ( – 8, 6) and (5, 10) is
(a) (0, 9)
(b) (0, 3)
(c) (1, 3)
(d) (3, 3)
Solution:
Centroid of the triangle whose Vertices are (3, -7), (-8, 6) and (5, 10) is
\(\left( \frac { 3-8+5 }{ 3 } ,\frac { -7+6+10 }{ 3 } \right) or\left( 0,\frac { 9 }{ 3 } \right) \)
or (0, 3) (b)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 11 Section Formula MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the A.P. whose nth term is 7 – 3K. Also find the 20th term.
Solution:
T_n = 7 – 3n
Giving values 1, 2, 3, 4, … to n, we get
T₁ = 7 – 3 x 1 = 7 – 3 = 4
T₂ = 7 – 3 x 2 = 7 – 6 = 1
T₃ = 7 – 3 x 3 = 7 – 9 = -2
T₄ = 7 – 3 x 4 = 7 – 12 = -5
T₂₀ = 7 – 3 x 20 = 7 – 60 = -53
A.P. is 4, 1, -2, -5, …
20th term = -53

Question 2.
Find the indicated terms in each of following A.P.s:
(i) 1, 6, 11, 16, …; a₂₀
(ii) – 4, – 7, – 10, – 13, …, a₂₅, a_n
Solution:
(i) 1, 6, 11, 16, …
Here, a = 1, d = 6 – 1 – 5
a₂₀ = a + (n – 1 )d
= 1 + (20 – 1) x 5
= 1 + 19 x 5
= 1 + 95
= 96

Question 3.
Find the nth term and the 12th term of the list of numbers: 5, 2, – 1, – 4, …
Solution:
5, 2, -1, -4, …
Here, a = 5 d = 2 – 5 = -3
(i) T_n = a + (n – 1)d
= 5 + (n – 1) (-3)
= 5 – 3n + 3
= 8 – 3n
(ii) T₁₂ = a + 11d
= 5 + 11(-3)
= 5 – 33
= -28

Question 4.
Find the 8th term of the A.P. whose first term is 7 and common difference is 3.
Solution:
First term (a) = 7
and common difference (d) = 3
A.P. = 7, 10, 13, 16, 19, …
T₈ = a + (n – 1)d
= 7 + (8 – 1) x 3
= 7 + 7 x 3
= 7 + 21
= 28

Question 5.
(i) If the common difference of an A.P. is – 3 and the 18th term is – 5, then find its first term.
(ii) If the first term of an A.P. is – 18 and its 10th term is zero, then find its common difference.
Solution:
(i) Common difference (d) = -3
T₁₈ = -5
a + (n – 1 )d = Tn
a + (18 – 1) (-3) = -5

Question 6.
Which term of the A.P.
(i) 3, 8, 13, 18, … is 78?
(ii) 7, 13, 19, … is 205 ?
(iii) 18, \(15 \frac { 1 }{ 2 } \), 13, … is – 47 ?
Solution:
(i) 3, 8, 13, 18, … is 78
Let 78 is nth term
Here, a = 3, d = 8 – 3 = 5

Question 7.
(i) Check whether – 150 is a term of the A.P. 11, 8, 5, 2, …
(ii) Find whether 55 is a term of the A.P. 7, 10, 13, … or not. If yes, find which term is it.
(iii) Is 0 a term of the A.P. 31,28, 25,…? Justify your answer.
Solution:
(i) A.P. is 11, 8, 5, 2, …
Here, a = 11, d = 8 – 11 = -3
Let -150 = n, then

Question 8.
(i) Find the 20th term from the last term of the A.P. 3, 8, 13, …, 253.
(ii) Find the 12th from the end of the A.P. – 2, – 4, – 6, …; – 100.
Solution:
(i) A.P. is 3, 8, 13, …, 253
12th term from the end
Last term = 253
Here, a = 3, d = 8 – 3 = 5

Question 9.
Find the sum of the two middle most terms of the A.P.
\(-\frac { 4 }{ 3 } ,-1,-\frac { 2 }{ 3 } ,…,4\frac { 1 }{ 3 } \)
Solution:
Given
A.P. is \(-\frac { 4 }{ 3 } ,-1,-\frac { 2 }{ 3 } ,…,4\frac { 1 }{ 3 } \)

Question 10.
Which term of the A.P. 53, 48, 43,… is the first negative term ?
Solution:
Let nth term is the first negative term of the A.P. 53, 48, 43, …
Here, a = 53, d = 48 – 53 = -5
.’. T_n = a + (n – 1 )d
= 53 + (n – 1) x (-5)
= 53 – 5n + 5
= 58 – 5n
5n = 58
\(n= \frac { 58 }{ 5 } \)
= \(11 \frac { 3 }{ 5 } \)
∴ 12th term will be negative.

Question 11.
Determine the A.P. whose fifth term is 19 and the difference of the eighth term from the thirteenth term is 20.
Solution:
In an A.P.,
T₅ = 19
T₁₃ – T₈ = 20
Let a be the first term and d be the common difference

Question 12.
Determine the A.P. whose third term is 16 and the 7th term exceeds the 5th term by 12
Solution:
T₃ = 16
T₇ – T₅ = 12
Let a be the first term and d be the common difference

Question 13.
Find the 20th term of the A.P. whose 7th term is 24 less than the 11th term, first term being 12.
Solution:
T₁₁ – T₇ = 24
a= 12
Let a be the first term and d be the common difference, then
(a + 10d) – (a + 6d) = 24

Question 14.
Find the 31st term of an A.P. whose 11th term is 38 and 6th term is 73.
Solution:
T₁₁ = 38, T₆ = 73
Let a be the first term and d be the common difference, then
a + 10d = 38..(i)
a + 5d = 73…(ii)

Question 15.
If the seventh term of an A.P. is \(\\ \frac { 1 }{ 9 } \) and its ninth term is \(\\ \frac { 1 }{ 7 } \), find its 63rd term.
Solution:
a₇ = \(\\ \frac { 1 }{ 9 } \)
⇒ a + 6d = \(\\ \frac { 1 }{ 9 } \) ….(i)
a₉ = \(\\ \frac { 1 }{ 7 } \)
⇒ a + 8d = \(\\ \frac { 1 }{ 7 } \)……(ii)

Question 16.
(i) The 15th term of an A.P. is 3 more than twice its 7th term. If the 10th term of the A.P. is 41, find its nth term.
(ii) The sum of 5th and 7th terms of an A.P. is 52 and the 10th term is 46. Find the A.P.
(iii) The sum of 2nd and 7th terms of an A.P. is 30. If its 15th term is 1 less than twice its 8th term, find the A.P.
Solution:
(i) Let a be the first term and d be a common difference.
We have,



∴ The A.P formed is 1, 6, 11, 16,….

Question 17.
If 8th term of an A.P. is zero, prove that its 38th term is triple of its 18th term.
Solution:
T₈ = 0
To prove that T₃₈ = 3 x T₁₈
Let a be the first term and d be the common difference

Question 18.
Which term of the A.P. 3, 10, 17,… will be 84 more than its 13th term?
Solution:
A.P. is 3, 10, 17, …
Here, a = 3, d – 10 – 3 = 7
T₁₃ = a + 12d
= 3 + 12 x 7
= 3 + 84
= 87

Question 19.
If the nth terms of the two A.g.s 9, 7, 5, … and 24, 21, 18, … are the same, find the value of n. Also, find that term
Solution:
nth term of two A.P.s 9, 7, 5,… and 24, 21, 18, … are same
In the first A.P. 9, 7, 5, …
a = 9 and d = 7 – 9 = -2
T_n = a + (n – 1)d
= 9 + (n – 1)(-2)

Question 20.
(i) How many two digit numbers are divisible by 3 ?
(ii) Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
(iii) How many numbers lie between 10 and 300, which when divided by 4 leave a remainder 3?
Solution:
(i) Two digits numbers divisible by 3 are
12, 15, 18, 21, …, 99
Here, a = 13, d = 15 – 12 = 3 and l = 99
Let number divisible by 3 and n

Question 21.
If the numbers n – 2, 4n – 1 and 5n + 2 are in A.P., find the value of n.
Solution:
n – 2, 4n – 1 and 5n + 2 are in A.P.
∴ 2(4n – 1) = n – 2 + 5n + 2
8n – 2 = 6n
⇒ 8n – 6n = 2
⇒ 2n = 1
⇒ \(n \frac { 2 }{ 2 } \) = 1
∴ n = 1

Question 22.
The sum of three numbers in A.P. is 3 and their product is – 35. Find the numbers.
Solution:
Sum of three numbers which are in A.P. = 3
Their product = -35
Let three numbers which are in A.P.
a – d, a, a + d
a – d + a + a + d = 3
⇒ 3a = 3 ,
⇒ a = \(\\ \frac { 3 }{ 3 } \) = 1

Question 23.
The sum of three numbers in A.P. is 30 and the ratio of first number to the third number is 3 : 7. Find the numbers.
Solution:
Sum of three numbers in A.P. = 30
Ratio between first and the third number = 3 : 7
Let numbers be
a – d, a, a + d, then
a – d + a + a + d = 30

Question 24.
The sum of the first three terms of an A.P.is 33. If the product of the first and the third terms exceeds the second term by 29, find the A.P.
Solution:
Let the three numbers in A.P. are
a – d, a, a + d
Now, a – d + a + a + d = 33
⇒ 3a = 33
⇒ a = \(\\ \frac { 33 }{ 3 } \) = 11

Question 25.
A man starts repaying a loan as first instalment of Rs 500. If he increases the instalment by Rs 25 every month, what,amount will he pay in the 30th instalment?
Solution:
First instalment of loan = Rs 500
Increases Rs 25 every month
Here, a = 500, d = 25
Total instalments (n) = 30
We have to find T₃₀
T₃₀ = a + (n – 1 )d = a + 29d
= 500 + 29 x 25
= 500 + 725
= Rs 1225

Question 26.
Ramkali saved Rs 5 in the first week of a year and then increased her savings by Rs 1.75. If in the rcth week, her weekly savings become Rs 20.75, find n.
Solution:
Savings in the first week = Rs 5
Increase every week = Rs 1.75
No. of weeks = n

Question 27.
Justify whether it is true to say that the following are the nth terms of an A.P.
(i) 2n – 3
(ii) n² + 1
Solution:
(i) 2n – 3
Giving the some difference values to n such as 1, 2, 3, 4, … then
2 x 1 – 3 = 2 – 3 = -1
2 x 2 – 3 = 4 – 3 = 1
2 x 3 – 3 = 6 – 3 = 3
2 x 4 – 3 = 8 – 3 = 5

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
For the following A.P.s, write the first term a and the common difference d:
(i) 3, 1, – 1, – 3, …
(ii) \(\frac { 1 }{ 3 } ,\frac { 5 }{ 3 } ,\frac { 9 }{ 3 } ,\frac { 13 }{ 3 } ,…. \)
(iii) – 3.2, – 3, – 2.8, – 2.6, …
Solution:
(i) 3, 1, -1, -3, …
Here first term (a) = 3
and the common difference (d)
= 1 – 3 = -2,
– 1 – 1 = -2,…
= -2

Question 2.
Write first four terms of the A.P., when the first term a and the common difference d are given as follows :
(i) a = 10, d = 10
(ii) a = – 2, d = 0
(iii) a = 4, d = – 3
(iv) a = \(\\ \frac { 1 }{ 2 } \), d = \(– \frac { 1 }{ 2 } \)
Solution:
(i) a = 10, d = 10
∴ A.P. = 10, 20, 30, 40, …
(ii) a = -2, d = 0
∴ A.P. = -2, -2, -2, -2, ….

Question 3.
Which of the following lists of numbers form an A.P.? If they form an A.P., find the common difference d and write the next three terms :
(i) 4, 10, 16, 22,…
(ii) – 2, 2, – 2, 2,…..
(iii) 2, 4, 8, 16,….
(iv) 2, \(\\ \frac { 5 }{ 2 } \), 3, \(\\ \frac { 7 }{ 2 } \),……
(v) – 10, – 6, – 2, 2,….
(vi) 1², 3², 5², 7²,….
(vii) 1, 3, 9, 27,….
(viii) √2, √8, √18, √32,….
(ix) 3, 3 + √2, 3 + √2, 3 + 3√2,…..
(x) √3, √6, √9, √12,……
(xi) a, 2a, 3a, 4a,…….
(xii) a, 2a + 1, 3a + 2, 4a + 3,….
Solution:
(i) 4, 10, 16, 22,…
Here a = 4, d = 10 – 4 = 6, 16 – 10 = 6, 22 – 16 = 6
∵ common difference is same
∵ It is in A.P
and next three terms are 28, 34, 40

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Choose the correct answer from the given four options (1 to 33) :

Question 1.
The list of numbers – 10, – 6, – 2, 2, … is
(a) an A.P. with d = – 16
(b) an A.P with d = 4
(c) an A.P with d = – 4
(d) not an A.P
Solution:
-10, -6, -2, 2, … is
an A.P. with d = – 6 – (-10)
= -6 + 10 = 4 (b)

Question 2.
The 10th term of the A.P. 5, 8, 11, 14, … is
(a) 32
(b) 35
(c) 38
(d) 185
Solution:
10th term of A.P. 5, 8, 11, 14, …
{∵ a = 5, d = 3}
a + (n – 1)d = 5 + (10 – 1) x 3
= 5 + 9 x 3
= 5 + 27
= 32 (a)

Question 3.
The 30th term of the A.P. 10, 7, 4, … is
(a) 87
(b) 77
(c) – 77
(d) – 87
Solution:
30th term of A.P. 10, 7, 4, … is
30th term = a + (n – 1)d

Question 4.
The 11th term of the A.P. – 3, \(– \frac { 1 }{ 2 } \), 2, … is
(a) 28
(b) 22
(c) – 38
(d) – 48
Solution:
Given
-3, \(– \frac { 1 }{ 2 } \), 2, …

Question 5.
The 4th term from the end of the A.P. – 11, – 8, – 5, …, 49 is
(a) 37
(b) 40
(c) 43
(d) 58
Solution:
4th term from the end of the A.P. -11, -8, -5, …, 49 is
Here, a = -11, d = -8 – (-11) = -8 + 11 = 3 and l = 49 .

Question 6.
The 15th term from the last of the A.P. 7, 10, 13, …,130 is
(a) 49
(b) 85
(c) 88
(d) 110
Solution:
15th term from the end of A.P. 7, 10, 13,…, 130
Here, a = 7, d = 10 – 7 = 3, l = 130
15th term from the end = l – (n – 1)d
= 130 – (15 – 1) x 3
= 130 – 42
= 88 (c)

Question 7.
If the common difference of an A.P. is 5, then a₁₈ – a₁₃ is
(a) 5
(b) 20
(c) 25
(d) 30
Solution:
Common difference of an A.P. (d) = 5
a₁₈ – a₁₃ = a + 17d – a – 12d = 5d = 5 x 5 = 25 (c)

Question 8.
In an A.P., if a₁₈ – a₁₄ = 32 then the common difference is
(a) 8
(b) – 8
(c) – 4
(d) 4
Solution:
If a₁₈ – a₁₄ = 32, then d = ?
(a + 17d) – a – 13d = 32
⇒ a + 17d – a – 13d = 32
⇒ 4d = 32
⇒ \(d \frac { 32 }{ 4 } \) = 8 (a)

Question 9.
In an A.P., if d = – 4, n = 7, a_n = 4, then a is
(a) 6
(d) 7
(c) 20
(d) 28
Solution:
In an A.P., d = -4, x = 7, a_n = 4 then a = ?
a_n = a(n – 1)d = 4
a₇ = a + (7 – 1)d = 4
⇒ a + 6d = 4
⇒ a + 6 x (-4) = 4
a – 24 = 4
⇒ a = 4 + 24 = 28 (d)

Question 10.
In an A.P., if a = 3.5, d = 0, n = 101, then a_n will be
(a) 0
(b) 3.5
(c) 103.5
(d) 104.5
Solution:
In an A.P.
a = 3.5, d= 0, n = 101, then a_n = ?
a_n = a₁₀₁ = a + (101 – 1)d
= 3.5 + 100d
= 3.5 + 100 x 0
= 3.5 + 0
= 3.5 (b)

Question 11.
In an A.P., if a = – 7.2, d = 3.6, a_n = 7.2, then n is
(a) 1
(b) 3
(c) 4
(d) 5
Solution:
In an A.P.
a = – 7.2, d = 3.6, a_n = 7.2, n = ?
a_n = 7.2
a + (n – 1)d = 7.2
– 7.2 + (n – 1) 3.6 = 7.2
(n – 1) x 3.6 = 7.2 + 7.2 = 14.4
(n – 1) = \(\\ \frac { 14.4 }{ 3.6 } \) = 4
n = 4 + 1 = 5 (d)

Question 12.
Which term of the A.P. 21, 42, 63, 84,… is 210?
(a) 9th
(b) 10th
(c) 11th
(d) 12th
Solution:
Which term of an A.P. 21, 42, 63, 84, … is 210
Let 210 be nth term, then
Here, a = 21, d = 42 – 21 =21
210 = a + (n – 1)d
210 = 21 + (n – 1) x 21
⇒ 210 – 21 = 21(n – 1)
⇒ \(\\ \frac { 189 }{ 21 } \) = n – 1
⇒ 9 = n – 1
⇒ n = 9 + 1 = 10
.’. It is 10th term. (b)

Question 13.
If the last term of the A.P. 5, 3, 1, – 1,… is – 41, then the A.P. consists of
(a) 46 terms
(b) 25 terms
(c) 24 terms
(d) 23 terms
Solution:
Last term of an A.P. 5, 3, 1, -1, … is -41
Then A.P. will consist of ……. terms
Here, a = 5, d = 3 – 5 = – 2 and n =?
l = -41
l = -41
l = -41 = a + (n – 1 )d
-41 = 5 + (n – 1) (-2)
-41 – 5 = (n – 1) (-2)
⇒ \(\\ \frac { -46 }{ -2 } \) = n – 1
⇒ n – 1 = 23
⇒ n = 23 + 1 = 24
A.P. consists of 24 terms. (c)

Question 14.
If k – 1, k + 1 and 2k + 3 are in A.P., then the value of k is
(a) – 2
(b) 0
(c) 2
(d) 4
Solution:
k – 1, k + 1 and 2k + 3 are in A.P.
2(k+ 1) = (k – 1) + (2k + 3)
⇒ 2k + 2 = k – 1 + 2k + 3
⇒ 2k + 2 – 3k + 2
⇒ 3k – 2k = 2 – 2
⇒ k = 0 (b)

Question 15.
The 21st term of an A.P. whose first two terms are – 3 and 4 is
(a) 17
(b) 137
(c) 143
(d) – 143
Solution:
First two terms of an A.P. are – 3 and 4
a = -3, d = 4 – (-3) = 4 + 3 = 7
21st term = a + 20d
= -3 + 20(7)
= -3 + 140
= 137 (b)

Question 16.
If the 2nd term of an A.P. is 13 and the 5th term is 25, then its 7th term is
(a) 30
(b) 33
(c) 37
(d) 38
Solution:
In an A.P.
2nd term = 13 ⇒ a + d = 13 …(i)
5th term = 25 ⇒ a + 4d = 25 …(ii)
Subtracting (i) and (ii),
3d = 12
⇒ d = \(\\ \frac { 1 }{ 3 } \)
Substitute the value of d in eq. (i), we get
a = 13 – 4 = 9
7th term = a + 6d = 9 + 6 x 4 = 9 + 24 = 33 (b)

Question 17.
If the first term of an A.P. is – 5 and the common difference is 2, then the sum of its first 6 terms is
(a) 0
(b) 5
(c) 6
(d) 15
Solution:
First term (a) of an A.P. = -5
Common difference (d) is 2
Sum of first 6 terms = \(\frac { n }{ 2 } \left[ 2a+\left( n-1 \right) d \right] \)
= \(\frac { 6 }{ 2 } \left[ 2\times \left( -5 \right) +\left( 6-1 \right) \times 2 \right] \)
= 3[-10 + 5 x 2]
= 3 x [-10 – 10]
= 3 x 0 = 0 (a)

Question 18.
The sum of 25 terms of the A.P.\(-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } \) is
(a) 0
(b) \(– \frac { 2 }{ 3 } \)
(c) \(– \frac { 50 }{ 3 } \)
(d) – 50
Solution:
Sum of 25 terms of an A.P.
\(-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } ,-\frac { 2 }{ 3 } \) is

Question 19.
In an A.P., if a = 1, a_n = 20 and S_n = 399, then n is
(a) 19
(b) 21
(c) 38
(d) 42
Solution:
In an A.P., a = 1, a_n = 20, S_n = 399, n is ?
a_n = a + (n – 1 )d = 20
1 +(n – 1)d = 20
(n – 1)d = 20 – 1 = 19 …(i)

Question 20.
In an A.P., if a = – 5, l = 21. and S_n = 200, then n is equal to
(a) 50
(b) 40
(c) 32
(d) 25
Solution:
In an A.P.
a = -5, l = 21, S_n = 200, n = ?
l = a + (n – 1)d = -5 + (n – 1 )d
21 = -5 + (n – 1)d

Question 21.
In an A.P., if a = 3 and S₈ = 192, then d is
(a) 8
(b) 7
(c) 6
(d) 4
Solution:
In an A.P.
a = 3, S₈ =192, d = ?

Question 22.
The sum of first five multiples of 3 is
(a) 45
(b) 55
(c) 65
(d) 75
Solution:
First 5 multiples of 3 :
3, 6, 9, 12, 15
Here, a = 3, d = 6 – 3 = 3

Question 23.
The number of two digit numbers which are divisible by 3 is
(a) 33
(b) 31
(c) 30
(d) 29
Solution:
Two digit number which are divisible by 3 is 12, 15, 18, 21, … 99
Here, a = 12, d = 3, l = 99
l = a_n = a + (n – 1)d
⇒ 12 + (n – 1) x 3 = 99
⇒ (n – 1)3 = 99 – 12 = 87
⇒ n – 1 = \(\\ \frac { 87 }{ 3 } \) = 29
⇒ n = 29 + 1 = 30 (c)

Question 24.
The number of multiples of 4 that lie between 10 and 250 is
(a) 62
(b) 60
(c) 59
(d) 55
Solution:
Multiples of 4 lying between 10 and 250 12, 16, 20, 24, …, 248
Here, a = 12, d = 16 – 12 = 4, l = 248

Question 25.
The sum of first 10 even whole numbers is
(a) 110
(b) 90
(c) 55
(d) 45
Solution:
Sum of first 10 even whole numbers
Even numbers are 0, 2, 4, 6, 8, 10, 12, 14, 16, 18
Here, a = 0, d = 2, n = 10

Question 26.
The list of number \(\\ \frac { 1 }{ 9 } \) , \(\\ \frac { 1 }{ 3 } \), 1, – 3,… is a
(a) GP. with r = – 3
(b) G.P. with r = \(– \frac { 1 }{ 3 } \)
(c) GP. with r = 3
(d) not a G.P.
Solution:
The given list of numbers
\(\\ \frac { 1 }{ 9 } \) , \(\\ \frac { 1 }{ 3 } \), 1, – 3,…

Question 27.
The 11th of the G.P. \(\\ \frac { 1 }{ 8 } \) , \(– \frac { 1 }{ 4 } \) , 2, – 1, … is
(a) 64
(b) – 64
(c) 128
(d) – 128
Solution:
11th of the G.P.
\(\\ \frac { 1 }{ 8 } \) , \(– \frac { 1 }{ 4 } \) , 2, -1, … is

Question 28.
The 5th term from the end of the G.P. 2, 6, 18, …, 13122 is
(a) 162
(b) 486
(c) 54
(d) 1458
Solution:
5th term from the end of the G.P. 2, 6, 18, …, 13122 is
Here, a = 2, r = \(\\ \frac { 6 }{ 2 } \) = 3, l = 13122

Question 29.
If k, 2(k + 1), 3(k + 1) are three consecutive terms of a G.P., then the value of k is
(a) – 1
(b) – 4
(c) 1
(d) 4
Solution:
k, 2(k + 1), 3(k + 1) are in G.P.
[2(k + 1)]² = k x 3(k + 1)
⇒ 4(k + 1)² = 3k(k + 1)
⇒ 4 (k + 1) = 3 k
(Dividing by k + 1 if k + 1 ≠ 0) 4
⇒ 4k + 4 = 3k
⇒ 4k – 3k = -4
⇒ k = -4 (b)

Question 30.
Which term of the G.P. 18, – 12, 8, … is \(\\ \frac { 512 }{ 729 } \) ?
(a) 12th
(b) 11th
(c) 10th
(d) 9th
Solution:
Which term of the G.P.
18, -12, 8,… \(\\ \frac { 512 }{ 729 } \)
Let it be nth term

Question 31.
The sum of the first 8 terms of the series 1 + √3 + 3 + … is
Solution:
Sum of first 8 terms of 1 + √3 + 3 + … is
Here a = 1, \(r=\frac { \sqrt { 3 } }{ 1 } =\sqrt { 3 } \) , n = 8

Question 32.
The sum of first 6 terms of the G.P. 1, \(– \frac { 2 }{ 3 } \) ,\(\\ \frac { 4 }{ 9 } \) ,… is
(a) \(– \frac { 133 }{ 243 } \)
(b) \(\\ \frac { 133 }{ 243 } \)
(c) \(\\ \frac { 793 }{ 1215 } \)
(d) none of these
Solution:
Sum of first 6 terms of G.P.
1, \(– \frac { 2 }{ 3 } \) ,\(\\ \frac { 4 }{ 9 } \) ,…

Question 33.
If the sum of the GP., 1,4, 16, … is 341, then the number of terms in the GP. is
(a) 10
(b) 8
(c) 6
(d) 5
Solution:
The sum of G.P. 1, 4, 16, … is 341
Let n be the number of terms,

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
Find the values of a and below
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
Solution:
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
comparing the corresponding elements
a + 3 = 2a + 1
⇒ 2a – a =3 – 1
⇒ a = 2
b² + 2 = 3b
⇒ b² – 3b + 2 = 0
⇒ b² – b – 2b + 2 = 0
⇒ b (b – 1) – 2 (b – 1) = 0
⇒ (b – 1) (b – 2) = 0.
Either b – 1 = 0, then b = 1
or b – 2 = 0, then b = 2
Hence a = 2, b = 2 or 1

Question 2.
Find a, b, c and d if \(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)
Solution:
Given
\(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)

Question 3.
Find X if Y = \(\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \) and 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
Solution:
Given
2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
⇒ 2X = 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \) – Y

Question 4.
Determine the matrices A and B when
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) and 2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \)
Solution:
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) …..(i)
2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \) …….(ii)
Multiplying (i) by 1 and (ii) by 2

Question 5.
(i) Find the matrix B if A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \) and A² = A + 2B
(ii) If A = \(\begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix} \), B = \(\begin{bmatrix} 0 & 1 \\ -2 & 5 \end{bmatrix} \)
and C = \(\begin{bmatrix} -2 & 0 \\ -1 & 1 \end{bmatrix} \) find A(4B – 3C)
Solution:
A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \)
let B = \(\begin{bmatrix} a & b \\ c & d \end{bmatrix} \)

Question 6.
If A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \), B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \) compute (AB)C = (CB)A ?
Solution:
Given
A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \),
B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and
C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \)

Question 7.
If A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \) find the each of the following and state it they are equal:
(i) (A + B)(A – B)
(ii)A² – B²
Solution:
Given
A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and
B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)

Question 8.
If A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \) find A² – 5A – 14I
Where I is unit matrix of order 2 x 2
Solution:
Given
A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \)

Question 9.
If A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \) and A² = 0 find p and q
Solution:
Given
A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \) and A² = I, find x,y
Solution:
Given
A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \)

Question 11.
If \(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \) find a,b,c and d
Solution:
Given
\(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \)

Question 12.
Find a and b if
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)
Solution:
Given
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)
Find (i) 2A – 3B (ii) A² (iii) BA
Solution:
Given
A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and
B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.