RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2
Other Exercises
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS
Question 1.
Two opposite angles of a parallelogram are (3x- 2)° and (50 – x)°. Find the measure of each angle of the parallelogram.
Solution:
∵ Opposite angles of a parallelogram are equal
∴ 3x – 2 = 50 – x
⇒ 3x + x – 50 + 2
⇒ 4x = 52
⇒ x = \(\frac { 52 }{ 4 }\) = 13
∴ ∠A = 3x – 2 = 3 x 13 – 2 = 39° – 2 = 37°
∠C = 50° -x = 50° – 13 = 37°
But∠A + B = 180°
∴ 37° + ∠B = 180°
⇒ ∠B = 180° – 37° = 143°
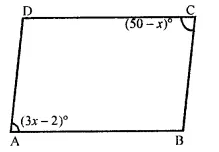
and ∠D = ∠B (Opposite angles of a ||gm)
∴ ∠D = 143°
Hence angles and 37°, 143°, 37°, 143°
Question 2.
If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
Solution:
Let in ||gm ABCD,
∠A =x
Then ∠B = \(\frac { 2 }{ 3 }\) x
But, ∠A + ∠B = 180° (Sum of two adjacent angles of a ||gm)
⇒ x + \(\frac { 2 }{ 3 }\)x = 180°
⇒ \(\frac { 5 }{ 3 }\)x = 180°
⇒ x = 180° x \(\frac { 3 }{ 5 }\) = 108°
∴ ∠A = 108°
and ∠B = 108° x \(\frac { 2 }{ 3 }\) = 72°
But, ∠A = ∠C and ∠B = ∠D (Opposite angles of a ||gm)
∴ ∠C = 108°, ∠D = 72°
Hence angles are 108°, 72°, 108°, 72°
Question 3.
Find the measure of all the angles of a parallelogram, if one angle is 24° less than twice the smallest angle.
Solution:
Let smallest angle of a ||gm = x
Then second angle = 2x – 24°
But these are consecutive angles
∴ x + (2x- 24°) = 180°
⇒ x + 2x – 24° = 180°
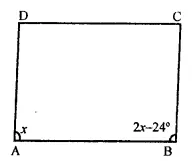
⇒ 3x = 180° + 24° = 204°
⇒ x =\(\frac { { 204 }^{ \circ } }{ 3 }\) = 68°
∴ Smallest angle = 68°
and second angle = 2x 68° – 24°
= 136°-24° = 112°
∵ The opposite angles of a ||gm are equal Other two angles will be 68° and 112°
∴ Hence angles are 68°, 112°, 68°, 112°
Question 4.
The perimeter of a parallelogram is 22 cm. If the longer side measures 6.5 cm what is the measure of the shorter side?
Solution:
In a ||gm ABC,
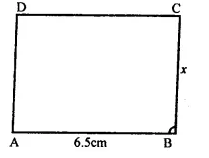
Perimeter = 22cm
and longest side = 6.5 cm
Let shorter side = x
∴ 2x (6.5 + x) = 22
⇒ 13 + 2x = 22
⇒ 2x = 22 – 13 = 9
⇒ x = \(\frac { 9 }{ 2 }\) = 4.5
∴ shorter side = 4.5cm
Question 5.
In a parallelogram ABCD, ∠D = 135°, determine the measure of ∠A and ∠B.
Solution:
In ||gm ABCD,
∠D = 135°
But, ∠A + ∠D = 180° (Sum of consecutive angles)
⇒∠A+ 135° = 180°
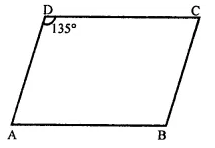
⇒ ∠A = 180° – 135° = 45°
∵ ∠B = ∠D (Opposite angles of a ||gm)
∴ ∠B = 135°
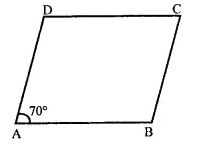
Question 6.
ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D.
Solution:
In ||gm ABCD,
∠A = 70°
But ∠A + ∠B = 180° (Sum of consecutive angles)
⇒ 70° + ∠B = 180°
⇒ ∠B = 180° – 70° = 110°
But ∠C = ∠A and ∠D = ∠B (Opposite angles of a ||gm)
∠C = 70° and ∠D = 110°
Hence ∠B = 110°, ∠C = 70° and ∠D = 110°
Question 7.
In the figure, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute ∠CDB and ∠ADB.
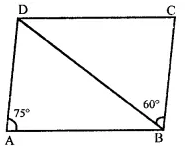
Solution:
In ||gm ABCD,
∠A + ∠B = 180°
(Sum of consecutive angles) But, ∠A = 75°
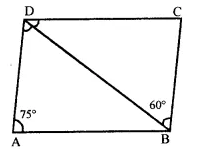
∴ ∠B = 180° – ∠A = 180° – 75° = 105°
∴ DBA = 105° -60° = 45°
But ∠CDB = ∠DBA (alternate angles)
= 45°
and ∠ADB = ∠DBC = 60°
Question 8.
Which of the following statements are true (T) and which are false (F)?
(i) In a parallelogram, the diagonals are equal.
(ii) In a parallelogram, the diagonals bisect each other.
(iii) In a parallelogram, the diagonals intersect each other at right angles.
(iv) In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram.
(v) If all the angles of a quadrilateral are equal, it is a parallelogram.
(vi) If three sides of a quadrilateral are equal, it is a parallelogram.
(vii) If three angles of a quadrilateral are equal, it is a parallelogram.
(viii)If all the sides of a quadrilateral are equal it is a parallelogram.
Solution:
(i) False, Diagonals of a parallelogram are not equal.
(ii) True.
(iii) False, Diagonals bisect each other at right angles is a rhombus or a square only.
(iv) False, In a quadrilateral, if opposite sides are equal and parallel, then it is a ||gm.
(v) False, If all angles are equal, then it is a square or a rectangle.
(vi) False, If opposite sides are equal and parallel then it is a ||gm
(vii) False, If opposite angles are equal, then it is a parallelogram.
(viii)False, If all the sides are equal then it is a square or a rhombus but not parallelogram.
Question 9.
In the figure, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A and ∠B meet at P, prove that AD = DP, PC= BC and DC = 2AD.
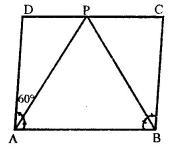
Solution:
Given : In ||gm ABCD,
∠A = 60°
Bisector of ∠A and ∠B meet at P.
To prove :
(i) AD = DP
(ii) PC = BC
(iii) DC = 2AD
Construction : Join PD and PC
Proof : In ||gm ABCD,
∠A = 60°
But ∠A + ∠B = 180° (Sum of excutive angles)
⇒ 60° + ∠B = 180°
∴ ∠B = 1809 – 60° = 120°
∵ DC || AB
∠PAB = ∠DPA (alternate angles)
⇒ ∠PAD = ∠DPA (∵ ∠PAB = ∠PAD)
∴ AB = DP
(PA is its angle bisector, sides opposite to equal angles)
(ii) Similarly, we can prove that ∠PBC = ∠PCB (∵ ∠PAB = ∠BCA alternate angles)
∴ PC = BC
(iii) DC = DP + PC
= AD + BC [From (i) and (ii)]
= AD + AB = 2AB (∵BC = AD opposite sides of the ||gm)
Hence DC = 2AD
Question 10.
In the figure, ABCD is a parallelogram and E is the mid-point of side BC. If DE and AB when produced meet at F, prove thatAF = 2AB.
Solution:
Given : In ||gm ABCD,
E a mid point of BC
DE is joined and produced to meet AB produced at F
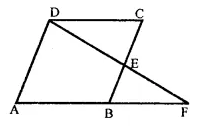
To prove : AF = 2AB
Proof : In ∆CDE and ∆EBF
∠DEC = ∠BEF (vertically opposite angles)
CE = EB (E is mid point of BC)
∠DCE = ∠EBF (alternate angles)
∴ ∆CDE ≅ ∆EBF (SAS Axiom)
∴ DC = BF (c.p.c.t.)
But AB = DC (opposite sides of a ||gm)
∴ AB = BF
Now, AF = AB + BF = AB + AB = 2AB
Hence AF = 2AB
Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.