RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.1
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.2
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.3
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables Ex 13.4
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables VSAQS
- RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS
Mark the correct alternative in each of the following:
Question 1.
The opposite sides of a quadrilateral have
(a) no common point
(b) one common point
(c) two common points
(d) infinitely many common points
Solution:
The opposite sides of a quadrilateral have no common point. (a)
Question 2.
The consecutive sides of a quadrilateral have
(a) no common point
(b) one common point
(c) two common points
(d) infinitely many common points
Solution:
The consecutive sides of a quadrilateral have one common point. (b)
Question 3.
PQRS is a quadrilateral, PR and QS intersect each other at O. In which of the following cases, PQRS is a parallelogram?
(a) ∠P = 100°, ∠Q = 80°, ∠R = 100°
(b) ∠P = 85°, ∠Q = 85°, ∠R = 95°
(c) PQ = 7 cm, QR = 7 cm, RS = 8 cm, SP = 8 cm
(d) OP = 6.5 cm, OQ = 6.5 cm, OR = 5.2 cm, OS = 5.2 cm
Solution:
PQRS is a quadrilateral, PR and QS intersect each other at O. PQRS is a parallelogram if ∠P = 100°, ∠Q = 80°, ∠R = 100° (a)
Question 4.
Which of the following quadrilateral is not a rhombus?
(a) All four sides are equal
(b) Diagonals bisect each other
(c) Diagonals bisect opposite angles
(d) One angle between the diagonals is 60°
Solution:
A quadrilateral is not a rhombus if one angle between the diagonals is 60°. (d)
Question 5.
Diagonals necessarily bisect opposite angles in a
(a) rectangle
(b) parallelogram
(c) isosceles trapezium
(d) square
Solution:
Diagonals necessarily bisect opposite angles in a square. (d)
Question 6.
The two diagonals are equal in a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) trapezium
Solution:
The two diagonals are equal in a rectangle. (c)
Question 7.
We get a rhombus by joining the mid-points of the sides of a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) triangle
Solution:
We get a rhombus by joining the mid points of the sides of a rectangle. (c)
Question 8.
The bisectors of any two adjacent angles of a parallelogram intersect at
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution:
The bisectors of any two adjacent angles of a parallelogram intersect at 90°. (d)
Question 9.
The bisectors of the angle of a parallelogram enclose a
(a) parallelogram
(b) rhombus
(c) rectangle
(d) square
Solution:
The bisectors of the angles of a parallelogram enclose a rectangle. (c)
Question 10.
The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a
(a) parallelogram
(b) rectangle
(c) square
(d) rhombus
Solution:
The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram. (a)
Question 11.
The figure formed by joining the mid-points of the adjacent sides of a rectangle is a
(a) square
(b) rhombus
(c) trapezium
(d) none of these
Solution:
The figure formed by joining the mid-points of the adjacent sides of a rectangle is a rhombus. (b)
Question 12.
The figure formed by joining the mid-points of the adjacent sides of a rhombus is a
(a) square
(b) rectangle
(c) trapezium
(d) none of these
Solution:
The figure formed by the joining the mid-points of the adjacent sides of a rhombus is a rectangle. (b)
Question 13.
The figure formed by joining the mid-points of the adjacent sides of a square is a
(a) rhombus
(b) square
(c) rectangle
(d) parallelogram
Solution:
Tire figure formed by joining the mid-points of the adjacent sides of a square is a square. (b)
Question 14.
The figure formed by joining the mid-points of the adjacent sides of a parallelogram is a
(a) rectangle
(b) parallelogram
(b) rhombus
(d) square
Solution:
The figure formed by joining the mid-points of the adjacent sides of a parallelogram is a parallelogram. (b)
Question 15.
If one angle of a parallelogram is 24° less than twice the smallest angle, then the measure of the largest angle of the parallelogram is
(a) 176°
(b) 68°
(c) 112°
(d) 102°
Solution:
Let the smallest angle be x
The largest angle = 2x – 24°
But sum of two adjacent angles = 180°
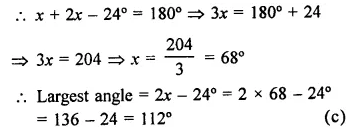
Question 16.
In a parallelogram ABCD, If ∠DAB = 75° and ∠DBC = 60°, then ∠BDC =
(a) 75°
(b) 60°
(c) 45°
(d) 55°
Solution:
In ||gm ABC,
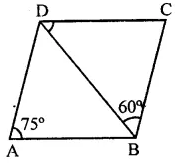
∠A = 75°, ∠DBC = 60°
But ∠A + ∠B = 180° (Sum of two consecutive angles)
⇒ 75° + ∠B = 180°
⇒ ∠B = 180°- 75“= 105°
But ∠DBC = 60°
∴ ∠DBA = 105°-60° = 45°
But ∠BDC = ∠DBA (Alternate angles)
∴ ∠BDC = 45° (c)
Question 17.
ABCD is a parallelogram and E and F are the centroids of triangles ABD and BCD respectively, then EF =
(a) AE
(b) BE
(c) CE
(d) DE
Solution:
In ||gm ABCD, BD is joined forming two triangles ABD and BCD
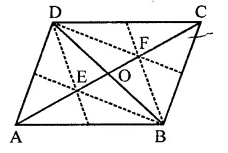
E and F are the centroid of ∆ABD and ∆BCD
Now E and F trisect AC
i.e. AE = EF = FC
∴ EF = AE (a)
Question 18.
ABCD is a parallelogram, M is the mid¬point of BD and BM bisects ∠B. Then, ∠AMB =
(a) 45°
(b) 60°
(c) 90°
(d) 75°
Solution:
In ||gm ABCD, M is mid-point of BD and
BM bisects ∠B
AM is joined
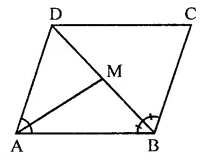
∴AM bisects ∠A
But ∠A + ∠B = 180° (Sum of two consecutive angles)
∴ ∠AMB = 90° (c)
Question 19.
If an angle of a parallelogram is two-third of its adjacent angle, the smallest angle of the parallelogram is
(a) 108°
(b) 54°
(c) 12°
(d) 81°
Solution:
Let adjacent angle of a ||gm = x
Then second angle = \(\frac { 2 }{ 3 }\) x
∴ x+ \(\frac { 2 }{ 3 }\) x= 180°
(Sum of two adjacent angles of a ||gm is 180°)
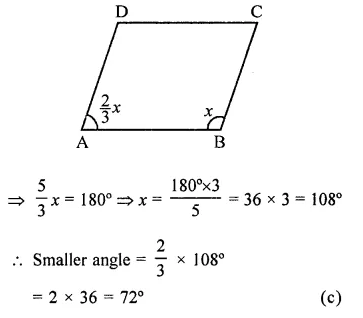
Question 20.
If the degree measures of the angles of quadrilateral are Ax, lx, 9x and 10JC, what is the sum of the measures of the smallest angle and largest angle?
(a) 140°
(b) 150°
(c) 168°
(d) 180°
Solution:
Sum of the angles of a quadrilateral = 360°
∴ 4x + 1x + 9x + 10x = 360°
⇒ 30x = 360°
⇒ x = \(\frac { { 360 }^{ \circ } }{ 30 }\) = 12°
Now sum of smallest and largest angle = 4 x 12° + 10 x 12°
= 48° + 120° = 168° (c)
Question 21.
If the diagonals of a rhombus are 18 cm and 24 cm respectively, then its side is equal to
(a) 16 cm
(b) 15 cm
(c) 20 cm
(d) 17 cm
Solution:
Diagonals of a rhombus are 18 cm and 24 cm But diagonals of a rhombus bisect each other at right angles
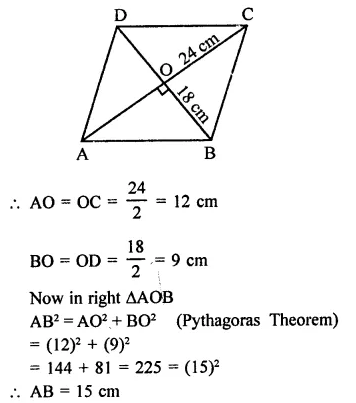
![]()
Question 22.
ABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC = 35°, then ∠ABC =
(a) 70°
(b) 110°
(c) 90°
(d) 120°
Solution:
In ||gm ABCD, AC is its diagonal which bisect ∠BAD
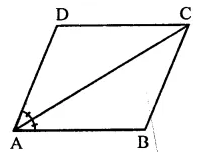
∠BAD = 35°
∴ ∠BAD = 2 x 35° = 70°
But ∠A + ∠B = 180° (Sum of consecutive angles)
⇒ 70° + ∠B = 180°⇒ ∠B = 180° – 70°
∴ ∠B = 110°
⇒ ABC = 110° (b)
Question 23.
In a rhombus ABCD, if ∠ACB = 40°, then ∠ADB =
(a) 70°
(b) 45°
(c) 50°
(d) 60°
Solution:
In rhombus ABCD, ∠ACB = 40°
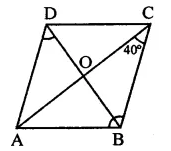
∴ ∠BCD = 2 x ∠ACB
= 2 x 40° = 80°
But ∠BCD + ∠ADC = 180° (Sum of consecutive angles of ||gm)
⇒ 80° + ∠ADC = 180°
⇒ ∠ADC = 180° – 80° = 100°
∴ ∠ADB = \(\frac { 1 }{ 2 }\)∠ADC = \(\frac { 1 }{ 2 }\)x 100° = 50° (c)
Question 24.
In ∆ABC, ∠A = 30°, ∠B = 40° and ∠C = 110°. The angles of the triangle formed by joining the mid-points of the sides of this triangle are
(a) 70°, 70°, 40°
(b) 60°, 40°, 80°
(c) 30°, 40°, 110°
(d) 60°, 70°, 50°
Solution:
In ∆ABC,
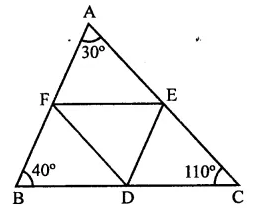
∠A = 30°, ∠B = 40°, ∠C = 110°
D, E and F are mid-points of the sides of the triangle. By joining them in order,
DEF is a triangle formed
Now BDEF, CDFE and AFDE are ||gms
∴ ∠A = ∠D = 30°
∠B = ∠E = 40°
∠C = ∠F= 110°
∴ Angles are 30°, 40°, 110° (c)
Question 25.
The diagonals of a parallelogram ABCD intersect at O. If ∠BOC = 90° and ∠BDC = 50°, then ∠OAB =
(a) 40°
(b) 50°
(c) 10°
(d) 90°
Solution:
In ||gm ABCD, diagonals AC and BD intersect each other at O
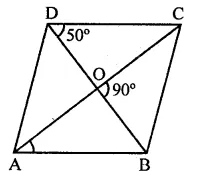
BOC = 90°, ∠BDC = 50°
∵ ∠BOC = 90°
∴ Diagonals of ||gm bisect each other at 90°
∴∠COD = 90°
In ∆COD,
∠OCD = 90° – 50° = 40°
But ∠OAB = ∠OCD (Alternate angles)
∴∠OAB = 40° (a)
Question 26.
ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and BC respectively. If AB = 12 cm, MN = 14 cm, then CD =
(a) 10 cm
(b) 12 cm
(c) 14 cm
(d) 16 cm
Solution:
In trapezium AB || DC
M and N are mid-points of sides AD and BC and MN are joined
AB = 12 cm, MN = 14 cm
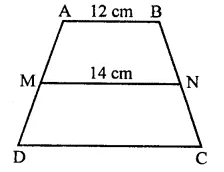
∵ MN = \(\frac { 1 }{ 2 }\)(AB + CD)
⇒ 2MN = AB + CD
⇒ 2 x 14 = 12 + CD
CD = 2 x 14 – 12 = 28 – 12 = 16 cm (d)
Question 27.
Diagonals of a quadrilateral ABCD bisect each other. If ∠A = 45°, then ∠B =
(a) 115°
(b) 120°
(c) 125°
(d) 135°
Solution:
Diagonals AC and BD of quadrilateral ABCD bisect each other at O
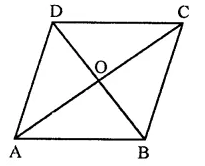
∴ AO = OC, BO = OD
∴ ABCD is a ||gm ∠A = 45°
But ∠A + ∠B = 180° (Sum of consecutive angles)
∴ ∠B = 180° – ∠A = 180° – 45°
= 135° (d)
Question 28.
P is the mid-point of side BC of a paralleogram ABCD such that ∠BAP = ∠DAP. If AD = 10 cm, then CD =
(a) 5 cm
(b) 6 cm
(c) 8 cm
(d) 10 cm
Solution:
In ||gm ABCD, P is mid-point of BC
AD = 10cm
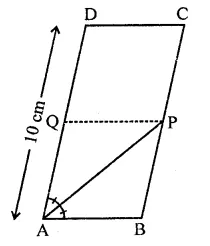
∠BAP = ∠DAP
Through P, draw PQ || AB
∴ ABPQ is rhombus
∴ AB = BP = AQ
= \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) x 10 = 5 cm
But CD = AB (Opposite sides of ||gm)
∴ CD = 5 cm (a)
Question 29.
In ∆ABC, E is the mid-point of median AD such that BE produced meets AC at E If AC = 10.5 cm, then AF =
(a) 3 cm
(b) 3.5 cm
(c) 2.5 cm
(d) 5 cm
Solution:
In ∆ABC, E is the mid-point of median AD
Such that BE produced meets AC at F
AC = 10.5 cm
Draw DG || AF
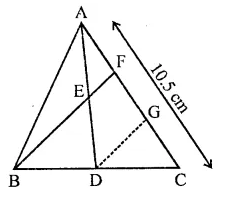
In ∆ADG
E is mid-point of AD and EF || DG
∴ F is mid-point of AG
⇒ AF = FG …(i)
In ∆BCF
D is mid-point of BC and DG || BF
∴ G is mid-point of FC
∴ FG = GC …(i)
From (i) and (ii)
AF = FG = GC = \(\frac { 1 }{ 3 }\) AC
But AC = 10.5 cm
∴ AF = \(\frac { 1 }{ 3 }\) AC = \(\frac { 1 }{ 3 }\) x 10.5 = 3.5 cm (b)
Question 30.
ABCD is a parallelogram and E is the mid-point of BC. DE and AB when produced meet at F. Then, AF =

Solution:
In ||gm ABCD, E is mid-point of BC DE and AB are produced to meet at F
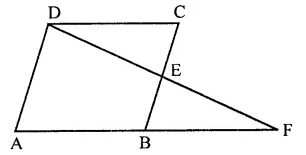
∵ E is mid point of BC
∴ BE = EC
In ∆BEF and ∆CDE
BE = EC
∠BEF = ∠CED (Vertically opposite angle)
and ∠EBF = ∠ECD (Alternate angles)
∴ ∆BEF ≅ ∆CDE (ASA criterian)
∴ DC = BF
But DC = AB
∴ AB = BF
AF = AB + BF = AB + AB
= 2AB (b)
Question 31.
In a quadrilateral ABCD, ∠A + ∠C is 2 times ∠B + ∠D. If ∠A = 140° and ∠D = 60°, then ∠B =
(a) 60°
(b) 80°
(c) 120°
(d) None of these
Solution:
In quadrilateral ABCD
⇒ ∠A + ∠C = 2(∠B + ∠D)
⇒ ∠A + ∠C = 2∠B + 2∠D
Adding 2∠A + 2∠C both sides
2∠A + 2∠C + ∠A + ∠C = 2∠A + 2∠B + 2∠C + 2∠D
⇒ 3∠A + 3∠C = 2(∠A + ∠B + ∠C + ∠D)
⇒ 3(∠A + ∠C) = 2 x 360° = 720°
∴ ∠A + ∠C = \(\frac { { 720 }^{ \circ } }{ 3 }\) = 240°
⇒ 40° + ∠C = 240° (∵ ∠A = 40°)
∠C = 240° – 40° = 200°
Now 2(∠B + ∠D) = ∠A + ∠C = 240°
∠B + ∠D = \(\frac { { 240 }^{ \circ } }{ 2 }\) = 120°
∴ ∠B = 60° = 120°
∴ ∠B = 60° (a)
Question 32.
The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, then ∠DPC =
(a) 70°
(b) 90°
(c) 80°
(d) 100°
Solution:
In rectangle ABCD, diagonals AC and BD intersect each other at P
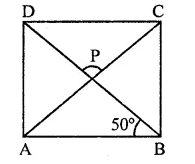
∠ABD = 50°
∴ ∠CAB = ∠ABD = 50° (∵ AP = BP)
Now in ∆APB
∠CAB + ∠ABD + ∠APB = 180° (Angles of a triangle)
⇒ ∠PAB + ∠PBA + ∠APB = 180°
⇒ 50° + 50° + ∠APB = 180°
⇒ ∠APB = 180° – 50° – 50° = 80°
But ∠DPC = ADB (Vertically opposite angles)
∴ ∠DPC = 80° (c)
Hope given RD Sharma Class 9 Solutions Chapter 13 Linear Equations in Two Variables MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.