RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.2
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.2
Other Exercises
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.1
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.2
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS
Question 1.
In the figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD. [NCERT]
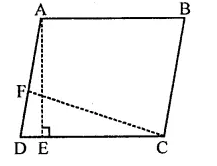
Solution:
In ||gm ABCD,
Base AB = 16 cm
and altitude AE = 8 cm
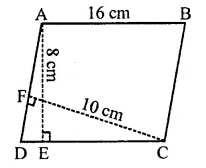
∴ Area = Base x Altitude
= AB x AE
= 16 x 8 = 128 cm2
Now area of ||gm ABCD = 128 cm2
Altitude CF = 10 cm
∴ Base AD = \(\frac { Area }{ Altitude }\) = \(\frac { 128 }{ 10 }\) = 12.8cm
Question 2.
In Q. No. 1, if AD = 6 cm, CF = 10 cm, AE = 8 cm, find AB.
Solution:
Area of ||gm ABCD,
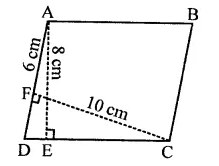
= Base x Altitude
= AD x CF
= 6 x 10 = 60 cm2
Again area of ||gm ABCD = 60 cm2
Altitude AE = 8 cm
∴ Base AB =\(\frac { Area }{ Altitude }\) = \(\frac { 60 }{ 8 }\) = \(\frac { 15 }{ 2 }\) cm = 7.5 cm
Question 3.
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and CD respectively, then find the area of parallelogram AEFD.
Solution:
Area of ||gm ABCD = 124 cm2
E and F are the mid points of sides AB and CD respectively. E, F are joined.
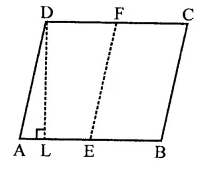
Draw DL ⊥ AB
Now area of ||gm ABCD = Base x Altitude
= AB x DL = 124 cm2
∵ E and F are mid points of sides AB and CD
∴ AEFD is a ||gm
Now area of ||gm AEFD = AE x DL
= \(\frac { 1 }{ 2 }\)AB x DL [∵ E is mid point of AB]
= \(\frac { 1 }{ 2 }\) x area of ||gm ABCD
= \(\frac { 1 }{ 2 }\) x 124 = 62 cm2
Question 4.
If ABCD is a parallelogram, then prove that ar(∆ABD) = ar(∆BCD) = ar(∆ABC) = ar(∆ACD) = \(\frac { 1 }{ 2 }\)ar( ||gm ABCD).
Solution:
Given : In ||gm ABCD, BD and AC are joined
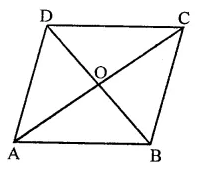
To prove : ar(∆ABD) = ar(∆BCD) = ar(∆ABC) = ar(∆ACD) = \(\frac { 1 }{ 2 }\)ar(||gm ABCD)
Proof: ∵ Diagonals of a parallelogram bisect it into two triangles equal in area When BD is the diagonal, then
∴ ar(∆ABD) = ar(∆BCD) = \(\frac { 1 }{ 2 }\)ar(||gm ABCD) …(i)
Similarly, when AC is the diagonal, then
ar(∆ABC) = ar(∆ADC) = \(\frac { 1 }{ 2 }\)ar(||gm ABCD) …(ii)
From (i) and (ii),
ar(∆ABD) = ar(∆BCD) = ar(∆ABC) = ar(∆ACD) = \(\frac { 1 }{ 2 }\) ar(||gm ABCD)
Hope given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.