RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.1
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.2
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals Ex 14.3
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS
- RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals MCQS
Question 1.
If ABC and BDE are two equilateral triangles such that D is the mid-ponit of BC, then find ar(∆ABC) : ar(∆BDE).
Solution:
ABC and BDE are two equilateral triangles and D is the mid-point of BC
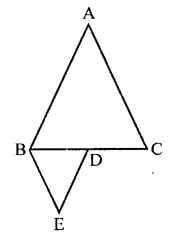
Let each side of AABC = a
Then BD = \(\frac { a }{ 2 }\)
∴ Each side of triangle BDE will be \(\frac { a }{ 2 }\)
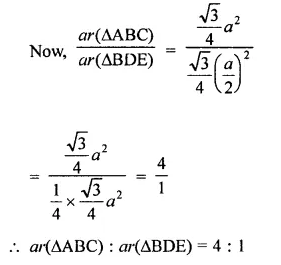
Question 2.
In the figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.
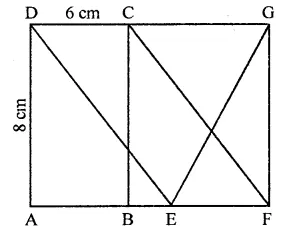
Solution:
In rectangle ABCD,
CD = 6 cm, AD = 8 cm
∴ Area of rectangle ABCD = CD x AD
= 6 x 8 = 48 cm2
∵ DC || AB and AB is produced to F and DC is produced to G
∴ DG || AF
∵ Rectangle ABCD and ||gm CDEF are on the same base CD and between the same parallels
∴ ar(||gm CDEF) = ar(rect. ABCD)
= 48 cm2
Question 3.
In the figure of Q. No. 2, find the area of ∆GEF.
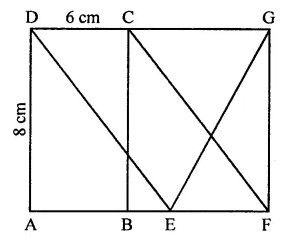
Solution:

Question 4.
In the figure, ABCD is a rectangle with sides AB = 10 cm and AD = 5 cm. Find the area of ∆EFG.
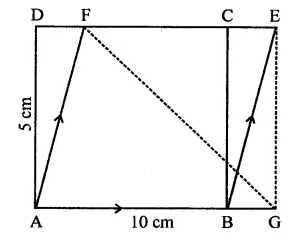
Solution:
ABCD is a rectangle in which
AB = 10 cm, AD = 5 cm
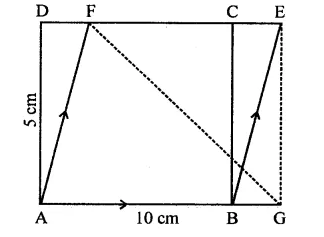
∵ ABCD is a rectangle
∴DC || AB,
DC is produced to E and AB is produced to G
∴DE || AG
∵ Rectangle ABCD and ||gm ABEF are on the same base AB and between the same parallels
∴ ar(rect. ABCD) = ar(||gm ABEF)
= AB x AD = 10 x 5 = 50 cm2
Now ||gm ABEF and AEFG are on the same
base EF and between the same parallels
∴ area ∆EFG = \(\frac { 1 }{ 2 }\) ar(||gm ABEF)
= \(\frac { 1 }{ 2 }\) x 50 = 25 cm2
Question 5.
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find or(∆RAS).
Solution:
In quadrant PLRM, rectangle PQRS is in scribed
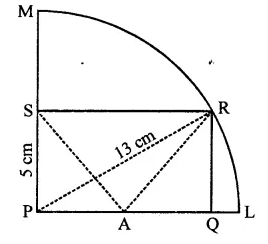
Radius of the circle = 13 cm
A is any point on PQ
AR and AS are joined, PS = 5 cm
In right ∆PRS,
PR2 = PS2 + SR2
⇒ (132 = (5)2+ SR2
⇒ 169 = 25 + SR2
⇒ SR2 = 169 – 25 = 144 = (12)2
∴ SR = 12 cm
Area of rect. PQRS = PS x SR = 5x 12 = 60 cm2
∵ Rectangle PQRS and ARAS are on the same
base SR and between the same parallels
∴ Area ARAS = \(\frac { 1 }{ 2 }\) area rect. PQRS 1
= \(\frac { 1 }{ 2 }\) x 60 = 30 cm2
Question 6.
In square ABCD, P and Q are mid-point of AB and CD respectively. If AB = 8 cm and PQ and BD intersect at O, then find area of ∆OPB.
Solution:
In sq. ABCD, P and Q are the mid points of sides AB and CD respectively PQ and BD are joined which intersect each other at O
Side of square AB = 8 cm
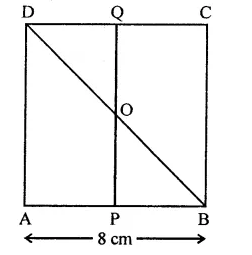
∴ Area of square ABCD = (side)2
∵ Diagonal BD bisects the square into two triangle equal in area
∴ Area ∆ABD = \(\frac { 1 }{ 2 }\) x area of square ABCD
= \(\frac { 1 }{ 2 }\) x 64 = 32 cm2
∵ P is mid point of AB of AABD, and PQ || AD
∴ O is the mid point of BD
∴ OP = \(\frac { 1 }{ 2 }\)AD = \(\frac { 1 }{ 2 }\) x 8 = 4 cm
and PB = \(\frac { 1 }{ 2 }\) AB = \(\frac { 1 }{ 2 }\) x 8 = 4 cm
∴ Area ∆OPB = \(\frac { 1 }{ 2 }\)PB x OP
= \(\frac { 1 }{ 2 }\) x4x4 = 8 cm2
Question 7.
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AE respectively. If area of ∆ABC is 16 cm2, find the area of ∆DEF.
Solution:
In ∆ABC, D is mid point of BC. E and F are the mid points of DC and AE respectively area of ∆ABC = 16 cm2
FD is joined
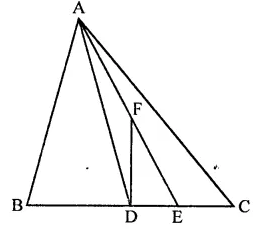
∵ D is mid point of BC
∴ AD is the median and median divides the triangle into two triangles equal in area
area ∆ADC = \(\frac { 1 }{ 2 }\) ar(∆ABC)
= \(\frac { 1 }{ 2 }\) x 16 = 8 cm2
Similarly, E is mid point of DC
∴ area (∆ADE) = \(\frac { 1 }{ 2 }\) ar(∆ADC)
= \(\frac { 1 }{ 2 }\) x 8 = 4 cm2
∵ F is mid point of AE of ∆ADE
∴ ar(∆DEF) = \(\frac { 1 }{ 2 }\)area (∆ADE)
= \(\frac { 1 }{ 2 }\) x 4 = 2 cm2
Question 8.
PQRS is a trapezium having PS and QR as parallel sides. A is any point on PQ and B is a point on SR such that AB || QR. If area of ∆PBQ is 17 cm2, find the area of ∆ASR.
Solution:
In trapezium PQRS,
PS || QR
A and B are points on sides PQ and SR
Such that AB || QR
area of ∆PBQ = 17 cm2
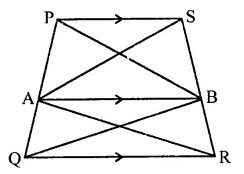
∆ABQ and ∆ABR are on the same base AB and between the same parallels
∴ ar(∆ABQ) = ar(∆ABR) …(i)
Similarly, ∆ABP and ∆ABS are on the same base and between the same parallels
∴ ar(ABP) = ar(∆ABS) …(ii)
Adding (i) and (ii)
ar( ∆ABQ) + ar( ∆ABP)
= ar(∆ABR) + ar(∆ABS)
⇒ ar(∆PBQ) = ar(∆ASR)
Put ar(PBQ) = 17 cm2
∴ ar(∆ASR) = 17 cm2
Question 9.
ABCD is a parallelogram. P is the mid-point of AB. BD and CP intersect at Q such that CQ : QP = 3 : 1. If ar(∆PBQ) = 10 cm2, find the area of parallelogram ABCD.
Solution:
In ||gm ABCD, P is mid point on AB,
PC and BD intersect each other at Q
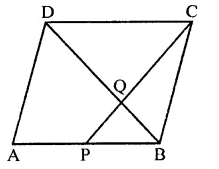
CQ : QP = 3 : 1
ar(∆PBQ) = 10 cm2
In ||gm ABCD,
BD is its diagonal
∴ ar(∆ABD) = ar(∆BCD) = \(\frac { 1 }{ 2 }\) ar ||gm ABCD
∴ ar(||gm ABCD) = 2ar(∆ABD) …(i)
In ∆PBC CQ : QP = 3 : 1
∵ ∆PBQ and ∆CQB have same vertice B
∴ 3 x area ∆PBQ = ar(∆CBQ)
⇒ area(∆CBQ) = 3 x 10 = 30 cm2
∴ ar(∆PBC) = 30 + 10 = 40 cm2
Now ∆ABD and ∆PBC are between the
same parallel but base PB = \(\frac { 1 }{ 2 }\) AB
∴ ar(∆ABD) = 2ar(∆PBC)
= 2 x 40 = 80 cm2
But ar(||gm ABCD) = 2ar(∆ABD)
= 2 x 80 = 160 cm2
Question 10.
P is any point on base BC of ∆ABC and D is the mid-point of BC. DE is drawn parallel to PA to meet AC at E. If ar(∆ABC) = 12 cm2, then find area of ∆EPC.
Solution:
P is any point on base of ∆ABC
D is mid point of BC
DE || PA drawn which meet AC at E
ar(∆ABC) = 12 cm2
AD and PE are joined
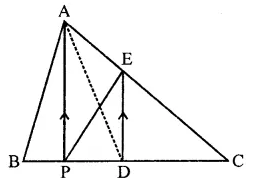
∵ D is mid point of BC
∴ AD is median
∴ ar(∆ABD) = ar(∆ACD)
= \(\frac { 1 }{ 2 }\) (∆ABC) = \(\frac { 1 }{ 2 }\) x 12 = 6 cm2 …(i)
∵ ∆PED and ∆ADE are on the same base DE and between the same parallels
∴ ar(∆PED) = ar(∆ADE)
Adding ar(∆DCE) to both sides,
ar(∆PED) + ar(∆DCE) = ar(∆ADE) + ar(∆DCE)
ar(∆EPC) = ar(∆ACD)
⇒ ar(∆EPC) = ar(∆ABD) = 6 cm2 [From (i)]
∴ ar(∆EPC) = 6 cm2
Hope given RD Sharma Class 9 Solutions Chapter 14 Quadrilaterals VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.