RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2D

RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2D.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2A
• RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2B
• RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2C
• RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2D
• RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2E
• RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2F

Find the H.C.F. of the numbers in each of the following, using the prime factorization method :

Question 1.
Solution:
We have

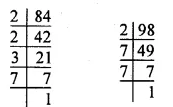
84 = 2 x 2 x 3 x 7
= 2² x 3 x 7
98 = 2 x 7 x 7 = 2 x 7²
∴H.C.F. =2 x 7 = 14.

Question 2.
Solution:
We have

So, 170 = 2 x 5 x 17
238 = 2 x 7 x 17
∴ H.C.F. of 170 and 238 = 2 x 17 = 34

Question 3.
Solution:
We have

So, 504 = 2 x 2 x 2 x 3 x 3 x 7 = 2³ x 3² x 7
980 = 2 x 2 x 5 x 7 x 7 = 2² x 5 x 7²
∴ H.C.F. of 504 and 980 = 2² x 7
= 4 x 7 = 28.

Question 4.
Solution:
We have

So, 72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
108 = 2 x 2 x 3 x 3 x 3 = 2² x 3³
180 = 2 x 2 x 3 x 3 x 5 = 2² x 3² x 5
∴ H.C.F. of 72, 108,
180 = 2² x 3²
= 4 x 9 = 36

Question 5.
Solution:
We have

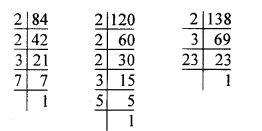
84 = 2 x 2 x 3 x 7 = 2² x 3 x 7
120 = 2 x 2 x 2 x 3 x 5 = 2³ x 3 x 5
138 = 2 x 3 x 23
∴ H.C.F. of 84, 120 and 138 = 2 x 3 = 6

Question 6.
Solution:
We have

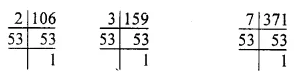
106 = 2 x 53
159 = 3 x 53
371 = 7 x 53
∴ H.C.F. of 106, 159, 371 = 53

Question 7.
Solution:
We have

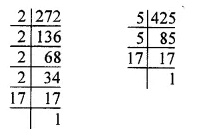
272 = 2 x 2 x 2 x 2 x 17 = 2⁴ x 17
425 = 5 x 5 x 17
= 5² x 17
∴ H.C.F. of 272 and 425 = 17.

Question 8.
Solution:
We have

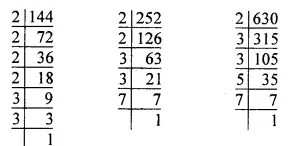
So, 144 = 2 x 2 x 2 x 2 x 3 x 3 = 2⁴ x 3²
252 = 2 x 2 x 3 x 3 x 7 = 2² x 3² x 7
630 = 2 x 3 x 3 x 5 x 7 = 2 x 3² x 5 x 7
∴ H.C.F. of 144, 252 and 630 = 2 x 3²
= 2 x 9 = 18.

Question 9.
Solution:
We have

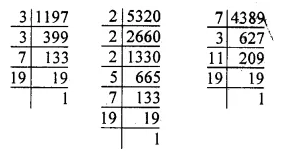
So, 1197 = 3 x 3 x 7 x 19 = 3² x 7 x 19
5320 = 2 x 2 x 2 x 5 x 7 x 19 = 2³ x 5 x 7 x 19
4389 = 7 x 3 x 11 x 19
∴ H.C.F. of 1197, 5320,
4389 = 7 x 19 = 133.

Find the H.C.F. of the numbers in each of the following using division method:

Question 10.
Solution:
By division method, we have :

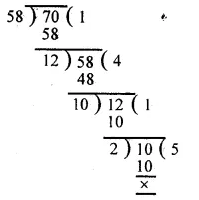
∴ H.C.F. of 58 and 70 = 2.

Question 11.
Solution:
By division method, we have

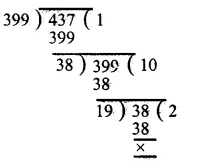
∴ H.C.F. of 399 and 437 = 19

Question 12.
Solution:
By division method, we have

∴ H.C.F. of 1045 and 1520 = 95.

Question 13.
Solution:
By division method, we have

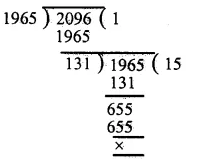
∴ H.C.F. of 1965 and 2096 = 131

Question 14.
Solution:
By division method, we have

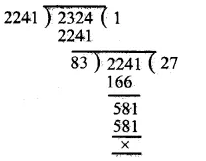
∴ H.C.F. of 2241 and 2324 = 83.

Question 15.
Solution:
First, we find the H.C.F. of 658 and 940

∴ H.C.F. of 658 and 940 is 94.
Now, we find the H.C.F. of 94 and 1128.

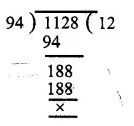
∴ H.C.F. of 94 and 1128 = 94
Hence, H.C.F. of 658, 940 and 1128 = 94.

Question 16.
Solution:
First, we find the H.C.F. of 754 and 1508

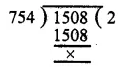
∴ H.C.F. of 754 and 1508 is 754
Now, we find the H.C.F. of 754 and 1972

∴ H.C.F. of 754 and 1972 = 58
Hence, the H.C.F. of 754,1508 and 1972 = 58.

Question 17.
Solution:
First, we find the H.C.F. of 391 and 425

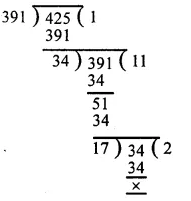
∴ H.C.F. of 391 and 425 is 17.
Now, we find the H.C.F. of 17 and 527

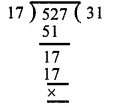
∴ H.C.F. of 17 and 527 is 17 Hence, H.C.F. of 391, 425 and 527 = 17.

Question 18.
Solution:
First, we find the H.C.F. of 1794 and 2346

H.C.F. of 1794 and 2346 is 138.
Now, we find the H.C.F. of 138 and 4761

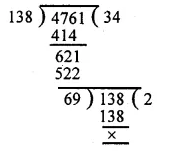
∴ H.C.F. of 138 and 4761 is 69.
Hence, the H.C.F. of 1794, 2346 and 4761 = 69.

Show that the following pairs are co-primes :

Question 19.
Solution:
First, we find the H.C.F. of 59, 97.

∴H.C.F. of 59 and 97 is 1.
Hence 59 and 97 are co-prime.

Question 20.
Solution:
First, we find the H.C.F. of 161 and 192.

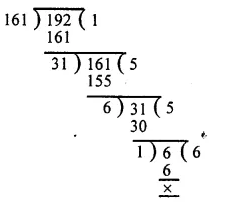
∴ H.C.F. of 161 and 192 is 1.
Hence 161 and 192 are co-prime.

Question 21.
Solution:
First, we find the H.C.F. of 343 and 432

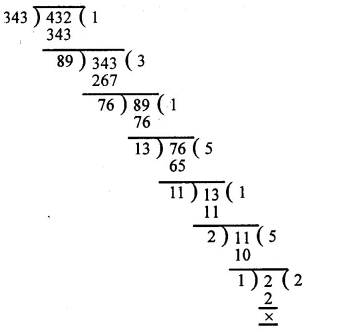
∴ H.C.F. of 343 and 432 is 1.
Hence 343 and 432 are co-prime.

Question 22.
Solution:
First, we find the H.C.F. of 512 and 945.

∴ H.C.F. of 512 and 945 is 1.
Hence 512 and 945 are co-prime.

Question 23.
Solution:
First, we find the H.C.F. of385 and 621

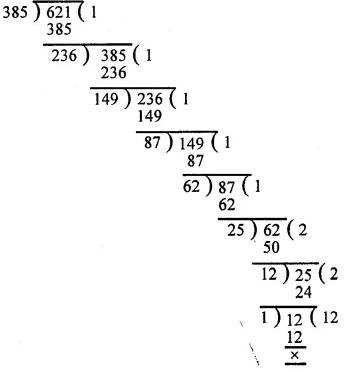
∴ H.C.F. of 385 and 621 is 1.
Hence the numbers 385 and 621 are co-prime

Question 24.
Solution:
First, we find the H.C.F. of 847 and 1014.

∴ H.C.F. of 847 and 1014 is 1.
Hence 847 and 1014 are co-prime.

Question 25.
Solution:
Clearly, we have to find the greatest number which divides (615 – 6) and (963 – 6) exactly.
So, the required number = H.C.F. of 615 – 6 = 609 and 963 – 6 = 957

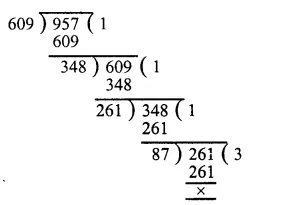
The required greatest number = 87.

Question 26.
Solution:
Clearly, we have to find the greatest number which divides 2011 – 9 = 2002 and 2623 – 5 = 2618.
So, the required greatest number = H.C.F. of 2002 and 2618

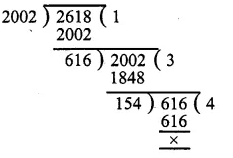
∴ Required greatest number = 154.

Question 27.
Solution:
Clearly, we have to find the greatest number which divides (445 4), (572 – 5) and (699 – 6). So, the required number = H.C.F. of 441, 567 and 693. First we find the H.C.F. of 441 and 567

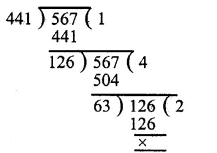
∴ H.C.F. of 441 and 567 is 63

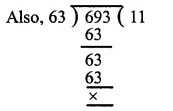
So H.C.F. of 63 and 693 is 63
Hence the required number = 63.

Question 28.
Solution:
(i) The given fraction = \(\\ \frac { 161 }{ 207 } \)
First we find the H.C.F. of 161 and 207

Question 29.
Solution:
Lengths of three pieces of timber = 42 metres, 49 metres, 63 metres Greatest possible length of each plank = H.C.F. of 42 metres, 49 metres and 63 metres
First we find the H.C.F. of 42 and 49

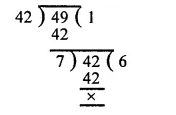
∴ H.C.F. of 42 and 49 = 7
Now we find the H.C.F. of 7 and 63

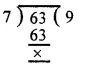
So, the H.C.F. of 7 and 63 is 7
∴ H.C.F. of 42 metres, 49 metres of 63 metres = 7 metres
Hence required possible length of each plank = 7 metres.

Question 30.
Solution:
Quantity of milk in three different containers = 403 L, 434 L and 465 L Clearly, the maximum capacity of the required container = H.C.F. of 403 L, 434 L, 465 L, we have

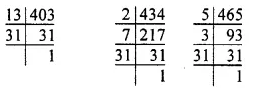
∴ 403 = 13 x 31
434 = 2 x 7 x 31
465 = 5 x 3 x 31
So the H.C.F. of 403 L, 434 L and 465 L = 31 L
Maximum capacity of the required container = 31 L.

Question 31.
Solution:
The given fruits = 527 apples, 646 pears and 748 oranges
Clearly, the greatest number of fruits in each heap = H.C.F. of 527, 646 and 748 we have

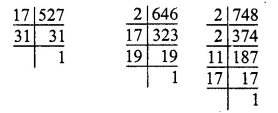
∴ 527 = 17 x 31
646 = 2 x 17 x 19
748 = 2 x 2 x 11 x 17
So, the H.C.F. of 527, 646 and 748 = 17
∴ Required number of fruits in each heap = 17
Total number of fruits = 527 + 646 + 748 = 1921
Number of heaps = \(\frac { Total\quad number\quad of\quad fruits }{ Number\quad of\quad fruits\quad in\quad one\quad heap } \)
= \( \frac { 1921 }{ 17 } \)
=113

Question 32.
Solution:
The given lengths are :
7 metres = 7 x 100 cm
= 700 cm 3 metres 85 cm
= (3 x 100 + 85) cm
= 385 cm
12 metres 95 cm = (12 x 100 + 95) cm
= 1295 cm
Clearly, the length of the required longest tape = H.C.F. of 700 cm, 385 cm and 1295 cm
We have

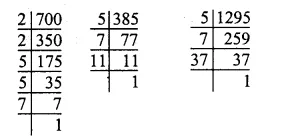
So, 700 = 2 x 2 x 5 x 5 x 7
= 2² x 5² x 7
385 = 5 x 7 x 11
1295 = 5 x 7 x 37
∴ H.C.F. of 700, 385 and 1295 = 5 x 7 = 35
∴ The required length of the longest tape
= 35 cm.

Question 33.
Solution:
Length of the courtyard = 18 m 72 cm = (18 x 100 + 72) cm = 1872 cm
Breadth of the courtyard = 13 m 20 cm = (13 x 100 + 20) cm = 1320 cm
Greatest side of each of the square tiles = H.C.F. of 1872 cm and 1320 cm
Now

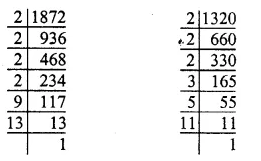
1872 = 2 x 2 x 2 x 2 x 9 x 13
= 2⁴ x 3² x 13
1320 = 2 x 2 x 2 x 3 x 5 x 11
= 2³ x 3 x 5 x 11
So, the H.C.F. of 1872 and 1320
= 2³ x 3 = 8 x 3 = 24
Greatest side of the square tile = 24 cm
Now Area of the courtyard = Length x Breadth = 1872 x 1320 cm²
Area of one square tile = Side x Side
= 24 x 24 cm²
∴ Least possible number of such tiles
= \(\frac { Area\quad of\quad the\quad courtyard }{ Area\quad of\quad the\quad tile } \)
= \( \frac { 1872\times 1320 }{ 24\times 24 } \)
= 78 x 55
= 4290

Question 34.
Solution:
Let the two prime numbers be 13 and 17, we find the H.C.F. of 13 and 17 as under

Hope given RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.