RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2E.

Other Exercises

Find the L.C.M. of the numbers given below:

Question 1.
Solution:
We have
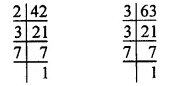
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 1.1
42 = 2 x 3 x 7
63 = 3 x 3 x 7
= 3² x 7
∴ L.C.M. of 42 and 63 = 2 x 3² x 7
= 2 x 9 x 7
= 18 x 7
= 126

Question 2.
Solution:
We have
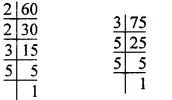
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 2.1
So, 60 = 2 x 2 x 3 x 5
= 2² x 3 x 5
75 = 3 x 5 x 5 = 3 x 5²
∴L.C.M. of 60 and 75 = 2² x 3 x 5²
= 4 x 3 x 25
= 4 x 75 = 300

Question 3.
Solution:
We have
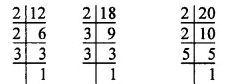
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 3.1
So, 12 = 2 x 2 x 3 = 2² x 3
18 = 2 x 3 x 3 = 2 x 3²
20 = 2 x 2 x 5 = 2² x 5
∴L.C.M. of 12, 18 and 20 = 2² x 3² x 5
=4 x 9 x 5
= 20 x 9
= 180

Question 4.
Solution:
We have
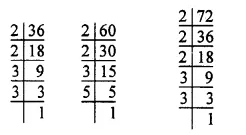
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 4.1
36 = 2 x 2 x 3 x 3 = 2² x 3²
60 = 2 x 2 x 3 x 5 = 2² x 3 x 5
72 = 2 x 2 x 2 x 3 x 3 = 2³ x 3²
∴ L.C.M. of 36, 60 and 72 = 2³ x 3² x 5
=8 x 9 x 5
= 40 x 9
= 360

Question 5.
Solution:
We have
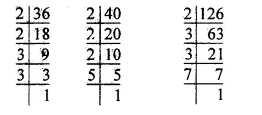
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 5.1
36 = 2 x 2 x 3 x 3 = 2² x 3²
40 = 2 x 2 x 2 x 5 = 2³ x 5
126 = 2 x 3 x 3 x 7 = 2 x 3² x 7
∴ L.C.M. of 36, 40 and 126 .
= 2³ x 3² x 5 x 7
= 8 x 9 x 5 x 7
= 72 x 35
= 2520

Question 6.
Solution:
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 6.1
∴ L.C.M. of given numbers
= 2 x 2 x 2 x 7 x 2 x 5 x 11
= 8 x 14 x 55
= 112 x 55 = 6160

Question 7.
Solution:
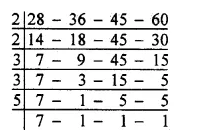
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 7.1
∴L.C.M. of given numbers = 2 x 2 x 3 x 3 x 5 x 7
= 36 x 35
= 1260

Question 8.
Solution:
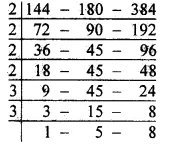
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 8.1
∴L.C.M. of given numbers
= 2 x 2 x 2 x 2 x 3 x 3 x 5 x 8
= 16 x 9 x 40
= 144 x 40
= 5760

Question 9.
Solution:
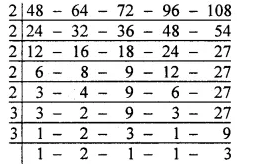
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 9.1
∴L.C.M. of given numbers = 2 x 2 x 2 x 2 x 2 x 3 x 3 x 2 x 3
= 32 x 54
= 1728

Find the H.C.F. and L.C.M. of :

Question 10.
Solution:
First we find the H.C.F. of the given numbers as under :
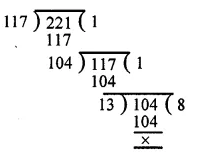
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 10.1
∴ H.C.F. of 117 and 221 = 13
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 117\times 221 }{ 13 } \)
= 9 x 221 = 1989
∴ H.C.F. = 13 and L.C.M. = 1989

Question 11.
Solution:
First we find the H.C.F. of 234 and 572 as under :
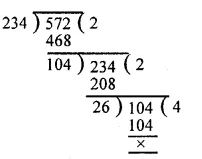
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 11.1
H.C.F. of 234 and 572 = 26
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 234\times 572 }{ 26 } \)
= 9 x 572
= 5148

Question 12.
Solution:
First we find the H.C.F. of 693 and 1078 as under :
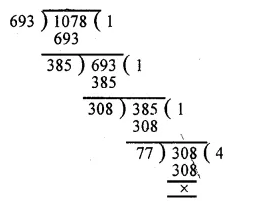
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 12.1
H.C.F. of 693 and 1078 = 77 Product of numbers
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 693\times 1078 }{ 77 } \)
= 9 x 1078
= 9702
H.C.F. = 77 and L.C.M. = 9702

Question 13.
Solution:
First we find the H.C.F. of 145 and 232 as under :
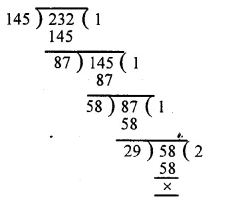
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 13.1
H.C.F. of 145 and 232 = 29
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 145\times 232 }{ 29 } \)
= 5 x 232 = 1160
H.C.F. = 29 and L.C.M. = 1160

Question 14.
Solution:
First we find the H.C.F. of 861 and 1353 as under :
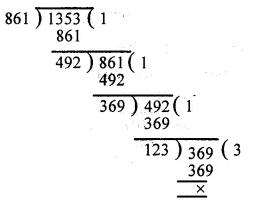
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 14.1
H.C.F. of 861 and 1353 = 123
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 861\times 1353 }{ 123 } \)
= 7 x 1353 = 9471
H.C.F. = 123 and L.C.M. = 9471

Question 15.
Solution:
First we find the H.C.F. of 2923 and 3239 as under :
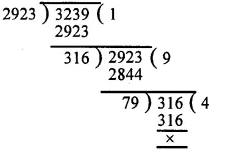
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 15.1
H.C.F. of 2923 and 3239 = 79
Now L.C.M. = \(\frac { product\quad of\quad numbers }{ their\quad H.C.F } \)
= \(\frac { 2923\times 3239 }{ 79 } \)
= 37 x 3239= 119843
H.C.F. = 79 and L.C.M. = 119843

Question 16.
Solution:
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 16.1

Question 17.
Solution:
We know that
L.C.M = \(\frac { product\quad of\quad the\quad number }{ their\quad H.C.F } \)
= \(\\ \frac { 2160 }{ 12 } \)
= 180

Question 18.
Solution:
We know that
L.C.M = \(\frac { product\quad of\quad the\quad number }{ their\quad H.C.F } \)
= \(\\ \frac { 2560 }{ 320 } \)
= 8

Question 19.
Solution:
We know that
One number x The other number
= H.C.F. x L.C.M.
.’. The other number
= \(\\ \frac { H.C.F\times L.C.M }{ One\quad number } \)
= \(\\ \frac { 145\times 2175 }{ 725 } \)
= \(\\ \frac { 2175 }{ 5 } \)
= 435
Required number = 435

Question 20.
Solution:
We know that
One number x The other number
= H.C.F. x L.C.M.
The other number
= \(\\ \frac { H.C.F\times L.C.M }{ One\quad number } \)
= \(\\ \frac { 131\times 8253 }{ 917 } \)
= \(\\ \frac { 8253 }{ 7 } \)
Required number = 1179

Question 21.
Solution:
Required least number = L.C.M. of 15, 20, 24, 32 and 36
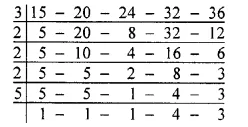
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 21.1
L.C.M. = 3 x 2 x 2 x 2 x 5 x 4 x 3
= 24 x 60
= 1440
Hence, required least number = 1440

Question 22.
Solution:
Clearly, required least number = (L.C.M. of the given numbers + 9)
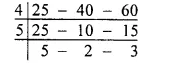
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 22.1
L.C.M. of the given numbers
= 4 x 5 x 5 x 2 x 3
= 600
Required least number
= 600 + 9
= 609

Question 23.
Solution:
First we find the L.C.M. of the given numbers as under :
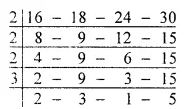
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 23.1
L.C.M of the given numbers = 2 x 2 x 2 x 3 x 2 x 3 x 5
= 24 x 30 = 720
Now least number of five digits = 10000 Dividing 10000 by 720, we get

Clearly if we add 80 to 640, it will become 720 which is exactly divisible by 720.
Required least number of five digits = 10000 + 80 = 10080

Question 24.
Solution:
The greatest number of five digits exactly divisible by the given numbers = The greatest number of five digits exactly divisible by the L.C.M. of given numbers.
Now
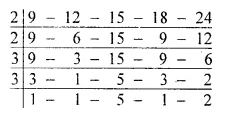
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 24.1
L.C.M. of given numbers
= 2 x 2 x 3 x 3 x 5 x 2 = 360
Now greatest number of five digits = 99999
Dividing 99999 by 360, we get

Required greatest number of five digits
= 99999 – 279
= 99720

Question 25.
Solution:
Three bells will again toll together after an interval of time which is exactly divisible by 9, 12, 15 minutes.
Required time = L.C.M. of 9, 12, 15 minutes

L.C.M. of 9, 12, 15 minutes = 3 x 3 x 4 x 5 minutes
= 9 x 20 minutes
= 180 minutes
Required time = 180 minutes
= \(\\ \frac { 180 }{ 60 } \)
= 3 hours

Question 26.
Solution:
Required distance = L.C.M. of 36 cm, 48 cm and 54 cm
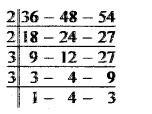
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 26.1
L.C.M. of 36 cm, 48 cm. 54 cm
= 2 x 2 x 3 x 3 x 4 x 3 cm
= 36 x 12 cm
= 432 cm
= 4 m 32 cm
Required distance = 4 m 32 cm

Question 27.
Solution:
Required time = L.C.M. of 48 seconds, 72 seconds and 108 seconds
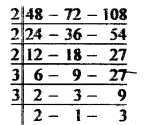
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 27.1
L.C.M. of 48 sec., 72 sec. and 108 sec.
= 2 x 2 x 2 x 3 x 3 x 2 x 3 sec.
= 24 x 18 sec.
= 432 sec.
Required time = 432 sec.
= \(\\ \frac { 432 }{ 60 } \)
= 7 m in 12 sec

Question 28.
Solution:
Lengths of three rods = 45 cm, 50 cm and 75 cm
Required least length of the rope = L.C.M. of 45 cm, 50 cm, 75 cm
We have
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 28.1

Question 29.
Solution:
The time after which both the devices will beep together = L.C.M. of 15 minutes and 20 minutes
Now,
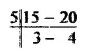
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 29.1
L.C.M. of 15 minutes and 20 minutes
= 5 x 3 x 4
= 60 minutes
= 1 hour
Both the devices will beep together after 1 hour from 6 a.m.
Required time = 6 + 1
= 7 a.m.

Question 30.
Solution:
The circumferences of four wheels = 50 cm, 60 cm, 75 cm and 100 cm
Required least distance = L.C.M. of 50 cm, 60 cm, 75 cm and 100 cm Now,
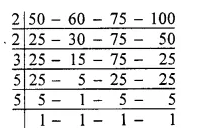
RS Aggarwal Class 6 Solutions Chapter 2 Factors and Multiples Ex 2E 30.1
L.C.M. of 50 cm, 60 cm, 75 cm, 100 cm
= 2 x 2 x 3 x 5 x 5 cm
= 300 cm = 3 m
Required least distance = 3 m.

Hope given RS Aggarwal Solutions Class 6 Chapter 2 Factors and Multiples Ex 2E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.