RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15A
These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A.
Other Exercises
- RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
- RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
- RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
- RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D
Question 1.
Solution:
In ∆ABC,
∠A = 72°, ∠B = 63°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ 72° + 63° + ∠C = 180°
⇒ 135° + ∠C = 180°
⇒ ∠C= 180°- 135° = 45°
Question 2.
Solution:
In. ∆PQR,
∠E = 105°, and ∠F = 40°
But ∠D + ∠E+ ∠F= 180° (sum of angles of a triangle)
⇒ ∠D + 105°+ 40°= 180°
⇒ ∠ D + 145° = 180°
⇒ ∠D = 180°- 145°
⇒ ∠D = 35°
Question 3.
Solution:
In ∆XYZ,
∠ X = 90°, ∠ Z = 48°
But ∠X + ∠Y + ∠Z = 180° (Sum of angles of a triangle)
⇒ 90° + ∠ Y + 48° = 180°
⇒ 138°+ ∠ Y = 180°
⇒ ∠Y = 180° – 138° = 42°
⇒ ∠Y = 42°
Question 4.
Solution:
Sum of angles of a triangle = 180°
and ratio in the three angles = 4 : 3 : 2

Question 5.
Solution:
In a right triangle
Sum of the two acute angles = 90°
One angle = 30°
Second angle = 90° – 36° = 54°
Question 6.
Solution:
In a right triangle
Sum of two acute angles = 90°
and ratio of these two angles = 2 : 1
Let first angle = 2x
Then second angle = x
2x + x = 90°
⇒ 3x = 90°
⇒ x = \(\frac { 90 }{ 3 }\) = 30°
First angle = 2x = 2 x 30° = 60°
and second angle = x = 1 x 30° = 30°
Question 7.
Solution:
In a triangle,
Measure of one angle = 100°
Sum of other two angles = 180° – 100° = 80°
(Sum of angles of a triangles)
But, these two angles are equal.
Measure of each angle = \(\frac { 80 }{ 2 }\) = 40°
Question 8.
Solution:
Sum of angles of a triangle = 180°
Let third angle = x
then, each equal angles = 2x
x + 2x + 2x = 180°
⇒ 5x = 180°
⇒ x = \(\frac { 180 }{ 5 }\) = 36°
Each equal angle = 2x = 2 x 36° = 72°
and third angle = 36°
Question 9.
Solution:
In a triangle ABC,
Let ∠A = ∠B + ∠C
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
⇒ ∠A + ∠A = 180° (∠B + ∠C = ∠A)
⇒ 2A = 180°
⇒ ∠ A = \(\frac { 180 }{ 2 }\) = 90°
∠ A = 90°
Hence, ∆ABC is a right triangle.
Question 10.
Solution:
In a ∆ABC,
2 ∠A = 3 ∠B = 6 ∠C = 1 (suppose)
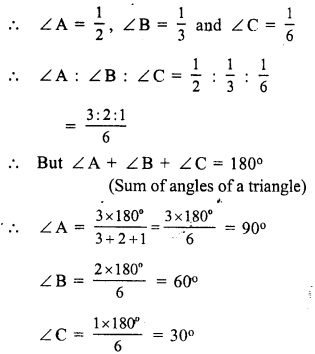
Question 11.
Solution:
In an equilateral triangle,
All sides are equal.
All angles are also equal.
Each angle = \(\frac { 180 }{ 3 }\) = 60°
(Sum of angles of a triangle = 180°)
Question 12.
Solution:
In the given figure,
ABC is a triangle in which DE || BC,
∠A = 65° and ∠B = 55°
DE || BC and ADB is the transversal
⇒ ∠ ADE = ∠ B (corresponding angles) = 55° (∠B = 55°)
In ∆ADE,
∠A + ∠ADE + ∠AED = 180° (sum of angles of a triangle)
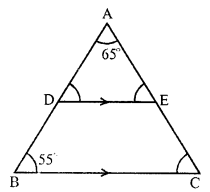
⇒ 65° + 55° + ∠AED = 180°
⇒ ∠ 120° + ∠AED = 180°
⇒ ∠AED = 180°- 120° = 60°
∠AED = 60°
D || BC and AEC is the transversal
∠ C = ∠ AED (A corresponding angles)
∠C = 60°
Hence ∠ADE = 55°, ∠AED = 60° and ∠ C = 60°
Question 13.
Solution:
(i) No. In a triangle, only one right angle is possible as if there are two right angles, then The third angle will be ∠ero which is not possible.
(ii) No. In a triangle only one obtuse angle is possible as if there are two obtuse angles, then the sum of these two angles will be greater than 180° which is not possible.
(iii) Yes. two acute can arc possible.
(iv) No. The sum of these three angles will be greater than 180° which is not possible in a triangle.
(v) No. The sum of these angles will be less than 180° which is not possible.
(vi) Yes. The sum of there three angle will be in 180° which is possible.
Question 14.
Solution:
(i) Yes, it can be a right triangle also
(ii) Yes, if right triangle has its sides different then it is possible.
(iii) No, a right triangle cannot be an equilateral triangle as an equilateral triangle has each side 60°.
(iv) Yes, it is possible, if its sides opposite to acute angles are equal.
Question 15.
Solution:
(i) A right triangle cannot have an obtuse angle.
(ii) The acute angles of a right triangle are complementary.
(iii) Each acute angle of an isosceles right triangle measures 45°.
(iv) Each angle of an equilateral triangle measures 60°.
(v) The side opposite the right angle of the right triangle is called the hypotenuse.
(vi) The sum of the lengths of the sides of a triangle is called its perimeter.
Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.