RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15D

RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15D

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D

Question 1.
Solution:
In right triangle ABC, ∠B = 90° AB = 9cm, BC = 12cm

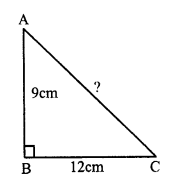
By Pythagoras Theorem,
AC² = AB² + BC² = (9)² + (12)² = 81 + 144 = 225
AC = √225 = 15 cm

Question 2.
Solution:
In right ∆ABC, ∠B = 90°
AC = 26cm, AB = 10cm
By Pythagoras Theorem
AC² = AB² + BC²

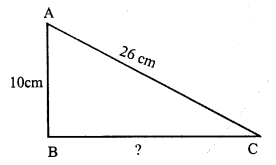
⇒ (26)² = (10)² + BC²
⇒ 676 = 100 + BC²
⇒ BC² = 676 – 100 = 576 = (24)²
⇒ BC = 24 cm

Question 3.
Solution:
In right ∆ABC, ∠C = 90°,
AB = 7.5cm, BC = 4.5cm
By Pythagoras Theorem
AB² = BC² + AC²

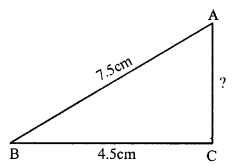
⇒ (7.5)² = (4.5)² + AC²
⇒ 56.25 = 20.25 + AC²
⇒ AC² = 56.25 – 20.25 = 36.00 = (6)²
⇒ AC = 6cm

Question 4.
Solution:
In ∆ABC, ∠B = 90°
Let each leg = x cm

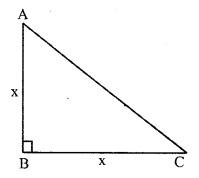
By Pythagoras Theorem,
x² + x² = AC²
⇒ 2x² = 50
⇒ x² = 25 = (5)²
⇒ x = 5
Length of each equal leg = 5cm

Question 5.
Solution:
A triangle is a right-angled,
If (Hypotenuse)² = sum of squares or other two sides
If (39)² = (15)² + (36)² (Hypotenuse is the longest side)
If 1521 = 225 + 1296
If 1521 = 1521 Which is true.
It is a right-angled triangle.

Question 6.
Solution:
In ∆ABC, ∠C = 90°

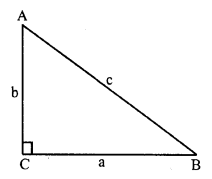
a = 6cm, b = 4.5cm.
By Pythagoras Theorem
c² = a² + b² = (6)² + (4.5)² = 36.00 + 20.25 = 56.25 = (7.5)²
c = 7.5 cm

Question 7.
Solution:
A triangle will be a right angled
if (longest side)² = Sum of squares of other two sides
(i) a = 15cm, b = 20cm, c = 25cm.
Here, longest side = c ,
The triangle will be right angled
if c² = a² + b²
if (25)² = (15)² + (20)²
if 625 = 225 + 400 = 625 Which is true.
It is a right angled triangle.
(ii) a = 9cm, b = 12cm, c = 16cm
∆ABC is a right angled triangle if
c² = a² + b²
if (16)² = (9)² + (12)²
if 256 = 81 + 144 = 225
⇒ 256 = 225
Which is not true
Triangle is not a right angled triangle.
(iii) a = 10cm, b = 24cm, c = 26cm
The triangle ABC is a right angled triangle
if c² = a² + b²
if (26)² = (10)² + (24)²
if 676 = 100 + 576
if 676 = 676 Which is true.
The triangle is a right angled triangle.

Question 8.
Solution:
In ∆ABC,
∠B = 35° and ∠C = 55°
∠A = 180°- (∠B + ∠C) = 180° – (35° + 55°) = 180° – 90° = 90°
∆ABC is a right angled triangle
By Pythagoras Theorem,
BC² = AB² + AC²
(iii) is hue

Question 9.
Solution:
AB is a ladder and it is 15 m long B is window and BC = 12 m
In right ∆ABC
AB² = AC² + BC² (By Pythagoras Theorem)
⇒ (15)² = x² + (12)²
⇒ (15)² = x² + (12)²
⇒ 225 = x² + 144
⇒ x² = 225 – 144
⇒ x² = 81 = (9)²
x = 9 m
Distance of the foot of ladder from the wall = 9 m

Question 10.
Solution:
Let AB be the ladder and AC be the height.

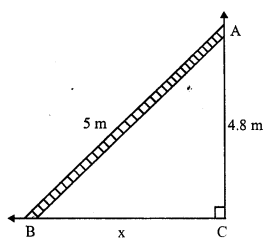
Length of ladder AB = 5m
and height CA = 4.8m
Let distance of the ladder from the wall BC = x
Now in right angled ∆ABC, ∠C = 90°
AB² = AC² + BC² (By Pythagoras Theorem)
⇒ (5)² = (4.8)² + x²
⇒ 25 = 23.04 + x²
⇒ x² = 25.00 – 23.04 = 1.96 = (1.4)²
⇒ x = 1.4
The foot of ladder are 1.4m away from the wall.

Question 11.
Solution:
Let AB be the tree which broke at D and its top A touches the ground at C
their BD = 5m, BC = 12m,
Let AD = x m, then CD = x m
Now, in right ∆ABC,
CD² = BD² + BC²
(By Pythagoras Theorem)

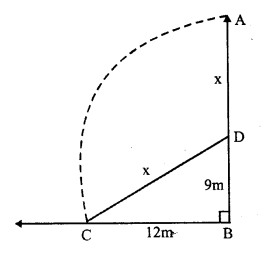
CD² = (9)² + (12)² = 81 + 144 = 225 = (15)²
CD = 15m,
AD = x = 15m
Height of the tree AB = AD + BD = 15 + 9 = 24m

Question 12.
Solution:
AB and CD are two poles and they are 12,m apart
AB = 18 m, CD = 13m and BD = 12 m

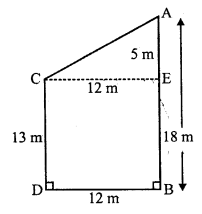
From C, draw CE || BD Then
CE = BD = 12 m
and AE = AB – EB = AB – CD = 18 – 13 = 5 m
Join AC
Now in right ∆ACE
AC² = CE² + AE²
(By Pythagoras Theorem)
AC² = (12)² + (5)² = 144 + 25 = 169 = (13)²
AC = 13 m
Distance between their tops = 13 m

Question 13.
Solution:
A man starts from O and goes 35m due west and then 12m due north, then
In rights ∆OAB,
OA = 35 m
AB = 12 m

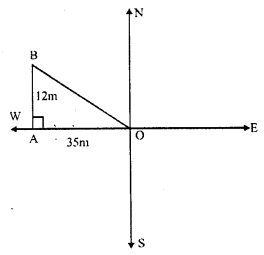
OB² = OA² + AB² (By Pythagoras Theorem)
= (35)² + (12)² = 1225 + 144 = 1369 = (37)²
OB = 37
Hence he is 37m away from the starting point

Question 14.
Solution:
A man goes 3km due north and then 4km east.

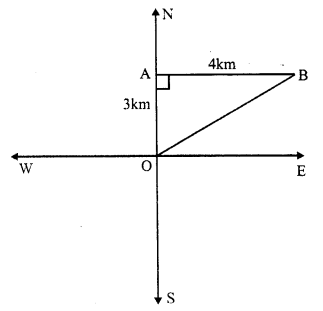
In right angled ∆OAB,
OA = 3km.
AB = 4km.
OB² = OA² + AB² (By Pythagoras Theorem)
= (3)² + (4)² = 9 + 16 = 25 = (5)²
OB = 5km
Hence he is 5km from the initial position.

Question 15.
Solution:
ABCD is a rectangle whose sides
AB = 16cm and BC = 12cm.
AC is its diagonal
In right angled ∆ABC
AC² = AB² + BC²
(By Pythagoras Theorem)
= (16)² + (12)² = 256 + 144 = 400 = (20)²
AC = 20cm
Hence length of diagonal AC = 20 cm

Question 16.
Solution:
ABCD is a rectangle and AC is its diagonal

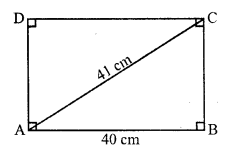
AB = 40 cm and AC = 41 cm
Now in right ∆ABC
AC² = AB² + BC² (By Pythagoras Theorem)
⇒ (41)² = (40)² + BC²
⇒ 1681 = 1600 + BC²
⇒ BC² = 1681 – 1600 = 81 = (9)²
⇒ BC = 9 cm
Now perimeter of rectangle ABCD = 2 (AB + BC)
= 2 (40 + 9) = 2 x 49 = 98 cm

Question 17.
Solution:
Perimeter of rhombus ABCD = 4 x Side
Diagonal AC = 30 cm and BD = 16 cm
The diagonals of rhombus bisect each other at right angles
AO = OC = \(\frac { 30 }{ 2 }\) = 15 cm
and BO = OD = \(\frac { 16 }{ 2 }\) = 8 m
Now in right ∆AOB,
AB² = AO² + BO² = (15)² + (8)² = 225 + 64 = 289 = (17)²
AB = 17 cm
Now perimeter = 4 x side = 4 x 17 = 68 cm

Question 18.
Solution:
(i) In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
(ii) If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right angled.
(iii) Of all the line segments that can be drawn to a given line from a given point outside it, the perpendicular is the shortest.

Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.