RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15C

RS Aggarwal Class 7 Solutions Chapter 15 Properties of Triangles Ex 15C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15A
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15B
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C
• RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15D

Question 1.
Solution:
We know that in a triangle, sum of any two sides is greater than the third side. Therefore :
(i) 1cm, 1cm, 1cm
It is possible to draw a triangle
(1 + 1) cm > 1cm (sum of two sides is greater than the third)
(ii) 2cm, 3cm, 4cm
It is also possible to draw the triangle
(2 + 3) cm > 4cm (sum of two sides is greater than third side)
(iii) 7cm, 8cm, 15cm
It is not possible to draw the triangle
(7 + 8)cm not > 15cm
But (7 + 8) cm = 15 cm
(iv) 3.4 cm, 2.1 cm, 5.3 cm
It is possible to draw the triangle
(3.4 + 2.1) cm > 5.3 cm
⇒ 5.5cm > 5.3 cm
(v) 6cm, 7cm, 14cm
It is not possible to draw
(6 + 7) cm not > 14cm
i.e. 13cm not > 14cm (13cm < 14cm)

Question 2.
Solution:
Two sides of a triangle are 5 cm and 9 cm long
Then the third side will be less then (5 + 9) or less than 14 cm

Question 3.
Solution:
(i) In ∆APB,
PA + PB > AB (sum of two sides is greater than its third side)
(ii) In ∆PBC,
PB + PC > BC (sum of two sides is greater than its third side)
(iii) In ∆PAC,
AC < PA + PC (PA + PC > AC)

Question 4.
Solution:
Proof: AM is the median of ∆ABC
M is mid-point of BC

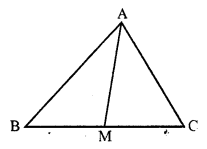
In ∆ABM,
AB + BM > AM ….(i)
(Sum of any two sides of a triangle is greater than its third side)
Similarly in ∆ACM,
AC + MC > AM ….(ii)
Adding (i) and (ii)
AB + BM + AC + MC > 2 AM
⇒ AB + AC + BM + MC > 2AM
⇒ AB + AC + BC > 2AM
Hence proved.

Question 5.
Solution:
Given: In ∆ABC, P is a point on BC.
AP is joined.
To prove :
(AB + BC + AC) > 2AP
Proof : In ∆ABP,
AB + BP > AP …(i) (Sum of two sides is greater than third)
Similarly in ∆ACP,

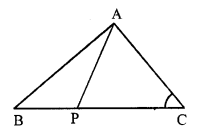
AC + PC > AP …(ii)
Adding (i) and (ii)
AB + BP + AC + PC > AP + AP
⇒ AB + BP + PC + CA > 2AP
⇒ AB + BC + CA > 2AP
Hence proved.

Question 6.
Solution:
ABCD is a quadrilateral AC and BD are joined.
Proof: Now in ∆ABC
AB + BC > AC ….(i)

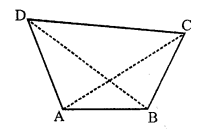
(Sum of any two sides of a triangle is greater than its third side)
Similarly in ∆ADC,
AD + CD > AC ….(ii)
In ∆ABD,
AB + AD > BD ….(iii)
and in ∆BCD,
BC + CD > BD ……..(iv)
Adding (i), (ii), (iii) and (iv)
AB + BC + CD + AD + AB + AD + BC + CD > AC + AC + BD + BD
⇒ 2 (AB + BC + CD + AD) > 2(AC + BD)
⇒ AB + BC + CD + AD > AC + BD
Hence proved.

Question 7.
Solution:
Given : O is any point outside of the ∆ABC
To prove : 2(OA + OB + OC) > (AB + BC + CA)
Construction : Join OA, OB and DC.
Proof: In ∆AOB,

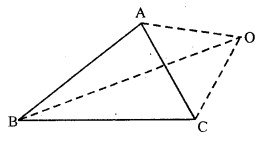
OA + OB > AB ….(i) (Sum of two sides of a triangle is greater than its third side)
Similarly in ∆BOC,
OB + OC > BC …(ii)
and in ∆COA
OC + OA > CA …(iii)
Adding (i), (ii) and (iii), we get:
OA + OB + OB + OC + OC + OA > AB + BC + CA
2 (OA + OB + OC) > (AB + BC + CA)
Hence proved.

Hope given RS Aggarwal Solutions Class 7 Chapter 15 Properties of Triangles Ex 15C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.