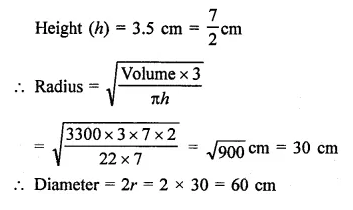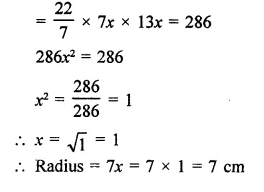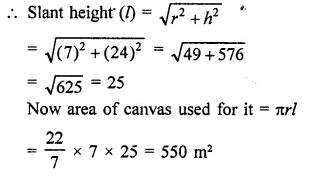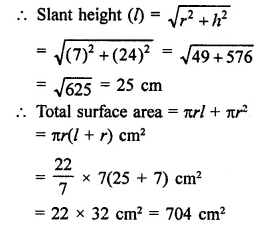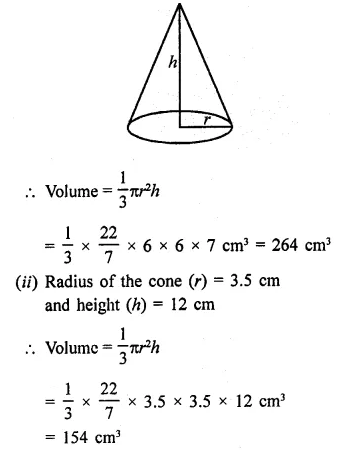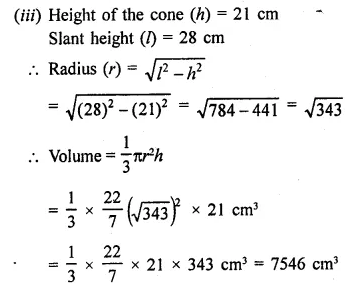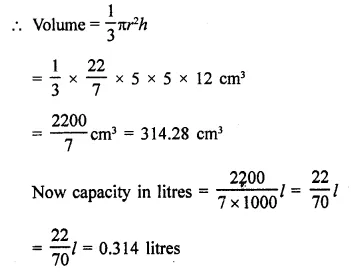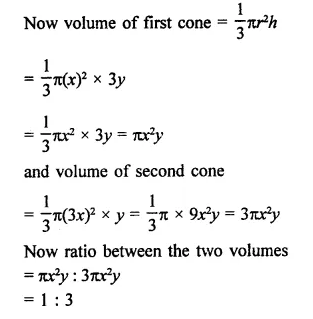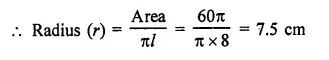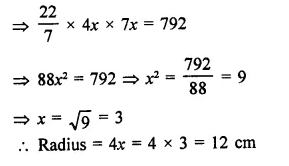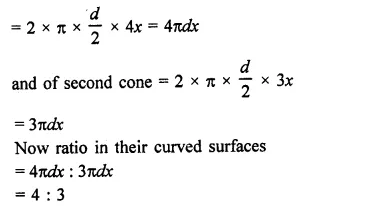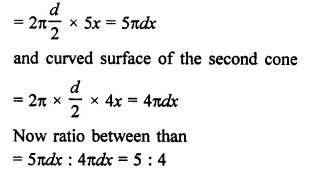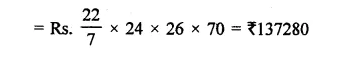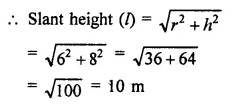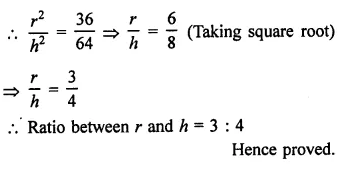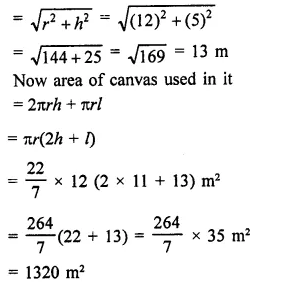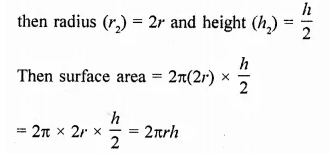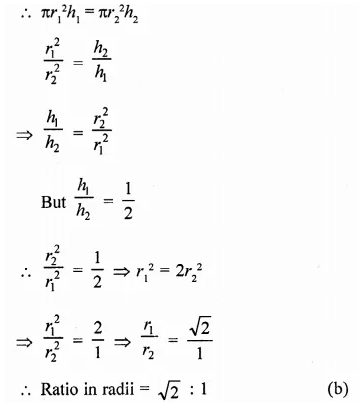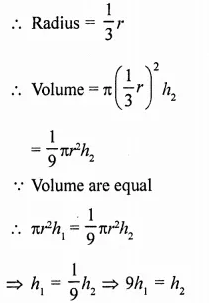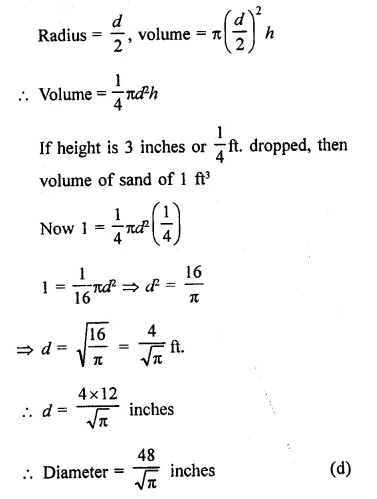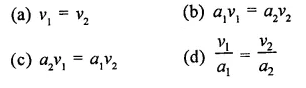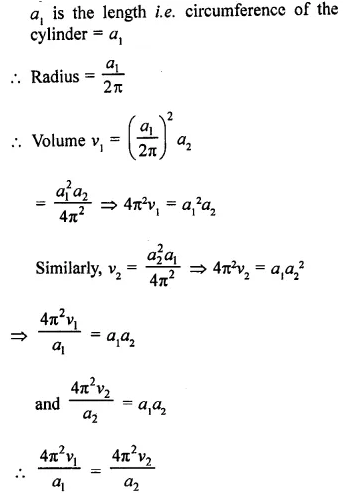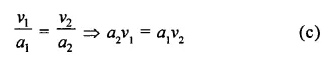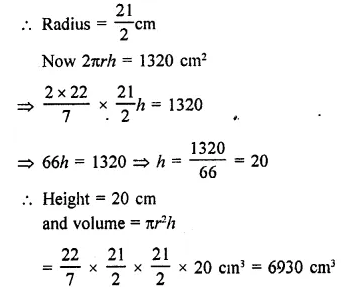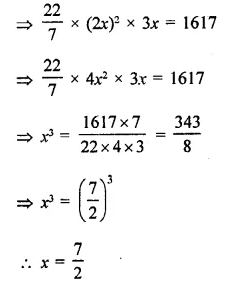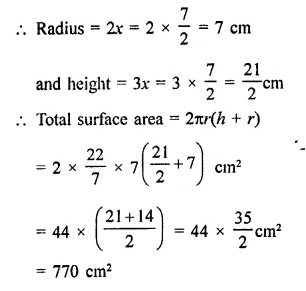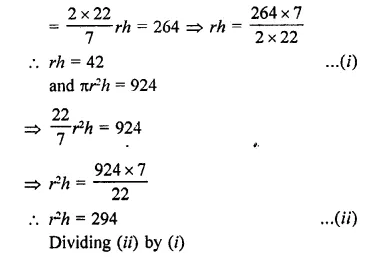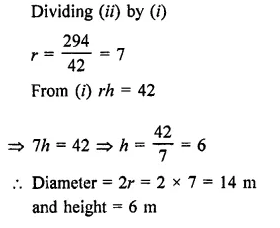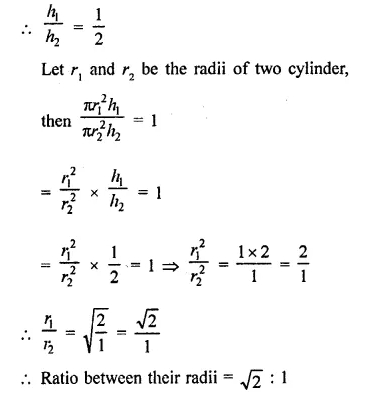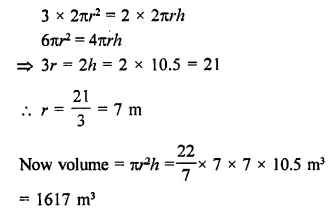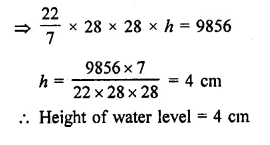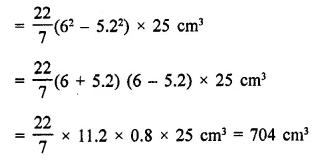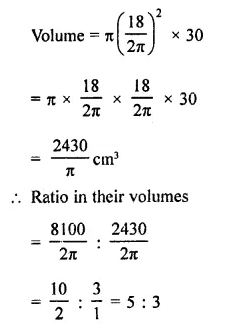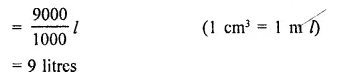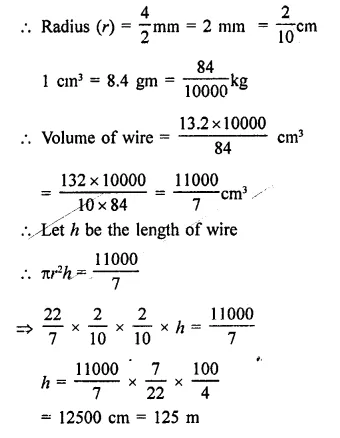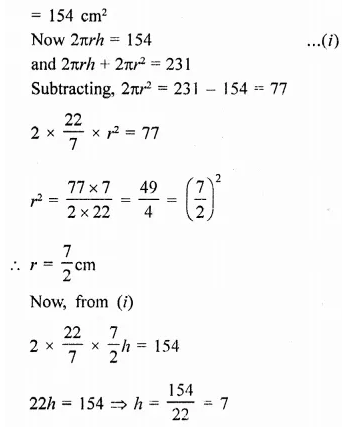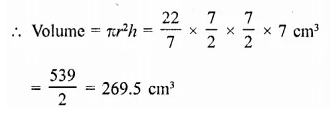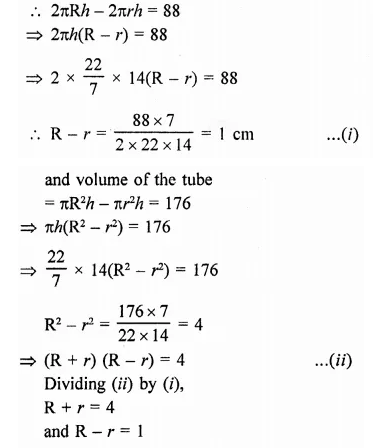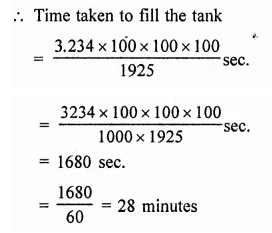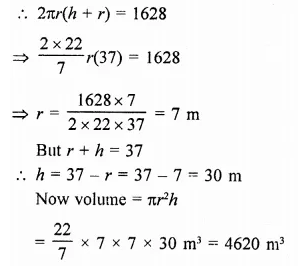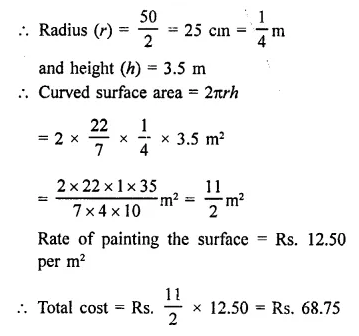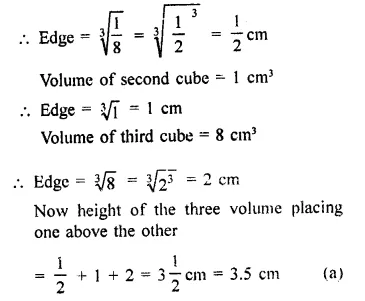Tag: Maths Class 9 RD Sharma Solutions

RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.2
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere VSAQS
• RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere MCQS

Question 1.
Find the surface area of a sphere of radius.
(i) 10.5 cm
(ii) 5.6 cm
(iii) 14 cm
Solution:
In a sphere,
(i) Radius (r) = 10.5 cm
Surface area = 4πr²

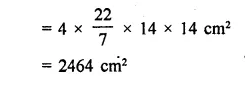
Question 2.
Find the surface area of a sphere of diameter
(i) 14 cm
(ii) 21 cm
(iii) 3.5 cm
Solution:
(i) Diameter of a sphere = 14 cm
Radius (r) = \(\frac { 14 }{ 2 }\) = 7 cm

Question 3.
Find the total surface area of a hemisphere and a solid hemisphere each of radius 10 cm. [Use π = 3.14]
Solution:
(i) Radius of hemisphere = 10 cm
∴ Total surface area of hemisphere = 2πr²
= 2 x 3.14 x 10 x 10 cm²
= 628 cm²
(ii) Total surface area of solid hemisphere
= 3πr² = 3 x 3.14 x 10 x 10 cm²
= 942 cm²

Question 4.
The surface area of a sphere in 5544 cm², find the diameter.
Solution:
Let r be the radius of a sphere, then Surface area = 4πr²

Question 5.
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹4 per 100 cm². [NCERT]
Solution:
Inner diameter of a hemispherical bowl = 10.5 cm

Question 6.
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of painting it at the rate of ₹2 per sq. m.
Solution:
Radius of dome (hemispherical) = 63 dm
Area of curved surface

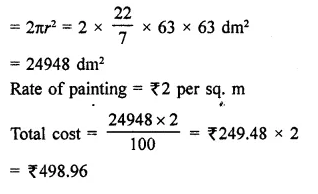
Question 7.
Assuming the earth to be a sphere of radius 6370 km, how many square kilometres is area of the land, if three-fourth of the earth’s surface is covered by water?
Solution:
Radius of earth (sphere) = 6370 km
Water on the earth = \(\frac { 3 }{ 4 }\) % total area

Question 8.
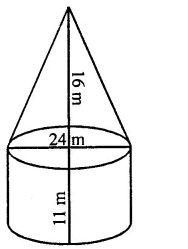
A cylinder of same height and radius is placed on the top of a hemisphere. Find the curved surface area of the shape if the length of the shape be 7 cm.
Solution:
Total height of the so formed shape = 7 cm

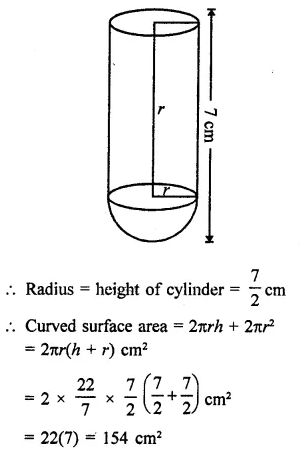
Question 9.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Solution:
Diameter of moon = \(\frac { 1 }{ 4 }\) of diameter of earth
Let radius of earth = r km
Then radius of moon = \(\frac { 1 }{ 4 }\) r km
Now surface area of earth = 4πr²

Question 10.
A hemi-spherical dome of a building needs to be painted. If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is ₹5 per 100 cm². [NCERT]
Solution:
Circumference of the base of dome (r) = 17.6 m

Question 11.
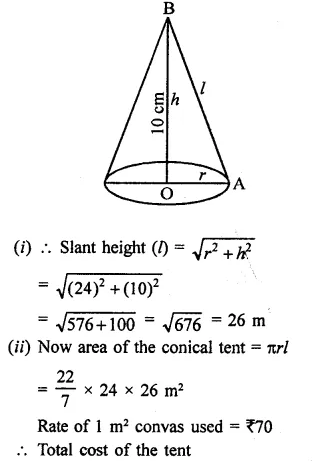
A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 16 cm and its height is 15 cm. Find the cost of painting the toy at ₹7 per 100 cm².
Solution:
Diameter of toy = 16 cm
Radius (r) = \(\frac { 16 }{ 2 }\) = 8 cm
Height of conical part (h) = 15 cm

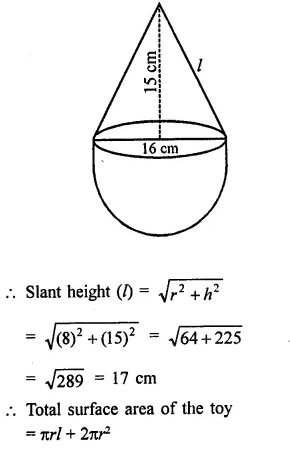
Question 12.
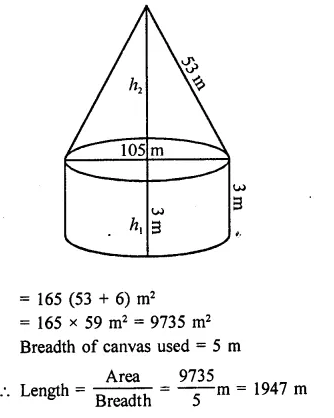
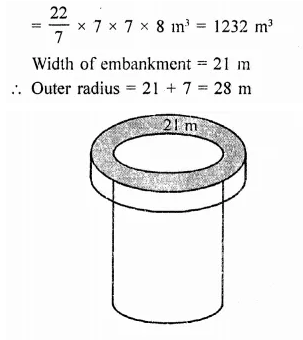
A storage tank consists of a circular cylinder with a hemisphere adjoined on either end. If the external diameter of the cylinder be 1.4 m and its length be 8 m, find the cost of painting it on the outside at the rate of ₹10 per m².
Solution:
Diameter of the tank = 1.4 m
∴ Radius (r) = \(\frac { 1.4 }{ 2 }\) m = 0.7 m
and height of cylindrical portion = 8m

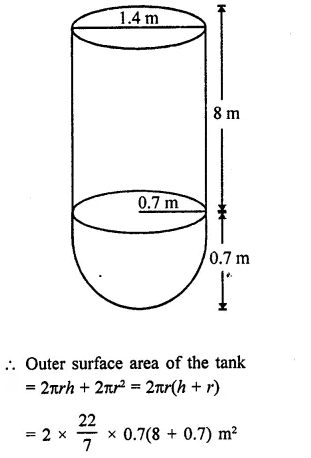
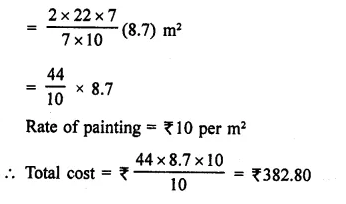
Question 13.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in the figure. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm² and black paint costs 5 paise per cm². [NCERT]

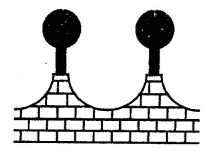
Solution:
Diameter of each spheres = 21 cm
∴ Radius (R) = \(\frac { 21 }{ 2 }\) cm
Radius of each cylinder (r) = 1.5 cm
and height (h) = 7 cm

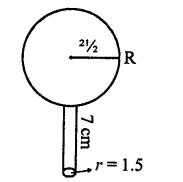
Now surface area of one sphere = 4πR²

Hope given RD Sharma Class 9 Solutions Chapter 21 Surface Areas and Volume of a Sphere Ex 21.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Mark the correct alternative in each of the following:
Question 1.
The number of surfaces of a cone has, is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
Number of surfaces of a cone are 2 (b)

Question 2.
The area of the curved surface of a cone of radius 2r and slant height \(\frac { 1 }{ 2 }\), is

Solution:
Radius of a cone = 2r

Question 3.
The total surface area of a cone of radius \(\frac { r }{ 2 }\) and length 2l, is

Solution:

Question 4.
A solid cylinder is melted and cast into a cone of same radius. The heights of the cone and cylinder are in the ratio
(a) 9 : 1
(b) 1 : 9
(c) 3 : 1
(d) 1 : 3
Solution:
Let r be the radius and h be the height of cylinder, then volume = πr²h
Now volume of cone = πr²h
r is the radius

Question 5.
If the radius of the base of a right circular cone is 3r and its height is equal to the radius of the base, then its volume is

Solution:
Radius of the base of a cone (R) = 3r
and height (H) = 3r

Question 6.
If the volumes of two cones are in the ratio 1 : 4 and their diameters are in the ratio 4 : 5, then the ratio of their heights, is
(a) 1 : 5
(b) 5 : 4
(c) 5 : 16
(d) 25 : 64
Solution:
Ratio in the volumes of two cones =1:4
and ratio in their diameter = 4:5
Let h₁, h₂ be their heights

Question 7.
The curved surface area of one cone is twice that of the other while the slant height of the latter is twice that of the former. The ratio of their radii is
(a) 2 : 1
(b) 4 : 1
(c) 8 : 1
(d) 1 : 1
Solution:
Let r be the radius and l be the slant height
∴ Curved surface area of first cone = πr₁l₁
and let curved surface area of second cone = πr₂l₂

Question 8.
If the height and radius of a cone of volume V are doubled, then the volume of the cone, is
(a) 3V
(b) 4V
(c) 6V
(d) 8V
Solution:
Let r and h be the radius and height of a cone, then

Question 9.
The ratio of the volume of a right circular cylinder and a right circular cone of the same base and height, is
(a) 1 : 3
(b) 3 : 1
(c) 4 : 3
(d) 3 : 4
Solution:
Let r be the radius and h be the height of a right circular cylinder and a right circular cone, and V₁ and V₂ are their volumes, the V₁ =  πr²h and

Question 10.
A right cylinder and a right circular cone have the same radius and same volumes. The ratio of the height of the cylinder to that of the cone is
(a) 3 : 5
(b) 2 : 5
(c) 3 : 1
(d) 1 : 3
Solution:
Let r be the radius of cylinder and cone and volumes are equal
and h₁, and h₂ be their have h₂ is respectively

Question 11.
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, the ratio of their curved surface areas, is
(a) 4 : 5
(b) 25 : 16
(c) 16 : 25
(d) 5 : 4
Solution:
∵ Diameters of two cones are equal
∴ Their radii are also be equal
Let r be their radius of each cone,
and ratio in their slant heights = 5:4
Let slant height of first cone (h₁) = 5x
Then height of second cone (h₂) = 4x

Question 12.
If the heights of two cones are in the ratio of 1 : 4 and the radii of their bases are in the ratio 4 : 1, then the ratio of their volumes is
(a) 1 : 2
(b) 2 : 3
(c) 3 : 4
(d) 4 : 1
Solution:
Ratio in the heights of two cones =1 : 4
and ratio in their radii of their bases = 4 : 1
Let height of the first cone = x
and height of the second cone = 4x
Radius of the first cone = 4y
and radius of the second cone = y

Question 13.
The slant height of a cone is increased by 10%. If the radius remains the same, the curved surface area is increased by
(a) 10%
(b) 12.1%
(c) 20%
(d) 21%
Solution:
Let r be radius and l be the slant height of a cone, then curved surface area = πrl
If slant height is increased by 10%, then

Question 14.
The height of a solid cone is 12 cm and the area of the circular base is 6471 cm². A plane parallel to the base of the cone cuts through the cone 9 cm above the vertex of the cone, the area of the base of the new cone so formed is
(a) 9π cm²
(b) 16π cm²
(c) 25π cm²
(d) 36π cm²
Solution:
Height of a solid cone (h) = 12 cm
Area of circular base = 64π cm²

Question 15.
If the base radius and the height of a right circular cone are increased by 20%, then the percentage increase in volume is approximately
(a) 60
(b) 68
(c) 73
(d) 78
Solution:
In first case,
Let r be radius and h be height, in volume

Question 16.
If h, S and V denote respectively the height, curved surface area and volume of a right circular cone, then 3πVh³ – S2h² + 9V² is equal to
(a) 8
(b) 0
(c) 4π
(d) 32π²
Solution:
h = height, S = curved surface area
V = volume of a cone
Let r be the radius of the cone, then

Question 17.
If a cone is cut into two parts by a horizontal plane passing through the mid¬point of its axis, the ratio of the volumes of upper and lower part is
(a) 1 : 2
(b) 2 : 1
(c) 1 : 7
(d) 1 : 8
Solution:
∴ ∆PDC ~ ∆PBA (AA axiom)
and O’ is mid point of PO

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Question 1.
The height of a cone is 15 cm. If its volume is 500π cm³, then find the radius of its base.
Solution:
Volume of cone = 500π cm³
and height (h) = 15 cm

Question 2.
If the volume of a right circular cone of height 9 cm is 48π cm³, find the diameter of its base.
Solution:
Volume of a cone = 48π cm³
Height (h) = 9 cm

Question 3.
If the height and slant height of a cone are 21 cm and 28 cm respectively. Find its volume.
Solution:
Height of a cone (h) = 21 cm
and slant height (l) = 28 cm

Question 4.
The height of a conical vessel is 3.5 cm. If its capacity is 3.3 litres of milk. Find the diameter of its base.
Solution:
Capacity of conical vessel = 3.3 litres
Volume = 3.3 m³
= 3.3 x 1000 = 3300 cm²

Question 5.
If the radius and slant height of a cone are in the ratio 7 : 13 and its curved surface area is 286 cm2, find its radius.
Solution:
Two ratio in radius and slant height of a cone = 7 : 13
Let radius (r) = 7x
and slant height (1) = 13x
Curved surface area = πrl

Question 6.
Find the area of canvas required for a conical tent of height 24 m and base radius 7 m.
Solution:
Base radius of the closed cone (r) = 7 cm
and vertical height (h) = 24 cm

Question 7.
Find the area of metal sheet required in making a closed hollow cone of base radius 7 cm and height 24 cm. making a closed hollow cone of base radius 7 cm and height 24 cm.
Solution:
Base radius of the closed cone (r) = 7 cm
and vertical height (h) = 24 cm

Question 8.
Find the length of cloth used in making a conical pandal of height 100 m and base radius 240 m, if the cloth is 100π m wide.
Solution:
Height of conical pandal (A) = 100 m
Base radius (r) = 240 m

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Question 1.
Find the volume of a right circular cone with:
(i) radius 6 cm, height 7 cm
(ii) radius 3.5 cm, height 12 cm
(iii) height 21 cm and slant height 28 cm. [NCERT]
Solution:
(i) Radius of a cone (r) = 6 cm
and height (h) = 7 cm

Question 2.
Find the capacity in litres of a conical vessel with:
(i) radius 7 cm, slant height 25 cm,
(ii) height 12 cm, slant height 13 cm. [NCERT]
Solution:
(i) Radius of the conical vessel (r) = 7 cm
Slant height (h) = 25 cm

Question 3.
Two cones have their heights in the ratio 1 : 3 and the radii of their bases in the ratio 3:1. Find the ratio of their volumes.
Solution:
Ratio in the heights of two cones =1:3
and ratio in their radii = 3: 1
Let radius of first cone (r₁) = x
and of second cone (r₂) = 3x
and height of first cone (h₁) = 3y
and of second cone (h₂)

Question 4.
The radius and the height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cubic metre, find the slant height and the radius (Use π = 3.14).
Solution:
Ratio in the radius and height of a cone = 5 : 12
Volume = 314 cm³
Let radius (r) = 5x
and height (h) = 12x

Question 5.
The radius and height of a right circular cone are in the ratio 5 : 12 and its volume is 2512 cubic cm. Find the slant height and radius of the cone. (Use π = 3.14).
Solution:
Ratio in the radius and height of a right circular cone = 5 : 12
Volume = 2512 cm³
Let radius (r) = 5x
Then height (h) = 12x

Question 6.
The ratio of volumes of two cones is 4 : 5 and the ratio of the radii of their bases is 2:3. Find the ratio of their vertical heights.
Solution:
Ratio in volumes of two cones = 4:5
and ratio in radii = 2:3
Let radius of the first cone (r₁) = 2x
Then radius of second cone (r₂) = 3x
Let h₁, h₂ be their heights respectively

Question 7.
Ratio between their vertical heights = 9:5 7. A cylinder and a cone have equal radii of their bases and equal heights. Show that their volumes are in the ratio 3:1.
Solution:
Let r be the radius and h be the height of a cylinder and a cone, then
Volume of cylinder = πr²h

Question 8.
If the radius of the base of a cone is halved, keeping the height same, what is the ratio of the volume of the reduced cone to that of the original cone?
Solution:
Let r be the radius and h be the height of the cone, then
Volume = \(\frac { 1 }{ 3 }\) πr²h
By halving the radius and same height the

Question 9.
A heap of wheat is in the form of a cone of diameter 9 m and height 3.5 m. Find its volume. How much canvas cloth is required to just cover the heap? (Use π = 3.14). [NCERT]
Solution:
Diameter of conical heap of wheat = 9 m

Question 10.
Find the weight of a solid cone whose base is of diameter 14 cm and vertical height 51 cm, supposing the material of which it is made weighs 10 grams per cubic cm.
Solution:
Diameter of the base of solid cone = 14 cm
and vertical height (h) = 51 cm

Question 11.
A right angled triangle of which the sides containing the right angle are 6.3 cm and 10 cm in length, is made to turn round on the longer side. Find the volume of the solid, thus generated. Also, find its curved surface area.
Solution:
Length of sides of a right angled triangle are 6.3 cm and 10 cm
By turning around the longer side, a cone is formed in which radius (r) = 6.3 cm
and height (h) = 10 cm

Question 12.
Find the volume of the largest right circular cone that can be fitted in a cube whose edge is 14 cm.
Solution:
Side of cube = 14 cm ,
Radius of the largest cone that can be fitted

Question 13.
The volume of a right circular cone is 9856 cm³. If the diameter of the base is 28 cm, find:
(i) height of the cone
(ii) slant height of the cone
(iii) curved surface area of the cone. [NCERT]
Solution:
Volume of a right circular cone = 9856 cm³
Diameter of the base = 28 cm

Question 14.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres? [NCERT]
Solution:
Diameter of the top of the conical pit = 3.5 m

Question 15.
Monica has a piece of Canvas whose area is 551 m². She uses it to have a conical tent made, with a base radius of 7 m. Assuming that all the stitching margins and wastage incurred while cutting, amounts to approximately 1 m². Find the volume of the tent that can be made with it. [NCERT]
Solution:
Area of Canvas = 551 m²
Area of wastage = 1 m²
Actual area = 551 – 1 = 550 m²
Base radius of the conical tent = 7 m

Let l be the slant height and h be the vertical

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1
• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.2
• RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data MCQS

Question 1.
What do you understand by the word ‘statistics’ in (i) singular form, (ii) plural forms.
Solution:
The word ‘statistics’ is used in both its singular as well as its plural senses.
In singular sense, statistics piay be defined as the science of collection, presentation, analysis and interpretation of numerical data.
In plural sense, statistics means numerical facts or observations collected with definite purpose.
For example, income and expenditure of persons in a particular locality, number of males and females in a particular town are statistics.

Question 2.
Describe some fundamental characteristics of statistics.
Solution:
Statistics in plural sense have the following characteristics:
(i) A single observation does not form statistics. Statistics are a sum total of observations.
(ii) Statistics are expressed quantitatively and not qualitatively.
(iii) Statistics are collected with a definite purpose.
(iv) Statistics in an experiment are comparable and can be classified into various groups.

Question 3.
What are (i) primary data? (ii) secondary data? Which of the two – the primary or the secondary data – is more reliable and why?
Solution:
(i) Primary data : When an investigator collects the data himself with a definite plan Or design in his mind, it is called primary data.
(ii) Secondary data : Data which are not originally collected rather obtained from the published or unpublished, sources are called secondary data.
Primary data are reliable and relevent because they are original in character and are collected by some individuals or by some institutions or by research bodies.

Question 4.
Why do we group data?
Solution:
When the number of observations is large, then arranging data in ascending or descending order is tedius job and it does not tell us much except minimum or maximum(s) of data. So, to make it easily understandable and clear, we tabulate data in the form of a table.

Question 5.
Explain the meaning of the following terms:
(i) variate
(ii) class intervals
(iii) class size
(iv) class mark
(v) frequency
(vi) class limits
(vii) true class limits.
Solution:
(i) Variate : The observations of a data are called variate.
(ii) Class intervals : When the presentations of data in classes, or groups, then groups are called classes or class intervals.
(iii) Class size : The difference between upper limit and lower limit is called class size.
(iv) Class mark : The mean of lower limit and upper limit is called class mark or mid value. Therefore class mark
= \(\frac { lower limit + upper limit }{ 2 }\)
(v) Frequency : The number of times an observation occurs in the given data, is called frequency of that observation.
(vi) Class limits : Every class has two limits : lower limit and upper limit.
(vii) True class limits : Whenever inclusive method is used, it is necessary tp make an adjustment to determine the correct class intervals, and to have continuity. If a-b is a class in inclusive method, then in order to change it into exclusive method, it becomes
a – \(\frac { h }{ 2 }\) – b + \(\frac { h }{ 2 }\) where h = \(\frac { 1 }{ 2 }\) [lower limit of a class – upper limit of previous class]

Question 6.
The ages of ten students of a group are given below. The ages have been recorded in years and months.
8-6, 9-0, 8-4, 9-3, 7-8, 8-11, 8-7, 9-2, 7¬10, 8-8
(i) What is the lowest age?
(ii) What is the highest age?
(iii) Determine the range?
Solution:
From the given data
(i) Lowest age is 7 years 8 months
(ii) The highest age is 9 years, 3 months
(iii) Range = Highest term – Lowest term
= 9 years 3 months – 7 years 8 months
= 1 years 7 months

Question 7.
The monthly pocket money of six friends is given below:
₹45, ₹30, ₹40, ₹50, ₹25, ₹45
(i) What is the highest pocket money?
(ii) What is the lowest pocket money?
(iii) What is the range?
(iv) Arrange the amounts of pocket money in ascending order.
Solution:
From the given data
(i) Highest pocket money = ₹50
(ii) Lowest pocket money = ₹25
(iii) Range = Highest term – Lowest term = ₹50-₹25 = ₹25
(iv) In ascending order : ₹25, ₹30, ₹40, ₹45, ₹45, ₹50

Question 8.
Write the class-size in each of the following:
(i) 0-4,5-9,10-14
(ii) 10-19, 20-29, 30-39
(iii) 100-120, 120-140, 160-180
(iv) 0-0.25, 0.25-0.50, 0.50-0.75
(v) 5-5,01, 5.01-5.02, 5.02-5.03
Solution:
(i) In 0-4, 5-9, 10-14
0-4 means from 0 to 4, similarly 5-9 means 5 to 9 and 10-14 means 10 to 14
class-size is 5
(ii) In 10-19, 20-29, 30-39
Here 10-19, means 10 to 19, 20-29 means 20 to 29 and 30-39 means 30 to 39
Class-size = 10
(iii) 100-120, 120-140, 160-180
Here 100-120, 120-140, 160-180
Then 120 – 100 = 20, 140 – 120 = 20, 180 – 160 = 20 is class-size = 20
(iv) 0-0.25, 0.25-0.50, 0.50-0.75
Here 0.25 – 0 = 0.25, 0.50 – 0.25 = 0.25 and 0.75 – 0.50 = 0.25
∴ Class-size = 0.25
(v) 5-5.01, 5.01-5.02, 5.02-5.03
Here 5.01 – 5 = 0.01, 5.02 – 5.01 = 0.01 and 5.03 – 5.02 = 0.01
∴ Class-size = 0.01

Question 9.
The final marks in mathematics of 30 students are as follows:
53, 61, 48, 60, 78, 68, 55, 100, 67, 90
75, 88, 77, 37, 84, 58, 60, 48, 62, 56
44, 58, 52, 64, 98, 59, 70, 39, 50, 60
(i) Arrange these marks in the ascending order,30 to 39 one group, 40 to 49 second group, etc.
Now answer the following:
(ii) What is the highest score?
(iii) What is the lowest score?
(iv) What is the range?
(v) If 40 is the pass mark how many have failed?
(vi) How many have scored 75 or more?
(vii) Which observations between 50 and 60 have not actually appeared?
(viii)How many have scored less than 50?
Solution:
(i) Arranging in ascending order:
37, 39, 44, 48, 48, 50, 52, 53, 55, 56, 58, 58, 59, 60, 60, 60, 61, 62, 64, 67, 68, 70, 75, 77, 78, 84, 88, 90, 98, 100

(ii) Highest score =100
(iii) Lowest score = 37
(iv) Range =  Highest score – Lowest score = 100 – 37 = 63
(v) If 40 is marks, then the number of students who failed = 2
(vi) No. of students who scored 75 or more = 8
(vii) Between 50 and 60, the scores which are missing 51, 54, 57
(viii) Number of students who scored less then 50 = 2 + 3 = 5

Question 10.
The weights of new born babies (in kg) in a hospital on a particular day are as follows:
2.3, 2.2, 2.1, 2.7, 2.6, 3.0, 2.5, 2.9, 2.8, 3.1, 2.5, 2.8, 2.7, 2.9, 2.4
(i) Rearrange the weights in descending order.
(ii) Determine the highest weight.
(iii) Determine the lowest weight.
(iv) Determine the range.
(v) How many babies were bom on that day?
(vi) How many babies weigh below 2.5 kg?
(vii) How many babies weigh more than 2.8 kg?
(viii)How many babies weigh 2.8 kg?
Solution:
(i) Weights in descending order are
3.1, 3.0, 2.9, 2.9, 2.8, 2.8, 2.7, 2.7, 2.6, 2.5, 2.5, 2.4, 2.3, 2.2, 2.1
(ii) Highest weight = 3.1
(iii) Lowest weight = 2.1
(iv) Range = Highest weight – Lowest wight = 3.1 – 2.1 = 1.0
(v) No. of babies who bom = 15
(vi) No. of babies whose weights are below 2.5 kg = 4
(vii) No. of babies whose weight are more than 2.8 kg = 4.
(viii) No. of babies whose weight is 2.8 kg = 2

Question 11.
The number of runs scored by a cricket player in 25 innings are as follows:
26, 35, 94, 48, 82, 105, 53, 0, 39, 42, 71, 0, 64, 15, 34, 67, 0, 42, 124, 84, 54, 48, 139, 64, 47.
(i) Rearrange these runs in ascending order.
(ii) Determine the player, is highest score.
(ii) How many times did the player not score a run?
(iv) How many centuries did he score?
(v) How many times did he score more than 50 runs?
Solution:
(i) Arranging in ascending order
0, 0, 0, 15, 26, 34, 35, 39, 42, 42, 47, 48, 48, 53, 54, 64, 64, 67, 71, 82, 84, 94, 105, 124, 139
(ii) Highest score is 139
(iii) 3 times when his score is 0
(iv) No. of times, he made century = 3
(v) No. of times his score more then 50 runs = 12

Question 12.
The class size of a distribution is 25 and the first class-interval is 200-224. There are seven class-intervals.
(i) Write the class-intervals.
(ii) Write the class-marks of each interval
Solution:
Class size = 25
First class is 200-224
∴ Number of class = 7
∴ Class interval will be
(i) 200-224, 225-249, 250-274, 275-299, 300-324, 325-349, 350-374

Question 13.
Write the class size and class limits in each of the following:
(i) 104, 114, 124, 134, 144, 154 and 164
(ii) 47, 52, 57, 62, 67, 72, 77, 82, 87, 92, 97 and 102
(iii) 12.5, 17.5, 22.5, 27.5, 32.5, 37.5, 42.5, 47.5
Solution:
(i) 104, 114, 124, 134, 144, 154 and 164
Here class size = 114 – 104 = 10
Here in first class, 104 – \(\frac { 10 }{ 2 }\)
= 104 – 5 = 99 and 104 + 5 = 109
∴ Class will be 99-109
In this way other classes will be 109-119, 119-129, 129-139, 139-149, 149-159, 159¬169
(ii) In 47, 52, 57, 62, 67, 72, 77, 82, 87, 92, 97, 102
Here class size = 52 – 47 = 5
∴ In first class, 47 – \(\frac { 5 }{ 2 }\) and 47 + \(\frac { 5 }{ 2 }\)
= 44.5-49.5
In this way other classes will be = 49.5-54.5, 54.5-59.5, 59.5-64.5, 64.5-69.5,69.5-74.5, 74.5-79.5, 79.5-84.5, 84.5-89.5, 89.5-94.5,94.5-99.5, 99.5-104.5 070 12.5, 17.5, 22.5, 27.5, 32.5, 37.5, 42.5, 47.5
Here class interval (size) = 17.5 – 12.5 = 5
In the class = 12.5 – \(\frac { 5 }{ 2 }\) , 12.5 + \(\frac { 5 }{ 2 }\)
⇒ 12.5 – 2.5, 12.5 + 2.5
⇒ 10, 15
∴ First class will be 10-15
In this way other classes 15-20, 20-25, 25-30, 30-35, 35-40, 40-45, 45-50

Question 14.
Following data gives the number of children in 41 families:
1, 2, 6, 5, 1, 5, 1, 3, 2, 6, 2, 3, 4, 2, 0, 0, 4, 4, 3, 2, 2, 0, 0, 1, 2, 2, 4, 3, 2, 1, 0, 5, 1, 2, 4, 3, 4, 1, 6, 2, 2.
Represent it in the form of a frequency distribution.
Solution:
Frequency distribution table is given below:

Question 15.
The marks scored by 40 students of class IX in mathematics are given below:
81, 55, 68, 79, 85, 43, 29, 68, 54, 73, 47, 35, 72, 64, 95, 44, 50, 77, 64, 35, 79, 52, 45, 54, 70, 83, 62, 64, 72, 92, 84, 76, 63, 43, 54, 38, 73, 68, 52, 54.
Prepare a frequency distribution with class size of 10 marks.
Solution:
Maximum marks = 95,
minimum marks = 29,
range = 95 – 29 = 66
Frequency distribution is given below

Question 16.
The heights (in cm) of 30 students of class IX are given below:155, 158, 154, 158, 160, 148, 149, 150, 153, 159, 161, 148, 157, 153, 157, 162, 159, 151, 154, 156, 152, 156, 160, 152, 147, 155, 163, 155, 157, 153.
Prepare a frequency distribution table with 160-164 as one of the class intervals.
Solution:
Maximum height = 163 cm,
minimum height = 147 cm,
range 163 – 147 = 16
Frequency distribution of the given data is given below

Question 17.
The monthly wages of 30 workers in a factory are given below:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 836, 878,840, 868, 890, 806, 840, 890.
Represent the data in the form of a frequency distribution with class size 10.
Solution:
Highest wage = ₹890,
lower wage = ₹804,
range = 890 – 804 = 86
Frequency distribution table is given below

Question 18.
The daily maximum temperatures (in degree Celsius) recorded in a certain city during the month of November are as follows:
25.8, 24.5, 25.6, 20.7, 21.8, 20.5, 20.6, 20.9, 22.3, 22.7, 23.1, 22.8, 22.9, 21.7, 21.3, 20.5, 20.9, 23.1, 22.4, 21.5, 22.7, 22.8, 22.0, 23.9, 24.7, 22.8, 23.8, 24.6, 23.9, 21.1
Represent them as a frequency distribution table with class size 1°C.
Solution:
Maximum temperature = 25.8
Minimum temperature = 20.5
Range = 25.8 – 20.5 = 5.3
Frequency distribution table is given below:

Question 19.
Construct a frequency table with equal class intervals from the following data on the monthly wages (in rupees) of 28 labourers working in a factory, taking* one of the class intervals as 210-230 (230 not included):
220, 268, 258, 242, 210, 268, 272, 242, 311, 290, 300, 320, 319, 304, 302, 318, 306, 292, 254, 278, 210, 240, 280, 316, 306, 215, 256, 236.
Solution:
Maximum wages = ₹320
Minimum wages = ₹210
Range = 320 – 210 = 110
Required frequency table is given below:

Question 20.
The blood groups of 30 students of class VIII are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O
Represent this data in the form of a frequency distribution table. Find out which is the most common and which is the rarest blood group among these students. (NCERT)
Solution:
Frequency distribution table is given below:

Question 21.
Three coins were tossed 30 times. Each time the number of heads occuring was noted down as follow:
0 1 2 2 1 2 3 1 3 0
1 3 1 1 2 2 0 1 2 1
3 0 0 1 1 2 3 2 2 0
Prepare a frequency distribution table for the data given above. (NCERT)
Solution:
Frequency distribution table is given below:

Question 22.
Thirty children were asked about the number of hours they watched T.V. programmes in the previous week. The results were found as follows:
1 6 2 35 12 5 8 4 8
10 3 4 12 2 8 15 1 17 6
3 2 8 5 9 6 8 7 14 12
(i) Make a grouped frequency distribution table for this data, taking class width 5 and one of the class intervals as 5-10.
(ii) How many children watched television for 15 or more hours a week? (NCERT)
Solution:
Highest number of hours = 17
Lowest number of hours = 1
(i) The frequency table is given below:

(ii) No. of children watching T.V. for 15 or more hours a week = 2

Question 23.
The daily minimum temperatures in degrees Celsius recorded in a certain Arctic region are as follows:
-12.5, -10.8, -18.6, -8.4, -10.8, -4.2, -4.8, -6.7, -13.2, -11.8, -2.3, 1.2, 2.6, 0, 2.4, 0, 3.2, 2.7, 3.4, 0, -2.4, -2.4, 0, 3.2, 2.7, 3.4, 0, -2.4, -5.8, -8.9, -14.6, -12.3, -11.5,-7.8,-2.9.
Represent them as frequency distribution table taking -19.9 to -15 as the first class interval.
Solution:
Maximum temperature = -18.6
Minimum temperature = 3.4
Range = 3.4 – (-18.6) = 3.4 + 18.6 = 22
The required frequency distribution table is given below:

Hope given RD Sharma Class 9 Solutions Chapter 22 Tabular Representation of Statistical Data Ex 22.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.2
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone VSAQS
• RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone MCQS

Question 1.
Find the curved surface area of a cone, if its slant height is 60 cm and the radius of its base is 21 cm.
Solution:
Radius of the base of the cone = 21 cm
and slant height (l) = 60 cm

Question 2.
The radius of a cone is 5 cm and vertical height is 12 cm. Find the area of the curved surface.
Solution:
Radius of the base of a cone = 5 cm
Vertical height (h) = 12 cm

Question 3.
The radius of a cone is 7 cm and area of curved surface is 176 cm2. Find the slant height.
Solution:
Curved surface area of a cone = 176 cm²
and radius (r) = 1 cm²

Question 4.
The height of a cone is 21 cm. Find the area of the base if the slant height is 28 cm.
Solution:
Height of the cone (h) = 21 cm
Slant height (l) = 28 cm
∴ l² = r² + h²
⇒ r² = l²– h² = (28)² – (21 )²
⇒ 784 – 441 = 343 …(i)
Now area of base = πr²
= \(\frac { 22 }{ 7 }\) x 343 [From (i)]
= 22 x 49 = 1078 cm²

Question 5.
Find the total surface area of a right circular cone with radius 6 cm and height 8 cm.
Solution:
Radius of base of cone (r) = 6 cm
and height (h) = 8 cm

Question 6.
Find the curved surface area of a cone with base radius 5.25 cm and slant height 10 cm. [NCERT]
Solution:
Radius of base of a cone (r) = 5.25 cm
and slant height (l) = 10 cm
Curved surface area = πrl

Question 7.
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m. [NCERT]
Solution:
Slant height of a cone (l) = 21 m
and diameter of its base = 24 m
∴ Radius (r) = \(\frac { 24 }{ 2 }\) = 12 m
Now total surface area = πr(l + r)

Question 8.
The area of the curved surface of a cone is 60π cm². If the slant height of the cone be 8 cm, find the radius of the base.
Solution:
Curved surface area of a cone = 6071 cm²
Slant height (l) = 8 cm

Question 9.
The curved surface area of a cone is 4070 cm² and its diameter is 70 cm. What is the slant height ? (Use π = 22/7).
Solution:
Surface area of a cone = 4070 cm²
Diameter of its base = 70 cm

Question 10.
The radius and slant height of a cone are in the ratio of 4 : 7. If its curved surface area is 792 cm², find its radius. (Use π = 22/7)
Solution:
Curved surface area of a cone = 792 cm²
Ratio in radius and slant height = 4:7
Let radius = 4x
Then slant height = 7x
∴ Curved surface area πrl = 792

Question 11.
A Joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps. [NCERT]
Solution:
Radius of the base of a conical cap (r) = 7 cm
and height (h) = 24 cm

Question 12.
Find the ratio of the curved surface areas of two cones if their diameters of the bases are equal and slant heights are in the ratio 4 : 3.
Solution:
Let diameters of each cone = d
Then radius (r) = \(\frac { d }{ 2 }\)
Ratio in their slant heights = 4 : 3
Let slant height of first cone = 4x
and height of second cone = 3x
Now curved surface area of the first cone = 2πrh

Question 13.
There are two cones. The curved surface area of one is twice that of the other. The slant height of the later is twice that of the former. Find the ratio of their radii.
Solution:
In two cones, curved surface of the first cone = 2 x curved surface of the second cone
Slant height of the second cone = 2 x slant height of first cone
Let r₁ and r₂ be the radii of the two cones
and let height of the first cone = h
Then height of second cone = 2h
∴ Curved surface of the first cone = 2πr₁h

Question 14.
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, find the ratio of their curved surfaces.
Solution:
Let diameter of one cone = d
and diameter of second cone = d
∴ Radius of the first cone (r) = \(\frac { d }{ 2 }\)
and of second cone (r₂) = \(\frac { d }{ 2 }\)
Ratio in their slant heights = 5:4
Let slant height of the first cone = 5x
Then that of second cone = 4x
Now curved surface of the first cone = 2πrh

Question 15.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find the radius of the base and total surface area of the cone. [NCERT]
Solution:
Area of curved surface of a cone = 308 cm²
and slant height (l) = 14 cm

Question 16.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of Rs. 210 per 100 m². [NCERT]
Solution:
Slant height of a cone (l) = 25 m

Question 17.
A conical tent is 10 m high and the radius of its base is 24 m. Find the slant height of the tent. If the cost of 1 m² canvas is Rs. 70, find the cost of the canvas required to make the tent. [NCERT]
Solution:
Height of conical tent (A) = 10 m
Radius of the base (r) = 24 m

Question 18.
The circumference of the base of a 10 m height conical tent is 44 metres. Calculate the length of canvas used in making the tent if width of canvas is 2 m. (Use π = 22/7)
Solution:
Circumference of the base of a conical tent = 44 m

Question 19.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6 m? Assum that the extra length of material will be required for stitching margins and wastage in cutting is approximately 20 cm. (Use π = 3.14) [NCERT]
Solution:
Height of the conical tent (h) = 8 m
and radius of the base (r) = 6 m

Now curved surface area of the tent = πrl = 3.14 x 6 x 10 = 188.4 m
Width of tarpaulin used = 3 m
∴ Length = 188.4 , 3 = 62.8 m
Extra length required = 20 cm = 0.2 m
∴ Total length of tarpaulin = 62.8 + 0.2 = 63 m

Question 20.
A bus stop is barricated from the remaining part of the road, by using 50 hollow cones made of recycled card-board. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is ₹12 per m², what will be the cost of painting these cones. (Use π = 3.14 and \(\sqrt { 1.04 } \) = 1.02) [NCERT]
Solution:
Diameter of the base of tent = 40 cm
∴ Radius of the base of cone (r) = \(\frac { 40 }{ 2 }\)

Question 21.
A cylinder and a cone have equal radii of their bases and equal heights. If their curved surface areas are in the ratio 8 : 5, show that the radius of each is to the height of each as 3 : 4.
Solution:
Let radius of cylinder = r
and radius of cone = r
and let height of cylinder = h
and height of cone = h

Question 22.
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of the canvas required for the tent.
Solution:
Diameter of the cylindrical portion = 24 m 24
∴ Radius (r) = \(\frac { 24 }{ 2 }\) = 12 m
Height of cylindrical portion = 11 m
and total height = 16 m

∴ Height of conical portion = 16 – 11 = 5 m
∴ Slant height of the conical portion (l)

Question 23.
A circus tent is cylindrical to a height of 3 meters and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
Solution:
Diameter of the cylindrical tent = 105 m

 

Hope given RD Sharma Class 9 Solutions Chapter 20 Surface Areas and Volume of A Right Circular Cone Ex 20.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Mark correct alternative in each of the following:
Question 1.
In a cylinder, if radius is doubled and height is halved, curved surface area will be
(a) halved
(b) doubled
(c) same
(d) four times
Solution:
Let radius of the first cylinder (r₁) = r
and height (h₁) = h
Surface area = 2πrh
If radius is doubled and height is halved

∴ Their surface area remain same (c)

Question 2.
Two cylindrical jars have their diameters in the ratio 3:1, but height 1:3. Then the ratio of their volumes is
(a) 1 : 4
(b) 1 : 3
(c) 3 : 1
(d) 2 : 5
Solution:
Sol. Ratio in the diameters of two cylinder = 3:1
and ratio in their heights = 1:3
Let radius of the first cylinder (r₁) = 3x
and radius of second (r₂) = x
and height of the first (h₁) = y
and height of the second (h₂) = 3y
Now volume of the first cylinder = πr²h
= π(3x)² x y = 9πx²y
and of second cylinder = π(x²) (3y)
∴ Ratio between then = 9πx²y : 3πx²y
= 3 : 1 (c)

Question 3.
The number of surfaces in right cylinder is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
The number of surfaces of a right cylinder is three. (c)

Question 4.
Vertical cross-section of a right circular cylinder is always a
(a) square
(b) rectangle
(c) rhombus
(d) trapezium
Solution:
The vertical cross-section of a right circular cylinder is always a rectangle. (b)

Question 5.
If r is the radius and h is height of the cylinder the volume will be

Solution:
Volume of a cylinder = πr²h (b)

Question 6.
The number of surfaces of a hollow cylindrical object is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
The number of surfaces of a hollow cylindrical object is 4. (d)

Question 7.
If the radius of a cylinder is doubled and the height remains same, the volume will be
(a) doubled
(b) halved
(c) same
(d) four times
Solution:
If r be the radius and h be the height, then volume = πr2h
If radius is doubled and height remain same,
the volume will be
= π(2r)²h = π x 4r²h
= 4πr²h = 4 x Volume
The volume is four times (d)

Question 8.
If the height of a cylinder is doubled and radius remains the same, then volume will be
(a) doubled
(b) halved
(c) same
(d) four times
Solution:
If r be the radius and h be the height, then volume of a cylinder = πr²h
If height is doubled and radius remain same, then volume = πr²(2h) = 2πr²h
∴ Its doubled (a)

Question 9.
In a cylinder, if radius is halved and height is doubled, the volume will be
(a) same
(b) doubled
(c) halved
(d) four times
Solution:
Let r be radius and h be height, then Volume = πr²h
If radius is halved and height is doubled

Question 10.
If the diameter of the base of a closed right circular cylinder be equal to its height h, then its whole surface area is

Solution:
Let diameter of the base of a cylinder (r) = h
Then its height (h) = h

Question 11.
A right circular cylindrical tunnel of diameter 2 m and length 40 m is to be constructed from a sheet of iron. The area of the iron sheet required in m², is
(a) 40π
(b) 80π
(c) 160π
(d) 200π
Solution:
Diameter of a cylindrical tunnel = 2 m
∴ Radius (r) = \(\frac { 2 }{ 2 }\) = 1m
and length (h) = 40 m
Curved surfae area = 2πrh = 2 x π x 1 x 40 = 80π (b)

Question 12.
Two circular cylinders of equal volume have their heights in the ratio 1 : 2. Ratio of their radii is

Solution:
Let r₁ and h₁ be the radius and height of the
first cylinder, then
Volume = πr₁²h₁
Similarly r₁ and h₂ are the radius and height of the second cylinder
∴ Volume = πr²h₂
But their volumes are equal,

Question 13.
The radius of a wire is decreased to one- third. If volume remains the same, the length will become
(a) 3 times
(b) 6 times
(c) 9 times
(d) 27 times
Solution:
In the first case, r and h1, be the radius and height of the cylindrical wire
∴ Volume = πr²h₁ …(i)
In second case, radius is decreased to one third

∴ In second case height is 9 times (c)

Question 14.
If the height of a cylinder is doubled, by what number must the radius of the base be multiplied so that the resulting cylinder has the same volume as the original cylinder?

Solution:
Let r be the radius and h be the height then volume = πr²h
If height is doubled and volume is same and let x be radius then πr²h = π(x)² x 2h

Question 15.
The volume of a cylinder of radius r is 1/4 of the volume of a rectangular box with a square base of side length x. If the cylinder and the box have equal heights, what is r in terms of x?

Solution:
Let r be the radius and h be the height, then volume = πr²h
This volume is \(\frac { 1 }{ 4 }\) of the volume of a rectangular box
∴ Volume of box = 4πr²h
Let side of base of box = x and height h,
then volume = x²h
∴ 4πr²h = x²h

Question 16.
The height ft of a cylinder equals the circumference of the cylinder. In terms of ft, what is the volume of the cylinder?

Solution:
In a cylinder,
h = circumference of the cylinder

Question 17.
A cylinder with radius r and height ft is closed on the top and bottom. Which of the following expressions represents the total surface area of this cylinder?
(a) 2πr(r + h)
(b) πr(r + 2h)
(c) πr(2r + h)
(d) 2πr² + h
Solution:
r is the radius of the base and ft is the height of a closed cylinder
Then total surface area = 2πr(r + h ) (a)

Question 18.
The height of sand in a cylindrical-shaped can drops 3 inches when 1 cubic foot of sand is poured out. What is the diameter, in inches, of the cylinder?

Solution:
Let h be the height and d be the diameter of a cylinder, then

Question 19.
Two steel sheets each of length a₁ and breadth a₂ are used to prepare the surfaces of two right circular cylinders – one having volume v₁ and height a₂ and other having volume v₂ and height a₁. Then,

Solution:
Length of each sheet = a₁
and breadth = a₂
Volume of cylinder = πr²h
In first case,
v₁ is volume and a₂ is the height

Question 20.
The altitude of a circualr cylinder is increased six times and the base area is decreased to one-ninth of its value. The factor by which the lateral surface of the cylinder increases, is

Solution:
In first case,
Let r be the radius and h be the height of the cylinder. Then,
∴ Lateral surface area = 2πrh
In second case,

Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Question 1.
Write the number of surface of a right circular cylinder.
Solution:
Three, two circular and one curved.

Question 2.
Write the ratio of total surface area to the curved surface area of a cylinder of radius r and height h.
Solution:
∵ Radius = r
and height = h
∴ Curved surface area = 2πrh
and total surface area = 2πr(h + r)
∴ Ratio = 2πr(h + r) : 2πrh
= h + r : h

Question 3.
The ratio between the radius of the base and height of a cylinder is 2 : 3. If its volume is 1617 cm3, find the total surface area of the cylinder.
Solution:
Ratio in radius and height of the cylinder = 2 : 3
Let radius (r) = 2x
Then height (h) = 3x
∴ Volume = πr²h

Question 4.
If the radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3, then find the ratio of their volumes.
Solution:
Ratio of radii of two cylinder = 2:3
Let radius of first cylinder (r₁) = 2x
and second cylinder (r₂) = 3x
and ratio in their heights = 5:3
Let height of first cylinder (h₁) = 5y
and height of second (h₂) = 3y
∴ Volume of the first cylinder =πr²h
= π x (2x)² x 5y = 20πx²y
and volume of second cylinder = π(3x)2 x 3y = 27πx²y
Now ratio between then,
= 20πx²y: 21πx²y
= 20 : 27

Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Question 1.
A soft drink is available in two packs – (i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and
(ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much? [NCERT]
Solution:
In first case, in a rectangular container of soft drink, the length of base = 5 cm
and Width = 4 cm
Height = 15 cm
∴ Volume of soft drink = lbh = 5 x 4 x 15 = 300 cm³
and in second case, in a cylindrical container, diameter of base = 7 cm

∴ The soft drink in second container is greater and how much greater = 385 cm – 380 cm² = 85 cm²

Question 2.
The pillars of a temple are cylindrically shaped. If each pillar has a circular base of radius 20 cm and height 10 m. How much concrete mixture would be required to build 14 such pillars? [NCERT]
Solution:
Radius of each pillar (r) = 20 cm

Question 3.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm³ of wood has a mass of 0.6 gm. [NCERT]
Solution:
Inner diameter of a cylindrical wooden pipe = 24 cm

Question 4.
If the lateral surface of a cylinder is 94.2 cm² and its height is 5 cm, find:
(i) radius of its base
(ii) volume of the cylinder [Use π = 3.14] [NCERT]
Solution:
Lateral surface area of a cylinder = 94.2 cm2

Question 5.
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it? [NCERT]
Solution:
The capacity of a closed cylindrical vessel = 15.4 l

Question 6.
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients? [NCERT]
Solution:
Diameter of the cylindrical bowl = 7 cm
∴ Radius (r) = \(\frac { 7 }{ 2 }\)cm
Level of soup in it = 4 cm
∴ Volume of soup in one bowl for one patient

Question 7.
A hollow garden roller, 63 cm wide with a girth of 440 cm, is made of 4 cm thick iron. Find the volume of the iron.
Solution:
Width of hollow cylinder (A) = 63 cm
Girth = 440 cm

Question 8.
The cost of painting the total outside surface of a closed cylindrical oil tank at 50 paise per square decimetre is ₹ 198. The height of the tank is 6 times the radius of the base of the tank. Find the volume corrected to 2 decimal places.
Solution:
Rate of painting = 50 paise per dm²
Total cost = ₹198

Question 9.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5:3. Calculate the ratio of their volumes and the ratio of their curved surfaces.
Solution:
Ratio in radii of two cylinders = 2:3
and ratio in their heights = 5:3
Let radius of the first cylinder (r₁) = 2x
and radius of second cylinder (r₂) = 3x
and height of first cylinders (h₁) = 5y
and height of second cylinder (h₂) = 3y
(i) Now volume of the first cylinder = πr²h = π(2x)² x 5y = 20πx²2y
and volume of tlie second cylinder = π(3x)² x 3y = π x 9×2 x 3y = 27πx²y
Now ratio in their volume
= 20πx²y : 21πx²y = 20 : 27
(ii) Curved surface area of first cylinder = 2πrh = 2π x 2x x 5y =20πxy
and curved surface area of second cylinder = 2π x 3x x = 1 8πxy
∴ Ratio in their curved surface area
= 20πxy : 18πxy = 10 : 9

Question 10.
The ratio between the curved surface area and the total surface area of a right circular cylinder is 1 : 2. Find the volume of the cylinder, if its total surface area is 616 cm².
Solution:
Ratio in curved surface area and total surface area of a cylinder =1:2
Total surface area = 616 cm²

Question 11.
The curved surface area of a cylinder is 1320 cm² and its base had diameter 21 cm. Find the height and the volume of the cylinder. [Use π = 22/7]
Solution:
Curved surface area of a cylinder = 1320 cm²
Diameter of the base = 21 cm

Question 12.
The ratio between the radius of the base and the height of a cylinder is 2 : 3. Find the total surface area of the cylinder, if its volume is 1617 cm³.
Solution:
Ratio between radius and height of a cylinder = 2:3
Volume =1617 cm³
Let radius (r) = 2x
Then height (h) = 3x
∴ Volume = πr²h

Question 13.
A rectangular sheet of paper, 44 cm x 20 cm, is rolled along its length of form a cylinder. Find the volume of the cylinder so formed.
Solution:
Length of sheet = 44 cm
Breadth = 20 cm
By rolling along length, the height of cylinder (h) = 20cm
and circumference of the base = 44cm

Question 14.
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m3. Find the diameter and the height of the pillar.
Solution:
Curved surface area of a pillar = 264 m²
and volume = 924 m³
Let r be the radius and It be height, then 2πrh = 264

Question 15.
Two circular cylinders of equal volumes have their heights in the ratio 1 : 2. Find the ratio of their radii.
Solution:
Volumes of two cylinders are equal Ratio in their height h₁ :h₂ = 1: 2

Question 16.
The height of a right circular cylinder is 10.5 m. Three times the sum of the areas of its two circular faces is twice the” area of the curved surface. Find the volume of the cylinder.
Solution:
Height of a right circular cylinder = 10.5 m
3 x sum of areas of two circular faces
= 2 x area of curved surface
Let r be that radius,

Question 17.
How many cubic metres of earth must be dugout to sink a well 21 m deep and 6 m diameter? Find the cost of plastering the inner surface of the well at ₹9.50 per m².
Solution:
Diameter of a well = 6 m
∴ Radius (r) = \(\frac { 6 }{ 2 }\) = 3 m
Depth (h) = 21 m
∴ Volume of earth dugout = πr²h

Question 18.
The trunk of a tree is cylindrical and its circumference is 176 cm. If the length of the trunk is 3 m. Find the volume of the timber that can be obtained from the trunk.
Solution:
Circumference of a cylindrical trunk of a tree = 176 cm

Question 19.
A cylindrical container with diameter of base 56 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 32 cm x 22 cm x 14 cm. Find the rise in the level of the water when the solid is completely submerged.
Solution:
Diameter of cylindrical container = 56 cm
∴ Radius (r) = \(\frac { 56 }{ 2 }\) = 28 cm
Dimensions of a rectangular solid are = 32 cm x 22 cm x 14 cm
∴ Volume of solid = lbh
= 32 x 22 x 14 = 9856 cm³
∴ Volume of water in the container = 9856 cm³
Let h be the level of water, then
πr2h = 9856

Question 20.
A cylindrical tube, open at both ends, is made of metal. The internal diameter of the tube is 10.4 cm and its length is 25 cm. The thickness of the metal is 8 mm everywhere. Calculate the volume of the metal.
Solution:
Length of metallic tube = 25 cm
Inner diameter = 10.4 cm
∴ Radius (r) = \(\frac { 10.4 }{ 2 }\) = 5.2 cm
Thickness of metal = 8 mm
∴ Outer radius (R) = 5.2 + 0.8 = 6.0 cm
Volume of metal used = π(R² – r²) x h

Question 21.
From a tap of inner radius 0.75 cm, water flows at the rate of 7 m per second. Find the volume in litres of water delivered by the pipe in one hour.
Solution:
Inner radius of a tap = 0.75 cm
Speed of flow of water in it = 7 m/s
Time = 1 hour
∴ Length of flow of water (h)
= 7 x 60 x 60 m = 25200 m
∴ Volume of water = πr²h

Question 22.
A rectangular sheet of paper 30 cm x 18 cm can be transformed into the curved surface of a right circular cylinder in two ways i.e., either by rolling the paper along its length or by rolling it along its breadth. Find the ratio of the volumes of the two cylinders thus formed.
Solution:
Size of rectangular sheet = 30 cm x 18 cm
∴ Length of sheet = 30 cm
and breadth = 18 cm
By folding length wise,
Height = 18 cm
and circumference = 30 cm

Question 23.
How many litres of water flow out of a pipe having an area of cross-section of 5 cm² in one minute, if the speed of water in the pipe is 30 cm/sec?
Solution:
Area of the cross-section of the pipe = 5 cm²
Speed of water flow = 30 cm/sec
Period = 1 minute
∴ Flow of water in 1 minute = 30 x 60 cm = 1800 cm
Area of mouth of pipe = 5 cm²
∴ Volume = 1800 x 5 = 9000 cm³
Volume of water in litres = 9000 ml

Question 24.
Find the cost of sinking a tubewell 280 m deep, having diameter 3 m at the rate of ₹3.60 per cubic metre. Find also the cost of cementing its inner curved surface at ₹2.50 per square metre.
Solution:
Depth of well (h) = 280 m
Diameter = 3 m

Question 25.
Find the length of 13.2 kg of copper wire of diameter 4 mm, when 1 cubic cm of copper weighs 8.4 gm.
Solution:
Weights of copper wire = 13.2 kg
Diamter = 4 mm

Question 26.
A solid cylinder has a total surface area of 231 cm². Its curved surface area is \(\frac { 2 }{ 3 }\) of the total surface area. Find the volume of the cylinder.
Solution:
Surface area of solid cylinder = 231 cm²
and curved surface area = \(\frac { 2 }{ 3 }\) of 231 cm²

Question 27.
A well with 14 m diameter is dug 8 m deep. The earth taken out of it has been evenly spread all around it to a width of 21 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of a well = 14 m
∴ Radius (r) = y = 7 m
Depth (h) = 8 m
∴ Volume of the earth dugout = πr²h

Question 28.
The difference between inside and outside surfaces of a cylindrical tube 14 cm long is 88 sq. cm. If the volume of the tube is 176 cubic cm, find the inner and outer radii of the tube.
Solution:
Length of cylindrical tube = 14 cm
Difference betveen the outer surface and inner surface = 88 cm²
and volume of the tube = 176 cm³
Let R and r be the outer and inner radius of the tube

Question 29.
Water flows out through a circular pipe whose internal diameter is 2 cm, at the rate of 6 metres per second into a cylindrical tank. The radius of whose base is 60 cm. Find the rise in the level of water in 30 minutes?
Solution:
Internal diameter of the pipe = 2 cm
∴ Radius (r) = \(\frac { 2 }{ 2 }\) = 1 cm
Speed of water flow = 6m per second Water in 30 minutes (h) = 6 x 60 x 30 m = 10800 m
Volume of water = πr²h

Question 30.
A cylindrical water tank of diameter 1.4 m and height 2.1 m is being fed by a pipe of diameter 3.5 cm through which water flows at the rate of 2 metre per second. In how much time the tank will be filled?
Solution:
Diameter of cylindrical tank = 1.4 m
∴ Radius (r) = \(\frac { 1.4 }{ 2 }\) = 0.7 m
and height (h) = 2.1 m
∴ Volume of water in the tank = πr²h

Question 31.
The sum of the radius of the base and height of a solid cylinder is 37 m. If the total surface area of the solid cylinder is 1628 m². Find the volume of the cylinder.
Solution:
Sum of radius and height of a cylinder = 37 m
Let r be the radius and h be the height, then r + h = 37m …(i)
Total surface area of a solid cylinder = 1628m³

Question 32.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 10 m 10
∴ Radius (r) = \(\frac { 10 }{ 2 }\) = 5 m
Depth (h) = 8.4 m
∴ Volume of earth dugout = πr²h

Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1

Other Exercises

• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.2
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder VSAQS
• RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder MCQS

Question 1.
Curved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7 m, find its height. [NCERT]
Solution:
Curved surface area of a cylinder = 4.4 m²
Radius (r) = 0.7 m

Question 2.
In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system. [NCERT]
Solution:
Diameter of the pipe = 5 cm

Question 3.
A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of 12.50 per m². [NCERT]
Solution:
Diameter of cylindrical pillar = 50 cm

Question 4.
It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square metres of the sheet are required for the same? [NCERT]
Solution:
Height of cylinder (h) = 1 m = 100 cm
Diameter of box = 140 cm

Question 5.
The total surface area of a hollow cylinder which is open from both sides is 4620 sq. cm, area of base ring is 115.5 sq. cm and height 7 cm. Find the thickness of the cylinder.
Solution:
Total surface area of a hollow cylinder open from both sides = 4620 cm²
Area of base of ring = 115.5 cm²
Height (h) = 7 cm
Let outer radius (R) = R
and inner radius = r

Question 6.
Find the ratio between the total surface area of a cylinder to its curved surface area, given that its height and radius are 7.5 cm and 3.5 cm.
Solution:
Radius of the cylinder (r) = 3.5 cm
and height (h) = 7.5 cm
Total surface area = 2πr (h + r)
and curved surface area = 2πrh

Question 7.
A cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70 cm and its height is 1.4 m, calculate the cost of tin-coating at the rate of ₹3.50 per 1000 cm².
Solution:
Radius of the base of a cylindrical vessel (r) = 70 cm
and height (h) = 1.4 m = 140 cm
Total surface area (excluding upper lid) on both sides = 2πrh x 2 + πr² x 2

Question 8.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find:
(i) inner curved surface area.
(ii) the cost of plastering this curved surface at the rate of ₹40 per m². [NCERT]
Solution:
Inner diameter of a well = 3.5 m

Question 9.
The students of a Vidyalaya were asked to participate s a competition for making and decorating pen holders in the shape of a cylinder with a base, using cardboard. Each pen holder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition? [NCERT]
Solution:
Radius of cylinderical pen holder (r) = 3 cm
Height (h) = 10.5 cm
∴ Surface area of the pen holder

Question 10.
The diameter of roller 1.5 m long is 84 cm. If it takes 100 revolutions to level a play¬ground, find the cost of levelling this ground at the rate of 50 paise per square metre.
Solution:
Diameter of a roller = 1.5 m
∴ Radius = \(\frac { 1.5 }{ 2 }\) = 0.75 m = 75 cm
and length (h) = 84 cm

Question 11.
Twenty cylindrical pillars of the Parliament House are to be cleaned. If the diameter of each pillar is 0.50 m and height is 4 m. What will be the cost of cleaning them at the rate of ₹2.50 per square metre? [NCERT]
Solution:
Number of pillars = 20
Diameter of one pillar = 0.50 m

Question 12.
A solid cylinder has total surface area of 462 cm². Its curved surface area is one- third of its total surface area. Find the radius and height of the cylinder.
Solution:
Total surface of solid cylinder = 462 cm²
Curved surface area = \(\frac { 1 }{ 3 }\) of total surface area

Question 13.
The total surface area of a hollow metal cylinder, open at both ends of external radius 8 cm and height 10 cm is 338 π cm². Taking r to be inner radius, obtain an equation in r and use it to obtain the thickness of the metal in the cylinder.
Solution:
Total surface area of a hollow metal cylinder = 338π cm²
Let R be the outer radius, r be inner radius and h be the height of the cylinder of the cylinder
∴ 2πRh + 2πrh + 2πR² – 2πr² = 338π
R = 8 cm, h = 10 cm
⇒ 2πh (R + r) + 2π(R² – r²) = 338π
⇒ Dividing by 2π , we get
⇒ h(R + r) + (R² – r²) = 169
⇒ 10(8 + r) + (8 + r) (8 – r) = 169
⇒ 80 + 10r + 64 – r² = 169
⇒ 10r – r² + 144 – 169 = 0
⇒ r² – 10r + 25 = 0
⇒ (r-5)² = 0
⇒ r = 5
∴ Thickness of the metal = R – r = 8 – 5 = 3 cm

Question 14.
Find the lateral curved surface area of a cylinderical petrol storage tank that is 4.2m in diameter and 4.5 m high. How much steel was actually used, if \(\frac { 1 }{ 12 }\) of steel actually used was wasted in making the closed tank? [NCERT]
Solution:
Diameter of a cylinderical tank = 4.2 m

 

Hope given RD Sharma Class 9 Solutions Chapter 19 Surface Areas and Volume of a Circular Cylinder Ex 19.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS

Other Exercises

• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS
• RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS

Mark correct alternative in each of the following:
Question 1.
The length of the longest rod that can be fitted in a cubical vessel of edge 10 cm long, is
(a) 10 cm
(b) 10\(\sqrt { 2 } \) cm
(c) 10\(\sqrt { 3 } \) cm
(d) 20 cm
Solution:
Edge of cuboid (a) = 10 cm
∴ Longest edge = \(\sqrt { 3 } \) a cm
= \(\sqrt { 3 } \) x 10 = 10\(\sqrt { 3 } \) cm (c)

Question 2.
Three equal cubes are placed adjacently in a row. The ratio of the total surface area of the resulting cuboid to that of the sum of the surface areas of three cubes, is
(a) 7 : 9
(b) 49 : 81
(c) 9 : 7
(d) 27 : 23
Solution:
Let a be the side of three equal cubes
∴ Surface area of 3 cubes
= 3 x 6a² = 18a²
and length of so formed cuboid = 3a
Breadth = a
and height = a
∴ Surface area = 2(lb + bh + hl)
= 2[3a x a + a x a+a x 3a] = 2[3a² + a² + 3a²] = 2 x 7a² = 14a²
∴ Ratio in the surface areas of cuboid and three cubes = 14a² : 18a²= 7:9 (a)

Question 3.
If the length of a diagonal of a cube is 8 \(\sqrt { 3 } \) cm, then its surface area is
(a) 512 cm²
(b) 384 cm²
(c) 192 cm²
(d) 768 cm²
Solution:
Length of the diagonal of cube = 8 \(\sqrt { 3 } \) cm

Question 4.
If the volumes of two cubes are in the ratio 8:1, then the ratio of their edges is
(a) 8 : 1
(b) 2\(\sqrt { 2 } \) : 1
(c) 2 : 1
(d) none of these
Solution:
Let volume of first cube = 8x³
and of second cube = x³

Question 5.
The volume of a cube whose surface area is 96 cm², is
(a) 16\(\sqrt { 2 } \) cm³
(b) 32 cm³
(c) 64 cm³
(d) 216 cm³
Solution:
Surface area of a cube = 96 cm²

Question 6.
The length, width and height of a rectangular solid are in the ratio of 3 : 2 : 1. If the volume of the box is 48 cm³, the total surface area of the box is
(a) 27 cm²
(b) 32 cm²
(c) 44 cm²
(d) 88 cm²
Solution:
Ratio in the dimensions of a cuboid =3 : 2 : 1
Let length = 3x
Breadth = 2x
and height = x
Then volume = lbh = 3x x 2x x x = 6×3
∴ 6x³ = 48 ⇒ x³= \(\frac { 48 }{ 6 }\) = 8 = (2)³
∴ x = 2
∴ Length (l) = 3 x 2 = 6 cm
Breadth (b) = 2 x 2 = 4 cm
Height (h) = 1 x 2 = 2 cm
Now surface area = 2[lb + bh + hl]
= 2[6 x 4 + 4 x 2 + 2 x 6] cm²
= 2[24 + 8-+ 12] = 2 x 44 cm²
= 88 cm² (d)

Question 7.
If the areas of the adjacent faces of a rectangular block are in the ratio 2:3:4 and its volume is 9000 cm3, then the length of the shortest edge is
(a) 30 cm
(b) 20 cm
(c) 15 cm
(d) 10 cm
Solution:
Ratio in the areas of three adjacent faces of a cuboid = 2 : 3 : 4
Volume = 9000 cm³
Let the area of faces be 2x, 3x, Ax and
Let a, b, and c be the dimensions of the cuboid, then
∴ 2x = ab, 3x = be, 4x = ca
∴ ab x be x ca = 2x x 3x x 4x
a²b²c² = 24 x 3
But volume = abc = 9000 cm³

Question 8.
If each edge of a cube, of volume V, is doubled, then the volume of the new cube is
(a) 2V
(b) 4V
(c) 6V
(d) 8V
Solution:
Let a be the edge of a cube whose Volume = V
∴ a3 = V
By doubling the edge, we get 2a
Then volume = (2a)3 = 8a³
∴ Volume of new cube = 8a³ = 8V (d)

Question 9.
If each edge of a cuboid of surface area S is doubled, then surface area of the new cuboid is
(a) 2S
(b) 4S
(c) 6S
(d) 8S
Solution:
Let each edge of a cube = a
Then surface area = 6a²
∴ S = 6a²
Now doubling the edge, we get
New edge of a new cube = 2a
∴ Surface area = 6(2a)²
= 6 x 4a² = 24a²
= 4 x 6a² = 4S (b)

Question 10.
The area of the floor of a room is 15 m2. If its height is 4 m, then the volume of the air contained in the room is
(a) 60 dm³
(b) 600 dm³
(c) 6000 dm³
(d) 60000 dm³
Solution:
Area of a floor of a room = 15 m²
Height (h) = 4 m
∴ Volume of air in the room = Floor area x Height
= 15 m² x 4 m = 60 m³
= 60 x 10 x 10 x 10 dm² = 60000 dm² (d)

Question 11.
The cost of constructing a wall 8 m long, 4 m high and 20 cm thick at the rate of ₹25 per m³ is
(a) ₹16
(b) ₹80
(c) ₹160
(d) ₹320
Solution:
Length of wall (l) = 8 m
Breadth (b) = 20 cm = \(\frac { 1 }{ 5 }\) m
Height (h) = 4 m

Question 12.
10 cubic metres clay in uniformaly spread on a land of area 10 acres. The rise in the level of the ground is
(a) 1 cm
(b) 10 cm
(c) 100 cm
(d) 1000 cm
Solution:
Volume of clay = 10 m³
Area of land = 10 acres
= 10 x 100 = 1000 m²
∴ Rise of level by spreading the clay

Question 13.
Volume of a cuboid is 12 cm³. The volume (in cm³) of a cuboid whose sides are double of the above cuboid is
(a) 24
(b) 48
(c) 72
(d) 96
Solution:
Volume of cuboid = 12 cm³
By doubling the sides of the cuboid the
volume will be = 12 cm³ x 2 x 2 x 2
= 96 cm³ (d)

Question 14.
If the sum of all the edges of a cube is 36 cm, then the volume (in cm3) of that cube is
(a) 9
(b) 27
(c) 219
(d) 729
Solution:
Sum of all edges of a cube = 36 cm
No. of edge of a cube are 12
∴ Length of its one edge = \(\frac { 36 }{ 12 }\) = 3 cm
Then volume = (edge)³ = (3)³ cm³
= 27 cm³ (b)

Question 15.
The number of cubes of side 3 cm that can be cut from a cuboid of dimensions 9 cm x 9 cm x 6 cm, is
(a) 9
(b) 10
(c) 18
(d) 20
Solution:
Dimensions of a cuboid = 9 cm x 9 cm x 6 cm

Question 16.
On a particular day, the rain fall recorded in a terrace 6 m long and 5 m broad is 15 cm. The quantity of water collected in the terrace is
(a) 300 litres
(b) 450 litres
(c) 3000 litres
(d) 4500 litres
Solution:
Dimension of a terrace = 6mx5m
Level of rain on it = 15 cm
∴ Volume of water collected on it

Question 17.
If A₁, A₂ and A₃ denote the areas of three adjacent faces of a cuboid, then its volume is

Solution:
Let l, b, h be the dimensions of the cuboid
∴ A₁= lb, A₂ = bh, A₃ = hl
∴ A₁ A₂ A₃ = lb.bh.hl = l₂b₂h₂

Question 18.
If l is the length of a diagonal of a cube of volume V, then

Solution:
Volume of a cube = V
and longest diagonal = l

Question 19.
If V is the volume of a cuboid of dimensions x, y, z and A is its surface area, then \(\frac { A }{ V }\)

Solution:
A is surface area, V is volume and x, y and z are the dimensions
Then V = xyz
A = 2[xy + yz + zx]

Question 20.
The sum of the length, breadth and depth of a cuboid is 19 cm and its diagonal is 5\(\sqrt { 5 } \) cm. Its surface area is
(a) 361 cm²
(b) 125 cm²
(c) 236 cm²
(d) 486 cm²
Solution:
Let x, y, z be the dimensions of a cuboid,
then x + y + z = 19 cm

Question 21.
If each edge of a cube is increased by 50%, the percentage increase in its surface area is
(a) 50%
(b) 75%
(c) 100%
(d) 125%
Solution:
Let in first case, edge of a cube = a
Then surface area = 6a²
In second case, increase in side = 50%

Question 22.
A cube whose volume is 1/8 cubic centimeter is placed on top of a cube whose volume is. 1 cm³. The two ,cubes are then placed on top of a third cube whose volume is 8 cm³. The height of the stacked cubes is
(a) 3.5 cm
(b) 3 cm
(c) 7 cm
(d) none of these
Solution:
Volume of first cube = \(\frac { 1 }{ 2 }\) cm³

Hope given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.