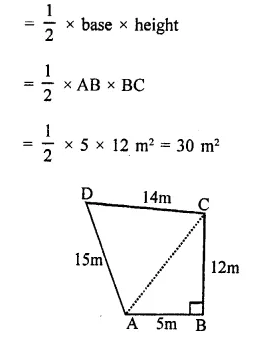
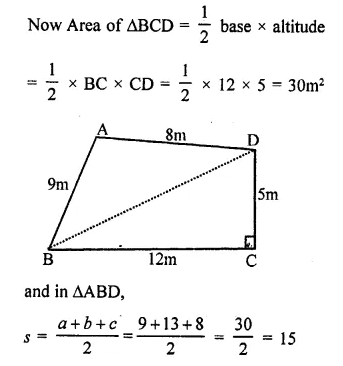
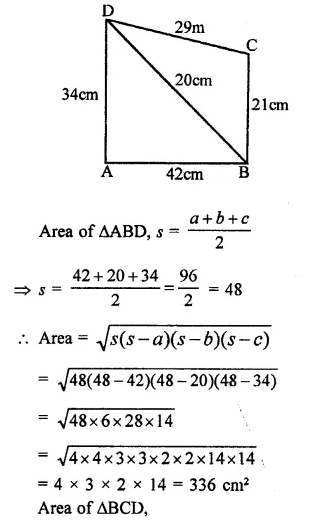
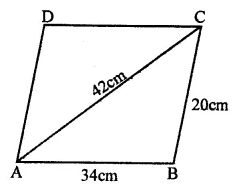
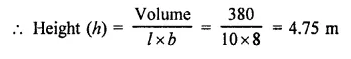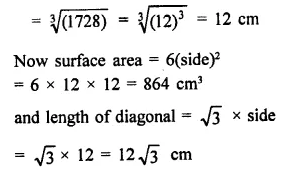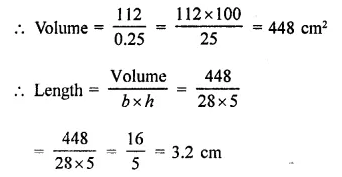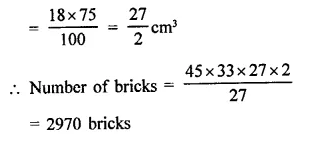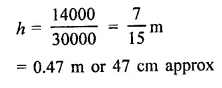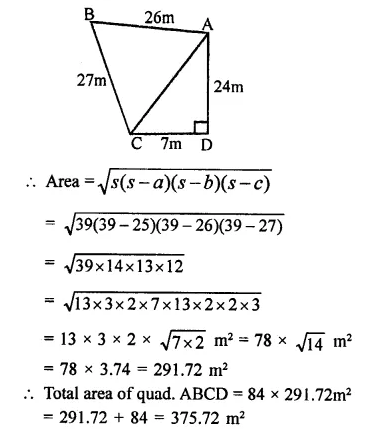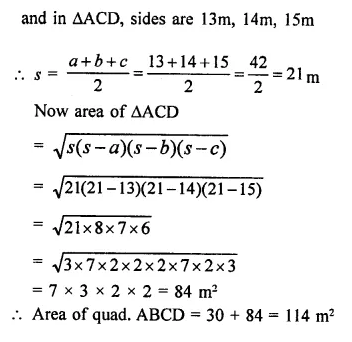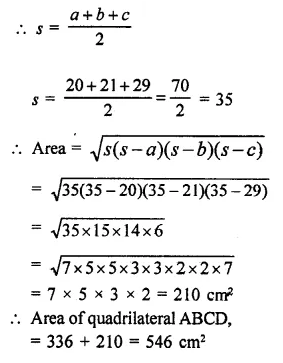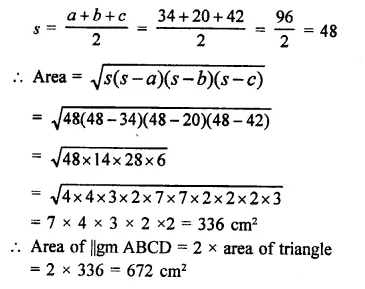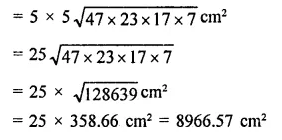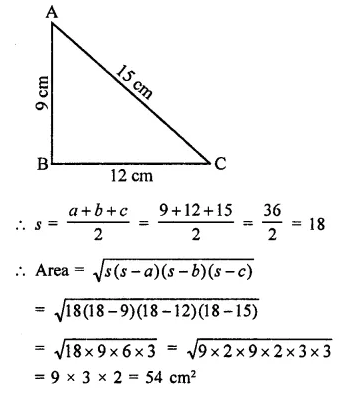RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.1
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube Ex 18.2
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS
- RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube MCQS
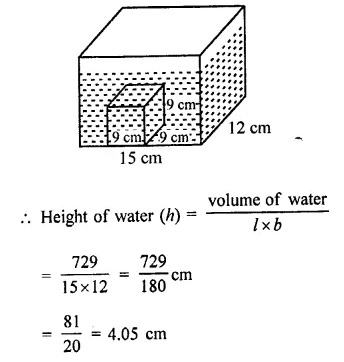
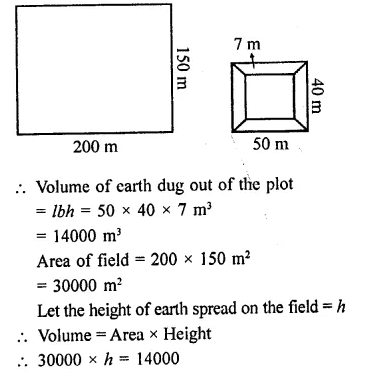
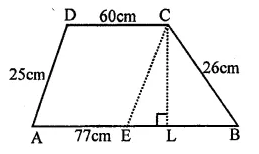
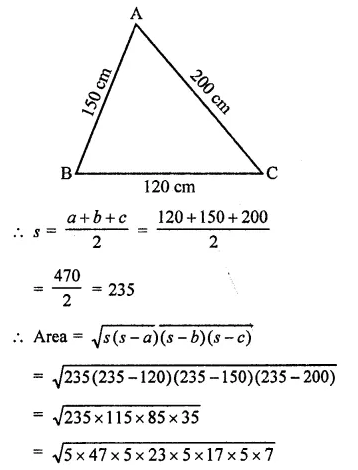
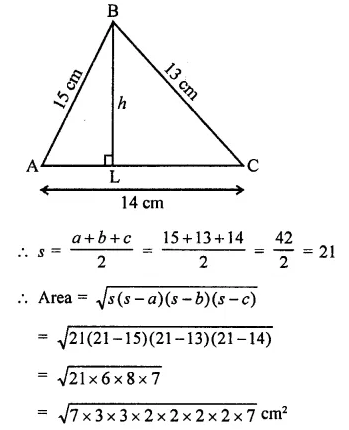
Question 1.
If two cubes of side 6 cm are joined face to face, then find the volume of the resulting cuboid.
Solution:
Side of a cube = 6 cm
∴ By joining two such cubes, the length of so
formed cuboid (l) = 6 x 2 = 12 cm
Breadth (b) = 6 cm
Height (h) = 6 cm
∴ Volume = lbh = 12 x 6 x 6 cm3
= 432 cm3
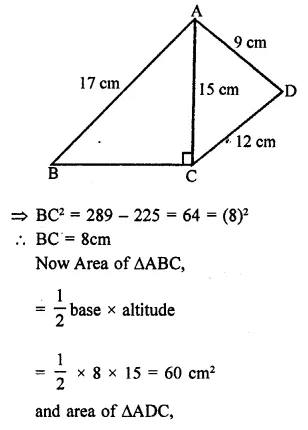
Question 2.
Three cubes of metal whose edges are in the ratio 3 : 4 : 5, are melted down into a single cube whose diagonals is 12 \(\sqrt { 3 } \) cm. Find the edges of three cubes.
Solution:
Ratio in the sides of three cubes = 3 : 4 : 5
Let side of first cube = 3x
and side of second cube = 4x
and side of third cube = 5x
∴ Sum of volume of three cubes
= (3x)3 + (4x)3 + (5x)3
= 27x3 + 64x3 + 125x3 = 216x3
∴ Volume of the cube formed Jby melting these three cubes = 216x3
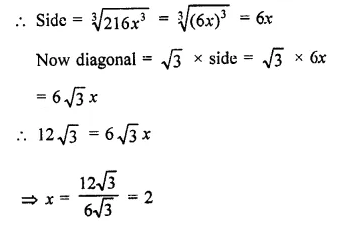
∴ Side of first cube = 3x = 3 x 2 = 6 cm
Side of second cube = 4x = 4×2 = 8 cm
and side of third cube = 5.r = 5 x 2 = 10 cm
Question 3.
If the perimeter of each face of a cube is 32 cm, find its lateral surface area. Note that four faces which meet the base of a cube are called its lateral faces.
Solution:
Perimeter of each face of a cube = 32 cm
∴ Length of edge = \(\frac { 32 }{ 4 }\) = 8 cm
and lateral surface area of the cube = 4 x (side)2
= 4 x 8 x 8 = 256 cm2
Question 4.
Find the edge of a cube whose surface area is 432 m2.
Solution:

Question 5.
A cuboid has total surface area of 372 cm2 and its lateral surface area is 180 cm2, find the area of its base.
Solution:
Total surface area of a cuboid = 372 cm2
and lateral surface area = 180 cm2
∴ Area of base and roof = 372 – 180 = 192 cm2
and area of base = \(\frac { 192 }{ 2 }\) = 96 cm2
Question 6.
Three cubes of each side 4 cm are joined end to end. Find the surface area of the resulting cuboid.
Solution:
By joining three cubes of side 4 cm each, end is end, we get a cuboid
Length of cuboid = 4 x 3 = 12 cm
Breadth = 4 cm
and height = 4 cm
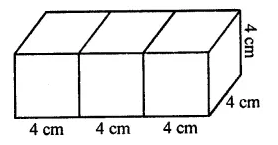
∴ Surface area = 2(lb + bh + hl)
= 2[12 x4+4×4 + 4x 12] cm2
= 2[48 + 16 + 48] cm2
= 2 x 112 = 224 cm2
Question 7.
The surface area of a cuboid is 1300 cm2. If its breadth is 10 cm and height is 20 cm, find its length.
Solution:
Surface area of a cuboid = 1300 cm2
Breadth (b) = 10 cm
and height (h) = 20 cm
Let l be the length, then
= 2 (lb + bh + hl) = 1300
lb+ bh + hl = \(\frac { 1300 }{ 2 }\) = 650
l x 10 + 10 x 20 + 20 x l = 650
10l + 20l + 200 = 650
⇒ 30l = 650 – 200 = 450
⇒ l = \(\frac { 450 }{ 30 }\) = 15
∴ Length of cuboid = 15 cm
Hope given RD Sharma Class 9 Solutions Chapter 18 Surface Areas and Volume of a Cuboid and Cube VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.