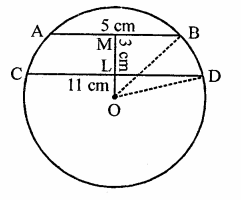
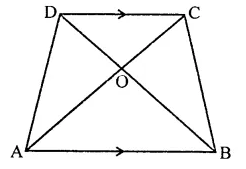
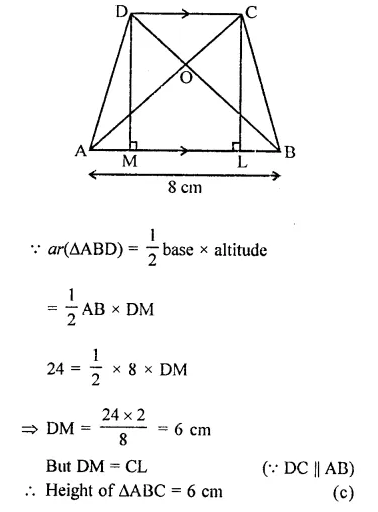
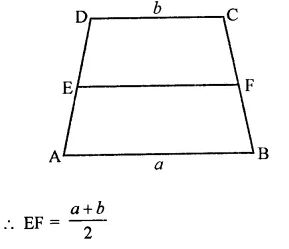
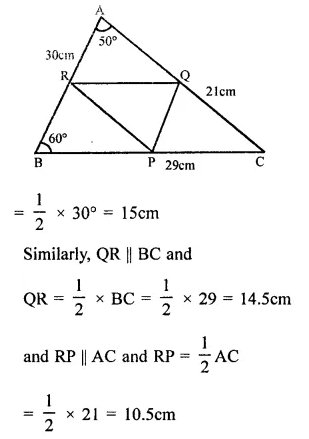
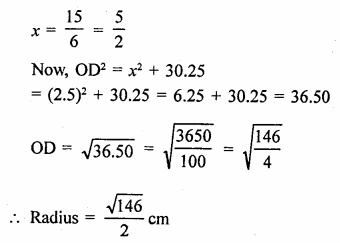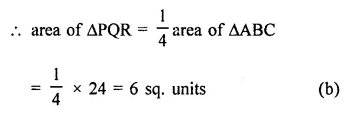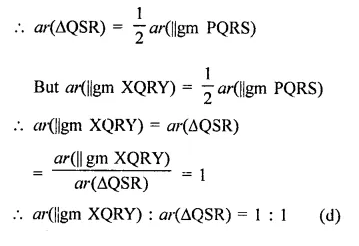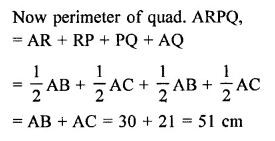RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
Other Exercises
- RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
- RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
- RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3
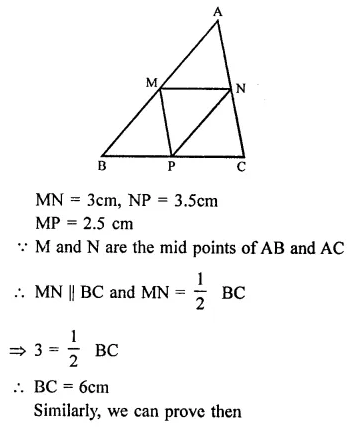
Question 1.
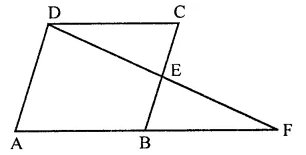
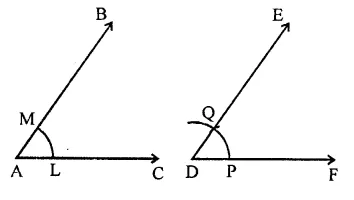
Draw an angle and label it as ∠BAC. Construct another angle, equal to ∠BAC.
Solution:
Steps of construction :
(i) Draw an angle BAC.
(ii) Draw a line DF.
(iii) With centre A and D, draw arcs of equal radius which intersect AC at L and AB at M and DF at P.
(iv) Cut off PQ = LM and join DQ and produce it to E, then
∠EDF = ∠BAC.
Question 2.
Draw an obtuse angle. Bisect it. Measure each of the angles so obtained.
Solution:
Steps of construction :
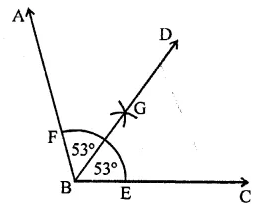
(i) Draw an angle ABC which is an obtuse i.e. more than 90°.
(ii) With centre B and a suitable radius draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
ThenBD is die bisector of ∠ABC.
On measuring each part, we find each angle = 53°.
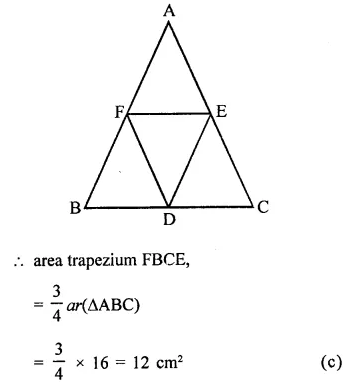
Question 3.
Using your protractor, draw an angle of measure 108°. With this angle as given, draw an angle of 54°.
Solution:
Steps of construction :
(i) With the help of protractor draw an angle ABC = 108°.
As 54° = \(\frac { 1 }{ 2 }\) x 108°
∴ We shall bisect it.
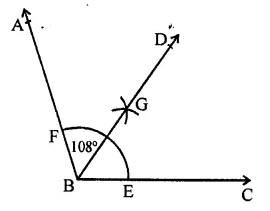
(ii) With centre B and a suitable radius, draw an arc meeting BC at E and AB at F.
(iii) With centre E and F, and radius more than half of EF, draw arcs intersecting each other at G
(iv) Join BG and produce it to D.
Then ∠DBC = 54°.
Question 4.
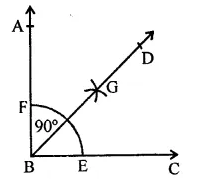
Using protractor, draw a right angle. Bisect it to get an angle of measure 45°.
Solution:
Steps of construction :
(i) Using protractor, draw a right angle ∆ABC.
i. e. ∠ABC = 90°.
(ii) With centre B and a suitable radius, draw an arc which meets BC at E and BA at F.
(iii) With centre E and F, draw arcs intersecting each other at G.
(iv) Join BG and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC =\(\frac { 1 }{ 2 }\) x 90° = 45°.
Question 5.
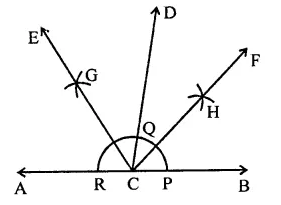
Draw a linear pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
Solution:
Steps of construction :
(i) Draw a linear pair ∠DCA and ∠DCB.
(ii) Draw the bisectors of ∠DCA and ∠DCB. Forming ∠ECF on measuring we get ∠ECF = 90°.
Verification : ∵∠DCA + ∠DCB = 180°
⇒ \(\frac { 1 }{ 2 }\) ∠DCA + \(\frac { 1 }{ 2 }\) ∠DCB = 180° x \(\frac { 1 }{ 2 }\) = 90°
∴ ∠ECF = 90°
i.e. EC and FC are perpendicular to each other.
Question 6.
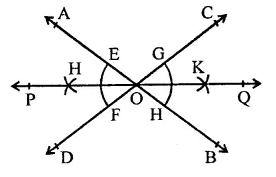
Draw a pair of vertically opposite angles. Bisect each of the two angles. Verify that the bisecting rays are in the same line
Solution:
Steps of construction :
(i) Draw two lines AB and CD intersecting each other at O.
(ii) Draw the bisector of ∠AOD and also the bisector of ∠BOC. Which are OP and OQ respectively. We see that OP and OQ are in the same straight line.
Question 7.
Using ruler and compasses only, draw a right angle.
Solution:
Steps of construction :
(i) Draw a line segment BC.
(ii) With centre B and a suitable radius, draw an arc meeting BC at E.
(iii) With centre E and same radius, cut off arcs EF and FG.
(iv) Bisect arc FG at H.
(v) Join BH and produce it to A.
Then ∠ABC = 90°.
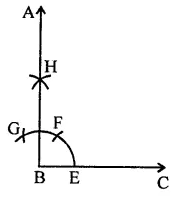
Question 8.
Using ruler and compasses only, draw an angle of measure 135°.
Solution:
Steps of construction :
(i) Draw a line DC and take a point B on it.
(ii) With centre B and a suitable radius draw an arc meeting BC at P.
(iii) With centre P, cut off arcs PQ, QR and RS.
(iv) Bisect as QR at T and join BT and produce it to E.
(v) Now bisect the arc KS at RL.
(vi) Join BL and produce it to A.
Now ∠ABC = 135°.
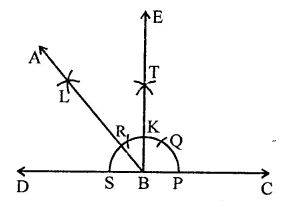
Question 9.
Using a protractor, draw an angle of measure 72°. With this angle as given, draw angles of measure 36° and 54°.
Solution:
Steps of construction :
(i) Draw an angle ABC = 12° with the help of protractor.
(ii) With centre B and a suitable radius, draw an arc EF.
(iii) With centre E and F, draw arcs intersecting
each other at G and produce it to D.
Then BD is the bisector of ∠ABC.
∴ ∠DBC = 72° x \(\frac { 1 }{ 2 }\) = 36°.
(iv) Again bisect ∠ABD in the same way then PB is the bisector of ∠ABD.
∴ ∠PBC = 36° + \(\frac { 1 }{ 2 }\) x 36°
= 36° + 18° = 54°
Hence ∠PBC = 54°
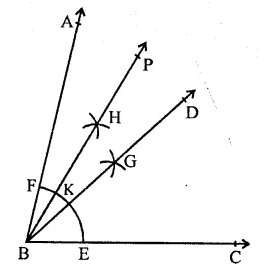
Question 10.
Construct the following angles at the initial point of a given ray and justify the construction:
(i) 45°
(ii) 90°
Solution:
(i) 45°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) With centre E, cut off equal arcs EF and FG.
(d) Bisect FG at H.
(e) Join BH and produce to X so that ∠XBC = 90°.
(f) Bisect ∠XBC so that ∠ABC = 45°.
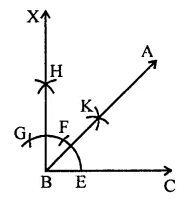
(ii) 90°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E and with centre E cut off arcs from E, EF = FG
(c) Now bisect the arc EG at H.
(d) Join BH and produce it to A.
∴ ∠ABC = 90°.
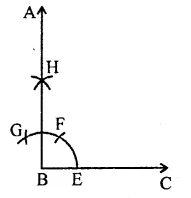
Question 11.
Construct the angles of the following measurements:
(i) 30°
(ii) 75°
(iii) 105°
(iv) 135°
(v) 15°
(vi) 22 \(\frac { 1 }{ 2 }\)°
Solution:
(i) 30°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) Cut off arcs EF and bisect it at G.
So that ∠ABC = 30°.
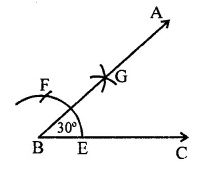
(ii) 75°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF = FG from E.
(d) Bisect the arc FG at K and join BK so that ∠KBC = 90°.
(e) Now bisect arc HF at L and join BL and produce it to A so that ∠ABC = 75°.
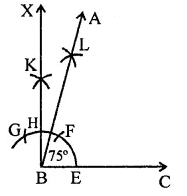
(iii) 105°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius draw an arc meeting BC at E.
(c) From E, cut off arc EF = FG and divide FG at H.
(d) Join BH meeting the arc at K.
(e) Now bisect the arc KG at L.
Join BL and produce it to A.
Then ∠ABC = 105°.
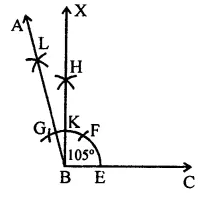
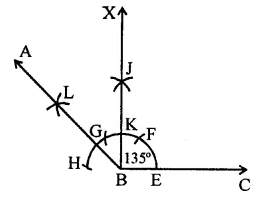
(iv) 135°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) From E, cut off EF = FG = GH.
(d) Bisect arc FG at K, and join them.
(e) Bisect arc KH at L.
(f) Join BL and produce it to A, then ∠ABC = 135°.
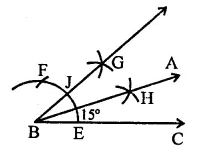
(v) 15°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc meeting BC at E.
(c) Cut off arc EF from E and bisect it at G. Then ∠GBC = 30°.
(d) Again bisect the arc EJ at H.
(e) Join BH and produce it to A.
Then ∠ABC = 15°.
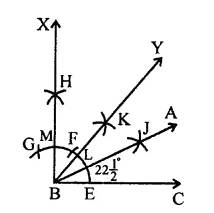
(vi) 22 \(\frac { 1 }{ 2 }\)°
Steps of construction :
(a) Draw a line segment BC.
(b) With centre B and a suitable radius, draw an arc and from E, cut off EF = FG
(c) Bisect FG at H so that ∠HBC = 90°.
(d) Now bisect ∠HBC at K. So that ∠YBC = 45°.
(e) Again bisect ∠YBC at J. So thttt ∠ABC = 22 \(\frac { 1 }{ 2 }\)°
Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.