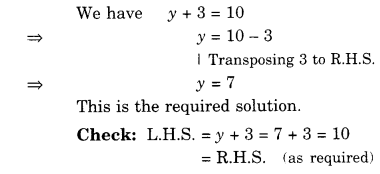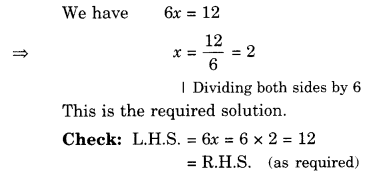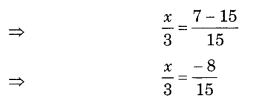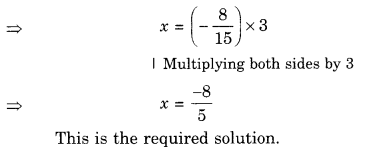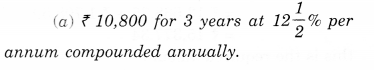Tag: NCERT Solutions for Class 8 Maths

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1.

• Direct and Indirect Proportions Class 8 Ex 13.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 13
Chapter Name	Direct and Indirect Proportions
Exercise	Ex 13.1
Number of Questions Solved	10
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1

Question 1.
Following are the car parking charges near a railway station up to
4 hours ₹ 60
8 hours ₹ 100
12 hours ₹ 140
24 hours ₹ 180
Check if the parking charges are in direct proportion to the parking time.
Solution.
We have
\(\frac { 60 }{ 4 } =\frac { 15 }{ 1 } \)
\(\frac { 100 }{ 8 } =\frac { 25 }{ 2 } \)
\(\frac { 140 }{ 12 } =\frac { 35 }{ 3 } \)
\(\frac { 180 }{ 24 } =\frac { 15 }{ 2 } \)
Since all the values are not the same, therefore, the parking charges are not in direct proportion to the parking time.

Question 2.
A mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of the base. In the following table, find the parts othe f base that need to be added.

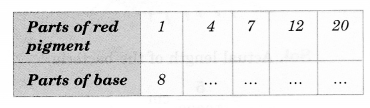
Solution.
Sol. Let the number of parts of red pigment is x and the number of parts of the base is y.
As the number of parts of red pigment increases, a number of parts of the base also increases in the same ratio. So it is a case of direct proportion.
We make use of the relation of the type

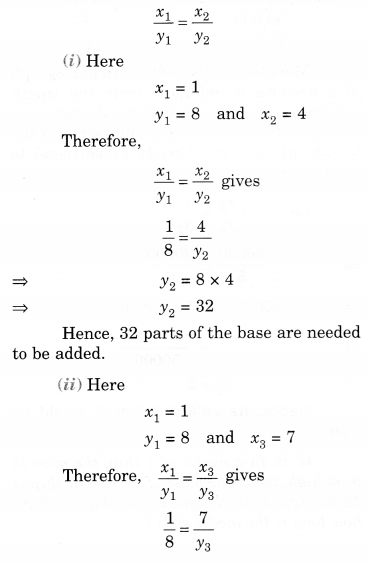
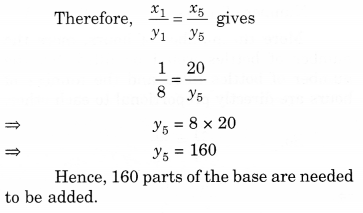
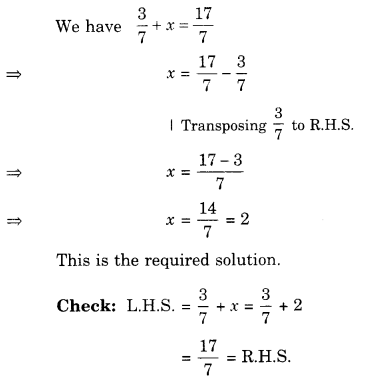
Question 3.
In Question 2 above, if 1 part of a red pigment requires 75 mL of the base, how much red pigment should we mix with 1800 mL of base?
Solution.
Let the number of parts of red pigment is x and the amount of base be y mL.
As the number of parts of red pigment increases, the amount of base also increases in the same ratio. So it is a case of direct proportion. We make use of the relation of the type.

Question 4.
A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
Solution.
Let the machine fill x bottles in five hours. We put the given information in the form of a table as shown below :
Number of bottles filled 840 x2
Number of hours 6 5
More the number of hours, more the number of bottles would be filled. So, the number of bottles filled and the number of hours are directly proportional to each other.
So, \(\frac { { x }_{ 1 } }{ { x }_{ 2 } } =\frac { { y }_{ 1 } }{ { y }_{ 2 } } \)
⇒ \(\frac { 840 }{ { x }_{ 2 } } =\frac { 6 }{ 5 } \)
⇒ \(6{ x }_{ 2 }=840\times 5\)
⇒ \({ x }_{ 2 }=\frac { 840\times 5 }{ 6 } \)
⇒ \({ x }_{ 2 }=700\)
Hence, 700 bottles will be filled.

Question 5.
A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria ? If the photograph is enlarged 20,000 times only, what would be its enlarged length?

Solution.
Actual length of the bacteria
= \(\frac { 5 }{ 50000 } \)cm
= \(\frac { 1 }{ 10000 } \) = \({ 10 }^{ -4 }\)cm
10000
Let the enlarged length be y2 cm. We put the given information in the form of a table as shown below:
Number of times Length attained
photograph enlarged (in cm)
50.000 5
20.000 y₂
More the number of times a photograph of a bacteria is enlarged, more the length attained. So, the number of times a photograph of a bacteria is enlarged and the length attained are directly proportional to each other.
So,\(\frac { { x }_{ 2 } }{ { y }_{ 2 } } =\frac { { x }_{ 2 } }{ { y }_{ 2 } } \)
⇒ \(\frac { 50000 }{ 5 } =\frac { 20000 }{ { y }_{ 2 } } \)
⇒ \(50000{ y }_{ 2 }=5\times 20000\)
⇒ \({ y }_{ 2 }=\frac { 5\times 20000 }{ 50000 } \)
⇒ \({ y }_{ 2 }=2\)
Hence, its enlarged length would be
2 cm.

Question 6.
In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28 m, how long is the model ship ?

Solution.

Question 7.
Suppose 2 kg of sugar contains 9 x 106 crystals. How many sugar crystals are there in
(i) 5 kg of sugar?
(ii) 1.2 kg of sugar?
Solution.
Suppose the amount of sugar is x kg and the number of crystals is y.
We put the given information in the form of a table as shown below:

As the amount of sugar increases, the number of crystals also increases in the same ratio. So it is a case of direct proportion. We make use of the relation of the type \(\frac { { x }_{ 1 } }{ { y }_{ 1 } } =\frac { { x }_{ 2 } }{ { y }_{ 2 } } \)

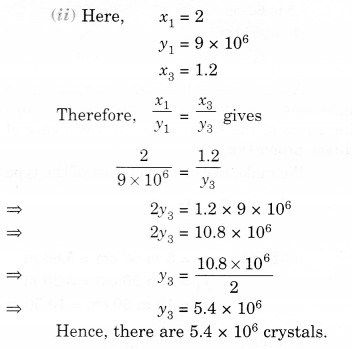
Question 8.
Rashmi has a roadmap with a scale of 1 cm representing 18 km. She drives on a T’oad for 72 km. What would be her distance covered in the map?
Solution.
Let the distance covered in the map be x cm. Then,
1 : 18 = x : 72
⇒ \(\frac { 1 }{ 18 } =\frac { x }{ 72 }\)
⇒ \(x=\frac { 72 }{ 18 } \)
⇒ x = 4
Hence, the distance covered in the map would be 4 cm.

Question 9.
A5 m 60 cm high vertical pole casts a shadow 3 m 20 cm long. Find at the same time
(i) the length of the shadow cast by another pole 10 m 50 cm high
(ii) the height of a pole which casts a shadow 5 m long.
Solution.
Let the height of the vertical pole be x m and the length of the shadow be y m.
We put the given information in the form of a table as shown below:

Question 10.
A loaded truck travels 14 km. in 25 minutes. If the speed remains the same, how far can it travel in 5 hours?
Solution.
Two quantities x and y which vary in direct proportion have the relation

 

We hope the NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 13 Direct and Indirect Proportions Ex 13.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1.

• Factorisation Class 8 Ex 14.2
• Factorisation Class 8 Ex 14.3
• Factorisation Class 8 Ex 14.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 14
Chapter Name	Factorisation
Exercise	Ex 14.1, Ex 14.2, Ex 14.3, Ex 14.4
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1

Question 1.
Find the common factors of the given terms:

Solution.

Question 2.
Factorise the following expressions:

Solution.

Question 3.
Factorise:

Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.1.

• Linear Equations in One Variable Class 8 Ex 2.2
• Linear Equations in One Variable Class 8 Ex 2.3
• Linear Equations in One Variable Class 8 Ex 2.4
• Linear Equations in One Variable Class 8 Ex 2.5
• Linear Equations in One Variable Class 8 Ex 2.6

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 2
Chapter Name	Linear Equations in One Variable
Exercise	Ex 2.1, Ex 2.2, Ex 2.3, Ex 2.4, Ex 2.5, Ex 2.6
Number of Questions Solved	1
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.1

Question 1.
Solve the following equations:

Solution.
1. x-2 = 7

2. y+3=10

3. 6=z+2

4. \(\frac { 3 }{ 7 } +x=\frac { 17 }{ 7 } \)

5. 6x=12

6. \(\frac { t }{ 5 } =10\)

7. \(\frac { 2x }{ 3 } =18\)

8. \(1.6=\frac { y }{ 1.5 }\)

9. 7x-9=16

10. 14y-8=13

11. 17+6p=9

12. \(\frac { x }{ 3 } +1=\frac { 7 }{ 15 } \)

 

We hope the NCERT Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 2 Linear Equations in One Variable Ex 2.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1.

• Squares and Square Roots Class 8 Ex 6.2
• Squares and Square Roots Class 8 Ex 6.3
• Squares and Square Roots Class 8 Ex 6.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 6
Chapter Name	Squares and Square Roots
Exercise	Ex 6.1
Number of Questions Solved	9
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1

Question 1.
What will be the unit digit of the squares of the following numbers ?
(i) 81
(ii) 272
(iii) 799
(iv) 3853
(v) 1234
(vi) 26387
(vii) 52698
(viii) 99880
(ix) 12796
(x) 55555
Solution.
(i) 81
∵ \(1\times 1\)
∴ The unit digit of the square of the number 81 will be 1.

(ii) 272
∵ \(2\times 2\)
∴ The unit digit of the square of the number 272 will be 4.

(iii) 799
∵ \(9\times 9\)
∴ The unit digit of the square of the number 799 will be 1.

(iv) 3853
∵ \(3\times 3\)
∴ The unit digit of the square of the number 3853 will be 9

(v) 1234
∵ \(4\times 4\)
∴ The unit digit of the square of the number 1234 will be 6.

(vi) 26387
∵ \(7\times 7\)
∴ The unit digit of the square of the number 26387 will be 9.

(vii) 52698
∵ \(8\times 8\)
∴ The unit digit of the square of the number 52698 will be 4.

(viii) 99880
∵ \(0\times 0\)
∴ The unit digit of the square of the number 99880 will be 0.

(ix) 12796
∵ \(6\times 6\)
∴ The unit digit of the square of the number 12796 will be 6.

(x) 55555
∵ \(5\times 5\)
∴ The unit digit of the square of the number 55555 will be 5.

Question 2.
The following numbers are obviously not perfect squares. Give reason.
(i) 1057
(ii) 23453
(iii) 7928
(iv) 222222
(v) 64000
(vi) 89722
(vii) 222000
(viii) 505050.
Solution.
(i) 1057
The number 1057 is not a perfect square because it ends with 7 at unit’s place whereas the square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(ii) 23453
The number 23453 is not a perfect square because it ends with 3 at unit’s place whereas the square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(iii) 7928
The number 7928 is not a perfect square because it ends with 8 at unit’s place whereas the square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(iv) 222222
The number 222222 is not a perfect square because it ends with 2 at unit’s place whereas the Square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(v) 64000
The number 64000 is not a square number because it has 3 (an odd number of) zeros at the end whereas the number of zeros at the end of a square number ending with zeros is always even.

(vi) 89722
The number 89722 is not a square number because it ends in 2 at unit’s place whereas the square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place.

(vii) 222000
The number 222000 is not a square number because it has 3 (an odd number of) zeros at the end whereas the number of zeros at the end of a square number ending with zeros is always even.

(viii) 505050
The number 505050 is not a square number because it has 1 (an odd number of) zeros at the end whereas the number of zeros at the end of a square number ending with zeros is always even.

Question 3.
The squares of which of the following would be odd numbers ?
(i) 431
(ii) 2826
(iii) 7779
(v) 82004.
Solution.
(i) 431
∵ 431 is an odd number
∴ Its square will also be an odd number.

(ii) 2826
∵ 2826 is an even number
∴ Its square will not be an odd number.

(iii) 7779
∵ 7779 is an odd number
∴ Its square will be an odd number.

(iv) 82004
∵ 82004 is an even number
∴ Its square will not be an odd number.

Question 4.
Observe the following pattern and find the missing digits:

Solution.

Question 5.
Observe the following pattern and supply the missing numbers:

Solution.

Question 6.
Using the given pattern, find the missing numbers:

Solution.

Question 7.
Without adding, find the sum:
(i) 1 + 3 + 5+7 + 9
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 +17 + 19
(iii) 1+3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 +23.
Solution.
(i)
l + 3 + 5 + 7 + 9 = sum of first five odd natural numbers = \({ 5 }^{ 2 }\) = 25

(ii)
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = sum of first ten odd natural numbers = \({ 10 }^{ 2 }\) = 100

(iii)
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 = sum of first twelve odd natural numbers = \({ 12 }^{ 2 }\)= 144.

Question 8.
(i) Express 49 as the sum of 7 odd numbers.
(ii) Express 121 as the sum of 11 odd numbers.
Solution.
(i)
49 (= \({ 7 }^{ 2 }\))
= 1 + 3 + 5 + 7 + 9 + 11 + 13

(ii)
121 (= \({ 11 }^{ 2 }\))
= 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21.

Question 9.
How many numbers lie between squares of the following numbers ?
(i) 12 and 13
(ii) 25 and 26
(iii) 99 and 100.
Solution.
(i) 12 and 13
Here, n = 12
∴ 2n = 2 x 12 = 24
So, 24 numbers lie between squares of i the numbers 12 and 13.

(ii) 25 and 26
Here, n = 25
∴ 2n = 2 x 25 = 50
So, 50 numbers lie between squares of the numbers 25 and 26.

(iii) 99 and 100
Here, n = 99
∴ 2n = 2 x 99 = 198
So, 198 numbers lie between squares of of the numbers 99 and 100.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1 are part help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.1 are part, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1.

• Data Handling Class 8 Ex 5.2
• Data Handling Class 8 Ex 5.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 5
Chapter Name	Data Handling
Exercise	Ex 5.1
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1

Question 1.
For which of these would you use a histogram to show the data?
(a) The number of letters for different areas in a postman’s bag.
(b) The height of competitors in an athletics meet.
(c) The number of cassettes produced by 5 companies.
(d) The number of passengers boarding trains from 7:00 a.m. to 7:00 p.m at a station.
Give reasons for each.
Solution.
For (b) and (d) because in these two cases data can be grouped into class intervals.

Question 2.
The shoppers who come to a departmental store are marked as man (M), woman (W), boy (B) or girl (G). The following list gives the shoppers who came during the first hour in the morning.
WWWGBWWMGGMMWWWWG
BMWBGGMWWMMWW
WMWBWGMWWWWGWMMWW
MWGWMGWMMBGGW
Make a frequency distribution table using tally marks. Draw a bar graph to illustrate it.
Solution.

Question 3.
The weekly wages (in of 30 workers in a factory are:
830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860,
832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 835, 836,
878, 840, 868, 890, 806, 840.
Solution.

Question 4.
Draw a histogram for the frequency table made for the data in Question 3, and answer the following questions:
(i) Which group has the maximum number of workers?
(ii) How many workers earnt 850 and more?
(iii) How many workers earn less than? 850?
Solution.

(i) Group 830—840, has the maximum number of workers.
(ii) 1 + 3 + 1 + 1 + 4 = 10, workers earn ? 850 and more.
(iii) 3 + 2 + l + 9 + 5 = 20, workers earn less than ? 850.

Question 5.
The number of hours for which students of a particular class watched television during holidays is shown through the given graph:

Answer the following:
(i) For how many hours did the maximum number of students watch TV?
(ii) How many students watched TV for less than 4 hours?
(iii) How many students spent more than 5 hours watching TV?
Solution.
(i) The maximum number of students watch TV for 4 to 5 hours.
(ii) 4 + 8 + 22 = 34 students watch TV for less than 4 hours.
(iii) 8 + 6 = 14 students spend more than 5 hours in watching TV.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.1, drop a comment below and we will get back to you at the earliest.

In Online Education NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3.

• Mensuration Class 8 Ex 11.1
• Mensuration Class 8 Ex 11.2
• Mensuration Class 8 Ex 11.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 11
Chapter Name	Mensuration
Exercise	Ex 11.3
Number of Questions Solved	10
Category	NCERT Solutions

Online Education NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3

Question 1.
There are two cuboidal boxes as shown in the adjoining figure. Which box requires the lesser amount of material to make?

Solution.

Question 2.
A suitcase with measures 80 cm x 48 cm x 24 cm is to be covered with a tarpau¬lin cloth. How many meters of tarpaulin of width 96 cm is required to cover 100 such suitcases?
Solution.

Question 3.
Find the side of a cube whose surface area is 600 \({ cm }^{ 2 }\).
Solution.
Let the side of the cube be a cm.
Then, Total surface area of the cube = 6\({ a }^{ 2 }\)
According to the question,
6\({ a }^{ 2 }\)= 600
⇒ \({ a }^{ 2 }\) = \(\frac { 600 }{ 6 } \)
⇒ \({ a }^{ 2 }\) = 100
⇒ a = \(\sqrt { 100 } \)
⇒ a = 10 cm
Hence, the side of the cube is 10 cm.

Question 4.
Rukhsar painted the outside of the cabinet of measure 1 m x 2 m x 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?

Solution.

Question 5.
Daniel is painting the walls and ceiling of a cuboidal hall with length, breadth, and height of 15 m, 10 m and 7 m respectively. From each can of paint 100 \({ m }^{ 2 }\) of area is painted.
How many cans of paint will she need to paint the room?
Solution.
l = 15 m
b = 10 m
h = 7 m
Surface area to be painted

Hence, she will need 5 cans of paint to paint the room.

Question 6.
Describe how the two figures at the right are alike and how they are different. Which box has a larger lateral surface area?

Solution.
Similarity → Both have the same heights.
Difference → One is a cylinder, the other is a cube;
The cylinder is a solid obtained by revolving a rectangular area about its one side whereas a cube is a solid enclosed by six square faces; a cylinder has two circular faces whereas a cube has six square faces.

Question 7.
A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How many sheets of metal is required?

Solution.

Question 8.
The lateral surface area of a hollow cylinder is 4224 \({ cm }^{ 2 }\). It is cut along its height and formed a rectangular sheet of width 33 cm. Find the perimeter of rectangular sheet?
Solution.
Lateral surface area of the hollow cylinder = 4224 \({ cm }^{ 2 }\)

Question 9.
A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and length is 1 m.
Solution.
Diameter of the road roller = 84 cm

Question 10.
A company packages its milk powder in the cylindrical container whose base has a diameter of 14 cm and height 20 cm. The company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label?
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.3, drop a comment below and we will get back to you at the earliest.

In Online Education NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2.

• Mensuration Class 8 Ex 11.1
• Mensuration Class 8 Ex 11.3
• Mensuration Class 8 Ex 11.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 11
Chapter Name	Mensuration
Exercise	Ex 11.2
Number of Questions Solved	11
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2

Question 1.
The shape of the top surface of a table is a trapezium. Find its area, if its parallel sides are 1 m and 1.2 man the d perpendicular distance between them is 0.8 m.
Solution.
Area of the top surface of the table

= \(\frac { 1 }{ 2 } h(a+b)\)
= \(\frac { 1 }{ 2 } \times 0.8\times (1.2+1)\)
= \(0.88{ m }^{ 2 }\)

Question 2.
The area of a trapezium is 34 cm2 and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the another parallel side.
Solution.
Area of trapezium
= \(\frac { 1 }{ 2 } h(a+b)\)

⇒ \(34=\frac { 1 }{ 2 } \times 4(10+b)\)
⇒ \(34=2\times (10+b)\)
⇒ \(10+b=\frac { 34 }{ 2 } \)
⇒ 10 + b=17
⇒ b = 17 – 10
⇒ b = 7 cm
Hence, the length of another parallel side is 7 cm.

Question 3.
Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC

Solution.
Fence of the trapezium shaped field ABCD = 120 m
⇒ AB + BC + CD + DA = 120
⇒ AB + 48 + 17 + 40 = 120
⇒ AB + 105 = 120
⇒ AB = 120 – 105
⇒ AB = 15 m
∴ Area of the field
= \(\frac { (BC+AD)\times AB }{ 2 } \)
= \(\frac { (48+40)\times 16 }{ 2 } \) = 660 \({ m }^{ 2 }\)

Question 4.
The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.

Solution.
Area of the field
= \(\frac { 1 }{ 2 } d({ h }_{ 1 }+{ h }_{ 2 })\)
= \(\frac { 24\times (8+13) }{ 2 } \) = \(\frac { 24\times 21 }{ 2 } \)
= 12 x 21 = 252\({ m }^{ 2 }\)

Question 5.
The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.
Solution.
Area of the rhombus

= \(\frac { 1 }{ 2 } \times { d }_{ 1 }\times { d }_{ 2 }\)
= \(\frac { 1 }{ 2 } \times 7.5\times 12\)
= 45 \({ m }^{ 2 }\)

Question 6.
Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.
Solution.
Area of the rhombus
= base (b) x altitude (h) = 5
= 5 x 4.8 = 24 \({ cm }^{ 2 }\)

Question 7.
The floor of a building consists of 3,000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor, if the cost per \({ m }^{ 2 }\) is ₹ 4.
Solution.
Area of a tile

Question 8.
Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10,500 \({ m }^{ 2 }\) and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.
Solution.
Let the length of the side along the road be x m. Then, the length of the side along the river is 2x m.
Area of the field = 10,500 square metres

Question 9.
Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.
Solution.
Area of the octagonal surface

Question 10.
There is a pentagonal shaped park as shown in the figure. For finding its area Jyoti and Kavita divided it in two different ways.

Find the area of this park using both ways. Can you suggest some other way of finding its area ?
Solution.

Question 11.
Diagram of the adjacent picture frame has outer dimensions = 24 cm x 28 cm and inner dimensions 16 cm x 20 cm. Find the area of each section of the frame, if the width of each section the same.

Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 11 Mensuration Ex 11.2, drop a comment below and we will get back to you at the earliest.

In Online Education NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.3.

• Comparing Quantities Class 8 Ex 8.1
• Comparing Quantities Class 8 Ex 8.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 8
Chapter Name	Comparing Quantities
Exercise	Ex 8.3
Number of Questions Solved	12
Category	NCERT Solutions

Online Education NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.3

Question 1.
Calculate the amount and compound interest on


Solution.
(a) By using year by year calculation

(b) By using year by year calculation

(c) By using half year by half year calculation

(d) By using half-year by half-year calculation

Question 2.
Kamala borrowed ₹ 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan?
(Hint: Find A for 2 years if interest is compounded yearly and then find SI on the 2nd year amount for \(\frac { 4 }{ 12 } \) year)
Solution.

Question 3.
Fabina borrows ₹ 12,500 at 12% per annum for 3 years at simple interest and Radha borrows the same amount for the same time period at 10% per annum, compounded annually. Who pays more interest and by how much ?
Solution.
For Fabina

Question 4.
I borrowed ₹ 12,000from Jamshed at 6% per annum simple interest for 2 years. Had I borrowed this sum at 6% per annum compound interest, what excess amount would I have to pay?
Solution.
At simple interest
P = ₹ 12000
R = 6% per annum

Question 5.
Vasudevan invested ₹ 60,000 on interest at the rate of 12% per annum compounded half yearly. What amount would he get
(i) after 6 months?
(ii) after 1 year?
Solution.
(i) after 6 months
P = ₹ 60,000
R = 12% per annum

(ii) after 1 year

Question 6.
Arif took a loan of ₹ 80,000 from a bank. If the rate of interest is 10% per annum, find the difference in amounts he would be paying after \(1\frac { 1 }{ 2 } \) years if the interest is
(i) compounded annually
(ii) compounded half yearly
Solution.
(i) compounded annually

(ii) compounded half yearly

Question 7.
Maria invested ₹ 8,000 in business. She would be paid interest at the rate of 5% per annum compounded annually. Find
(i) the amount credited against her name at the end of the second year.
(ii) the interest for the 3rd year.
Solution.
(i)

(ii)

Question 8.
Find the amount and the compound interest on ₹ 10,000 for \(1\frac { 1 }{ 2 } \) years at 10% per annum, compounded half yearly. Would this interest be more than the interest he would get if it was compounded annually?
Solution.

Question 9.
Find the amount which Ram will get on ₹ 4,096 if he gave it for 18 months at \(12\frac { 1 }{ 2 } % \) per annum, interest being compounded half yearly.
Solution.

Question 10.
The population of a place increased to 54,000 in 2003 at a rate of 5% per annum.
(i) find the population in 2001.
(ii) what would he its population in 2005?
Solution.
(i)
Let the population in 2001 be P.
R = 5% p.a.
n = 2 years

(ii)
initial population in 2003

Question 11.
In a Laboratory, the count of bacteria in a certain experiment was increasing at the rate of 2.5% per hour. Find the bacteria at the end of 2 hours, if the count was initially 5,06,000.
Solution.
Initial count of bacteria

Question 12.
A scooter was bought at ₹ 42,000. It’s value depreciated at the rate of 8% per annum. Find its value after one year.
Solution.
Initial value of the scooter

We hope the NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.3, drop a comment below and we will get back to you at the earliest.

In Online Education NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1.

• Exponents and Powers Class 8 Ex 12.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 12
Chapter Name	Exponents and Powers
Exercise	Ex 12.1
Number of Questions Solved	7
Category	NCERT Solutions

Online Education NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1

Question 1.
Evaluate :
(i) \({ 3 }^{ -2 }\)
(ii) \({ -4 }^{ -2 }\)
(iii) \(({ \frac { 1 }{ 2 } ) }^{ -5 }\)
Solution.

Question 2.
Simplify and express the result in power notation with positive exponent.

Solution.

Question 3.
Fmd the value of:

Solution.

Question 4.
Evaluate
(i) \(\frac { { 8 }^{ -1 }\times { 5 }^{ 3 } }{ { 2 }^{ -4 } } \)
(ii) \(({ 5 }^{ -1 }\times { 2 }^{ -1 })\times { 6 }^{ -1 }\)
Solution.

Question 5.
Find the value of m for which \({ 5 }^{ m }+{ 5 }^{ -3 }={ 5 }^{ 5 }\)
Solution.

Question 6.
Evaluate :

Solution.

Question 7.
Simplify:
(i) \(\frac { 25\times { t }^{ -4 } }{ { 5 }^{ -3 }\times 10\times { t }^{ -8 } } \) (t ≠ 0)
(ii) \(\frac { { 3 }^{ -5 }\times { 10 }^{ -5 }\times 125 }{ { 5 }^{ -7 }\times { 6 }^{ -5 } } \)
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1, drop a comment below and we will get back to you at the earliest.

In Online Education NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.2.

• Factorisation Class 8 Ex 14.1
• Factorisation Class 8 Ex 14.3
• Factorisation Class 8 Ex 14.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 14
Chapter Name	Factorisation
Exercise	Ex 14.2
Number of Questions Solved	5
Category	NCERT Solutions

Online Education NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.2

Question 1.
Factorise the following expressions:

Solution.

Question 2.
Factorise:

Solution.

Question 3.
Factorise the expressions:

Solution.

Question 4.
Factorise:

Solution.

Question 5.
Factorise the following expressions:

Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.2, drop a comment below and we will get back to you at the earliest.