Tag: RD Sharma Maths Solutions Class 10

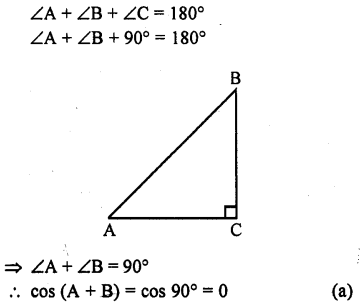
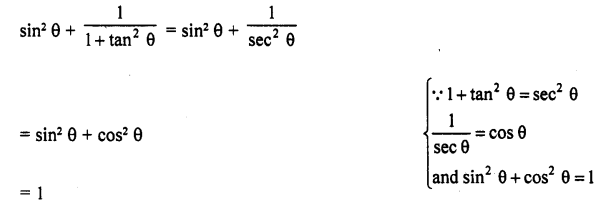
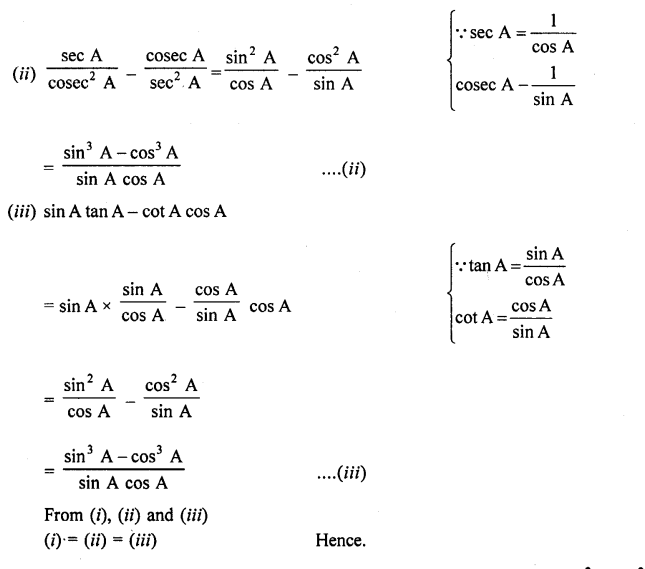
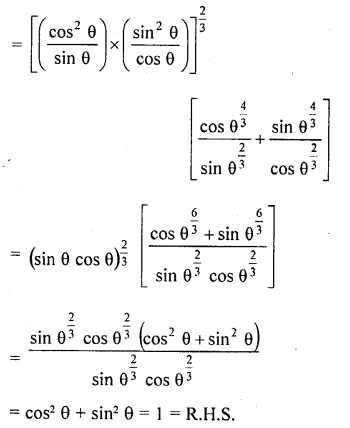
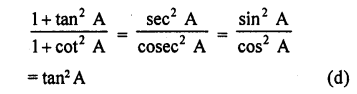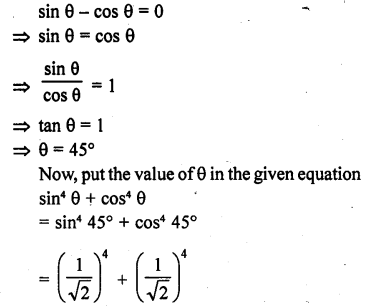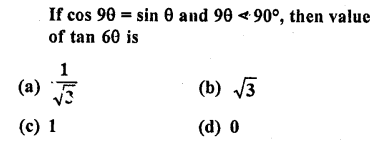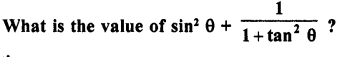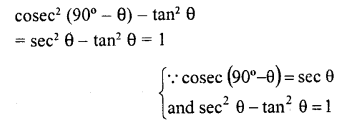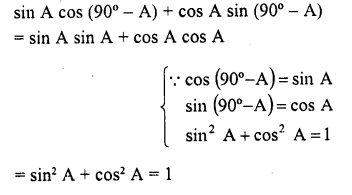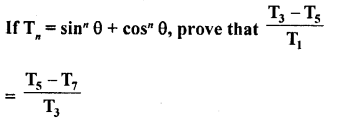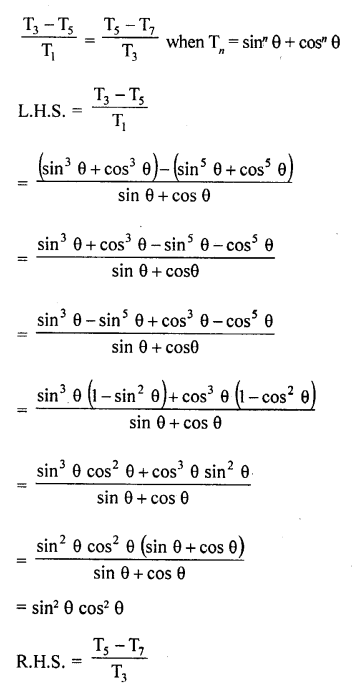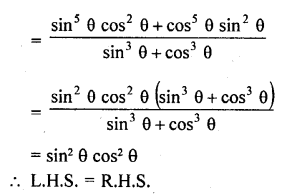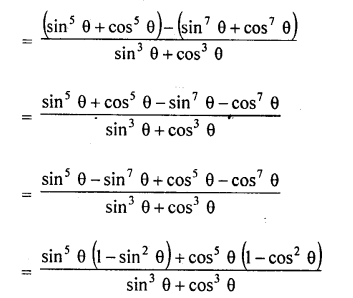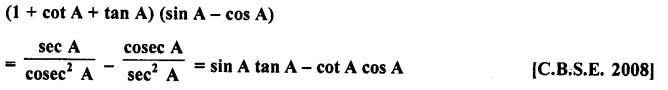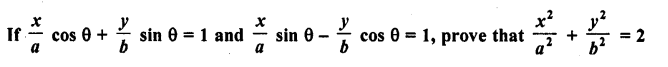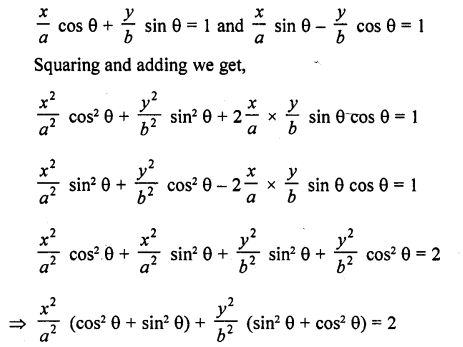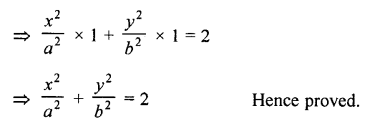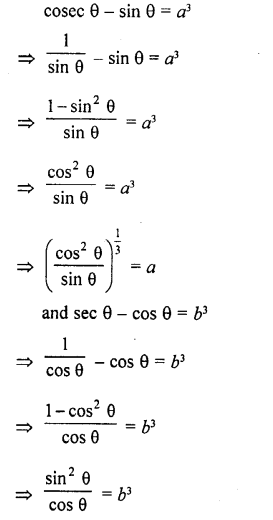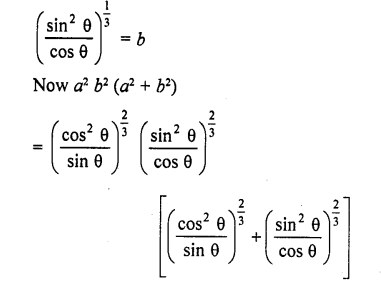RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.1
• RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2
• RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.3

Question 1.
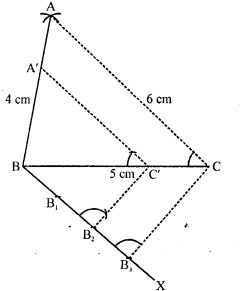
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are (2/3) of the corresponding sides of it.
Solution:
Steps of construction :
(i) Draw a line segment BC = 5 cm.
(ii) With centre B and radius 4 cm and with centre C and radius 6 cm, draw arcs intersecting each other at A.
(iii) Join AB and AC. Then ABC is the triangle.
(iv) Draw a ray BX making an acute angle with BC and cut off 3 equal parts making BB₁ = B₁B₂= B₂B₃.
(v) Join B₃C.
(vi) Draw B’C’ parallel to B₃C and C’A’ parallel to CA then ΔA’BC’ is the required triangle.

Question 2.
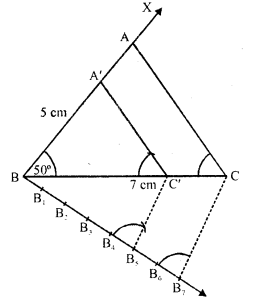
Construct a triangle similar to a given ΔABC such that each of its sides is (5/7)^th of the corresponding sides of ΔABC. It is given that AB = 5 cm, BC = 7 cm and ∠ABC = 50°.
Solution:
Steps of construction :
(i) Draw a line segment BC = 7 cm.
(ii) Draw a ray BX making an angle of 50° and cut off BA = 5 cm.
(iii) Join AC. Then ABC is the triangle.
(iv) Draw a ray BY making an acute angle with BC and cut off 7 equal parts making BB, =B₁B₂=B₂B₃=B₃B₄=B₄B_s=B₅B₆=B₆B₇
(v) Join B₇ and C
(vi) Draw B₅C’ parallel to B₇C and C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.

Question 3.
Construct a triangle similar to a given ∠ABC such that each of its sides is \(\frac { 2 }{ 3 }\)rd of the corresponding sides of ΔABC. It is given that BC = 6 cm, ∠B = 50° and ∠C = 60°.
Solution:
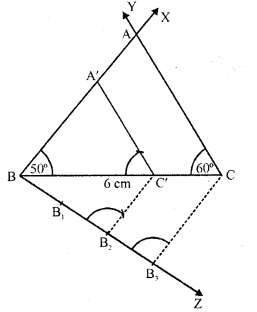
Steps of construction :
(i) Draw a line segment BC = 6 cm.
(ii) Draw a ray BX making an angle of 50° and CY making 60° with BC which intersect each other at A. Then ABC is the triangle.
(iii) From B, draw another ray BZ making an acute angle below BC and intersect 3 equal parts making BB₁ =B₁B₂ = B₂B₂
(iv) Join B₃C.
(v) From B₂, draw B₂C’ parallel to B₃C and C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.

Question 4.
Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to \(\frac { 3 }{ 4 }\)th of the corresponding sides of ΔABC.
Solution:
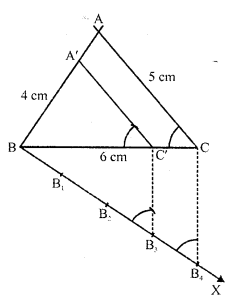
Steps of construction :
(i) Draw a line segment BC = 6 cm.
(ii) With centre B and radius 4 cm and with centre C and radius 5 cm, draw arcs’intersecting eachother at A.
(iii) Join AB and AC. Then ABC is the triangle,
(iv) Draw a ray BX making an acute angle with BC and cut off 4 equal parts making BB₁=  B₁B₂ = B₂B₃ = B₃B₄.
(v) Join B₄ and C.
(vi) From B₃C draw C₃C’ parallel to B₄C and from C’, draw C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.

Question 5.
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac { 7 }{ 5 }\) of the corresponding sides of the first triangle.
Solution:
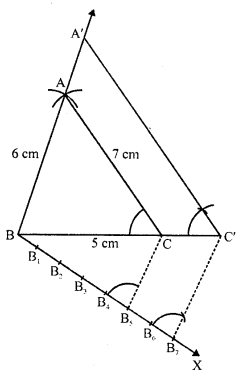
Steps of construction :
(i) Draw a line segment BC = 5 cm.
(ii) With centre B and radius 6 cm and with centre C and radius 7 cm, draw arcs intersecting eachother at A.
(iii) Join AB and AC. Then ABC is the triangle.
(iv) Draw a ray BX making an acute angle with BC and cut off 7 equal parts making BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇.
(v) Join B₅ and C.
(vi) From B₇, draw B₇C’ parallel to B₅C and C’A’ parallel CA. Then ΔA’BC’ is the required triangle.

Question 6.
Draw a right triangle ABC in which AC = AB = 4.5 cm and ∠A = 90°. Draw a triangle similar to ΔABC with its sides equal to (\(\frac { 5 }{ 4 }\))th ot the corresponding sides of ΔABC.
Solution:
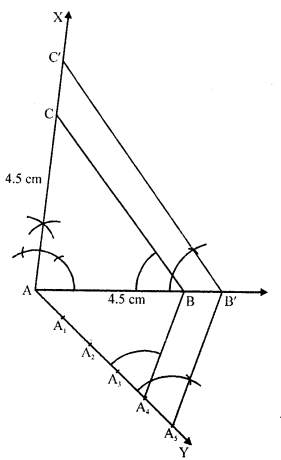
Steps of construction :
(i) Draw a line segment AB = 4.5 cm.
(ii) At A, draw a ray AX perpendicular to AB and cut off AC = AB = 4.5 cm.
(iii) Join BC. Then ABC is the triangle.
(iv) Draw a ray AY making an acute angle with AB and cut off 5 equal parts making AA₁ = A₁A₂ = A₂A₃ =A₃A₄ = A₄A₅
(v) Join A₄ and B.
(vi) From 45, draw 45B’ parallel to  A₄B and  B’C’ parallel to BC.
Then ΔAB’C’ is the required triangle.

Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 5 cm and 4 cm. Then construct another triangle whose sides are \(\frac { 5 }{ 3 }\) times the corresponding sides of the given triangle.  (C.B.S.E. 2008)
Solution:
Steps of construction :
(i) Draw a line segment BC = 5 cm.
(ii) At B, draw perpendicular BX and cut off BA = 4 cm.
(iii )join Ac , then ABC is the triangle
(iv) Draw a ray BY making an acute angle with BC, and cut off 5 equal parts making BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
(v) Join B₃ and C.
(vi) From B₅, draw B₅C’ parallel to B₃C and C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.

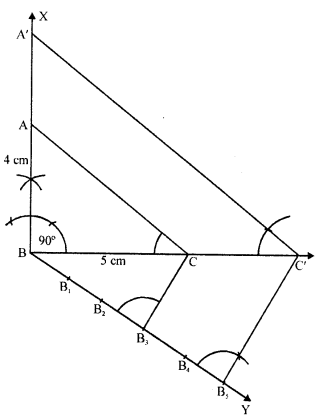
Question 8.
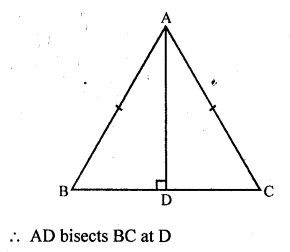
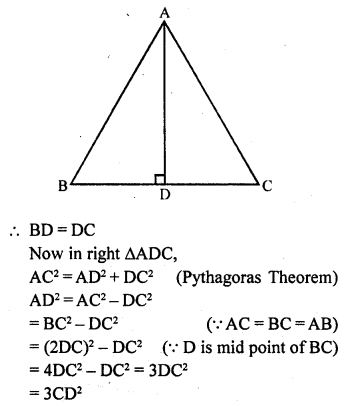
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are \(\frac { 3 }{ 2 }\) times the corresponding sides of the isosceles triangle.
Solution:
Steps of construction :
(i) Draw a line segment BC = 8 cm and draw its perpendicular bisector DX and cut off DA = 4 cm.
(ii) Join AB and AC. Then ABC is the triangle.
(iii) Draw a ray DY making an acute angle with OA and cut off 3 equal parts making DD₁ = D₁D₂ =D₂D₃ = D₃D₄
(iv) Join D₂
(v) Draw D₃A’ parallel to D₂A and A’B’ parallel to AB meeting BC at C’ and B’ respectively.
Then ΔB’A’C’ is the required triangle.

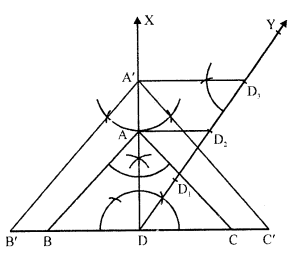
Question 9.
Draw a ΔABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a trianglewhose sides are \((\frac { 3 }{ 4 } )\)th of the corresponding sides of the ΔABC.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6 cm.
(ii) At B, draw a ray BX making an angle of 60° with BC and cut off BA = 5 cm.
(iii) Join AC. Then ABC is the triangle.
(iv) Draw a ray BY making an acute angle with BC and cut off 4 equal parts making BB₁= B₁B₂  B₂B₃=B₃B₄.
(v) Join B₄ and C.
(vi) From B₃, draw B₃C’ parallel to B₄C and C’A’ parallel to CA.
Then ΔA’BC’ is the required triangle.

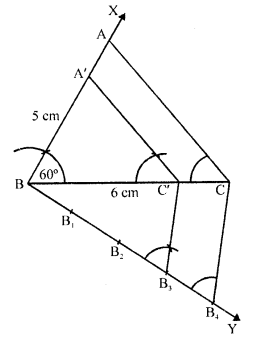
Question 10.
Construct a triangle similar to ΔABC in which AB = 4.6 cm, BC = 5.1 cm,∠A = 60° with scale factor 4 : 5.
Solution:
Steps of construction :
(i) Draw a line segment AB = 4.6 cm.
(ii) At A, draw a ray AX making an angle of 60°.
(iii) With centre B and radius 5.1 cm draw an arc intersecting AX at C.
(iv) Join BC. Then ABC is the triangle.
(v) From A, draw a ray AX making an acute angle with AB and cut off 5 equal parts making AA₁ = A₁A₂ = A₂A₃ = A₃A₄=A₄A₅.
(vi) Join A₄ and B.
(vii) From A₅, drawA₅B’ parallel to A₄B and B’C’ parallel to BC.
Then ΔC’AB’ is the required triangle.

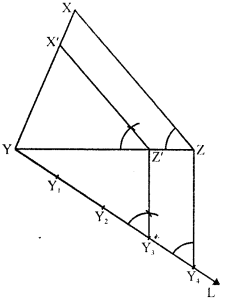
Question 11.
Construct a triangle similar to a given ΔXYZ with its sides equal to \((\frac { 3 }{ 2 })\) th of the corresponding sides of ΔXYZ. Write the steps of construction.                      [CBSE 1995C]
Solution:
Steps of construction :
(i) Draw a triangle XYZ with some suitable data.
(ii) Draw a ray YL making an acute angle with XZ and cut off 5 equal parts making YY₁= Y₁Y₂ = Y₂Y₃ = Y₃Y₄.
(iii) Join Y₄ and Z.
(iv) From Y₃, draw Y₃Z’ parallel to Y₄Z and Z’X’ parallel to ZX.
Then ΔX’YZ’ is the required triangle.

Question 12.
Draw a right triangle in which sides (other than the hypotenuse) are of lengths 8 cm and 6 cm. Then construct another triangle whose sides are \(\frac { 3 }{ 4 }\) times the corresponding sides of the first triangle.
Solution:
(i) Draw right ΔABC right angle at B and BC = 8 cm and BA = 6 cm.
(ii) Draw a line BY making an a cut angle with BC and cut off 4 equal parts.
(iii) Join 4C and draw 3C’ || 4C and C’A’ parallel to CA.
The BC’A’ is the required triangle.

Question 13.
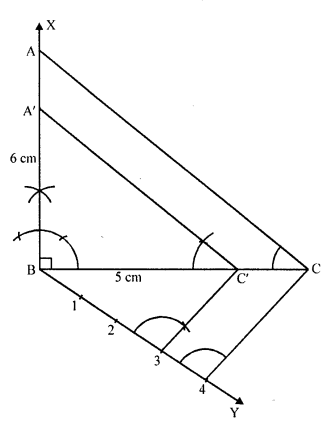
Construct a triangle with sides 5 cm, 5.5 cm and 6.5 cm. Now construct another triangle, whose sides are 3/5 times the corresponding sides of the given triangle. [CBSE 2014]
Solution:
Steps of construction:
(i) Draw a line segment BC = 5.5 cm.
(ii) With centre B and radius 5 cm and with centre C and radius 6.5 cm, draw arcs which intersect each other at A
(iii) Join BA and CA.
ΔABC is the given triangle.
(iv) At B, draw a ray BX making an acute angle and cut off 5 equal parts from BX.
(v) Join C5 and draw 3D || 5C which meets BC at D.
From D, draw DE || CA which meets AB at E.
∴ ΔEBD is the required triangle.

Question 14.
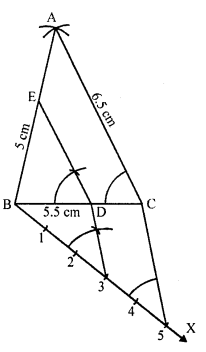
Construct a triangle PQR with side QR = 7 cm, PQ = 6 cm and ∠PQR = 60°. Then construct another triangle whose sides are 3/5 of the corresponding sides of ΔPQR. [CBSE 2014]
Solution:
Steps of construction:
(i) Draw a line segment QR = 7 cm.
(ii) At Q draw a ray QX making an angle of 60° and cut of PQ = 6 cm. Join PR.
(iii) Draw a ray QY making an acute angle and cut off 5 equal parts.
(iv) Join 5, R and through 3, draw 3, S parallel to 5, R which meet QR at S.
(v) Through S, draw ST || RP meeting PQ at T.
∴ ΔQST is the required triangle.

Question 15.
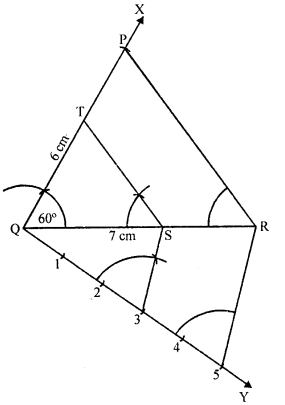
Draw a ΔABC in which base BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are \(\frac { 3 }{ 4 }\) of the corresponding sides of ΔABC.    [CBSE 2017]
Solution:
Steps of construction:

1. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
2.  Draw a ray BX, which makes an acute angle ∠CBX below the line BC.
3. Locate four points B₁, B₂, B₃and B₄ on BX such that BB₁ = B₁B₂=B₂B₃ = B₃B₄.
4. Join B₄C and draw a line through B₃ parallel to B₄C intersecting BC to C’.
5. Draw a line through C’ parallel to the line CA to intersect BA at A’.

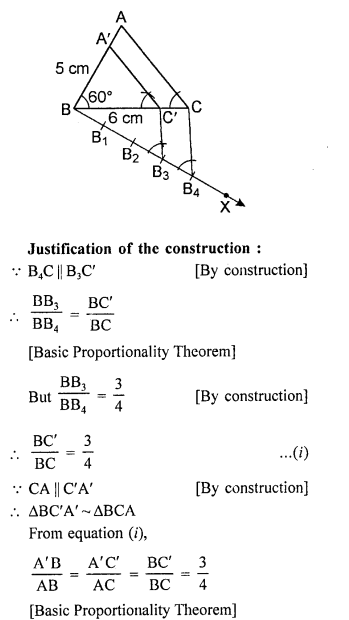
Question 16.
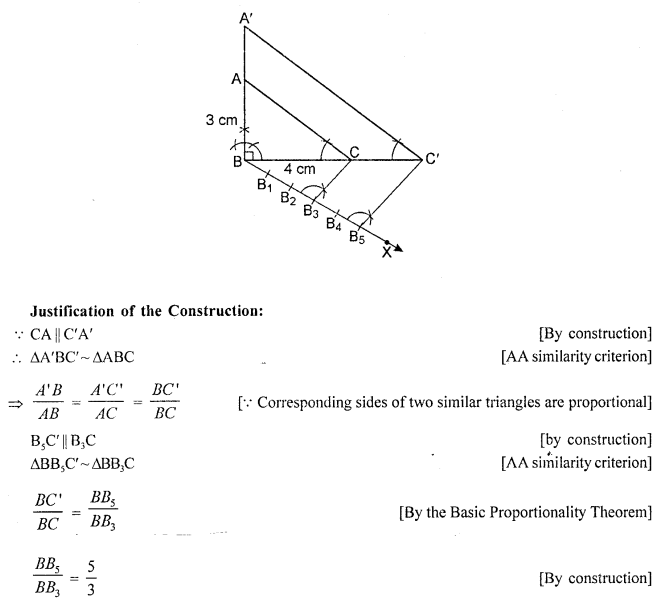
Draw a right triangle in which the sides (other than the hypotenuse) arc of lengths 4 cm and 3 cm. Now, construct another triangle whose sides are \(\frac { 5 }{ 3 }\) times the corresponding sides of the given triangle. [CBSE 2017]
Solution:
Steps of construction:

1. Draw a right triangle ABC in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. ∠B = 90°.
2. Draw a line BX, which makes an acute angle ∠CBX below the line BC.
3. Locate 5 points B₁, B₂, B₃, B₄ and B₅ on BX such that BB₁ = B₁B₂=B₂B₃=B₃B₄=B₄B₅.
4. Join B₃ to C and draw a line through B₅ parallel to B₃C, intersecting the extended line segment BC at C’.
5. Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’.

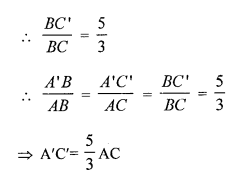
Question 17.
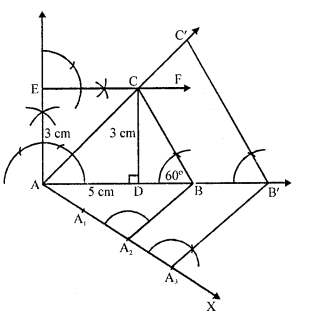
Construct a ΔABC in which AB = 5 cm, ∠B = 60°, altitude CD = 3 cm. Construct a ΔAQR similar to ΔABC such that side of ΔAQR is 1.5 times that of the corresponding sides of ΔACB.
Solution:
Steps of construction :
(i) Draw a line segment AB = 5 cm.
(ii) At A, draw a perpendicular and cut off AE = 3 cm.
(iii) From E, draw EF || AB.
(iv) From B, draw a ray making an angle of 60 meeting EF at C.
(v) Join CA. Then ABC is the triangle.
(vi) From A, draw a ray AX making an acute angle with AB and cut off 3 equal parts making A A₁= A₁A₂ = A₂A₃.
(vii) Join A₂ and B.
(viii) From A , draw A^B’ parallel to A₂B and B’C’ parallel toBC.
Then ΔC’AB’ is the required triangle.

Hope given RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1
• RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2
• RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS
• RD Sharma Class 10 Solutions Chapter 8 Circles MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
In the figure, PA and PB are tangents to the circle drawn from an external point P. CD is a third tangent touching the circle at Q. If PB = 10 cm and CQ = 2 cm, what is the length PC ?

Solution:
In the figure, PA and PB are the tangents to the circle drawn from P
CD is the third tangent to the circle drawn at Q
PB = 10 cm, CQ = 2 cm

PA and PB are tangents to the circle
PA = PB = 10 cm
Similarly CQ and CA are tangents to the circle
CQ = CA = 2 cm
PC = PA – CA = 10 – 2 = 8 cm

Question 2.
What is the distance between two parallel tangents of a circle of radius 4 cm ?
Solution:
TT’ and SS’ are two tangents of a circle with centre O and radius 4 cm and TT’ || SS’
OP and OQ are joined

Now OP is the radius and TPT’ is the tangent
OP ⊥ TPT’
Similar OQ ⊥ SS’
But TT’ || SS’
POQ is the diameter
Which is 4 x 2 = 8 cm
Distance between the two parallel tangents is 8 cm

Question 3.
The length of tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What is the radius of the circle ?
Solution:
PA is a tangent to the circle from P at a distance of 5 cm from the centre O
PA = 4 cm
OA is joined and let OA = r

Now in right ∆OAP,
OP² = OA² + PA²
=> (5)² = r² + (4)²
=> 25 = r + 16
=> r² = 25 – 16 = 9 = (3)²
r = 3
Radius of the circle = 3 cm

Question 4.
Two tangents TP and TQ are drawn from an external point T to a circle with centre O as shown in the following figure. If they are inclined to each other at an angle of 100°, then what is the value of ∠POQ ?

Solution:
TP and TQ are the tangents from T to the circle with centre O and ∠PTQ = 100°
OT, OP and OQ are joined
OP and OQ are radius
OP ⊥ PT and OQ ⊥ QT
Now in quadrilateral OPTQ,
∠POQ + ∠OPT + ∠PTQ + ∠OQT = 360° (Sum of angles of a quadrilateral)
=> ∠POQ + 90° + 100° + 90° = 360°
=> ∠POQ + 280° = 360°
=> ∠POQ = 360° – 280° = 80°
Hence ∠POQ = 80°

Question 5.
What is the distance between two parallel tangents to a circle of radius 5 cm?
Solution:
In a circle, the radius is 5 cm and centre is O

TT’ and SS’ are two tangents at P and Q to the circle
Such that TT’ || SS’
Join OP and OQ
OP is radius and TPT’ is the tangent
OP ⊥ TT’
Similarly OQ ⊥ SS’
POQ is the diameter of the circle
Now length of PQ = OP + OQ = 5 + 5 = 10 cm
Hence distance between the two parallel tangents = 10 cm

Question 6.
In Q. No. 1, if PB = 10 cm, what is the perimeter of ∆PCD ?
Solution:
In the figure, PB = 10 cm, CQ = 2 cm

PA and PB are tangents to the give from P
PA = PB = 10 cm
Similarly, CA and CQ are the tangents
CA = CQ = 2 cm
and DB and DQ are the tangents
DB = DQ
Now, perimeter of ∆PCD
PC + PD + CQ + DQ
= PC + CQ + PD + DQ
= PC + CA + PD + DB {CQ = CA and DQ = DB}
= PA + PB = 10 + 10 = 20 cm

Question 7.
In the figure, CP and CQ are tangents to a circle with centre O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then find the length of BR. (C.B.S.E. 2009)

Solution:
Given : In the figure, CP and CQ are tangents to a circle with centre O
ARB is a third tangent to the circle at R
CP = 11 cm, BC = 7 cm

To find : The length of BR
BQ and BR are tangents to the circle drawn from B
BQ = BR ….(i)
Similarly CQ = CP
=> BC + BQ = CP = 11 (CP = 11 cm and BC = 7 cm)
=> 7 + BQ = 11
=> BQ = 11 – 7
BQ = 4 cm
But BQ = BR
BR = 4 cm

Question 8.
In the figure, ∆ABC is circumscribing a circle. Find the length of BC. (C.B.S.E. 2009)

Solution:
∆ABC is circumscribing a circle which touches it at P, Q and R
AC = 11 cm, AR = 4 cm, BR = 3 cm
Now we have to find BC
AR and AQ are tangents to the circle from A
AQ = AR = 4 cm
Then CQ = AC – AQ = 11 – 4 = 7 cm
Similarly,
CP and CQ are tangents from C
CP = CQ = 7 cm
and BP and BR are tangents from B
BP = BR = 3 cm
Now BC = BP + CP = 3 + 7 = 10 cm

Question 9.
In the figure, CP and CQ are tangents from an external point C to a circle with centre O. AB is another tangent which touches the circle at R. If CP = 11 cm and BR = 4 cm, find the length of BC. [CBSE 2010]

Solution:
CP and CQ are the tangents to the circle from C.
AB is another tangent to the same circle which touches at R and meets the first two tangents at A and B. O is the centre of the circle.
OC is joined
CP = 11 cm, BR = 4 cm
CP and CQ are tangents to the circle
CP = CQ = 11 cm
Similarly from B, CR and BQ are the tangents
BQ = BR = 4 cm
Now BC = CQ – BQ = 11 – 4 = 7 cm

Question 10.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
Two concentric circles with centre O, have radii 5 cm and 3 cm
AB is a chord which touches the smaller circle at P
OP is joined which is radius of smaller circle

P is mid-point of AB
OP = 3 cm and OA = 5 cm
Now in right ∆OAP
OA² = OP² + AP²
(5)² = (3)² + AP²
=> 25 = 9 + AP²
=> AP² = 25 – 9 = 16 = (4)²
AP = 4 cm
AB = 2 AP = 2 x 4 cm = 8 cm

Question 11.
In the given figure, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB. [CBSE 2015]

Solution:
In the given figure,
PA and PB are tangents to the circle from P
PA = PB
∠APB = 50°, OA is joined
To find ∠OAB
In ∆PAB
PA = PB

Question 12.
In the figure, PQ is a chord of a circle and PT is the tangent at P such that ∠QPT = 60°. Then, find ∠PRQ. [NCERT Exemplar]

Solution:
∠OPQ = ∠OQP = 30°, i.e., ∠POQ = 120°
Also, ∠PRQ = \(\frac { 1 }{ 2 }\) reflex ∠POQ

Question 13.
In the figure, PQL and PRM are tangents to the circle with centre O at the points Q and R respectively and S is a point on the circle such that ∠SQL = 50° and ∠SRM = 60°. Then, find ∠QSR. [NCERT Exemplar]

Solution:
Here ∠OSQ = ∠OQS = 90° – 50° = 40°
and ∠RSO = ∠SRO = 90° – 60° = 30°.
Therefore, ∠QSR = 40° + 30° = 70°

Question 14.
In the figure, BOA is a diameter of a circle and the tangent at a point P meets BA produced at T. If ∠PBO = 30°, then find ∠PTA. [NCERT Exemplar]

Solution:
As ∠BPA = 90°,
∠PAB = ∠OPA = 60°
Also OP ⊥ PT.
Therefore, ∠APT = 30°
and ∠PTA = 60° – 30° = 30°

Hope given RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios VSAQS
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :

Question 1.
Write the maximum and minimum values of sin θ.
Solution:
Maximum value of sin θ = 1
and minimum value of sin θ = 0

Question 2.
Write the maximum and minimum values of cos 0.
Solution:
Maximum value cos θ=1 and minimum value of cos θ = θ

Question 3.
What is the maximum value of \(\frac { 1 }{ sec\theta }\) ?
Solution:
Maximum value of \(\frac { 1 }{ sec\theta }\) or cos θ = 1

Question 4.
What is the maximum value of \(\frac { 1 }{ cosec\theta }\)
Solution:
Maximum value of \(\frac { 1 }{ cosec\theta }\) or sin θ = 1

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.
If tan A = \(\frac { 3 }{ 4 }\) and A + B = 90°, then what is the value of cot B ?
Solution:

Question 11.
If A + B = 90°, cos B = \(\frac { 3 }{ 5 }\), what is the value of sin A.
Solution:

Question 12.
Write the acute angle θ satisfying √3 sin θ = cos θ.
Solution:

Question 13.
Write the Value of cos 1° cos 2° cos 3° ……. cos 179° cos 180°.
Solution:

Question 14.
Write the Value of tan 10′ tan 15° tan 75° tan 80°.
Solution:

Question 15.
If A + B = 90° and tan A = \(\frac { 3 }{ 4 }\) what is cot B?
Solution:

Question 16.
If tan A = \(\frac { 5 }{ 12 }\), find the value of (sin A + cos A) sec A. (C.B.S.E. 2008)
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.1
• RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.2
• RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.3

Question 1.
Determine a point which divides a line segment of length 12 cm internally in the ratio 2 : 3. Also justify your construction.
Solution:
Steps of construction :
(i) Draw a line segment AB = 12 cm.
(ii) Draw a ray AX at A making an acute angle with AB.
(iii) From B, draw another ray BY parallel to AX.
(iv) Cut off 2 equal parts from AX and 3 equal parts from BY.
(v) Join 2 and 3 which intersects AB at P.
P is the required point which divides AB in the ratio of 2 : 3 internally.

Question 2.
Divide a line segment of length 9 cm internally in the ratio 4 : 3. Also, give justification of the construction.
Solution:
Steps of construction :
(i) Draw a line segment AB = 9 cm.
(ii) Draw a ray AX making an acute angle with AB.
(iii) From B, draw another ray BY parallel to AX.
(iv) Cut off 4 equal parts from AX and 3 parts from BY.
(v) Join 4 and 3 which intersects AB at P.
P is the required point which divides AB in the ratio of 4 : 3 internally.

Question 3.
Divide a line segment of length 14 cm internally in the ratio 2 : 5. Also justify your construction.
Solution:
Steps of construction :
(i) Draw a line segment AB = 14 cm.
(ii) Draw a ray AX making an acute angle with AB.
(iii) From B, draw another ray BY parallel to AX.
(iv) From AX, cut off 2 equal parts and from B, cut off 5 equal parts.
(v) Join 2 and 5 which intersects AB at P.
P is the required point which divides AB in the ratio of 2 : 5 internally.

Question 4.
Draw a line segment of length 8 cm and divide it internally in the ratio 4 : 5.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8 cm.
(ii) Draw a ray AX making an acute angle with ∠BAX = 60° withAB.

(iii) Draw a ray BY parallel to AX by making an acute angle ∠ABY = ∠BAX.
(iv) Mark four points A₁, A₂, A₃, A₄ on AX and five points B₁, B₂, B₃, B₄, B_s on BY in such a way that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ .
(v) Join A₄B₅.
(vi) Let this line intersect AB at a point P.
Thus, P is the point dividing the line segment AB internally in the ratio of 4 : 5.

 

Hope given RD Sharma Class 10 Solutions Chapter 9 Constructions Ex 9.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Mark the correct alternative in each of the folloiwng :
Question 1.
If sec θ + tan θ = x, then sec θ =

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.
sec⁴ A – sec² A is equal to
(a) tan² A – tan⁴ A
(b) tan⁴ A – tan² A
(c) tan⁴ A + tan² A          
(d) tan² A + tan⁴ A
Solution:

Question 6.
cos⁴ A – sin⁴ A is equal to
(a) 2 cos² A + 1        
(b) 2 cos² A – 1
(c) 2 sin² A – 1           
 (d) 2 sin² A + 1
Solution:
cos⁴ A – sin⁴ A = (cos² A + sin² A) (cos² A – sin² A)
= 1 (cos² A – sin² A) = cos² A – (1 – cos² A)
= cos² A – 1 + cos² A
= 2 cos² A – 1            (b)

Question 7.

Solution:

Question 8.

Solution:

Question 9.
The value of (1 + cot θ – coscc θ) (1 + tan θ + sec θ) is
(a) 1                          
(b) 2
(c) 4                          
(d) 0
Solution:

Question 10.

Solution:

Question 11.
(cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ) is equal 
(a) 0                          
(b) 1
(c) -1
(d) None of these
Solution:

Question 12.
If x = a cos θ and y = b sin θ, then b²x² + a²y² =
(a) a²b²                             
(b) ab
(c) a⁴b⁴                      
(d) a² + b²
Solution:
x = a cos θ, y = b sin θ                       …(i)
bx = ab cos θ, ay = ab sin θ          ….(ii)
Adding (i) and (ii) we get,
b²x²+ a²y² = a²b² cos²  θ + a²b² sin²  θ
= a²b² (cos²  θ + sin²  θ)
= a²b² x 1
= a²b²                         (a)

Question 13.
If x = a sec θ and y-b tan θ, then b²x² – a²y²
(a) ab
(b) a² – b²
(c) a² + b²
(d) a²b²
Solution:
x = a sec θ and y = b tan θ
b²x² – a²y² = b² (a sec θ)² – a² (b tan θ)²
= a²b² sec² θ – a²b² tan²  θ
= a²b² (sec²  θ – tan²  θ)
= a²b² x 1
= a²b²                       (d)

Question 14.

Solution:

Question 15.
2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) is equal to
(a) 0                
(b) 1
(c) -1               
(d) None of these
Solution:
.

Question 16.
If a cos θ + b sin θ = 4 and a sin θ – b cos θ = 3, then a² + b² =
(a) 7                 
(b) 12
(c) 25                         
(d) None of these
Solution:
a cos θ + b sin θ = 4
a sin θ – b cos θ = 3
Squaring and adding
a² cos²  θ + b²  sin² θ  + 2ab sin θ cos θ=16
a² sin² θ + b²  cos² θ  – 2ab sin θ  cos θ = 9
a² (cos² θ + sin² θ) + b² (sin² θ + cos² θ) = 25 (∵ sin² θ + cos² θ=1)
⇒ a² x 1 + b² x 1 = 25
⇒  a² + b² = 25                                           (c)

Question 17.
If a cot θ + b cosec θ = p and b cot θ + a cosec θ = q, then p² – q² =
(a)   a² – b²                  
(b) b² – a²
(c)  a² + b²                  
(d)  b – a
Solution:
a cot θ + b cosec θ = p
b cot θ + a cosec θ = q
Squaring and subtracting,
p² – q²  = (a cot θ + b cosec θ)² – (b cot θ + a cosec θ)²
= a² cot² θ + b² cosec² θ + 2ab cot θ cosec θ – (b² cot² θ + a² cosec² θ + 2ab cot θ cosec θ)
= a² cot² θ +  b²  cosec² θ + lab cot θ cosec θ – b² cot²  θ – a² cosec² θ – lab cot θ cosec θ
= a² (cot² θ – cosec² θ) + b² (cosec² θ – cot^{2 θ})
= -a² (cosec² θ – cot² θ) + b² (cosec² θ – cot² θ)
= -a² x 1 + b² x 1 = b² – a²                                    (b)

Question 18.
The value of sin² 29° + sin² 61° is
(a) 1
(b) 0
(c) 2sin² 29“                 
(d)  2cos² 61°
Solution:
sin² 29° + sin² 61° = sin² 29° + sin² (99° – 29°)
= sin² 29 + cos² 29°              (a)
(sin² θ + cos² θ=1)

Question 19.
If x = r sin θ cos φ, y = r sin θ sin φ and z – r cos θ, then
(a) x² +y² + z² = r²      
(b)   x² +y² – z² = r²
(c) x²– y²+ z² = r²      
(d)   z² + y² – x² = r²
Solution:

Question 20.
If sin θ + sin²  θ=1, then cos²  θ + cos⁴  θ
(a) -1                         
(b) 1
(c) 0                           
(d) None of these
Solution:
sin θ + sin² θ=1
⇒ sin θ = 1- sin² θ
⇒ sin θ = cos² θ
cos² θ + cos⁴ θ = sin θ + sin² θ     {∵ cos² θ = sin θ}
⇒  cos² θ + cos⁴ θ=1                                 (b)
{∵ sin θ + sin² θ = 1 (given)}

Question 21.
If a cos θ + b sin θ = m and a sin θ – b cos θ = it, then a² + b² =
(a) m² – it²        
(b) m²n²
(c) n² – m²        
(d) m² + n²
Solution:
a cos θ + b sin θ = m
a sin θ – b cos θ = n
Squaring and adding
a² cos² θ + b² sin² θ   + lab sin  θ cos θ = m²
a² sin² θ + b² cos² θ   – 2ab sin  θ cos θ = n²
a² (cos² θ + sin² θ) + b² (sin² θ + cos² θ) = m² + n²     {sin² θ + cos² θ=1}
⇒   a² + 1 + b² x 1 = m² – n²
⇒  a² + b² = m² + n²
Hence a² + b² = m² + n²          (d)

Question 22.
If cos A + cos² A = 1, then sin² A + sin⁴ A = 
(a) -1                         
(b) 0                            
(c) 1                           
(d) None of these
Solution:
cos A + cos² A = 1
⇒ cos A = 1 – cos² A
⇒  cos A = sin² A
Now, sin² A + sin⁴ A = cos A + cos² A = 1 (∵ cos A + cos² A = 1) (given)
∴ sin² A + sin⁴ A = 1                              (c)

Question 23.

Solution:

Question 24.

Solution:

Question 25.
9sec² A – 9tan² A is equal to
(a) 1
(b) 9
(c) 8                           
(d) 0
Solution:
9sec² A – 9tan² A = 9 (sec² A – tan² A)
= 9 x 1       (∵ sec² A – tan² A = 1)
= 9                        (b)

Question 26.
(1 + tan θ + sec θ) (1 + cot θ – cosec θ) =
(a) 0
(b) 1
(c) 1                           
(d) -1
Solution:

Question 27.
(sec A + tan A) (1 – sin A) =
(a) sec A
(b) sin A
(c) cosec A                        
(d) cos A
Solution:

Question 28.

Question 29.
If sin θ cos θ = 0, then the value of sin⁴ θ + cos⁴ θ is

Solution:

Question 30.
The value of sin (45° + θ) – cos (45° – θ) is equal to
(a) 2 cos θ                  
(b) 0
(c) 2 sin θ
(d) 1
Solution:
sin (45° + θ) – cos (45° – θ)
= sin (45° + θ) – sin (90° – 45° + θ)
= sin (45° + θ) – sift (45° + θ)
= 0                                                     (b)

Question 31.
If ΔABC is right angled at C, then the value of cos (A + B) is

Solution:

Question 32.

Solution:
cos (9θ) = sin θ
⇒ sin (90° – 9θ) = sin θ
⇒ 90° – 90 = θ
⇒ 9θ = 90°
⇒  θ= 10
tan 6θ = tan 6
= tan 60° = \(\sqrt { 3 } \)        (b)

Question 33.
If cos (α + β) =0 , then sin (α – β) can be reduced to 
(a) cos β
(b) cos 2β
(c) sin α
(d) sin 2α
Solution:
cos (α + β) = 0
⇒ α + β = 90°                       [∵ cos 90° = 0]
⇒  θ = 90° – β                                          …(i)
sin (α – β) = sin (90° – β – β) [using (i)]
= sin (90° – 2β)
= cos 2β [∵ sin (90° – θ) = cos θ]         (b)

Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.1
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.2
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios VSAQS
• RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios MCQS

Question 1.
Evaluate the following :

Solution:

Question 2.
Evaluate the following :

Solution:

Question 3.
Express each one of the following in terms of trigonometric ratios of angles lying between 0° and 45°
(i) sin 59° + cos 56°
(ii) tan 65° + cot 49“
(iii) sec 76° + cosec 52°
(iv) cos 78° + sec 78°
(v) cosec 54° + sin 72°
(vi) cot 85″ + cos 75°
(vii) sin 67° + cos 75°
Solution:
(i) sin 59° + cos 56°
= sin (90° – 31°) + cos (90° – 34°)
= cos 31° +sin 34°
(ii) tan 65° + cot 49°
= tan (90° – 25°) + cot (90° – 41°)
= cot 25° + tan 41°
(iii) sec 76° + cosec 52°
= sec (90° – 14°) + cosec (90 0 – 38°)
= cosec 14° + sec 38°
(iv) cos 78° + sec 78°
= cos (90° – 12°) + sec (90°- 12°)
= sin 12° + cosec 12°
(v) cosec 54° + sin 72°
= cosec (90° – 36°) + sin (90°-18°)
= sec 36° + cos 18°
(vi) cot 85° + cos 75°
= cot (90° – 5°) + cos (90° – 15°)
= tan 5° + sin 15°
(vii) sin 67° + cos 75°
= sin (90° – 23°) + cos (90° – 15°)
= cos 23° + sin 15°

Question 4.
Express cos 75° + cot 75° in terms of angles between 0° and 30°.
Solution:
cos 75° + cot 75° = cos (90° – 15°) + cot (90°-15°)
= sin 15° + tan 15°

Question 5.
If sin 3A = cos (A – 26°), where 3A is an acute angle, And the value of A.
Solution:
sin 3A = cos (A – 26°)
⇒ cos (90° – 3A) = cos (A – 26°)
Comparing,
90° – 3A = A – 26°
⇒ 90° + 26° = A + 3A ⇒ 4A = 116°

Question 6.
If A, B, C are the interior angles of a triangle ABC, prove

Solution:

Question 7.
Prove that :

Solution:

Question 8.
Prove the following :

Solution:

Question 9.
Evaluate :


Solution:

Question 10.
If sin θ= cos (θ – 45°), where θ and (θ – 45°) are acute angles, find the degree measure of θ.
Solution:

Question 11.
If A, B, C are the interior angles of a AABC, show that :
(i) \(sin\frac { B+C }{ 2 } cos\frac { A }{ 2 }\)
(ii) \(cos\frac { B+C }{ 2 } sin\frac { A }{ 2 }\)
Solution:

Question 12.
If 2θ + 45° and 30° – θ are acute angles, find the degree measures of θ satisfying sin (20 + 45°) = cos (30° – θ).
Solution:

Question 13.
If θ is a positive acute angle such that sec θ = cosec 60°, And the value of 2 cos2 θ-1.
Solution:

Question 14.
If cos 2 θ – sin 4 θ, where 2 θ and 4 θ are acute angles, find the value of θ.
Solution:

Question 15.
If sin 3 θ = cos (θ – 6°), where 3 θ and θ – 6° are acute angles, find the value of θ.
Solution:

Question 16.
If sec 4A = cosec (A – 20°), where 4A is an acute angle, find the value of A.
Solution:

Question 17.
If sec 2A = cosec (A – 42°), where 2A is an acute angle, find the value of A. (C.B.S.E. 2008)
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 10 Trigonometric Ratios Ex 10.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1
• RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2
• RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS
• RD Sharma Class 10 Solutions Chapter 8 Circles MCQS

Question 1.
Fill in the blanks :
(i) The common point of a tangent and the circle is called ……….
(ii) A circle may have ………. parallel tangents.
(iii) A tangent to a circle intersects it in ……….. point(s).
(iv) A line intersecting a circle in two points is called a …………
(v) The angle between tangent at a point on a circle and the radius through the point is ………..
Solution:
(i) The common point of a tangent and the circle is called the point of contact.
(ii) A circle may have two parallel tangents.
(iii) A tangents to a circle intersects it in one point.
(iv) A line intersecting a circle in two points is called a secant.
(v) The angle between tangent at a point, on a circle and the radius through the point is 90°.

Question 2.
How many tangents can a circle have ?
Solution:
A circle can have infinitely many tangents.

Question 3.
O is the centre of a circle of radius 8 cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB.
Solution:
Radius OA = 8 cm, ST is the tangent to the circle at A and AB = 15 cm

OA ⊥ tangent TS
In right ∆OAB,
OB² = OA² + AB² (Pythagoras Theorem)
= (8)² + (15)² = 64 + 225 = 289 = (17)²
OB = 17 cm

Question 4.
If the tangent at a point P to a circle with centre O cuts a line through O at Q such that PQ = 24 cm and OQ = 25 cm. Find the radius of the circle.
Solution:
OP is the radius and TS is the tangent to the circle at P

OQ is a line
OP ⊥ tangent TS
In right ∆OPQ,
OQ² = OP² + PQ² (Pythagoras Theorem)
=> (25)² = OP² + (24)²
=> 625 = OP² + 576
=> OP² = 625 – 576 = 49
=> OP² = (7)²
OP = 7 cm
Hence radius of the circle is 7 cm

 

Hope given RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Question 1.
If cos θ = \(\frac { 4 }{ 5 }\) , find all other trigonometric ratios of angle θ
Solution:


Question 2.
If sin θ = \(\frac { 1 }{ \sqrt { 2 } }\) , find all other trigono­metric ratios of angle θ
Solution:

Question 3.
If tan θ = \(\frac { 1 }{ \sqrt { 2 } }\), find the value of \(\frac { { cosec }^{ 2 }-{ sec }^{ 2 } }{ { cosec }^{ 2 }+cot^{ 2 } }\) 
Solution:
<

Question 4.
If tan θ = \(\frac { 3 }{ 4 }\), find the value of \(\frac { 1-cosheta }{ 1+cosheta }\) 
 (C.B.S.E. 1995)
Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.
If \(\sqrt { 3 } \) tan θ = 3sin θ , find the value of sin² θ  – cos² θ .          (C.B.S.E. 2001)
Solution:

Question 11.

Solution:

Question 12.
If sin θ + cos θ = \(\sqrt { 2 } \)cos (90° – θ), find cot θ
Solution:

Question 13.
If 2sin² θ – cos² θ = 2, then find the value of θ. [NCERT Exemplar]
Solution:

Question 14.
If \(\sqrt { 3 } \) tan θ-1=0, find the value of sin² – cos² θ. [NCERT Exemplar]
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.2
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS
• RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
Define an identity.
Solution:
An identity is an equation which is true for all values of the variable (s) involved.

Question 2.
What is the value of (1 – cos² θ) cosec² θ?
Solution:

Question 3.
What is the value of (1 + cot² θ) sin² θ ?
Solution:
(1 + cot² θ) sin² θ = cosec² sin² θ                           {1 + cot² θ = cosec² θ}
= (cosec θ sin θ)² = (l)² = 1                                      (∵ sin θ cosec θ=1)

Question 4.

Solution:

Question 5.
If sec θ + tan θ = x, write the value of sec θ – tan θ in terms of x.
Solution:
sec θ+ tan θ = x
We know that
sec² θ – tan² θ=1                                                                    .
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1                               {a² – b² = (a + b) (a – b)}
⇒  x (sec θ – tan θ) = 1
⇒  sec θ – tan θ = \(\frac { 1 }{ x }\)

Question 6.
If cosec θ – cot θ = α, write the value of cosec θ + cot α.
Solution:
cosec θ – cot θ = α
We know that,
cosec²  θ – cot²  θ=1
⇒  (cosec θ – cot θ) (cosec θ + cot θ) = 1
⇒  a (cosec θ + cot θ) = 1                                                {a² – b² = (a + b) (a – 6)}
⇒  cosec θ + cot θ = 1/α

Question 7.
Write the value of cosec² (90° – θ) – tan²θ
Solution:

Question 8.
Write the value of sin A cos (90° – A) + cos A sin (90° – A)
Solution:

Question 9.

Solution:

Question 10.
If x = a sin θ and y = b cos θ, what is the value of b²x² + a²y² ?
Solution:
x = a sin θ, y = b cos θ

Question 11.
If sin θ = \(\frac { 4 }{ 5 }\), What is the value of cot θ + cosec θ ?
Solution:

Question 12.
What is the value of 9 cot²  θ-9 cosec²  θ?
Solution:
9 cot²  θ – 9 cosec²  θ
= -(9cosec²  θ – 9cot²  θ)
= -9 (cosec²  θ – cot² θ) = -9 x 1
= -9                                                       {∵  cosec²  θ – cot² θ=1}

Question 13.

Solution:

Question 14.

Solution:

Question 15.
What is the value of (1 + tan² θ) (1 – sin θ) (1 + sin θ) ?
Solution:

Question 16.
If cos A = \(\frac { 7 }{ 25 }\), find the value of tan A +cot A. (C.B.S.E. 2008)
Solution:

Question 17.
If sin θ = \(\frac { 1 }{ 3 }\), then find the value of 2 cot² θ + 2. (C.B.S.E. 2009)
Solution:

Question 18.
If cos θ = \(\frac { 3 }{ 4 }\), then find the value of 9 tan² θ + 9.
Solution:

Question 19.
If sec²  θ (1 + sin θ) (1 – sin θ) = k, then find the value of k. (C.B.S.E. 2009)
Solution:

Question 20.
If cosec²  θ (1 + cos θ) (1 – cos θ) = λ, then find the value of λ.
Solution:
cosec²  θ (1 + cos θ) (1 – cos θ) = λ
⇒ cosec² θ (1 – cos² θ) = λ                      {(a + b) (a – b) = a¹ – b²)}
⇒  cosec² θ x sin θ = λ             (1 – cos² θ = sin² θ)
⇒ 1 = λ                                      (sin θ cosec θ=1)
∴ λ = 1

Question 21.
If sin² θ cos² θ (1 + tan² θ) (1 + cot² θ) = λ, then find the value of λ.
Solution:
sin² θ cos² θ (1+ tan² θ) (1 + cot² θ) = λ
sin² θ cos² θ (sec² θ) (cosec² θ) = λ

Question 22.


Solution:

Question 23.
If cosec θ = 2x and cot θ = \(\frac { 2 }{ x }\), find the value of 2 ( x² – \(\frac { 1 }{ x2 }\)           [CBSE 2010]
Solution:

Question 24.
Write ‘True’ or ‘False’ and justify your answer in each of the following:
(i) The value of sin θ is x + \(\frac { 1 }{ x }\), where ‘x’ is a positive real number.
(ii) cos θ = \(\frac { { a }^{ 2 }+{ b }^{ 2 } }{ 2ab }\) , where a and b are two lab distinct numbers such that ab > 0.
(iii) The value of cos² 23 – sin² 67 is positive.
(iv) The value of the expression sin 80° – cos 80° is negative.
(v) The value of sin θ + cos θ is always greater than 1.
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.1
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.2
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.3
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.4
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.5
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.6
• RD Sharma Class 10 Solutions Chapter 7 Triangles Ex 7.7
• RD Sharma Class 10 Solutions Chapter 7 Triangles Revision Exercise
• RD Sharma Class 10 Solutions Chapter 7 Triangles VSAQS
• RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS

Mark the correct alternative in each of the following.
Question 1.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3
(b) 4 : 9
(c) 81 : 16
(d) 16 : 81
Solution:
(d) Triangles are similar and the ratio of their sides is 4 : 9
The ratio of the areas of two similar triangles are proportion to the square oT their corresponding sides
Ratio in their areas = (4)² : (9)² = 16 : 81

Question 2.
The areas of two similar triangles are in respectively 9 cm² and 16 cm². The ratio of their corresponding sides is
(a) 3 : 4
(b) 4 : 3
(c) 2 : 3
(d) 4 : 5
Solution:
(a) Ratio in the areas of two similar triangles = 9 cm² : 16 cm² = 9 : 16
The areas of similar triangles are proportional to the squares of their corresponding sides
Ratio in their corresponding sides = √\(\frac { 9 }{ 16 }\) = \(\frac { 3 }{ 4 }\) = 3 : 4

Question 3.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm² and 81 cm² respectively. If the longest side of larger ∆ABC be 36 cm, then. The longest side of the smaller triangle ∆DEF is :
(a) 20 cm
(b) 26 cm
(c) 27 cm
(d) 30 cm
Solution:
(c) Area of the larger triangle ABC = 144 cm²
and area of smaller ∆DEF = 81 cm²
Longest side of larger triangle = 36 cm
Let the longest side of smaller triangle = x cm
The ratio of the areas of two similar triangles is proportional to the squares of their corresponding sides

Question 4.
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangles ABC and BDE is :
(a) 2 : 1
(b) 1 : 2
(c) 4 : 1
(d) 1 : 4
Solution:
(c) ∆ABC and ∆BDE are equilateral triangles and D is the mid-point of PC
∆ABC and ∆BDE are both equilateral triangles

Question 5.
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
(a) 16 cm
(b) 12 cm
(c) 8 cm
(d) 4 cm
Solution:
(a)

Question 6.

(a) 2 : 5
(b) 4 : 25
(c) 4 : 15
(d) 8 : 125
Solution:
(b)

Question 7.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
(a) 2 cm
(b) 4 cm
(c) 6 cm
(d) 8 cm
Solution:
(c) In ∆ABC, XY || BC
AB = 4BX, YC = 2 cm

Question 8.
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
(a) 12 m
(b) 14 m
(c) 13 m
(d) 11 m
Solution:
(c) Let length of pole AB = 6 m
and of pole CD = 11 m
and distance between their foot = 12 m
i.e., BD = 12 m

Question 9.
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
(a) 1.1 cm
(b) 4 cm
(c) 4.4 cm
(d) 5.5 cm
Solution:
(c) In ∆ABC, DE || BC
AD : DB = 3 : 1, EA = 3.3 cm

Question 10.
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
(a) 35°
(b) 65°
(c) 75°
(d) 85°
Solution:
(c) In ∆ABC and ∆DEF,
∠A = ∠E = 40°
AB : ED = AC : EF, ∠F = 65°

Question 11.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:
(a) ∆ABC ~ ∆DEF
∠A = 47°, ∠E = 83°
∆ABC and ∆DEF are similar
∠A = ∠D, ∠B = ∠E and ∠C = ∠F
∠A = 47°
∠B = ∠E = 83°
But ∠A + ∠B + ∠C = 180° (Sum of angles of a triangle)
47° + 83° + ∠C = 180°
=> 130° + ∠C = 180°
=> ∠C = 180° – 130°
=> ∠C = 50°

Question 12.
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
(a) 1 : 4
(b) 1 : 2
(c) 2 : 3
(d) 4 : 5
Solution:
(a) D, E and F are the mid points of the sides. BC, CA and AB respectively of ∆ABC
DE, EF and FD are joined

Question 13.
In an equilateral triangle ABC, if AD ⊥ BC, then
(a) 2AB² = 3AD²
(b) 4AB² = 3AD²
(c) 3AB² = 4AD²
(d) 3AB² = 2AD²
Solution:
(c) In equilateral ∆ABC,
AD ⊥ BC

Question 14.
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD² =
(a) \(\frac { 3 }{ 2 }\) DC²
(b) 2 DC²
(c) 3 CD²
(d) 4 DC²
Solution:
(c) In equilateral ∆ABC, AD ⊥ BC
AD bisects BC at D

Question 15.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
(a) 11.3 cm
(b) 2.5 cm
(c) 3.5 cm
(d) None of these
Solution:
(b) In ∆ABC, AD is the bisector of ∠BAC
AB = 6 cm, AC = 5 cm, BD = 3 cm

Question 16.
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
(a) 4 cm
(b) 6 cm
(c) 3 cm
(d) 8 cm
Solution:
(a) In ∆ABC, AD is the bisector of ∠BAC
AB = 8 cm, BD = 6 cm and DC = 3 cm

Question 17.
ABCD is a trapezium such that BC || AD and AB = 4 cm. If the diagonals AC and BD intersect at O such that \(\frac { AO }{ OC }\) = \(\frac { DO }{ OB }\) = \(\frac { 1 }{ 2 }\) , then BC =
(a) 7 cm
(b) 8 cm
(c) 9 cm
(d) 6 cm
Solution:
(b) In trapezium ABCD, BC || AD
AD = 4 cm, diagonals AC and BD intersect

=> x = 8
BC = 8 cm

Question 18.
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4 (AN² + CM²) =
(a) 4 AC²
(b) 5 AC²
(c) \(\frac { 5 }{ 4 }\) AC²
(d) 6 AC²
Solution:
(b) In right ∆ABC, ∠B = 90°
M and N are the mid points of AB and BC respectively

Question 19.
If in ∆ABC and ∆DEF, \(\frac { AB }{ DE }\) = \(\frac { BC }{ FD }\), then ∆ABC ~ ∆DEF when
(a) ∠A = ∠F
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠B = ∠E
Solution:
(c)

Question 20.

Solution:
(a)

Question 21.
∆ABC ~ ∆DEF, ar (∆ABC) = 9 cm², ar (∆DEF) = 16 cm². If BC = 2.1 cm, then the measure of EF is
(a) 2.8 cm
(b) 4.2 cm
(c) 2.5 cm
(d) 4.1 cm
Solution:
(a) ∆ABC ~ ∆DEF
ar (∆ABC) = 9 cm², ar (∆DEF) =16 cm²,
BC = 2.1 cm
∆ABC ~ ∆DEF

Question 22.
The length of the hypotenuse of an isosceles right triangle whose one side is 4√2 cm is
(a) 12 cm
(b) 8 cm
(c) 8√2 cm
(d) 12√2 cm
Solution:
(b) In isosceles right ∆ABC

∠B = 90°, AB = BC = 4√2
AC = √2
equal side = √2 x 4√2 = 8 cm

Question 23.
A man goes 24 m due west and then 7 m due north. How far is he from the starting point ?
(a) 31 m
(b) 17 m
(c) 25 m
(d) 26 m
Solution:
(c) In the figure, O is starting point OA = 24 m and AB = 7 m

By Pythagoras Theorem
OB² = OA² + AB²
= (24)² + (7)² = 576 + 49 = 625 = (25)²
OB = 25 m

Question 24.
∆ABC ~ ∆DEF. If BC = 3 cm, EF = 4 cm and ar (∆ABC) = 54 cm², then ar (∆DEF)
(a) 108 cm²
(b) 96 cm²
(c) 48 cm²
(d) 100 cm²
Solution:
(b)

Question 25.
∆ABC ~ ∆PQR such that ar (∆ABC) = 4 ar (∆PQR). If BC = 12 cm, then QR =
(a) 9 cm
(b) 10 cm
(c) 6 cm
(d) 8 cm
Solution:
(c) ∆ABC ~ ∆PQR
ar (∆ABC) = 4ar (∆PQR), BC = 12 cm
∆ABC ~ ∆PQR

Question 26.
The areas of two similar triangles are 121 cm² and 64 cm² respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangles is
(a) 11 cm
(b) 8.8 cm
(c) 11.1 cm
(d) 8.1 cm
Solution:
(b) Areas of two similar triangles are 121 cm² and 64 cm²
Median of first triangle = 12.1 cm

In ∆ABC, area ∆DEF
AD and PS are their corresponding median
∆ABC ~ ∆DEF

Question 27.
In an equilateral triangle ABC if AD ⊥ BC, then AD² =
(a) CD²
(b) 2 CD²
(c) 3 CD²
(d) 4 CD²
Solution:
(c) In equilateral ∆ABC, AD ⊥ BC

Question 28.
In an equilateral triangle ABC if AD ⊥ BC, then
(a) 5 AB² = 4 AD²
(b) 3 AB² = 4 AD²
(c) 4 AB² = 3 AD²
(d) 2 AB² = 3 AD²
Solution:
(b) In equilateral ∆ABC, AD ⊥ BC

Question 29.
In an isosceles triangle ABC if AC = BC and AB² = 2 AC², then ∠C =
(a) 30°
(b) 45°
(c) 90°
(d) 60°
Solution:
(c) In isosceles ∆ABC, AC = BC

and AB2 = 2 AC² = AC² + AC²
= AC² + BC² ( AC = BC)
By converse of Pythagoras Theorem,
∠C = 90°

Question 30.
∆ABC is an isosceles triangle in which ∠C = 90°. If AC = 6 cm, then AB =
(a) 6√2 cm
(b) 6 cm
(c) 2√6 cm
(d) 4√2 cm
Solution:
(a) ∆ABC is an isosceles with ∠C= 90°

AC = BC
AC = 6 cm
AB² = AC² + BC² (Pythagoras Theorem)
(6)² + (6)² = 36 + 36 = 72 (AC = BC)
AB = √72 = √(36 x 2) = 6√2 cm

Question 31.
If in two triangles ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true ?
(a) \(\frac { BC }{ DF }\) = \(\frac { AC }{ DE }\)
(b) \(\frac { AB }{ DE }\) = \(\frac { BC }{ DF }\)
(c) \(\frac { AB }{ EF }\) = \(\frac { AC }{ DE }\)
(d) \(\frac { BC }{ DF }\) = \(\frac { AB }{ EF }\)
Solution:
(b) In two triangles ABC and DEF
∠A = ∠E, ∠B = ∠F

Question 32.
In the figure, the measures of ∠D and ∠F are respectively
(a) 50°, 40°
(b) 20°, 30°
(c) 40°, 50°
(d) 30°, 20°

Solution:
(b) In ∆ABC
∠A = 180° – (∠B + ∠C)

Question 33.
In the figure, the value of x for which DE || AB is
(a) 4
(b) 1
(c) 3
(d) 2

Solution:
(b)

Question 34.
In the figure, if ∠ADE = ∠ABC, then CE =
(a) 2
(b) 5
(c) \(\frac { 9 }{ 2 }\)
(c) 3

Solution:
(c) In the figure ∠ADE = ∠ABC
AB = 2, DB = 3, AE = 3
Let EC = x
∠ADE = ∠ABC
But these are corresponding angles DE || BC
∆ADE ~ ∆ABC

Question 35.
In the figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively
(a) 12, 10
(b) 14, 6
(c) 10, 7
(d) 16, 8

Solution:
(d) In the figure RS || DB || PQ
CP = PD = 11 cm DR = RA = 3 cm
In ∆ABD
RS || BD and AR = RD
RS = \(\frac { 1 }{ 2 }\) BD
y = \(\frac { 1 }{ 2 }\) x or x = 2y
Only 16, 8 is possible

Question 36.
In the figure, if PB || CF and DP || EF, then \(\frac { AD }{ DE }\) =
(a) \(\frac { 3 }{ 4 }\)
(b) \(\frac { 1 }{ 3 }\)
(c) \(\frac { 1 }{ 4 }\)
(d) \(\frac { 2 }{ 3 }\)

Solution:
(b) In the figure, PB || CF, DP || EF
AB = 2 cm, AC = 8 cm
BC = AC – AB = 8 – 2 = 6 cm
In ∆ACF, BP || CF

\(\frac { AD }{ DE }\) = \(\frac { 1 }{ 3 }\)

Question 37.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
(a) 5√2
(b) 10√2
(c) \(\frac { 5 }{ \surd 2 }\)
(d) 10√3 [ICSE 2014]
Solution:
(b)

AB² = OA² + OB² (Pythagoras Theorem)
AB² = 10² + 10²
AB² = 2 (10)²
AB = 10√2

Question 38.
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
(a) 100 m
(b) 120 m
(c) 25 m
(d) 200 m
Solution:
(a) Height of a stick = 20 m
and length of its shadow = 10 m
At the same time
Let height of tower = x m
and its shadow = 50 m
20 : x = 10 : 50
x x 10 = 20 x 50
=> x = \(\frac { 20 x 50 }{ 10 }\) = 100
Height of tower = 100 m

Question 39.
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is :
(a) 4 : 5
(b) 5 : 4
(c) 3 : 2
(d) 5 : 7
Solution:
(a) The corresponding angles of two isosceles triangles are equal These are similar Ratio in their areas = 16 : 25
The ratio of areas of similar triangles are proportion to the squares of their corresponding altitudes (heights)
Ratio in their altitudes = \(\surd \frac { 16 }{ 25 } =\frac { 4 }{ 5 }\)
= i.e., 4 : 5

Question 40.
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ~ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
(a) 7.5 cm
(b) 15 cm
(c) 22.5 cm
(d) 30 cm
Solution:
(b) ∆DEF ~ ∆ABC
AB = 3 cm, BC = 2 cm, CA = 2.5 cm, EF = 4 cm
∆s are similar

Question 41.
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then :
(a) BC = CY
(b) BC = BY
(c) BC ≠ CY
(d) BC ≠ BY
Solution:
(a) In ∆ABC, XY || BC
BY is the bisector of ∠XYC

∠XYB = ∠CXB ….(i)
XY || BC
∠XYB = ∠XBC (Alternate angles) ……….(ii)
From (i) and (ii)
∠CYB = ∠YBC
BC = CY

Question 42.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
(a) \(\frac { 13 }{ 2 }\) cm
(b) \(\frac { 60 }{ 13 }\) cm
(c) \(\frac { 13 }{ 60 }\) cm
(d) \(\frac { 2\surd 15 }{ 13 }\) cm
Solution:
(b) In ∆ABC,
∠A = 90°, AB = 5 cm, AC = 12 cm

Question 43.
In a ∆ABC, perpendicular AD from A on BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
(a) ∆ABC is isosceles
(b) ∆ABC is equilateral
(c) AC = 2 AB
(d) ∆ABC is right-angled at A
Solution:
(d) In ∆ABC, AD ⊥ BC
BD = 8 cm, DC = 2 cm, AD = 4 cm

In right ∆ACD,
AC² = AD² + CD² (Pythagoras Theorem)
= (4)² + (2)² = 16 + 4 = 20
and in right ∆ABD,
AB² = AD² + DB²
= (4)² + (8)2 = 16 + 64 = 80
and BC² = (BD + DC)² = (8 + 2 )² = (10)² = 100
AB² + AC² = 80 + 20 = 100 = BC²
∆ABC is a right triangle whose ∠A = 90°

Question 44.
In a ∆ABC, point D is on side AB and point G is on side AC, such that BCED is a trapezium. If DE : BC = 3:5, then Area (∆ADE) : Area (BCED) =
(a) 3 : 4
(b) 9 : 16
(c) 3 : 5
(d) 9 : 25
Solution:
(b)

In ∆ABC, D and E are points on the side AB and AC respectively, such that BCED is a trapezium DE : BC = 3 : 5
In ∆ABC, DE || BC
∆ADE ~ ∆ABC

Question 45.
If ABC is an isosceles triangle and D is a point on BC such that AD ⊥ BC, then
(a) AB² – AD² = BD.DC
(b) AB² – AD² = BD² – DC²
(c) AB² + AD² = BD.DC
(d) AB² + AD² = BD² – DC²
Solution:
(a) If ∆ABC, AB = AC
D is a point on BC such that

AD ⊥ BC
AD bisects BC at D
In right ∆ABD,
AB² = AD² + BD²
AB² – AD² = BD² = BD x BD = BD x DC (BD = DC)

Question 46.
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then , \(\frac { BD }{ DC }\) =
(a) \(\left( \frac { AB }{ AC } \right) ^{ 2 }\)
(b) \(\frac { AB }{ AC }\)
(c) \(\left( \frac { AB }{ AD } \right) ^{ 2 }\)
(d) \(\frac { AB }{ AD }\)
Solution:
(a) In right angled ∆ABC, ∠A = 90°
AD ⊥ BC

Question 47.
If E is a point on side CA of an equilateral triangle ABC such that BE ⊥ CA, then AB² + BC² + CA² =
(a) 2 BE²
(b) 3 BE²
(c) 4 BE²
(d) 6 BE²
Solution:
(c) ∆ABC is an equilateral triangle
BE ⊥ AC

Question 48.
In a right triangle ABC right-angled at B, if P and Q are points on the sides AB and AC respectively, then
(a) AQ² + CP² = 2 (AC² + PQ²)
(b) 2 (AQ² + CP²) = AC² + PQ²
(c) AQ² + CP² = AC² + PQ²
(d) AQ + CP = \(\frac { 1 }{ 2 }\) (AC + PQ)
Solution:
(c) In right ∆ABC, ∠B = 90°
P and Q are points on AB and BC respectively
AQ, CP and PQ are joined

In right ∆ABC,
AC² = AB² + BC² ….(i)
(Pythagoras Theorem)
Similarly in right ∆PBQ,
PQ² = PB² + BQ² ………(ii)
In right ∆ABQ
AQ² = AB² + BQ² ….(iii)
and in right ∆CPB,
CP² = PB² + BC² ….(iv)
Adding (iii) and (iv)
AQ² + CP² = AB² + BQ² + PB² + BC²
= AB² + BC² + BQ² + PB²
= AC² + PQ2 {From (i) and (ii)}

Question 49.
If ∆ABC ~ ∆DEF such that DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm, then perimeter of ∆ABC is
(a) 18 cm
(b) 20 cm
(c) 12 cm
(d) 15 cm
Solution:
(d) ∆ABC ~ ∆DEF
DE = 3 cm, EF = 2 cm, DF = 2.5 cm, BC = 4 cm

Question 50.
If ∆ABC ~ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
(a) 36 cm
(b) 30 cm
(c) 34 cm
(d) 35 cm
Solution:
(d) ∆ABC ~ ∆DEF
AB = 9.1 cm and DE = 6.5 cm
Perimeter of ∆DEF = 25 cm

Question 51.
In an isosceles triangle ABC, if AB = AC = 25 cm and BC = 14 cm, then the measure of altitude from A on BC is
(a) 20 cm
(b) 22 cm
(c) 18 cm
(d) 24 cm
Solution:
(d) ∆ABC is an isosceles triangle in which AB = AC = 25 cm, BC = 14 cm

From A, draw AD ⊥ BC
D is mid-point of BC
BD = \(\frac { 1 }{ 2 }\) BC = \(\frac { 1 }{ 2 }\) x 14 = 7 cm
Now in right ∆ABD
AD² = AB² – BD²
= (25)² – (7)² = 625 – 49 = 576 = (24)²
AD = 24 cm

Hope given RD Sharma Class 10 Solutions Chapter 7 Triangles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Prove the following trigonometric identities :
Question 1.
(1 – cos² A) cosec² A = 1
Solution:
(1 – cos² A) cosec² A = 1
L.H.S. = (1 – cos² A) cosec² A = sin² A cosec² A  (∵ 1 – cos² A = sin² A)
= (sin A cosec A)² = (l)² = 1 = R.H.S.  {sin A cosec A = 1 }

Question 2.
(1 + cot² A) sin² A = 1
Solution:
(1 + cot² A) sin² A = 1
L.H.S. = (1 + cot² A) (sin² A)
= cosec² A sin² A {1 + cot² A = cosec² A}
= [cosec A sin A]²
= (1)²= 1 = R.H.S. (∵ sin A cosec A = 1

Question 3.
tan² θ cos²  θ = 1- cos²  θ
Solution:

Question 4.

Solution:

Question 5.
(sec² θ – 1) (cosec² θ – 1) = 1
Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.
tan²  θ – sin²  θ = tan²  θ sin² θ
Solution:

Question 17.
(sec θ + cos θ ) (sec θ – cos θ ) = tan²  θ + sin² θ
Solution:

Question 18.
(cosec θ + sin θ) (cosec θ – sin θ) = cot² θ + cos² θ
Solution:

Question 19.
sec A (1 – sin A) (sec A + tan A) = 1 (C.B.S.E. 1993)
Solution:

Question 20.
(cosec A – sin A) (sec A – cos A) (tan A + cot A) = 1
Solution:

Question 21.
(1 + tan²  θ) (1 – sin θ) (1 + sin θ) = 1
Solution:

Question 22.
sin² A cot² A + cos² A tan² A = 1 (C.B.S.E. 1992C)
Solution:

Question 23.

Solution:

Question 24.

Solution:

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Question 28.

Solution:

Question 29.

Solution:

Question 30.

Solution:

Question 31.
sec⁶ θ= tan⁶  θ + 3 tan²  θ sec²  θ + 1
Solution:

Question 32.
cosec⁶  θ = cot⁶  θ+ 3cot²θ cosec²  θ + 1
Solution:

Question 33.

Solution:

Question 34.

Solution:

Question 35.

Solution:

Question 36.

Solution:

Question 37.

Solution:

Question 38.

Solution:

Question 39.

Solution:

Question 40.

Solution:

Question 41.

Solution:

Question 42.

Solution:

Question 43.

Solution:

Question 44.

Solution:

Question 45.

Solution:

Question 46.

Solution:

Question 47.


Solution:

Question 48.

Solution:

Question 49.
tan² A + cot² A = sec² A cosec² A – 2
Solution:

Question 50.

Solution:

Question 51.

Solution:

Question 52.

Solution:

Question 53.

Solution:

Question 54.
sin² A cos² B – cos² A sin² B = sin² A – sin² B.
Solution:
L.H.S. = sin² A cos² B – cos² A sin² B
= sin² A (1 – sin² B) – (1 – sin² A) sin² B
= sin² A – sin² A sin² B – sin² B + sin² A sin² B
= sin² A – sin² B
Hence, L.H.S. = R.H.S.

Question 55.

Solution:

Question 56.
cot² A cosec² B – cot² B cosec² A = cot² A – cot² B
Solution:

Question 57.
tan² A sec² B – sec² A tan² B = tan² A – tan² B
Solution:

Prove the following identities: (58-75)
Question 58.
If x = a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x¹ – y² = a² – b¹. [C.B.S.E. 2001, 20O2C]
Solution:
x – a sec θ + b tan θ
y = a tan θ + b sec θ
Squaring and subtracting, we get
x²-y² = {a sec θ + b tan θ)² – (a tan θ + b sec θ)²
= (a² sec² θ + b² tan²  θ + 2ab sec θ x tan θ) – (a² tan²  θ + b² sec²  θ + 2ab tan θ sec θ)
= a² sec² θ + b tan²  θ + lab tan θ sec θ – a² tan²  θ – b² sec²  θ – 2ab sec θ tan θ
= a² (sec² θ – tan²  θ) + b² (tan²  θ – sec²  θ)
= a² (sec² θ – tan²  θ) – b² (sec²  θ – tan²  θ)
=  a² x 1-b² x 1 =a²-b² = R.H.S.

Question 59.
If 3 sin θ + 5 cos θ = 5, prove that 5 sin θ – 3 cos θ = ±3
Solutioon:

Question 60.
If cosec θ + cot θ = mand cosec θ – cot θ = n,prove that mn= 1
Solution:

Question 61.

Solution:

Question 62.

Solution:

Question 63.

Solution:

Question 64.

Solution:

Question 65.

Solution:

Question 66.
(sec A + tan A – 1) (sec A – tan A + 1) = 2 tan A
Solution:

Question 67.
(1 + cot A – cosec A) (1 + tan A + sec A) = 2
Solution:

Question 68.
(cosec θ – sec θ) (cot θ – tan θ) = (cosec θ + sec θ) (sec θ cosec θ-2)
Solution:

Question 69.
(sec A – cosec A) (1 + tan A + cot A) = tan A sec A – cot A cosec A
Solution:

Question 70.

Solution:

Question 71.

Solution:

Question 72.

Solution:

Question 73.
sec⁴ A (1 – sin⁴ A) – 2tan² A = 1
Solution:

Question 74.

Solution:

Question 75.

Solution:

Question 76.

Solution:

Question 77.
If cosec θ – sin θ = a³, sec θ – cos θ = b³, prove that a²b² (a² + b²) = 1
Solution:

Question 78.

Solution:

Question 79.

Solution:

Question 80.
If a cos θ + b sin θ = m and a sin θ – b cos θ = n, prove that a² + b² = m² + n² 
Solution:

Question 81.
If cos A + cos² A = 1, prove that sin² A + sin⁴ A = 1
Solution:
cos A + cos² A = 1
⇒ cos A = 1 – cos² A
⇒cos A = sin² A
Now, sin² A + sin⁴ A = sin² A + (sin² A)²
= cos A + cos² A = 1 = R.H.S.

Question 82.
If cos θ + cos²  θ = 1, prove that
sin¹² θ + 3 sin¹⁰  θ + 3 sin⁸  θ + sin⁶  θ + 2 sin⁴  θ + 2 sin²  θ-2 = 1
Solution:

Question 83.
Given that :
(1 + cos α) (1 + cos β) (1 + cos γ) = (1 – cos α) (l – cos β) (1 – cos γ)
Show that one of the values of each member of this equality is sin α sin β sin γ
Solution:

Question 84.

Solution:

Question 85.

Solution:

Question 86.
If sin θ + 2cos θ = 1 prove that 2sin θ – cos θ = 2. [NCERT Exemplar]
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities Ex 11.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.