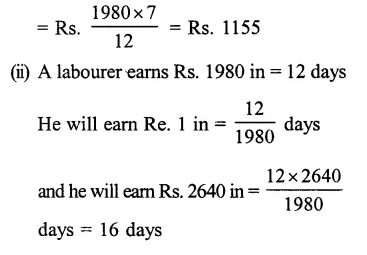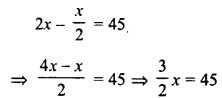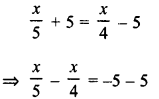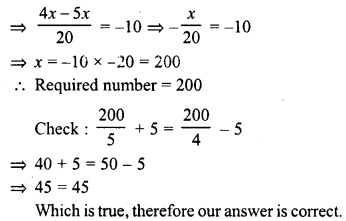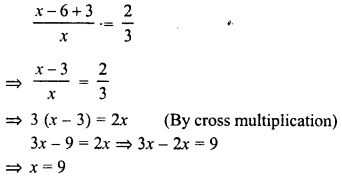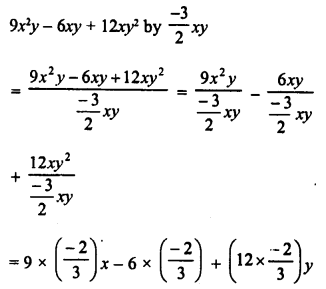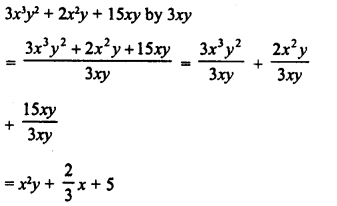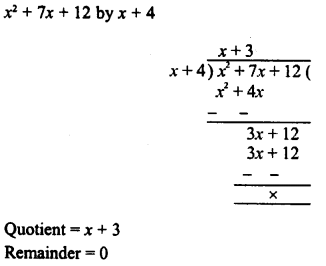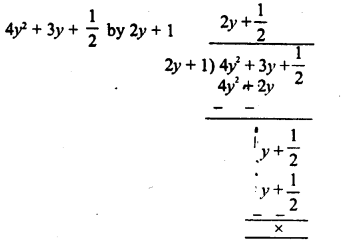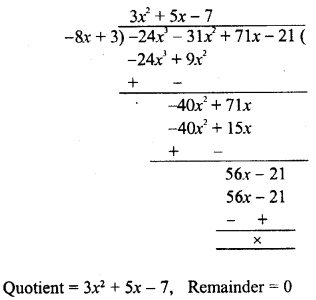HOTS Questions for Class 10 Science Chapter 9 Heredity and Evolution
These Solutions are part of HOTS Questions for Class 10 Science. Here we have given HOTS Questions for Class 10 Science Chapter 9 Heredity and Evolution
Question 1.
Observe the diagram carefully. What does it depict ? Identify the parts shown by lines.
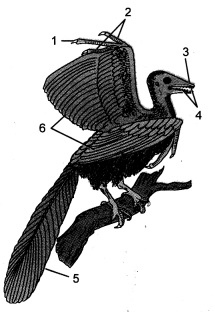
Answer:
Reconstruction of fossil bird Archaeopteryx.
- Claw
- Free fingers
- Beak
- Teeth
- Tail
- Feathers
More Resources
- HOTS Questions for Class 10 Science
- NCERT Solutions for Class 10 Science
- Value Based Questions in Science for Class 10
- NCERT Exemplar Solutions for Class 10 Science
- Previous Year Question Papers for CBSE Class 10 Science
Question 2.
Name the organism in which feathers appeared for the first time.
Answer:
Members of Dromaesaur family which were small dinosaurs.
Question 3.
Which one is the edible part in Kale, Kohlrabi, Broccoli, Brussel’s Sprout, Cabbage and Cauliflower ?
Answer:
Kale — Leaves,
Kohlrabi — Swollen stem,
Broccoli — Immature green flowers,
Brussel’s Sprout — Axillary buds,
Cabbage — Terminal bud,
Cauliflower — Immature inflorescence of sterile flowers.
Question 4.
Give an example where temperature determines the sex of the new bom.
Answer:
- Chrysema picta (a turtle). Temperature above 33°C produces females and below 28°C males.
- Agama agama (a lizard). High temperature produces males.
Question 5.
Name a recessive trait which is quite common in human beings.
Answer:
Blood group O (I°I°).
Question 6.
Why is variation beneficial for the species but not necessarily for the individual ? (CBSE Foreign 2010)
Answer:
Preadaptation is a variation which under normal conditions is of no advantage to the individual bearing it. However, it becomes highly useful in survival under changed environment, e.g, heat wave in temperate environment, insecticide or antibiotic resistance.
Hope given HOTS Questions for Class 10 Science Chapter 9 Heredity and Evolution are helpful to complete your science homework.
If you have any doubts, please comment below. Learn Insta try to provide online science tutoring for you.